Water Supply Pipeline Risk Index Assessment Based on Cohesive Hierarchical Fuzzy Inference System
Abstract
1. Introduction
2. Related Work
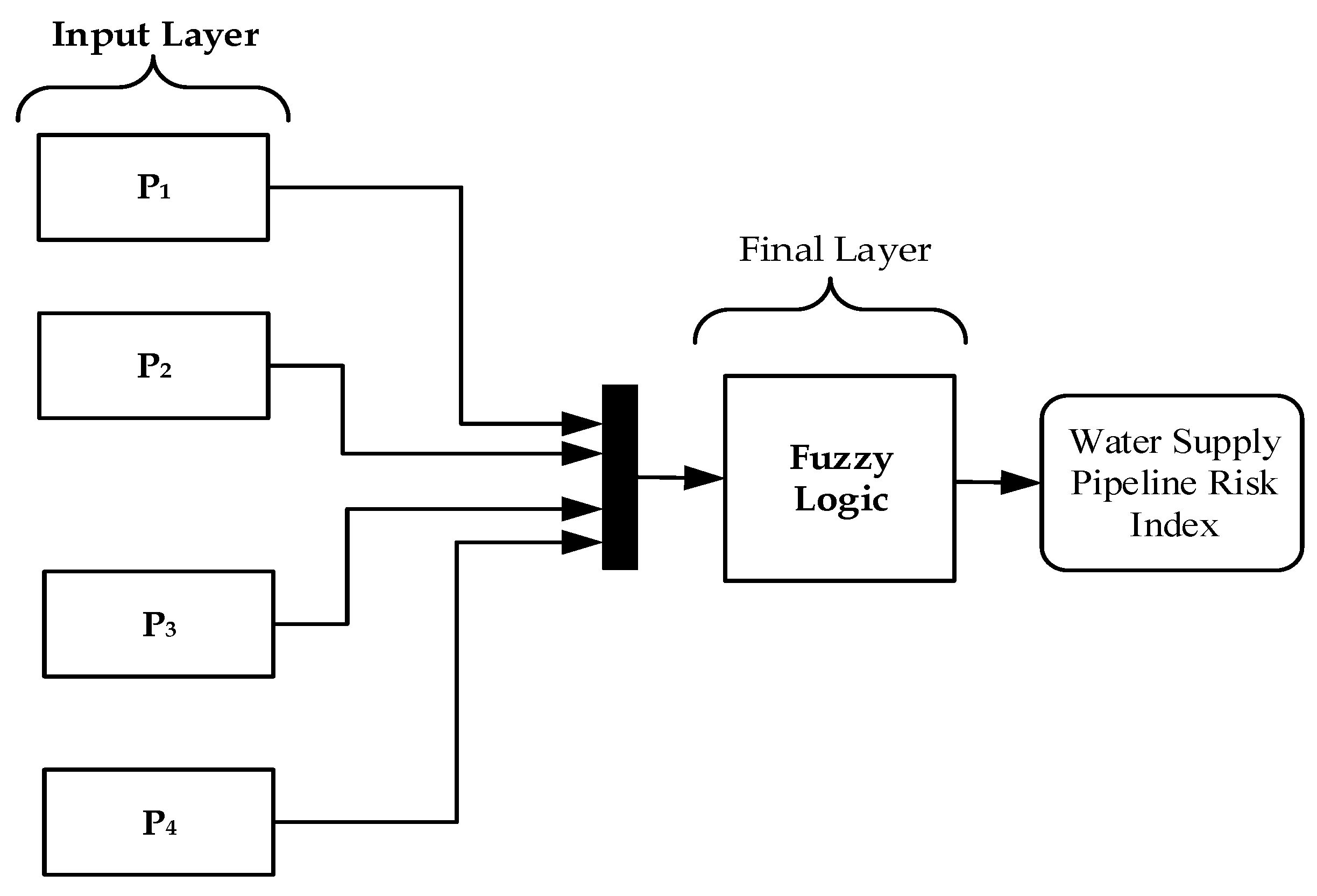
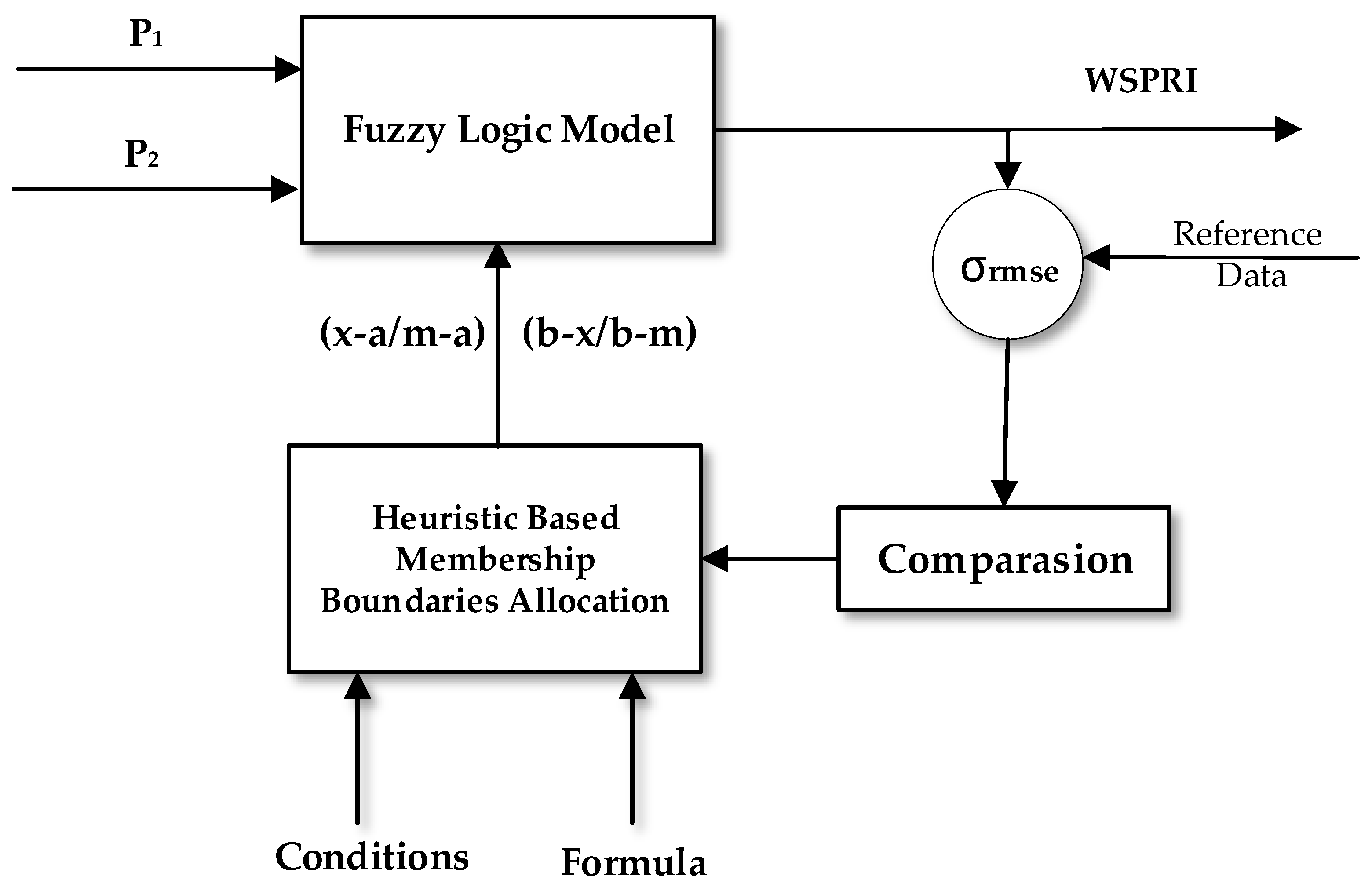
3. Proposed Water Supply Pipeline Risk Index Methodology
| Algorithm_1: Pseudo code for a cohesive hierarchical fuzzy inference system |
| Input (P1, P2, P3, X4) |
| Output: WSPRI |
| Begin: |
| 1. RI ← ∅; |
| 2. ML (P1, P2, P3, X4) { |
| i. FIS_1(P1, P2) { |
| • µ(P1) // change the numeric input value to P1 to fuzzy value |
| • µ(P2) // change the numeric input value to P2 to fuzzy value |
| for j ← 1 to 30 do |
| ▪ Rule inferencing |
| ▪ µ(zj) // Rule implication |
| od |
| • µ(y1) ← Aggregate (): // Apply aggregation |
| • b1 ← µ(y1) |
| • return PR1 |
| ii. FIS_2(P3, P4) { |
| • µ(P3) // change the numeric input value to P3 to fuzzy value |
| • µ(P4) // change the numeric input value to P4 to fuzzy value |
| for j ← 1 to 30 do |
| ▪ Inferencing of rules |
| ▪ µ(zj) // implication of rules |
| od |
| • µ(g2) ← Aggregate (): // Aggregation |
| • m2 ←µ(g2) |
| • return PR2 |
| } [PR1, PR2] ← ML (P1, P2, P3, P4) |
| 3. FL (PR1, PR2) |
| iii. FIS_3 (PR1, PR2) { |
| • µ(PR1) // change the numeric input value to PR1 to fuzzy value |
| • µ(PR2) // change the numeric input value to PR2 to fuzzy value |
| for j ← 1 to 25 do |
| ▪ Inferencing of rules |
| ▪ µ(zj) // implication of rules |
| od |
| • µ(g3) ← Aggregate (): // Aggregation |
| • m2 ←µ(g3) |
| • return WSPRI |
| WSPRI = FL (PR1, PR2) |
| End |
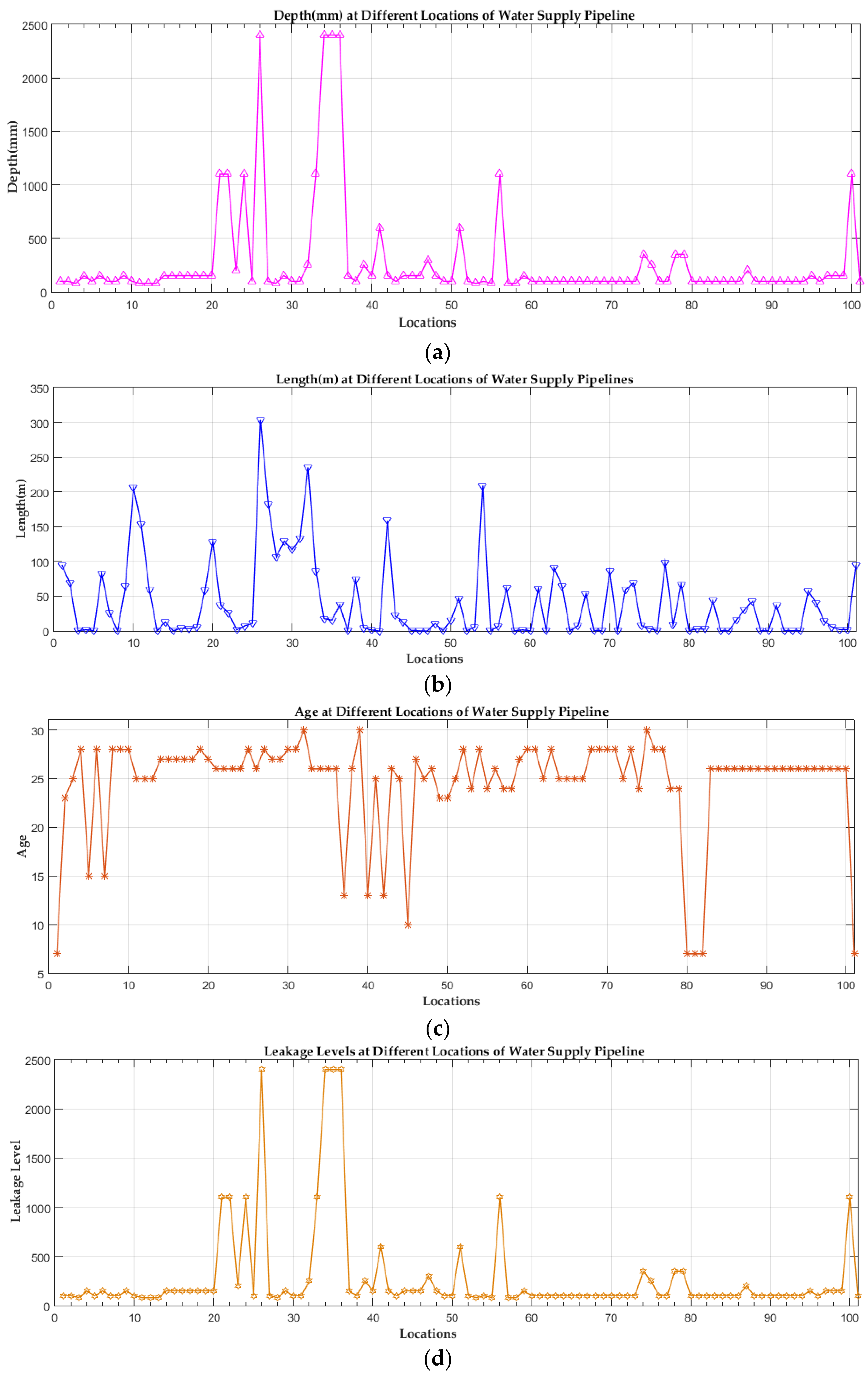
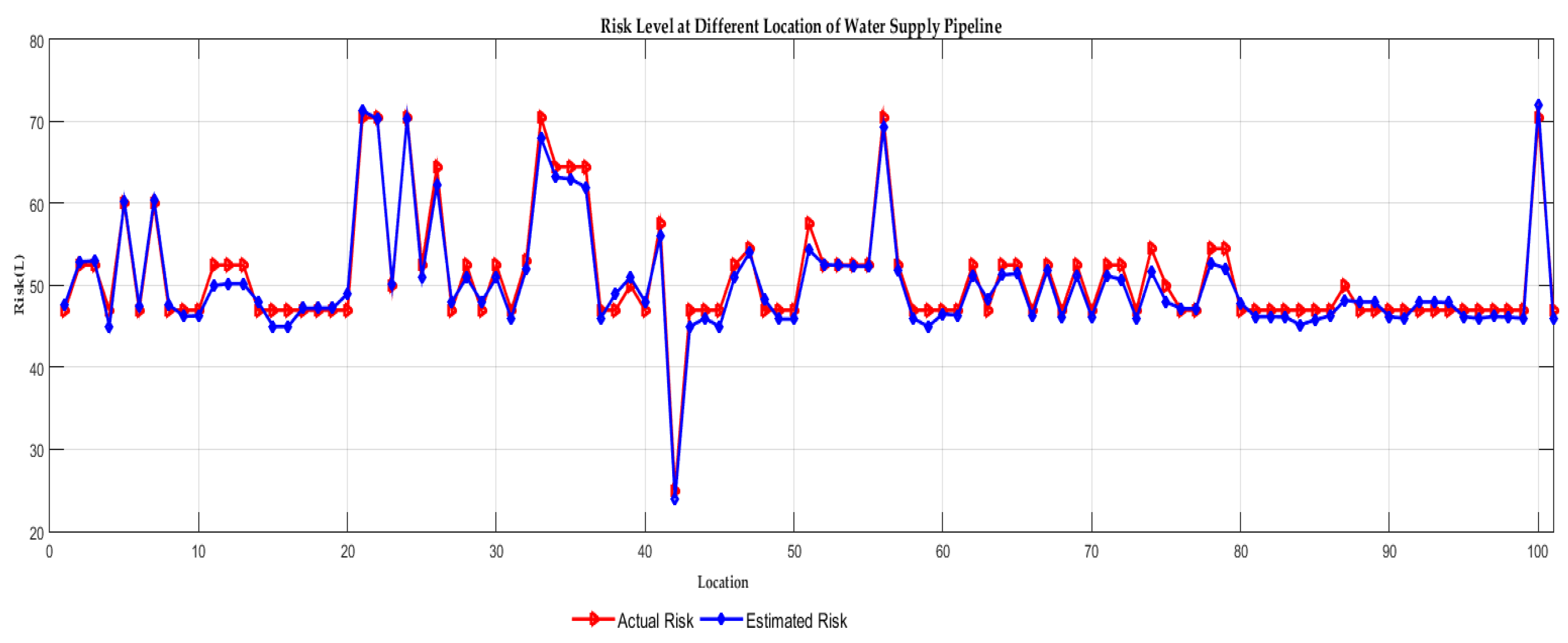
4. Implementation and Experimental Results
4.1. Implementation
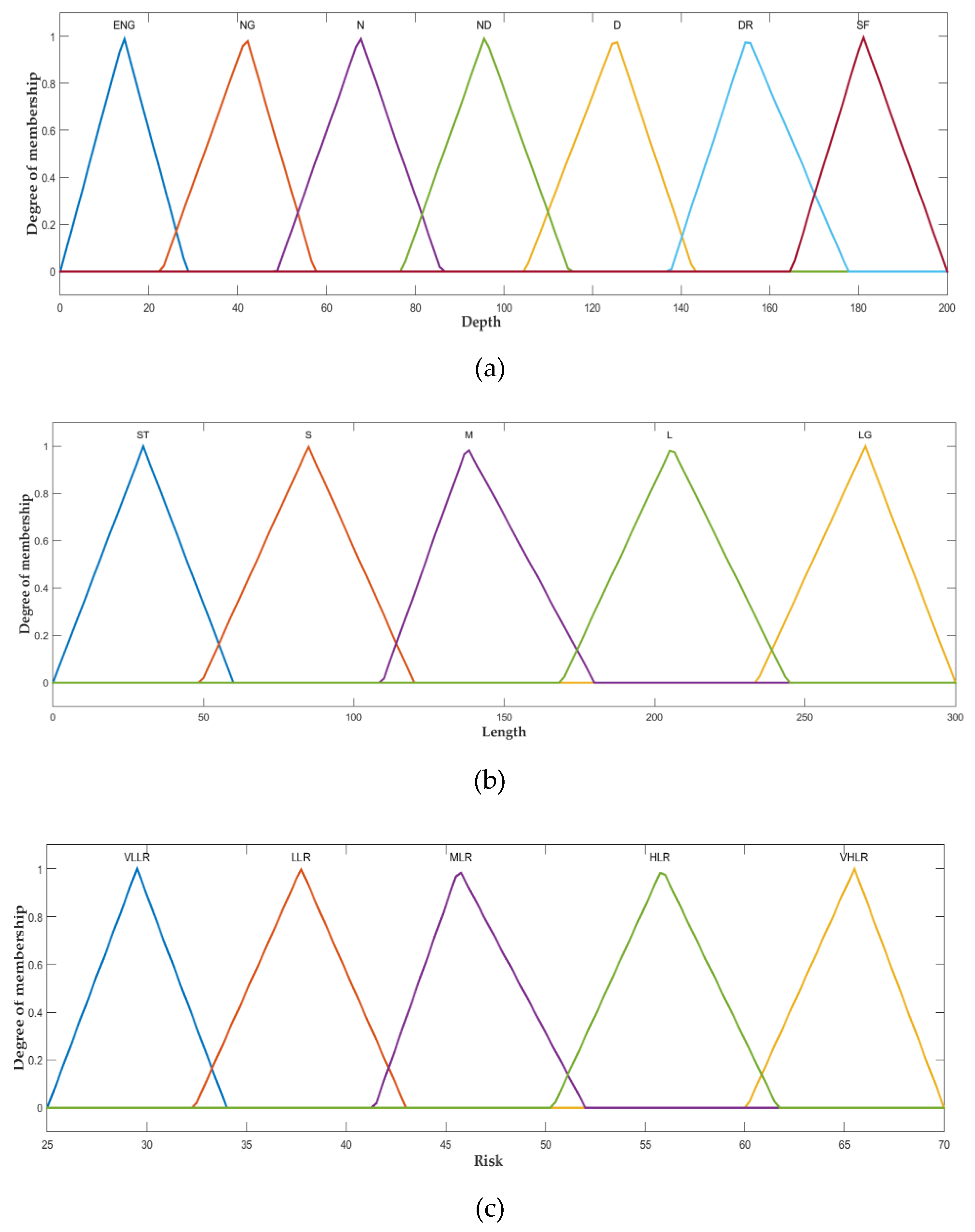
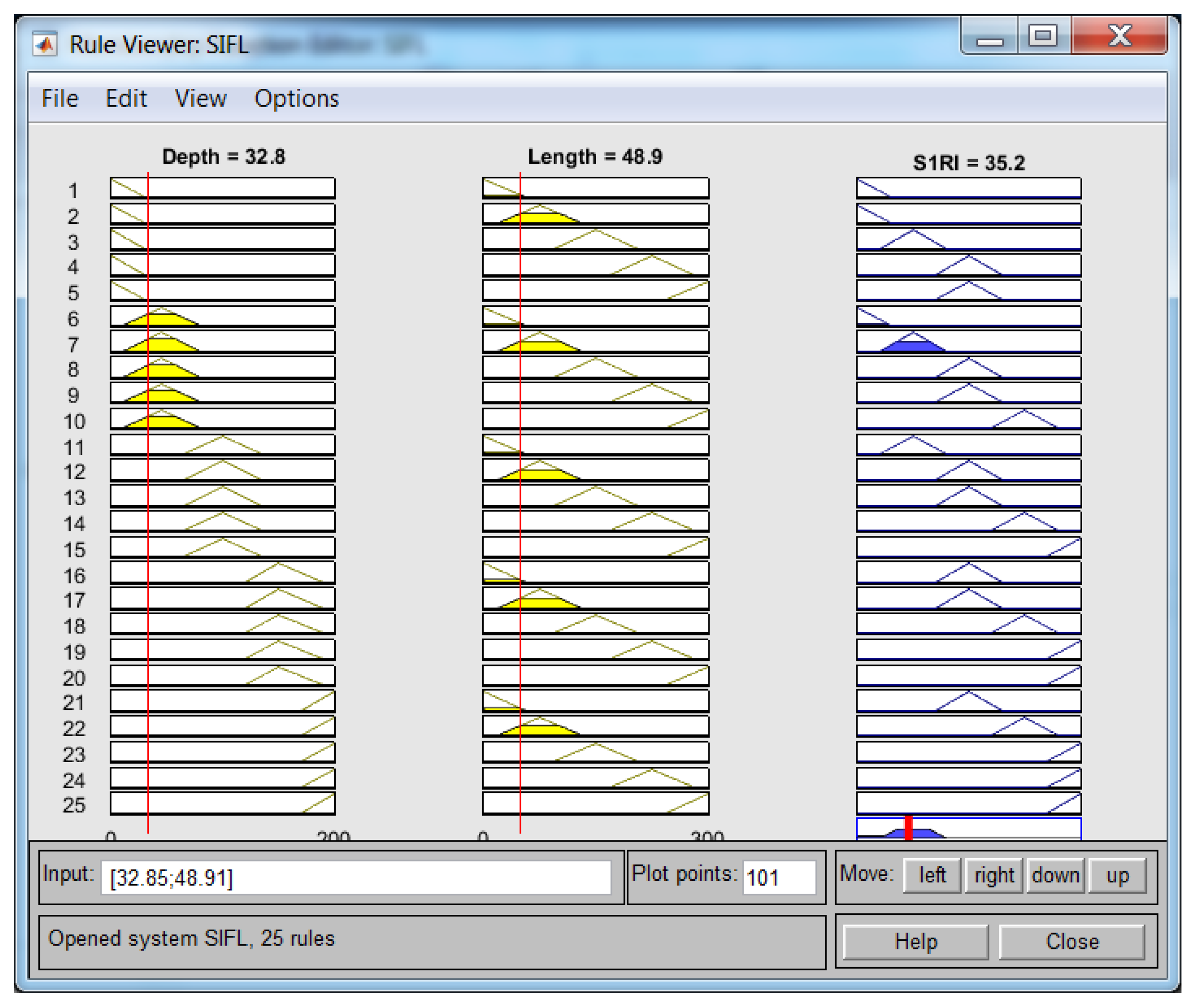
4.2. Results of CHFIS Model
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Kleiner, Y.; Rajani, B. Considering time-dependent factors in the statistical prediction of water main breaks. In Proceedings of the American Water Works Association Infrastructure Conference, Baltimore, MD, USA, 12 March 2000; pp. 12–15. [Google Scholar]
- Kleiner, Y.; Rajani, B. Forecasting variations and trends in water-main breaks. J. Infrastruct. Syst. 2002, 8, 122–131. [Google Scholar] [CrossRef]
- Kiefner, J.; Rosenfeld, M. The Role of Pipeline Age in Pipeline Safety; INGAA: Worthington, DC, USA, 2012; Available online: https://www.ingaa.org/File.aspx?id=19307 (accessed on 27 March 2019).
- Christodoulou, S.E. Water network assessment and reliability analysis by use of survival analysis. Water Resour. Manag. 2011, 25, 1229–1238. [Google Scholar] [CrossRef]
- Inanloo, B.; Tansel, B.; Shams, K.; Jin, X.; Gan, A. A decision aid GIS-based risk assessment and vulnerability analysis approach for transportation and pipeline networks. Saf. Sci. 2016, 84, 57–66. [Google Scholar] [CrossRef]
- Christodoulou, S.; Aslani, P.; Deligianni, A. Integrated GIS-based management of water distribution networks. In Proceedings of the International Conference on Computing and Decision Making in Civil and Building Engineering, Montreal, QC, Canada, 14–16 June 2006; pp. 858–865. [Google Scholar]
- Tang, X.; Liu, Y.; Zheng, L.; Ma, C.; Wang, H. Leak detection of water pipeline using wavelet transform method. In International Conference on Environmental Science and Information Application Technology, Wuhan, China, 4–5 July 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 217–220. [Google Scholar]
- Caleyo, F.; Velazquez, J.; Valor, A.; Hallen, J. Probability distribution of pitting corrosion depth and rate in underground pipelines: A monte carlo study. Corros. Sci. 2009, 51, 1925–1934. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Lee, M.-L.; Chung, H.-Y.; Yu, F.-M. Modeling of hierarchical fuzzy systems. Fuzzy Sets and Syst. 2003, 138, 343–361. [Google Scholar] [CrossRef]
- Satici, A.C.; Poonawala, H.; Spong, M.W. Robust optimal control of quadrotor UAVs. IEEE Access 2013, 1, 79–93. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Model predictive quadrotor control: Attitude, altitude and position experimental studies. IET Control. Theory Appl. 2012, 6, 1812–1827. [Google Scholar]
- Fayaz, M.; Ullah, I.; Park, D.-H.; Kim, K.; Kim, D. An integrated risk index model based on hierarchical fuzzy logic for underground risk assessment. Appl. Sci. 2017, 7, 1037. [Google Scholar] [CrossRef]
- Fayaz, M.; Ahmad, S.; Ullah, I.; Kim, D. A Blended Risk Index Modeling and Visualization Based on Hierarchical Fuzzy Logic for Water Supply Pipelines Assessment and Management. Processes 2018, 6, 61. [Google Scholar] [CrossRef]
- What is Raspberry pi. Available online: https://www.raspberrypi.org/help/what-is-a-raspberry-pi/ (accessed on 4 November 2018).
- Available online: http://www.arduino.cc/ (accessed on 5 November 2018).
- Fayaz, M.; Ullah, I.; Kim, D.-H. Underground Risk Index Assessment and Prediction Using a Simplified Hierarchical Fuzzy Logic Model and Kalman Filter. Processes 2018, 6, 103. [Google Scholar] [CrossRef]
- Li, D.; Yao, W. Risk assessment of long-distance water transmission pipeline based on fuzzy similarity evaluation approach. Proceedings of 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Changsha, China, 13–15 August 2016; pp. 1096–1102. [Google Scholar]
- Tripathy, D.P.; Ala, C.K. Risk assessment in underground coalmines using fuzzy logic in the presence of uncertainty. J. Inst. Eng. 2018, 99, 157–163. [Google Scholar] [CrossRef]
- Chen, C.-T.; Lin, C.-T.; Huang, S.-F. A fuzzy approach for supplier evaluation and selection in supply chain management. Int. J. Product. Econ. 2006, 102, 289–301. [Google Scholar] [CrossRef]
- Gul, M.; Guneri, A.F. A fuzzy multi criteria risk assessment based on decision matrix technique: A case study for aluminum industry. J. Loss Prev. Process. Ind. 2016, 40, 89–100. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, J.; Diao, M.; Wu, W.; Wang, T.; Qi, S. A case study on risk assessment of long distance water supply system. Procedia Eng. 2014, 70, 1762–1771. [Google Scholar] [CrossRef]
- Zhao, X.; Hwang, B.-G.; Gao, Y. A fuzzy synthetic evaluation approach for risk assessment: A case of singapore’s green projects. J. Clean. Product. 2016, 115, 203–213. [Google Scholar] [CrossRef]
- Chang, C.-W.; Tao, C.-W. A simplified implementation of hierarchical fuzzy systems. Soft Comput. 2018, 1–11. Available online: https://link.springer.com/article/10.1007%2Fs00500-018-3111-3 (accessed on 27 March 2019).
- Fayaz, M.; Ullah, I.; Kim, D. An optimized fuzzy logic control model based on a strategy for the learning of membership functions in an indoor environment. Electronics 2019, 8, 132. [Google Scholar] [CrossRef]

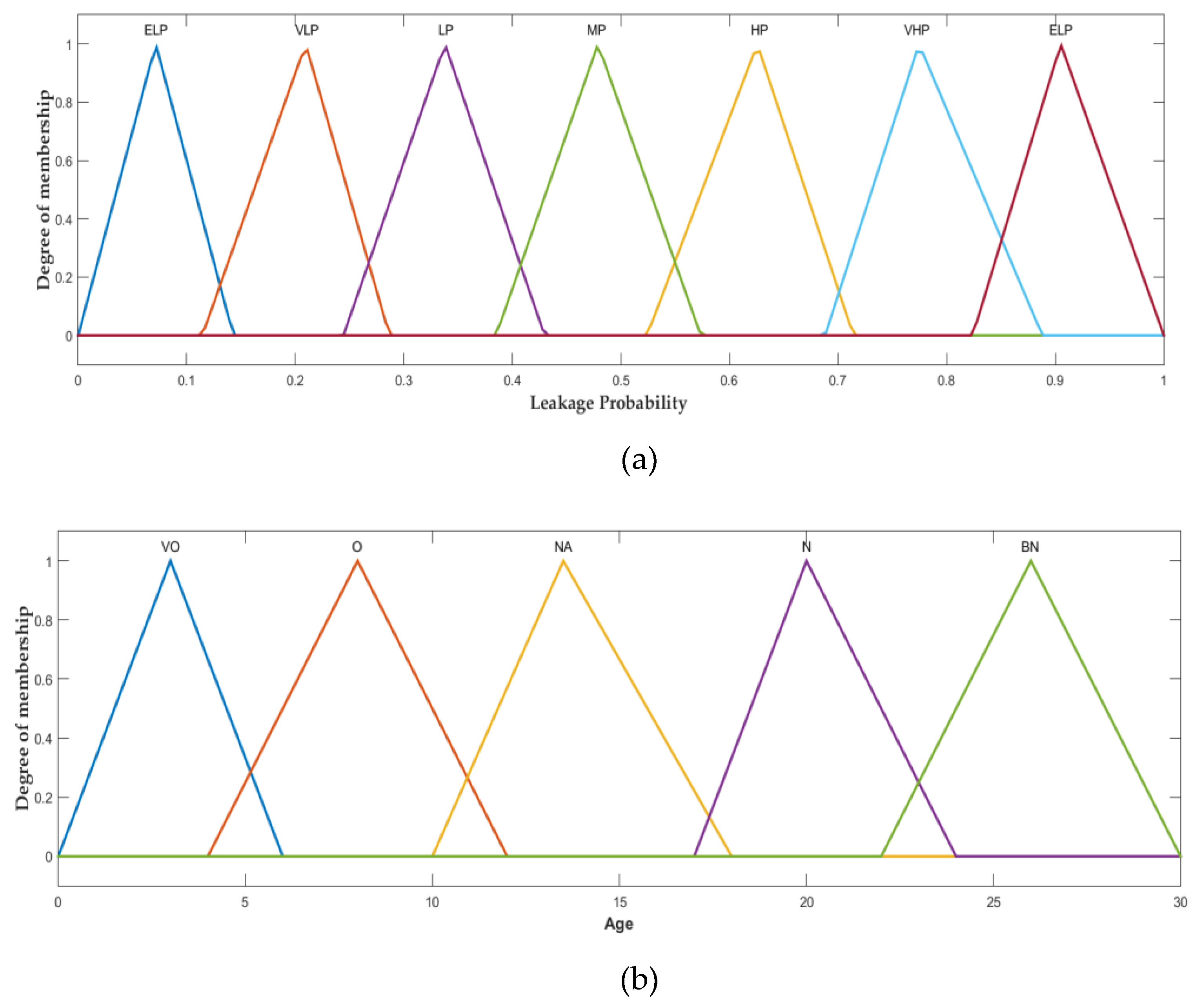
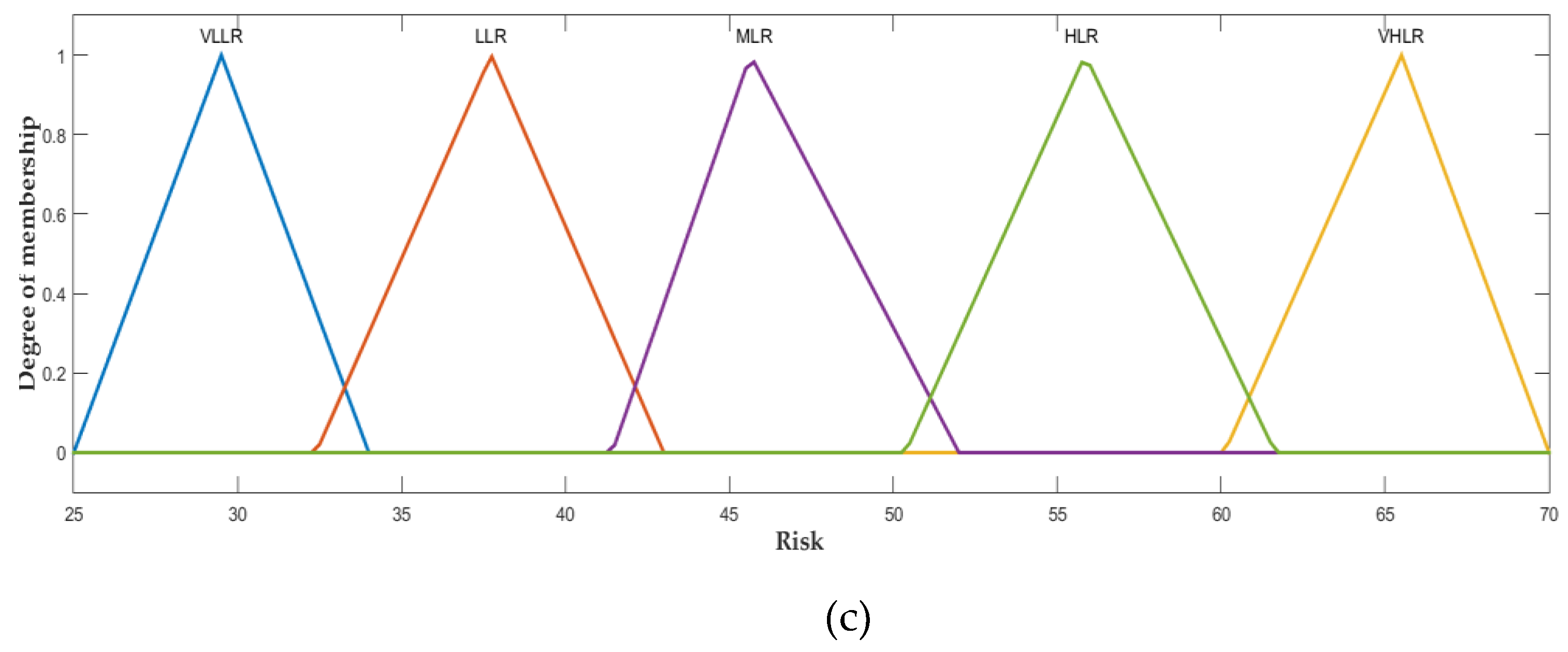
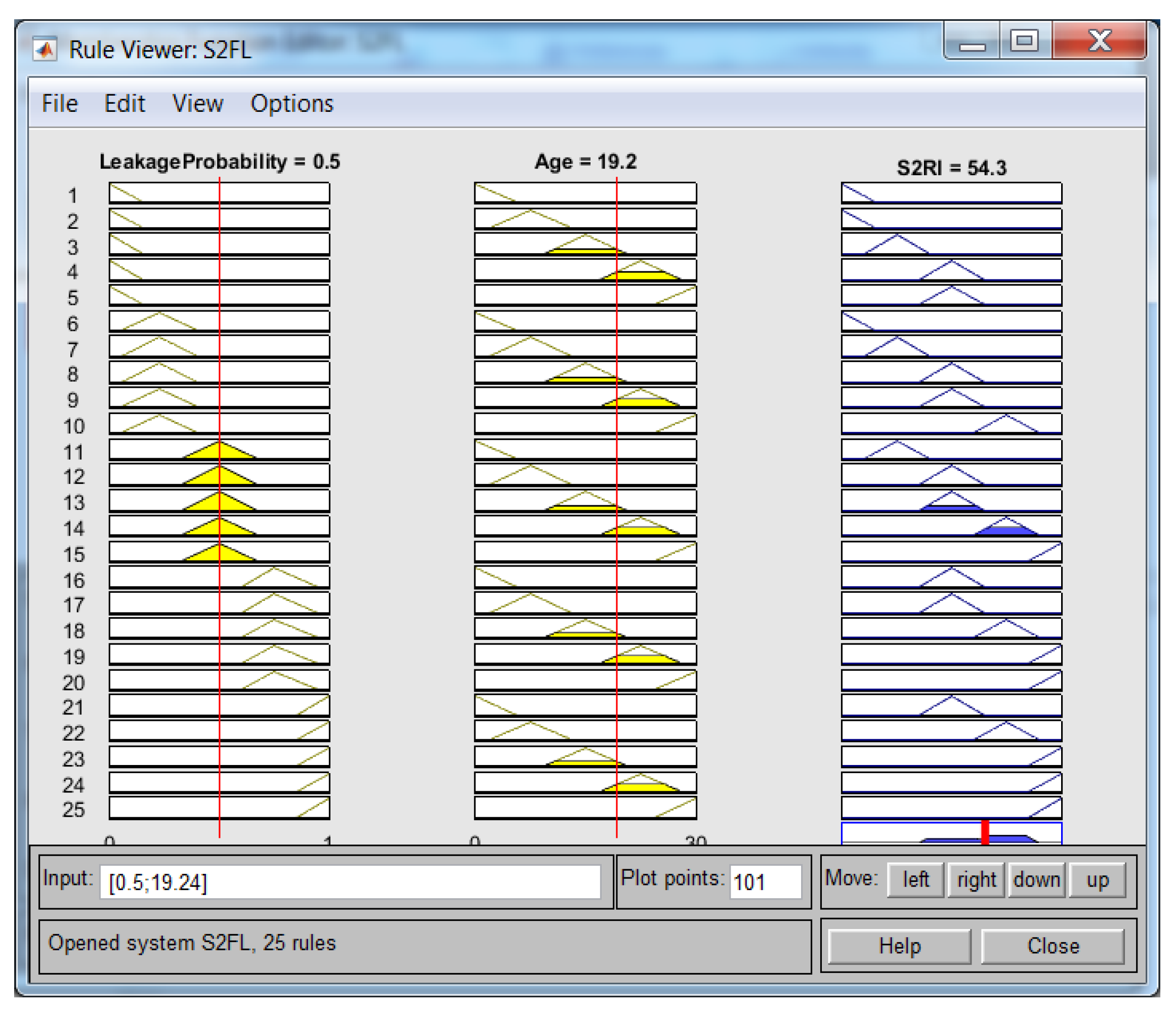
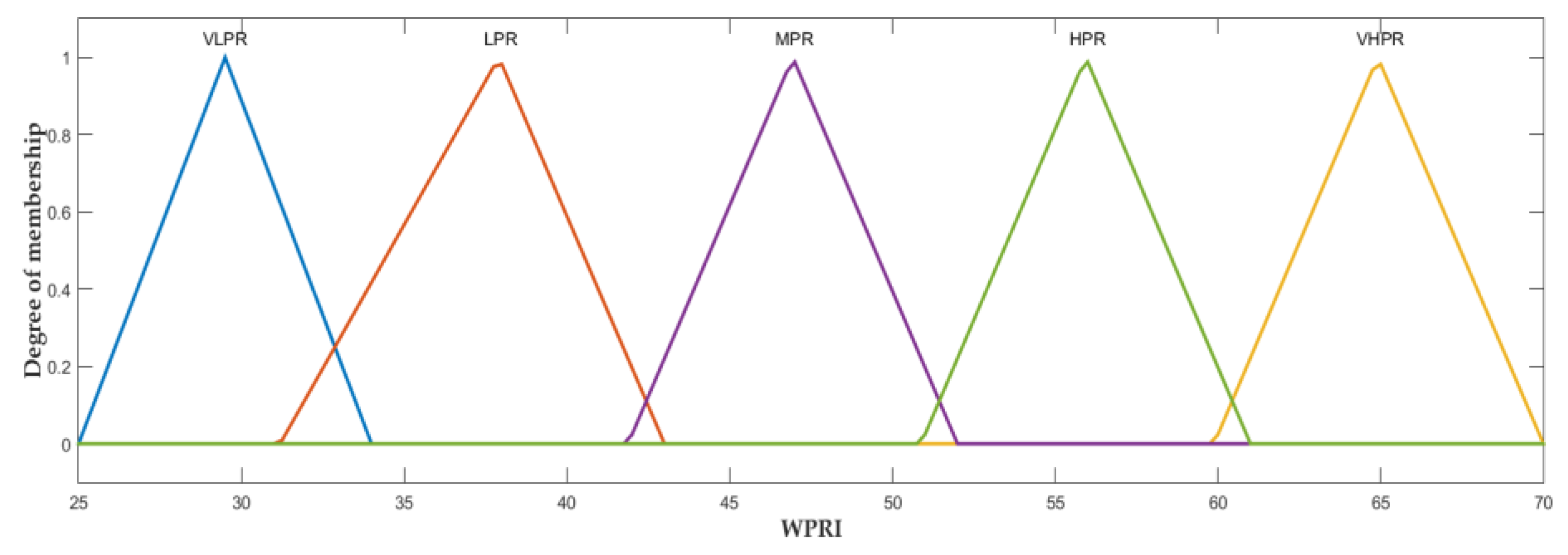


| Model | Number of Rules |
|---|---|
| Proposed Cohesive hierarchical fuzzy logic model | 85 |
| Conventional fuzzy logic model | 900 |
| Simplified hierarchical fuzzy logic model [17] | 175 |
| P1 | NG | N | ND | D | DR | VT | |
|---|---|---|---|---|---|---|---|
| P2 | |||||||
| ST | VLLR | VLLR | LLR | MLR | MLR | VHLR | |
| S | LLR | LLR | MLR | MLR | HLR | LLR | |
| M | LLR | MLR | MLR | HLR | VHLR | LLR | |
| L | MLR | MLR | HLR | VHLR | VHLR | MLR | |
| LG | MLR | HLR | VHR | VHLR | VHLR | HLR | |
| P3 | VLP | VHL | MLP | HLP | VHP | EHP | |
|---|---|---|---|---|---|---|---|
| P4 | |||||||
| OD | VLLR | VLLLR | LLR | MLR | MLR | VHLR | |
| O | VLLR | LLR | MLR | MLR | HLR | VHLR | |
| MA | LLR | MLR | MLR | HLR | VHLR | VHLR | |
| N | MLR | MLR | HLR | VHLR | VHLR | VHLR | |
| BN | MLR | HLR | VHLR | VHLR | VHLR | VHLR | |
| PR1 | VLLR | LLR | MLR | HLR | VHLR | |
|---|---|---|---|---|---|---|
| PR2 | ||||||
| VLLR | VLR | VLR | LR | MR | MR | |
| LLR | VLR | LR | MR | MR | HR | |
| MLR | LR | MR | MR | HR | VHR | |
| HLR | MR | MR | HR | VHR | VHR | |
| VHLR | MR | HR | VHR | VHR | VHR | |
| Component | Description |
|---|---|
| Hardware | Raspberry PI 3 Model B |
| Operating System | Raspbian |
| Memory | 1GB |
| Actuators | LEDs |
| IDE | Vim, PyCharm (Remote Access) |
| Programming Language | Python 3 |
| Libraries | CoAP Server, GPIO |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fayaz, M.; Ahmad, S.; Hang, L.; Kim, D. Water Supply Pipeline Risk Index Assessment Based on Cohesive Hierarchical Fuzzy Inference System. Processes 2019, 7, 182. https://doi.org/10.3390/pr7040182
Fayaz M, Ahmad S, Hang L, Kim D. Water Supply Pipeline Risk Index Assessment Based on Cohesive Hierarchical Fuzzy Inference System. Processes. 2019; 7(4):182. https://doi.org/10.3390/pr7040182
Chicago/Turabian StyleFayaz, Muhammad, Shabir Ahmad, Lei Hang, and DoHyeun Kim. 2019. "Water Supply Pipeline Risk Index Assessment Based on Cohesive Hierarchical Fuzzy Inference System" Processes 7, no. 4: 182. https://doi.org/10.3390/pr7040182
APA StyleFayaz, M., Ahmad, S., Hang, L., & Kim, D. (2019). Water Supply Pipeline Risk Index Assessment Based on Cohesive Hierarchical Fuzzy Inference System. Processes, 7(4), 182. https://doi.org/10.3390/pr7040182






