A Systematic Grey-Box Modeling Methodology via Data Reconciliation and SOS Constrained Regression
Abstract
1. Introduction
2. Problem Statement
- Proposing a good candidate structure often implies certain knowledge of the interactions and phenomena taking place in the process, which are normally too complex to model or are not well understood.
- Some parameters may not be identifiable within reasonable precision with a scarce set of measured variables y.
Pursued Goal
3. Materials and Methods
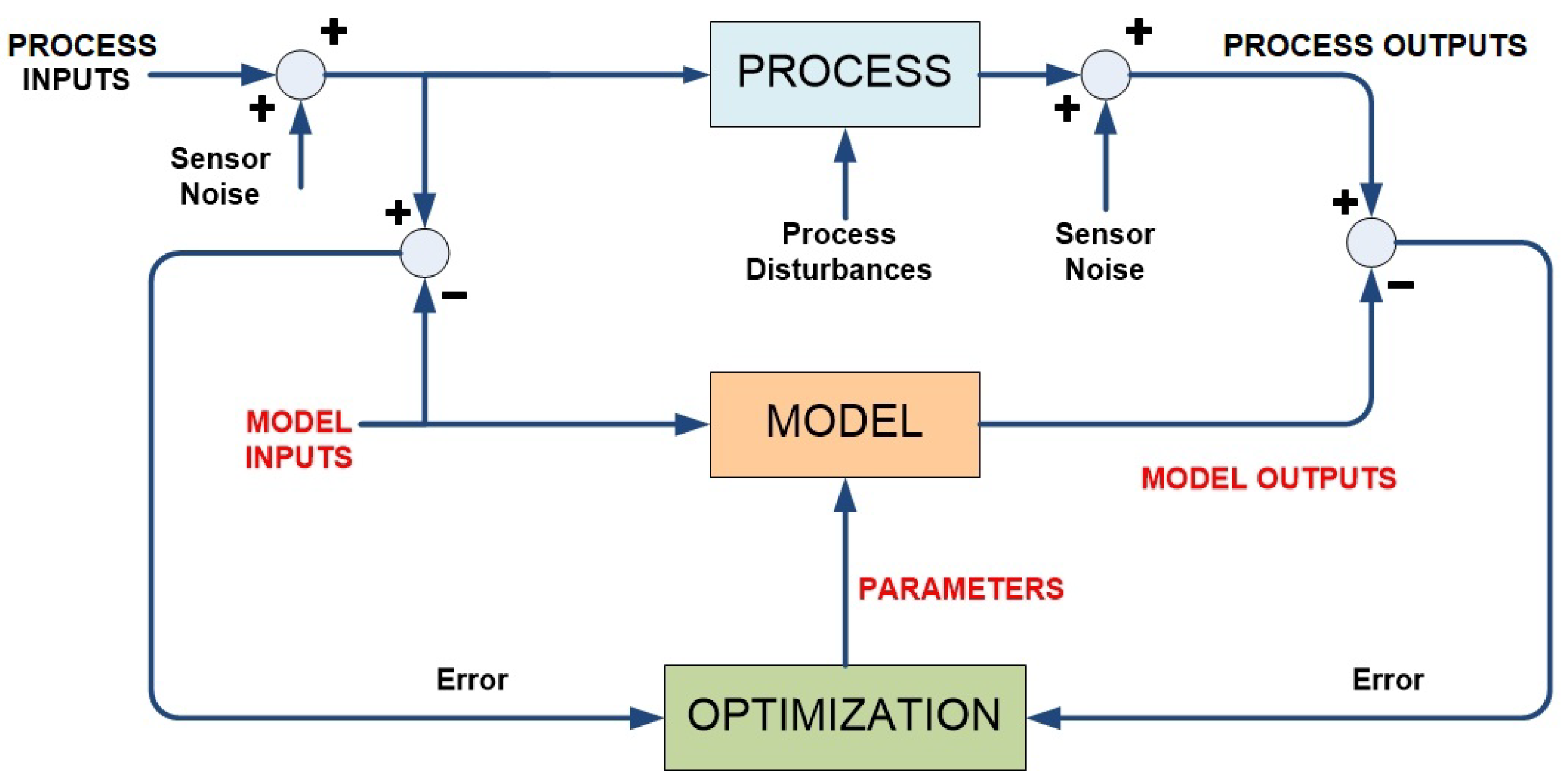
3.1. Dynamic Data Reconciliation
- , being the process measured variables with their analogies in the model, and are the sensors’ standard deviations.
- , , , are vectors of possibly nonlinear functions comprising the model equations (f and h), the measured outputs (vector c) and additional constraints such as upper and lower bounds in some variables or/and their variation over time (vector g).
- are the free model variables whose value will be estimated by the DR. These are supposed to vary conforming a wide-sense stationary process w whose power spectral density is limited by bandwidths . Bandwidths and gains can be set according to an engineering guess on the variation of the mean values of and via the sensitivity matrix of in y as proposed in ([28] Chap. 3), respectively. For instance, a limit case of and would represent a constant parameter.
- is a user-defined parameter to tune the slope of the fair estimator [16], i.e., the insensitivity to outliers.
3.2. Sum-of-Squares Programming
SOS Optimization
3.3. Polynomial Regression with Regularization
4. Proposed Modeling Methodology
- Regression. Identify relationships between variables with any x, u and/or z, and formulate a constrained regression problem to obtain algebraic equations . Finally, these equations are added to the first-principles ones (1) in order to get a complete model of the process.
5. SOS Constrained Regression
- is enforced by:
- Using Lemma 3, is enforced by:
6. Illustrative Examples
6.1. SOS Constrained Regression versus Regularization
6.1.1. Least Squares with Regularization
6.1.2. SOS Constrained Regression
- [P-2]
- Positive curvature in , tending to zero when (dashed-dotted pink curve in Figure 3):
- [P-3]
- Upper bound on p in and bounded negative curvature in (dashed green curve):
- [P-4]
- Symmetrically bounding the slope between two values in (dotted blue curve):
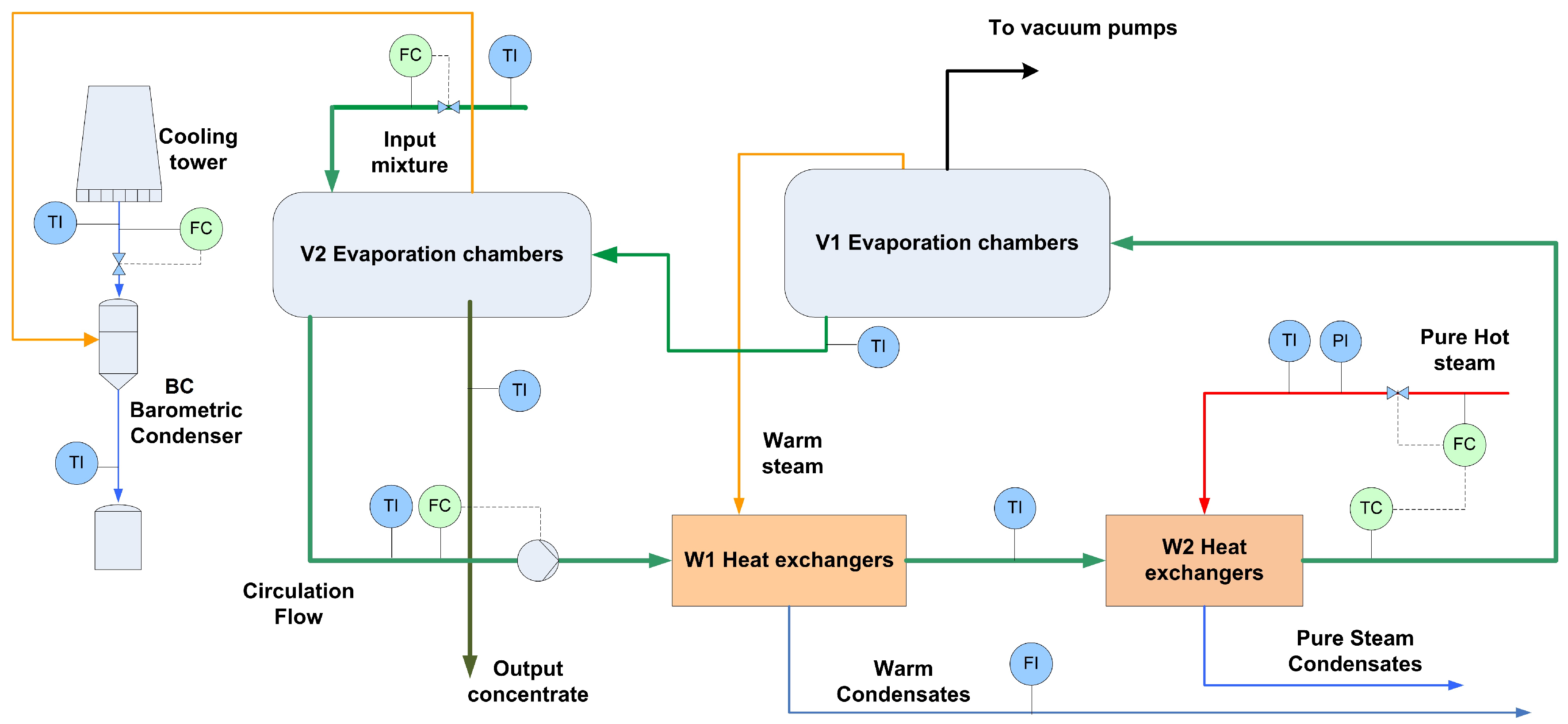
6.2. Modeling the Heat-Transfer in an Evaporation Plant
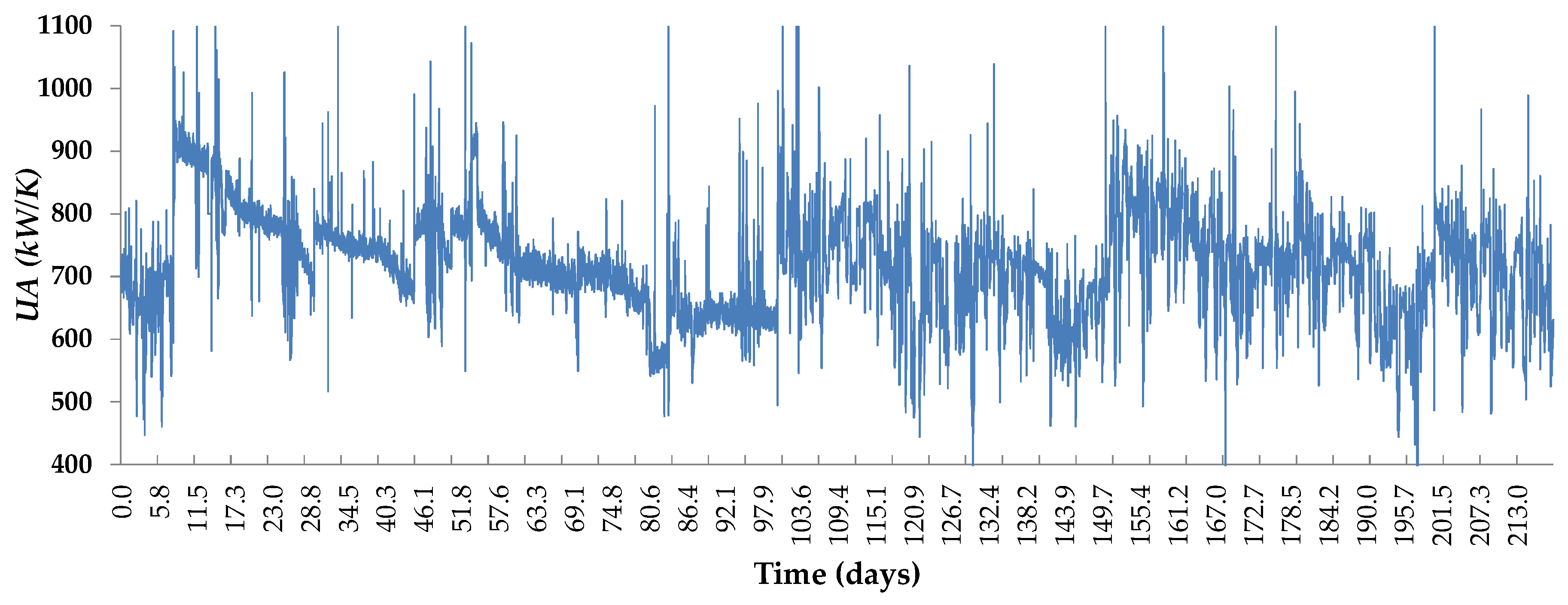
6.2.1. Stage 1: Estimation
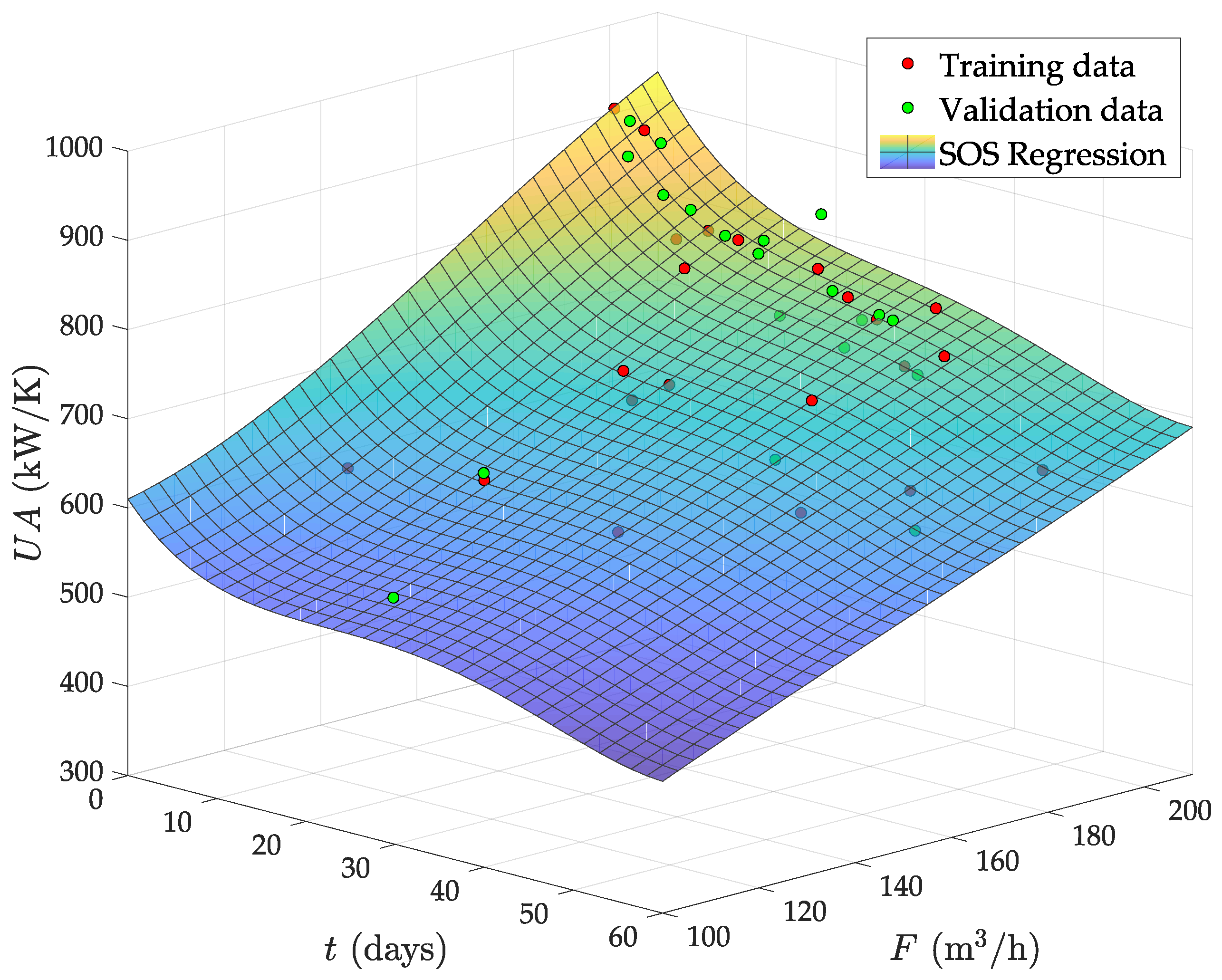
6.2.2. Stage 2: Regression
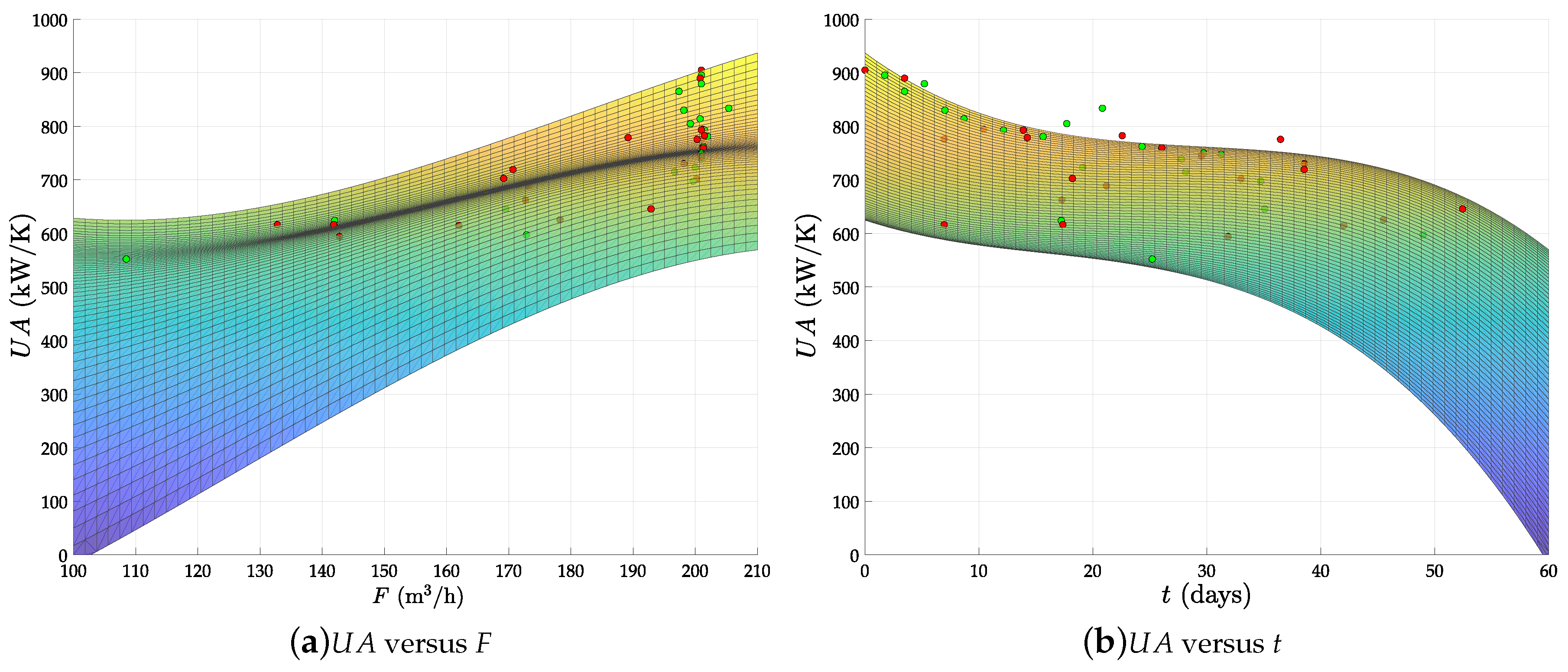
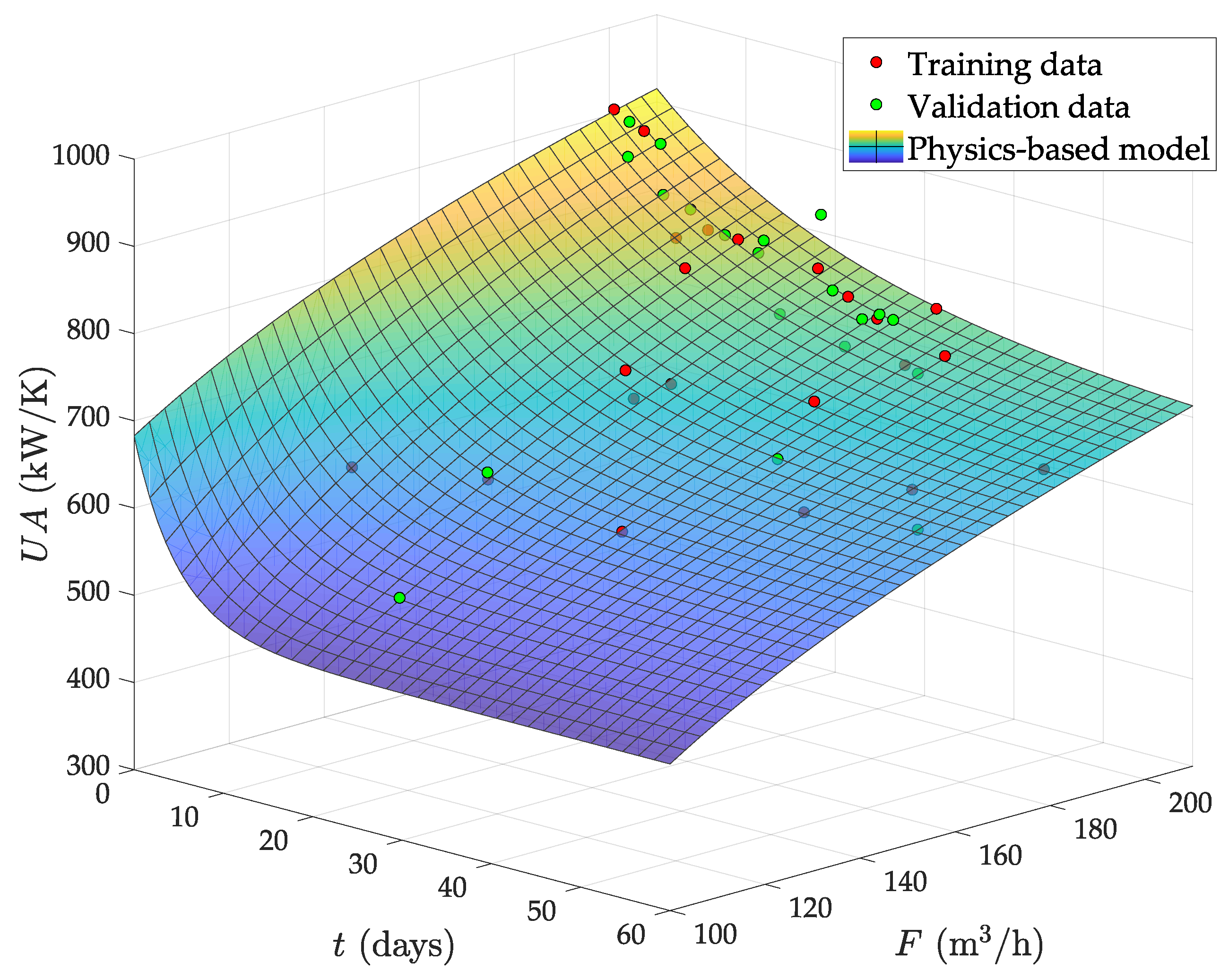
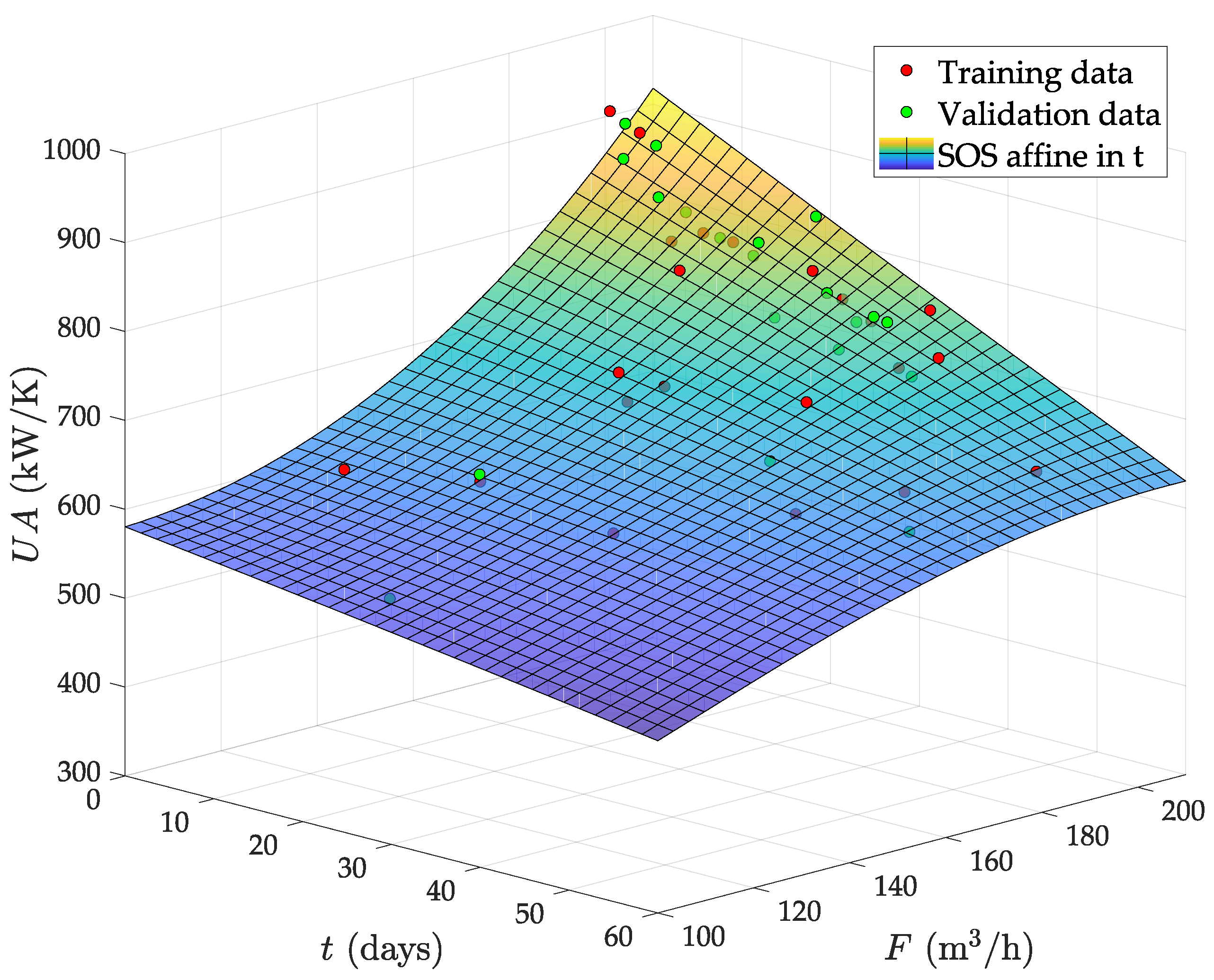
- The circulating flow is fixed by a pump in this plant. Therefore, the fouling due to deposition of organic material must tend to a saturation limit with the time. This is because the flow speed increases as the effective pipe area reduces by fouling and, from basic physics, the deposition of particles in the pipes must always decrease with the flow speed. Therefore, the abrupt falling of the from day 30 onwards is not possible. Indeed, the predicted even reaches zero and negative values after two months of operation with low F.
- With a nearly constant exchange area, always decreases as F does, by convective thermodynamics. Hence, the mild increase observed at low F when the evaporator is fully clean (see Figure 7a) is also physically impossible.
6.2.3. Comparison with Previous Works
7. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Davies, R. Industry 4.0: Digitalization for Productivity and Growth; Document pe 568.337; European Parliamentary Research Service: Brussels, Belgium, 2015. [Google Scholar]
- Krämer, S.; Engell, S. Resource Efficiency of Processing Plants: Monitoring and Improvement; John Wiley & Sons: Weinheim, Germany, 2017. [Google Scholar]
- Palacín, C.G.; Pitarch, J.L.; Jasch, C.; Méndez, C.A.; de Prada, C. Robust integrated production-maintenance scheduling for an evaporation network. Comput. Chem. Eng. 2018, 110, 140–151. [Google Scholar] [CrossRef]
- Maxeiner, L.S.; Wenzel, S.; Engell, S. Price-based coordination of interconnected systems with access to external markets. Comput. Aided Chem. Eng. 2018, 44, 877–882. [Google Scholar]
- Afram, A.; Janabi-Sharifi, F. Black-box modeling of residential HVAC system and comparison of gray-box and black-box modeling methods. Energy Build. 2015, 94, 121–149. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: San Francisco, CA, USA, 2016. [Google Scholar]
- Olsen, I.; Endrestøl, G.O.; Sira, T. A rigorous and efficient distillation column model for engineering and training simulators. Comput. Chem. Eng. 1997, 21, S193–S198. [Google Scholar] [CrossRef]
- Galan, A.; de Prada, C.; Gutierrez, G.; Sarabia, D.; Gonzalez, R. Predictive Simulation Applied to Refinery Hydrogen Networks for Operators’ Decision Support. In Proceedings of the 12th IFAC Symposium on Dynamics and Control of Process Systems, Including Biosystems (DYCOPS), Florianópolis, Brazil, 23–26 April 2019. [Google Scholar]
- Kar, A.K. A hybrid group decision support system for supplier selection using analytic hierarchy process, fuzzy set theory and neural network. J. Comput. Sci. 2015, 6, 23–33. [Google Scholar] [CrossRef]
- Kalliski, M.; Pitarch, J.L.; Jasch, C.; de Prada, C. Apoyo a la Toma de Decisión en una Red de Evaporadores Industriales. Revista Iberoamericana de Automática e Informática Industrial 2019, 16, 26–35. [Google Scholar] [CrossRef]
- Zorzetto, L.; Filho, R.; Wolf-Maciel, M. Processing modelling development through artificial neural networks and hybrid models. Comput. Chem. Eng. 2000, 24, 1355–1360. [Google Scholar] [CrossRef]
- Cellier, F.E.; Greifeneder, J. Continuous System Modeling; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Zou, W.; Li, C.; Zhang, N. A T–S Fuzzy Model Identification Approach Based on a Modified Inter Type-2 FRCM Algorithm. IEEE Trans. Fuzzy Syst. 2018, 26, 1104–1113. [Google Scholar] [CrossRef]
- Neumaier, A. Solving Ill-Conditioned and Singular Linear Systems: A Tutorial on Regularization. SIAM Rev. 1998, 40, 636–666. [Google Scholar] [CrossRef]
- Kim, S.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An Interior-Point Method for Large-Scale ℓ1-Regularized Least Squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Llanos, C.E.; Sanchéz, M.C.; Maronna, R.A. Robust Estimators for Data Reconciliation. Ind. Eng. Chem. Res. 2015, 54, 5096–5105. [Google Scholar] [CrossRef]
- de Prada, C.; Hose, D.; Gutierrez, G.; Pitarch, J.L. Developing Grey-box Dynamic Process Models. IFAC-PapersOnLine 2018, 51, 523–528. [Google Scholar] [CrossRef]
- Cozad, A.; Sahinidis, N.V.; Miller, D.C. A combined first-principles and data-driven approach to model building. Comput. Chem. Eng. 2015, 73, 116–127. [Google Scholar] [CrossRef]
- Cozad, A.; Sahinidis, N.V. A global MINLP approach to symbolic regression. Math. Programm. 2018, 170, 97–119. [Google Scholar] [CrossRef]
- Reemtsen, R.; Rückmann, J.J. Semi-Infinite Programming; Springer Science & Business Media: New York, NY, USA, 1998; Volume 25. [Google Scholar]
- Parrilo, P.A. Semidefinite programming relaxations for semialgebraic problems. Math. Programm. 2003, 96, 293–320. [Google Scholar] [CrossRef]
- Nauta, K.M.; Weiland, S.; Backx, A.C.P.M.; Jokic, A. Approximation of fast dynamics in kinetic networks using non-negative polynomials. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 1144–1149. [Google Scholar]
- Tan, K.; Li, Y. Grey-box model identification via evolutionary computing. Control Eng. Pract. 2002, 10, 673–684. [Google Scholar] [CrossRef]
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; MOS-SIAM Series on Optimization: Philadelphia, PA, USA, 2010; Volume 10. [Google Scholar]
- Schuster, A.; Kozek, M.; Voglauer, B.; Voigt, A. Grey-box modelling of a viscose-fibre drying process. Math. Comput. Model. Dyn. Syst. 2012, 18, 307–325. [Google Scholar] [CrossRef]
- Tulleken, H.J. Grey-box modelling and identification using physical knowledge and bayesian techniques. Automatica 1993, 29, 285–308. [Google Scholar] [CrossRef]
- Leibman, M.J.; Edgar, T.F.; Lasdon, L.S. Efficient data reconciliation and estimation for dynamic processes using nonlinear programming techniques. Comput. Chem. Eng. 1992, 16, 963–986. [Google Scholar] [CrossRef]
- Bendig, M. Integration of Organic Rankine Cycles for Waste Heat Recovery in Industrial Processes. Ph.D. Thesis, Institut de Génie Mécanique, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2015. [Google Scholar]
- Lasserre, J.B. Sufficient conditions for a real polynomial to be a sum of squares. Archiv der Mathematik 2007, 89, 390–398. [Google Scholar] [CrossRef]
- Parrilo, P.A. Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2000. [Google Scholar]
- Papachristodoulou, A.; Anderson, J.; Valmorbida, G.; Prajna, S.; Seiler, P.; Parrilo, P. SOSTOOLS version 3.00 sum of squares optimization toolbox for MATLAB. arXiv, 2013; arXiv:1310.4716. [Google Scholar]
- Hilbert, D. Ueber die Darstellung definiter Formen als Summe von Formenquadraten. Mathematische Annalen 1888, 32, 342–350. [Google Scholar] [CrossRef]
- Scherer, C.W.; Hol, C.W.J. Matrix Sum-of-Squares Relaxations for Robust Semi-Definite Programs. Math. Programm. 2006, 107, 189–211. [Google Scholar] [CrossRef]
- Putinar, M. Positive Polynomials on Compact Semi-algebraic Sets. Indiana Univ. Math. J. 1993, 42, 969–984. [Google Scholar] [CrossRef]
- Pitarch, J.L. Contributions to Fuzzy Polynomial Techniques for Stability Analysis and Control. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2013. [Google Scholar]
- Scherer, C.; Weiland, S. Linear Matrix Inequalities in Control; Lecture Notes; Dutch Institute for Systems and Control: Delft, The Netherlands, 2000; Volume 3, p. 2. [Google Scholar]
- Wilson, Z.T.; Sahinidis, N.V. The ALAMO approach to machine learning. Comput. Chem. Eng. 2017, 106, 785–795. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS) 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Gill, P.; Murray, W.; Saunders, M. SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Sanchis, J.; Blasco, X.; Martínez, M. Design of Continuous Controllers Using a Multiobjective Differential Evolution Algorithm with Spherical Pruning. In Applications of Evolutionary Computation; Di Chio, C., Cagnoni, S., Cotta, C., Ebner, M., Ekárt, A., Esparcia-Alcazar, A.I., Goh, C.K., Merelo, J.J., Neri, F., Preuß, M., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 532–541. [Google Scholar]
- Andersson, J.; Åkesson, J.; Diehl, M. CasADi: A Symbolic Package for Automatic Differentiation and Optimal Control. In Recent Advances in Algorithmic Differentiation; Forth, S., Hovland, P., Phipps, E., Utke, J., Walther, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 297–307. [Google Scholar]
- Hart, W.E.; Laird, C.D.; Watson, J.P.; Woodruff, D.L.; Hackebeil, G.A.; Nicholson, B.L.; Siirola, J.D. Pyomo—Optimization Modeling in Python; Springer Science & Business Media: New York, NY, USA, 2017; Volume 67. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Programm. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Sahinidis, N.V. BARON: A general purpose global optimization software package. J. Glob. Optim. 1996, 8, 201–205. [Google Scholar] [CrossRef]
- Pitarch, J.L.; Palacín, C.G.; de Prada, C.; Voglauer, B.; Seyfriedsberger, G. Optimisation of the Resource Efficiency in an Industrial Evaporation System. J. Process Control 2017, 56, 1–12. [Google Scholar] [CrossRef]
- Pitarch, J.L.; Palacín, C.G.; Merino, A.; de Prada, C. Optimal Operation of an Evaporation Process. In Modeling, Simulation and Optimization of Complex Processes HPSC 2015; Bock, H.G., Phu, H.X., Rannacher, R., Schlöder, J.P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 189–203. [Google Scholar]
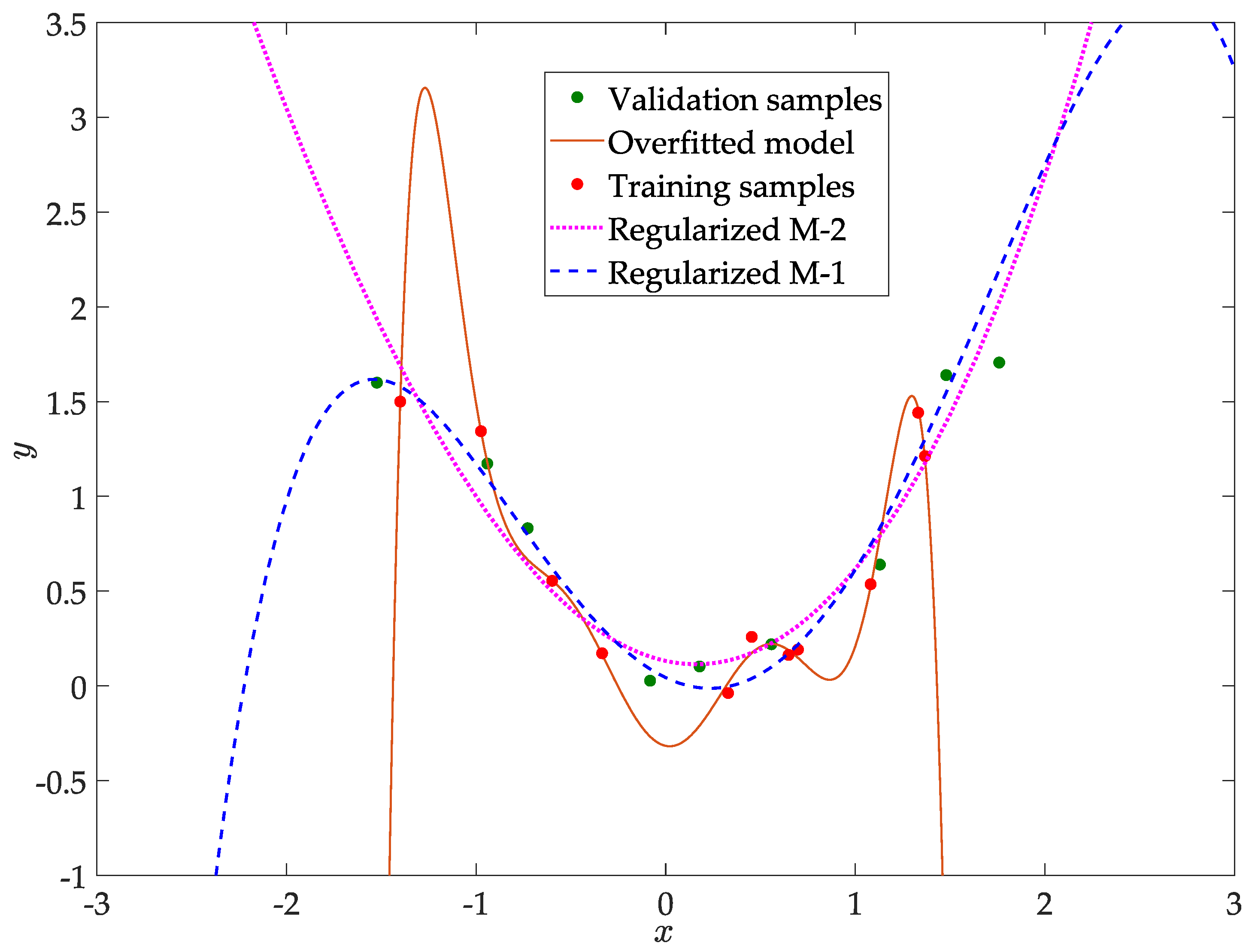
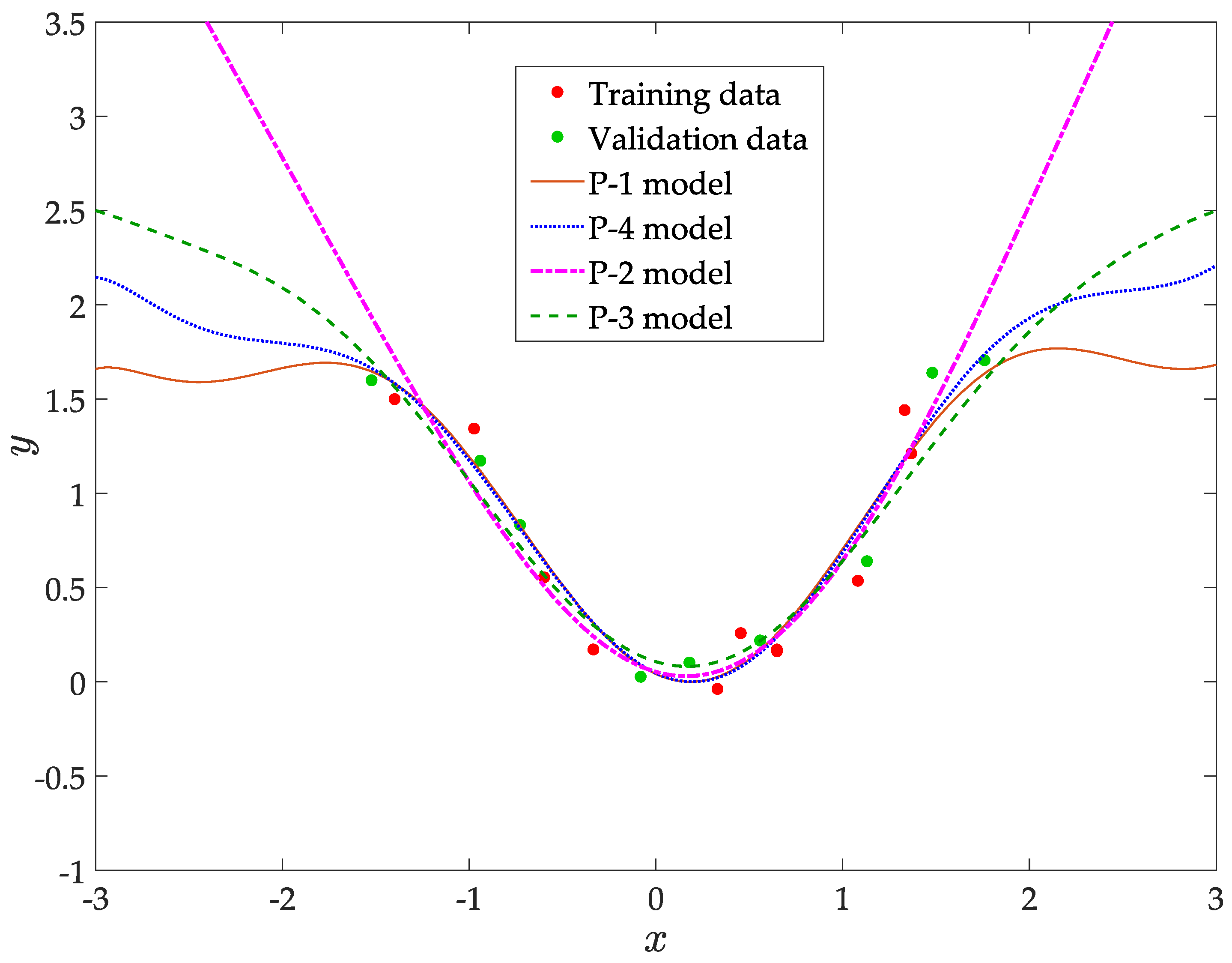
| Training Error | Validation Error | Total | ||
|---|---|---|---|---|
| M-1 | 0.01 | 0.1517 | 1.84 | 2 |
| 0.1 | 0.206 | 0.366 | 0.572 | |
| 0.4 | 0.218 | 0.324 | 0.541 | |
| 1 | 0.23 | 0.372 | 0.602 | |
| 10 | 0.34 | 0.49 | 0.83 | |
| 100 | 0.416 | 0.55 | 0.967 | |
| M-2 | 0.001 | 0.184 | 1.021 | 1.2 |
| 0.01 | 0.231 | 0.834 | 1.065 | |
| 0.5 | 0.405 | 0.422 | 0.826 | |
| 2 | 0.63 | 0.42 | 1.05 | |
| 10 | 1.671 | 1.698 | 3.37 |
| Constraint | Training Error | Validation Error | Total |
|---|---|---|---|
| P-1 | 0.26 | 0.15 | 0.41 |
| P-2 | 0.31 | 0.364 | 0.674 |
| P-3 | 0.372 | 0.255 | 0.627 |
| P-4 | 0.257 | 0.144 | 0.4 |
| Method | Training Error | Validation Error | Total | Relative Deterioration |
|---|---|---|---|---|
| LS regularized | 13,448 | 14,282 | 27,730 | - |
| SOS constrained | 14,751 | 13,362 | 28,113 | 1.36% |
| SOS affine | 20,147 | 15,131 | 35,278 | 21.39% |
| Physics-based model | - | - | 37,361 | 25.78% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitarch, J.L.; Sala, A.; de Prada, C. A Systematic Grey-Box Modeling Methodology via Data Reconciliation and SOS Constrained Regression. Processes 2019, 7, 170. https://doi.org/10.3390/pr7030170
Pitarch JL, Sala A, de Prada C. A Systematic Grey-Box Modeling Methodology via Data Reconciliation and SOS Constrained Regression. Processes. 2019; 7(3):170. https://doi.org/10.3390/pr7030170
Chicago/Turabian StylePitarch, José Luis, Antonio Sala, and César de Prada. 2019. "A Systematic Grey-Box Modeling Methodology via Data Reconciliation and SOS Constrained Regression" Processes 7, no. 3: 170. https://doi.org/10.3390/pr7030170
APA StylePitarch, J. L., Sala, A., & de Prada, C. (2019). A Systematic Grey-Box Modeling Methodology via Data Reconciliation and SOS Constrained Regression. Processes, 7(3), 170. https://doi.org/10.3390/pr7030170







