Modeling, Management, and Control of an Autonomous Wind/Fuel Cell Micro-Grid System
Abstract
:1. Introduction
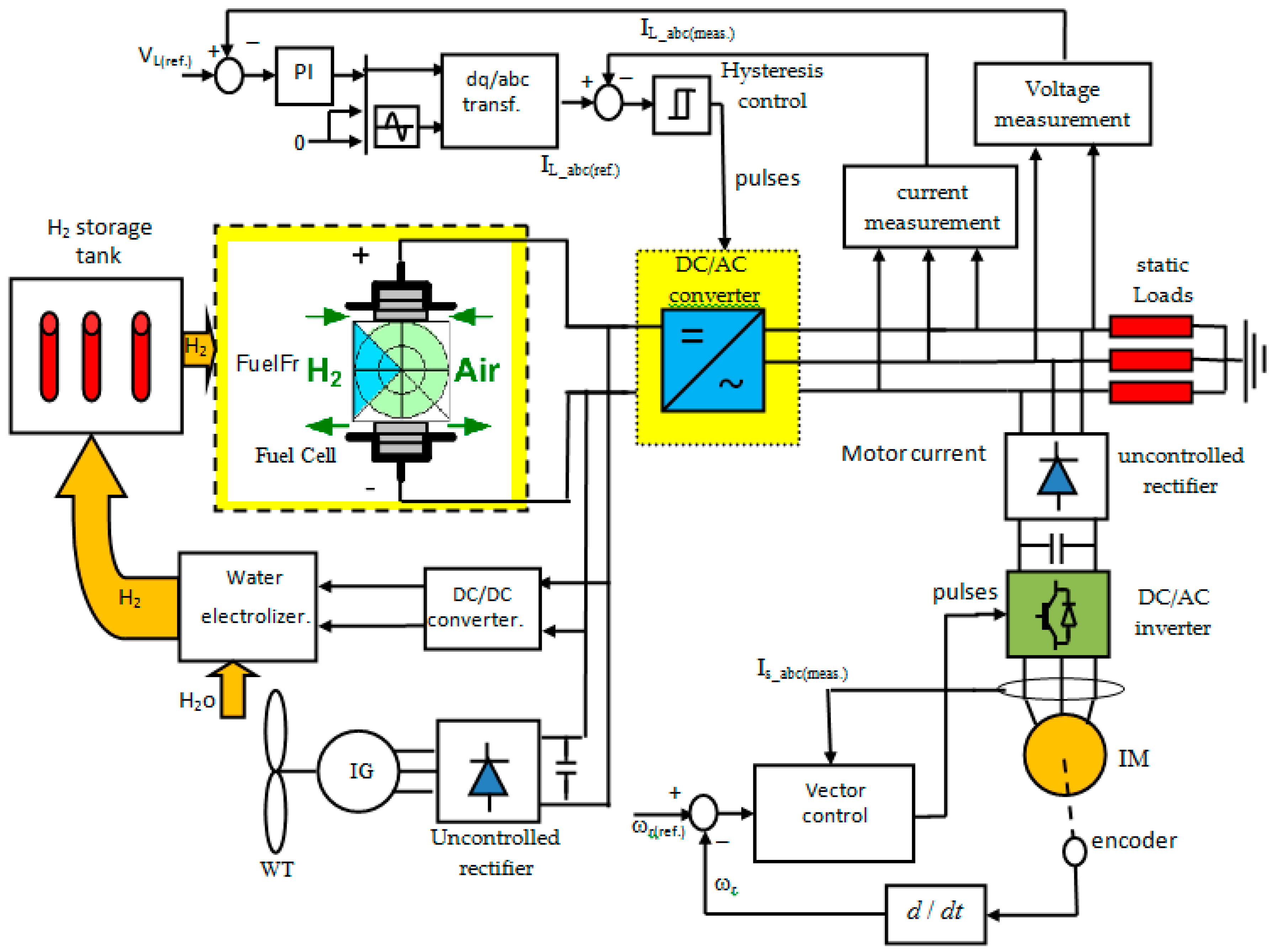
2. System Description
3. The Dynamic Model of the System
3.1. Wind Turbine Model
3.2. Dynamic Model of the Induction Machine
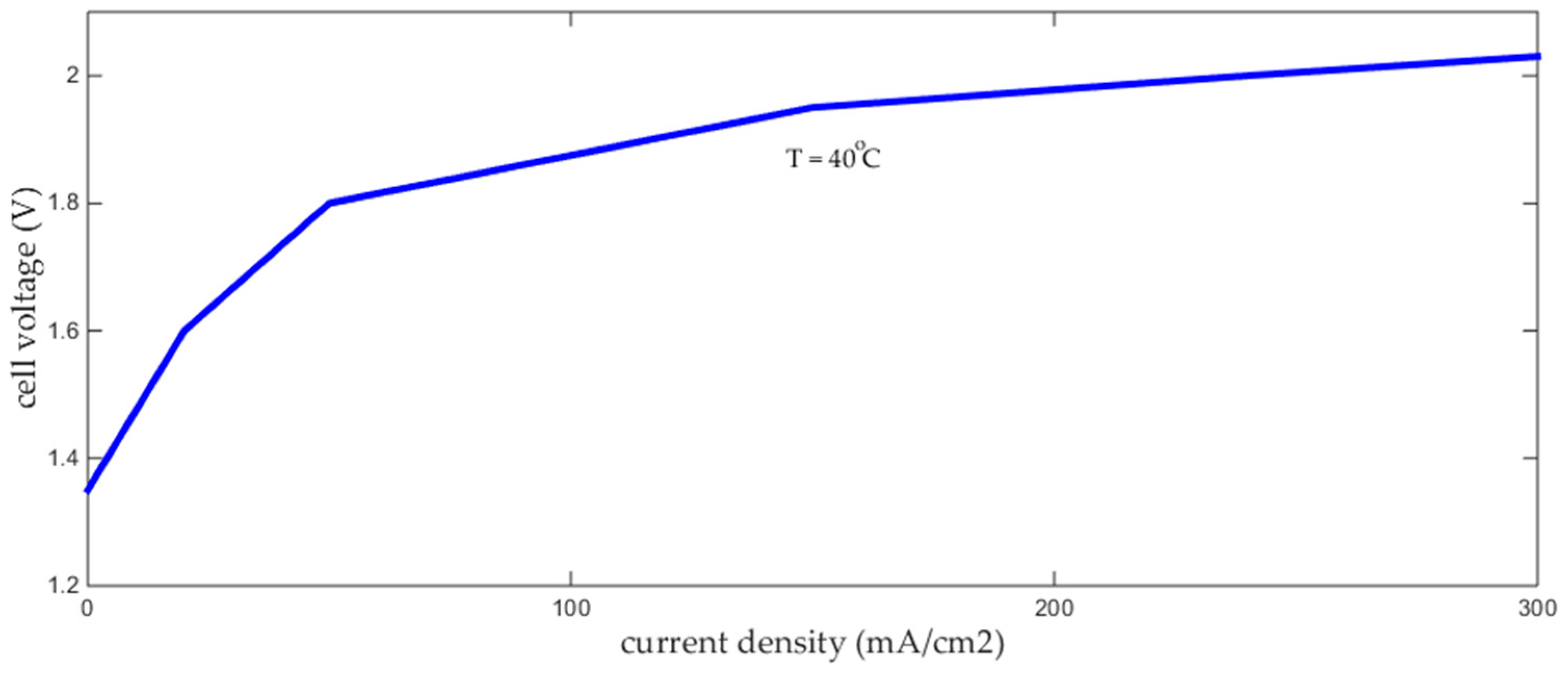
3.3. Fuel Cell Model
3.4. Uncontrolled Rectifier Model
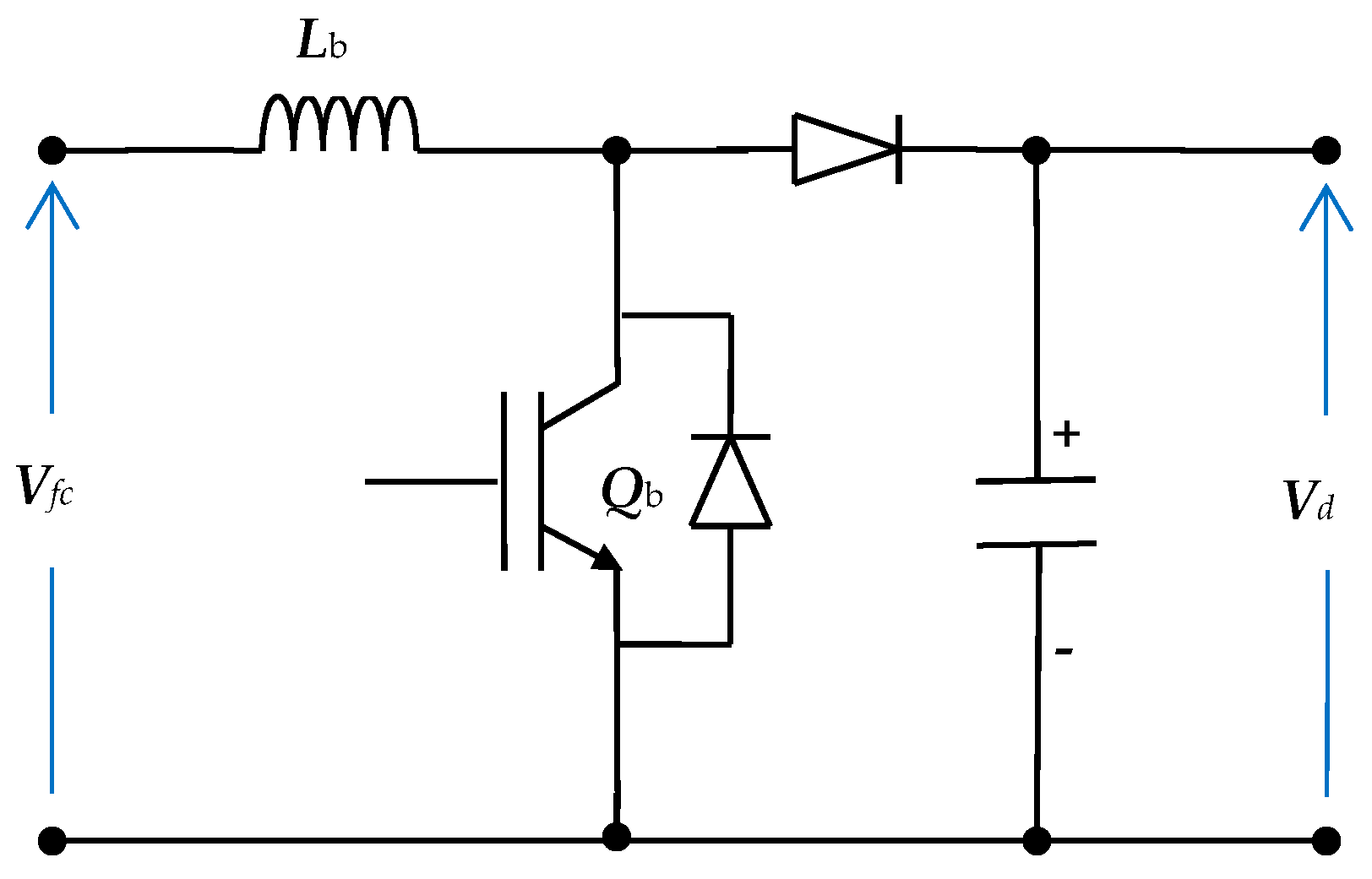
3.5. Boost Converter Model
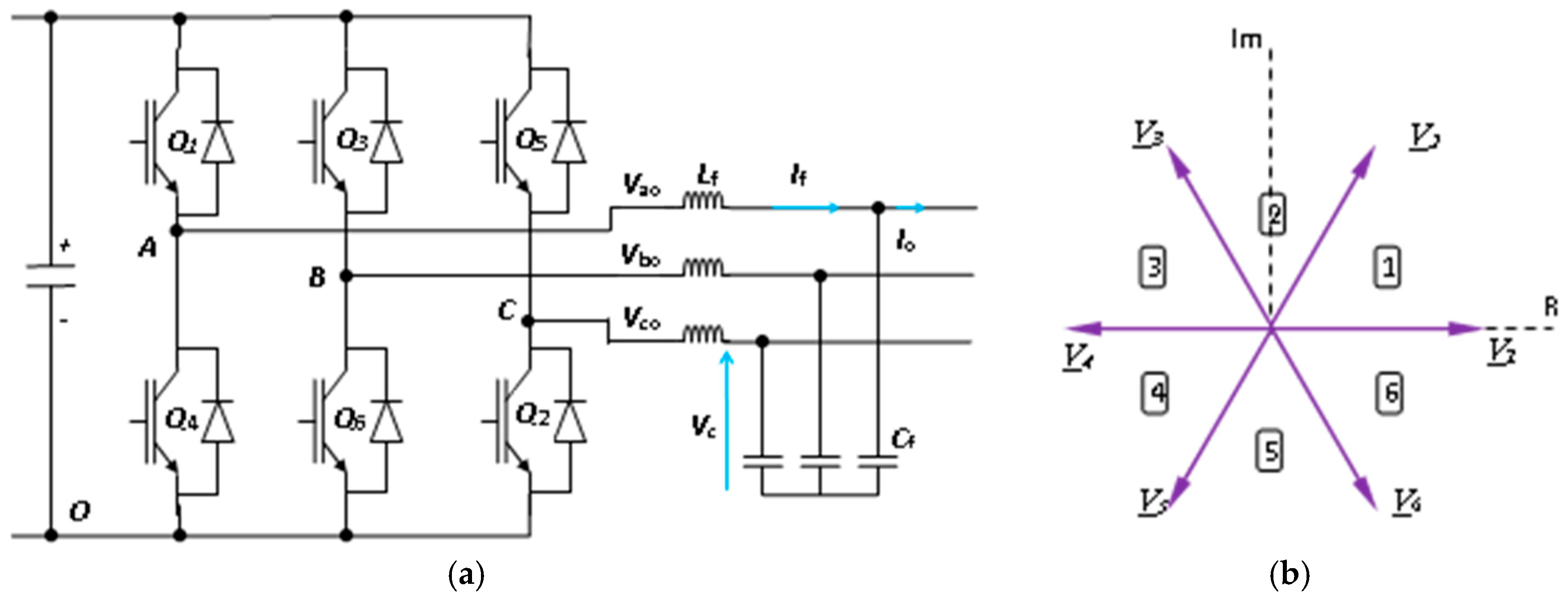
3.6. Main Power Inverter Model
4. System Controllers
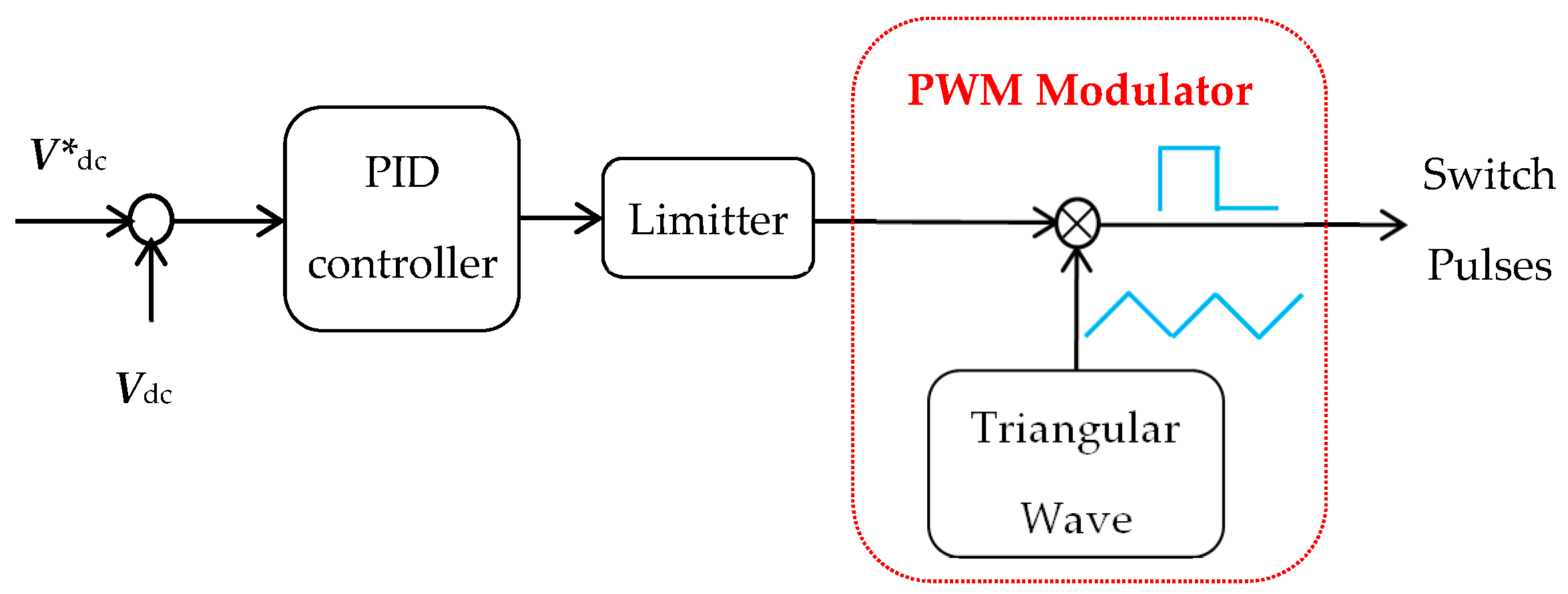
4.1. Main Inverter Controller
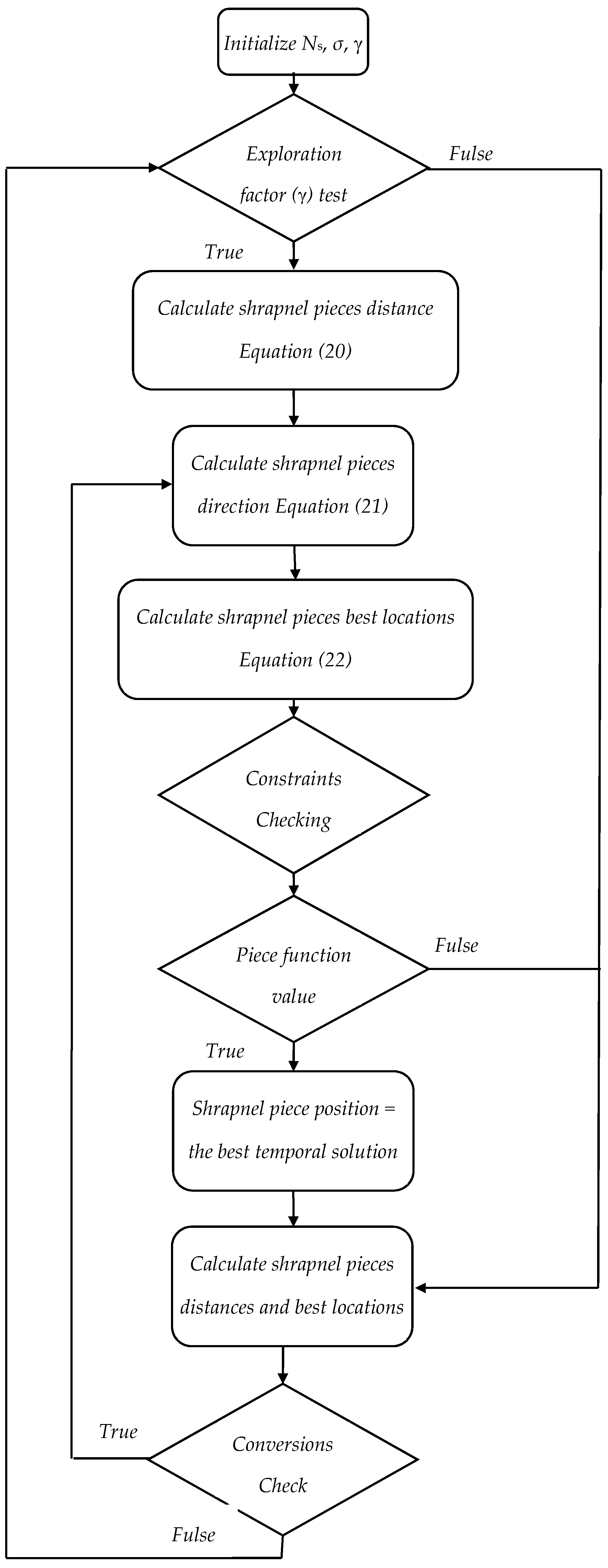
4.2. Mine Blast Optimization Algorithm
4.3. Boost Converter Controller
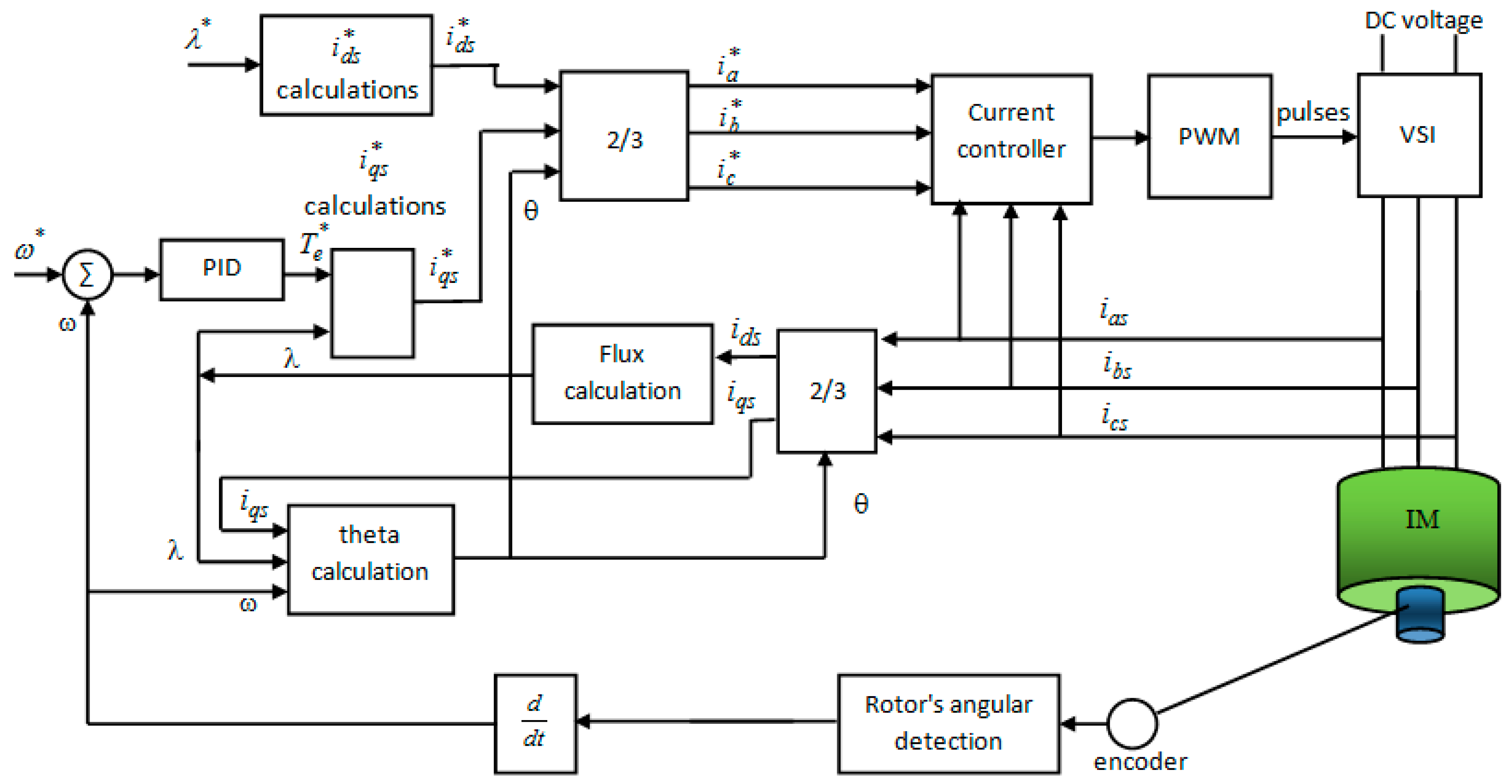
4.4. Induction Motor Controller
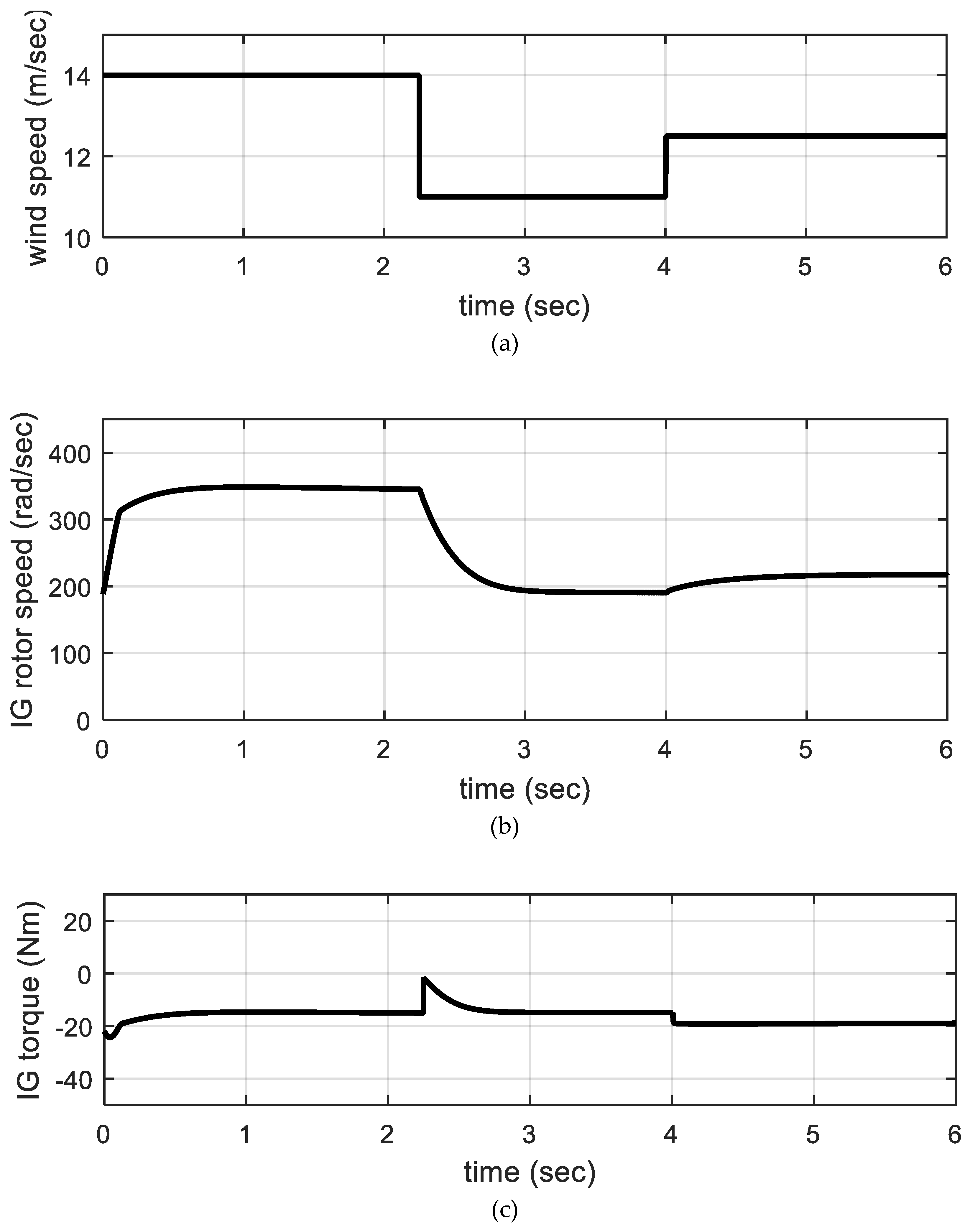
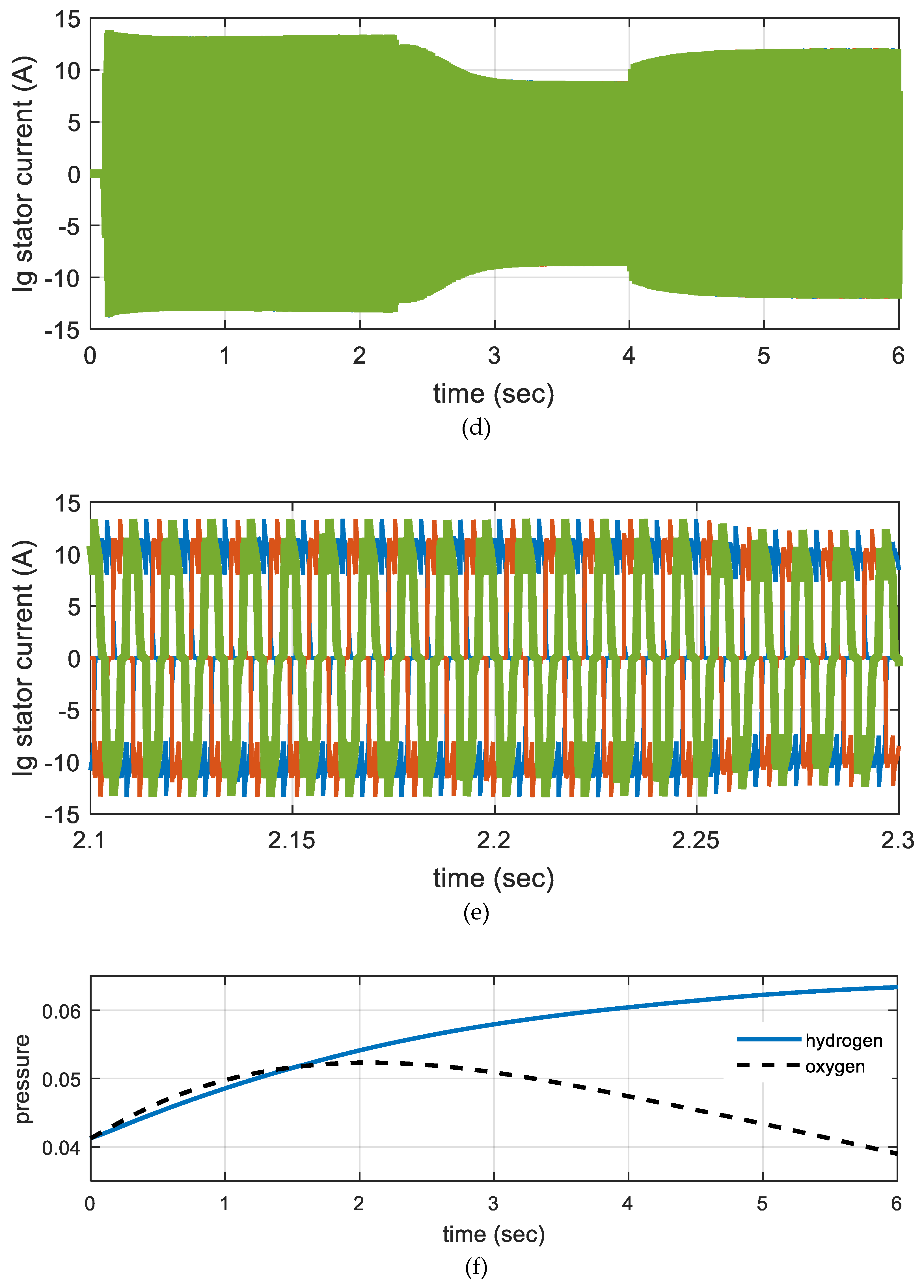
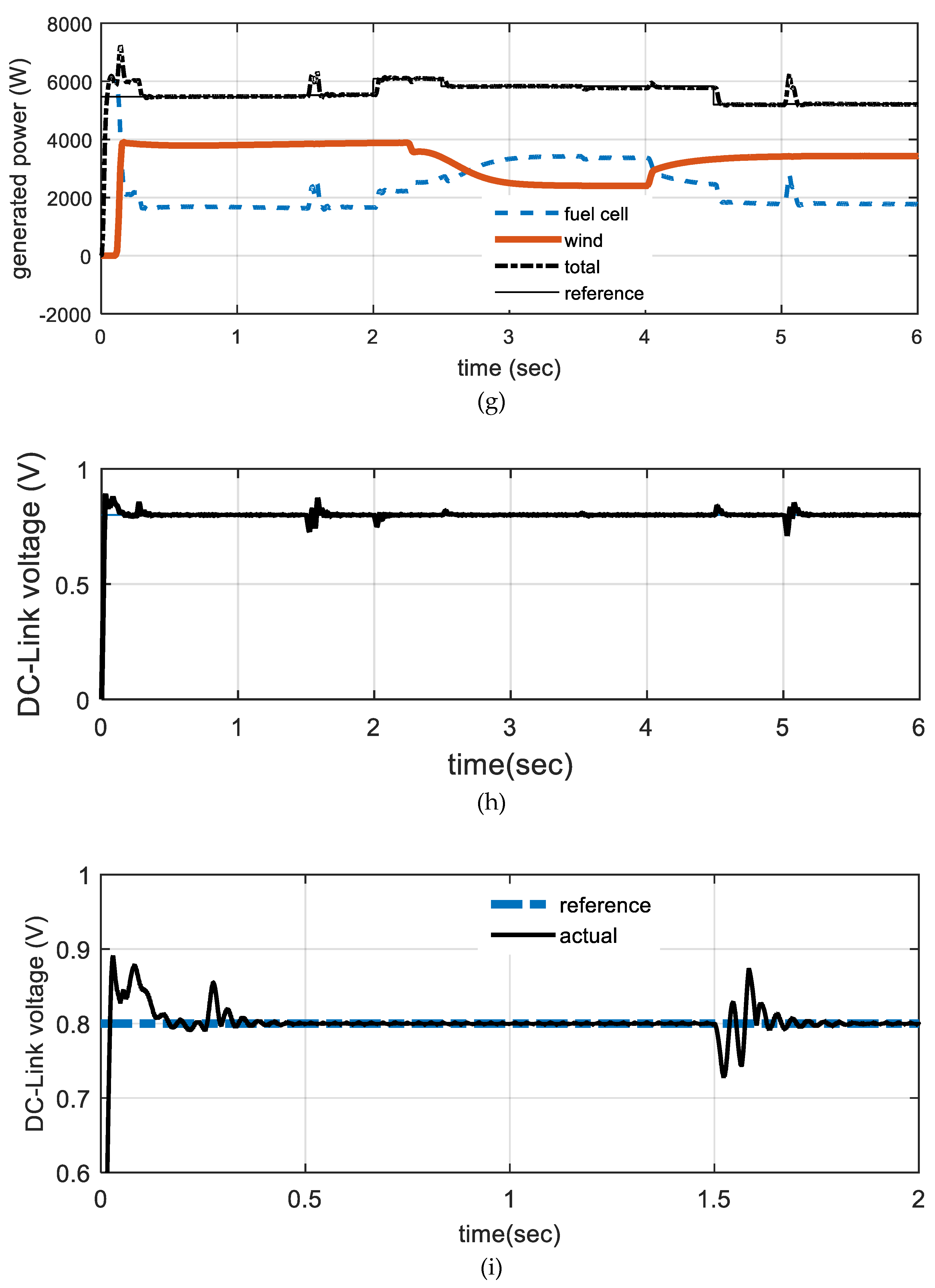
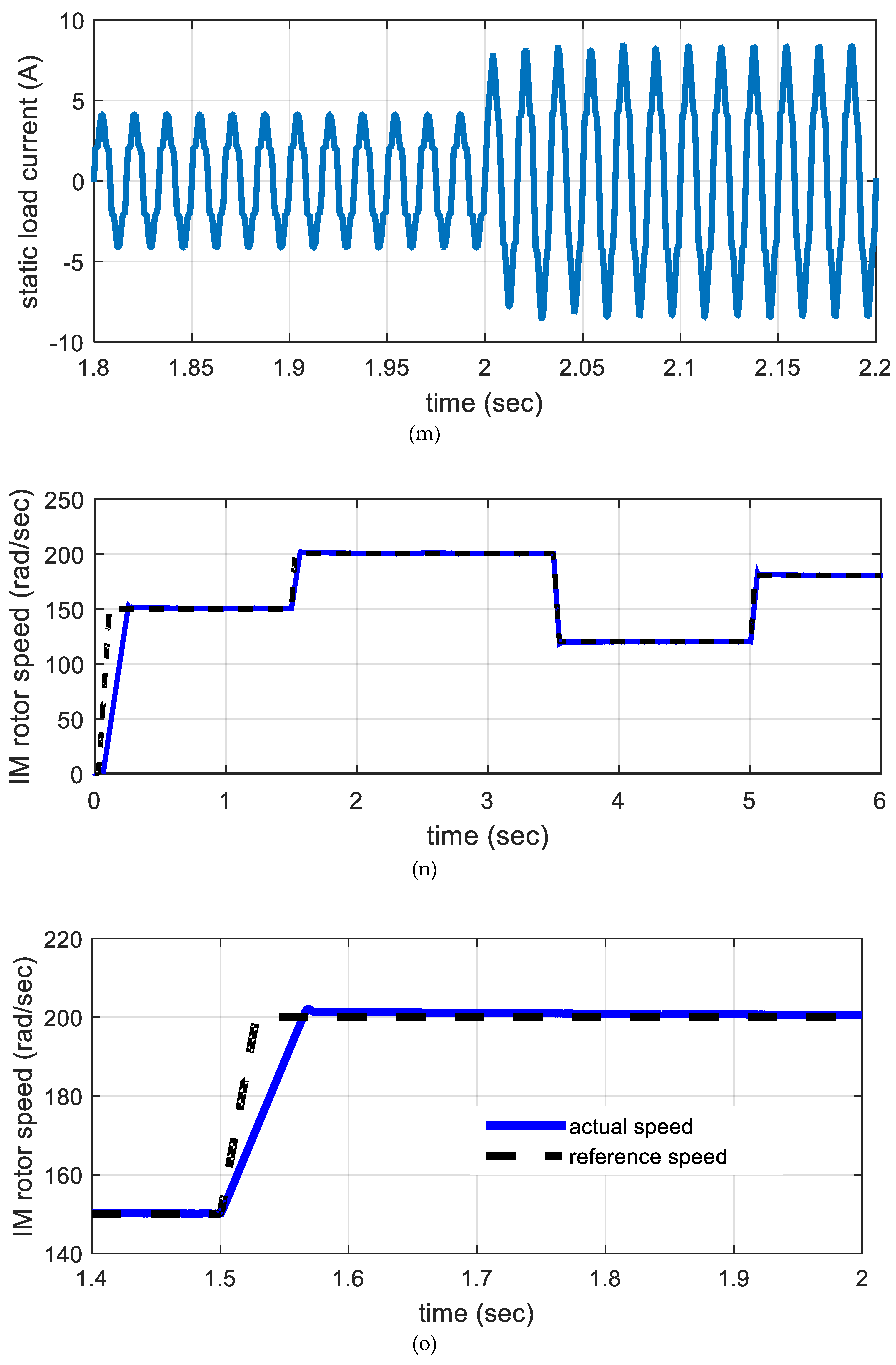
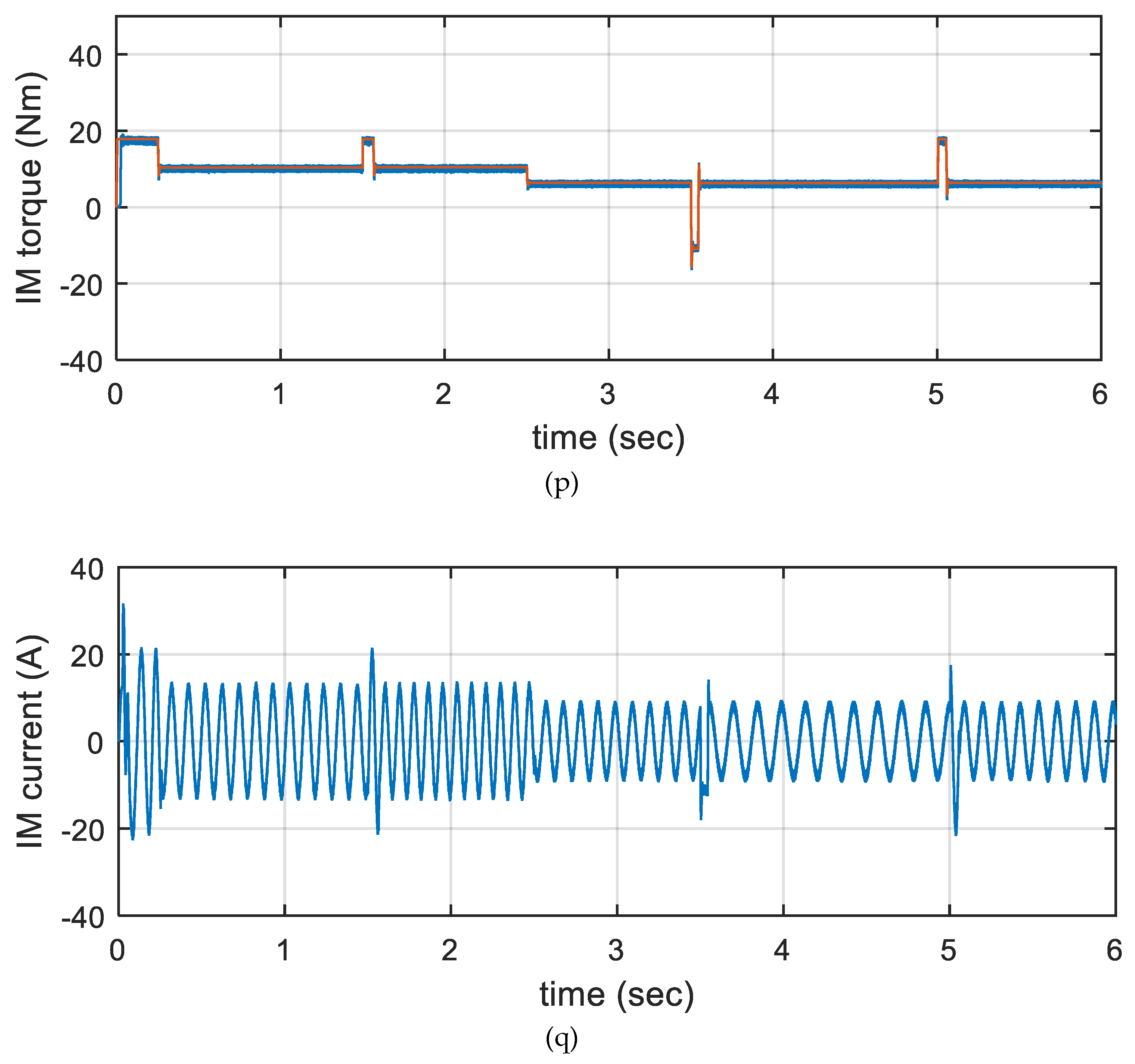
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclatures
| Pm | the power output of the wind turbine |
| β | the blade pitch angle (in degrees) |
| ρ | the air density (kg/m3) |
| vw | the wind speed |
| R | the radius of the turbine blade |
| Cp | the performance coefficient of the turbine |
| ωm | the turbine mechanical angular rotor speed |
| Tm | the wind turbine torque |
| Te | the electrical generator electromagnetic torque (N·m), |
| J | the combined inertia of the generator rotor and the wind turbine (kg·m) |
| B | the mechanical viscous friction (N·m·s/rad) |
| rr | the rotor resistance |
| vds, vqs | the stator d- and q-axis voltage components |
| ids, iqs | the stator d- and q-axis current components |
| λdr, λqr | the rotor d- and q-axis flux linkage components |
| Ls, Lr, Lm | the stator inductance, rotor, and mutual inductances |
| ωr | the motor speed, ωs is the motor synchronous speed |
| Tem | the motor electromagnetic torque (N·m) |
| Jm | the inertia of the IM rotor (kg·m) |
| Bm | the viscous friction of the coupling (N·m·s/rad) |
| E | the stack output voltage |
| Eo | the cell open circuit voltage at standard pressure |
| N | the number of cells in stack |
| F | the Faraday’s constant |
| n | the number of transferred electrons in the electrochemical reaction |
| R’ | the universal gas constant |
| T | the operating temperature |
| PH2 | the partial pressure of hydrogen |
| PO2 | the partial pressure of oxygen |
| PH2Oc | the partial pressure of gas water |
| Pstd | the standard pressure |
| Vdrop | the voltage losses |
| i | the output current density |
| in | the internal current density related to internal current losses |
| io | the exchange current density related to activation losses |
| iL | the limiting current density related to concentration losses |
| α | the area specific resistance related to resistive losses |
| (Ig, Vg) | the phase rms current and voltage of the IG |
| (Id, Vd) | the average rectifier output current and voltage |
| d | the duty ratio of the switch |
| (Vfc, Ifc) | the fuel cell output voltage and current |
| Vc | the output voltage, |
| Vi, | the inverter voltage |
| Io | the output current |
| If | the filter current |
| fa, fb, fc | the phase values, |
| F | the space vector of the quantity |
| (L, C) | the filter inductance and capacitance |
| zo | the first shot point, |
| SB, LB | are the problem upper and lower limits |
| γ | the exploration factor |
| Ns | the Shrapnel pieces |
| the shrapnel distance of the exploded mines | |
| F | the fitness function |
| the best location | |
| ts | the simulation time |
| Kp1, Ki1, Kp2, Ki2 | The PI control parameters to be estimated |
| Pw | electrical output power of wind generation system |
| PFC | electrical output power of fuel cell generation system |
| PSL | electrical power needed by the static load |
| PDL | electrical power needed by the dynamic load |
| PNet | the difference between the generated and demanded powers |
References
- REN21. Renewable energy Policy Network for the 21st Century. Global Status Report. 2018. Available online: http://www.ren21.net/gsr_2018_full_report_en (accessed on 20 November 2018).
- Meisen, P.; Loiseau, A. Ocean Energy Technologies for Renewable Energy Generation; Global Energy Network Institute (GENI): New York, NY, USA, 2009. [Google Scholar]
- Pena, R.; Cardenas, R.; Proboste, J.; Clare, J.; Asher, G. Wind–diesel generation using doubly fed induction machines. IEEE Trans. Energy Convers. 2008, 23, 202–214. [Google Scholar] [CrossRef]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar-wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Sanyal, S.K. Future of geothermal energy. In Proceedings of the 35th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 1–3 February 2010. [Google Scholar]
- Lazard’s Levelized Cost of Energy Analysis—Version 10. Available online: https://www.lazard.com/media/438038/levelized-cost-of-energy-v100.pdf (accessed on 23 December 2016).
- Nehrir, M.H.; Wang, C.; Strunz, K.; Aki, H.; Ramakumar, R.; Bing, J.; Miao, Z.; Salameh, Z. A Review of Hybrid Renewable/Alternative Energy Systems for Electric Power Generation: Configurations, Control, and Applications. IEEE Trans. Sustain. Energy 2011, 2, 392–403. [Google Scholar] [CrossRef]
- Barnard, M. 7 Factors Show Wind Solar 1st Choices. Available online: https://cleantechnica.com/2016/07/11/7-factors-show-wind-solar-1st-choices/ (accessed on 11 July 2016).
- Zhang, D.; Evangelisti, S.; Lettieri, P.; Papageorgiou, L.G. Economic and environmental scheduling of smart homes with microgrid: DER operation and electrical tasks. Energy Convers. Manag. 2016, 110, 113–124. [Google Scholar] [CrossRef]
- Koohi-Kamali, S.; Rahim, N.A. Coordinated control of smart microgrid during and after islanding operation to prevent under frequency load shedding using energy storage system. Energy Convers. Manag. 2016, 127, 623–646. [Google Scholar] [CrossRef]
- Camblong, H.; Baudoin, S.; Vechiu, I.; Etxeberria, A. Design of a SOFC/GT/SCs hybrid power system to supply a rural isolated microgrid. Energy Convers. Manag. 2016, 117, 12–20. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. A review on Integrated Renewable Energy System based power generation for stand-alone applications: Configurations, storage options, sizing methodologies and control. Renew. Sustain. Energy Rev. 2014, 38, 99–120. [Google Scholar] [CrossRef]
- The Energy Foundation Annual Report. Available online: http://www.ef.org/ten-signs-in-2016-that-show-the-clean-energy-economy-is-here-to-stay/ (accessed on 23 December 2016).
- Onar, O.C.; Uzunoglu, M.; Alam, M.S. Dynamic modeling, design and simulation of a wind/fuel cell/ultra-capacitor-based hybrid power generation system. J. Power Sources 2006, 161, 707–722. [Google Scholar] [CrossRef]
- Kassem, A.M.; Hassan, A.A. Performance improvements of a permanent magnet synchronous machine via functional model predictive control. J. Control Sci. Eng. 2012, 2012, 7. [Google Scholar] [CrossRef]
- Ribeiro, P.F.; Johnson, B.K.; Crow, M.L.; Arsoy, A.; Liu, Y. Energy storage systems for advanced power applications. Proc. IEEE 2001, 89, 1744–1756. [Google Scholar] [CrossRef]
- Rastler, D. Electricity Energy Storage Technology Options: A White Paper Primer on Applications, Costs, and Benefits; Technical Report; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2010. [Google Scholar]
- Giraud, F.; Salameh, Z.M. Steady-state performance of a grid-connected rooftop hybrid wind–photovoltaic power system with battery storage. IEEE Trans. Energy Convers. 2001, 16, 1–7. [Google Scholar] [CrossRef]
- Yang, H.X.; Lu, L.; Zhou, W. A novel optimization sizing model for hybrid solar–wind power generation system. Solar Energy 2007, 81, 76–84. [Google Scholar] [CrossRef]
- Baziar, A.; Kavousi-Fard, A. Considering uncertainty in the optimal energy management of renewable micro-grids including storage devices. Renew. Energy 2013, 59, 158–166. [Google Scholar] [CrossRef]
- Ahmed, M.; Amin, U.; Aftab, S.; Ahmed, Z. Integration of Renewable Energy Resources in Microgrid. Energy Power Eng. 2015, 7, 12–29. [Google Scholar] [CrossRef]
- Delfino, B.; Fornari, F. Modeling and Control of an Integrated Fuel Cell/Wind Turbine System. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; p. 6. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel standalone hybrid solar/wind/fuel cell power generation system for remote areas. Solar Energy 2017, 146, 30–43. [Google Scholar] [CrossRef]
- Vidyanandan, K.V.; Senroy, N. Frequency regulation in microgrid using wind—Fuel cell—Diesel generator. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Hussaina, A.; Arifb, S.M.; Aslamc, M. Emerging renewable and sustainable energy technologies: State of the art. Renew. Sustain. Energy Rev. 2017, 71, 12–28. [Google Scholar] [CrossRef]
- Al-falahi, M.D.A.; Jayasinghe, S.D.G.; Enshaei, H. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Zhu, Y.; Tomsovic, K. Development of models for analyzing the load-following performance of micro-turbines and fuel cells. Electr. Power Syst. Res. 2002, 62, 1–11. [Google Scholar] [CrossRef]
- Khan, F.I.; Hawboldt, K.; Iqbal, M.T. Life Cycle Analysis of wind–fuel cell integrated system. Renew. Energy 2005, 30, 157–177. [Google Scholar] [CrossRef]
- Battista, H.D.; Mantz, R.J.; Garelli, F. Power conditioning for a wind/hydrogen energy system. J. Power Sources 2006, 155, 478–486. [Google Scholar] [CrossRef]
- Gorgun, H. Dynamic Modeling of a Proton Exchange Membrane (PEM) Electrolyzer. Int. J. Hydrogen Energy 2006, 31, 29–38. [Google Scholar] [CrossRef]
- Bizon, N. Optimal operation of fuel cell/wind turbine hybrid power system under turbulent wind and variable load. Appl. Energy 2018, 212, 196–209. [Google Scholar] [CrossRef]
- Mendis, N.; Muttaqi, K.M.; Sayeef, S.; Perera, S. Standalone operation of wind turbine-based variable speed generators with maximum power extraction capability. IEEE Trans. Energy Conv. 2012, 27, 822–834. [Google Scholar] [CrossRef]
- MATLAB Math Library User’s Guide’, by the Math Works. Inc. 2015. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/845043405443232/sl_using_r2015a.pdf (accessed on 1 March 2015).
- Chiu, L.Y.; Diong, B.; Gemmen, R.S. An improved small-signal model of the dynamic behavior of pem fuel cells. IEEE Trans. Ind. Appl. 2004, 40, 970–977. [Google Scholar] [CrossRef]
- Belyaev, P.V.; Mischenko, V.S.; Podberezkin, D.A.; Em, R.A. Simulation Modeling of Proton Exchange Membrane Fuel Cells. In Proceedings of the 2016 Dynamics of Systems, Mechanisms and Machines (Dynamics), Omsk, Russia, 15–17 November 2016; pp. 1–5. [Google Scholar] [CrossRef]
- SharifiAsl, S.M.; Rowshanzamir, S.; Eikani, M.H. Modelling and simulation of the steady-state and dynamic behavior of a PEM fuel cell. Energy 2010, 35, 1633–1646. [Google Scholar] [CrossRef]
- Kassem, A.M. Modeling and Robust Control Design of a Standalone Wind-Based Energy Storage Generation Unit Powering an Induction Motor Variable-Displacement Pressure Compensated Pump. IET Renew. Power Gener. 2016, 10, 275–286. [Google Scholar] [CrossRef]
- Rashid, M. Power Electronics Handbook, 2nd ed.; Elsevier Press: California, CA, USA, 2011. [Google Scholar]
- Ali, E.S.; Abd Elazim, S.M. Mine blast algorithm for environmental economic load dispatch with valve loading effect. Neural Comput. Appl. 2016, 30, 261–270. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Majumdar, S.; Mandal, K.; Chakraborty, N. Performance study of mine blast algorithm for automatic voltage regulator tuning. In Proceedings of the 2014 Annual IEEE India conference (INDICON), Pune, India, 11–13 December 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Trzynadlowski, A.M. The Field Orientation Principle in Control of Induction Motors, 1st ed.; Springer: New York, NY, USA, 1994. [Google Scholar]



| Parameter | Value |
|---|---|
| α | 642.3 |
| Ns | 100 |
| No. of variables | 2 |
| Max_iteration | 100 |
| Final distance | 0.0042351 |
| Number of function evaluations | 10,000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atawi, I.E.; Kassem, A.M.; Zaid, S.A. Modeling, Management, and Control of an Autonomous Wind/Fuel Cell Micro-Grid System. Processes 2019, 7, 85. https://doi.org/10.3390/pr7020085
Atawi IE, Kassem AM, Zaid SA. Modeling, Management, and Control of an Autonomous Wind/Fuel Cell Micro-Grid System. Processes. 2019; 7(2):85. https://doi.org/10.3390/pr7020085
Chicago/Turabian StyleAtawi, Ibrahem E., Ahmed M. Kassem, and Sherif A. Zaid. 2019. "Modeling, Management, and Control of an Autonomous Wind/Fuel Cell Micro-Grid System" Processes 7, no. 2: 85. https://doi.org/10.3390/pr7020085
APA StyleAtawi, I. E., Kassem, A. M., & Zaid, S. A. (2019). Modeling, Management, and Control of an Autonomous Wind/Fuel Cell Micro-Grid System. Processes, 7(2), 85. https://doi.org/10.3390/pr7020085





