Parallel Conical Area Community Detection Using Evolutionary Multi-Objective Optimization

Abstract

Detecting community structures helps to reveal the functional units of complex networks. In this paper, the community detection problem is regarded as a modularity-based multi-objective optimization problem (MOP), and a parallel conical area community detection algorithm (PCACD) is designed to solve this MOP effectively and efficiently. In consideration of the global properties of the selection and update mechanisms, PCACD employs a global island model and targeted elitist migration policy in a conical area evolutionary algorithm (CAEA) to discover community structures at different resolutions in parallel. Although each island is assigned only a portion of all sub-problems in the island model, it preserves a complete population to accomplish the global selection and update. Meanwhile the migration policy directly migrates each elitist individual to an appropriate island in charge of the sub-problem associated with this individual to share essential evolutionary achievements. In addition, a modularity-based greedy local search strategy is also applied to accelerate the convergence rate. Comparative experimental results on six real-world networks reveal that PCACD is capable of discovering potential high-quality community structures at diverse resolutions with satisfactory running efficiencies.

1. Introduction

Complex networks are used to represent many systems in the real world, such as communication networks, social networks, and wireless sensor networks [1,2]. A complex network is made up of nodes and edges, where nodes represent the objects in a system and each edge signifies a relation between a pair of nodes. Actually, a network often comprises a few communities that can be represented as clusters of nodes. In general, the number of edges within communities is much larger than that of the edges between them. Finding community structures by community detection algorithms helps to reveal some important information. For example, people with similar interests are in general in the same community in a social network. Most important of all, community structures could help us understand the functional units of complex networks.

In the area of community detection, most existing algorithms are optimization-based methods, which detect community structures by optimizing objective functions. A well known quality metric called modularity has been proposed by Newman and Girvan [3,4] and widely employed in community detection algorithms. However, a main drawback of optimization-based algorithms using only one objective of modularity is the resolution limit [5,6,7]. In other words, they are in general not able to find multiple potential structures at different resolutions.

Compared with traditional single-objective algorithms [8], multi-objective methods for community detection, which in general optimize two competing objectives of community structures simultaneously, do not require any parameter about the resolution scale [9]. Evolutionary algorithms (EAs), including genetic algorithms [10,11], swarm intelligence algorithms [12,13,14], and cross-entropy methods [15,16], are inspired from natural evolution and adaptation. Owing to their population-based nature, EAs are particularly suitable for solving multi-objective optimization problems (MOPs) and multi-objective evolutionary algorithms (MOEAs) are able to find community structures at different resolutions in one single run. Another advantage of MOEAs for community detection lies in that it is convenient to transform MOEAs into their parallel versions, which usually cost much less running time than their serial counterparts. In consideration of these advantages, it becomes more and more popular to regard community detection as one MOP with two competing objectives [6,7]. Then various MOEAs are customized and applied to solve the MOP of community detection effectively.

In the past several years, a large number of universal MOEAs [16,17] have been proposed. The majority of existing MOEAs are based on Pareto dominance, such as the improved non-dominated sorting genetic algorithm (NSGA-II) [18] and the improved strength Pareto (SPEA-II). As one of the most popular dominance-based MOEAs, NSGA-II has been widely applied in many fields in the past decade. Furthermore, a few dominance-based MOEAs are specially re-designed for community detection, including the multi-objective genetic algorithm for networks (MOGA-Net) [19] and the multi-objective community detection algorithm (MOCD) [20]. Particularly, MOCD is a MOEA based on the strength Pareto evolutionary algorithm-II (SPEA-II) framework for community detection. So far, there has been no efficient approach to non-dominated sorting of an entire population, which results in very high running complexities of dominance-based MOEAs for community detection.

In recent years, efficient decomposition-based MOEAs have become popular, including the MOEA based on decomposition (MOEA/D) [10] and the conical area evolutionary algorithm (CAEA) [21]. In this paper, the community detection is considered as a modularity-based multi-objective optimization problem and a parallel conical area community detection algorithm (PCACD) is presented to further cut down the running time of an efficient MOEA, CAEA, for solving this MOP. PCACD adopts a parallel process-based CAEA on distributed-memory clusters. However, because of the global characteristics of the selection and update mechanisms of CAEA, parallel CAEAs on distributed-memory clusters couldn’t directly utilize the local island model used in parallel MOEA/Ds. Instead, PCACD employs a parallel global island model, targeted elitist migration policy, and modularity-based local search strategy so that satisfactory speedup and community structures at different resolutions are successfully achieved.

The rest of this paper is organized as follows. First, related studies are introduced in Section 2. Then, Section 3 presents the details of our proposed method for community detection including the objective functions, local search, island model, and migration policy. Subsequently, experimental results are supplied and analyzed in Section 4. Finally, Section 5 concludes this paper.

2. Related Work

Up to now, community detection methods have been classified into three types: agglomerative hierarchical methods [22,23,24], divisive hierarchical methods [25,26], and optimization-based methods [8,19,20]. In agglomerative hierarchical methods, each node starts in its own cluster, and then pairs of clusters are merged in a bottom-up recursive manner. In divisive hierarchical methods, all nodes start in one single cluster, and then splits are performed in a top-down recursive manner. In order to determine which clusters should be combined for agglomerative methods, or where a cluster should be split for divisive methods, a measure of dissimilarity between sets of clusters is required for both hierarchical methods. Most of the existing community detection algorithms are optimization-based methods. Unlike both hierarchical methods, optimization-based methods attempt to define objective functions and then directly obtain the best community structure of a network by optimizing objective functions.

To assess the community structures of a network, Newman and Girvan [3,4] have proposed a very popular quality metric called modularity. Furthermore, the modularity metric has been widely employed as the objective function of some traditional optimization-based methods such as the Louvain algorithm for community detection [8]. The Louvain algorithm [8] is just a simple and efficient greedy optimization algorithm based on the single objective of modularity for identifying communities in large networks. It involves two simple steps of maximizing the local modularity and transforming every previously found community to one node of a new network. The procedure of the method repeats these two steps iteratively until the best modularity Q is found. Nevertheless, Fortunato and Barthelemy have pointed out that the optimization-based community detection algorithms using only one single objective of modularity have a primary disadvantage that they are not capable of discovering multiple potential structures at different resolutions [5,6,7]. Hence, various algorithms were proposed to compensate the disadvantage of limited resolution. Most of existing methods need to set a parameter in advance to define the resolution scale. If the end user has some knowledge of resolutions of the detected networks, the resolution parameter allows taking advantage of this information. Nevertheless, in most situations, it is very difficult to acquire the knowledge of resolutions and set in advance appropriate values of the resolution parameter for different networks.

Fortunately, MOEAs are able to find community structures at different resolutions in one single run. The majority of existing MOEAs are based on Pareto dominance. In recent years, decomposition-based MOEAs such as MOEA/D [10,27] and CAEA [11,21] have become popular. With respect to the running cost, MOEA/D [10] has a great advantage over dominance-based MOEAs. MOEA/D decomposes a MOP into a number of scalar objective optimization subproblems so that it does not have to examine non-dominance for a population anymore. Every offspring for a subproblem has to update its T neighbor subproblems locally in MOEA/D. By taking advantage of a conical partition strategy and a conical area indicator, the CAEA was designed to further improve the running efficiency of decomposition-based MOEAs for bi-objective optimization [21]. Unlike in MOEA/D, each offspring for a subproblem needs to update only the closest global subproblem in terms of convergence direction in CAEA rather than its T neighbor subproblems. Hence, for the identical population size and generation number, the proportion of running complexity between CAEA and MOEA/D is $O\left(1\right)$:$O\left(T\right)$, where T represents the number of neighbor subproblems. Although decomposition-based MOEAs improve the running efficiencies of dominance-based MOEAs to a certain extent, with the increase of the size of complex networks, a relatively large number of decision variables proportional to the number of nodes in the network bring them greater challenges. Particularly, the biggest one of them is that the calculation costs of objective functions become computationally fairly expensive for solving multi-objective community detection problems [28]. In order to further cut down the running time of decomposition-based MOEAs for expensive MOPs, several of these algorithms have been redesigned as parallel algorithms by applying parallel and distributed technologies [29]. There exist two main categories of parallel models for MOEAs: master-slave models [30] and island models [31]. The master-slave models parallelize only the objective calculation among the slave nodes. The island models parallelize the entire evolutionary procedure by dividing the large population into multiple separate small sub-populations. Because of the relative independence of the decomposed subproblems, the island models are more suitable for the parallelization of decomposition-based MOEAs than the master-slave model.

In addition, parallel decomposition-based MOEAs could be implemented at two levels: the thread level and process level. A few parallel MOEA/Ds at the thread level have been specially designed for shared-memory multi-processors [32,33]. These thread-based MOEA/Ds preserve all the islands inside the common shared memory physically while each thread evolves a logically separate but physically shared island. Until now, several parallel MOEA/Ds at the process level, such as the overlapped partitioning parallelization of MOEA/D (opMOEA/D) [29,34], have been developed for message-passing clusters with distributed memory. These process-based MOEA/Ds distribute the islands over the compute nodes of a cluster and each process evolves a logically and physically separate island on a compute node. In contrast to thread-based parallel MOEA/Ds, process-based parallel MOEA/Ds have two evident advantages. Not only they avoid race conditions that multiple threads attempt to access the shared memory at the same time, but also they generally offer better scalability for large sizes of computing clusters.

3. Parallel Conical Area Community Detection

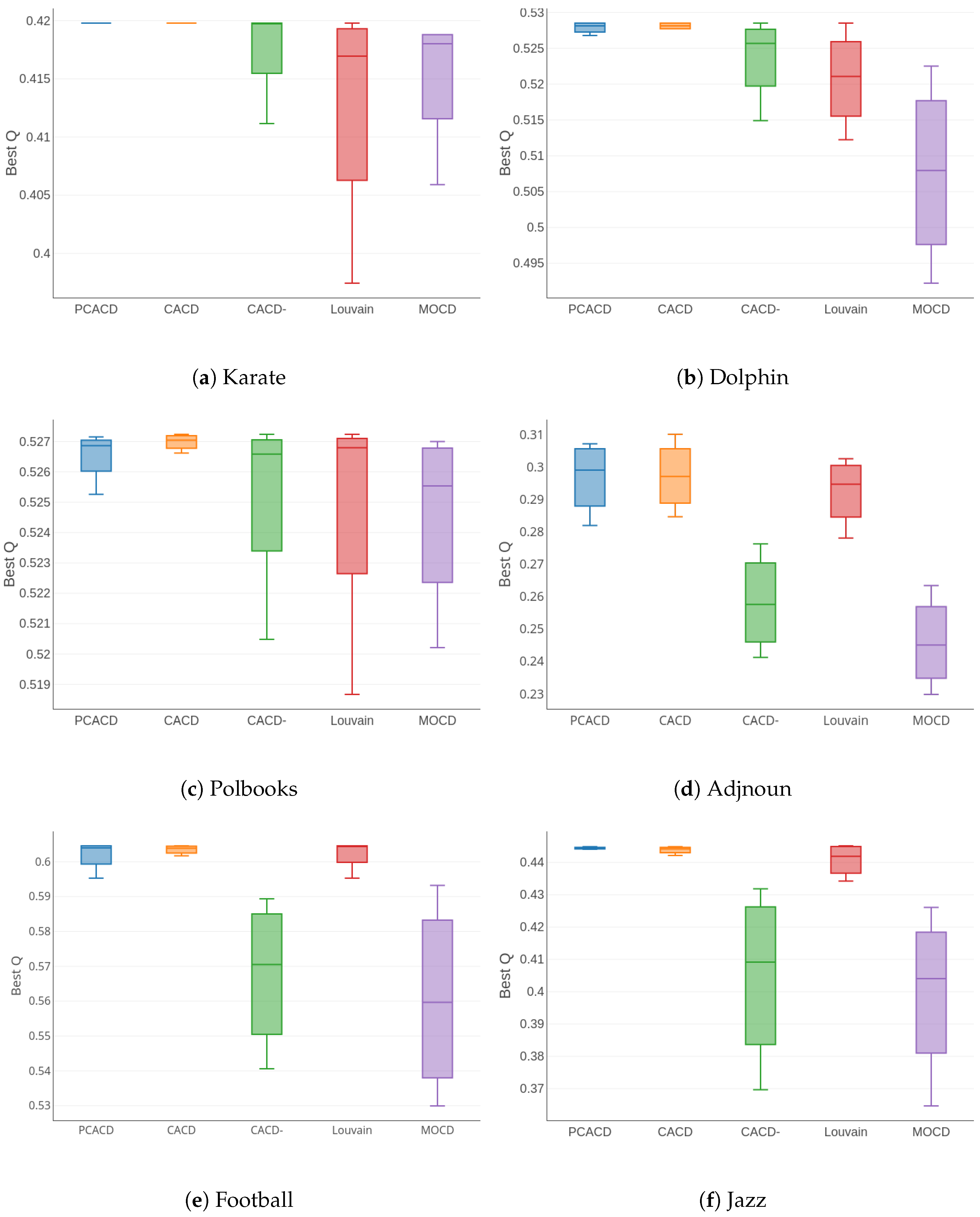
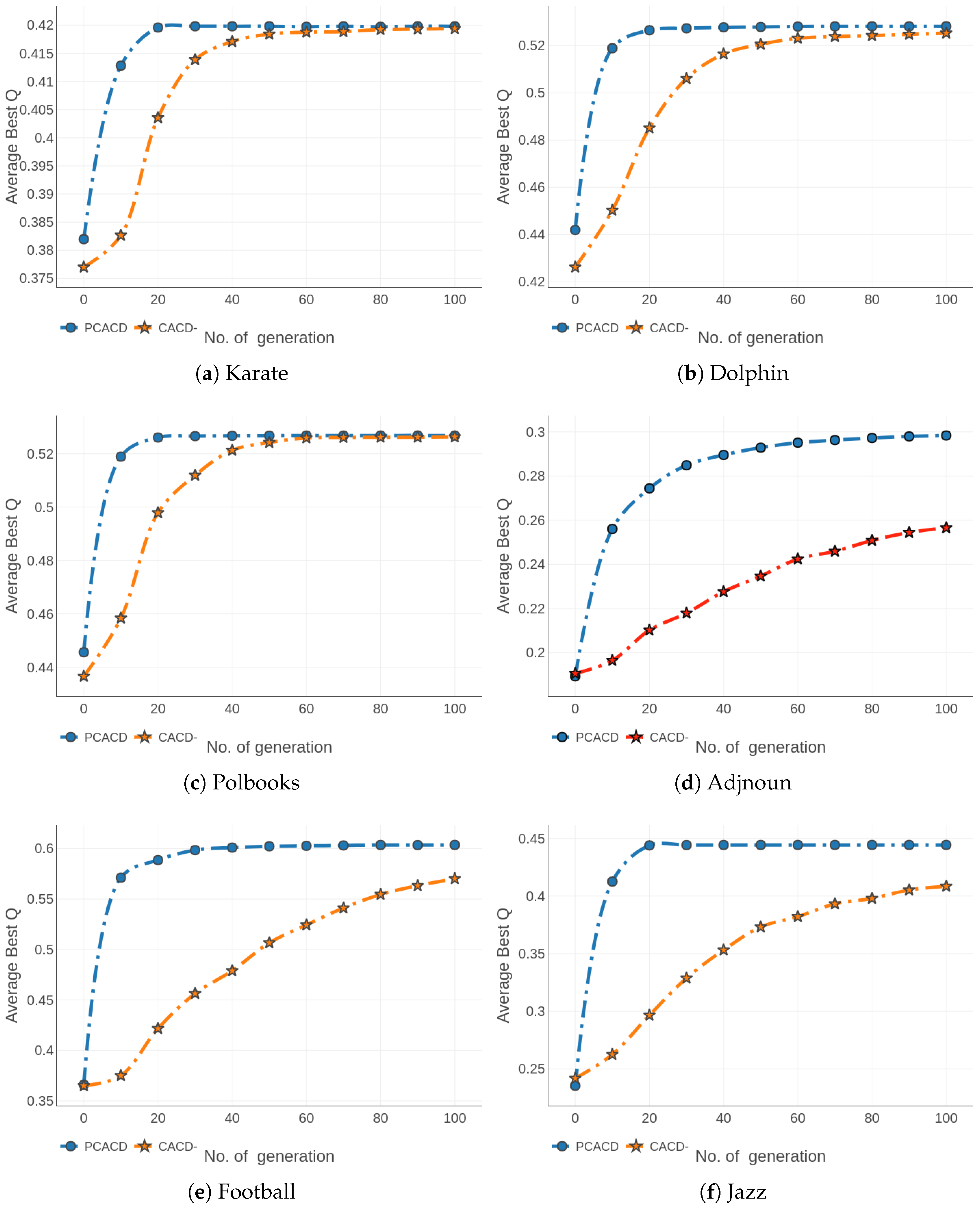
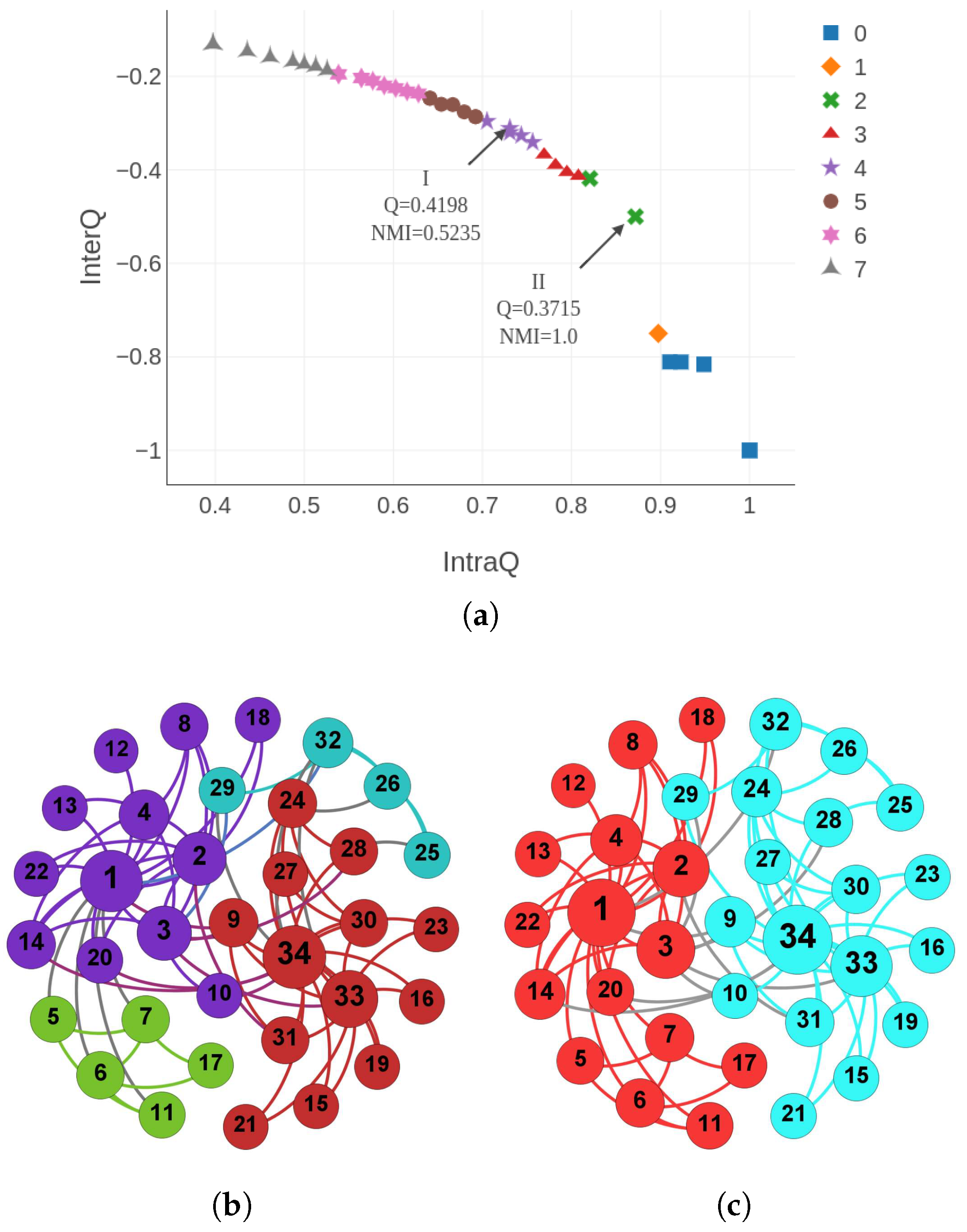
3.1. Chromosome Representation

Since the proposed method, PCACD, employs the framework of an efficient MOEA, CAEA, one of the top issues of PCACD is to determine an appropriate chromosome representation for the community detection problem. PCACD utilized an adjacency-based chromosome [35] to encode a solution, i.e., one community structure of the detected network. The major advantage of the adjacency-based chromosome representation lies in that it is able to conveniently avoid the generation of any invalid chromosome during crossover and mutation. Specifically, every chromosome $P_i$, $i\in [0,N-1]$, in a population has a fixed length of n where n denotes the total number of nodes in the network and N indicates the population size. The value of every gene $P_{ia}$, $a\in [1,n]$, in chromosome $P_i$ ranges from one to n. The gene $P_{ia}$ taking an integer value $b\in [1,n]$ signifies that both nodes, a and b, are classified as belonging to the same community in the community structure decoded from chromosome $P_i$. In consequence, a decoding procedure has to be applied for any adjacency-based chromosome before the evaluation of its objective functions. Figure 1 presents a simple example of an adjacency-based chromosome in the case of $n=6$ and the corresponding community structure decoded from this chromosome where all the nodes within the same connected subgraph were just classified into the same community. Fortunately, with the assistance of the backtracking method, this decoding procedure costs only linear time [35].

3.2. Modularity-Based Objective Functions and Local Search

As an optimization-based multi-objective method, PCACD transforms the community detection into a modularity-based bi-objective optimization problem (BOP) in order to discover potential community structures at different resolutions. The modularity metric, denoted as Q, was proposed by Newman and Girvan [3,4] for the purpose of assessing the quality of a network partition or community structure. It can be represented as

$$Q=\sum _{C\in X}\left[\frac{l_c}{m}-{\left(\frac{k_c}{2m}\right)}^2\right]=\sum _{C\in X}\frac{l_c}{m}-\sum _{C\in X}{\left(\frac{k_c}{2m}\right)}^2$$

(1)

where X denotes a partition or community structure of a network, C represents one of communities in this partition, $l_c$ represents the number of edges in community C, m denotes the total number of edges in this network, and $k_c$ denotes the degree of nodes within community C.

To obtain the largest modularity Q score, we should simultaneously maximize its first part ${\sum }_{C\in X}\frac{l_c}{m}$ and minimize the second part ${\sum }_{C\in X}{\left(\frac{k_c}{2m}\right)}^2$. In short, as the first term increases, the number of edges in the same community increases, which results in the generation of larger communities. In contrast, as the second part decreases, the degree of nodes within the same community declines, which tends to generate smaller communities. Therefore, maximizing modularity means finding an appropriate trade-off between these two potentially competing terms. As a consequence, these two terms of the modularity are often separated in order to avoid the resolution limit disadvantage of modularity-based single objective optimization methods [5]. Similarily, PCACD applies both of them as two competing objection functions to be optimized. Specifically, PCACD considers the community detection problem as the following modularity-based BOP to simultaneously maximize two objective functions, i.e., $IntraQ\left(X\right)={\sum }_{C\in X}\frac{l_c}{m}$ and $InterQ\left(X\right)=-{\sum }_{C\in X}{\left(\frac{k_c}{2m}\right)}^2$.

$$\begin{array}{ll}\mathrm{minimize}\hfill & F\left(X\right)=\left(IntraQ\right(X),InterQ(X\left)\right),\hfill \\ \mathrm{subject}\mathrm{to}\hfill & X\in \mathsf{\Omega }.\hfill \end{array}$$

(2)

In general, it is a little difficult for EAs to approach the local optimum partitions quickly only through their own crossover and mutation operators. Since PCACD aims to optimize the above modularity-based bi-objective community detection problem, a modularity-based greedy local search strategy is further applied to every generated offspring to accelerate the search process of PCACD with the aid of the heuristic tricks about community detection. To be specific, this local search strategy for each offspring consists of k loops of greedy merging operations, where k is set to one quarter of the total number n of the network’s nodes. In every loop of greedy merging operation, the local search strategy first chooses one node a from all the nodes of the network randomly. Then node a tries to move into the communities of its adjacent nodes one by one for the current chromosome $P_i$ and the best adjacent one $b^{☆}$ is picked such that the resulting community structure could reach the local highest modularity score. Thereafter, the gene $P_{ia}$ at locus a is assigned just the gene value $P_{i{b}^{☆}}$ at locus $b^{☆}$ for chromosome $P_i$. It signifies that the chosen node a is greedily merged into the community of its local best adjacent one $b^{☆}$.

3.3. Parallel Global Island Model

The proposed algorithm, PCACD, utilizes the framework of an efficient bi-objective optimization algorithm, CAEA, to solve the above bi-objective community detection problem. It means that the bi-objective community detection problem is decomposed into N scalar optimization subproblems. Moreover, to find a local nondominated solution in the corresponding decision subset ${\mathsf{\Omega }}^{\left(k\right)}$, each subproblem employs a conical area as its scalar objective [21]. In PCACD, each subproblem is associated with one individual in the current population and is responsible for searching for the best solution in its exclusive decision subset ${\mathsf{\Omega }}^{\left(k\right)}$ in terms of its conical area indicator.

In order to further reduce the running time of solving the bi-objective community detection problem, PCACD requires an island model to parallelize the CAEA. In general, parallel MOEA/Ds such as opMOEA/D [29] employ some local island models since a generated offspring for a subproblem needs to update only the neighbors of this subproblem locally in MOEA/D. In contrast, all the individuals in the population are essential for the global update mechanism in CAEA where a produced offspring globally chooses and updates one out of all the subproblems according to the direction of convergence. It results in the local island models for parallel MOEA/Ds not being suitable for parallel CAEAs radically.

Hence, PCACD employed a global island model to solve the bi-objective community detection problem in parallel. In this parallel island model, each island maintains an entire population in order to globally update subproblems in CAEA while it is in charge of the optimization of only a portion of the subproblems. In the initialization procedure, all subproblems are linearly partitioned into q groups where q denotes the number of parallel islands. Thereafter, each island is assigned an evolutionary task for one group out of them. That is, the size of the r-th group $P^{\left(r\right)}$, $r\in [0,q-1]$, equals

$$N^{\left(r\right)}=\left\{\begin{array}{cc}N/q+1,\hfill & \mathrm{if}r<N\%q,\hfill \\ N/q,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(3)

In the above equation, / and % denote the integer division and modulus operations respectively.

Formally, the k-th subproblem associated with the k-th reference direction or observation vector ${\lambda }^k$ in CAEA, denoted as $g\left(X\right|{\lambda }^k,{\mathbf{z}}^{*})$, employs the conical area [21] as its scalar objective in the form

$$\begin{array}{l}\mathrm{minimize}g\left(X\right|{\lambda }^k,{\mathbf{z}}^{*})=S(F\left(X\right)-{\mathbf{z}}^{*},{\mathbf{C}}^k),\hfill \\ \mathrm{subject}\mathrm{to}X\in \mathsf{\Omega }andF\left(X\right)-{\mathbf{z}}^{*}\in {\mathbf{C}}^k.\hfill \end{array}$$

(4)

In the above equation, X represents a community structure of the network, $F\left(X\right)$ denotes the objective vector consisting of IntraQ(X) and InterQ(X), ${\mathbf{C}}^k$ indicates the conical subregion associated with reference direction ${\lambda }^k$, $0\le k\le$$N-1$, ${\mathbf{z}}^{*}=(\underset{X\in \mathsf{\Omega }}{\min }\left\{IntraQ\left(X\right)\right\},\underset{X\in \mathsf{\Omega }}{\min }\left\{InterQ\left(X\right)\right\})$ represents the true ideal point for the given bi-objective community detection problem, and function $S(F\left(X\right)-{\mathbf{z}}^{*},{\mathbf{C}}^k)$ denotes the conical area of the portion not dominated by the first input vector, $F\left(X\right)-{\mathbf{z}}^r$, in the conical sub-region ${\mathbf{C}}^k$ [21]. It is worth noticing that, in practice, the true ideal point ${\mathbf{z}}^{*}$ should be replaced with the current attainable ideal point on the r-th island, written as ${\mathbf{z}}^r$, since ${\mathbf{z}}^{*}$ would be in general unknown and unavailable to PCACD.

According to the parallel island model, although the r-th island globally preserves all N solutions associated, respectively, with N sub-problems, the r-th island is assigned the optimization task of only the r-th group of sub-problems, $G^{\left\{r\right\}}=\left\{g\left(X\right|{\lambda }^k,{\mathbf{z}}^{*})\right|k\in N^{\left\{r\right\}}\}$, where $N^{\left\{r\right\}}=\{r{N}^{\left(r\right)}$, $r{N}^{\left(r\right)}+1$, ⋯, $(r+1)N^{\left(r\right)}-1\}$ if $r<N\%q$ and $N^{\left\{r\right\}}=\{r{N}^{\left(r\right)}+N\%q$, $r{N}^{\left(r\right)}+N\%q+1$, ⋯, $(r+1)N^{\left(r\right)}+N\%q-1\}$ otherwise. It signifies that, during the reproduction of each offspring on the r-th island, the first parent is bound to be one out of the current individuals associated with the r-th group of sub-problems $G^{\left\{r\right\}}$. The role of the other groups of sub-problems, $G^{\left\{j\right\}}$, $j\ne r$, on the r-th island is just to help this island to globally select the second parent and complete the global update process for each offspring.

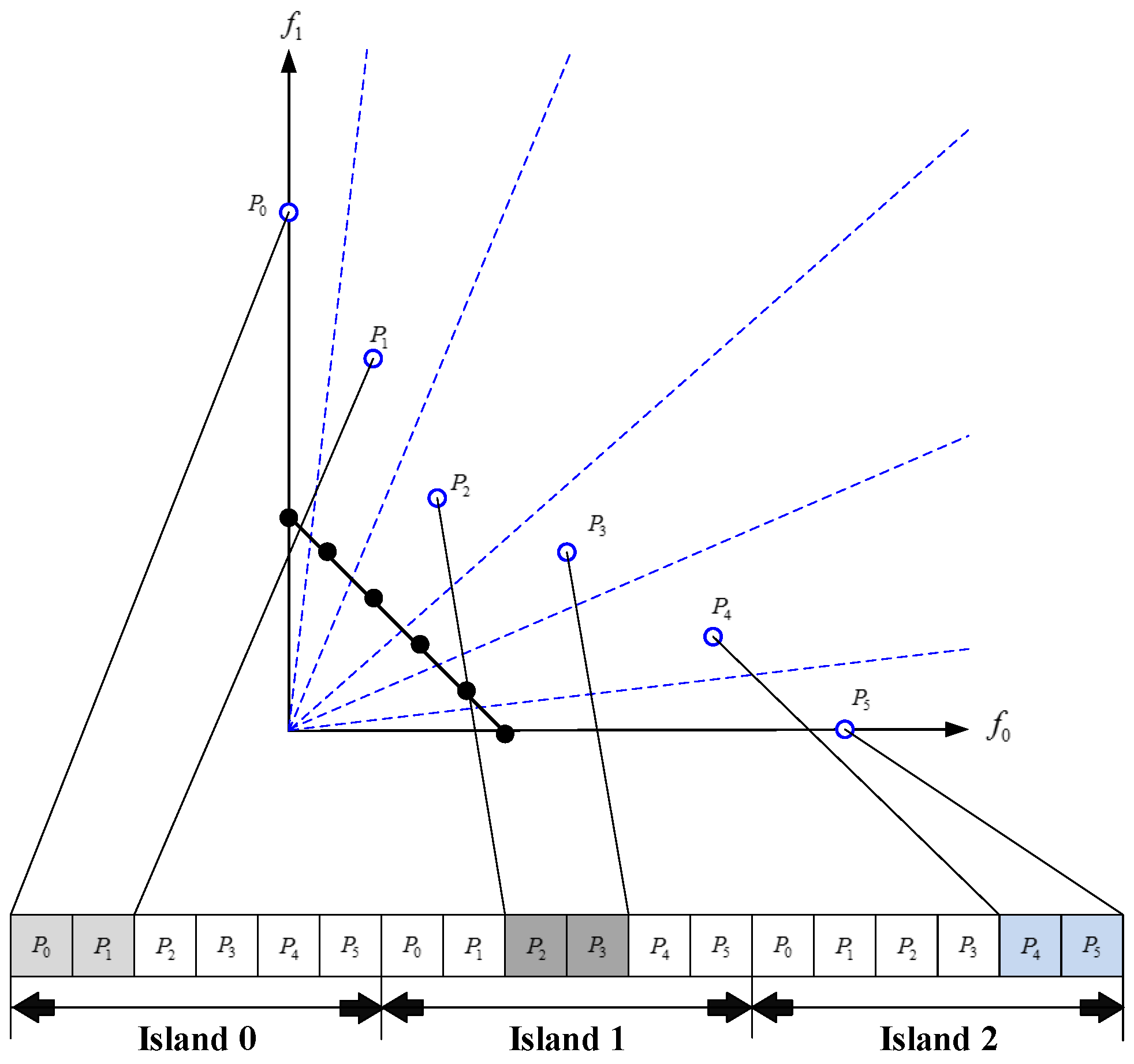
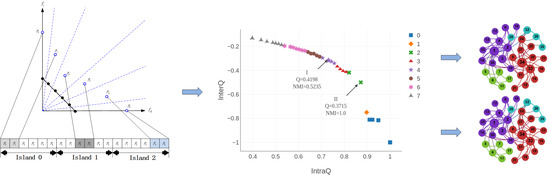
Figure 2 illustrates a simple example of the parallel global island model in case of $q=3$ and $N=6$. From the perspective of the objective space, the r-th island, $r\in \{0,1,2\}$, is actually responsible for optimizing $N^{\left(r\right)}=2$ sub-problems, $g\left(X\right|{\lambda }^{2r},{\mathbf{z}}^{*})$ and $g\left(X\right|{\lambda }^{2r+1},{\mathbf{z}}^{*})$, by evolving their respective associated individuals, $P_{2r}$ and $P_{2r+1}$, to approach the r-th fragment of Pareto front. In the meantime, the r-th island has to maintain an entire population of size $N=6$ in order to perform the global selection and update mechanisms of CAEA. This parallel island model is capable of helping PCACD to reduce the run time of its serial counterpart for community detection.

3.4. Targeted Elitist Migration

At the same time that the parallel global island model was employed for good speed-ups, an appropriate migration policy had to be utilized to share essential evolutionary achievements among islands so that the qualities of community structures obtained by PCACD do not degrade substantially. The migration policy has two crucial issues: the selection of migrants and migration topology. In a parallel MOEA/D, opMOEA/D [29], a local hybrid migration policy was used to shares both ideal points and elitist solutions in a local migration topology where all migrants on one island locally emigrate to one of only two islands linearly adjacent to it. However, as a parallel CAEA for the bi-objective community detection problem, PCACD adopted a targeted elitist migration policy on the account of the evident differences between the selection and update mechanisms of CAEA and MOEA/D.

To be specific, MOEA/D locally selected a pair of parent solutions associated with two neighbor sub-problems during reproduction. Since this pair of parent solutions were often very similar to each other, their offspring was also similar to them in general. Hence, this local selection mechanism of MOEA/D posed a great difficulty that one separate island could not achieve a satisfactory ideal point only on its own evolution in any parallel MOEA/D. Consequently, a better ideal point was very critical to every island in a parallel MOEA/D since it helped the island to explore an evidently wider front segment.

In contrast, CAEA globally chose the parents from the entire population rather than only from the neighbors. Hence, a new offspring reproduced had the chance to globally update one of all the individuals in the whole population. As a result, migration of ideal points was unnecessary to PCACD because the ideal point resulting from one island was generally capable of meeting the evolutionary requirements of this island. In consideration of the global property of the selection mechanism in CAEA, only elitist individuals were considered as migrants in PCACD. That is, once the individual associated with a sub-problem was successfully replaced at the last generation on the r-th island, a copy of the elitist individual replacing it would be transmitted to another certain island according to the migration topology in PCACD.

Apart from the selection of migrants, the migration topology also had a significant impact on the extent to which the migration accelerated the parallel evolutionary progress. Instead of locally updating several neighbor sub-problems in MOEA/D, one offspring needed to update one global sub-problem in accordance with the convergence direction in CAEA and PCACD. Hence it would be of great benefit to the further optimization of one successfully updated sub-problem in PCACD to directly migrate an elitist individual to the appropriate island, rather than simply to two linearly adjacent islands as the same as in opMOEA/CD. In consideration of this, a targeted migration topology was specially designed in PCACD to achieve the fast and accurate sharing of essential evolutionary achievements among islands. In light of the global island model, the optimization of the k-th sub-problem in PCACD, $0\le k\le N-1$, belongs to the $r^{\prime }$-th group and it is actually in the charge of the $r^{\prime }$-th island where $r^{\prime }=k/(\frac{N}{q}+1)$ if $k<N\%q(\frac{N}{q}+1)$, otherwise $r^{\prime }=N\%q+[k-N\%q(\frac{N}{q}+1)]/\frac{N}{q}$. Once the k-th sub-problem was successfully updated by a generated offspring on one island, the individual $P_k$ currently associated with this sub-problem, i.e., a copy of the offspring, would be regarded as an elitist one and it would migrate to the $r^{\prime }$-th island in accordance with this targeted migration topology.

Algorithm 1 presents the implementation procedure of the targeted elitist migration policy on the r-th island. It consists of two phases; (1) transmitting elitist individuals to other islands in Lines 1 to 10 and (2) receiving elitist individuals from other islands in Lines 11 to 18. In the first phase, it was determined whether the current k-th individual $P_k$ associated with the k-th subproblem $g\left(X\right|{\lambda }^k,{\mathbf{z}}^r)$ was an elitist individual in Line 2. If this is the case, the index $r^{\prime }$ of the destination island was figured out according to the targeted migration topology in Lines 3 to 7. Thereafter, as an elitist individual, a copy of the current individual $P_k$ associated with the k-th subproblem on this island was transmitted to the corresponding destination, i.e., the receive queue ${\beta }_{r^{\prime }}$ of elitist individuals on the $r^{\prime }$-th island in Line 8.

Algorithm 1TargetedElitistMigration(r)

1: for$k=0$to$N-1$do  2:     if the k-th sub-problem $g\left(X\right|{\lambda }^k,{\mathbf{z}}^r)$ was successfully updated at the last generation then  3:         if $k<N\%q(\frac{N}{q}+1)$ then  4:            $r^{\prime }\leftarrow$$k/(\frac{N}{q}+1)$;  5:         else  6:            $r^{\prime }\leftarrow$$N\%q+[k-N\%q(\frac{N}{q}+1)]/\frac{N}{q}$;   7:         end if 8:         Transmit a copy of the elitist individual $P_k$ to the receive queue ${\beta }_{r^{\prime }}$ of the $r^{\prime }$-th island;  9:     end if  10: end for  11: while the receive queue ${\beta }_r\ne \varnothing$ do  12:     Receive the first immigrator $X^{\prime }$ from queue ${\beta }_r$;  13:     $k^{\prime }\leftarrow floor(\frac{(N-1)(IntraQ\left(X^{\prime }\right)-{\mathrm{z}}_1^r)}{IntraQ\left(X^{\prime }\right)-{\mathrm{z}}_1^r+InterQ\left(X^{\prime }\right)-{\mathrm{z}}_2^r}+0.5)$;  14:     if $S(F\left(X^{\prime }\right)-{\mathbf{z}}^r,{\mathbf{C}}^{k^{\prime }})$ < $S(F\left(P_{k^{\prime }}\right)-{\mathbf{z}}^r,{\mathbf{C}}^{k^{\prime }})$ then  15:         $P_{k^{\prime }}\leftarrow$$X^{\prime }$;  16:     end if  17:     Delete $X^{\prime }$ from queue ${\beta }_r$;  18: end while

In the second phase, every immigrator $X^{\prime }$ from the other islands, i.e., every solution in the receive queue ${\beta }_r$ of elitist individuals on the r-th island, was utilized to update one subproblem on this island in a similar manner to one offspring in CAEA. To be specific, according to the definition of conical sub-problems in CAEA, the index $k^{\prime }$ of the sub-problem with which the immigrator $X^{\prime }$ should be associated was first figured out on this island by $k^{\prime }=floor(\frac{(N-1)(IntraQ\left(X^{\prime }\right)-{\mathrm{z}}_1^r)}{IntraQ\left(X^{\prime }\right)-z_{\mathrm{1}}^r+InterQ\left(X^{\prime }\right)-{\mathrm{z}}_2^r}+0.5)$ where $floor(·)$ indicates the bottom integral function in Line 13. Subsequently, if this immigrator $X^{\prime }$ was superior to the current individual $P_{k^{\prime }}$ associated with this sub-problem in terms of their respective conical area values, $S(F\left(X^{\prime }\right)-{\mathbf{z}}^r,{\mathbf{C}}^{k^{\prime }})$ and $S(F\left(P_{k^{\prime }}\right)-{\mathbf{z}}^r,{\mathbf{C}}^{k^{\prime }})$, the individual $P_{k^{\prime }}$ was replaced by this immigrator $X^{\prime }$ on this island in Lines 14 to 16. Then this immigrator was deleted from the queue of immigrators in Line 17. This operation was repeated until the queue of immigrators becomes empty in Line 11.

3.5. Framework of PCACD

The main framework of PCACD is presented in Algorithm 2. Each island or process is initialized on one processor in Lines 2 to 5. In Line 2, the r-th island generates N evenly distributed reference directions ${\lambda }^k$, $k=0,1,\cdots ,N-1$, for N sub-problems. Then, the r-th island divided all sub-problems linearly into q groups and calculated the size $N^{\left(r\right)}$ of the r-th group according to Equation (3) in Line 3. Meanwhile the r-th island was only assigned the optimization task of the r-th group of $N^{\left(r\right)}$ sub-problems, $G^{\left\{r\right\}}$. In Line 4, this island randomly initialized N individuals to form its whole population $P^{\left(r\right)}$ and associates them with N reference directions in terms of the directions and the conical area values in the same manner as CAEA. During the initialization of the population, each gene $P_{ia}$ of each initial individual was randomly assigned the index of one of its adjacent nodes and the adjacency-based chromosome representation avoided the generation of invalid community structures. Subsequently, these initial individuals in $P^{\left(r\right)}$ were utilized to update the local ideal point ${\mathbf{z}}^r$ on the r-th island in Line 5.

Algorithm 2 The main procedure of parallel conical area community detection algorithm (PCACD).

1: for each$r\in [0,q-1]$in parallel do        ▹ parallel q islands or processes  2:     Generate N evenly distributed reference directions ${\lambda }^k$, $k=0,1,\cdots ,N-1$;  3:     Divide all N sub-problems linearly into q groups, calculate the size $N^{\left(r\right)}$ of the r-th group, and assign the r-th island the optimization task of the r-th group of $N^{\left(r\right)}$ sub-problems, $G^{\left\{r\right\}}$;  4:     Initialize N individuals randomly to form its whole population $P^{\left(r\right)}$, evaluate them, and associate them with N reference directions in the same manner as CAEA;  5:     Utilize the initial individuals in $P^{\left(r\right)}$ to update the local ideal point ${\mathbf{z}}^r$ on the r-th island;  6:     $n_g\leftarrow 0$;  7:     while $n_g<N_g$ do        ▹ evolutionary loops  8:         for $i=0$ to $N^{\left(r\right)}-1$ do  9:            $parent1\leftarrow$ ParentSelection1(r);  10:            $parent2\leftarrow$ ParentSelection2(r);  11:            $child\leftarrow$ Reproduction($parent1$, $parent2$);  12:            $child\leftarrow$ LocalSearch($child$);  13:            ${\mathbf{z}}^r\leftarrow$ IdealPointUpdate($child$, ${\mathbf{z}}^r$);  14:            SubProblemUpdate($child$, r);  15:         end for  16:         TargetedElitistMigration(r);       ▹ targeted elitist migration  17:         $n_g\leftarrow n_g+1$;  18:     end while  19:     Synchronize with the root island and transmit all the individuals associated with the r-th group of sub-problems to the root island;  20:     if $r==0$ then        ▹ the 0-th island  21:         The root island gathers all the individuals associated with q groups of sub-problems from q islands and integrates them into a final entire population P;  22:     end if  23: end for

In Line 7, the r-th island will repeat the evolutionary loop if the current number $n_g$ of generations does not reach the maximum number $N_g$ of generations. Lines 8 to 15 represent one generation of evolution, and include important evolutionary operators such as selection, production, local search, and update. Note that function ParentSelection1(r) in Line 9 chooses the first parent individual, $parent1$, only from the current individuals associated with the r-th group of sub-problems $G^{\left\{r\right\}}$ on the r-th island for the reproduction of each offspring in accordance with the tournament selection based on the conical area. Function ParentSelection2(r) in Line 10 chooses the second parent individual globally, $parent2$, from the entire population on the r-th island in the same manner as CAEA. Subsequently, Reproduction($parent1$, $parent2$) generates an offspring $child$ from parents $parent1$ and $parent2$ through crossover and mutation in Line 11. Because it is preferable to maintain the effective connection components of the detected network during crossover, a two-point crossover rather than a uniform crossover is adopted in PCACD. The mutation operator randomly chooses several genes of an individual in terms of the mutation probability and then assigns each of them the index of the one randomly selected from its corresponding adjacent nodes. Next, LocalSearch($child$) applies the modularity-based greedy local search strategy to the offspring $child$ to accelerate the search in Line 12. Thereafter, function IdealPointUpdate($child$, ${\mathbf{z}}^r$) evaluates the offspring $child$ and utilizes it to update the local ideal point ${\mathbf{z}}^r$ on the r-th island in Line 13. At the end of one generation of evolution, SubProblemUpdate($child$, r) in Line 14 associates the offspring $child$ with the nearest sub-problem on the r-th island in accordance with the convergence direction and updates this sub-problem in terms of the conical area value in the same manner as CAEA.

After one generation of evolution, TargetedElitistMigration(r) presented in Algorithm 1 is called to transmit elitist solutions to other islands and receive elitist solutions from other islands in accordance with the targeted elitist migration policy in Line 16. When the entire evolution terminates, the r-th island synchronizes with the root island, i.e., the 0-th island, and transmits all the individuals associated with the r-th group of sub-problems to the root island in Line 19. Finally, the root process gathers all the individuals associated with q groups of sub-problems from q islands and integrates them into a final entire population P in Line 21.

3.6. Computational Complexity

The fitness evaluation and the local search were the most time-consuming operations for every parallel island of PCACD. Specifically, the fitness evaluation of an adjacency-based chromosome consisted of the backtracking-based decoding and the calculation of two objectives, $InterQ\left(X\right)$ and $IntraQ\left(X\right)$. Suppose that the detected network contained n nodes and m edges. The backtracking-based decoding and the calculation of objectives have complexities $O\left(n\right)$ and $O\left(m\right)$, respectively. Therefore, the complexity of the fitness evaluation of a chromosome is $O(m+n)$. Because $N_g$ generations of evolution were performed and in total about $\frac{1}{q}N$ chromosomes were generated and evaluated during every generation on every parallel island of PCACD, the complexity of every PCACD process without the local search strategy is $O\left(\frac{1}{q}{N}_{g}N(m+n)\right)$, where $N_g$ denoted the allowed maximum number of generations and N indicates the population size.

As mentioned earlier, the modularity-based local search strategy included $\frac{1}{4}n$ loops and every loop on average needed D fitness evaluations where $D=\frac{2m}{n}$ denotes the mean of degrees of all the nodes in the detected network. As a consequence, the computational complexity of the local search strategy was $O\left(nD\right(m+n\left)\right)=O\left(m\right(m+n\left)\right)$. Hence, every PCACD process including the local search strategy had the total complexity of $O\left(\frac{1}{q}{N}_{g}Nm(m+n)\right)$.

4. Experimental Results

In our experiments, PCACD was utilized to detect the community structures of some real-world networks. To illustrate the performances of PCACD at discovering community structures, four other community detection algorithms, i.e., the single objective Louvain algorithm [8], the multi-objective community detection algorithm (MOCD) [20], the serial version without the parallel global island model and the targeted elitist migration policy of PCACD, referred to as CACD, and a variant without the local search strategy of CACD, written as CACD-, were chosen for comparison with PCACD in our experiments. We applied these algorithms to detect six real-world networks in our experiments.

Table 1. Six detected real-world networks.

Name	Nodes	Edges	Average Degree	True Community Structure
Karate	34	78	4.588	Known
Dolphin	62	159	9.450	Known
Polbook	105	441	8.400	Known
Adjnoun	112	425	7.589	Unknown
Football	115	613	10.66	Known
Jazz	198	2742	27.70	Unknown

indicates the number of nodes, the number of edges, the average degree of nodes, and whether so far the true community structure has been known for each of these six real-world networks. Zachary’s karate club network [36] is a famous friendship network between members of a karate club at a US university, studied from 1970 to 1972. It is a small network including 34 members. The dolphin social network [37] is a social network of dolphins observed by Lusseau over a period of years. This network has 62 nodes and 159 edges, where the nodes represent dolphins while the edges indicate frequent communications between dolphins. The political book network [4] is a network about the American politics books published during the 2004 presidential election and sold by Amazon.com. The word adjacency network [38] denotes a network of common adjective and noun adjacencies for the novel David Copperfield by Charles Dickens, as described by Newman. The American college football network [25] is a complex social network based on the American University Football League, consisting of 115 nodes and 616 edges, with the nodes indicating the football teams and the edges representing whether there had been a match between these two teams. The jazz musician network [39] is a social network about the collaboration of jazz musicians. In this paper, these six real-world networks are referred to as Karate, Dolphin, Polbook, Adjnoun, Football, and Jazz, respectively.

For the sake of fairness, the common parameters of four MOEA-based algorithms, i.e., MOCD, PCACD, CACD, CACD-, were set to the same values. Specifically, the size N of the population was set to 100 and the maximum number $N_g$ of generations was 100. Meanwhile, the crossover probability $p_c$ and the mutation probability $p_m$ were set as 0.8 and 0.1, respectively. In addition, the probability $p_l$ of local search was unity for PCACD and CACD, which signified the modularity-based local search strategy was absolutely performed for each offspring. All the computing nodes were connected by Gigabit Ethernet and each of them was equipped with an Intel Core I5 3.20 GHz CPU and a memory size of 8 GB RAM in our experiments. In PCACD, each island was implemented by launching a corresponding process on an exclusive computing node. Unless otherwise stated, the total number q of processes launched in PCACD was set to 8. All these algorithms were implemented in C++ and the message passing interface (MPI) was additionally adopted to implement the communications between the parallel PCACD processes.

As suggested by Zhang and Li [10], Ying et al. [21], and Gong et al. [6], totally 30 runs of each algorithm have been conducted independently for each of the six networks in our experiments. To measure the effectiveness, the modularity Q was first used to assess the qualities of community structures obtained by five algorithms and then another metric, the normalized mutual information (NMI) [40], was adopted to reveal the capability of discovering potential community structures at different resolutions in our experiments. As for the efficiency, in addition to CPU time, we used the speedup metric to evaluate the parallel performance of the PCACD algorithm.

4.1. Qualities of Obtained Community Structures

With respect to the qualities of obtained community structures, Figure 3 presents the box plots of the best Q scores over 30 runs of each of five algorithms for six real-world networks, where the “best” denotes the highest one out of the Q scores of all obtained community structures in the final population in each run. From Figure 3, it is obviously observed that PCACD and its serial counterpart, CACD, achieved the distinctly higher qualities of community structures in terms of the modularity Q than the other three algorithms, i.e., CACD-, Louvain, and MOCD, for nearly all six networks. Figure 3 also clearly reveals that PCACD and CACD perform relatively more stably than Louvain for three networks such as Karate, Dolphin and Polbook, and so they do than MOCD and CACD- for all six networks. Particularly, in comparison with CACD, PCACD exhibits very similar overall results for networks Karate, Dolphin and Adjnoun, slightly less stable performances for networks Polbooks and Football, and slightly more stable performances for network Jazz. It signifies that, with the effective aids of the parallel global island model and targeted elitist migration policy, both eight parallel processes of PCACD and its serial counterpart, CACD, gain the nearly same satisfactory results in terms of the modularity.

Moreover, Figure 4 plots the convergence curves of average best Q scores over 30 runs of each of PCACD and CACD- for six real-world networks mentioned above, respectively, where the “best” denotes the highest one out of the Q scores of solutions in the current generation of population. It is evident from Figure 4 that the convergence speeds of PCACD are much better than those of CACD- for all six networks. Meanwhile, it is also inferred from Figure 3 that the Q scores achieved by CACD- and MOCD are also evidently worse than those by Louvain for three networks such as Karate, Dolphin and Polbook. Like CACD-, there was no local search strategy in MOCD. It implies that the modularity-based local search strategy also played an important role in community detection and helped to accelerate the convergence speed of PCACD.

4.2. Potential Community Structures at Diverse Resolutions

As a single objective optimization algorithm for community detection, the Louvain method is in general only able to output one community structure. In consequence, it has a limited capability to find potential community structures at diverse resolutions. Instead, as a MOEA, PCACD is capable to generate a cluster of non-dominated solutions in one single run. We can discover some other interesting community structures, apart from the community structure with the best Q score, from the set of non-dominated solutions at different resolutions achieved by PCACD. For presentational convenience, we take the Karate network whose true community structure has been known as an example in this subsection. Figure 5a plots the non-dominated front discovered by eight islands or processes of PCACD in the run with the median best Q score. In Figure 5a, the non-dominated solutions acquired by different PCACD processes are grouped by different shapes.

In addition to the modularity Q, we also employ the NMI metric to assess the qualities of obtained community structures. Specifically, the solution with the highest Q score and the one with the highest NMI score are marked as ‘I’ and ‘II’, respectively, in the final non-dominated front achieved by PCACD in Figure 5a. Different from the modularity Q, the NMI metric only makes sense for networks whose true community structures are known, since this metric needs to calculate the similarity between the ground truth community structure and any obtained one. The NMI value always falls in the range of [0, 1], and a larger NMI value indicates that these two community structures are more similar. In short, given the ground truth community structure $p^{*}$ and an obtained one $p^{\prime }$ for the detected network, if the NMI value of $p^{\prime }$, written as $NMI\left(p^{\prime }\right|p^{*})$, reach one, this implies that $p^{\prime }=p^{*}$. On the contrary, if these two community structures are completely different, then $NMI\left(p^{\prime }\right|p^{*})=0$.

Figure 5a also shows that solution “II” has the highest NMI score of 1.0 and the Q score of 0.3715 while solution “I” has the highest Q score of 0.4198 and the NMI score of 0.5235. Moreover, Figure 5b,c illustrate the community structures corresponding to solutions ‘I’ and ‘II’, respectively. It’s worth noting that the NMI score of 1.0 signifies that solution ‘II’ is exactly the same as the true community structure of the Karate network. From the obtained results for the Karate network, it can be inferred that the acquired community structure with the highest Q score is often different from the one with the highest NMI score. In fact, there is no necessary causal relationship between these two metrics. Moreover, it is impossible for the NMI metric to serve as a special optimization objective for any community detection algorithm since the calculation of NMI requires the true community structure $p^{*}$. Even so, a series of community structures in the uniformly distributed population of PCACD along the Pareto front in the bi-objective space are at diverse resolutions and beneficial to yield the potential true community structure with the highest NMI score through simultaneously maximizing two objective functions of IntraQ and InterQ. For example, solutions ‘I’ and ‘II’ just correspond to a high resolution and a low resolution, respectively, where each large community in solution ‘II’ substantially consists of two small communities in solution ‘I’, as shown in Figure 5b,c. Similarly, there might be still some other community structures at diverse resolutions in the front, which could help us reveal other interesting potential functional units of a complex network.

4.3. Running Time

With regard to the running cost,

Table 2. The CPU time (s) spent by each algorithm for six real-world networks (PCACD: parallel conical area community detection algorithm; CACD: conical area community detection algorithm; CACD-: conical area community detection algorithm variant without the local search strategy; MOCD: multi-objective community detection algorithm).

Network	PCACD	CACD	CACD-	Louvain	MOCD
Karate	17.86	102.36	67.10	0.18	184.14
Dolphin	29.83	164.06	94.32	0.26	299.28
Polbook	56.68	282.26	137.80	0.38	512.87
Adjnoun	51.09	311.70	135.44	0.53	501.90
Football	96.74	522.43	254.00	0.41	558.25
Jazz	144.88	970.70	277.13	0.87	1099.54

records the CPU time in seconds spent by each algorithm for six real-world networks. Figure 6 presents the speedup curves achieved by PCACD as the number p of parallel processes increases from one to eight for all six networks. It is evident from Table 2 that the Louvain algorithm spent far less running time than the other four algorithms based on MOEAs due to the characteristic of single objective greedy optimization. However, as mentioned earlier, since the Louvain algorithm only obtains one community structure generally, it is not good at discovering useful potential community structures at diverse resolutions. As for the algorithms using multi-objective optimization, it is obvious from Table 2 that CACD- runs faster than MOCD for all the six networks. It is in accordance with the fact that the computational complexity of CACD-, $O\left(N_{g}N(m+n)\right)$, is much lower than that of MOCD, $O\left(N_g{N}^2(m+n)\right)$ [20]. CACD has the computational complexity of $O\left(N_{g}Nm(m+n)\right)$ and takes about double the CPU time compared to CACD-, because of its local search strategy. Even so, CACD not only achieves the obviously better qualities of community structures, but also takes slightly less time than MOCD for these networks.

Ulteriorly, Figure 6 clearly indicates that, owing to the parallel global island model and targeted elitist migration policy, the speedups acquired by PCACD grow approximately in a line with the increase of the number p of parallel processes for all six networks in our experiments. Specifically, in the case of 8 parallel processes, PCACD achieves the speedups of around 7.0 and 5.0, respectively, for networks Jazz and Polbook. For the rest four networks, PCACD also gains the speedups of about 6.0. Moreover, it can be inferred from Table 2 that PCACD with 8 parallel processes performs the fastest among four algorithms using multi-objective optimization and spends much less CPU time than CACD, because of the low computational complexity, $O\left(\frac{1}{q}{N}_{g}Nm(m+n)\right)$, of every PCACD process.

5. Conclusions

In this paper, community detection is treated as a modularity-based bi-objective optimization problem. A parallel conical area community detection algorithm, PCACD, is proposed to solve this BOP. In order to reduce the running time, PCACD applies a global island model and targeted elitist migration policy to parallelize the CAEA for community detection due to the global characteristics of the selection and update mechanisms in CAEA. This global island model preserves an entire population on each island in order to implement the global selection and update while each island is in charge of the optimization of only a portion of subproblems. In the meantime, the targeted elitist migration policy migrates every elitist individual directly to the appropriate island in charge of the sub-problem associated with it to share essential evolutionary achievements and accelerate the convergence rate. In addition, PCACD adopts an adjacent-based chromosome representation and a modularity-based local search strategy to avoid invalid individuals and heighten the ability of finding the local best community structures. The experimental results on six real-world networks demonstrate that PCACD achieves high-quality community structures with satisfactory speedups in virtue of the global island model and targeted elitist migration policy. Furthermore, a cluster of non-dominated solutions produced by PCACD contributes to the discovery of interesting potential functional units at diverse resolutions of networks.

Our ongoing research focuses on developing parallel MOEAs for overlapping community detection. Meanwhile we are also interested in radically cutting down on the computational costs of MOEAs for dealing with expensive multi-objective community detection problems in large-scale complex networks with the aids of some other efficient strategies, such as surrogate-assisted approaches and hierarchical network reduction methods.