An Integrated LHS–CD Approach for Power System Security Risk Assessment with Consideration of Source–Network and Load Uncertainties
Abstract
:1. Introduction
- (1)
- A completed source–network–load probabilistic model with consideration of wind power and load demand correlations is proposed, and the proposed model could well reflect representative uncertainties of power system generation–transmission–consumption portion.
- (2)
- With the help of introducing LHS to sample the source–network–load demand uncertainties and adopting CD to handle wind power and load demand correlations by rearranging the sampling matrix, an integrated LHS–CD approach is tailored to handle power system generation–transmission–consumption uncertainties for security risk assessment.
- (3)
- Simulation results of the modified New England 39-bus system demonstrate that the proposed integrated LHS–CD approach is effective and efficient for power system security risk assessment with comprehensive consideration of source–network–load uncertainties.
2. Source–Network–Load Probabilistic Model for Power System Security Risk Assessment
2.1. Discrete Probabilistic Model of Transmission Line Outage
2.2. Power Source Probabilistic Model
2.2.1. Probabilistic Model of Correlated Wind Power Output
2.2.2. Probabilistic Model of Thermal Generator Operation State
2.3. Probabilistic Model of Correlated Load Demands
3. Integrated LHS–CD Approach for Power System Security Risk Assessment
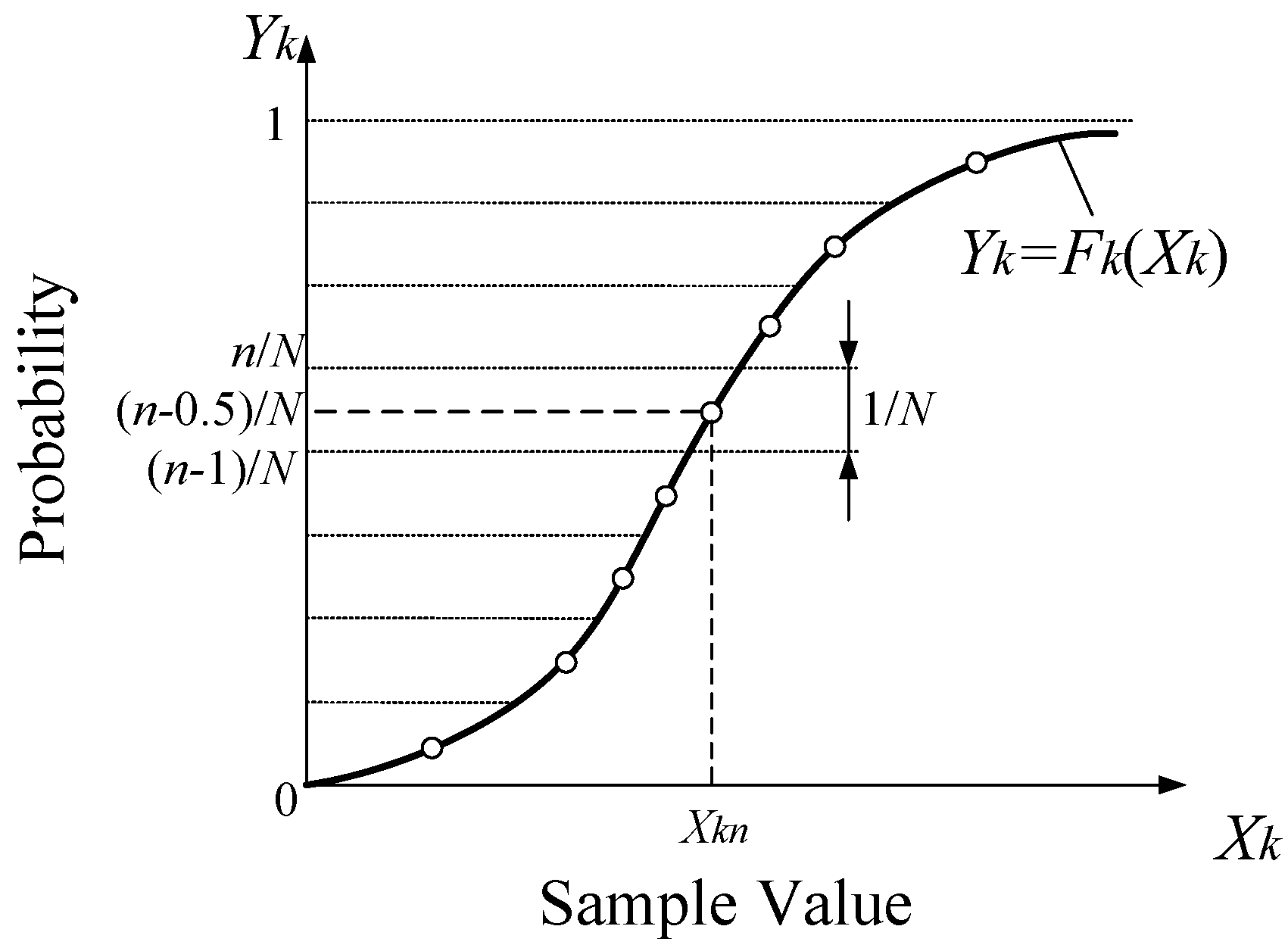
3.1. Sampling Based on LHS
3.2. Permutation Based on CD
3.2.1. CD-Based Permutation for Independent Random Input Variables
- (1)
- Generate a K × N random ordering matrix Lr, where the element in each row is an integer number 1 to N, which represents the rank position according to the element numerical value in a descending order in that row.
- (2)
- Calculate the correlation coefficient matrix CLr of the random ordering matrix Lr. Since CLr is a positive definite symmetric matrix, it could be decomposed by CD to obtain the lower triangular matrix Q.
- (3)
- Then a matrix G can be calculated based on the lower triangular matrix Q.It is not difficult to prove that the correlation coefficient matrix of matrix G is a unit matrix:
- (4)
- With the help of above transformation, there is no correlation between the row and column elements of matrix G, so the sample matrix of independent variables can be arranged according to G. However, since the elements in G may not be positive integers, it cannot be arranged directly according to G. The common solution is to obtain the ordering matrix L0 of G, and then the primary sample matrix XKN can be arranged according to L0 for obtaining a new sample matrix X0, which meets the characteristic of independent input variables.
3.2.2. CD-Based Permutation for Correlated Random Input Variables
- (1)
- Calculate the correlation coefficient matrix CZ from CX according to Formulas (16)–(20);
- (2)
- Use CD to obtain the lower triangular matrix B of CZ, i.e., CZ = BBT;
- (3)
- Sample K independent random variables of standard normal distribution N times to obtain WKN;
- (4)
- Calculate the normal distribution sample matrix Zc,KN = BWKN in Formula (22), which has the same correlations of the original input random variables X;
- (5)
- Obtain the ordering matrix Lz of Zc,KN;
- (6)
- Rearrange the sample matrix XKN generated in Formula (11) according to Lz, and the perfect sampled matrix is finally obtained.
3.3. LHS–CD for Generating the Correlated Sampling Matrix for Power System Source–Network–Load Uncertainties
4. Index for Power System Security Risk Assessment
4.1. Static Voltage Risk Index
4.2. Transmission Line Overloaded Risk Index
4.3. Main Steps of Proposed LHS–CD Approach for Power System Static Risk Assessment with Consideration of the Source–Network–Load Uncertainties
5. Simulation Results
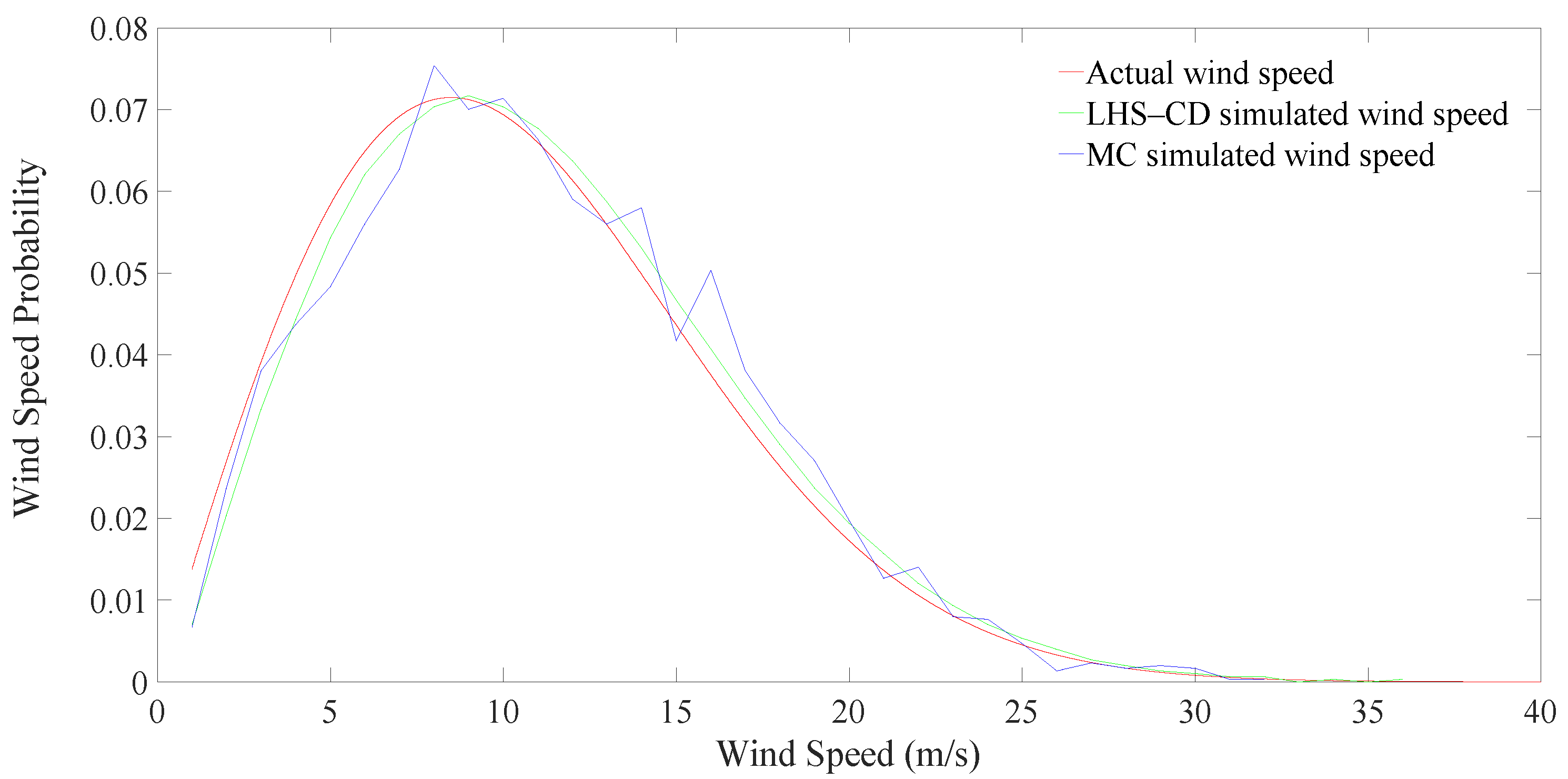
5.1. Comparison of MC and LHS–CD for Wind Speed Sampling
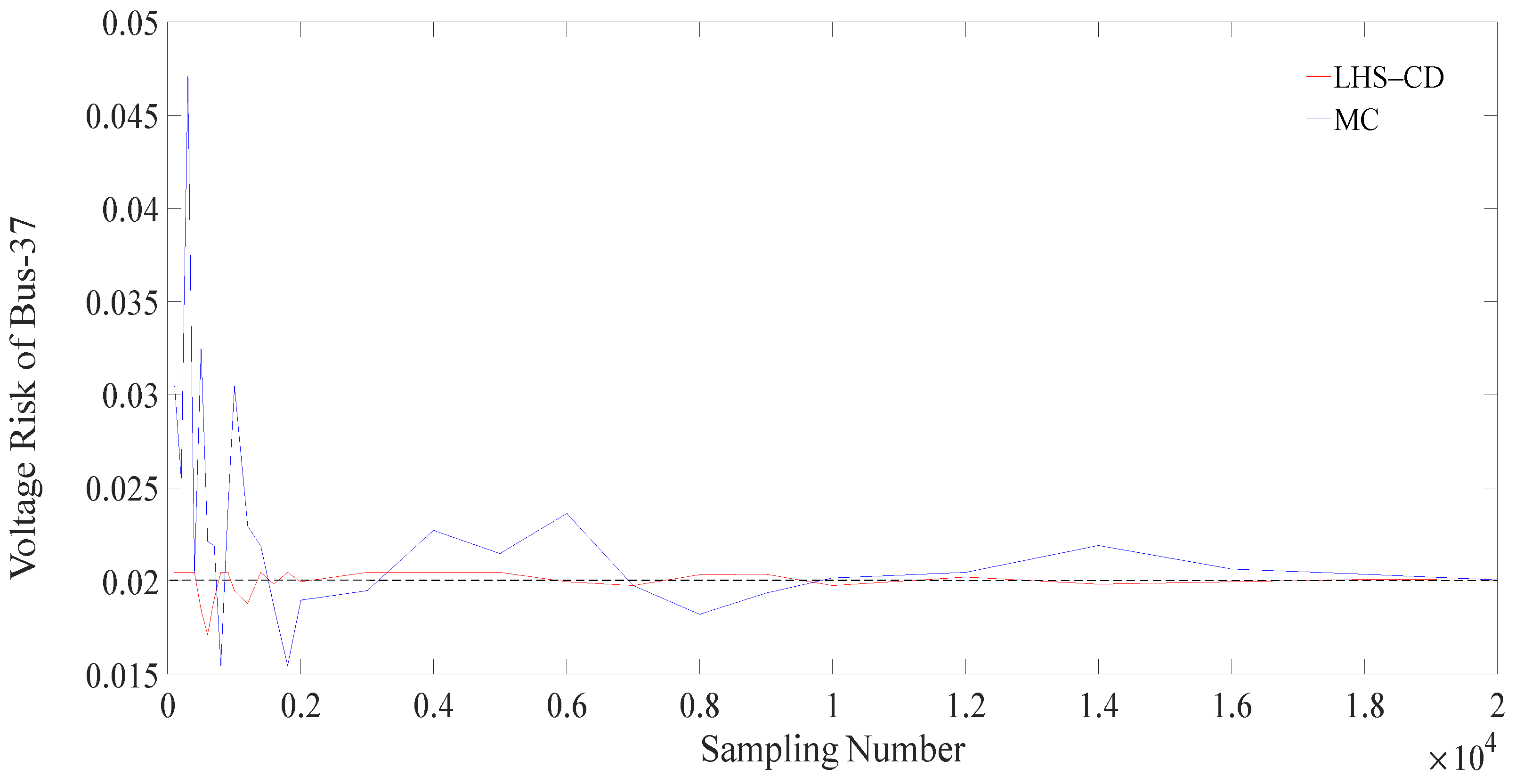
5.2. LHS–CD Convergence for Power Security Risk Assessment
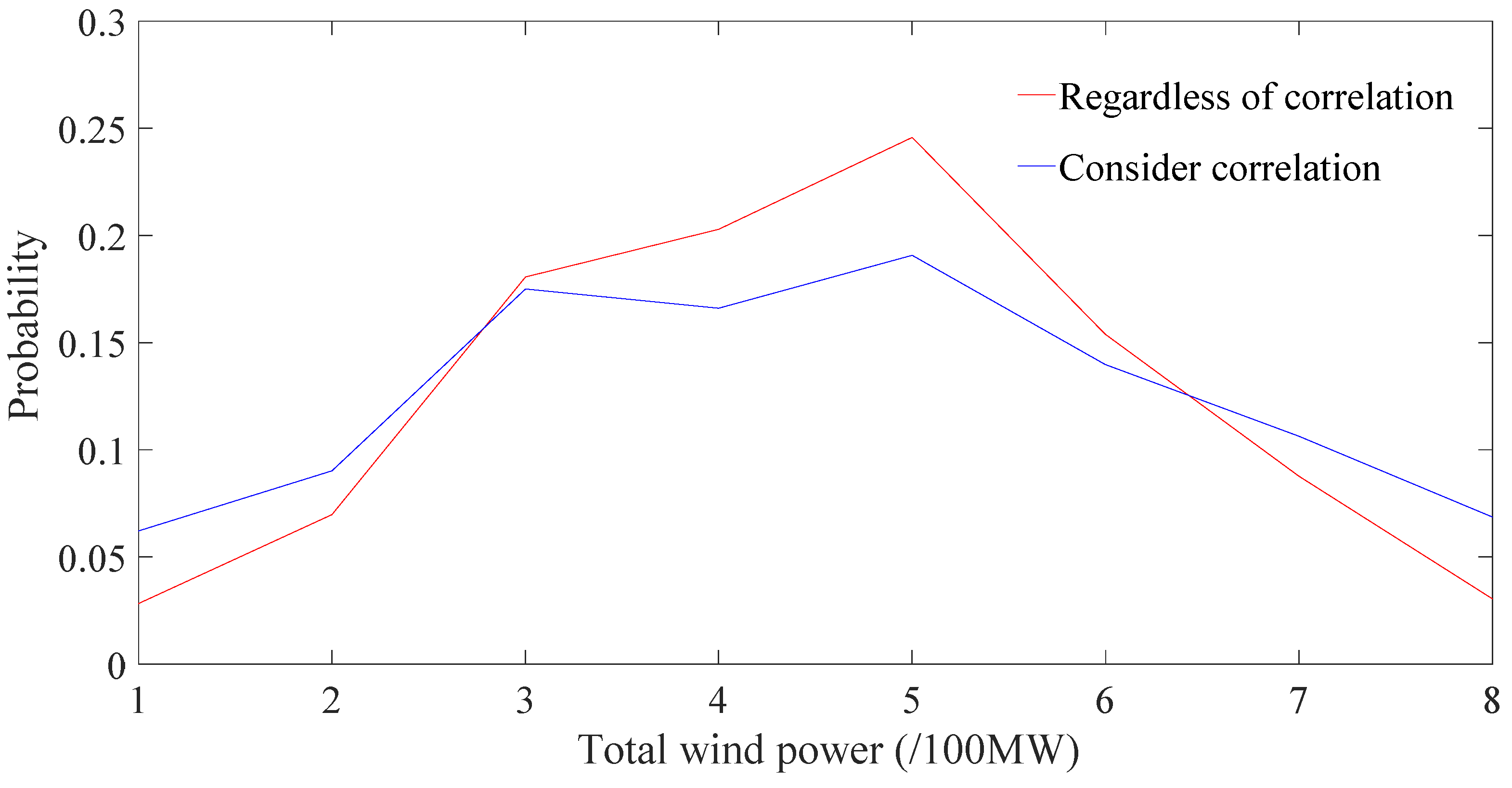
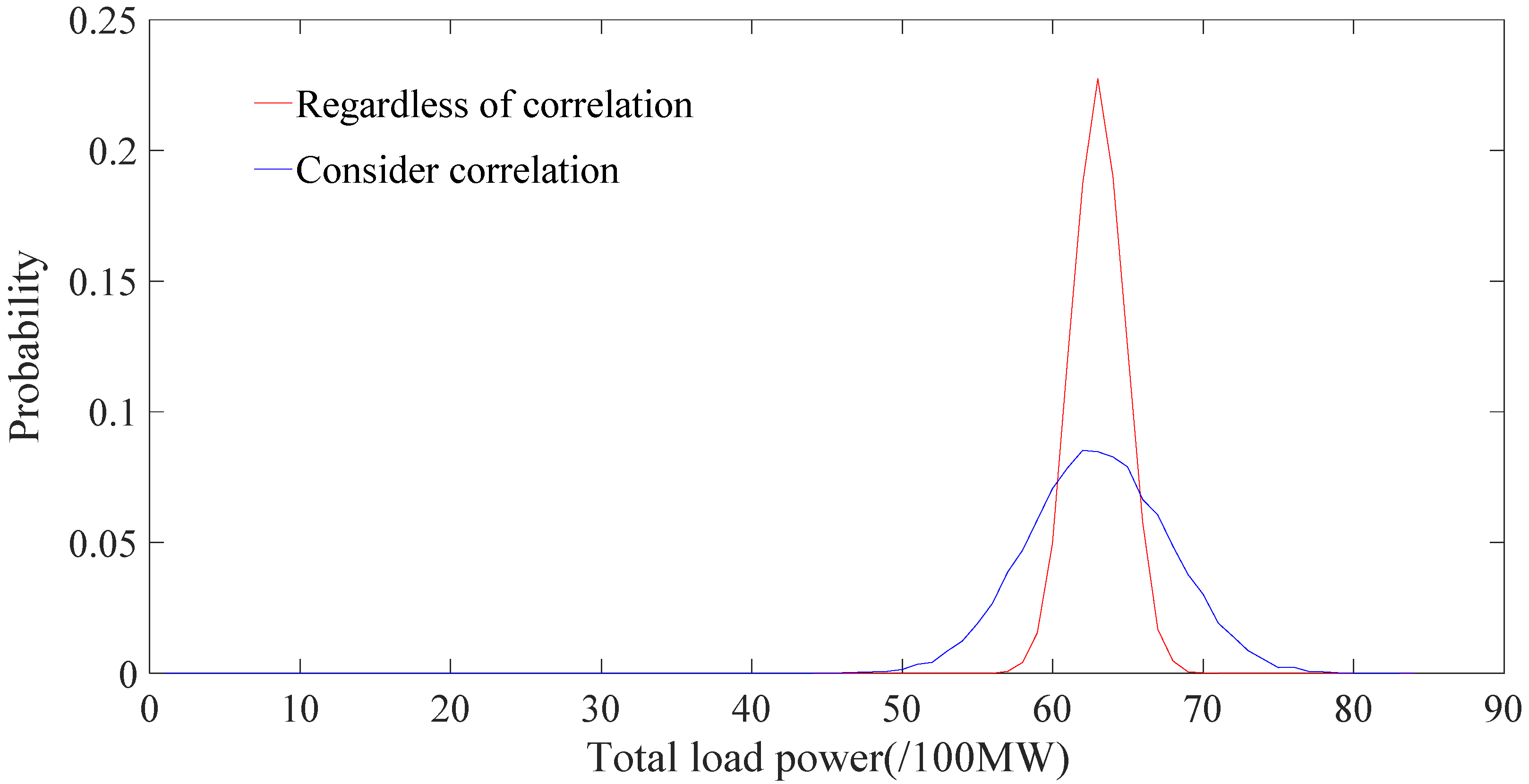
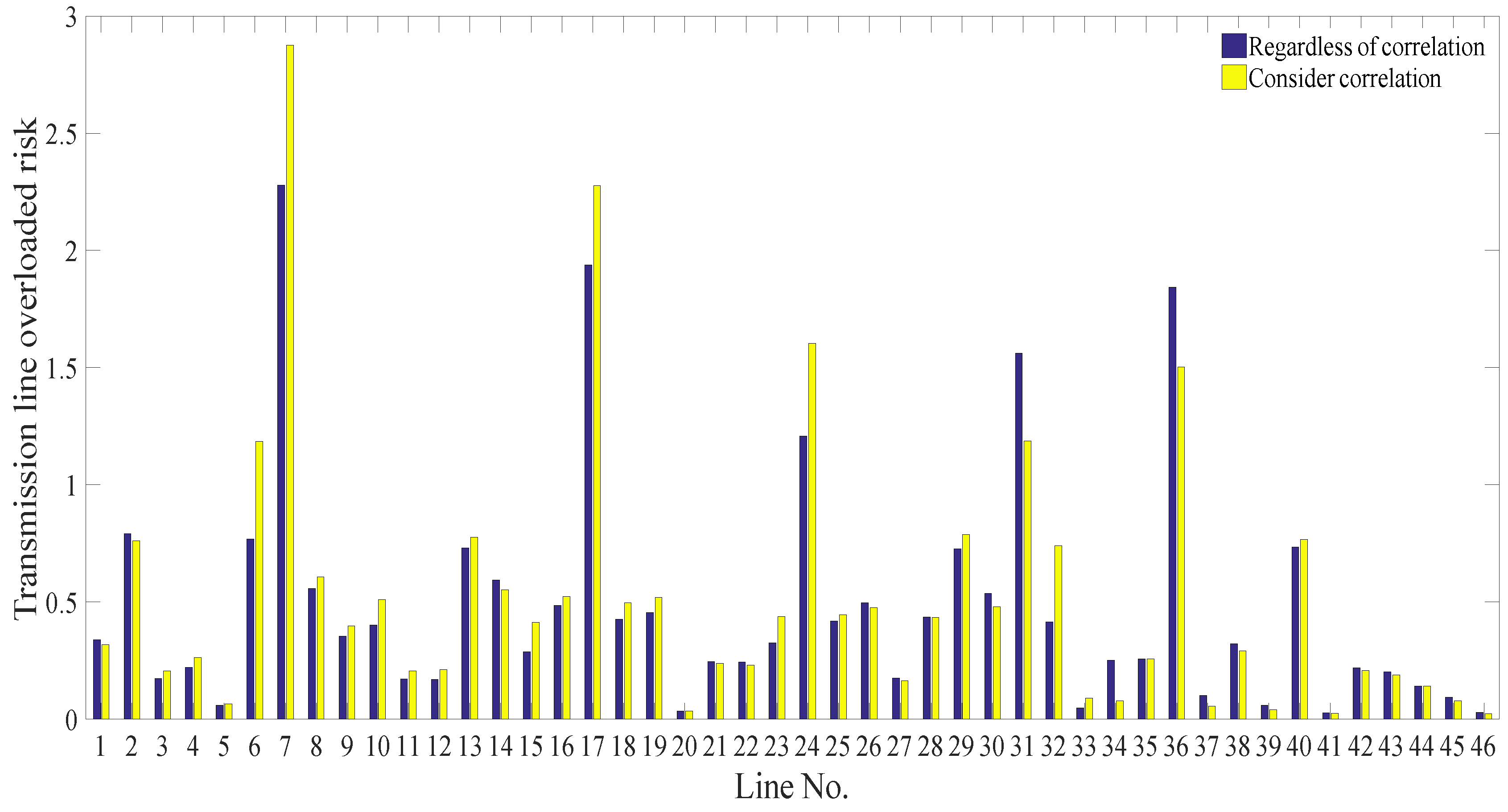
5.3. Influence of Wind Power Correlation and Load Correlation
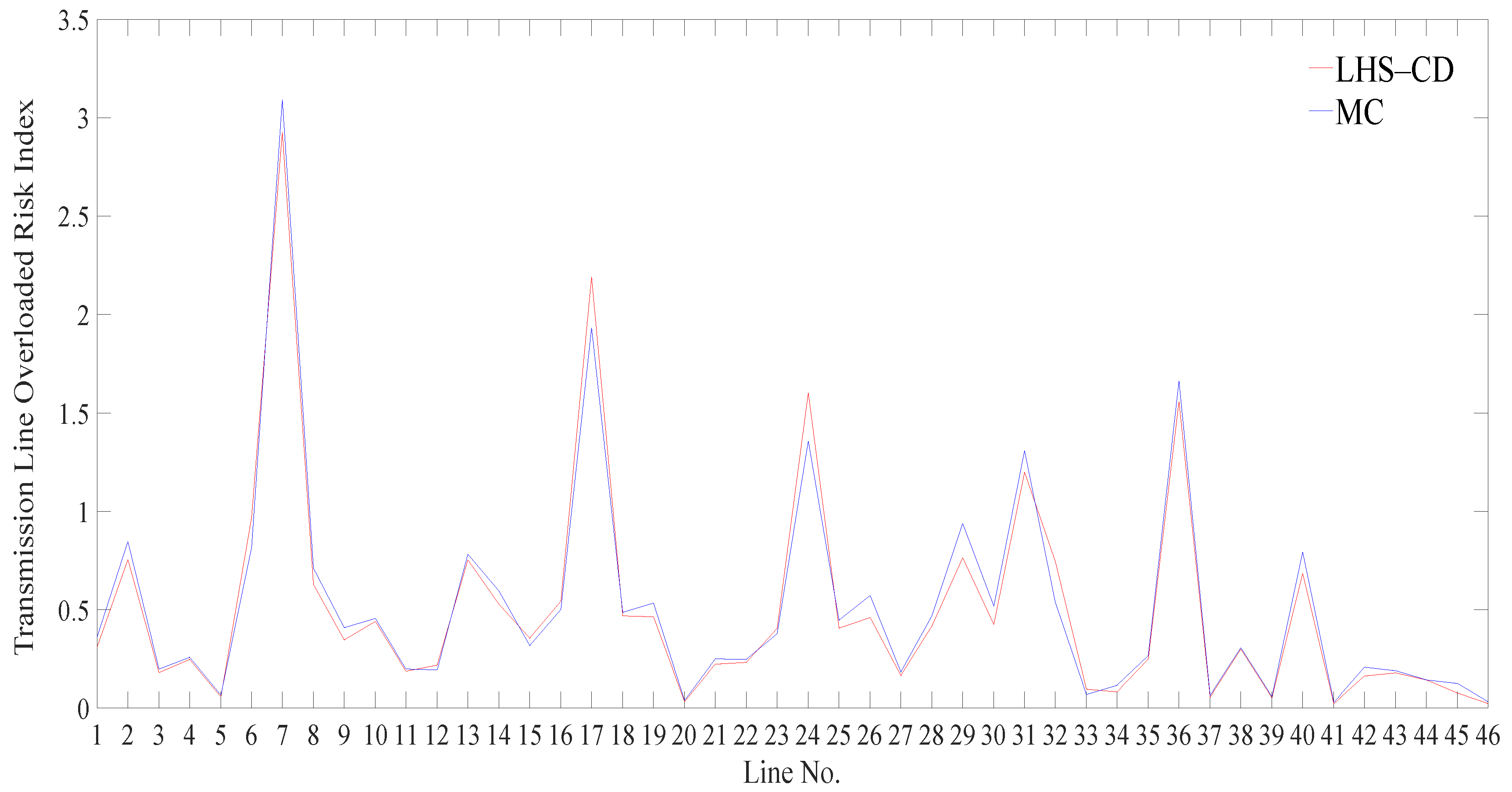
5.4. Accuracy of Security Risk Assessment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Operation state of the line r | |
| Outage probability of the transmission line r | |
| Ur | A random number uniformly distributed in [0,1] interval |
| v | Wind speed |
| k, c | Shape and scale parameter of wind speed |
| Vin, Vrate, Vcut | Cut-in speed, rated and cut-out wind speeds |
| Correlation coefficient matrix of wind farms | |
| Pi, Qi | Active and reactive power for load i |
| μPi, σPi | Mean and standard deviation of active power Pi |
| μQi, σQi | Mean and standard deviation of reactive power Qi. |
| Cload | Correlation coefficient matrix of load |
| RUi | Overridden voltage risk index of bus i |
| Uik | Voltage calculated at the kth sampling point |
| Ui_rate | Rated voltage of bus i |
| PUik | Probability of sample k |
| Sjk | Apparent power flow of transmission line j for the kth sampling point |
| Sj_rate | Rated apparent power of transmission line j |
References
- Feng, Y.; Wu, W.C.; Zhang, B.M.; Li, W. Power system operation risk assessment using credibility theory. IEEE Trans. Power Syst. 2008, 23, 1309–1318. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Du, D.; Cao, J. Overload risk assessment in grid-connected induction wind power system. In Proceedings of the Asia Simulation Conference/International Conference on System Simulation and Scientific Computing (AsiaSim and ICSC 2012), Shanghai, China, 27–30 October 2012; pp. 44–51. [Google Scholar]
- De, J.; Papaefthymiou, G.; Palensky, P. A framework for incorporation of infeed uncertainty in power system risk-based security assessment. IEEE Trans. Power Syst. 2018, 33, 613–621. [Google Scholar]
- Ding, T.; Li, C.; Yan, C.; Li, F.; Bie, Z. A bilevel optimization model for risk assessment and contingency ranking in transmission system reliability evaluation. IEEE Trans. Power Syst. 2016, 32, 3803–3813. [Google Scholar] [CrossRef]
- Negnevitsky, M.; Nguyen, D.H.; Piekutowski, M. Risk assessment for power system operation planning with high wind power penetration. IEEE Trans. Power Syst. 2015, 30, 1359–1368. [Google Scholar] [CrossRef]
- Deng, W.; Ding, H.; Zhang, B.; Lin, X.; Bie, P.; Wu, J. Multi-period probabilistic-scenario risk assessment of power system in wind power uncertain environment. IET Gener. Transm. Distrib. 2016, 10, 359–365. [Google Scholar] [CrossRef]
- Karki, R.; Thapa, S.; Billinton, R.B. A simplified risk-based method for short-term wind power commitment. IEEE Trans. Sustain. Energy 2012, 3, 498–505. [Google Scholar] [CrossRef]
- Xue, Y.; Yu, C.; Li, K.; Wen, F.; Ding, Y.; Wu, Q.; Yang, G. Adaptive ultra-short-term wind power prediction based on risk assessment. CSEE J. Power Energy Syst. 2016, 2, 59–64. [Google Scholar] [CrossRef]
- Wang, C.; Liu, F.; Wang, J.; Wei, W.; Mei, S. Risk-based admissibility assessment of wind generation integrated into a bulk power system. IEEE Trans. Sustain. Energy 2016, 7, 325–336. [Google Scholar] [CrossRef]
- Li, H.X.; Cai, D.F.; Li, Y.H. Probabilistic assessment of voltage stability margin in presence of wind speed correlation. J. Electr. Eng. Technol. 2013, 8, 719–728. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; Ghazi, R.; Ghayeni, M. Power system security assessment with high wind penetration using the farms models based on their correlation. IET Renew. Power Gener. 2018, 12, 893–900. [Google Scholar] [CrossRef]
- Pindoriya, N.M.; Jirutitijaroen, P.; Srinivasan, D.; Singh, C. Composite Reliability Evaluation Using Monte Carlo Simulation and Least Squares Support Vector Classifier. IEEE Trans. Power Syst. 2011, 26, 2483–2490. [Google Scholar] [CrossRef]
- Lei, H.T.; Singh, C. Non-sequential Monte Carlo simulation for cyber-induced dependent failures in composite power system reliability evaluation. IEEE Trans. Power Syst. 2017, 32, 1064–1072. [Google Scholar]
- Li, X.N.; Wu, F.Q.; Sun, X.F. Research on Reliability Evaluation Based on Monte Carlo Method. Appl. Mech. Mater. 2011, 130, 3859–3861. [Google Scholar] [CrossRef]
- Da Silva, A.L.M.; Fernandez, R.A.G.; Singh, C. Generating Capacity Reliability Evaluation Based on Monte Carlo Simulation and Cross-Entropy Methods. IEEE Trans. Power Syst. 2010, 25, 129–137. [Google Scholar] [CrossRef]
- Zhu, J.; Li, C.; Tang, A.H. Reliability evaluation of distribution network based on improved non sequential Monte Carlo method. In Proceedings of the 3rd International Conference on Mechatronics, Robotics and Automation (ICMRA), Shenzhen, China, 20–21 April 2015. [Google Scholar]
- Shu, Z.; Jirutitijaroen, P. Latin hypercube sampling techniques for power systems reliability analysis with renewable energy sources. IEEE Trans. Power Syst. 2011, 26, 2066–2073. [Google Scholar]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- He, H.; Zhou, Q.; Sun, T.; Cheng, H.; Zuo, Q. Reliability evaluation based on modified latin hypercube sampling and minimum load-cutting method. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015. [Google Scholar]
- Shu, Z.; Jirutitijaroen, P.; da Silva, A.M.L.; Singh, C. Accelerated State Evaluation and Latin Hypercube Sequential Sampling for Composite System Reliability Assessment. IEEE Trans. Power Syst. 2014, 29, 1692–1700. [Google Scholar] [CrossRef]
- Sun, C.; Bie, Z.; Xie, M.; Ning, G. Effects of wind speed probabilistic and possibilistic uncertainties on generation system adequacy. IET Gener. Transm. Distrib. 2015, 9, 339–347. [Google Scholar] [CrossRef]
- Giorsetto, P.; Utsurogi, K.F. Development of a New Procedure for Reliability Modeling of Wind Turbine Generators. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 134–143. [Google Scholar] [CrossRef]
- Billinton, R.; Bai, G. Generating capacity adequacy associated with wind energy. IEEE Trans. Energy Convers. 2004, 19, 641–646.20. [Google Scholar] [CrossRef]
- Li, Z.N.; Ai, X. Flatlands wind farm power generation and wake effect analysis based on Jensen model. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), HongKong, China, 8–11 December 2013. [Google Scholar]
- Liu, P.L.; Kiureghian, A.D. Multivariate distribution models with prescribed marginals and covariances. Probabilistic Eng. Mech. 1986, 1, 105–112. [Google Scholar] [CrossRef]
- Pai, M.A. Energy Function Analysis for Power System Stability; Springer: Boston, MA, USA, 1989; pp. 223–227. [Google Scholar]






| Wind Farm Connected Bus | Shape Parameter k | Scale Parameter c | Cut-In Speed Vin (m/s) | Cut-Out Speed Vcut (m/s) | Rated Speed Vrate (m/s) | Rated Power Prate (MVA) |
|---|---|---|---|---|---|---|
| 11 | 2 | 12 | 3 | 25 | 12 | 200 |
| 13 | 2 | 12 | 3 | 25 | 12 | 200 |
| 18 | 2 | 10 | 3 | 25 | 12 | 200 |
| 22 | 2 | 10 | 3 | 25 | 12 | 200 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, S.; Song, L.; Wu, Y.; Ma, Z.; Jing, J.; Ding, Z.; Li, G. An Integrated LHS–CD Approach for Power System Security Risk Assessment with Consideration of Source–Network and Load Uncertainties. Processes 2019, 7, 900. https://doi.org/10.3390/pr7120900
Xia S, Song L, Wu Y, Ma Z, Jing J, Ding Z, Li G. An Integrated LHS–CD Approach for Power System Security Risk Assessment with Consideration of Source–Network and Load Uncertainties. Processes. 2019; 7(12):900. https://doi.org/10.3390/pr7120900
Chicago/Turabian StyleXia, Shiwei, Liangyun Song, Yi Wu, Zhoujun Ma, Jiangping Jing, Zhaohao Ding, and Gengyin Li. 2019. "An Integrated LHS–CD Approach for Power System Security Risk Assessment with Consideration of Source–Network and Load Uncertainties" Processes 7, no. 12: 900. https://doi.org/10.3390/pr7120900
APA StyleXia, S., Song, L., Wu, Y., Ma, Z., Jing, J., Ding, Z., & Li, G. (2019). An Integrated LHS–CD Approach for Power System Security Risk Assessment with Consideration of Source–Network and Load Uncertainties. Processes, 7(12), 900. https://doi.org/10.3390/pr7120900






