Abstract
The injection pressure of the gasoline direct injection vehicle is currently developing from the low pressure to the high pressure, and the increase of the injection pressure has brought various damage problems to the high pressure pump structure. These problems should be solved urgently. In this paper, the damage problem of the high pressure pump unloading valve ball in a gasoline direct injection vehicle under high pressure conditions is studied. The theoretical calculation of the force of the pressure relief valve is carried out. Firstly, the equivalent friction coefficient is obtained by decoupling analysis of the statically indeterminate model. Based on this, a finite element model is established. The equivalent stress is obtained by numerical simulation. The equivalent stress is compared with the yield strength of the valve ball material to determine that the valve ball damage is a non-static damage. At the same time, the s-N curve of the probability of destruction of one-millionth of the material of the valve ball is given. Then, the fatigue numerical simulation is performed. A safety factor of 3.66 is obtained. In summary, the high pressure relief valve ball in the direct injection high pressure pump should not be a traditional structural damage under high pressure conditions. In the theoretical calculation, the tangential displacement and radial displacement of the ball are all on the micrometer level. It can be presumed that the surface damage of the valve ball is microscopic damage, such as fretting wear.
1. Introduction
Gasoline direct injection is the latest fuel supply technology for gasoline engines. The direct injection gasoline engine directly injects fuel into the cylinder. Compared with the previous carburetor oil supply and single or multi-point electronic fuel injection technology, it has the advantages of accurate oil supply, uniform oil and gas mixing, and high combustion efficiency. Therefore, the technology is used by many car manufacturers [1,2,3]. Furthermore, the increased pressure of the direct injection oil will make the spray atomization effect better, the combustion efficiency higher, and the generation of discharged particulate matter better suppressed, which make the technology more environmentally friendly [4,5,6]. More widely, for the process control [7,8,9] and fluid power control components [10,11], the pressurization technology seems to come into notice more frequently. However, with the increased pressure of the injection gasoline, the high pressure pump will have various types of damage problems under long-term working conditions, which affect normal functions. Li et al. [12] analyzed the pitting corrosion of a high pressure oil pump cam of a direct injection gasoline engine in a cylinder and proposed corrective measures. Wang et al. [13] performed contact stress analysis and fatigue analysis on the high pressure oil pump cam-roller mechanism, which verified the reliability of the mechanism. Lei et al. [14] carried out flow field analysis on the internal fluid of the whole high pressure oil pump and used the obtained oil pressure distribution data to analyze the structural strength of the oil pump structure, which provided research ideas and methods for the design and optimization of the high pressure oil pump. The object of this paper is the pressure relief valve of the high pressure oil pump of the direct injection gasoline vehicle. The surface damage of the valve ball and the valve seat under the high pressure and high frequency working conditions has caused the unloading function to be unachievable. In response to this problem, it is necessary to perform damage verification analysis on the unloading valve structure.
2. Model Analysis
This research object is a spherical unloading valve in the high pressure pump of the direct injection vehicle. Its structure is shown in Figure 1. The unloading valve is shown in Figure 2. The left side of the valve ball is subjected to an alternating oil pressure of 0 to 45 MPa and the right side is subjected to a constant oil pressure of p2. The left side of the valve ball is initially subjected to the preload force Ft of the spring. When the oil pressure p2 at the right end of the valve ball increases to a certain value, exceeding the spring force provided at the left end, and the left end oil pressure is changed to 0 MPa, the valve ball will be opened and the right side high pressure oil will be released to the left side, which acts as a safe unloading valve. The ball valve structural parameters and oil pressure parameters are shown in Table 1. The equivalent calculation is carried out according to the pressure, and the contact area between the valve ball and the valve seat is subjected to an equivalent oil pressure of 5–50 MPa.
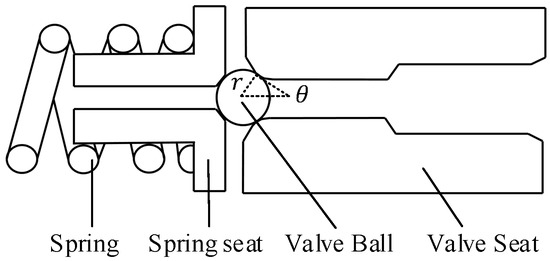
Figure 1.
The structure of the pressure relief valve.
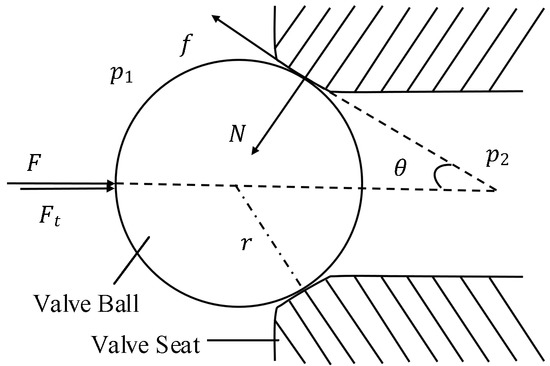
Figure 2.
The stress state of the pressure relief valve.

Table 1.
The parameters of structure and oil pressure.
The surface damage problem of the unloading valve ball in 500 h (the number of cycles is 1.728 × 109 times) will occur as shown in Figure 3. The most critical and most important damage mechanism under complex conditions may be hidden and cannot be directly seen in Figure 3, so further analysis and judgment is needed to reach a conclusion. Firstly, it is necessary to consider whether the valve ball will be structurally damaged from the perspective of static force and fatigue.
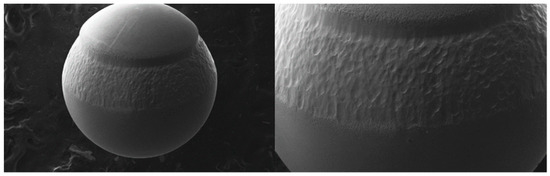
Figure 3.
The damage surface topography of the valve ball.
For the verification of the rationality of the structural design, the research can be divided into the following sections:
(1) The contact stress between the valve ball and the valve seat is obtained by theoretical calculation, and the value of the equivalent friction force of the contact part is calculated in this part, which provides a parameter basis for the simulation calculation;
(2) The theoretical calculation results are verified by simulation calculation, and the equivalent stress value and fatigue safety factor are obtained;
(3) The data obtained by the simulation are used to safely check for static and fatigue damage.
3. Theoretical Analysis
3.1. Structural Micro-Division
From the structure of the unloading valve, it can be known that the initial state of contact between the valve ball and the valve seat is a line contact on the circumference. In order to facilitate the analysis of the contact force, the structure is divided into n(n→∞) equal divisions as shown in Figure 4. The force of each micro-element is shown in Figure 5.
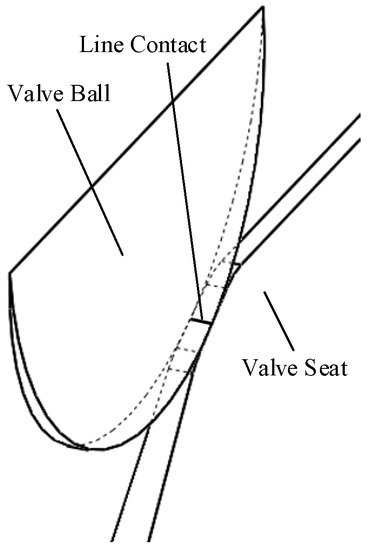
Figure 4.
The micro-division of the structure.
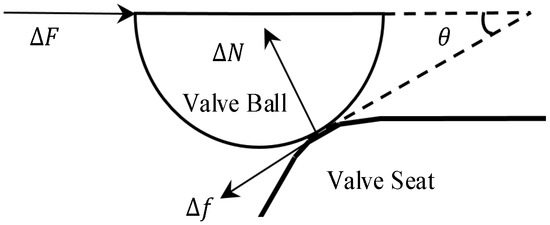
Figure 5.
The force of each micro-element.
Under uniform oil pressure and initial spring force, the maximum force that the ball is subjected to can be expressed as:
The force that each micro-element is subjected to can be expressed as:
It can be obtained from the force model of the micro-element that:
ΔN and Δf are the positive pressure and friction of the micro-element. From the Equation (3), the relationship between ΔN and Δf is not known; it cannot be solved directly, so it is necessary to obtain the equivalent friction coefficient between the two.
3.2. Equivalent Friction Coefficient Calculation
We can suppose a situation that a block on a horizontal plane is subjected to horizontal thrust F1 and forward pressure N1. When the horizontal thrust F1 is within the range of 0 ≤ F1 ≤ fmax = μ1N1 (μ1—maximum static friction between the two materials), the slider has no displacement. However, there is a slight slip Δx between the slider and the horizontal plane. It can be considered that the micro slip range in which the slider does not move is 0 ≤ Δx ≤ Δxmax. It can be also considered that the equivalent friction coefficient fx satisfies fx∝Δx [15].
The meaning of μx is the ratio of the value of non-critical equivalent friction to the positive pressure:
The relationship between the equivalent friction coefficient μx and the micro-slip Δx is experimentally verified and obtained by Dr. Liu [16]. μx and Δx are proportional to each other.
The valve ball and valve seat structure are steel materials, kf = 0.25 μm−1 [16].
The micro-element structure of the ball valve is analyzed, and its force deformation is shown in Figure 6. ΔX is the slight slippage of the valve ball under the action of the spring force that can be calculated from the Hertz contact theory in Section 3.3. Here, a is the half width of the contact between the valve ball and the valve seat under the action of positive pressure ΔN. The initial radius of the ball is r. After the force is deformed, the distance between the center point of the contact and the center of the sphere is r1, which can be expressed as:
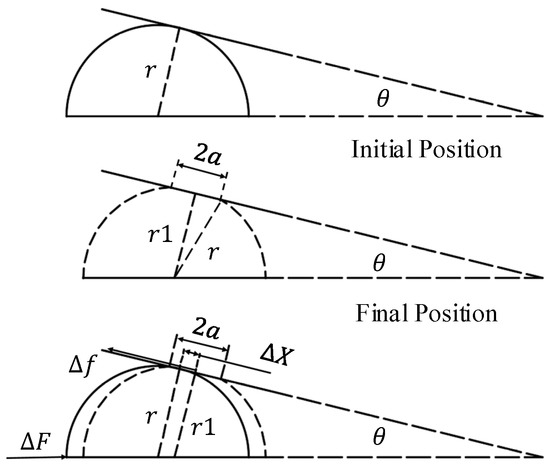
Figure 6.
The force model of the ball valve.
The micro-slip distance ΔX can be expressed as:
The relationship between ΔN and Δf in the force model of micro-element can be described as:
Therefore, the relationship between the equivalent friction and the positive pressure can be linked by the Hertz contact theory.
3.3. Structural Contact Stress Analysis
The contact part of the micro-element structure of the spherical unloading valve can be regarded as a model of contact between the cylinder and the plane. According to the Hertz contact theory [17], the contact half width a satisfies:
The maximum contact stress in the contact portion appears at the contact center, and the maximum value is:
where Δl is the length of the micro-element of the contact between the valve seat and the valve ball line, which satisfies:
E* is the equivalent elastic modulus, which satisfies:
E1 and E2 are the elastic modulus values of the valve ball and the valve seat material, respectively. υ1 and υ2 are the Poisson′s ratios of the valve ball and the valve seat material, respectively. E1 = 200 GPa, E2 = 213 GPa. υ1 = 0.3, υ1 = 0.29.
It can be obtained by solving Equations (1)–(3) and (6)–(12) that: ΔN = 145.4/n, Δf = 12.9/n. The equivalent friction coefficient is:
At the same time, the micro-slip distance Δx = 0.355 μm can be obtained; the contact half width a = 17.15 μm.
The maximum contact stress value of the contact between the valve ball and the valve seat is expressed as follows:
4. Simulation Analysis
The valve ball seat structure shown in Figure 7 is added to the ANSYS model. In order to facilitate the addition of force, a plane is selected on the left side of the valve ball. The elastic modulus and Poisson’s ratio parameters of the ball and seat are added to the material properties.
Figure 7.
The simulation structure of the pressure relief valve.
The s-N curve of the structural material needs to be known when calculating the fatigue safety factor of the structure. The material used for the valve ball and the valve seat is bearing steel 9Cr18, and its p′-s-N′ curve is used to set the material fatigue property parameters [18]. The meaning of the p′-s-N′ curve expression is that the life distribution of the material is a normal distribution form under the same stress level [19]. The lifetime of most tested materials is distributed at p′ = 0.5, the middle of the normal distribution curve. In this simulation, in order to meet the requirement of one-millionth of the destruction probability of the structure in engineering applications, it is necessary to fit the s-N′ curve data in the case of the probability p′ = 0.000001 according to the p1′ = 0.01, p2′ = 0.05, p3′ = 0.1 and p4′ = 0.5 data given by the material according to the normal distribution.
The fatigue life curve formula is as shown in Equation (15):
where N′ is the number of cycles; s (Pa) is the stress size; the values of C and m refer to Table 2.

Table 2.
Parameter values under different damage probabilities.
The s-N curve data table with a probability of destruction of one part per million is calculated as shown in Table 3. The meshing parameter is set for the structure, and the local mesh encryption is performed on the key contact portion of the calculation, as shown in Figure 8. The overall mesh size is 0.3 mm and the contact portion mesh is refined to 0.015 mm.

Table 3.
The data sheet of fatigue life curve.
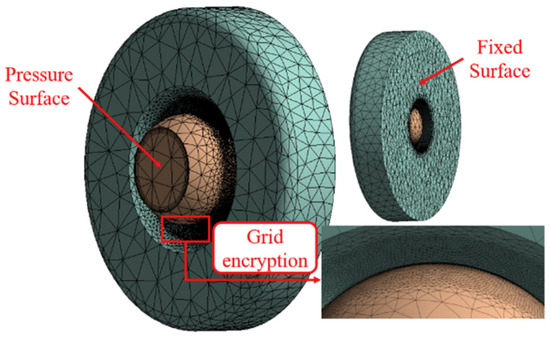
Figure 8.
Meshing and simulation boundary conditions.
The structural stress boundary conditions, i.e., the pressure acting surface and the fixed surface, are set. The contact portion was set to frictional contact and the coefficient of friction was defined as 0.0887 as calculated in Section 3.3. The pressure is calculated according to the maximum force under working conditions, that is 50 MPa oil pressure, equivalent to 78.58 N.
The fatigue simulation force is in the form of pulsating circulation. The force application is still the same as the external force in the static simulation. The alternating equivalent oil pressure is 5–50 MPa, and the minimum oil pressure σmin = 0.1 × 50 MPa = 5 MPa. The pulsating form is shown in Figure 9.
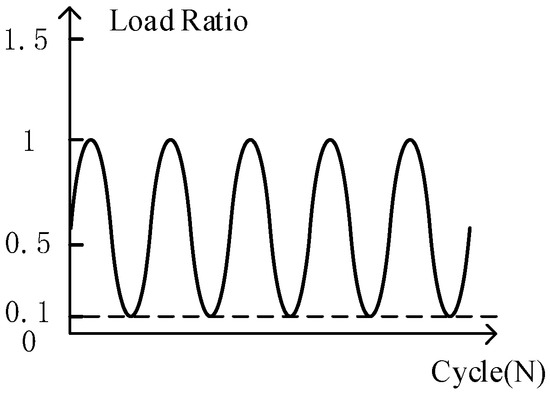
Figure 9.
Constant amplitude load ratio.
The contact stress distribution obtained by simulation is shown in Figure 10. The maximum contact stress value calculated by simulation is pmax′ = 1107.8 MPa, and the theoretical calculation result is pmax = 1220 MPa. The error between the two is about 9.2%, less than 10%, which verifies the correctness of the theoretical model. The overall equivalent stress distribution is obtained as shown in Figure 11. The maximum equivalent stress is 725.63 MPa. The yield strength of the ball and seat material is σt = 1900 MPa, and the tensile yield strength and compressive yield strength of the elastoplastic material are generally considered to be the same, i.e., σt = σc (σc is the compressive yield strength). The von Mises equivalent stress theoretical shear yield strength satisfies τs = σt/√3, and τs ≈ 1096 MPa can be calculated [20]. The check is performed with the minimum shear yield strength, which is much larger than the equivalent stress of 725.63 MPa that is theoretically calculated. It can be judged that the ball valve is safe under static conditions.
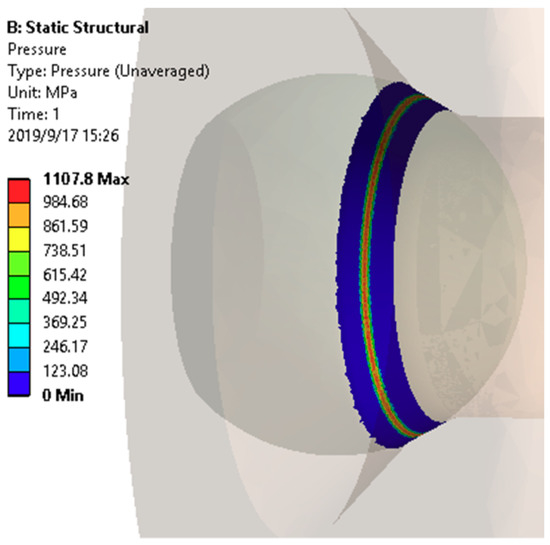
Figure 10.
The simulation results of contact stress.
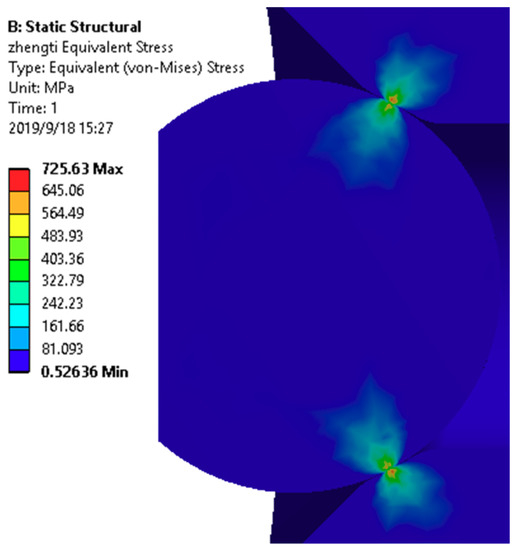
Figure 11.
The simulation results of equivalent stress.
The fatigue safety factor distribution of the whole structure under the stress condition of 1.728 × 109 times is shown in Figure 12; the maximum is 3.6558, which indicates that the structural ball will not suffer structural fatigue damage under the action of fatigue alone.
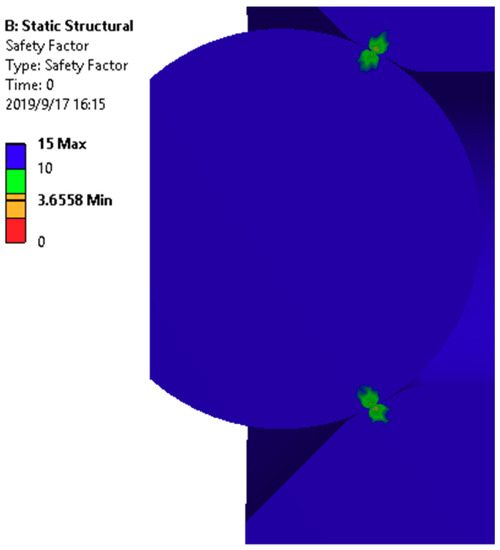
Figure 12.
The distribution of fatigue safety factor.
5. Discussion
In this paper, the calculation of the stress of valve ball and valve seat is solved by phenomenological mathematics, obtained by the experiment, and the result is verified by simulation. Through the static and fatigue check, the damage mechanism of the valve ball and the valve seat under working conditions is not static and fatigue damage.
For a further study of the damage mechanism, a high frequency test rig as shown in Figure 13 was designed. The loading force can reach more than 100 N and the operating frequency can reach 500 Hz. A 50-h experiment has been done between the valve ball and the valve seat at 500 Hz and 8–80 N. The damage mechanism needs further research to explain the experimental phenomena or to illustrate the problems in combination with the experiments.
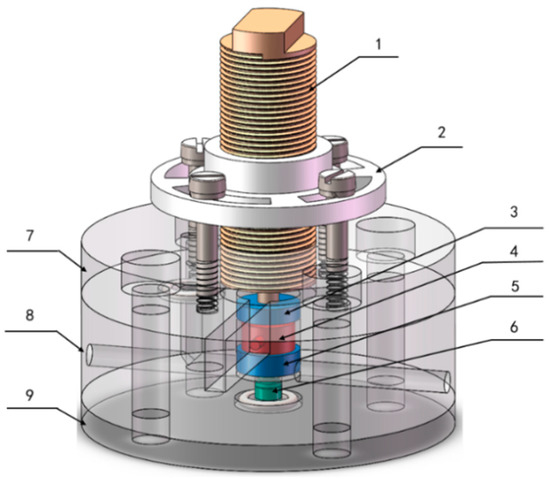
Figure 13.
Test bench, (1) piezoelectric actuator; (2) fixed disc; (3) cylinder 1; (4) force sensor; (5) cylinder 2; (6) testing object; (7–9) base.
The ball and seat wear band under the 50-h test is shown in Figure 14. The diameter of the ball is small. It is only a little more than a millimeter. Therefore, the amount of damage cannot be assessed by quality. At present, the best evaluation method is to take the damage surface morphology by microscopy and estimate the damage by width and depth.

Figure 14.
Damage zone (8–80 N, 500 Hz, 50 h).
Although the amount of damage can be estimated by microscopy, this method of evaluation is not particularly accurate. It is also impossible to monitor the damage during the experiment. The test bench can be improved to add better calculation methods. For example, a distance sensor can be added to monitor the depth of the damage zone to determine the depth of damage during the experiment.
6. Conclusions
The injection pressure of the gasoline direct injection vehicle is currently developing from low pressure to high pressure. The structural damage problems brought by the increase of the injection pressure should be solved urgently. Therefore, based on theoretical analysis and numerical analysis, the paper first determines whether there is traditional structural damage.
The theoretical stress calculation and static and fatigue simulation analysis of the unloading valve structure were carried out around the ball damage problem of the high pressure pump unloading valve in a gasoline direct injection vehicle. The following conclusions were obtained:
(1) According to the maximum static force of the valve ball, the theoretical calculation is carried out, the equivalent friction coefficient is obtained by solving the statically indeterminate problem, and the maximum contact stress value of 1220 MPa is obtained by the Hertz contact theory.
(2) Through simulation, the maximum contact stress is 1107.8 MPa and the maximum equivalent stress is 725.63 MPa under maximum static force. The simulated contact stress values are compared with the theoretical calculations and the difference between the two is less than 10%, which verifies the correctness of the theoretical model. At the same time, the equivalent stress is used for static checking, and it is judged that the unloading valve structure will not be damaged under the action of static force.
(3) By the simulation analysis, the fatigue safety factor of the unloading valve is 3.6558 under the condition of one-millionth of the failure probability and 1.728 × 109 cycles. It is verified that the traditional structural fatigue is not the cause of the ball failure of the unloading valve.
It can be seen from the above verification analysis that the damage of the ball valve structure is not caused by static force and fatigue damage; further analysis of the structural damage mechanism is needed. In the theoretical calculation, the tangential displacement (0.355 μm) and radial displacement (17.15 μm) of the valve ball are all in the micron range. The motion state belongs to the fretting category and the surface damage morphology of the valve ball is similar to the fretting damage. It can be preliminarily speculated that the surface damage of the valve ball is a fretting damage. The mechanism still needs further research.
Author Contributions
L.L. (Liang Lu) and Q.X. provided theoretical research methods; L.L. (Liang Lu) and Q.X. conceived and designed the experiments; Q.X. performed the experiments; M.Z. and L.L. (Liangliang Liu) analyzed the data; M.Z., L.L. (Liangliang Liu) and Z.W. contributed to the project supervision and management; Z.W. contributed to the problem research and provided research object and resources. Q.X. provided original draft preparation. L.L. (Liang Lu) provided review and editing of writing.
Funding
The authors are grateful to the National Natural Science Foundation of China (No. 51605333) and the Fundamental Research Funds for the Central Universities (kx0138020173443) for financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, S.C.; Li, J.; Li, D.G. Analysis on Development for Gasoline Direct Injection Technology. Veh. Engine 2007, 5, 8–13. [Google Scholar]
- Sun, Y.; Wang, Y.J.; Wang, J.X.; Shuai, S.J. New Progress of Gasoline Direct Injection Engines’ Research and Technical Problems. Intern. Combust. Engines 2002, 1, 6–10. [Google Scholar]
- Xia, S.M.; Qiu, X.W.; Zhao, X.S.; Feng, H.Q. Survey of Research Situation on Gasoline Direct Injection Technology of Automotive Gasoline Engine. Trans. Chin. Soc. Agric. Mach. 2003, 34, 168–171. [Google Scholar]
- Zhao, F.; Lai, M.C.; Harrington, D.L. Automotive spark-ignited direct-injection gasoline engines. Prog. Energy Combust Sci. 1999, 25, 437–562. [Google Scholar] [CrossRef]
- Pei, Y.Q.; Wang, K.; Zhang, D.; Liu, B.; Hu, T.G.; Ji, S.S. Spray Macroscopic Characteristics of GDI Injector Fueled with Ethanol Using Ultra-High Injection Pressure. Sci. Technol. 2018, 51, 755–762. [Google Scholar]
- Zhong, B.; Hong, W.; Su, Y.; Xie, F.X.; Han, L.P. Effects of Control Parameters on the Particulate Emission Characteristics of Turbocharged Gasoline Direct Injection Engine under Part Load. J. Xi’an Jiaotong Univer. 2016, 50, 95–100. [Google Scholar]
- Qian, J.Y.; Hou, C.W.; Wu, J.Y.; Gao, Z.X.; Jin, Z.J. Aerodynamics analysis of superheated steam flow through multi-stage perforated plates. Int. J. Heat Mass Transf. 2019, 141, 48–57. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Gao, Z.X.; Jin, Z.J. Mach number and energy loss analysis inside multi-stage Tesla valves for hydrogen decompression. Energy 2019, 179, 647–654. [Google Scholar] [CrossRef]
- Qian, J.Y.; Wu, J.Y.; Gao, Z.X.; Wu, A.; Jin, Z.J. Hydrogen decompression analysis by multi-stage Tesla valves for hydrogen fuel cell. Int. J. Hydrog. Energy 2019, 44, 13666–13674. [Google Scholar] [CrossRef]
- Lu, L.; Fu, X.; Ryu, S.; Yin, Y.B.; Shen, Z.X. Comprehensive discussions on higher back pressure system performance with cavitation suppression using high back pressure. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2019, 233, 2442–2455. [Google Scholar] [CrossRef]
- Lu, L.; Xie, S.H.; Yin, Y.B.; Ryu, S. Experimental and numerical analysis on the surge instability characteristics of the vortex flow produced large vapor cavity in u-shape notch spool valve. Int. J. Heat Mass Transf. 2020, 146, 118882. [Google Scholar] [CrossRef]
- Li, L.F.; Su, Z.G.; Cong, Z.Q.; et al. Failure Analysis and Corrective Actions of High Pressure Oil-pump Cam for Direct Injection Gasoline Engine. Intern. Combust. Engines 2014, 4, 37–39. [Google Scholar] [CrossRef]
- Wang, J.; Fu, J.; Huang, G.C.; Li, Y.Z.; He, Y.H.; Zhang, Q.H.; Lei, G. Contact analysis and fatigue calculation of the cam mechanism of fuel system. Mach. Tool Hydraul. 2017, 45, 77–80. [Google Scholar] [CrossRef]
- Lei, G.; Zhang, X.; Lai, L. Structural strength analysis of high-pressure oil pump under fluid-solid coupling conditions. Mach. Tool Hydraul. 2016, 44, 74–81. [Google Scholar] [CrossRef]
- Liu, D. Constitutive Relation of Bodies about Non-Critical Static Friction. Eng. Mech. 1999, 16, 94–97. [Google Scholar]
- Liu, D. The Formula of Non-Critical Static Friction and Its Application. J. Gansu Sci. 2006, 18, 27–29. [Google Scholar]
- Guan, C. Calculation of Critical Parameters for Hertz Contact Between Cylinder and Rigid Plane. Bearing 2013, 8, 4–7. [Google Scholar]
- Zhu, S.D.; Fang, X.W.; Wu, M.D.; Wu, G.C.; Lu, M.J. Mechanical Engineering Material Performance Data Sheet; China Machine Press: Beijing, China, 1995; ISBN 7-111-04313-8. [Google Scholar]
- He, C. Fatigue Test Dada Treatment and P-S-N Curve Function. Automob. Technol. Mater. 2007, 4, 42–44. [Google Scholar]
- Niu, J.; Liu, G.; Tian, J.; Zhang, Y.X.; Meng, L.P. Comparison of Yield Strength Theories with Experimental Results. Eng. Mech. 2014, 31, 181–187. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).