Pressure Drop and Cavitation Analysis on Sleeve Regulating Valve
Abstract
1. Introduction
2. Numerical Method
2.1. Mathematical Model
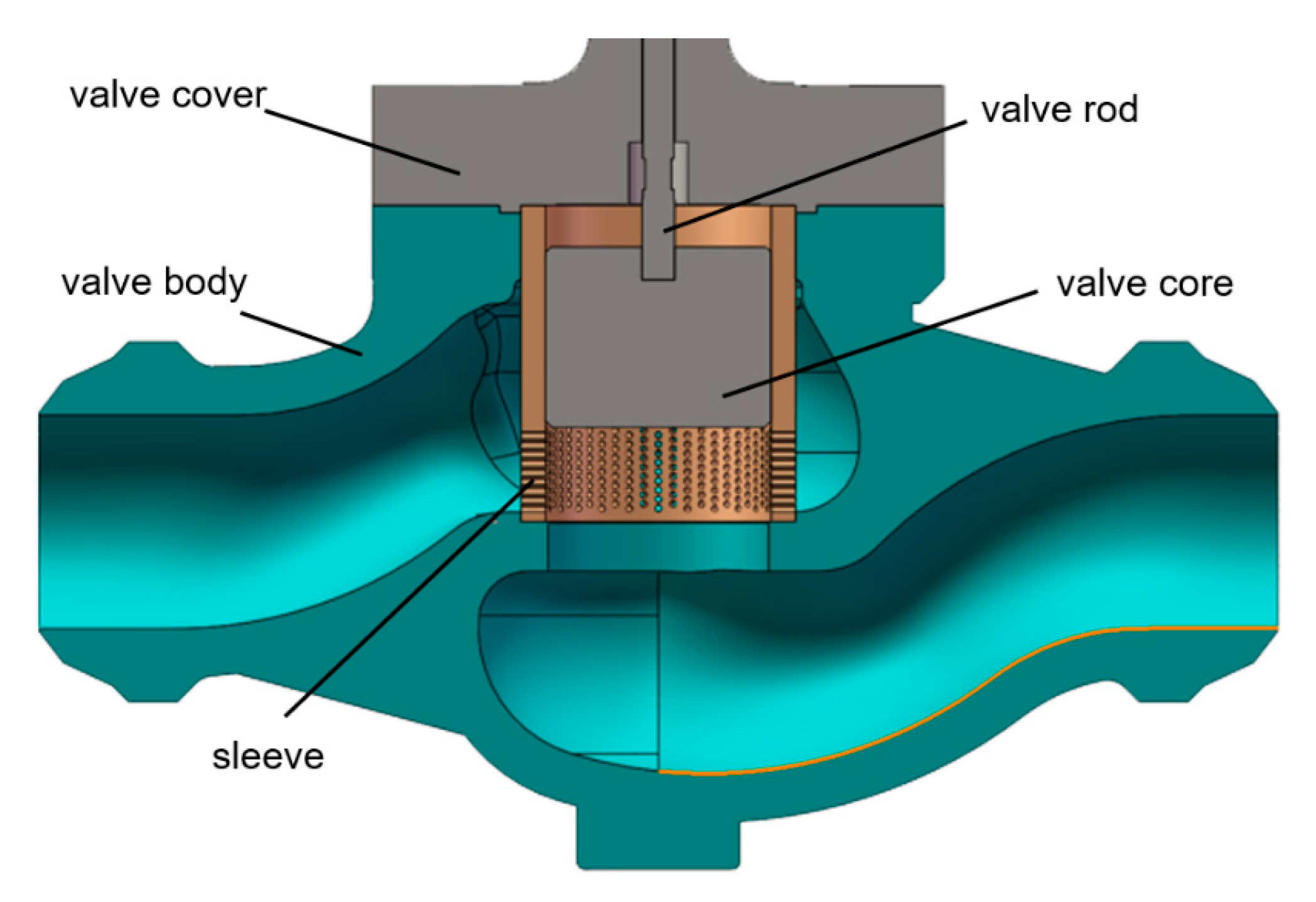
2.2. Geometrical Model
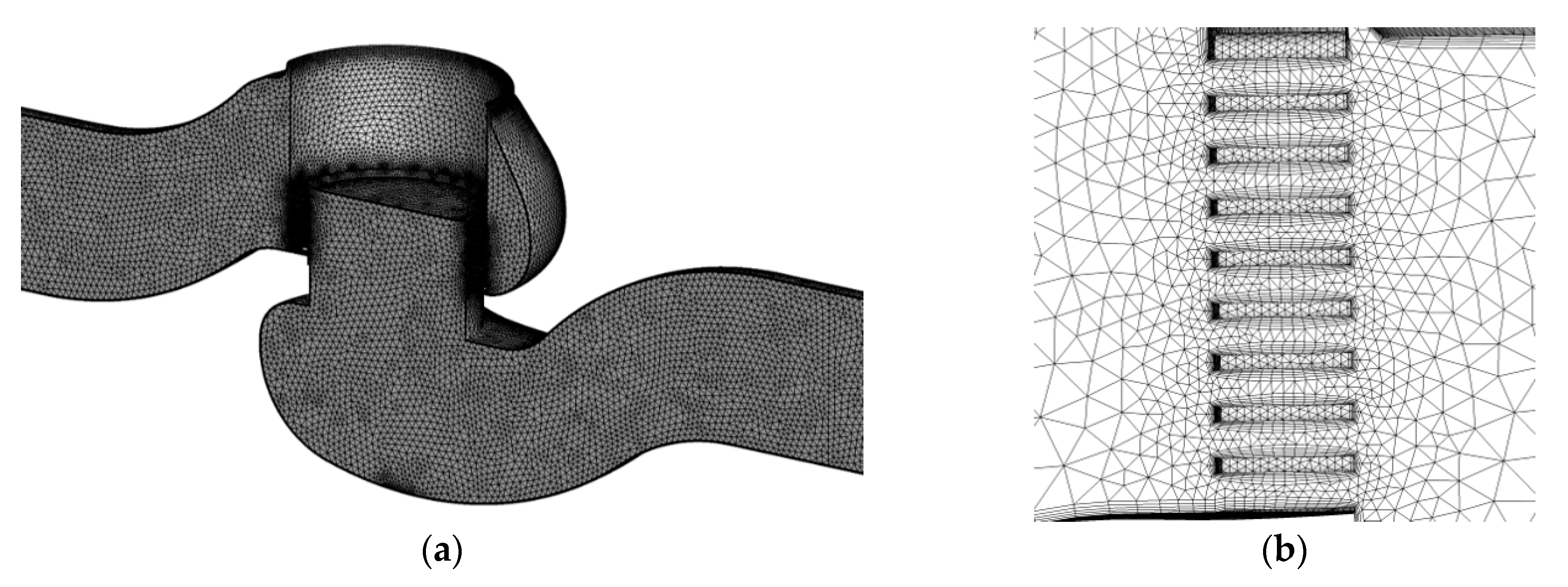
2.3. Mesh and Boundary Conditoms
3. Results and Discussion
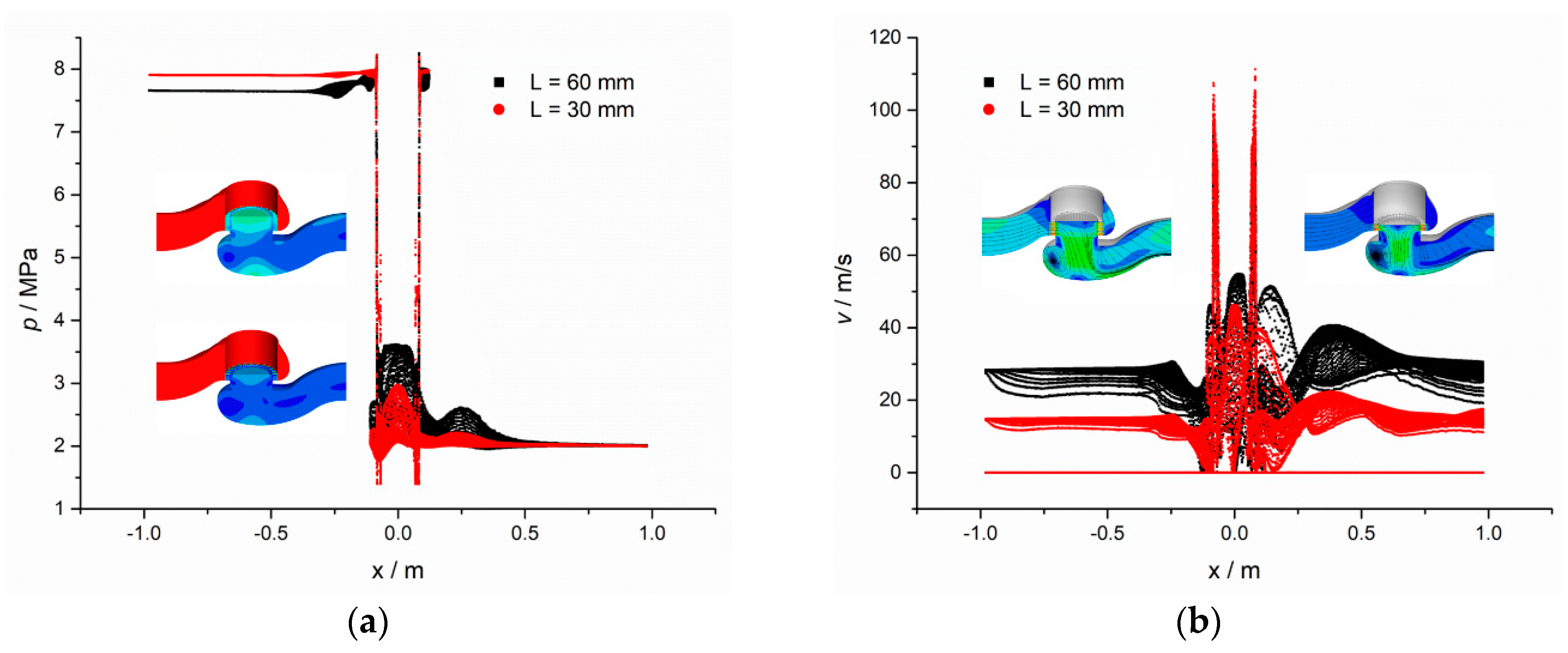
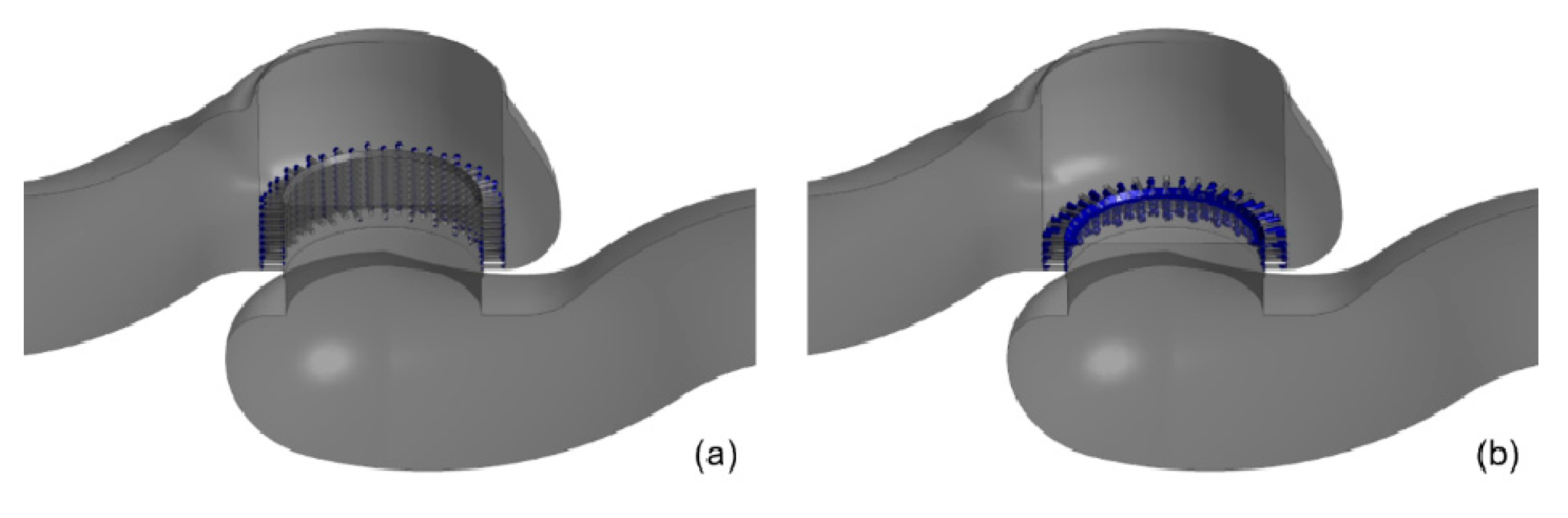
3.1. Comparsion between Full Opening State and Half Opening State
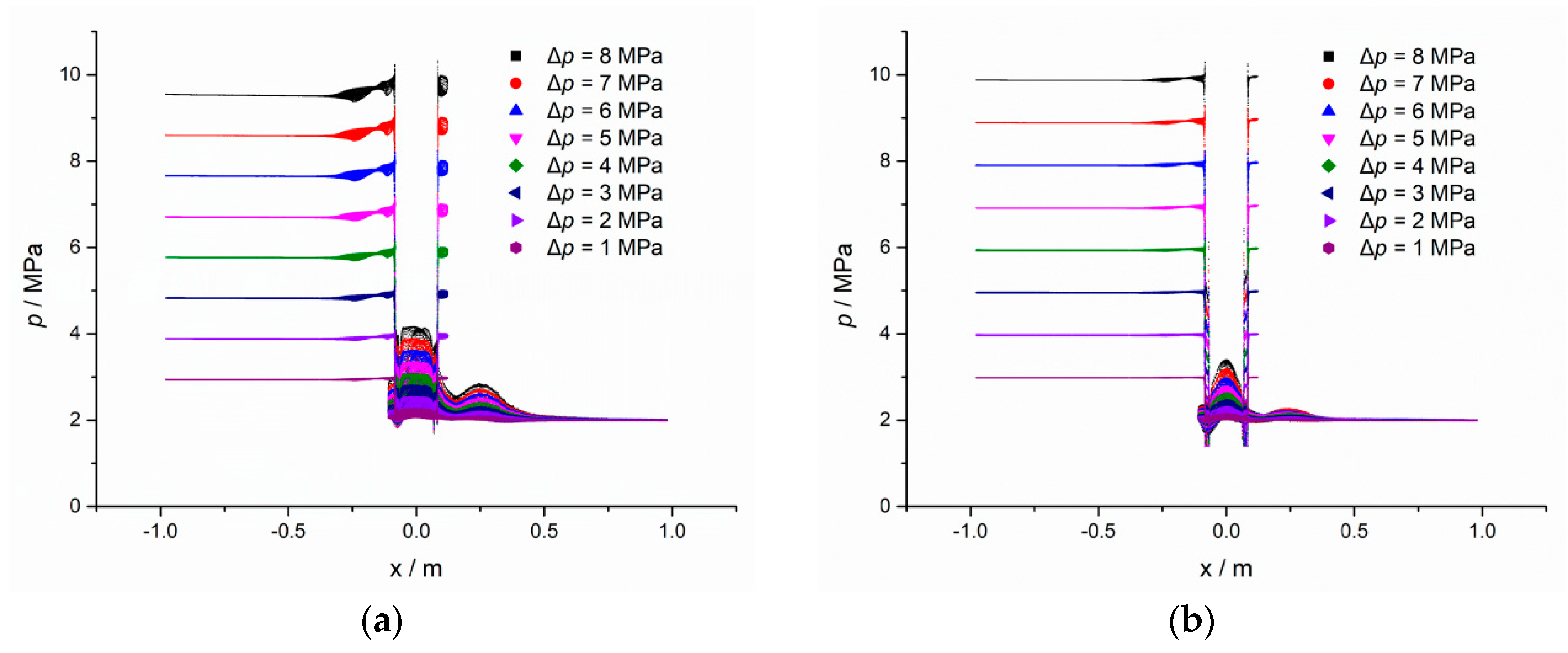
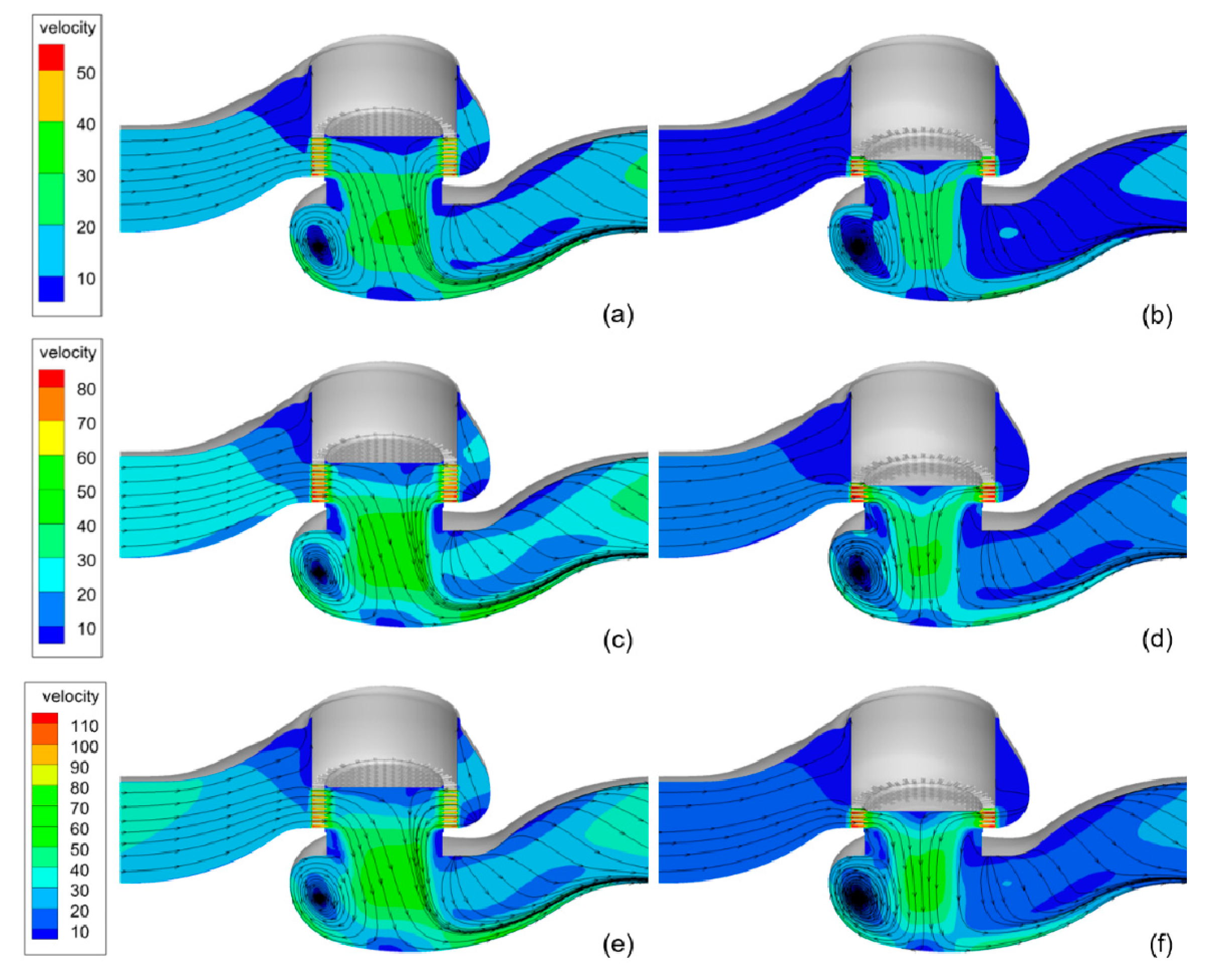
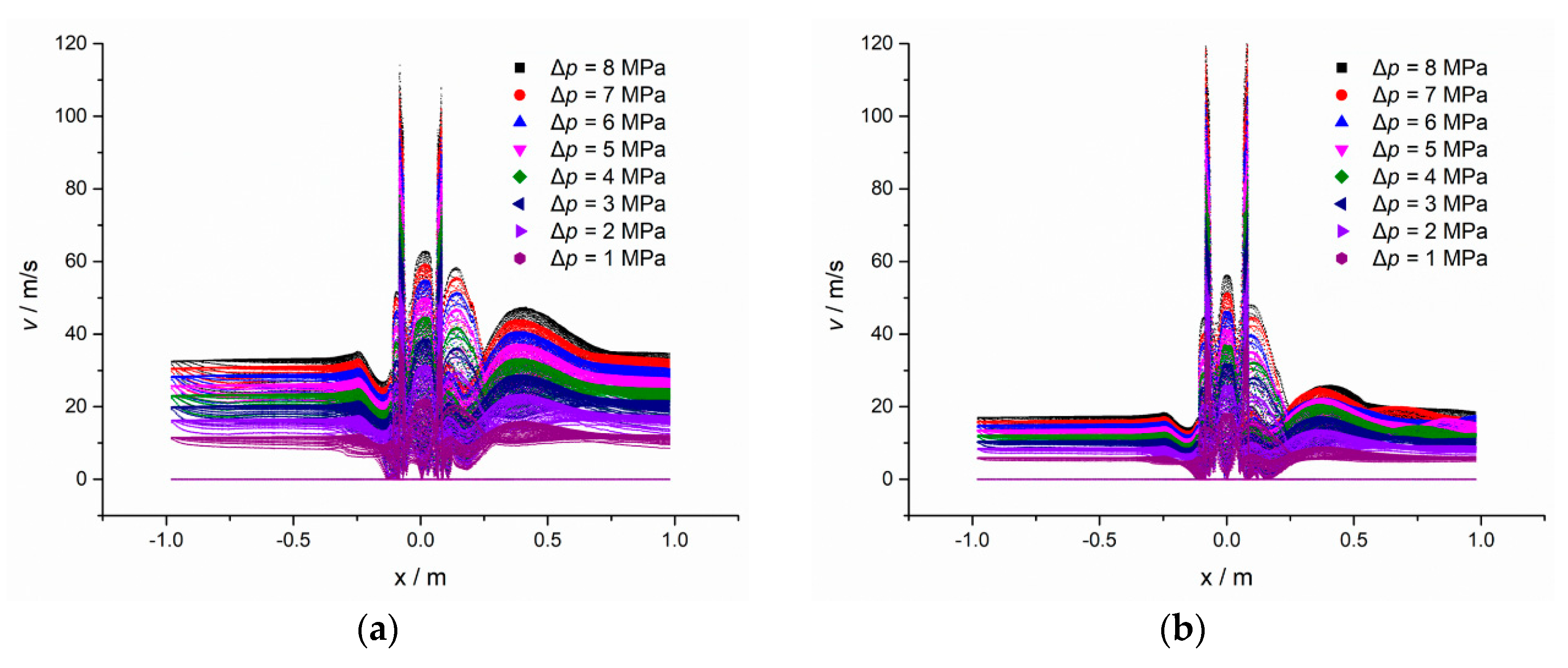
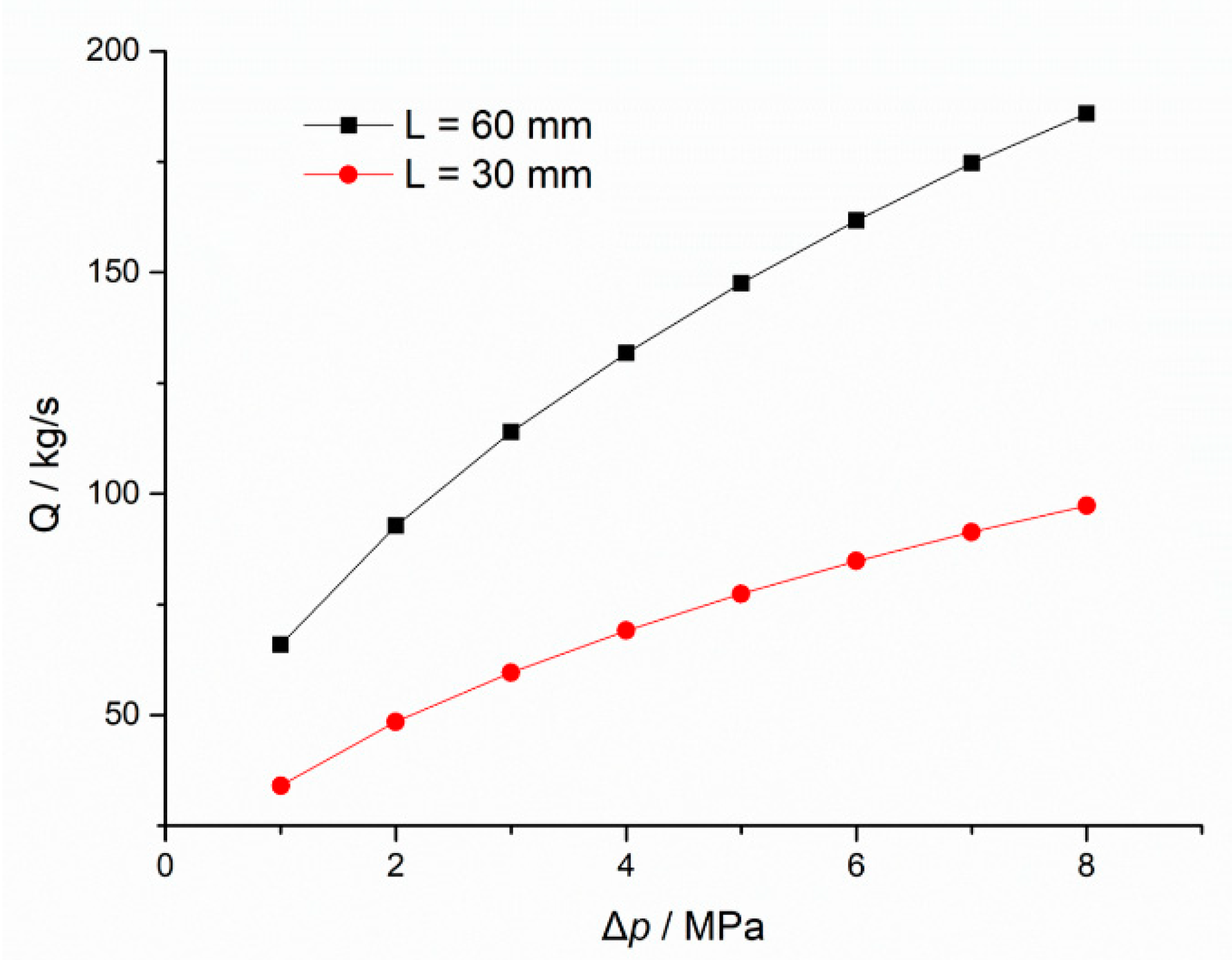
3.2. Flow Field Analysis for Different Pressure Difference
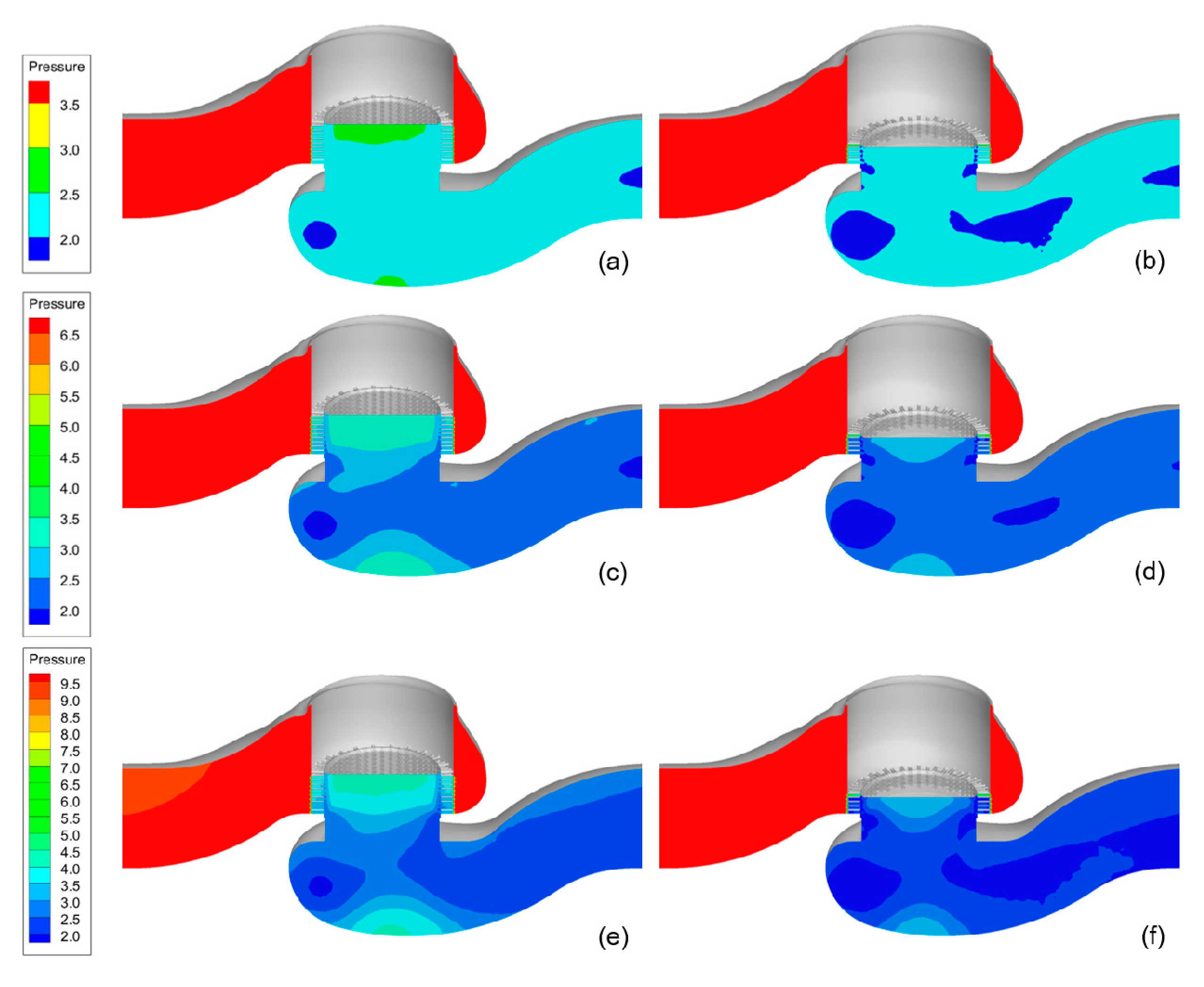
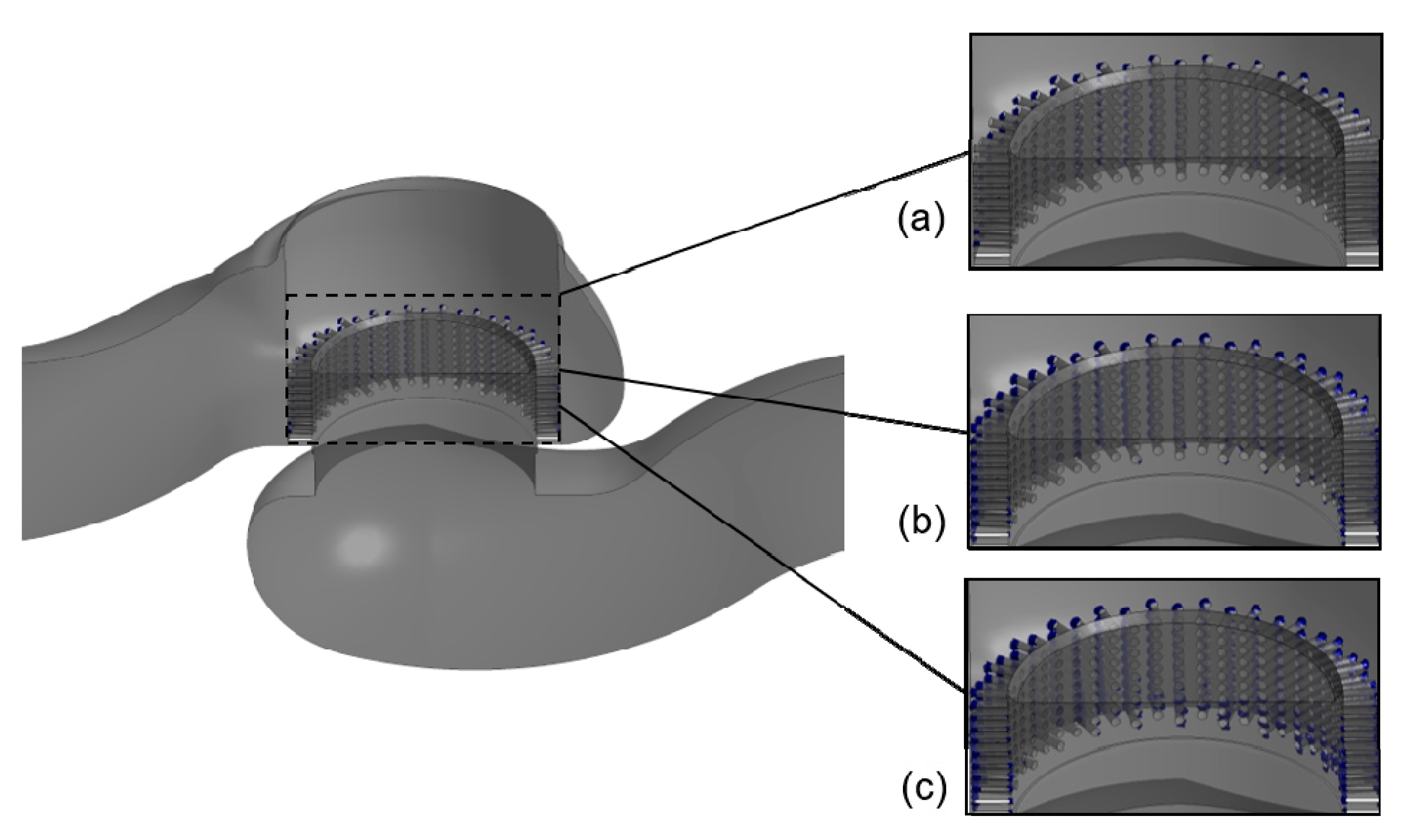
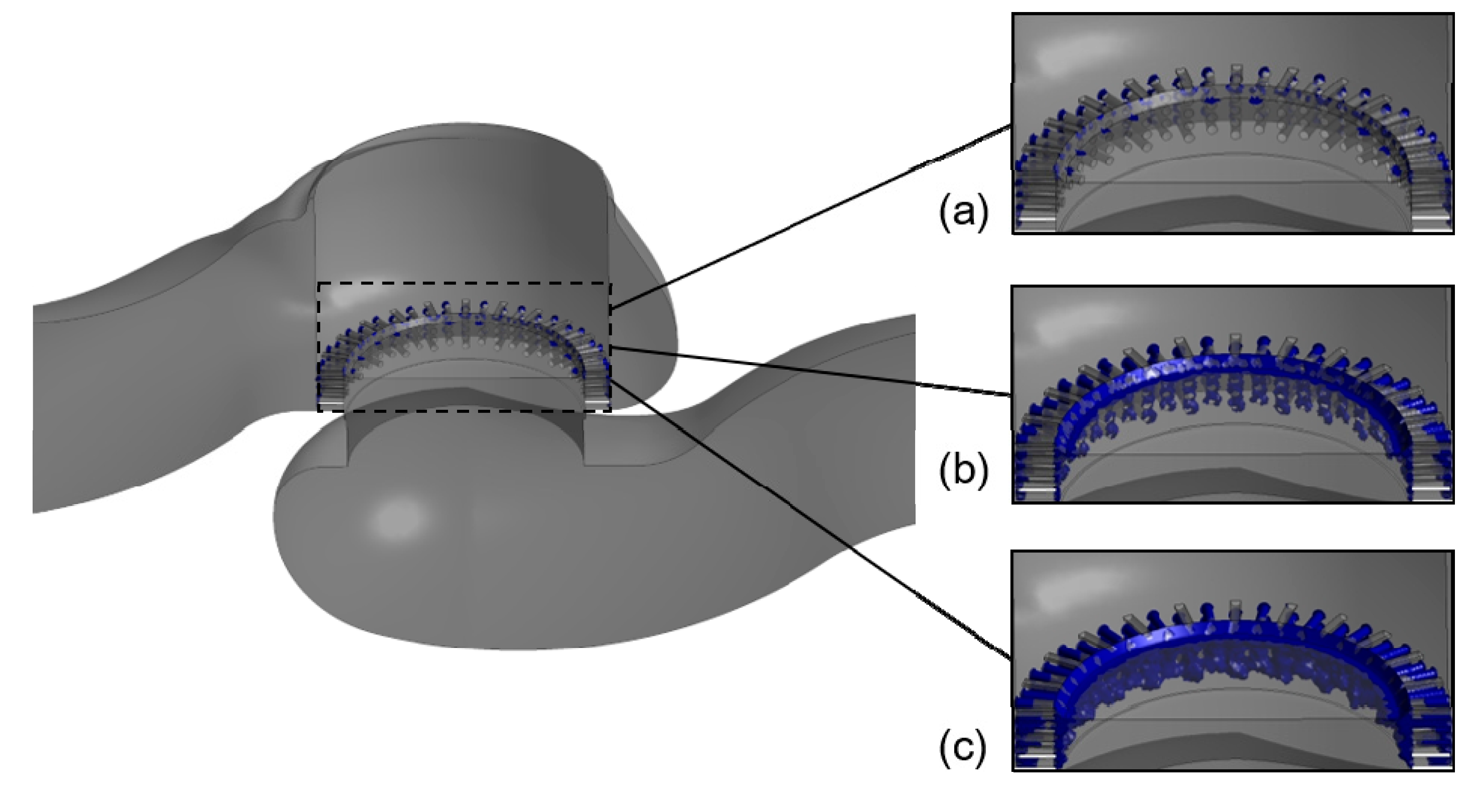
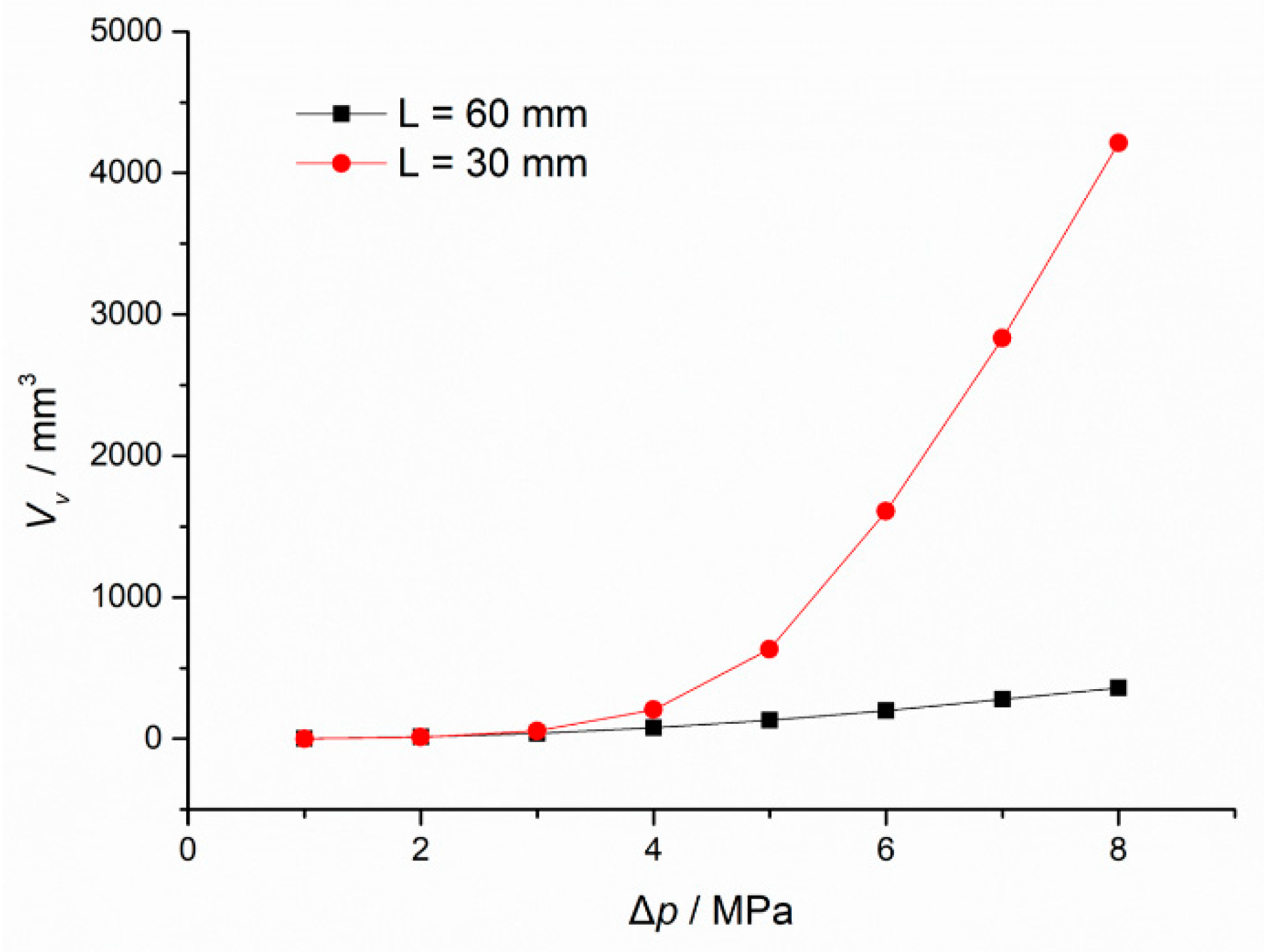
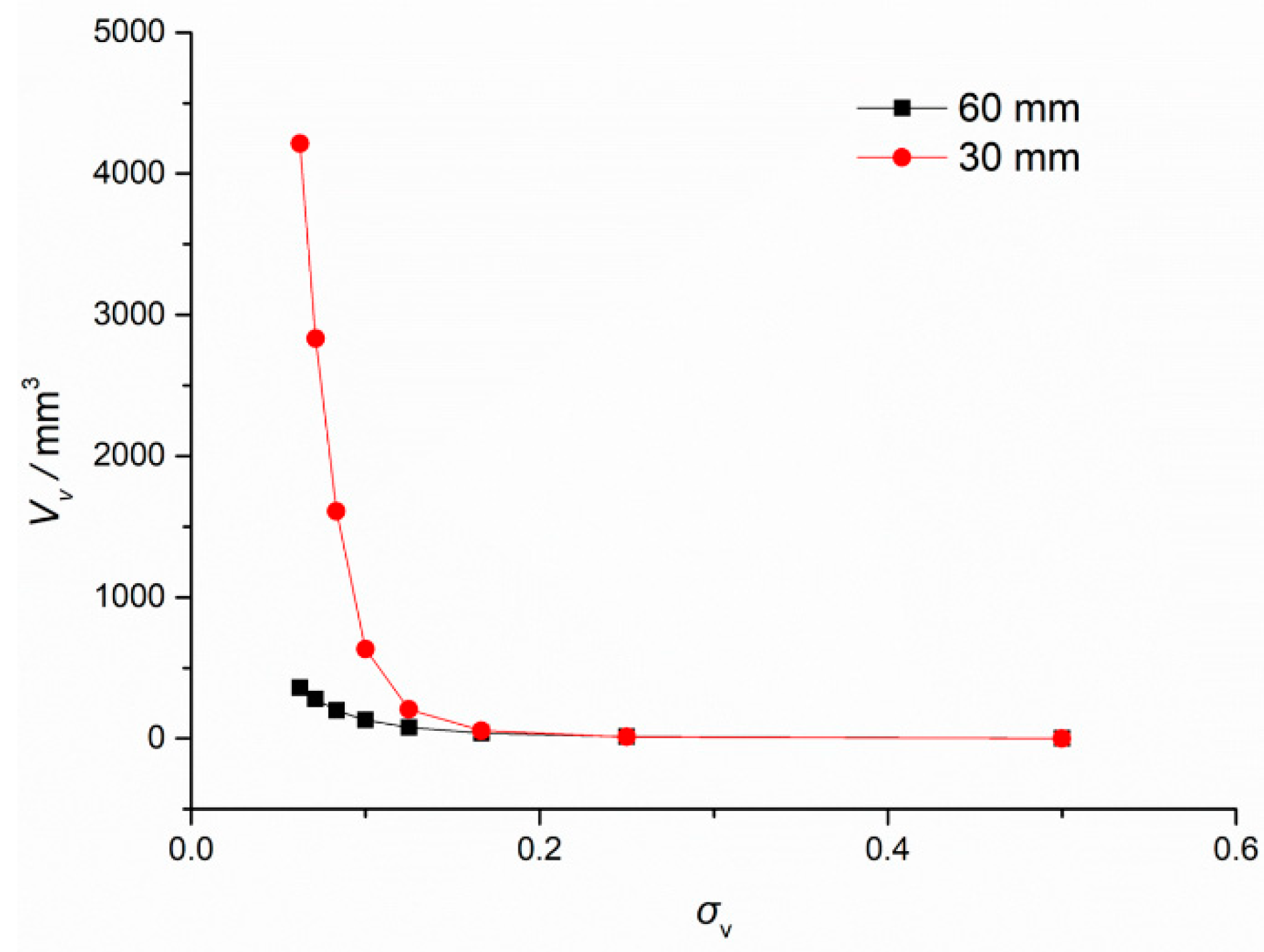
3.3. Cavitation Distribution Analysis for Difference Pressure Differences
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| p | pressure (MPa) |
| pv | saturation pressure of water (MPa) |
| t | time (s) |
| v | mass average velocity (m/s) |
| Vv | total vapor volume (m3) |
| Rb | bubble radius (m) |
| Rc | rates of breaking of vapor bubbles |
| α | vapor volume fraction |
| n | bubble number density |
| ρm | mixture density (kg/m³) |
| ρl | liquid density (kg/m³) |
| ρv | vapor density (kg/m³) |
| μm | mixture dynamic viscosity (Pa·s) |
| μl | liquid dynamic viscosity (Pa·s) |
| μv | vapor dynamic viscosity (Pa·s) |
| μt | turbulent viscosity (Pa·s) |
| vv | vapor phase velocity (m/s) |
| L | valve core displacement (mm) |
References
- Long, X.; Zhang, Y.; Wang, J.; Xu, M.; Lyu, Q.; Ji, B. Experimental investigation of the global cavitation dynamic behavior in a venturi tube with special emphasis on the cavity length variation. Int. J. Multiph. Flow 2017, 89, 290–298. [Google Scholar] [CrossRef]
- Liu, H.; Cao, S.; Luo, X. Study on the effect of inlet fluctuation on cavitation in a cone flow channel. ASME J. Fluids Eng. 2015, 137, 051301. [Google Scholar]
- Kim, J.; Song, S.J. Measurement of temperature effects on cavitation in a turbopump inducer. ASME J. Fluids Eng. 2016, 138, 011304. [Google Scholar] [CrossRef]
- Xiao, L.; Long, X. Cavitating flow in annular jet pumps. Int. J. Multiph. Flow 2015, 71, 116–132. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, W.; Pan, D.; Dubuisson, M. Numerical and experimental investigation of tip leakage vortex cavitation patterns and mechanisms in an axial flow pump. ASME J. Fluids Eng. 2015, 137, 121103. [Google Scholar] [CrossRef]
- Zhu, B.; Hongxun, C. Analysis of the staggered and fixed cavitation phenomenon observed in centrifugal pumps employing a gap drainage impeller. ASME J. Fluids Eng. 2016, 139, 031301. [Google Scholar] [CrossRef]
- Wang, C.; Hu, B.; Zhu, Y.; Luo, C.; Cheng, L. Numerical study on the gas-water two-phase flow in the self-priming process of self-priming centrifugal pump. Processes 2019, 7, 330. [Google Scholar] [CrossRef]
- Qian, J.; Chen, M.; Liu, X.; Jin, Z. A numerical investigation of flow of nanofluids through a micro Tesla valve. J. Zhejiang Univ. Sci. A 2019, 20, 50–60. [Google Scholar] [CrossRef]
- Qian, J.; Gao, Z.; Hou, C.; Jin, Z. A comprehensive review of cavitation in valves: Mechanical heart valves and control valves. Bio-Design Manuf. 2019, 2, 119–136. [Google Scholar] [CrossRef]
- Hassis, H. Noise caused by cavitating butterfly and monovar valve. J. Sound Vib. 1999, 225, 515–526. [Google Scholar] [CrossRef]
- Herbertson, L.H.; Reddy, V.; Manning, K.B.; Welz, J.P.; Deutsch, S. Wavelet transforms in the analysis of mechanical heart valve cavitation. J. Biomech. Eng. 2006, 128, 217–222. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Lin, W.; Tsukiji, T. Investigation of cavitation near the orifice of hydraulic valves. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2006, 220, 253–265. [Google Scholar] [CrossRef]
- Jin, Z.; Gao, Z.; Li, X.; Qian, J. Cavitation flow through a micro-orifice. Micromachines 2019, 10, 191. [Google Scholar] [CrossRef] [PubMed]
- Jia, W.H.; Yin, C.B. Numerical analysis and experiment research of cylinder valve port cavitating flow. In Proceedings of the Fourth International Conference on Experimental Mechanics, Singapore, 18–20 November 2009. [Google Scholar]
- Liu, Y.H.; Ji, X.W. Simulation of cavitation in rotary valve of hydraulic power steering gear. Sci. China 2009, 52, 3142–3148. [Google Scholar] [CrossRef]
- Lu, L.; Zou, J.; Fu, X. The acoustics of cavitation in spool valve with U-notches. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2011, 226, 540–549. [Google Scholar] [CrossRef]
- Li, S.; Aung, N.Z.; Zhang, S.; Cao, J.; Xue, X. Experimental and numerical investigation of cavitation phenomenon in flapper-nozzle pilot stage of an electrohydraulic servo-valve. Comput. Fluids 2013, 88, 590–598. [Google Scholar] [CrossRef]
- Kudźma, Z.; Stosiak, M. Studies of flow and cavitation in hydraulic lift valve. Arch. Civil Mech. Eng. 2015, 15, 951–961. [Google Scholar] [CrossRef]
- Qu, W.S.; Tan, L.; Cao, S.L.; Xu, Y.; Huang, J.; Xu, Q.H. Experiment and numerical simulation of cavitation performance on a pressure-regulating valve with different openings. IOP Conf. Ser. Mater. Sci. Eng. 2015, 72, 042035. [Google Scholar] [CrossRef]
- Ulanicki, B.; Picinali, L.; Janus, T. Measurements and analysis of cavitation in a pressure reducing valve during operation—A Case Study. Procedia Eng. 2015, 119, 270–279. [Google Scholar] [CrossRef][Green Version]
- Deng, J.; Pan, D.; Xie, F.; Shao, X. Numerical investigation of cavitation flow inside spool valve with large pressure drop. J. Phys. Conf. Ser. 2015, 656, 012067. [Google Scholar] [CrossRef]
- Ou, G.F.; Xu, J.; Li, W.Z.; Chen, B. Investigation on cavitation flow in pressure relief valve with high pressure differentials for coal liquefaction. Procedia Eng. 2015, 130, 125–134. [Google Scholar] [CrossRef]
- Yi, D.L.; Lu, L.; Zou, J.; Fu, X. Interactions between poppet vibration and cavitation in relief valve. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 1447–1461. [Google Scholar] [CrossRef]
- Okita, K.; Miyamoto, Y.; Kataoka, T.; Takagi, S.; Kato, H. Mechanism of noise generation by cavitation in hydraulic relief valve. J. Phys. Conf. Ser. 2015, 656, 012104. [Google Scholar] [CrossRef]
- Lu, L.; Xie, S.; Yin, Y.; Ryu, S. Experimental and numerical analysis on the surge instability characteristics of the vortex flow produced large vapor cavity in u-shape notch valve. Int. J. Heat Mass Transfer. 2020, 146, 118882. [Google Scholar] [CrossRef]
- Jin, Z.; Gao, Z.; Qian, J.; Wu, Z.; Sunden, B. A parametric study of hydrodynamic cavitation inside globe valve. ASME J. Fluids Eng. 2018, 140, 031208. [Google Scholar] [CrossRef]
- Qian, J.; Chen, M.; Gao, Z.; Jin, Z. Mach number and energy loss analysis inside multi-stage Tesla valves for hydrogen decompression. Energy 2019, 179, 647–654. [Google Scholar] [CrossRef]
- Qian, J.; Wu, J.; Gao, Z.; Wu, A.; Jin, Z. Hydrogen decompression analysis by multi-stage Tesla valves for hydrogen fuel cell. Int. J. Hydrogen Energy 2019, 44, 13666–13674. [Google Scholar] [CrossRef]
- Tao, J.; Lin, Z.; Ma, C.; Ye, J.; Zhu, Z.; Li, Y.; Mao, W. An experimental and numerical study of regulating performance and flow loss in a v-port ball valve. ASME. J. Fluids Eng. 2020, 142, 021207. [Google Scholar] [CrossRef]
- Baran, G.; Catana, I.; Magheti, I.; Safta, C.A.; Savu, M. Controlling the cavitation phenomenon of evolution on a butterfly valve. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012100. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, S.; Luo, X.; Shi, W. New approach of suppressing cavitation in water hydraulic components. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 4022–4034. [Google Scholar]
- Shi, W.; Cao, S.; Luo, X.; Zhang, Z.; Zhu, Y. Experimental research on the cavitation suppression in the water hydraulic throttle valve. J. Press. Vessel Technol. 2017, 139, 051302. [Google Scholar]
- Chern, M.J.; Hsu, P.H.; Cheng, Y.J.; Tseng, P.Y.; Hu, C.M. Numerical study on cavitation occurrence in globe valve. J. Energy Eng. 2013, 139, 25–34. [Google Scholar] [CrossRef]
- Qian, J.; Hou, C.; Wu, J.; Gao, Z.; Jin, Z. Aerodynamics analysis of superheated steam flow through multi-stage perforated plates. Int. J. Heat Mass Transfer 2019, 141, 48–57. [Google Scholar] [CrossRef]
- Yaghoubi, H.; Madani, S.A.H.; Alizadeh, M. Numerical study on cavitation in a globe control valve with different numbers of anti-cavitation trims. J. Cent. South Univ. 2018, 25, 2677–2687. [Google Scholar] [CrossRef]
- Liu, Q.; Ye, J.; Zhang, G.; Lin, Z.; Xu, H.; Jin, H.; Zhu, Z. Study on the metrological performance of a swirlmeter affected by flow regulation with a regulating valve. Flow Meas. Instrum. 2019, 67, 83–94. [Google Scholar] [CrossRef]
- Qian, J.; Wei, L.; Jin, Z.; Wang, J.; Zhang, H. CFD analysis on the dynamic flow characteristics of the pilot-control globe valve. Energy Convers. Manag. 2014, 87, 220–226. [Google Scholar] [CrossRef]
- Hou, C.; Qian, J.; Chen, F.; Jiang, W.; Jin, Z. Parametric analysis on throttling components of multi-stage high pressure reducing valve. Appl. Therm. Eng. 2018, 128, 1238–1248. [Google Scholar] [CrossRef]
- Schnerr, G.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]

| Grids | Flow Rate (kg/s) | Volume Fraction |
|---|---|---|
| 1,451,696 | 162.72 | 0.1296 |
| 1,705,067 | 162.14 | 0.2272 |
| 2,055,352 | 168.31 | 0.2676 |
| 2,407,840 | 167.74 | 0.2829 |
| 2,708,138 | 167.37 | 0.2585 |
| 3,138,669 | 167.01 | 0. 2323 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, C.; Jiang, C.-H.; Zhang, H.; Wu, J.-Y.; Jin, Z.-J. Pressure Drop and Cavitation Analysis on Sleeve Regulating Valve. Processes 2019, 7, 829. https://doi.org/10.3390/pr7110829
Qiu C, Jiang C-H, Zhang H, Wu J-Y, Jin Z-J. Pressure Drop and Cavitation Analysis on Sleeve Regulating Valve. Processes. 2019; 7(11):829. https://doi.org/10.3390/pr7110829
Chicago/Turabian StyleQiu, Chang, Cheng-Hang Jiang, Han Zhang, Jia-Yi Wu, and Zhi-Jiang Jin. 2019. "Pressure Drop and Cavitation Analysis on Sleeve Regulating Valve" Processes 7, no. 11: 829. https://doi.org/10.3390/pr7110829
APA StyleQiu, C., Jiang, C.-H., Zhang, H., Wu, J.-Y., & Jin, Z.-J. (2019). Pressure Drop and Cavitation Analysis on Sleeve Regulating Valve. Processes, 7(11), 829. https://doi.org/10.3390/pr7110829






