1. Introduction
Chemical industry parks are built in development zones and are based on the development of oil and chemicals. They have unique inner features, and their most important characteristic is that they are potentially dangerous. Due to the nature of chemical products, chemical industrial parks are potentially high risk: chemical plants are concentrated in the parks, and there are many major hazards such as inflammable, explosive, and toxic chemicals within them. When an accident occurs, the consequences can be very serious. Historical examples include the Bhopal tragedy [
1], the Piper Alpha [
2], the Flixborough disaster [
3], BP Texas City [
4], the West Fertilizer explosion [
5], the Tianjin explosion, etc. [
6] (details of these events are shown in
Table 1).Therefore, the safety management of chemical industry parks is very important.
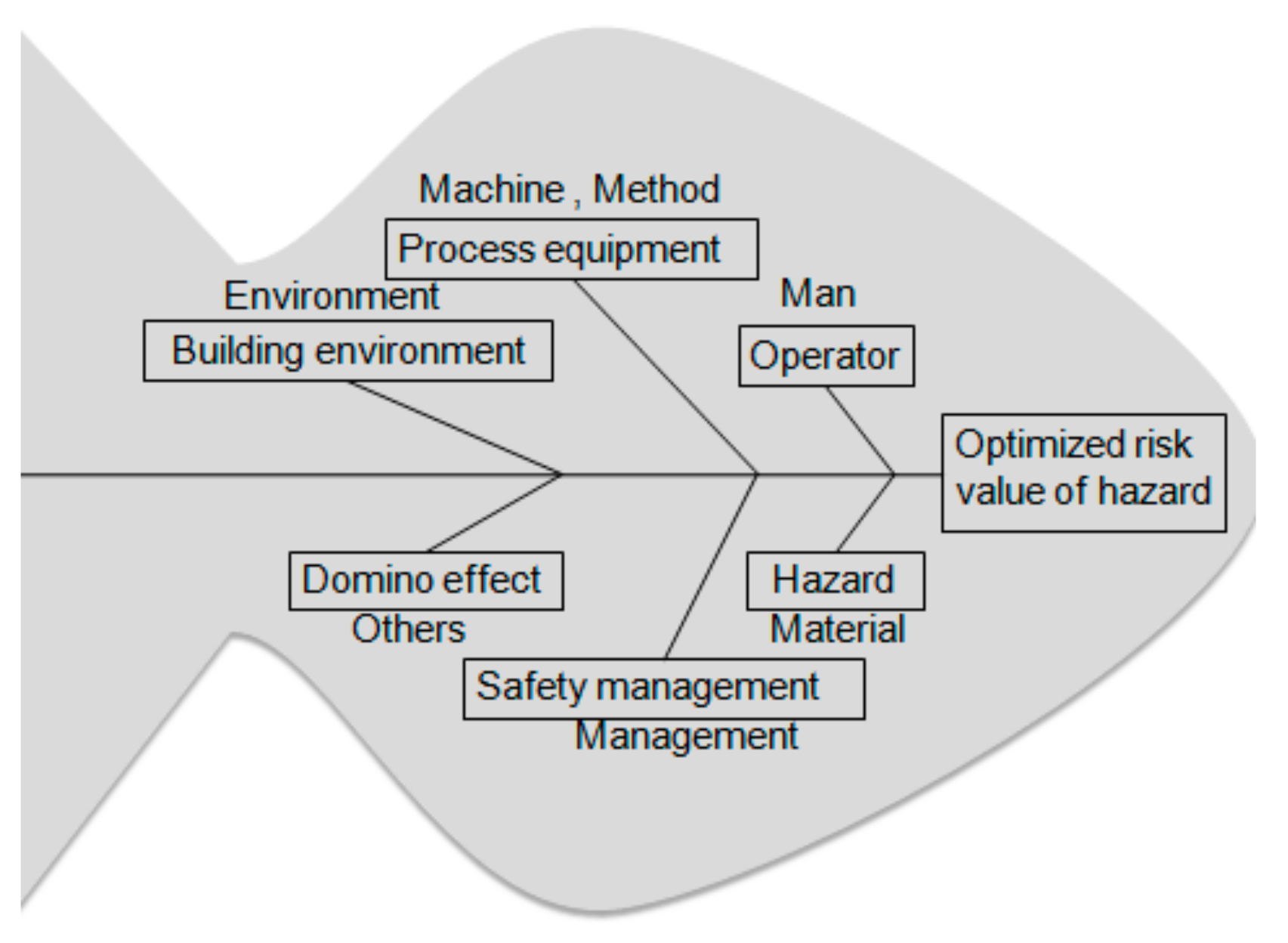
To prevent and control major chemical safety accidents, we need to take appropriate measures to strengthen the management of chemical industry parks. There are many factors affecting chemical safety accidents, mainly human, machine, material, method, environment, management, and others; if we can comprehensively monitor and manage these safety factors, we can detect potential safety problems in a timely manner and immediately rectify and improve them to prevent major accidents. Targeted management of the risk level of dangerous chemicals in chemical industry parks can be used to fully mobilize the limited resources of government departments and plants. The focus of such management, rational distribution, is one of the most ideal management tools currently used in chemical industry parks. Therefore, chemical industry parks should implement a combination of key management of major chemical hazards and real-time monitoring.
Comparatively more research has been invested in hazard risk assessment, and quantitative risk assessment methods have been used in the overall risk assessment and safety planning of chemical industry parks, for example, the U.K.’s Canvey Island research project in 1978, Italy’s Ravenna research project in 1979, and the Rijnmond research project in the Netherlands in 1979 [
7]. In 2002, the European Union research center launched the ARAMIS(accidental risk assessment methodology for industries) project and provided a comprehensive evaluation system [
8,
9] as a part of this project. In 2004, Khan F.I, Amyotte P.R proposed the comprehensive essential safety index (I2SI), which consists of two main sub-indices: the risk index (HI) and the underlying safety potential index [
10]. Khakzad et al. [
11] applied bow-tie and Bayesian network methods in conducting quantitative risk analysis of drilling operations. Abimbola et al. [
12] performed safety and risk analysis of a managed pressure drilling operation using Bayesian networks. Goerlandt et al. [
13] presented a review focusing on the validation of QRA (quantitative risk analysis) in a safety context. Valerie DE Dianous et al. [
14] studied the consequences and causes of all kinds of accidents faced by plants in the chemical industry and emphasized the use of the bow structure diagram method. Christian Delvosalle et al. [
15] analyzed the possible accident scenarios for various major hazards. Bahman [
16] proposed a new approach, which can predict and assess the impact of an accident in one process unit on the other process units that could be affected. Jonkman S.N et al. [
17] gave a model of quantitative risk measures for loss of life and economic damage. Selvik J.T et al. presented and discussed the RCM (reliability centered maintenance) framework to improve risk and uncertainty assessments. The QRA techniques used are based on standard methods, such as fault tree and event tree analysis, but also on more tailor-made methods and approaches to meet the great diversity of processes, hazardous materials, equipment types, and control schemes that characterize the chemical processing industry [
18,
19,
20]. In chemical risk research, governments are constantly exploring the best ways to solve problems via collaboration. Control standards and procedures related to major hazards are promulgated by the United Kingdom, France, the Netherlands, etc. [
21,
22,
23,
24,
25]. In terms of risk criteria, Kletz [
7] proposed that the highest risk of death among residents in the vicinity of chemical facilities is 10
−6 per year, and some companies in the United Kingdom, the United States, and Denmark use this risk standard. According to the risk assessment methods of major hazards and different occasions, the Dutch government has also established reference values for personal and social risks relating to chemical plants [
26,
27]. A risk index was devised to allow the assessment of the risk level originating from a given installation or site over the affected zone, and a Bayesian network methodology was developed to estimate the total probability of a major accident in a chemical plant [
28,
29,
30,
31,
32]. The current research detailed above, which is mainly used for chemical industry park planning and analysis, cannot be easily used for the dynamic safety management of existing chemical industry parks; in addition, only the main hazards themselves were considered in these studies, and other major factors that affect safety accidents, such as human, machine, material, method, and environment, were not considered.
To sum up, there are more mature safety assessment methods that have been developed at home and abroad, but these are mainly relatively static assessment methods for the planning of chemical industry parks. For example, Nancy Leveson [
33] presented a new accident model founded on basic systems theory concepts. The use of such a model provides a theoretical foundation for the introduction of new unique types of accident analysis, hazard analysis, and accident prevention strategies. Nancy Leveson [
34] also described a new method for identifying system-specific leading indicators based on the accident causal relationship of the STAMP (System-Theory Accident Model and Process) model and tools that were intended to be built on the model. There are fewer methods of dynamic assessment generally, and they do not take into account factors beyond the hazards themselves, such as the dynamic process of change in the production and storage of hazards or the combined effects of operators, process, equipment, the building environment, safety management, and the domino effect [
35]. The question that remains, and which we address in this paper, is how to carry out dynamic and quantitative assessment of the major hazards in a chemical industry park and provide an assessment result of the dangers in the chemical plants to the park managers promptly and intuitively, so that the park managers can detect the potential safety hazards in time and avoid the occurrence of major safety accidents. The six influencing factors of the model are all dynamic, and each inspection time point has a comprehensive quantitative value. The dynamic form can ensure that the calculated risk value is a real-time quantitative value, which is in line with the actual situation on site and ensures that this research will have great practical significance.
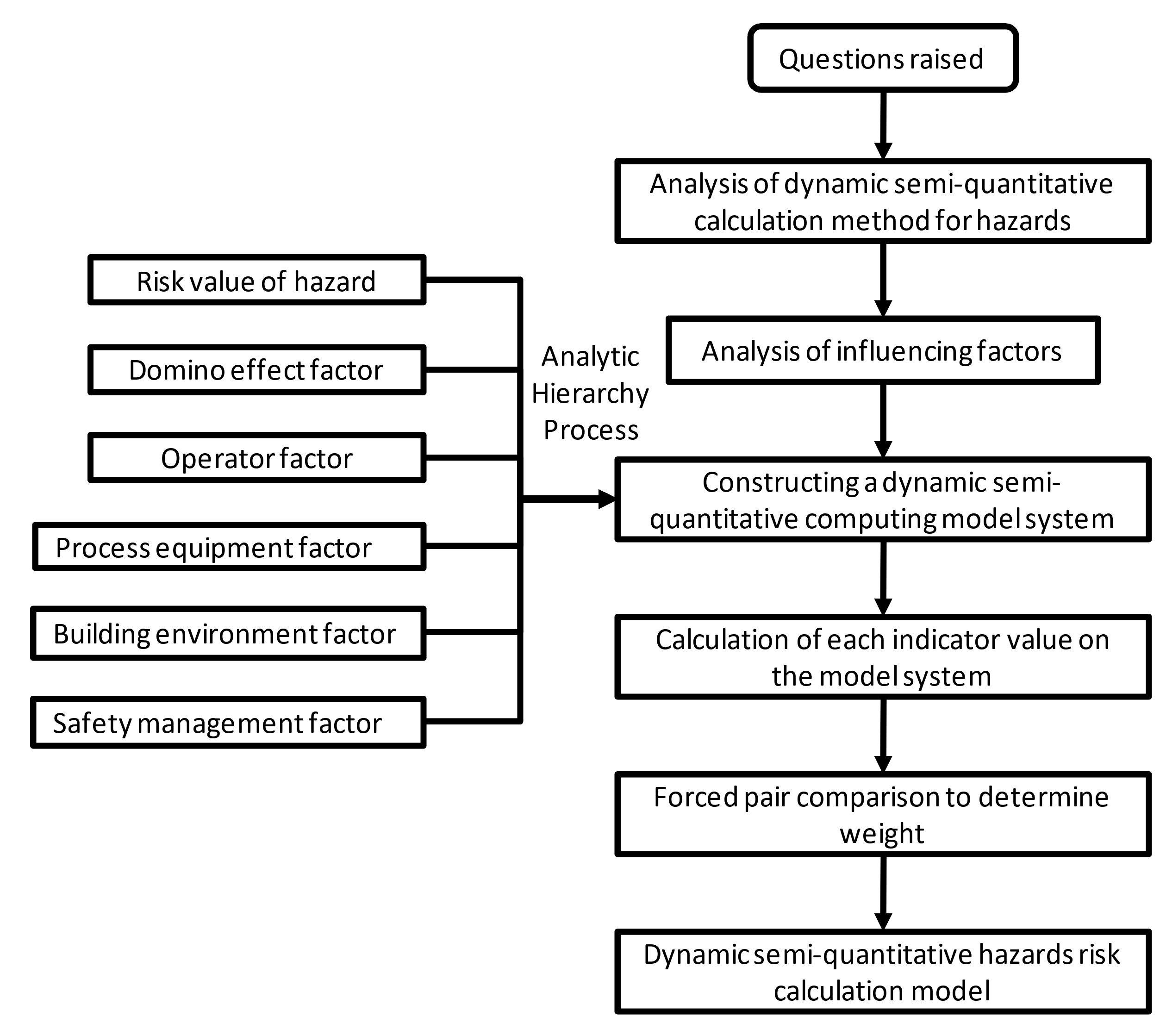
Therefore, this article is based on the research of dynamic semi-quantitative real-time monitoring and management methods for major hazards in chemical industry parks as they relate to the operators, process/equipment, risk, building environment, safety management, and domino effect. We analyze and calculate these six factors and give a dynamic semi-quantitative calculation model of chemical hazards based on an analytical hierarchy process [
36]. Using this model, the risk value of each chemical plant in a park can be accurately calculated, and the safety hazards of each chemical plant can be found according to the risk value. Our focus is on the improvement and tracking of safety hazards to reduce the probability of accidents.
3. Index Value Calculations via an Analytical Hierarchy Model
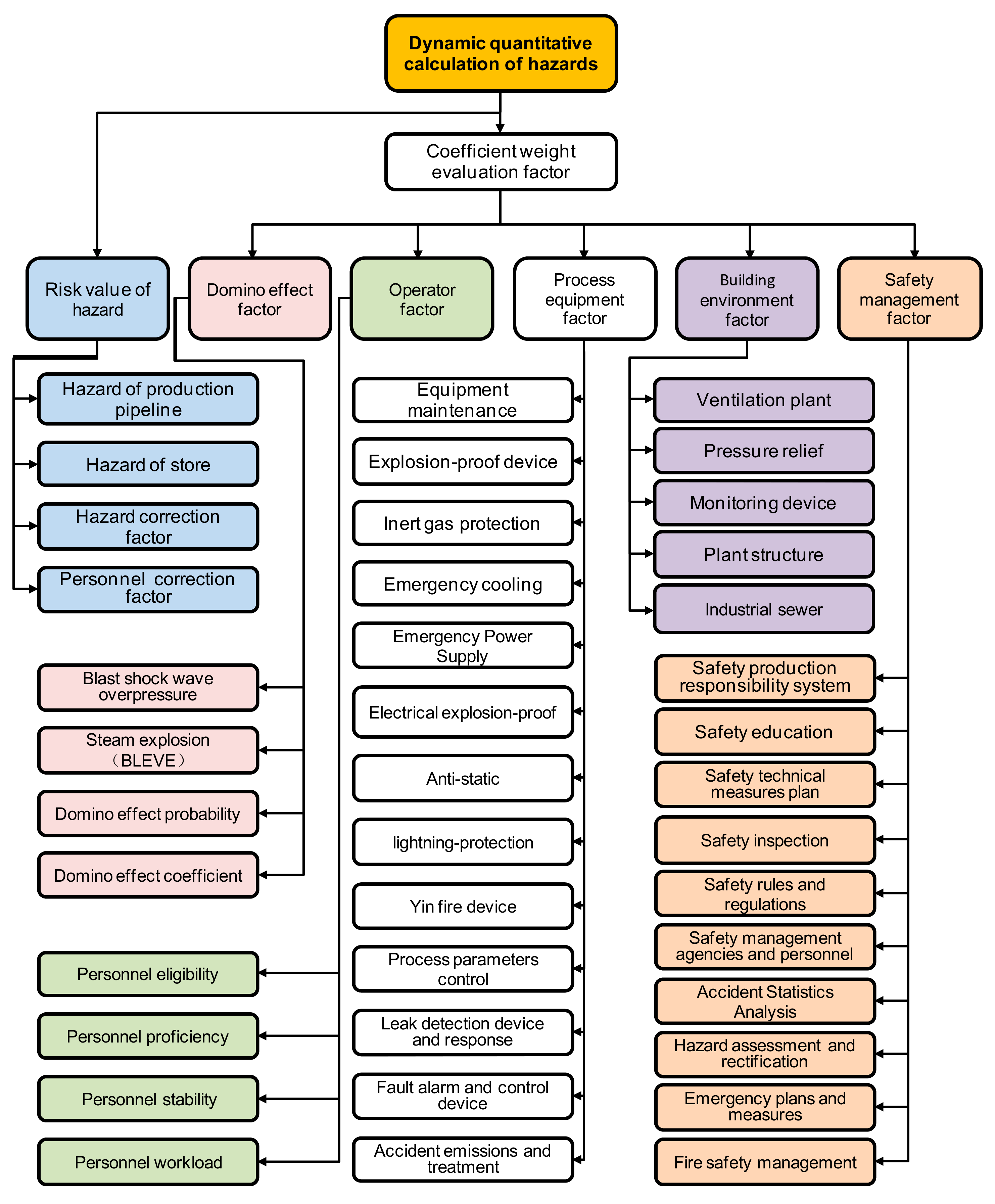
In the dynamic semi-quantitative calculation model for chemical hazards, the six weighting factors are the risk value factor of the hazard, domino effect factor, operator factor, process/equipment factor, building environment factor, and safety management factor. In this article we aimed to study the dynamic quantitative risk values of chemical hazards. The dynamic focus is on all quantitative and semi-quantitative data changes which need to be dynamically monitored, such as real-time changes in the output of hazards in the production pipeline according to the input value of the monitoring point. Therefore, a monitoring point setup matrix was chosen to calculate the overall dynamic quantitative data. The description of the letters used in the equations in this section is shown in
Table 8.
3.1. Risk Value Factor of a Hazard, Denoted a (Also R3)
From the previous analysis, we define the two matrix equations for the variable
q in the chemical hazards storage area and the variable
q’ in the production site, as shown in Equations (20) and (21).
When the chemical hazards in the storage area and production pipeline are determined, the correction factor and critical value of the hazard can be found in the table. The correction coefficient is
β, the chemical hazards storage critical mass is
Q, and the chemical hazards production site critical mass is
Q’, so the relative ratios in the available matrices are as shown in Equations (22) and (23).
According to Equations (2) to (4), we can calculate the risk value factor of hazard
ai as shown in Equation (24).
Therefore, the value of
a is as shown in Equation (25).
3.2. Domino Effect Factor, Denoted b
The parameters
q and
q’ can be read out from the risk value factors of a hazard, and their sum is a variable that affects the domino effect. The equation of total hazard mass can be obtained from Equations (20) and (21), and it is as shown in Equation (26).
We do not consider the impacts between various hazards, because the impact of each calculation is too complex to study here in detail. The
jth substance of all those where the monitoring point is located, defined as the data of the
jth row, can be obtained from Equation (26) and is shown in Equation (27).
3.2.1. Overpressure Explosion Model and Vapor Explosion Model Calculation
The specified overpressure explosion model is the Δp data set, the vapor explosion model is the q(r) data set, and b
1 is defined as shown in Equation (28).
- (1)
Overpressure explosion model
Taking the overpressure explosion model of the
ith monitoring point, we can get
from Equations (5) to (7), and (27), as shown in Equation (29).
We define the overpressure explosion model device container specification matrix as
with restrictions:
, according to the device container, to set the possible condition equations shown in
Table 9.
- (2)
Vapor explosion modell
Taking the vapor explosion model of the
ith monitoring point, we can get q
ji(r) and t
i from Equations (8) to (10), and (27), as shown in Equations (31) and (32).
We define the vapor explosion model device container specification matrix as shown in Equation (33).
With restrictions
, according to the device container, to set the possible condition equations in
Table 10.
3.2.2. Overpressure Explosion and Vapor Explosion Model Probability Calculations
We define the overpressure explosion probability as the
b3i data set and the vapor explosion probability as the
b’
3i data set; the explosion probability matrix can then be constructed as shown in Equations (34) to (36).
3.2.3. Domino Effect Coefficient
Because the multilayer domino effect is complicated, but the calculation method is the same, we only consider the domino effect for a single layer. According to Equation (12), the domino effect coefficient is as shown in Equation (37).
The output domino effect coefficient
b is as shown in Equation (38).
3.3. Operator Factor, Denoted c
In the calculation of the operator’s index coefficient, there are five items involved in the calculation of important information: the post (g), certificate (
t1), working age (
t2), accident-free time (
t3), and working time (
t4).We set the input matrix as shown in Equation (39).
This article uses real-time quantitative data, so there is no situation of different people in the same location; that is,
N = 1 and
M0 =
N0.When
gk =
gj (
k ≠
j,
k = 1,2,…,
n,
j = 1,2,…,
n), from Equations (13)–(15),
Hpi is as shown in Equation (40).
The elements
u in the set {
g1,
g2,…,
gn}
i can make up
Hp, so the operator risk is as shown in Equation (41).
From the calculation process, it can be seen that Hu has a maximum close to 1. Taking into account the limited impact of personnel factors, when the value is 0.8, the coefficient c is specified as 1. The worse the indicator, the greater the coefficient c. The highest value of Hu is 1 and the lowest value is specified as 0.6, so when the value is lower than 0.6, it is calculated using 0.6 instead. Therefore, the range of c values is 0.8 to 1.33.
When
Hui ≤ 0.6, we let
Hui = 0.6, and
ci is calculated as shown in Equation (42).
The coefficient
c is as shown in Equation (43).
3.4. Process/Equipment Factor, Denoted d
The process/equipment index factor includes a total of 13 second-level factors, namely, equipment maintenance, explosion-proof devices, inert gas protection, emergency cooling, emergency power supply, electrical explosion-proofing, anti-static, lightning protection, devices for preventing fire, process parameter control, leak detection device and response, fault alarm and control devices, and accidental discharge and treatment. There is a certain number of third-level index factors for each second-level index factor, and the scores for each third-level index factor are not the same. There are two kinds of calculation logic, “and” and “or”, for the third-level indices, with the highest total score being 310 points. Coefficient d is defined as 1 at 248 points (80%), and the worse the indicator, the greater the coefficient d. The highest is 310 points, and when the value is less than 186 points (60%), it is calculated using 186 points. Therefore, the range of d values is 0.8 to 1.33.
According to
Table 5, the score matrix
can be built for input data X
i, where
with restrictions as follows:
- (1)
The original input data are only 0 or 1, that is, X11, X12, …, XD5 ∈ {0,1};
- (2)
X11 + X12 ≤ 1;
- (3)
X31 + X32 ≤ 1;
- (4)
X41 + X42 ≤ 1;
- (5)
X5 = X51 + X52 ≤ 1;
- (6)
X6 = X61 + X62 + X63 + X64 + X65 + X66 + X67 + X68 + X69 ≤ 1;
- (7)
X7 = X71 + X72 + X73 + X74 + X75 ≤ 1;
- (8)
X8 = X81 + X82 + X83 + X84 + X85;
- (9)
X9 = X91 + X92 + X93;
- (10)
XA = XA1 + XA2 + XA3 ≤ 1;
- (11)
XB1 + XB2 ≤ 1.
According to the above score matrix, input data, and restrictions, we can get x
i, where x
i is the multiplication of matrix D and matrix X
i, as shown in Equation (44).
when x
i ≥ 186, the definition of value
d is as shown in Equation (45).
when x
i < 186, the definition of value
d is
.
The process/equipment index coefficient
d is as shown in Equation (46).
3.5. Building Environmental Factor, Denoted e
The building environmental index factor includes a total of five second-level factors, namely, ventilation plant, pressure relief, monitoring device, plant structure, and industrial sewer. There are a certain number of third-level index factors for each second-level index factor, and the third-level index factor scores are not the same. There are two kinds of calculation logic, “and” and “or”, for the third-level indices, with the highest total score being 89 points. Coefficient e is defined as 1at 71 points (80%), and the worse the indicator, the greater the coefficient e. The highest is 89 points, and when the value is less than 53 points (60%), it is calculated using 53 points. Therefore, the range of e values is 0.8 to 1.33.
According to
Table 4, the score matrix
can be built with input data Y
i such that Y
i= [Y
11 Y
21 Y
22 Y
23 Y
31 Y
32 Y
33 Y
41 Y
42 Y
43 Y
44 Y
45 Y
51 Y
52]
T and with restrictions as follows:
- (1)
The original input data are only 0 or 1, that is, Y11, Y21,…, Y52 ∈ {0,1};
- (2)
Y21 + Y22 + Y23 ≤ 1.
According to the above score matrix, input data, and restrictions, we can get y
i where y
i is the multiplication of matrix E and matrix Y
i, as shown in Equation (47).
when y
i ≥ 53, the definition of
e is as shown in Equation (48).
when y
i < 53, the definition of e is
.
The construction environmental index coefficient
e is as shown in Equation (49).
3.6. Safety Management Factor, Denoted f
The safety management index factor includes a total of 10 s-level factors, namely, safety production responsibility system, safety education, safety technical measures plan, safety inspection, safety rules and regulations, safety management agencies and personnel, statistical analysis of accidents, hazard assessment and rectification, contingency plans and measures, and fire safety management. There are a certain number of third-level index factors for each second-level index factor, and the third-level index factor scores are not the same. The total score is 100 points. At 80 points, coefficient f is defined as 1, and the worse the indicator, the greater the coefficient f. The highest is 100 points, and when the value is less than 60 points, it is calculated using 60 points. Therefore, the range of f values is 0.8 to 1.33.
According to
Table 5, score matrix
can be built for input data Z
i, where Z
i= [Z
1 Z
2 Z
3 Z
4 Z
5 Z
6 Z
7 Z
8 Z
9 Z
A]
T, with restrictions as follows:
- (1)
The original input data are only 0 or 1, that is, Z11, Z12,…, ZAA ∈ {0,1};
- (2)
Z1 = Z11 + Z12 + Z13 + Z14 + Z15 + Z16 + Z17 + Z18 + Z19;
- (3)
Z2 = Z21 + Z22 + Z23 + Z24 + Z25 + Z26 + Z27 + Z28;
- (4)
Z3 = Z31 + Z32 + Z33 + Z34;
- (5)
Z4 = Z41 + Z42 + Z43 + Z44 + Z45 + Z46 + Z47;
- (6)
Z5 = Z51 + Z52 + Z53 + Z54 + Z55 + Z56 + Z57 + Z58 + Z59 + Z5A + Z5B + Z5C + Z5D;
- (7)
Z6 = Z61 + Z62 + Z63 + Z64 + Z65;
- (8)
Z7 = Z71 + Z72 + Z73;
- (9)
Z8 = Z81 + Z82 + Z83 + Z84 + Z85 + Z86 + Z87 + Z88 + Z89;
- (10)
Z9 = Z91 + Z92 + Z93 + Z94 + Z95 + Z96 + Z97 + Z98 + Z99;
- (11)
ZA = ZA1 + ZA2 + ZA3 + ZA4 + ZA5 + ZA6 + ZA7 + ZA8 + ZA9 +ZAA.
According to the above score matrix, input data, and restrictions, we can get z
i, where z
i is the multiplication of matrix F and matrix Z
i as shown in Equation (50).
when z
i ≥ 60, the definition of
f is as shown in Equation (51).
when z
i < 60, the definition of
f is
.
The safety management index coefficient
f is as shown in Equation (52).
3.7. Calculation Results
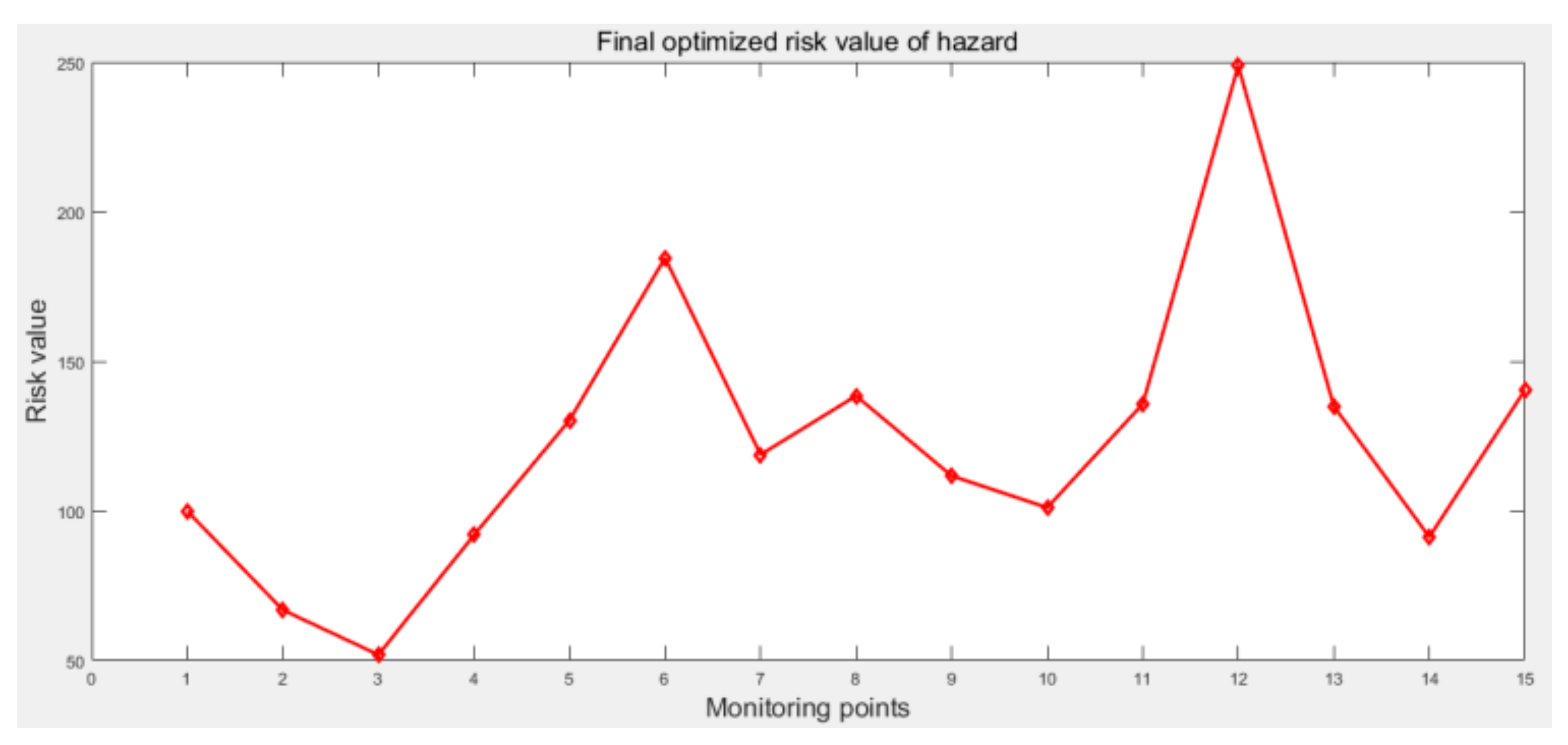
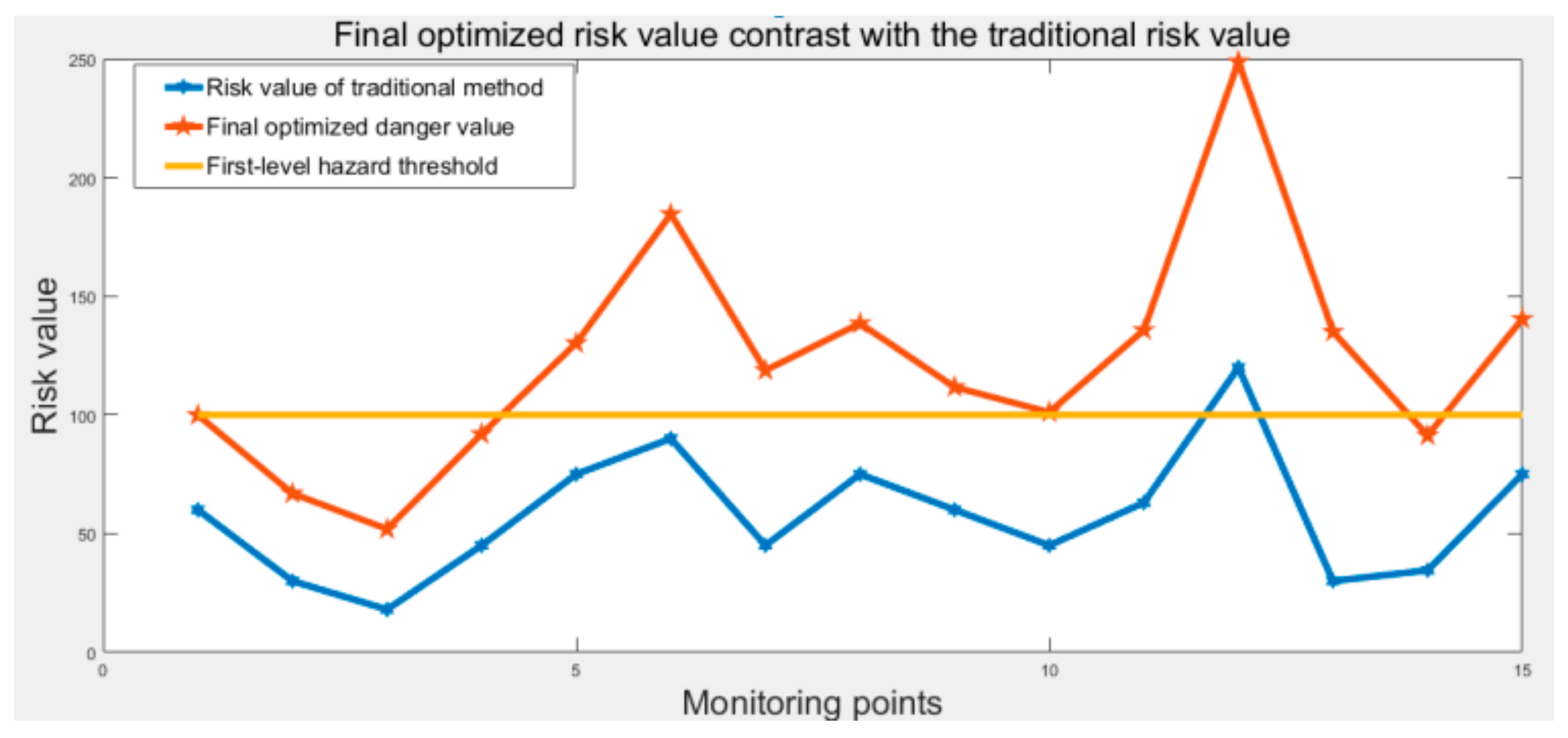
We used forced pair comparison (
Table 11) to calculate the final optimized risk value
R’ of the hazards.
R’ is as shown in Equation (53):
where
is a five-point indicator function of
i monitoring points.
5. Conclusions
In this article, we proposed and analyzed a new dynamic semi-quantitative risk calculation model for chemical plants that can be applied digitally. This model provides a sustainable, standardized, and comprehensive management strategy for the safety management of chemical plants and chemical industry park managers. The model and its determined parameters were applied to the dynamic semi-quantified safety management of chemical plants with in the chemical industry park of Quzhou, Zhejiang Province. From the point of view of the existing semi-quantitative model, the existing problems of the current model were analyzed, the current model was optimized, and a new dynamic semi-quantitative evaluation model scheme was proposed. The new model employs an analytical hierarchy process to comprehensively assess and compare the differences in the risk values of hazards among plants. The dynamic semi-quantitative calculation system for managing hazards is composed of six elements: operator, process/equipment, hazard risk, building environment, safety management, and domino effect. The model finally produces a dynamic quantification value, which can be used to compare the risk value of the chemical company from six angles directly reflected through the corresponding software, allowing it to play a greater role in the safety management of the plant. The establishment of this model involves many basic disciplines, such as management, mathematics, operations research, control science, computer science, etc. A combination of these basic disciplines was used to get this dynamic quantitative risk value. Of course, the model is not perfect, giving room to further optimize the threshold and some parameter settings in future to make the model more practical and accurate. In addition to the above research topics, future research should also explore other aspects of chemical safety management in order to establish a complete chemical safety management and emergency rescue system. At the same time, we will continue to study the systematic engineering needed to combine the many basic disciplines involved in the model and use the thinking of system engineering to establish a theoretical framework of modern safety engineering based on safety risk analysis management.