Novel Parallel Heterogeneous Meta-Heuristic and Its Communication Strategies for the Prediction of Wind Power
Abstract
1. Introduction
- It first proposes parallel heterogeneous model based on PSO and GWO.
- It introduces four new communication strategies to improve the abilities of exploration and exploitation.
- It dynamically changes the members of subgroup from the diversity of the population.
2. Preliminaries
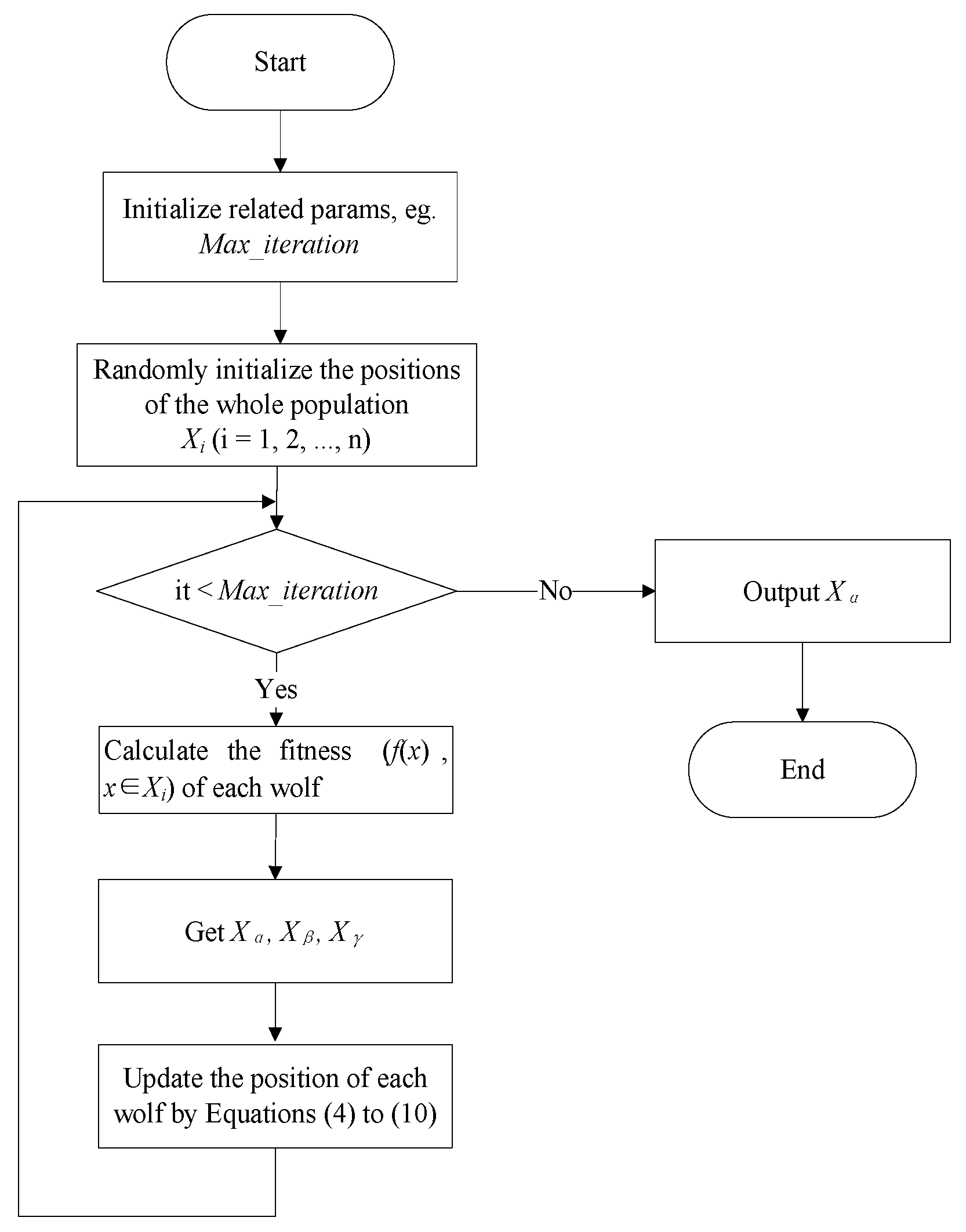
2.1. Particle Swarm Optimization
2.2. Grey Wolf Optimizer
2.3. Population-Based Parallelization
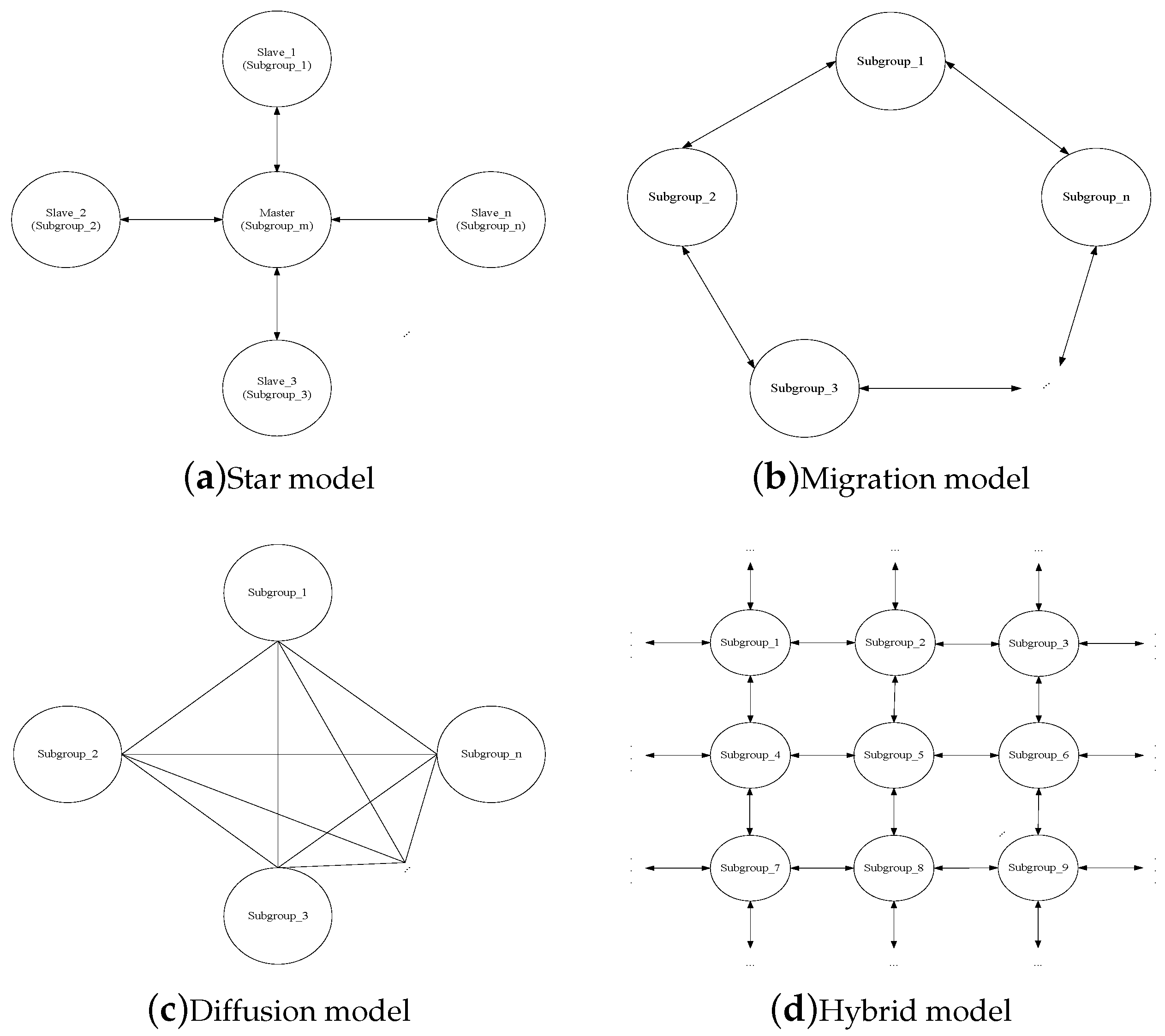
2.3.1. Communication Models
- Star model
- Migration model
- Diffusion model
- Hybrid model
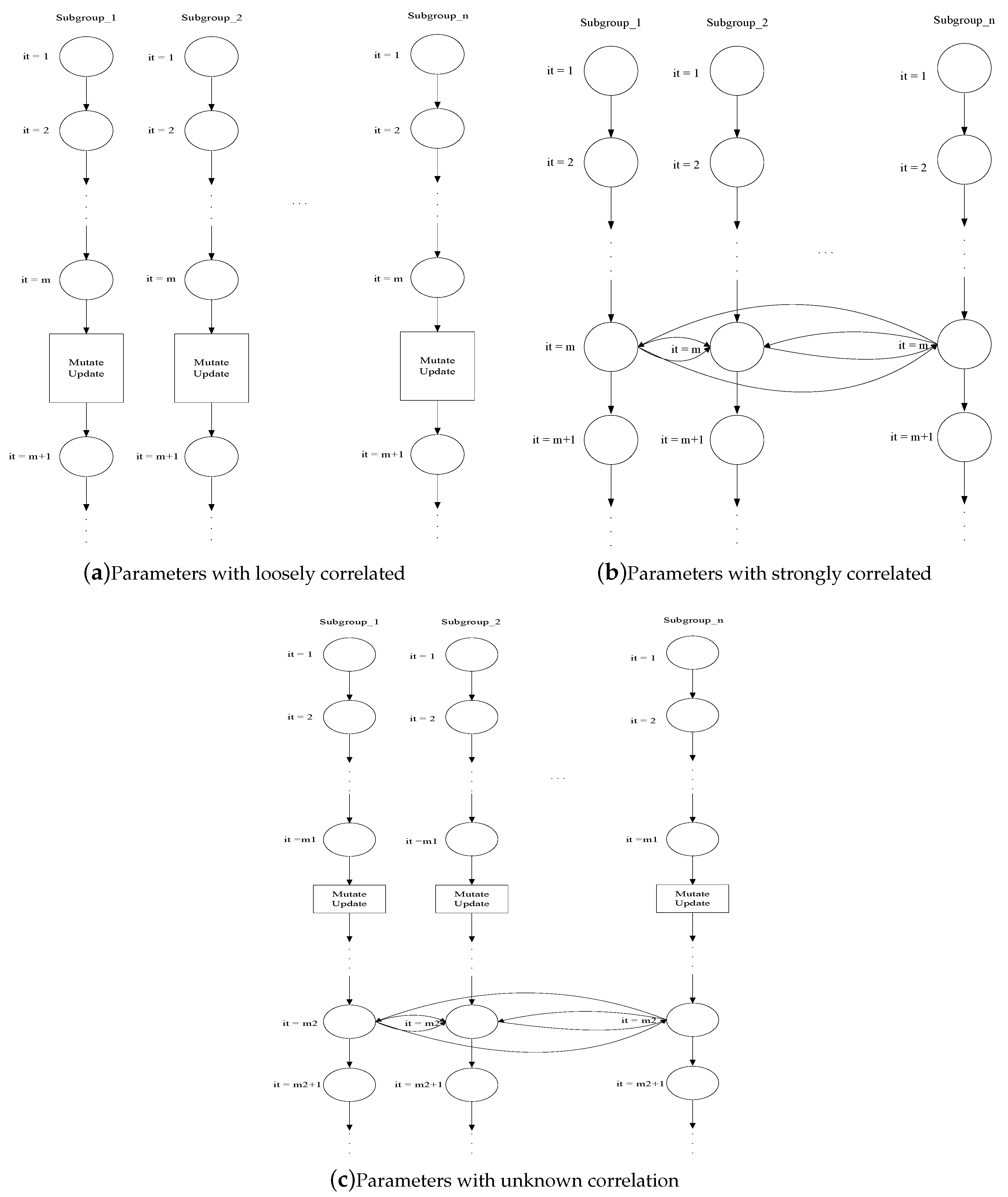
2.3.2. Communication Strategies
- Parameters with loosely correlated
- Parameters with strongly correlated
- Parameters with unknown correlation (Hybrid)
3. Novel Parallel Heterogeneous Algorithm
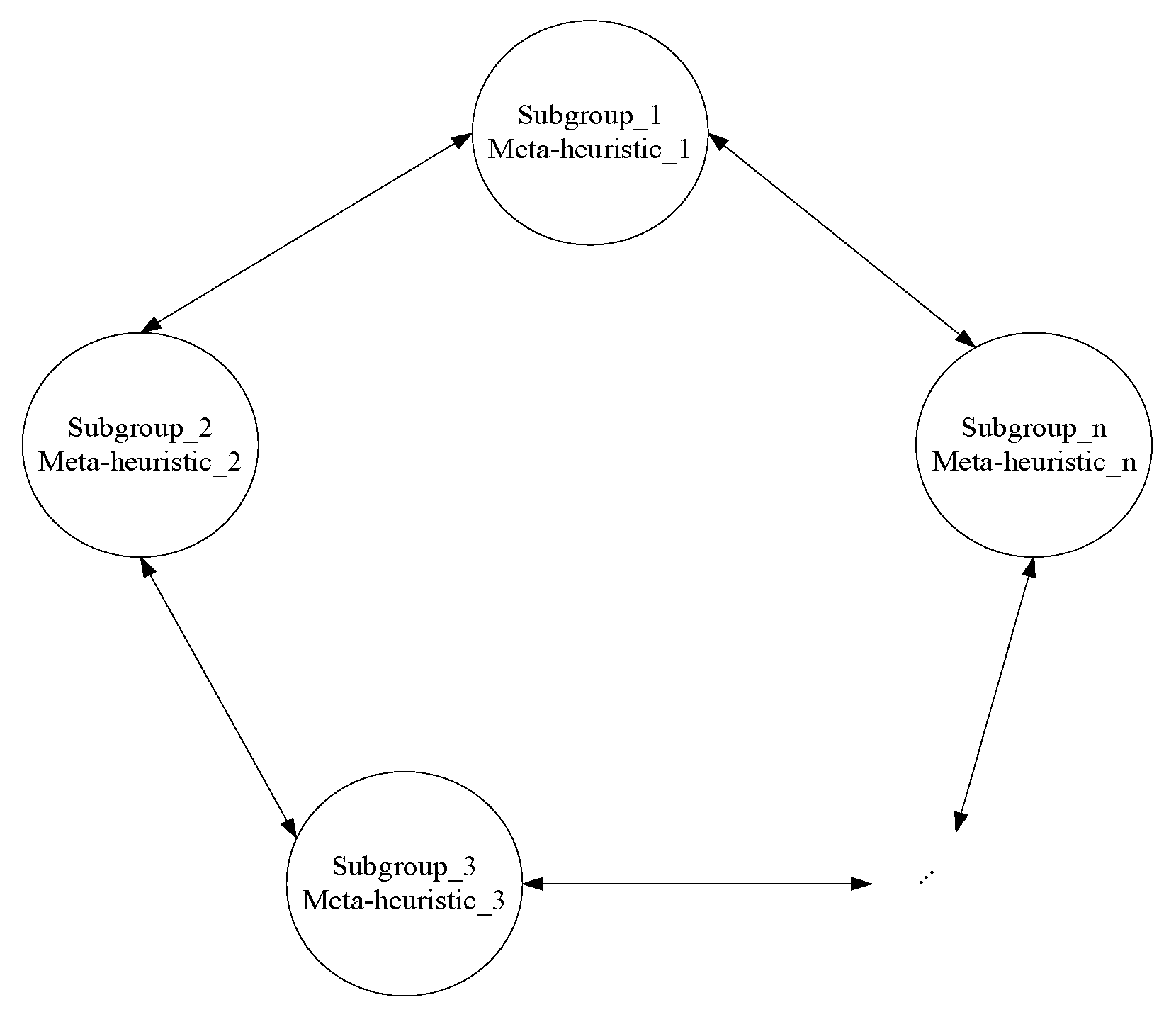
3.1. The Model of Parallel Heterogeneous Algorithm
3.2. New Communication Strategies
3.2.1. Communication Strategy with Ranking
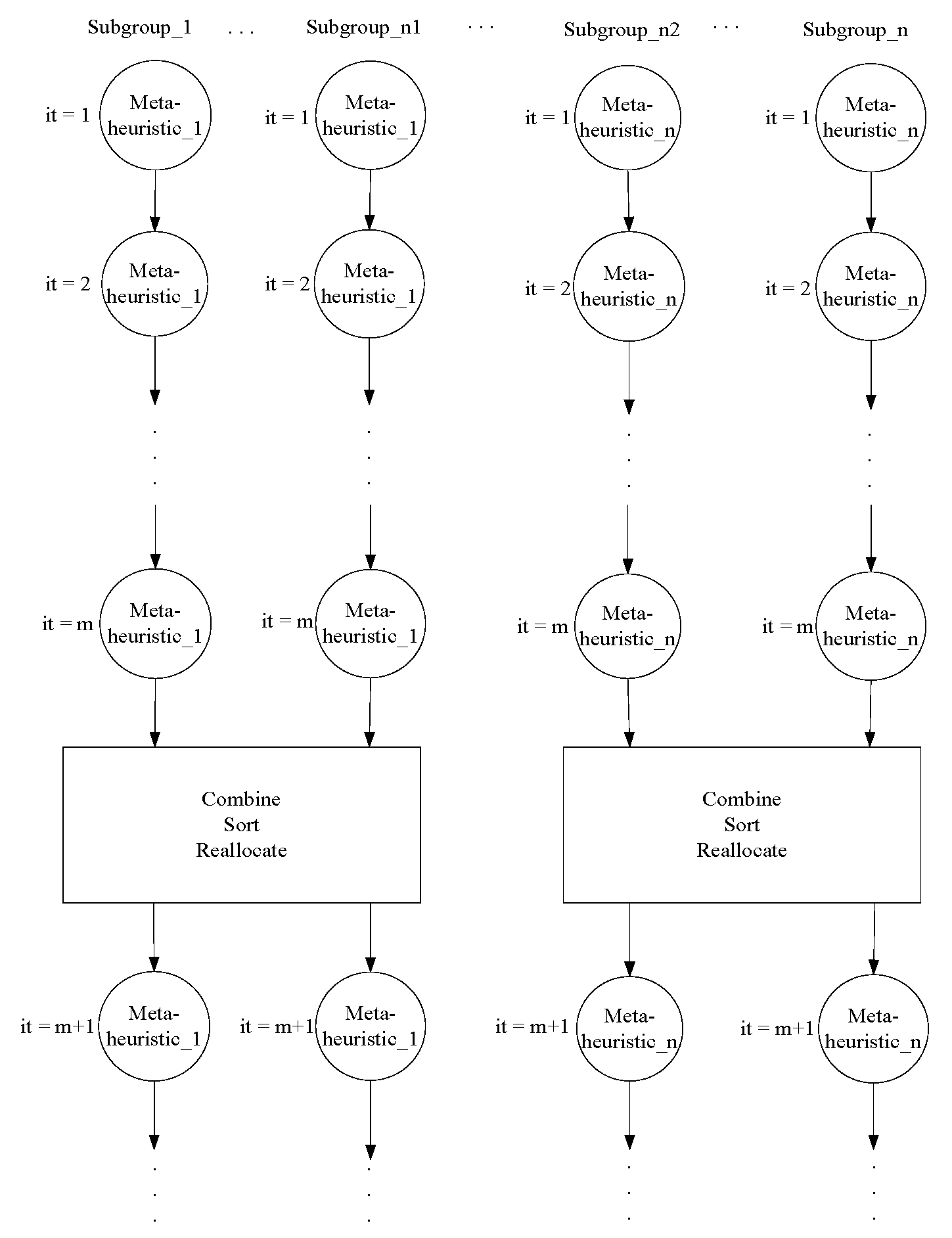
3.2.2. Communication Strategy with Combination
| Algorithm 1 Combination |
| //ngroups.number is the number of subgroups |
| for g = 1 : ngroups.number do |
| //ngroups.algorithms is the number of meta-heuristics |
| for j = 1 : ngroups.algorithms do |
| if j == groups(g).algorithm then |
| //ngroups.size is the number of subgroup |
| for l = 1 : ngroups.size do |
| temp(j,t(j)) = groups(g).pop(l); |
| t(j) = t(j) + 1; |
| end for |
| end if |
| end for |
| end for |
| for j = 1 : ngroups.algorithms do |
| i = 1; |
| temp(j) = SortPopulationByFitness(temp(j)); |
| for g = 1 : ngroups.number do |
| if j == groups(g).algorithm && i ≤ t(j) then |
| groups(g).pop(p(g)) = temp(j,i); |
| i = i + 1; |
| p(g) = p(g) + 1; |
| end if |
| end for |
| end for |
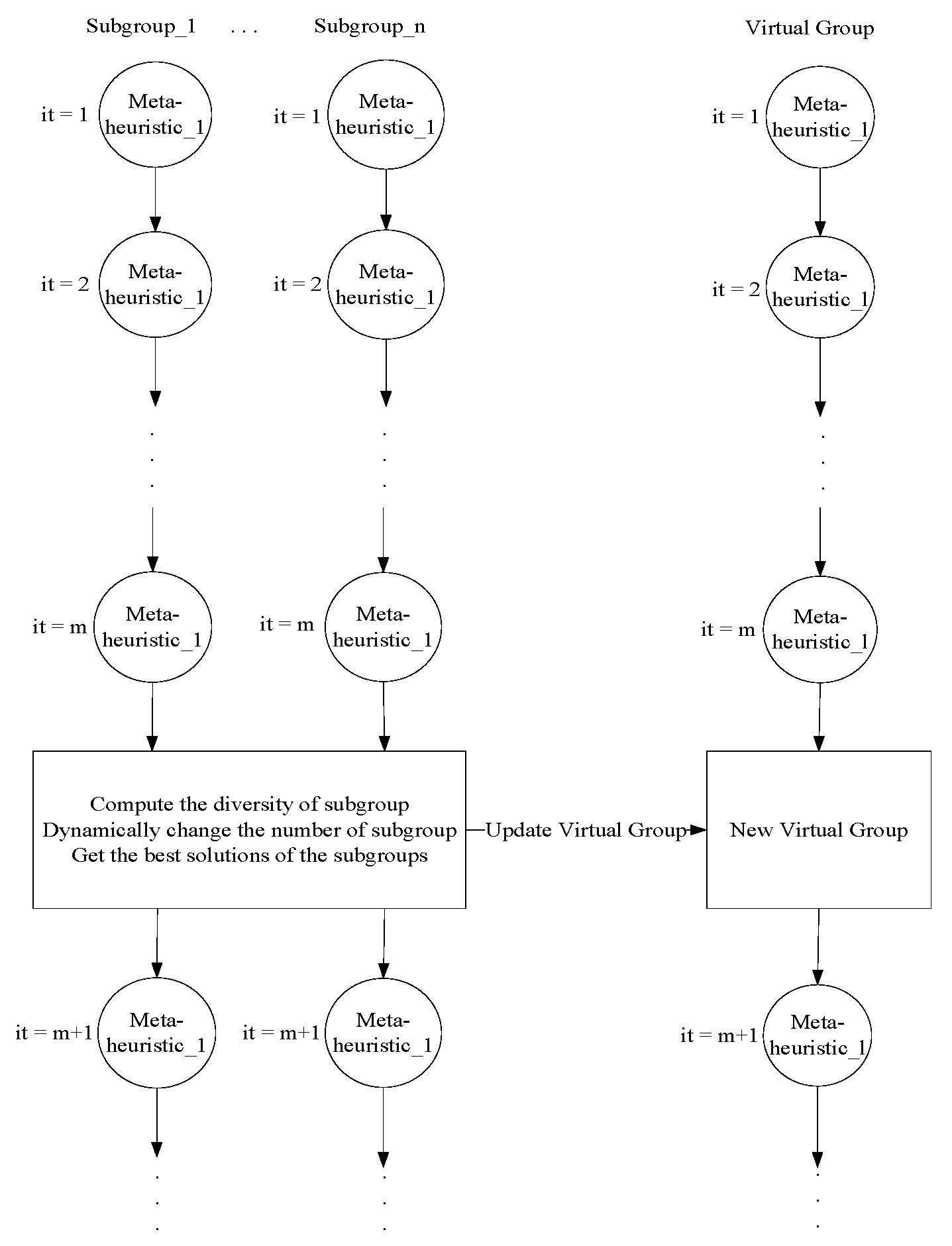
3.2.3. Communication Strategy with Dynamic Change
| Algorithm 2 Dynamic Change |
| Sort A //A is the best solutions of the subgroups |
| Sort B // B is the virtual group |
| for i = 1 : length(A), j = 1 : length(B) do |
| if f(A(i)) < B(j) then |
| B(j) = A(i); |
| ++i; |
| else |
| ++j; |
| end if |
| end for |
3.2.4. Hybrid Communication Strategy
4. Experimental Results and Analysis
4.1. Parameters Configuration
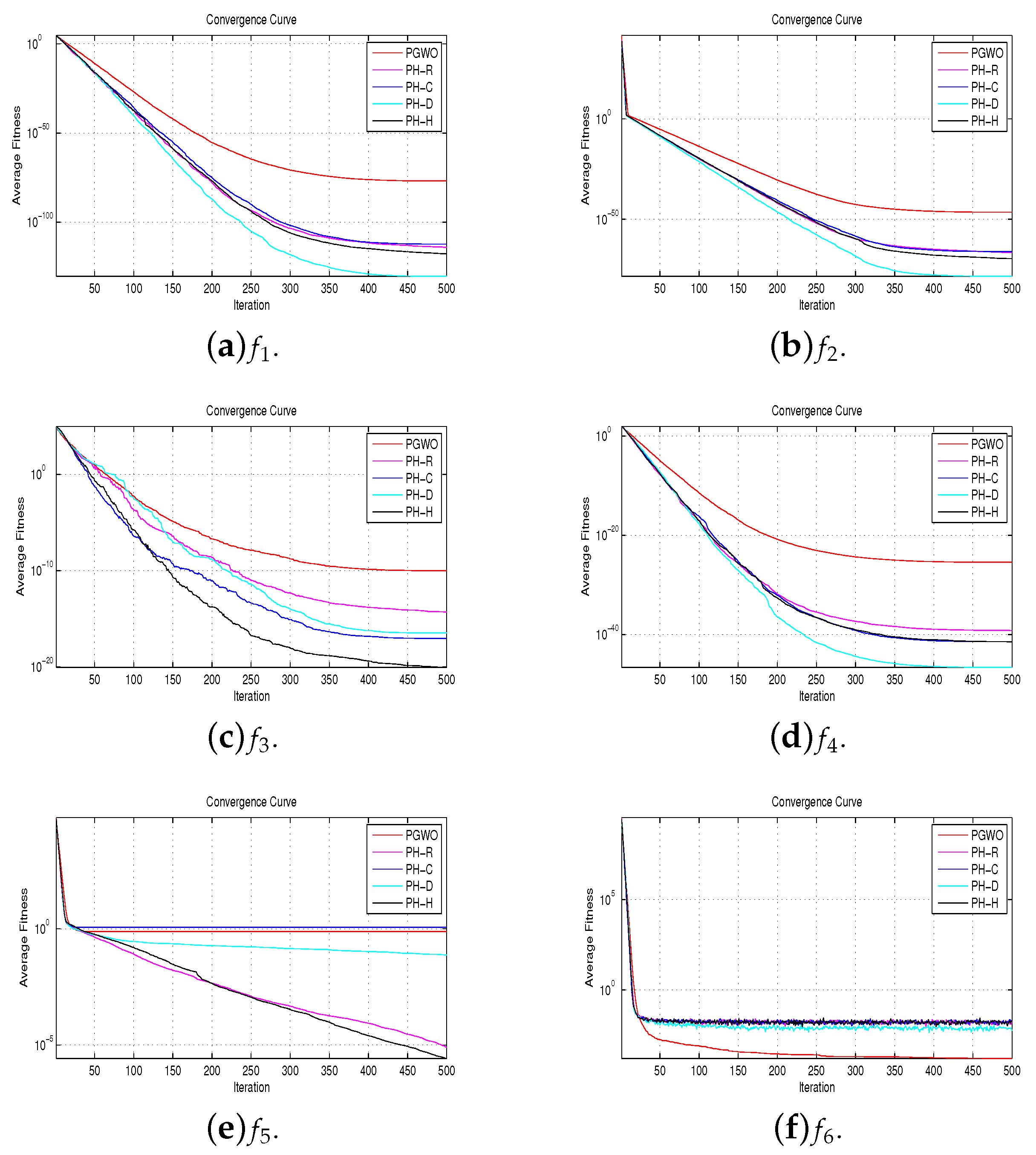
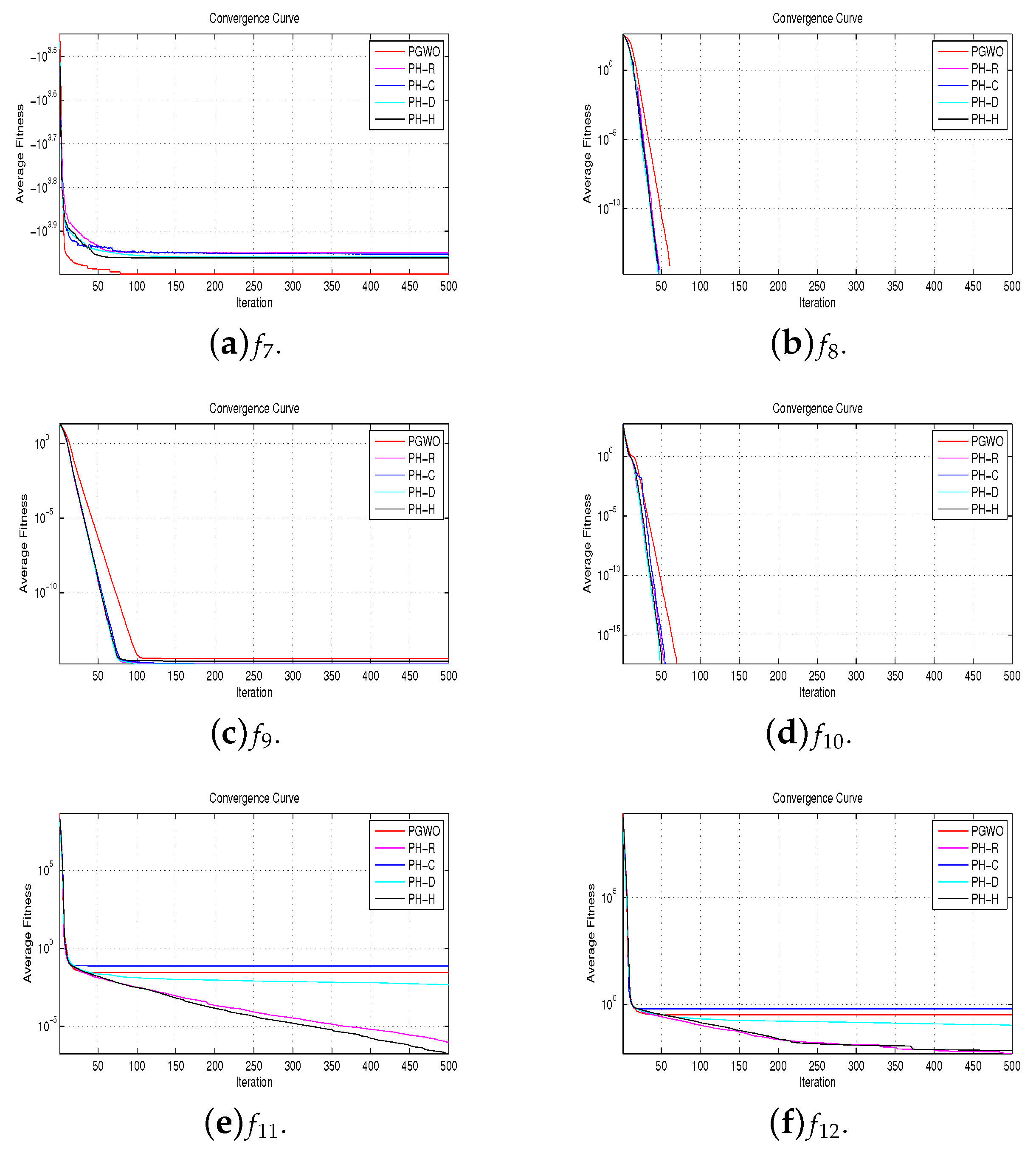
4.2. Unimodal Functions
4.3. Multimodal Functions
4.4. Fixed-Dimension Multimodal Functions
4.5. Composite Multimodal Functions
5. Application for Wind Power Forecasting
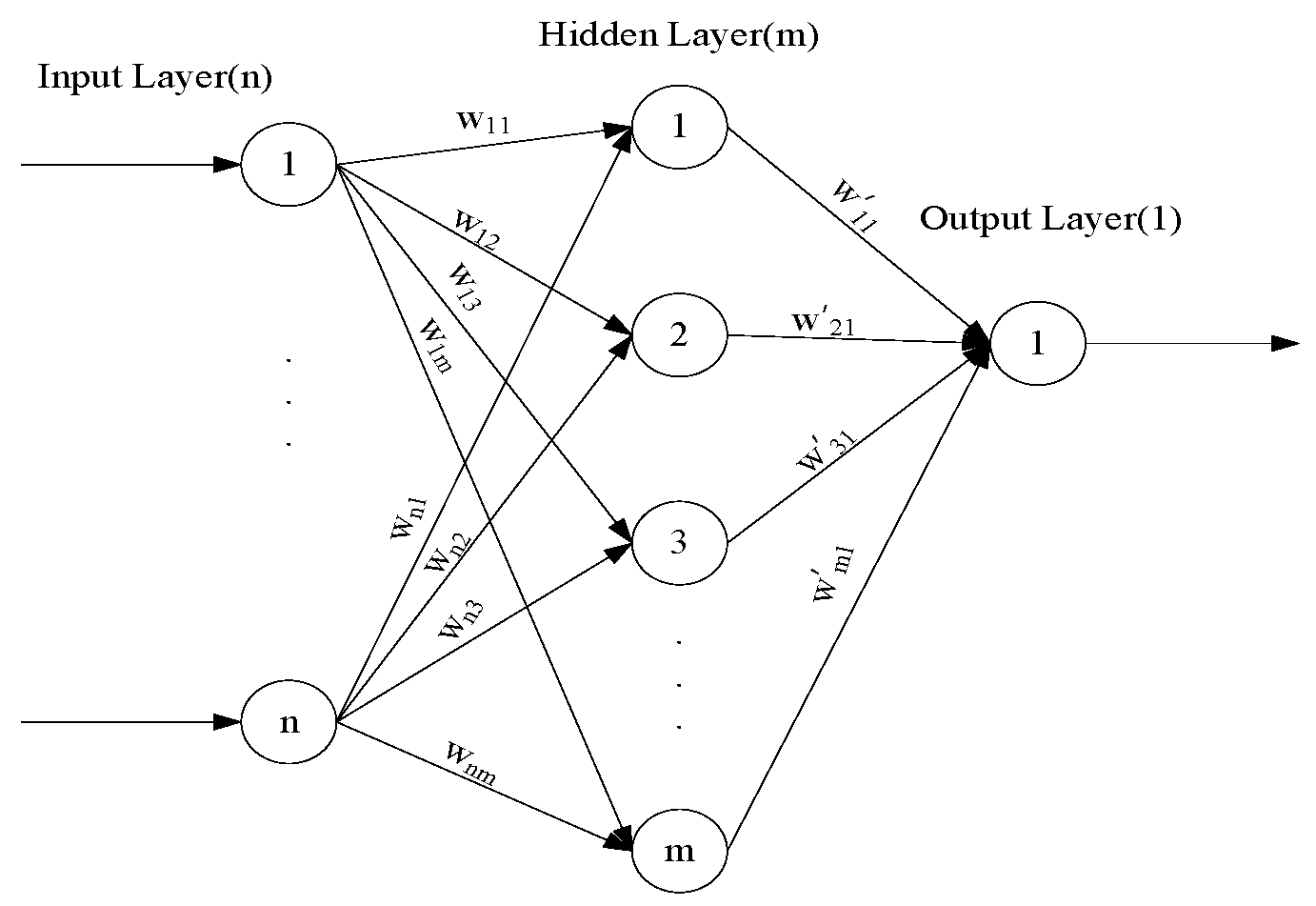
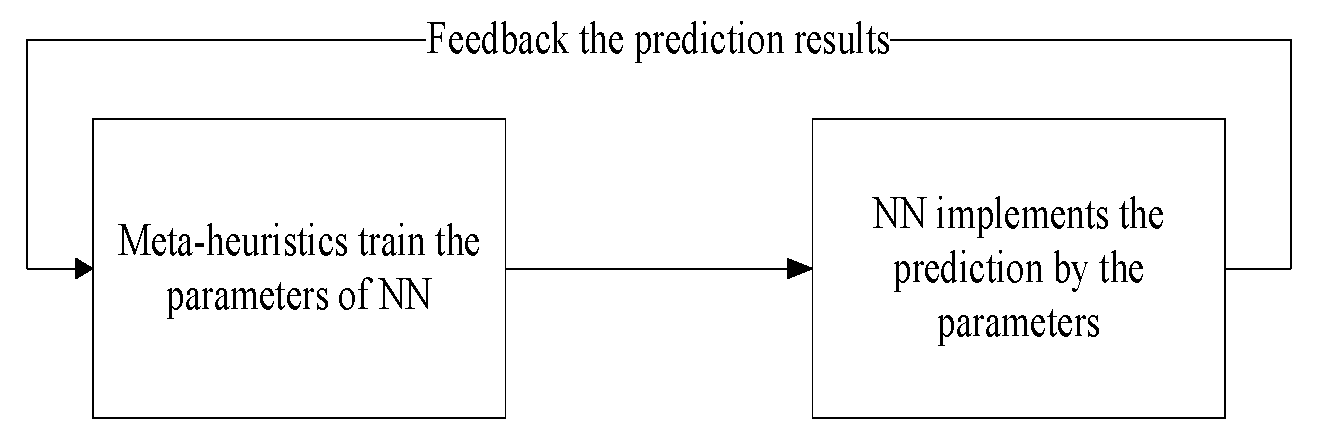
5.1. The Model of Wind Power Forecasting Based on Hybrid Neural Network
5.2. Simulation Results
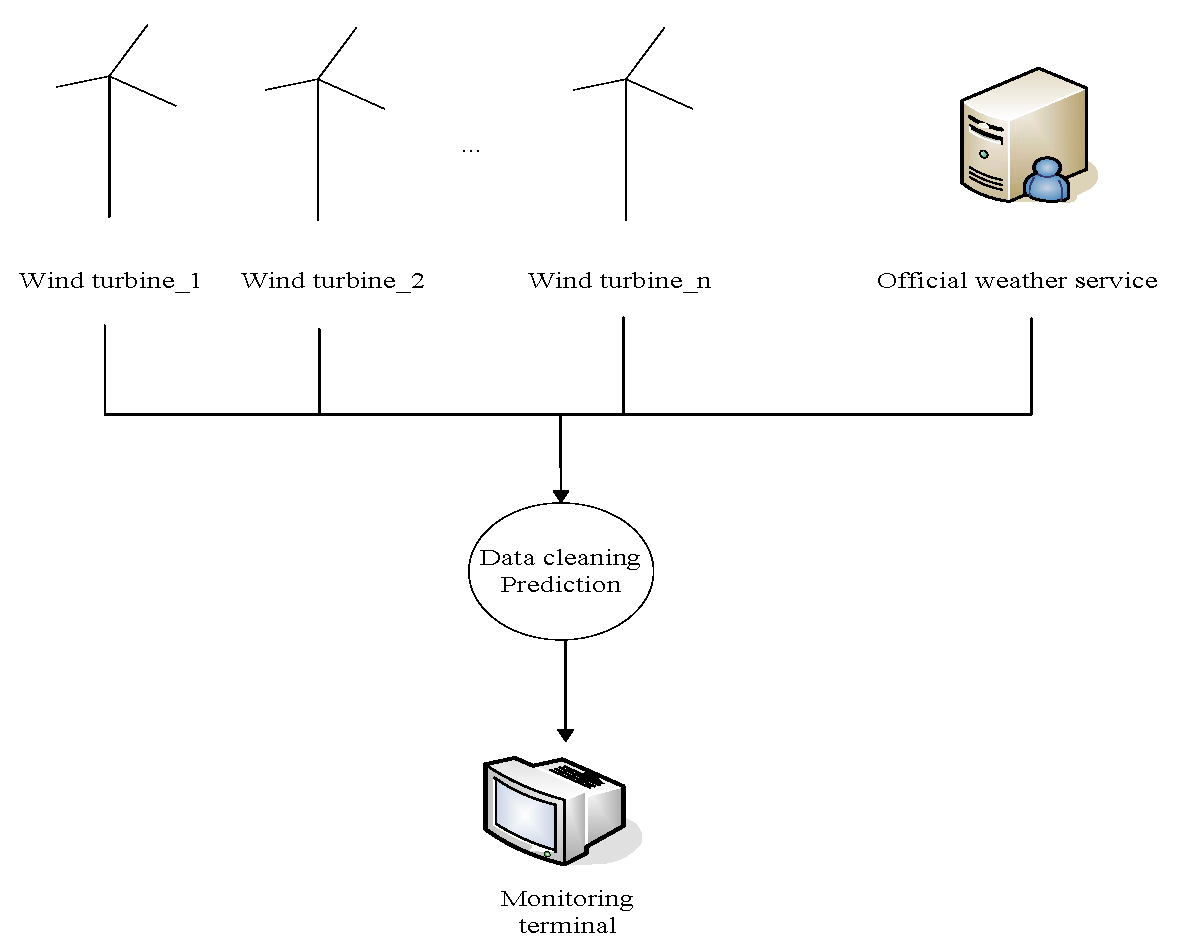
5.2.1. Data Preprocessing
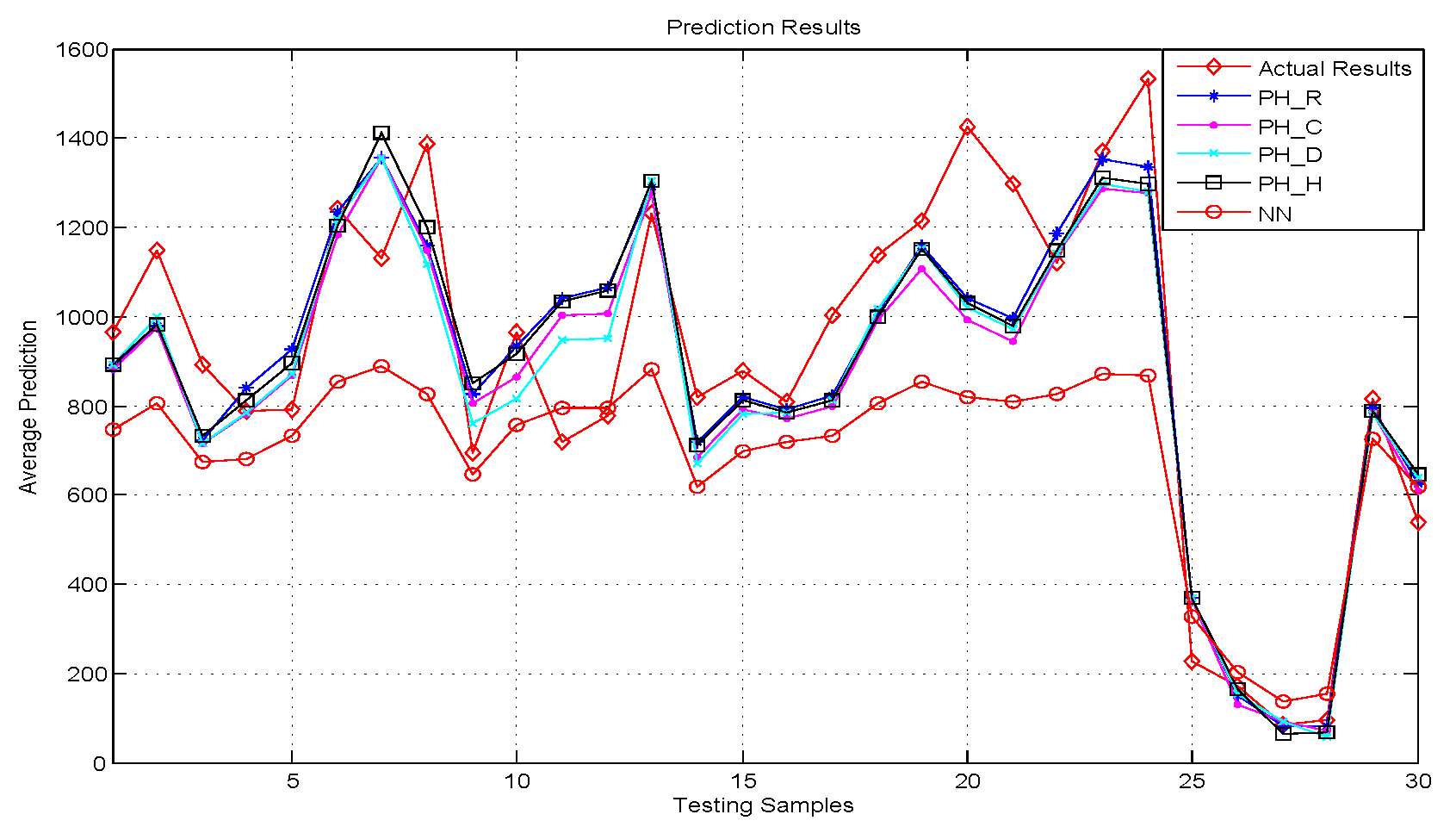
5.2.2. The Evaluation Performance of Hybrid Model
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar–wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Bhaskar, K.; Singh, S. AWNN-assisted wind power forecasting using feed-forward neural network. IEEE Trans. Sustain. Energy 2012, 3, 306–315. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Chen, C.; Li, Y.f. A hybrid statistical method to predict wind speed and wind power. Renew. Energy 2010, 35, 1857–1861. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y. Multi-objective dynamic unit commitment optimization for energy-saving and emission reduction with wind power. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; pp. 2074–2078. [Google Scholar]
- Wang, C.N.; Le, T.M.; Nguyen, H.K.; Ngoc-Nguyen, H. Using the Optimization Algorithm to Evaluate the Energetic Industry: A Case Study in Thailand. Processes 2019, 7, 87. [Google Scholar] [CrossRef]
- Hu, P.; Pan, J.S.; Chu, S.C.; Chai, Q.W.; Liu, T.; Li, Z.C. New Hybrid Algorithms for Prediction of Daily Load of Power Network. Appl. Sci. 2019, 9, 4514. [Google Scholar] [CrossRef]
- Morris, G.M.; Goodsell, D.S.; Halliday, R.S.; Huey, R.; Hart, W.E.; Belew, R.K.; Olson, A.J. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1998, 19, 1639–1662. [Google Scholar] [CrossRef]
- Pan, J.; McInnes, F.; Jack, M. Application of parallel genetic algorithm and property of multiple global optima to VQ codevector index assignment for noisy channels. Electron. Lett. 1996, 32, 296–297. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Shieh, C.S.; Huang, H.C.; Wang, F.H.; Pan, J.S. Genetic watermarking based on transform-domain techniques. Pattern Recognit. 2004, 37, 555–565. [Google Scholar] [CrossRef]
- Huang, H.C.; Pan, J.S.; Lu, Z.M.; Sun, S.H.; Hang, H.M. Vector quantization based on genetic simulated annealing. Signal Process. 2001, 81, 1513–1523. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Wang, H.; Sun, H.; Li, C.; Rahnamayan, S.; Pan, J.S. Diversity enhanced particle swarm optimization with neighborhood search. Inf. Sci. 2013, 223, 119–135. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; Volume 1, pp. 81–86. [Google Scholar]
- Chang, J.F.; Roddick, J.F.; Pan, J.S.; Chu, S. A parallel particle swarm optimization algorithm with communication strategies. J. Inf. Sci. Eng. 2005, 21, 809–818. [Google Scholar]
- Sun, C.L.; Zeng, J.C.; Pan, J.S. An improved vector particle swarm optimization for constrained optimization problems. Inf. Sci. 2011, 181, 1153–1163. [Google Scholar] [CrossRef]
- Wang, J.; Ju, C.; Ji, H.; Youn, G.; Kim, J.U. A Particle Swarm Optimization and Mutation Operator Based Node Deployment Strategy for WSNs; International Conference on Cloud Computing and Security; Springer: Boston, MA, USA, 2017; pp. 430–437. [Google Scholar]
- Liu, W.; Wang, J.; Chen, L.; Chen, B. Prediction of protein essentiality by the improved particle swarm optimization. Soft Comput. 2018, 22, 6657–6669. [Google Scholar] [CrossRef]
- Wang, J.; Ju, C.; Kim, H.j.; Sherratt, R.S.; Lee, S. A mobile assisted coverage hole patching scheme based on particle swarm optimization for WSNs. Clust. Comput. 2019, 22, 1787–1795. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evol. Comput. 2008, 13, 398–417. [Google Scholar] [CrossRef]
- Meng, Z.; Pan, J.S.; Kong, L. Parameters with adaptive learning mechanism (PALM) for the enhancement of differential evolution. Knowl.-Based Syst. 2018, 141, 92–112. [Google Scholar] [CrossRef]
- Meng, Z.; Pan, J.S.; Tseng, K.K. PaDE: An enhanced Differential Evolution algorithm with novel control parameter adaptation schemes for numerical optimization. Knowl.-Based Syst. 2019, 168, 80–99. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Penas, D.R.; Banga, J.R.; González, P.; Doallo, R. Enhanced parallel differential evolution algorithm for problems in computational systems biology. Appl. Soft Comput. 2015, 33, 86–99. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Appl. Intell. 2015, 43, 150–161. [Google Scholar] [CrossRef]
- Pan, J.S.; Dao, T.K.; Chu, S.C.; Nguyen, T.-T. A novel hybrid GWO-FPA algorithm for optimization applications. In Proceedings of the International Conference on Smart Vehicular Technology, Transportation, Communication and Applications, Kaohsiung, Taiwan, 6–8 November 2017; pp. 274–281. [Google Scholar]
- Song, X.; Tang, L.; Zhao, S.; Zhang, X.; Li, L.; Huang, J.; Cai, W. Grey Wolf Optimizer for parameter estimation in surface waves. Soil Dyn. Earthq. Eng. 2015, 75, 147–157. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Single and multi-objective optimal power flow using grey wolf optimizer and differential evolution algorithms. Electr. Power Components Syst. 2015, 43, 1548–1559. [Google Scholar] [CrossRef]
- Meng, Z.; Pan, J.S.; Xu, H. QUasi-Affine TRansformation Evolutionary (QUATRE) algorithm: A cooperative swarm based algorithm for global optimization. Knowl.-Based Syst. 2016, 109, 104–121. [Google Scholar] [CrossRef]
- Liu, N.; Pan, J.S.; Xue, J.Y. An Orthogonal QUasi-Affine TRansformation Evolution (O-QUATRE). In Proceedings of the 15th International Conference on IIH-MSP in Conjunction with the 12th International Conference on FITAT, Jilin, China, 18–20 July 2019; Volume 2, pp. 57–66. [Google Scholar]
- Pan, J.S.; Meng, Z.; Xu, H.; Li, X. QUasi-Affine TRansformation Evolution (QUATRE) algorithm: A new simple and accurate structure for global optimization. In Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, Morioka, Japan, 2–4 August 2016; pp. 657–667. [Google Scholar]
- Meng, Z.; Pan, J.S. QUasi-Affine TRansformation Evolution with External ARchive (QUATRE-EAR): An enhanced structure for differential evolution. Knowl.-Based Syst. 2018, 155, 35–53. [Google Scholar] [CrossRef]
- Weber, M.; Neri, F.; Tirronen, V. Shuffle or update parallel differential evolution for large-scale optimization. Soft Comput. 2011, 15, 2089–2107. [Google Scholar] [CrossRef]
- Pooranian, Z.; Shojafar, M.; Abawajy, J.H.; Abraham, A. An efficient meta-heuristic algorithm for grid computing. J. Comb. Optim. 2015, 30, 413–434. [Google Scholar] [CrossRef]
- Yang, Z.; Li, K.; Niu, Q.; Xue, Y. A novel parallel-series hybrid meta-heuristic method for solving a hybrid unit commitment problem. Knowl.-Based Syst. 2017, 134, 13–30. [Google Scholar] [CrossRef]
- Mussi, L.; Daolio, F.; Cagnoni, S. Evaluation of parallel particle swarm optimization algorithms within the CUDA™ architecture. Inf. Sci. 2012, 181, 4642–4657. [Google Scholar] [CrossRef]
- Schutte, J.F.; Reinbolt, J.A.; Fregly, B.J.; Haftka, R.T.; George, A.D. Parallel global optimization with the particle swarm algorithm. Int. J. Numer. Methods Eng. 2004, 61, 2296–2315. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.S.; Dao, T.K.; Nguyen, T.-T. A Novel Improved Bat Algorithm Based on Hybrid Parallel and Compact for Balancing an Energy Consumption Problem. Information 2019, 10, 194–215. [Google Scholar]
- Alba, E.; Luque, G.; Nesmachnow, S. Parallel metaheuristics: Recent advances and new trends. Int. Trans. Oper. Res. 2013, 20, 1–48. [Google Scholar] [CrossRef]
- Xue, X.; Chen, J. Optimizing ontology alignment through hybrid population-based incremental learning algorithm. Memetic Comput. 2019, 11, 209–217. [Google Scholar] [CrossRef]
- Lalwani, S.; Sharma, H.; Satapathy, S.C.; Deep, K.; Bansal, J.C. A Survey on Parallel Particle Swarm Optimization Algorithms. Arab. J. Sci. Eng. 2019, 44, 2899–2923. [Google Scholar] [CrossRef]
- Madhuri, D.K.; Deep, K. A state-of-the-art review of population-based parallel meta-heuristics. In Proceedings of the Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; pp. 9–11. [Google Scholar]
- Liao, D.Y.; Wang, C.N. Neural-network-based delivery time estimates for prioritized 300-mm automatic material handling operations. IEEE Trans. Semicond. Manuf. 2004, 17, 324–332. [Google Scholar] [CrossRef]
- Jeng-Shyang, P.; Lingping, K.; Tien-Wen, S.; Pei-Wei, T.; Waclav, S. α-fraction first strategy for hierarchical wireless sensor networks. J. Internet Technol. 2018, 19, 1717–1726. [Google Scholar]
- Nguyen, T.T.; Pan, J.S.; Dao, T.K. An Improved Flower Pollination Algorithm for Optimizing Layouts of Nodes in Wireless Sensor Network. IEEE Access 2019, 7, 75985–75998. [Google Scholar] [CrossRef]
- Pan, J.S.; Lee, C.Y.; Sghaier, A.; Zeghid, M.; Xie, J. Novel Systolization of Subquadratic Space Complexity Multipliers Based on Toeplitz Matrix-Vector Product Approach. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019. [Google Scholar] [CrossRef]
- Xue, X.; Chen, J.; Yao, X. Efficient User Involvement in Semiautomatic Ontology Matching. IEEE Trans. Emerg. Top. Comput. Intell. 2018. [Google Scholar] [CrossRef]
- Pan, J.S.; Kong, L.; Sung, T.W.; Tsai, P.W.; Snášel, V. A clustering scheme for wireless sensor networks based on genetic algorithm and dominating set. J. Internet Technol. 2018, 19, 1111–1118. [Google Scholar]






| Function | Space | Dim | fmin |
|---|---|---|---|
| [−100, 100] | 30 | 0 | |
| [−10, 10] | 30 | 0 | |
| [−100, 100] | 30 | 0 | |
| [−100, 100] | 30 | 0 | |
| [−100, 100] | 30 | 0 | |
| [−1.28, 1.28] | 30 | 0 |
| Function | Space | Dim | fmin |
|---|---|---|---|
| [−500, 500] | 30 | −12,569 | |
| [−5.12, 5.12] | 30 | 0 | |
| [−32, 32] | 30 | 0 | |
| [−600, 600] | 30 | 0 | |
| [−50, 50] | 30 | 0 | |
| [−50, 50] | 30 | 0 |
| Function | Space | Dim | fmin |
|---|---|---|---|
| [−65, 65] | 2 | 1 | |
| [−5, 5] | 4 | 0.00030 | |
| [−5, 5] | 2 | −1.0316 | |
| [−5, 5] | 2 | 0.398 | |
| [−2, 2] | 2 | 3 | |
| [1, 3] | 3 | −3.86 | |
| [0, 1] | 6 | −3.32 | |
| [0, 10] | 4 | −10.1532 | |
| [0, 10] | 4 | −10.4028 | |
| [0, 10] | 4 | −10.5363 |
| Function | Space | Dim | fmin |
|---|---|---|---|
| [−5, 5] | 30 | 0 | |
| [−5, 5] | 30 | 0 | |
| [−5, 5] | 30 | 0 | |
| [−5, 5] | 30 | 0 | |
| [−5, 5] | 30 | 0 | |
| [−5, 5] | 30 | 0 |
| Algorithm | Communication Strategy | Main Parameters Setting |
|---|---|---|
| PH-R | Ranking | |
| PH-C | Combination | |
| PH-D | Dynamic Change | |
| PH-H | Hybrid of Ranking and Combination |
| Function | PGWO | PH-R | PH-C | PH-D | PH-H | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| AVG | STSD | AVG | STSD | AVG | STSD | AVG | STSD | AVG | STSD | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | ||||||||
| Algorithm | Accuracy (%) |
|---|---|
| PH-R | 84.97 |
| PH-C | 83.89 |
| PH-D | 84.49 |
| PH-H | 83.67 |
| NN | 73.30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.-S.; Hu, P.; Chu, S.-C. Novel Parallel Heterogeneous Meta-Heuristic and Its Communication Strategies for the Prediction of Wind Power. Processes 2019, 7, 845. https://doi.org/10.3390/pr7110845
Pan J-S, Hu P, Chu S-C. Novel Parallel Heterogeneous Meta-Heuristic and Its Communication Strategies for the Prediction of Wind Power. Processes. 2019; 7(11):845. https://doi.org/10.3390/pr7110845
Chicago/Turabian StylePan, Jeng-Shyang, Pei Hu, and Shu-Chuan Chu. 2019. "Novel Parallel Heterogeneous Meta-Heuristic and Its Communication Strategies for the Prediction of Wind Power" Processes 7, no. 11: 845. https://doi.org/10.3390/pr7110845
APA StylePan, J.-S., Hu, P., & Chu, S.-C. (2019). Novel Parallel Heterogeneous Meta-Heuristic and Its Communication Strategies for the Prediction of Wind Power. Processes, 7(11), 845. https://doi.org/10.3390/pr7110845







