Abstract
High fluctuation in cyclic variations influences engine combustion negatively, leading to higher fuel consumption, lower performance, and drivability problems. This paper examines the impacts of injection strategies (injection pressure, injection timing and injection duration) on the cyclic variation of gasoline spark ignition (SI) optical engine under clean and fouled injectors. The principal oscillatory modes of the cycle to cycle variation have been identified, and the engine cycles over which these modes may persist are described. Through the wavelet power spectrum, the presence of short, intermediate and long-term periodicities in the pressure signal have been detected. It was noticed that depending on the clean and fouled injector, the long and intermediate-term periodicities may span many cycles, whereas the short-period oscillations tend to appear intermittently. Information of these periodicities could be helpful to promote efficient control strategies for better combustion. The outcomes report that the cyclic variation of the IMEP happens on multiple timescales, and thus, display complex dynamics. As the fouled injector used, mainly intermittent high-frequency fluctuations are recognized.
1. Introduction
Fuel consumption and engine emissions are considered as the key points in the design of an engine, downsizing, driving to the current trend of high compression ratios, and boosting proposed at enhancing efficiency in SI engines [1,2]. The higher temperatures and pressures associated with operating conditions lead to a rise of the auto-ignition tendency, resulting in knocking and restricting the optimization of SI engine operations [2,3,4]. Adopting high octane rating fuels leads to the protection of the engine parts from damage which are made via detonation (knock) of the engine as well as higher auto-ignition resistance [5]. Several techniques were used to decrease the pressure and temperature of the end gas including utilizing the charge cooling effect of direct injection [6], using exhaust gas recirculation (EGR) [7], and retarding the spark timing, decreasing [8] the effective compression ratio (CR) by variable valve operation [9]. Cycle-to-cycle variations (CCV) may become the limiting factor for the operational range of the engine design [10], lead to decreased efficiency due to potential detonation [11], and reduce HC emissions resulting from incomplete combustion [12]. Enhanced understanding of the CCV could afford important insights to design engines to be reliably run closer to detonation-limited conditions [13,14,15].
The CCVs in SI engine have generally been addressed in the literature [16,17,18,19]. It is one of the various factors which have to be admitted into consideration in modelling, control and design of SI engines. CCV is detected in the consecutive cycles of cylinder pressure even though the injection strategies and other control parameters are constant. Output engine power reduced as the fluctuations in CCV increased, as well drives to raise operational instabilities and total misfires, thus causing undesirable engine vibrations and noise [13]. Decreasing the CCV is an effective approach which leads to enhancing the performance and fuel consumption of gasoline engines. For this goal, Pan, et al. [20] illustrated the impacts of EGR ratio, CR, and boost pressure on a CCV port fuel injection engine. The authors have studied the impacts using both computational fluid dynamics (CFD) tools and experiments. The results of both the experiment and simulation revealed that the CCV increased as the ratio of EGR increased for its lower laminar flame speed. The CCV has been examined through wavelet analysis approach by Sen, et al. [21]. The enhancement in the engine power by 10% could be achieved by elimination of the CCV for the same fuel consumption in an SI engine [22]. According to Heywood [8], Ozdor [22] and Matekunas [23], the CCV could be defined via the parameters in four principal groups: combustion-relevant parameters, pressure-relevant parameters, flame front-relevant parameters, and exhaust gas-relevant parameters [24]. CCV is most recognized in SI engines, where they are produced by fluctuations in the burn rate for each successive cycle. This fluctuation could have several root causes: CCV in the amount of fuel, CCV in the cylinder gas motion, air and CCV of the mixture composition near the spark plug or exhaust gases present in the cylinder, leading to variations in combustion speed or local end-gas auto-ignition [10].
Cyclic variation in the combustion of the engine is typically quantified by utilizing chaotic and statistical approaches [25,26,27]. These techniques were adapted for the measurement of various patterns and their possible correlations. Standard statistical methods usually apply the coefficient of variation (COV) to determine the CCV of the maximum pressure or indicted mean effects pressure (IMEP), etc. The main weakness of conventional statistical approaches is that they give the temporal variations present in the data series. Conventional statistical approaches are incapable of considering the frequency domain (spectral characteristics) of the data. The wavelet transform is proposed to overcome the difficulties of the Fourier transform. Wavelet analysis eliminates the difficulties related to short time Fourier transform by utilizing adaptive usage of short windows for high-frequency information and long windows for retrieving low-frequency information. One of the chief features of wavelet transform is the capability to perform flexible localized analysis. Wavelet analysis has been employed successfully in characterizing the CCV in reciprocating engines [28,29,30,31,32]. Wavelets analysis are utilized to discover the amplitude as well as periodicities of CCV in engine combustion because wavelet transform gives a good spectral and temporal resolution [33,34].
However, recent researchers employed this method to analyze the in-cylinder pressure of ICE and evaluate CCV. Many investigations engaged in studying the effect of various engine parameters integrate with alternative fuels on CCV [35,36,37,38]. Other studies have investigated into the influence of different CR, injection pressure, fuel additive, and engine load on CCV [30,39,40,41]. Maurya and Akhil [30] found lower CCV for 200 bar of injection pressure compared to 170 and 220 bar using both statistical and wavelet methods. Law et al. [42] discovered that at 2000 rpm engine speed, the spark timing has no impact on the ignition, combustion and IMEP within the range of 2–5 bar. However, gasoline direct injection (GDI) engines with stratified mixtures have large CCV and low combustion efficiency at low engine speeds and high loads [43].
Based on the author’s knowledge, from the above literature survey, few researchers have done studies of the impact of injection strategies on CCV of an optical engine under a clean and fouled injector. Hence, it is essential to conduct a study on the effect of injection pressure, injection timing and injection duration under a clean and fouled injector on cycle to cycle variations to attain acceptable ringing intensity. Thus, the objective of the present study is to understand the influence of injection strategies on SI engine.
2. Experimental Setup
Data Acquisition
All the data analyzed in this work have been obtained from a gasoline direct injection optical engine. The tests were conducted in the Engine Laboratory at Tsinghua University. The optical engine’s cylinder head is modified from a production GDI engine, which makes many properties of this research engine comparable with a commercial engine. The engine specifications are listed in Table 1. A full-visible piston window was used in this study to offer full visibility of the combustion chamber. Figure 1 shows the configuration of the piston window.

Table 1.
Engine specifications.

Figure 1.
Configuration of the full-visible piston window.
Figure 1a shows a comparison of conventional piston windows and full-visible piston windows with the size same as the bore diameter (75 mm). The top of the full-visible window is flat, while the bottom is a curved surface to enlarge the visible area. The design principle for the curved surface is so that when parallel light comes from the bottom of the window, it can reach all the areas inside the combustion chamber, as shown in Figure 1b. According to the reversibility of the light path, the combustion chamber is fully visible when observed from the bottom of the full-visible window. The image distortion brought by the curved surface can be corrected by a coordinate transformation. The correction method is detailed in [37].
Figure 2a,b illustrates the experiment schema of a side view and bottom view image acquisition respectively. Bottom view images were taken by a Photron SA-X2 high-speed camera via the 45° mirror and the quartz window on the piston crown. The side view images were taken by a Phantom V710 high-speed camera through a fused silica window placed at the side of the combustion chamber. The in-cylinder pressure was recorded by the pressure transducer and combustion analyzer. The air–fuel ratio sensor, which was installed at the exhaust port, ensured that the engine always operated at an equivalence ratio of 1.0.
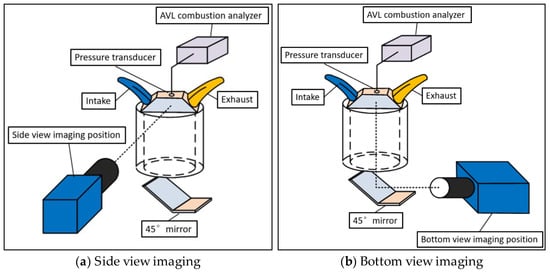
Figure 2.
Schematic of the experimental rig.
The engine was fueled with 93 octane commercial gasoline, and the speed was maintained at 1200 rpm; the engine operated at different injection pressures, injection timings and injection durations under a clean and fouled injector. Operating condition information is summarized in Table 2. A pressure transducer (Kistler, Model 6115CF) collected in-cylinder pressure data. An incremental rotary shaft encoder (BEI sensors, Model H25D, resolution 720 counts per turn) was used. Data of 100 consecutive cycles were acquired under every operating condition.

Table 2.
Experiment operating conditions.
Figure 3 shows the high levels of deposit formation at different parts of the injector, especially the deposit formation in the injector tip; in addition, apparent layers of deposits could be located near the injector tip-dome. Furthermore, a remarkable amount of the deposits gathered nearby the periphery of the hole.
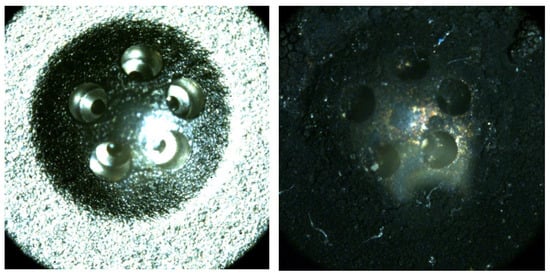
Figure 3.
Images of clean and fouling injector.
3. Wavelet Analysis and Results
The technique of wavelet analysis has been used widely to investigate the variations within the series of collected data in different scientific applications [44]. It has been adopted to indicate the presence and persistence for specified periodicities. In this technique, the signal processing is adopted to distinguish information for time and frequency simultaneously. The task for localization of these two conjugate variables is complex due to the lack of a specified method for the specific value of frequency indication at a provided time and vice versa. Thus, the wavelet analysis technique could be implemented efficiently to obtain a powerful analysis for observations of decomposing time and frequency together [45]. The time series of the IMEP is considered as a base parameter for conducting the wavelet transform. This parameter can be considered a significant indicator for the in-cylinder pressure and fuel combustion progress. Wavelet transform is suitable to analyze the time series with fluctuated power and variable different frequencies [46]. It is used in this study to analyze the IMEP time series for 100 consecutive engine cycles at equal time spacing.
In this analysis, the wavelet power spectrum (WPS) represents the amount of signal energy included at a particular range in a certain domain which is given by the square modulus of the Continuous Wavelet Transform (CWT) [47]. A surface based on both scale and time is used to depict WPS results. Noise analysis is adopted to indicate the significant cyclic variations at a significant level of 5%. Moreover, CWT is used to obtain the global wavelet spectrum (GWS) as another important indicator. GWS represents the average of the WPS for each scale over the whole collected cycles and depicts power as a function of frequency or period [44]. In this analysis, the region in which the edge effects within the range of data have a significant influence on the wavelet transform is represented by the cone of influence (COI). This cone represents the area where edge impacts become essential; the region inside the COI is recognized for analysis, and the area outside COI is ignored [30]. The results in the region under the U-curve of the cone of influence in the WPS may be unreliable due to the edge effects and should be carefully used [44].
Figure 4 illustrates the IMEP time series of the SI engine at different injection pressures, timings and durations under a clean and fouled injector. The cycle-by-cycle variation of IMEP near the best injection timing is strongly correlated to the cycle-by-cycle fluctuation of the concentration of unburned fuel existing at the cavity side during the later combustion period [48]. Huang et al. [49] stated that cycle to cycle variation could be more clearly demonstrated in the CoVIMEP rather than in the maximum cylinder pressure CoVPmax. The WPS and GWS of each of these time series are illustrated in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. The WPS is a contour plot that has the Fourier period on the y-axis and the cycles number (data series) on the x-axis in addition to the intensity of the variations in the data series expressed in the contour plot. The higher variation of the parameter is indicated by a stronger color in the contour plot.
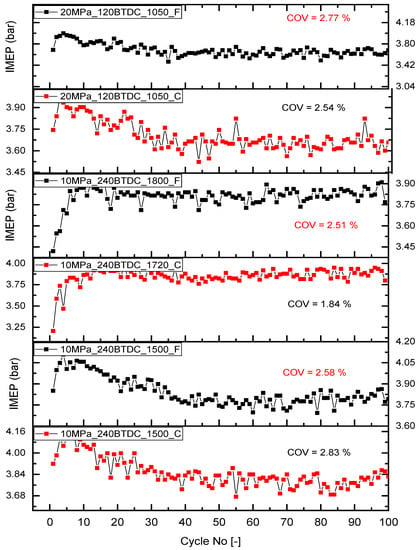
Figure 4.
IMEP of over 100 engine cycles under various injection strategies.
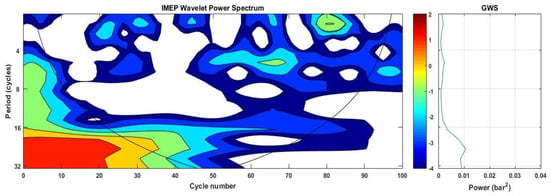
Figure 5.
Wavelet analysis of IMEP (WPS and GWS), 10MPa_240BTDC_1500_Foul.
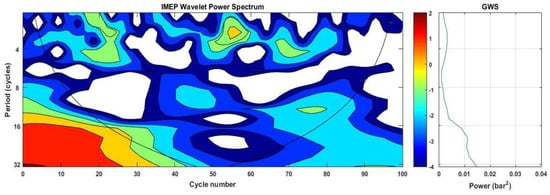
Figure 6.
Wavelet analysis of IMEP (WPS and GWS), 10MPa_240BTDC_1500_Clean.
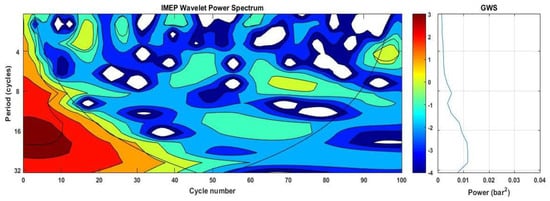
Figure 7.
Wavelet analysis of IMEP (WPS and GWS), 10MPa_240BTDC_1800_Foul.

Figure 8.
Wavelet analysis of IMEP (WPS and GWS), 10MPa_240BTDC_1720_Clean.
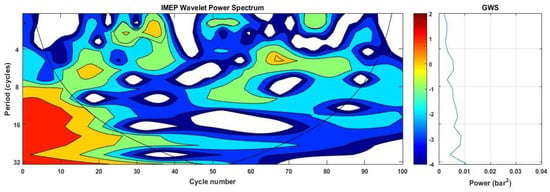
Figure 9.
Wavelet analysis of IMEP (WPS and GWS), 20MPa_120BTDC_1050_Foul.
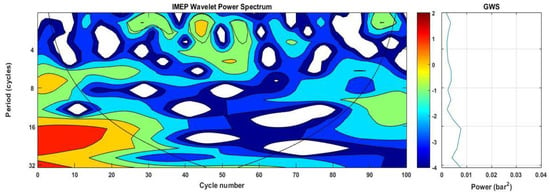
Figure 10.
Wavelet analysis of IMEP (WPS and GWS), 20MPa_120BTDC_1050_Clean.
WPS and GWS depict the results of wavelet analysis which were dedicated to assessing the effect of injector strategies on the engine cyclic variations. Based on the record length of 100 consecutive cycles of the IMEP time series, we limit our considerations to periodicities of less than 32 cycles. It was observed from the wavelet power spectrum (WPS) and global wavelet spectrum (GWS) represented in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 that the CCV of IMEP occurs at multiple timescales. Figure 5, Figure 7 and Figure 9 reveal that, in the fouled injector, the CCV display mainly higher frequency oscillations which tend to increase in the CCV with increasing fouling. Accordingly, it can be seen from Figure 9 that with a fouled injector under an injection parameter (20MPa_120BTDC_1050), there is strong power around the 16-cycle period, which persists approximately over 60 engine cycles. These strong periodic bands bordering the COI extend to smaller periodicities, indicating higher frequencies generated by the use of the fouled injector. Three low periodic bands are also observed; 4–6 cycle period spanning approximately 13–18 cycles; 2–4 cycle band lasting over 32–36 cycles; and 5–7 cycle period spanning approximately 65–70 cycles. Additionally, low-intermittent short-term periodicities are indicated. Figure 7 shows that injector deposits formation (fouled injector) leads to a slight increase in the engine cycle-to-cycle variations in which persistent low-frequency oscillations tend to develop. Slightly higher persistent oscillation developed in the region between 2–5 cycles spanning approximately 11–15 cycles lasting over nearly four engine cycles, as well another region between 7–9 cycles spanning approximately 64–75 cycles lasting over nearly 11 engine cycles. Additionally, low-intermittent short-term periodicities are indicated.
In particular, Figure 10 reveals that wavelet analysis of IMEP for the clean injector with 20MPa_120BTDC_1050_90 injection parameter shows low-frequency cycle-to-cycle variations with intermittent fluctuations. A persistent oscillation is indicated in the region before the four cycles period and between 4–8 cycles period lasting over nearly 41–43 engine cycles for each. In comparison, from the GWS for the results of the clean and fouled injector shown in Figure 6 and Figure 7, it is obvious that the lower spectral power isobtained with the clean injector, which increases slightly after injector deposits formation. This indicates a noticeable effect of deposits formation on engine cycle-to-cycle variations. These results agreed well with that of the COV obtained in this study.
4. Conclusions
Utilizing a continuous wavelet transform, this paper has analyzed the cyclic variations of IMEP. Various long, intermediate and short-term periodicities have been identified from the wavelet power spectrum of the pressure signal.
From a comparison of WPS, the following conclusions can be drawn. It is obvious that the lower spectral power is obtained with the clean injector, which increases slightly after injector deposits formation. This indicates a noticeable effect of deposits formation on engine cycle-to-cycle variations. These results agreed well with that of the COV obtained in this study. At the fouled injector, these periodicities tend to become lower or vanish altogether, and various short and intermediate-term periodicities are observed. Several of the short-term periodicities are intermittent in nature. In summary, wavelet analysis is a useful method for spectral analysis of CCV, and outcomes achieved could be employed for the improvement of effective strategies of engine control. Furthermore, from the GWS, it is obvious that the lower spectral power is obtained with the clean injector which increases slightly after injector deposits formation. This indicates a noticeable effect of deposits formation on engine cycle-to-cycle variations. These results agreed well with that of the COV obtained in this study.
Author Contributions
Z.Z., X.M.; methodology, O.M.A.; software, O.I.A. formal analysis, and writing—original draft preparation, S.S. and M.K., writing—review and editing.
Funding
The authors are grateful to the Natural Science Foundation of China (51636003) for supporting this research.
Acknowledgments
The authors acknowledge the financial support from the Natural Science Foundation of China under Grant 51636003.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Joshi, A. Review of Vehicle Engine Efficiency and Emissions. SAE Int. J. Engines 2018, 11, 1307–1330. [Google Scholar]
- Stone, R. Introduction to Internal Combustion Engines; Springer: Berlin, Germany, 1999; Volume 3. [Google Scholar]
- Zhen, X.; Wang, Y.; Xu, S.; Zhu, Y.; Tao, C.; Xu, T.; Song, M. The engine knock analysis—An overview. Appl. Energy 2012, 92, 628–636. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Reitz, R.D. Knocking combustion in spark-ignition engines. Prog. Energy Combust. Sci. Technol. 2017, 61, 78–112. [Google Scholar] [CrossRef]
- Kalghatgi, G. Developments in internal combustion engines and implications for combustion science and future transport fuels. Proc. Combust. Inst. 2015, 35, 101–115. [Google Scholar] [CrossRef]
- Kasseris, E.; Heywood, J. Charge cooling effects on knock limits in SI DI engines using gasoline/ethanol blends: Part 2-effective octane numbers. SAE Int. J. Fuels Lubr. 2012, 5, 844–854. [Google Scholar] [CrossRef]
- Wei, H.; Zhu, T.; Shu, G.; Tan, L.; Wang, Y. Gasoline engine exhaust gas recirculation–A review. Appl. Energy 2012, 99, 534–544. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; Mcgraw-Hill: New York, NY, USA, 1988; Volume 930. [Google Scholar]
- Li, T.; Gao, Y.; Wang, J.; Chen, Z. The Miller cycle effects on improvement of fuel economy in a highly boosted, high compression ratio, direct-injection gasoline engine: EIVC vs. LIVC. Energy Convers. Energy Convers. Manag. 2014, 79, 59–65. [Google Scholar] [CrossRef]
- Kyrtatos, P.; Brückner, C.; Boulouchos, K. Cycle-to-cycle variations in diesel engines. Appl. Energy 2016, 171, 120–132. [Google Scholar] [CrossRef]
- Maurya, R.K.; Agarwal, A.K. Experimental investigation on the effect of intake air temperature and air–fuel ratio on cycle-to-cycle variations of HCCI combustion and performance parameters. Appl. Energy 2011, 88, 1153–1163. [Google Scholar] [CrossRef]
- Badawy, T.; Bao, X.; Xu, H. Impact of spark plug gap on flame kernel propagation and engine performance. Appl. Energy 2017, 191, 311–327. [Google Scholar] [CrossRef]
- Willman, C.; Stone, R.; Davy, M.; Williams, B.A.O.; Ewart, P.; Shen, L.; Hung, D.L.S.; Liu, M.; Camm, J. Cycle-to-Cycle Variation Analysis of Two-Colour PLIF Temperature Measurements Calibrated with Laser Induced Grating Spectroscopy in a Firing GDI Engine. SAE Int. J. Engines 2019, 1, 0722. [Google Scholar]
- Pischinger, S.; Günther, M.; Budak, O. Abnormal combustion phenomena with different fuels in a spark ignition engine with direct fuel injection. Combust. Flame 2017, 175, 123–137. [Google Scholar] [CrossRef]
- Schulz, C.; Dreizler, A.; Ebert, V.; Wolfrum, J. Combustion diagnostics. In Springer Handbook of Experimental Fluid Mechanics. Springer Handbooks; Springer: Berlin, Germany, 2017. [Google Scholar]
- d’Adamo, A.; Breda, S.; Fontanesi, S.; Cantore, G. LES modelling of spark-ignition cycle-to-cycle variability on a highly downsized DISI engine. Sae Int. J. Engines 2015, 8, 2029–2041. [Google Scholar] [CrossRef]
- Sen, A.K.; Zheng, J.; Huang, Z. Dynamics of cycle-to-cycle variations in a natural gas direct-injection spark-ignition engine. Appl. Energy 2011, 88, 2324–2334. [Google Scholar] [CrossRef]
- Bode, J.; Schorr, J.; Krüger, C.; Dreizler, A.; Böhm, B. Influence of three-dimensional in-cylinder flows on cycle-to-cycle variations in a fired stratified DISI engine measured by time-resolved dual-plane PIV. Proc. Combust. Inst. 2017, 36, 3477–3485. [Google Scholar] [CrossRef]
- Gong, C.; Huang, K.; Chen, Y.; Jia, J.; Su, Y.; Liu, X. Cycle-by-cycle combustion variation in a DISI engine fueled with methanol. Fuel 2011, 90, 2817–2819. [Google Scholar] [CrossRef]
- Pan, M.; Shu, G.; Wei, H.; Zhu, T.; Liang, Y.; Liu, C. Effects of EGR, compression ratio and boost pressure on cyclic variation of PFI gasoline engine at WOT operation. Appl. Therm. Eng. 2014, 64, 491–498. [Google Scholar] [CrossRef]
- Sen, A.K.; Litak, G.; Yao, B.F.; Li, G.X. Analysis of pressure fluctuations in a natural gas engine under lean burn conditions. Appl. Therm. Eng. 2010, 30, 776–779. [Google Scholar] [CrossRef]
- Ozdor, N.; Dulger, M.; Sher, E. Cyclic variability in spark ignition engines a literature survey. SAE Trans. 1994, 103, 1514–1552. [Google Scholar]
- Matekunas, F.A. Modes and measures of cyclic combustion variability. Sae Trans. 1983, 92, 1139–1156. [Google Scholar]
- Kaleli, A.; Ceviz, M.A.; Erenturk, K. Controlling spark timing for consecutive cycles to reduce the cyclic variations of SI engines. Appl. Therm. Eng. 2015, 87, 624–632. [Google Scholar] [CrossRef]
- Maurya, R.K.; Agarwal, A.K. Experimental investigation of cyclic variations in HCCI combustion parameters for gasoline like fuels using statistical methods. Appl. Energy 2013, 111, 310–323. [Google Scholar] [CrossRef]
- Foakes, A.; Pollard, D. Investigation of a chaotic mechanism for cycle-to-cycle variations. Combust. Sci. Technol. 1993, 90, 281–287. [Google Scholar] [CrossRef]
- Maurya, R.K.; Nekkanti, A. Combustion instability analysis using wavelets in conventional diesel engine. In Mathematical Concepts and Applications in Mechanical Engineering and Mechatronics; IGI Global: Hershey, PA, USA, 2017; pp. 390–413. [Google Scholar] [CrossRef]
- Saxena, M.R.; Maurya, R.K. Effect of Diesel Injection Timing on Peak Pressure Rise Rate and Combustion Stability in RCCI Engine. SAE Int. J. Engines 2018, 1, 1731. [Google Scholar] [CrossRef]
- Sen, A.K.; Litak, G.; Edwards, K.D.; Finney, C.E.; Daw, C.S.; Wagner, R.M. Characteristics of cyclic heat release variability in the transition from spark ignition to HCCI in a gasoline engine. Appl. Energy 2011, 88, 1649–1655. [Google Scholar] [CrossRef]
- Maurya, R.K.; Akhil, N. Experimental Investigation on Effect of Compression Ratio, Injection Pressure and Engine Load on Cyclic Variations in Diesel Engine Using Wavelets. SAE Int. J. Engines 2018, 1, 5007. [Google Scholar] [CrossRef]
- Liu, Z.; Chiew, K.; Zhang, L.; Zhang, B.; He, Q.; Zimmermann, R. Rare category exploration via wavelet analysis: Theory and applications. Expert Syst. Appl. 2016, 63, 173–186. [Google Scholar] [CrossRef]
- Canakci, M.; Ozsezen, A.N.; Arcaklioglu, E.; Erdil, A. Prediction of performance and exhaust emissions of a diesel engine fueled with biodiesel produced from waste frying palm oil. Expert Syst. Appl. 2009, 36, 9268–9280. [Google Scholar] [CrossRef]
- Wu, J.-D.; Liu, C.-H. Investigation of engine fault diagnosis using discrete wavelet transform and neural network. Expert Syst. Appl. 2008, 35, 1200–1213. [Google Scholar] [CrossRef]
- Wu, J.-D.; Liu, C.-H. An expert system for fault diagnosis in internal combustion engines using wavelet packet transform and neural network. Expert Syst. Appl. 2009, 36, 4278–4286. [Google Scholar] [CrossRef]
- Galloni, E. Analyses about parameters that affect cyclic variation in a spark ignition engine. Appl. Therm. Eng. 2009, 29, 1131–1137. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Z.; Miao, H.; Wang, X.; Jiang, D. Study of cyclic variations of direct-injection combustion fueled with natural gas–hydrogen blends using a constant volume vessel. Int. J. Hydrog. Energy 2008, 33, 7580–7591. [Google Scholar] [CrossRef]
- Aleiferis, P.; Hardalupas, Y.; Taylor, A.; Ishii, K.; Urata, Y. Flame chemiluminescence studies of cyclic combustion variations and air-to-fuel ratio of the reacting mixture in a lean-burn stratified-charge spark-ignition engine. Combust. Flame 2004, 136, 72–90. [Google Scholar] [CrossRef]
- Ceviz, M.A.; Sen, A.K.; Küleri, A.K.; Öner, I.V. Engine performance, exhaust emissions, and cyclic variations in a lean-burn SI engine fueled by gasoline–hydrogen blends. Appl. Therm. Eng. 2012, 36, 314–324. [Google Scholar] [CrossRef]
- Santoso, W.B.; Rosli, A.; Bakar, R.; Ariyono, S.; Cholis, N. Study of cyclic variability in diesel-hydrogen dual fuel engine combustion. Int. J. Mech. Mechatron. Eng. IJMME-IJENS 2012, 12, 52–56. [Google Scholar]
- Barboza, A.; Sudhir, C.; Sharma, Y.N. Performance, Emissions & Cyclic Combustion Studies of CI engine using Jatropha B20 Fuel. Int. J. Earth Sci. Eng. 2012, 5, 1073–1077. [Google Scholar]
- Barboza, A.; Sharma, N.Y.; Sudhir, C. Cyclic combustion studies of a CI engine operating on jatropha B20 fuel. In Proceedings of the 2nd International Conference on Mechanical and Electrical Technology (ICMET), Singapore, 10–12 September 2010; pp. 43–46. [Google Scholar]
- Law, D.; Kemp, D.; Allen, J.; Kirkpatrick, G.; Copland, T. Controlled Combustion in an IC-Engine with a Fully Variable Valve Train. Sae Trans. 2001, 110, 192–198. [Google Scholar]
- Ikoma, T.; Abe, S.; Sonoda, Y.; Suzuki, H.; Suzuki, Y.; Basaki, M. Development of V-6 3.5-liter Engine Adopting New Direct Injection System. SAE Int. J. Engines 2006, 1, 1259. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Ali, O.M.; Mamat, R.; Abdullah, N.R.; Abdullah, A.A. Analysis of blended fuel properties and engine performance with palm biodiesel–diesel blended fuel. Renew. Energy 2016, 86, 59–67. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Ali, O.M.; Mamat, R.; Masjuki, H.H.; Abdullah, A.A. Analysis of blended fuel properties and cycle-to-cycle variation in a diesel engine with a diethyl ether additive. Energy Convers. Manag. 2016, 108, 511–519. [Google Scholar] [CrossRef]
- Fujikawa, T.; Nomura, Y.; Hattori, Y.; Kobayashi, T.; Kanda, M. Analysis of cycle-by-cycle variation in a direct injection gasoline engine using a laser-induced fluorescence technique. Int. J. Engine Res. 2003, 4, 143–153. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, L.; Jiang, D.; Ren, Y.; Liu, B.; Zeng, K.; Wang, Q. Study on cycle-by-cycle variations of combustion in a natural-gas direct-injection engine. Part D J. Automob. Eng. 2008, 222, 1657–1667. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).