Comparison of Irregularity Indices of Several Dendrimers Structures
Abstract
:1. Introduction
2. Main Results
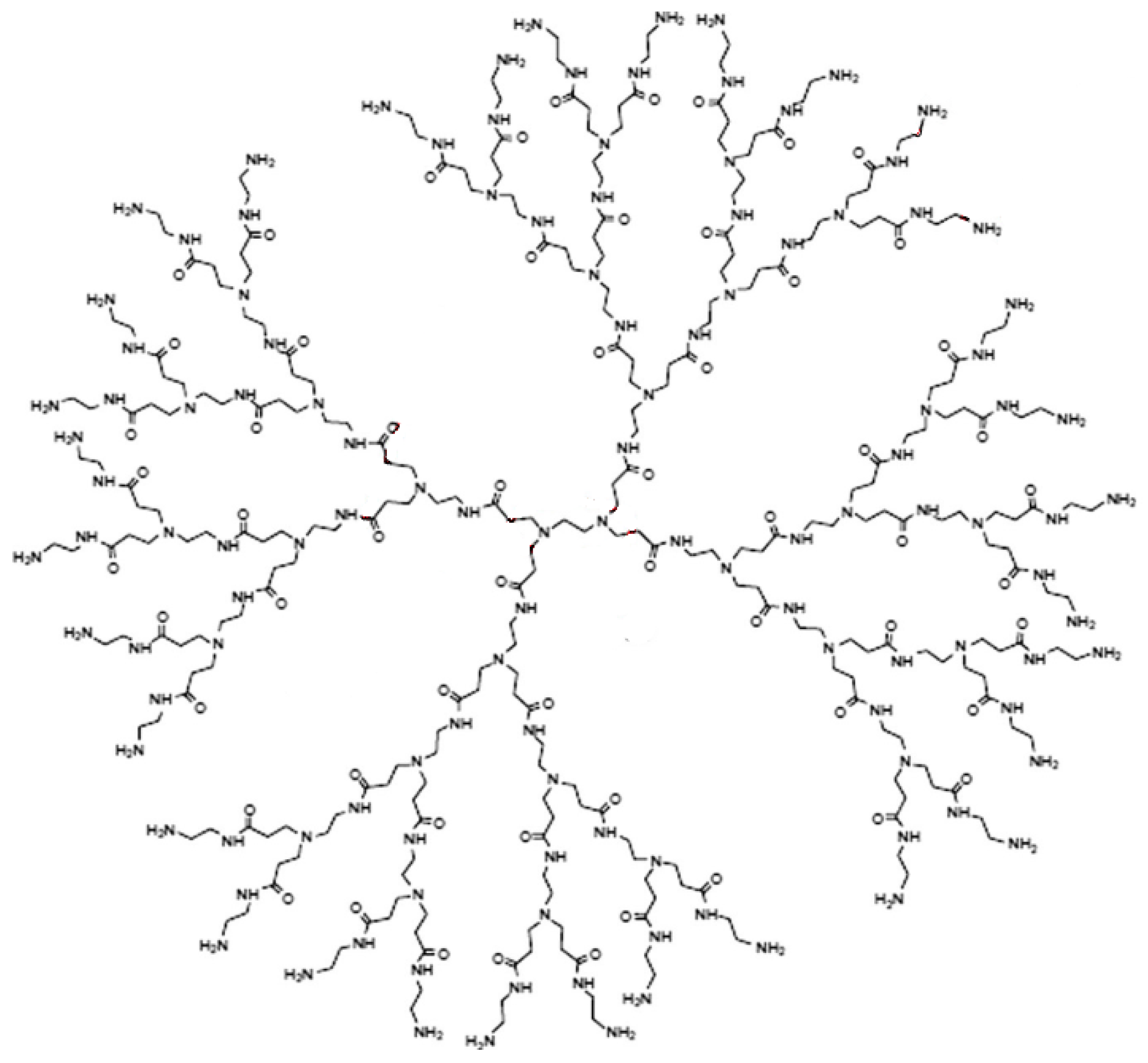
2.1. Irregularity Measures of PAMAM Dendrimers
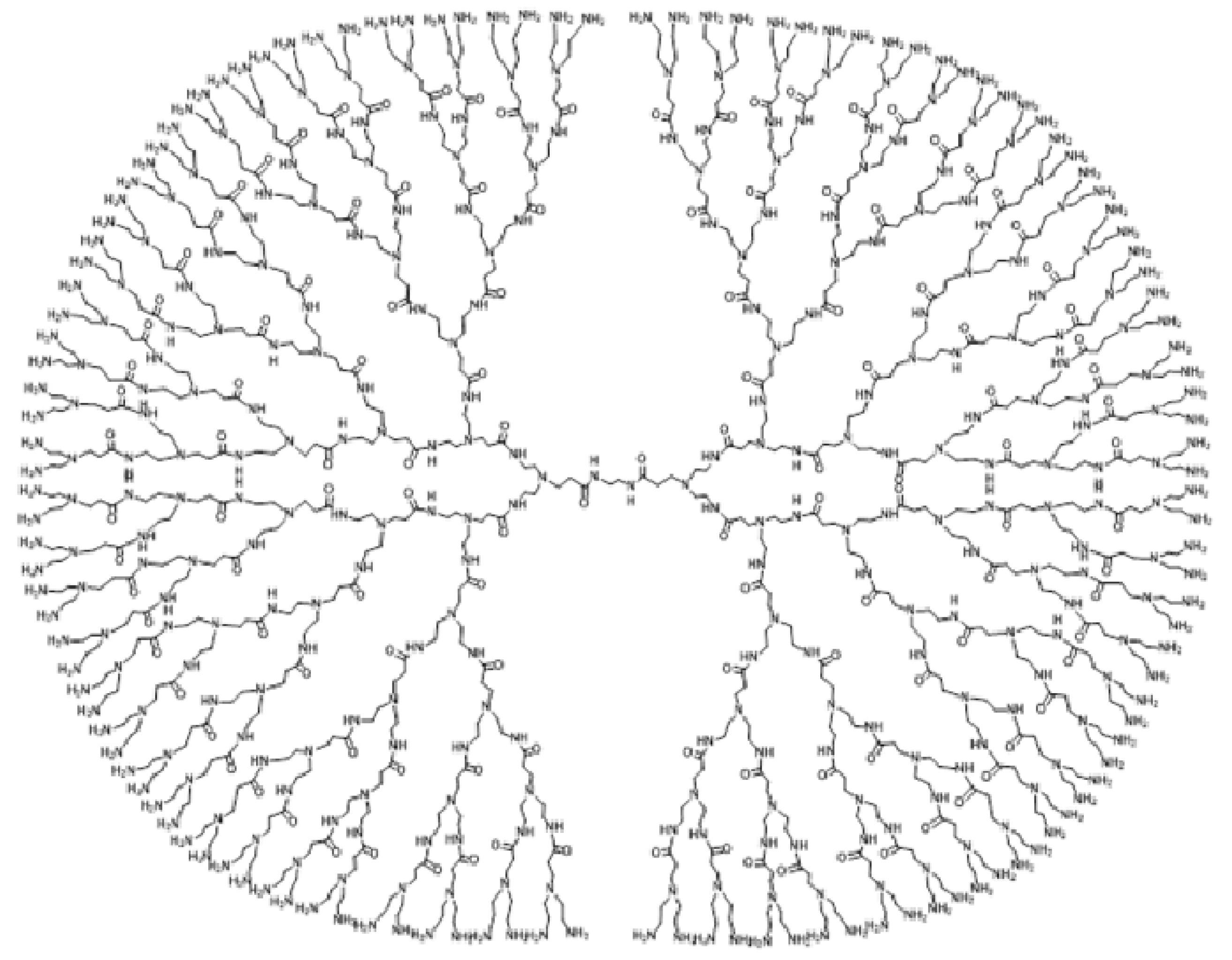
2.2. Irregularity Measures of PolyEThyleneAmidoAmine (PETAA) Dendrimers
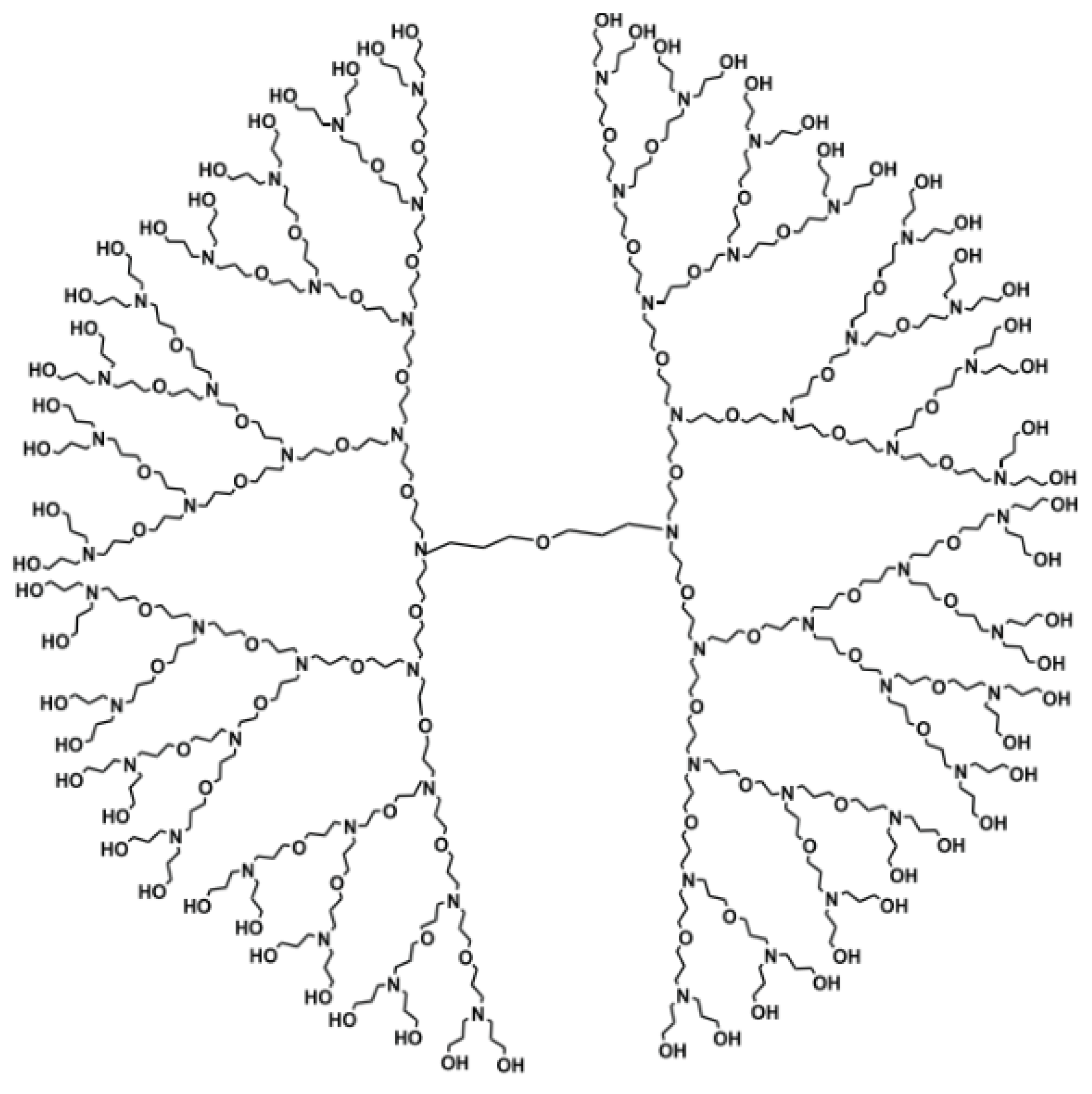
2.3. Irregularity Measures of Poly (propyl ether imine) (PETIM) Dendrimers
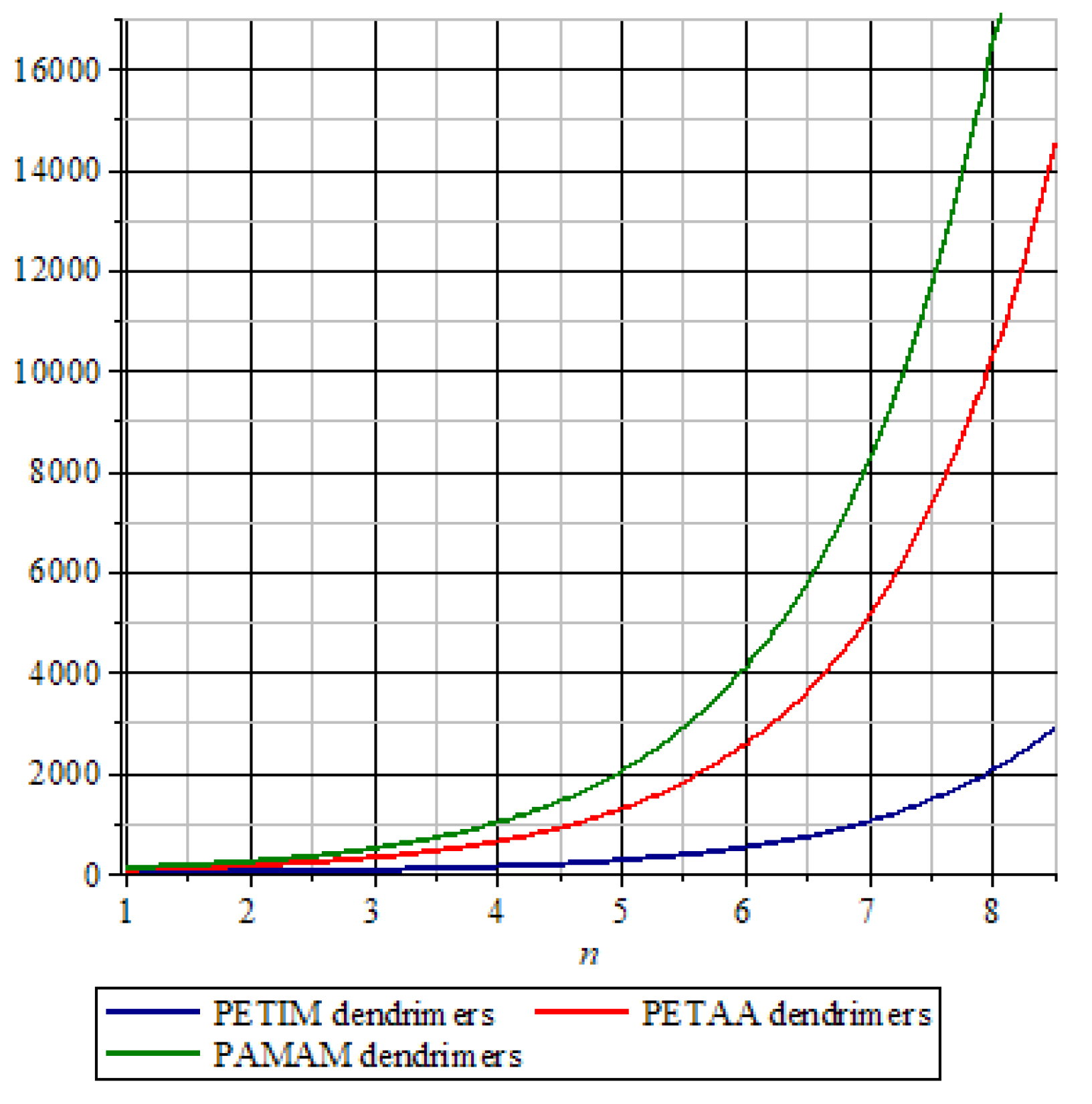
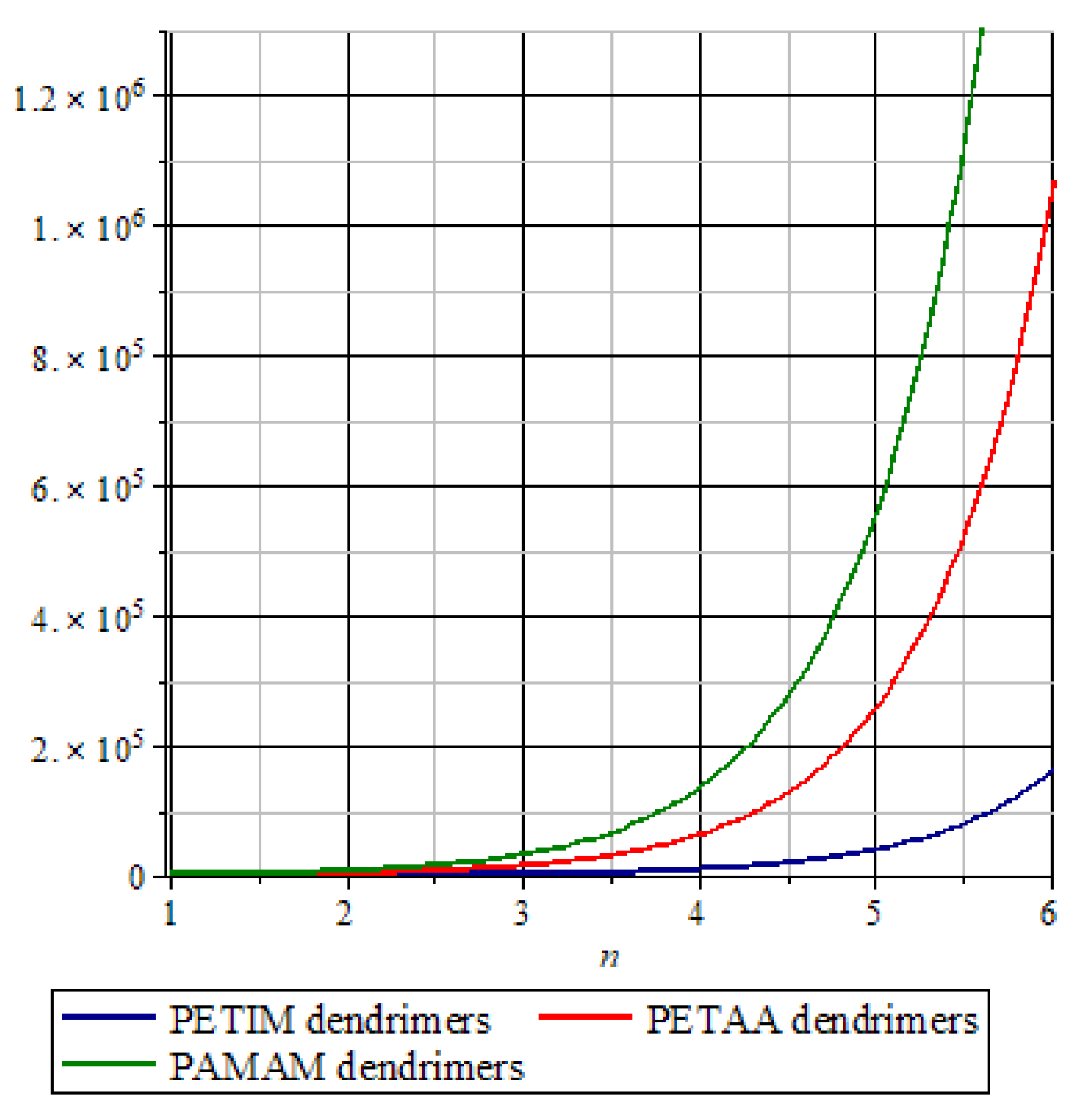
3. Graphical Analysis and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gozalbes, R.; Doucet, J.P.; Derouin, F. Application of topological descriptors in QSAR and drug design: History and new trends. Curr. Drug Targets Infect. Disord. 2002, 2, 93–102. [Google Scholar] [CrossRef] [PubMed]
- Amic, D.; Beaa, D.; Lucic, B.; Nikolic, S.; Trinajstic, N. The vertex connectivity index revisited. J. Chem. Inf. Comput. Sci. 1998, 38, 819–822. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, E.; Shao, Z.; Gutman, I.; Klobucar, A. Total domination and open packing in some chemical graphs. J. Math. Chem. 2018, 5, 1481–1492. [Google Scholar] [CrossRef]
- Nasiri, R.; Fath-Tabar, G.H. The second minimum of the irregularity of graphs. Electron. Notes Discret. Math. 2014, 45, 133–140. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, P.; Zhang, X.; Dimitrov, D.; Liu, J.B. On the maximum ABC index of graphs with prescribed size and without pendent vertices. IEEE Access 2018, 6, 27604–27616. [Google Scholar] [CrossRef]
- Ye, A.; Qureshi, M.I.; Fahad, A.; Aslam, A.; Jamil, M.K.; Zafar, A.; Irfan, R. Zagreb connection number index of nanotubes and regular hexagonal lattice. Open Chem. 2019, 17, 75–80. [Google Scholar] [CrossRef]
- Réti, T.; Sharafdini, R.; Dregelyi-Kiss, A.; Haghbin, H. Graph irregularity indices used as molecular descriptor in QSPR studies. Match Commun. Math. Comput. Chem. 2018, 79, 509–524. [Google Scholar]
- Albertson, M.O. The irregularity of a graph. Ars Combin. 1997, 46, 219–225. [Google Scholar]
- Luo, W.; Zhou, B. On the irregularity of trees, unicyclic graphs with given matching number. Util. Math. 2010, 83, 141–147. [Google Scholar]
- Hansen, P.; Mélot, H. Variable neighborhood search for extremal graphs. 9. bounding the irregularity of a graph. Discret. Math. Theor. Comput. Sci. 2005, 69, 253–264. [Google Scholar]
- Abdo, H.; Dimitrov, D. The irregularity of graphs under graph operations. Discuss. Math. Graph Theory 2014, 34, 263–278. [Google Scholar] [CrossRef]
- Abdo, H.; Brandt, S.; Dimitrov, D. The total irregularity of a graph. Discret. Math. Theor. Comput. Sci. 2014, 16, 201–206. [Google Scholar]
- Dimitrov, D.; Škrekovski, R. Comparing the irregularity, the total irregularity of graphs. Ars Math. Contemp. 2015, 9, 45–50. [Google Scholar] [CrossRef]
- Fath-Tabar, G.H. Old, new Zagreb indices of graphs. Match Commun. Math. Comput. Chem. 2011, 65, 79–84. [Google Scholar]
- Abdo, H.; Cohen, N.; Dimitrov, D. Graphs with maximal irregularity. Filomat 2014, 28, 1315–1322. [Google Scholar] [CrossRef]
- Nasiri, R.; Ellahi, H.R.; Gholami, A.; Fath-Tabar, G.H. The irregularity, total irregularity of Eulerian graphs. Iran. J. Math. Chem. 2018, 9, 101–111. [Google Scholar]
- Gutman, I.; Togan, M.; Yurttas, A.; Cevik, A.S.; Cangul, I.N. Inverse problem for sigma index. Match Commun. Math. Comput. Chem. 2018, 79, 491–508. [Google Scholar]
- Abdo, H.; Dimitrov, D.; Gutman, I. Graphs with maximal σ irregularity. Discret. Appl. Math. 2018, 250, 57–64. [Google Scholar] [CrossRef]
- Gutman, I. Stepwise irregular graphs. Appl. Math. Comput. 2018, 325, 234–238. [Google Scholar] [CrossRef]
- Bell, F.K. A note on the irregularity of graphs. Linear Algebra Appl. 1992, 161, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, F.; Aval, S.F.; Akbarzadeh, A.; Milani, M.; Nasrabadi, H.T.; Joo, S.W.; Hanifehour, Y.; Koshki, K.N.; Pashei-Asl, R. Dendrimers: Synthesis, applications, and properties. Nano Scale Res. Lett. 2014, 247, 1–10. [Google Scholar] [CrossRef]
- Buhleier, E.; Wehner, W.; Vogtle, F. Cascade and nonskid chain like syntheses of molecular cavity topologies. Synthesis 1978, 2, 155–158. [Google Scholar] [CrossRef]
- Tomalia, D.A.; Baker, H.; Dewald, J.R.; Hall, M.; Kallos, G.; Martin, S.; Roeck, J.; Ryder, J.; Smith, P. Dendritic macromolecules: Synthesis of starburst dendrimers. Macromolecules 1986, 19, 2466–2468. [Google Scholar] [CrossRef]
- Newkome, G.R.; Yao, Z.; Baker, G.R.; Gupta, V.K. Micelles. Part 1. Cascade molecules: A new approach to micelles. A [27]-arborol. J. Org. Chem. 1985, 50, 2003–2004. [Google Scholar] [CrossRef]
- Abdo, H.; Dimitrov, D.; Gao, W. On the irregularity of some molecular structures. Can. J. Chem. 2017, 95, 174–183. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Aamir, M.; Iqbal, Z.; Ishaq, M.; Aslam, A. On irregularity measures of some dendrimers structures. Mathematics 2019, 7, 271. [Google Scholar] [CrossRef]
- Gutman, I.; Hansen, P.; Mélot, H. Variable neighborhood search for extremal graphs 10. Comparison of irregularity indices for chemical trees. J. Chem. Inf. Model. 2005, 45, 222–230. [Google Scholar] [CrossRef]
- Iqbal, Z.; Aslam, A.; Ishaq, M.; Aamir, M. Characteristic study of irregularity measures of some nanotubes. Can. J. Phys. 2019. [Google Scholar] [CrossRef]
- Gao, W.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aamir, M.; Aslam, A. On eccentricity-based topological indices study of a class of porphyrin-cored dendrimers. Biomolecules 2018, 8, 71. [Google Scholar] [CrossRef]
- Gao, W.; Iqbal, Z.; Ishaq, M.; Aslam, A.; Aamir, M.; Binyamin, M.A. Bounds on topological descriptors of the corona product of F-sum of connected graphs. IEEE Access 2019, 7, 26788–26796. [Google Scholar] [CrossRef]
- Gao, W.; Iqbal, Z.; Ishaq, M.; Aslam, A.; Sarfraz, R. Topological aspects of dendrimers via distance-based descriptors. IEEE Access 2019, 7, 35619–35630. [Google Scholar] [CrossRef]
- Hussain, Z.; Munir, M.; Rafique, S.; Hussnain, T.; Ahmad, H.; Kwun, Y.C.; Kang, S.M. Imbalance-based irregularity molecular descriptors of nanostar dendrimers. Processes 2019, 7, 517. [Google Scholar] [CrossRef]
- Iqbal, Z.; Aamir, M.; Ishaq, M.; Shabri, A. On theoretical study of Zagreb indices and Zagreb polynomials of water-soluble perylenediimide-cored dendrimers. J. Inf. Math. Sci. 2018, 10, 647–657. [Google Scholar]
- Iqbal, Z.; Ishaq, M.; Aamir, M. On eccentricity-based topological descriptors of dendrimers. Iran. J. Sci. Technol. Trans. Sci. 2019, 43, 1523–1533. [Google Scholar] [CrossRef]
- Iqbal, Z.; Ishaq, M.; Aslam, A.; Gao, W. On eccentricity-based topological descriptors of water-soluble dendrimers. Z. Nat. 2018, 74, 25–33. [Google Scholar] [CrossRef]
- Kang, S.M.; Iqbal, Z.; Ishaq, M.; Sarfraz, R.; Aslam, A.; Nazeer, W. On eccentricity-based topological indices and polynomials of phosphorus-containing dendrimers. Symmetry 2018, 10, 237. [Google Scholar] [CrossRef]
- Zheng, J.; Iqbal, Z.; Fahad, A.; Zafar, A.; Aslam, A.; Qureshi, M.I.; Irfan, R. Some eccentricity-based topological indices and polynomials of poly(EThyleneAmidoAmine) (PETAA) dendrimers. Processes 2019, 7, 433. [Google Scholar] [CrossRef]
- Tomalia, D.A.; Baker, H.; Dewald, J.R.; Hall, M.; Kallos, G.; Martin, S.; Roeck, J.; Ryder, J.; Smith, P. Dendrimers II: Architecture, nanostructure and supramolecular chemistry. Macromolecules 1986, 19, 2466. [Google Scholar]
- Froehling, P.E. Dendrimers and dyes a review. Dyes Pigment. 2001, 48, 187–195. [Google Scholar] [CrossRef]
- Tomalia, D.A.; Baker, H.; Dewald, J.R.; Hall, M.; Kallos, G.; Martin, S.; Roeck, J.; Ryder, J.; Smith, P. A new class of polymers: Starburst-dendritic macromolecules. Polym. J. 1985, 17, 117–132. [Google Scholar] [CrossRef]
- Alper, J. Rising chemical stars could play many roles. Science 1991, 251, 1562–1564. [Google Scholar] [CrossRef]
- Araújo, R.V.; Santos, S.S.; Ferreira, E.I.; Giarolla, J. New advances in general biomedical applications of PAMAM dendrimers. Molecules 2018, 23, 2849. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: London, UK, 2008. [Google Scholar]
- Huang, B.; Tang, S.; Desai, A.; Lee, K.H.; Leroueil, P.R.; Baker, J.R. Novel Poly(EthyleneAmidoAmine) (PETAA) dendrimers produced through a unique and highly efficient synthesis. Polymer 2011, 52, 5975–5984. [Google Scholar] [CrossRef]
- Ramakrishna, T.; Jayaraman, N. Synthesis of poly(propyl ether imine) dendrimers and evaluation of their cytotoxic properties. J. Org. Chem. 2003, 69, 9694–9704. [Google Scholar]
- Jain, S.; Kaur, A.; Puri, R.; Utreja, P.; Jain, A.; Bhide, M.; Ratnam, R.; Singh, V.; Patil, A.S.; Jayaraman, N. Poly propyl ether imine (PETIM) dendrimer, A novel non-toxic dendrimer for sustained drug delivery. Eur. J. Med. Chem. 2010, 45, 4997–5005. [Google Scholar] [CrossRef]
- Liang, Z.; Gong, T.; Sun, X.; Tang, J.Z.; Zhang, Z. Chitosan oligomers as drug carriers for renal delivery of zidovudine. Carbohydr. Polym. 2012, 87, 2284–2290. [Google Scholar] [CrossRef]
- Jain, S.K.; Sharma, A.; Mahajan, M.; Sankar, R. In-vitro and in-vivo evaluation of poly (propyl ether imine) (PETIM) dendrimer for sustained delivery of zidovudine. J. Antivir. Antiretrovir. 2013, 5. [Google Scholar] [CrossRef]


| Growth Stage | ||||
|---|---|---|---|---|
| 74 | 1358 | 98 | 949/2500 | |
| 170 | 7030 | 226 | 4901/12,996 | |
| 362 | 31,622 | 482 | 22,021/58,564 | |
| 746 | 133,798 | 994 | 93,125/248,004 | |
| 1514 | 550,118 | 2018 | 382,789/1,020,100 |
| Growth Stage | ||||
|---|---|---|---|---|
| 51 | 656 | 63 | 454/1225 | |
| 115 | 3320 | 143 | 2290/6241 | |
| 243 | 14,792 | 303 | 10,186/27,889 | |
| 499 | 62,312 | 623 | 42,874/117,649 | |
| 1011 | 255,656 | 1263 | 175,834/483,025 |
| Growth Stage | ||||
|---|---|---|---|---|
| 10 | 57 | 10 | 146/625 | |
| 26 | 413 | 26 | 1018/5329 | |
| 58 | 2085 | 58 | 5066/28,561 | |
| 122 | 9269 | 122 | 22,378/130,321 | |
| 250 | 38,997 | 250 | 93,866/55,5025 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Iqbal, Z.; Irfan, R.; Chaudhry, M.A.; Ishaq, M.; Jamil, M.K.; Fahad, A. Comparison of Irregularity Indices of Several Dendrimers Structures. Processes 2019, 7, 662. https://doi.org/10.3390/pr7100662
Zhao D, Iqbal Z, Irfan R, Chaudhry MA, Ishaq M, Jamil MK, Fahad A. Comparison of Irregularity Indices of Several Dendrimers Structures. Processes. 2019; 7(10):662. https://doi.org/10.3390/pr7100662
Chicago/Turabian StyleZhao, Dongming, Zahid Iqbal, Rida Irfan, Muhammad Anwar Chaudhry, Muhammad Ishaq, Muhammad Kamran Jamil, and Asfand Fahad. 2019. "Comparison of Irregularity Indices of Several Dendrimers Structures" Processes 7, no. 10: 662. https://doi.org/10.3390/pr7100662
APA StyleZhao, D., Iqbal, Z., Irfan, R., Chaudhry, M. A., Ishaq, M., Jamil, M. K., & Fahad, A. (2019). Comparison of Irregularity Indices of Several Dendrimers Structures. Processes, 7(10), 662. https://doi.org/10.3390/pr7100662






