Robust Scheduling Optimization Model for Multi-Energy Interdependent System Based on Energy Storage Technology and Ground-Source Heat Pump
Abstract
:1. Introduction
2. Description of the CCHP System Based on Thermal Energy Storage and Ground-Source Heat Pump
3. Operation Performance Evaluation Indexes
3.1. Operation Strategy
3.2. Performance Indexes
3.2.1. Energy Performance Indexes
3.2.2. Economic Performance Indexes
3.2.3. Environmental Performance Indexes
4. Multi-Objective Operation Optimization Model
4.1. Objective Functions
4.2. Constraint Conditions
4.2.1. Energy Balance Constraints
4.2.2. Gas-Steam Combined Cycle Constraints
4.2.3. Auxiliary Subsystem Constraints
4.2.4. Power Source Output Constraints
4.2.5. Other Module Constraints
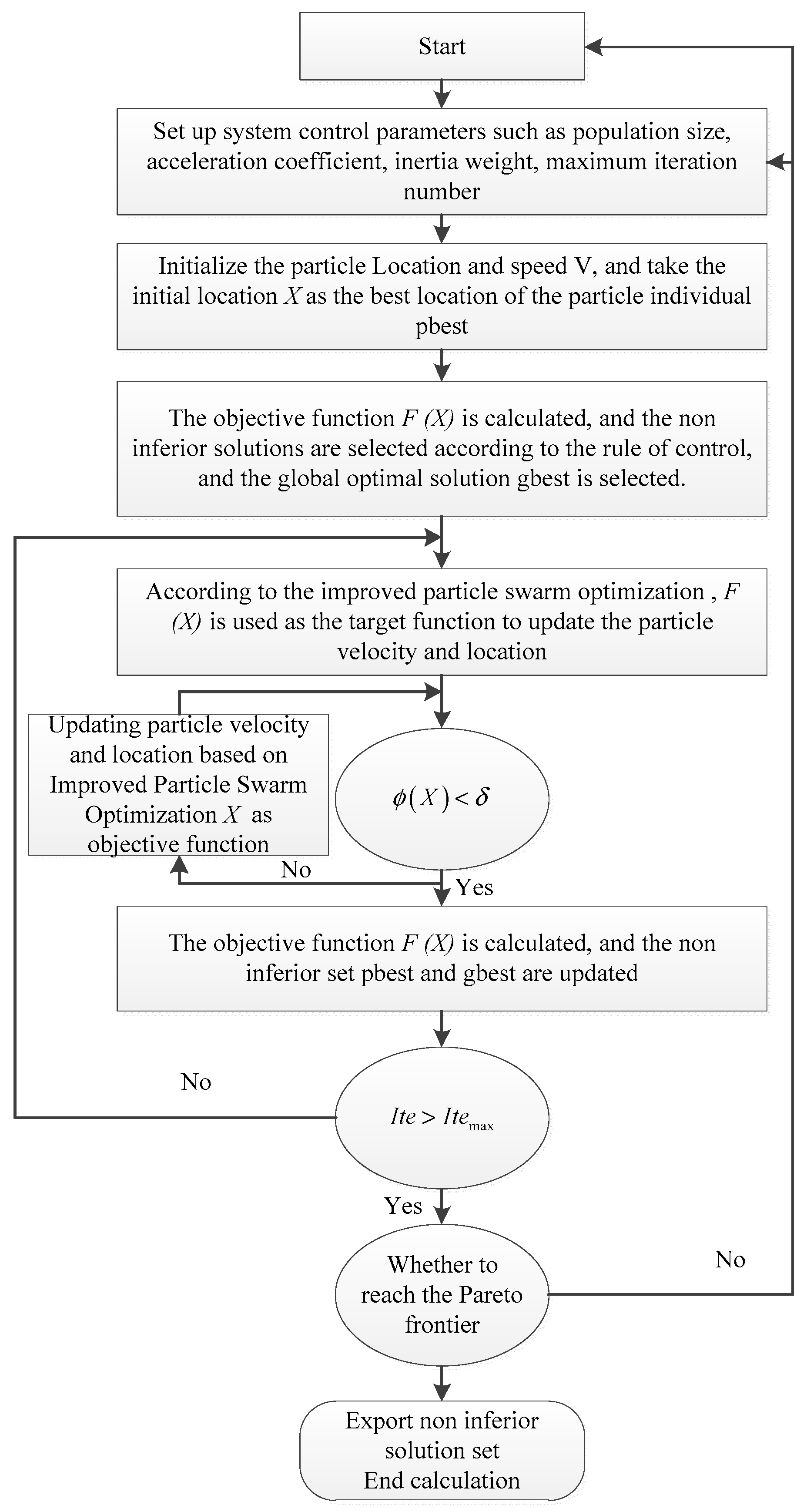
4.3. Solution Methodology
4.3.1. Wind Power Output Uncertainty Set
4.3.2. Basic Particle Swarm Optimization Algorithm
- (1)
- Parameter initialization. Initialize the particle population size , the acceleration factors and , the maximum particle velocity , the maximum iteration number , and so on. Initialize the speed and location of all particles. The initial location of the particle is set as the optimal location, and the initial particle global optimal location is set as the population optimal location.
- (2)
- Update the velocity and location of the particle according to Formulas (34) and (35);
- (3)
- Update the individual optimal location;
- (4)
- Update the particle population optimal location;
- (5)
- Check the terminating condition. If it is satisfied, the algorithm finishes; if not, return to step (2).
4.3.3. Multi-Objective Particle Swarm Optimization Algorithm
4.3.4. Improvement of the PSO Algorithm Based on the Dynamic Object Method (DOM) Constraint Mechanism
5. Example Analysis
5.1. Basic Data
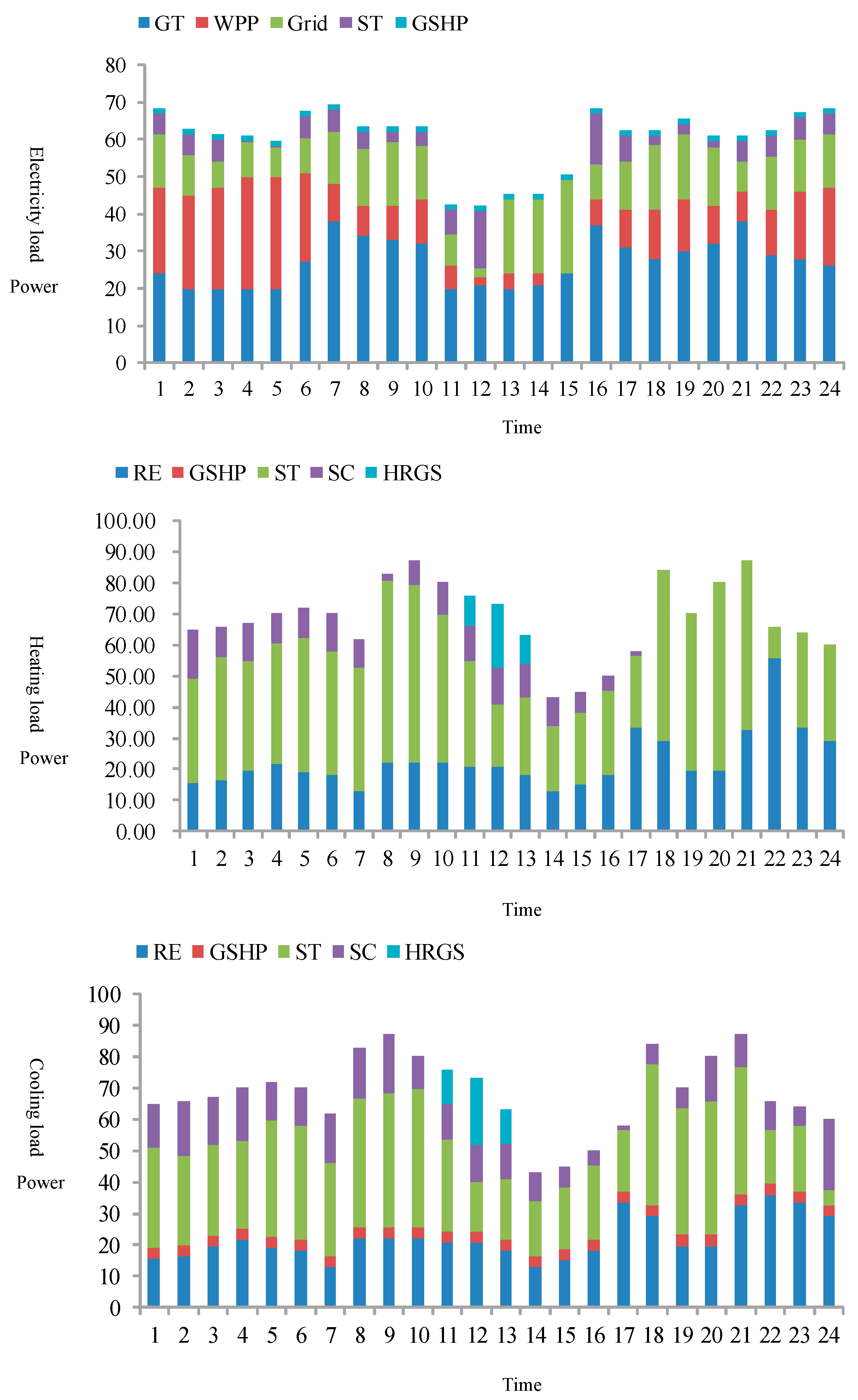
5.2. Operation Results with Signal Objective
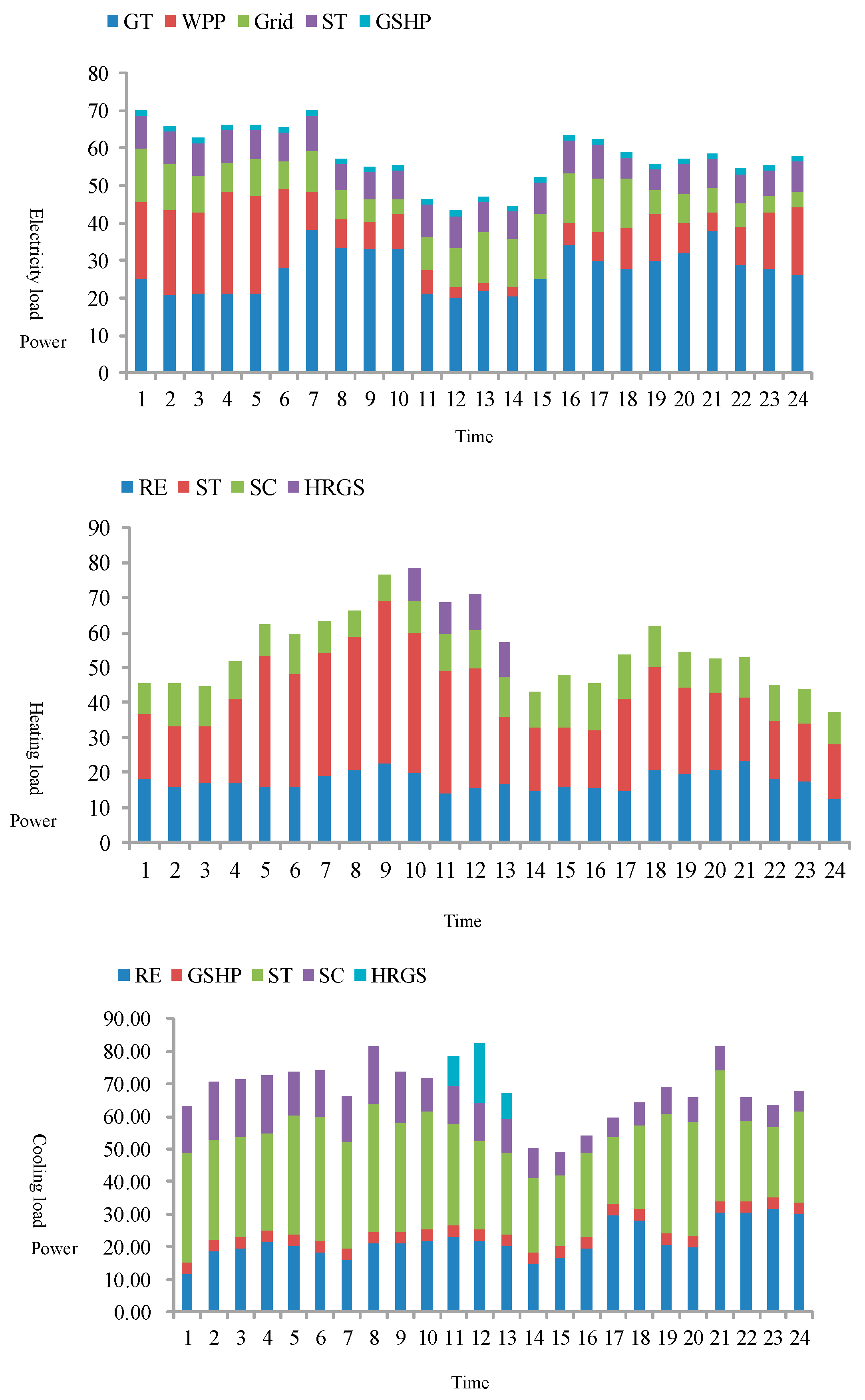
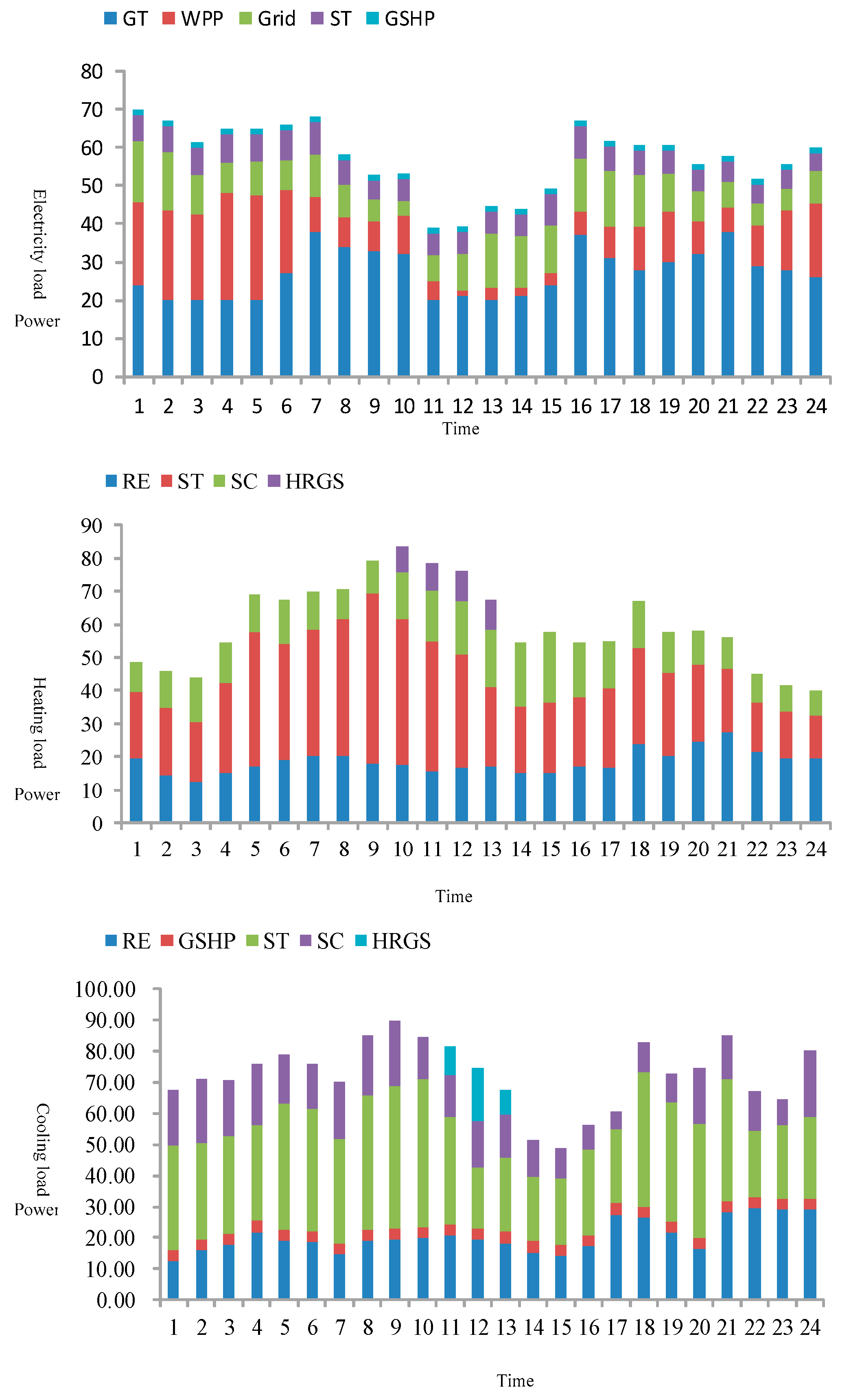
5.2.1. Operation Result in Scenario 1
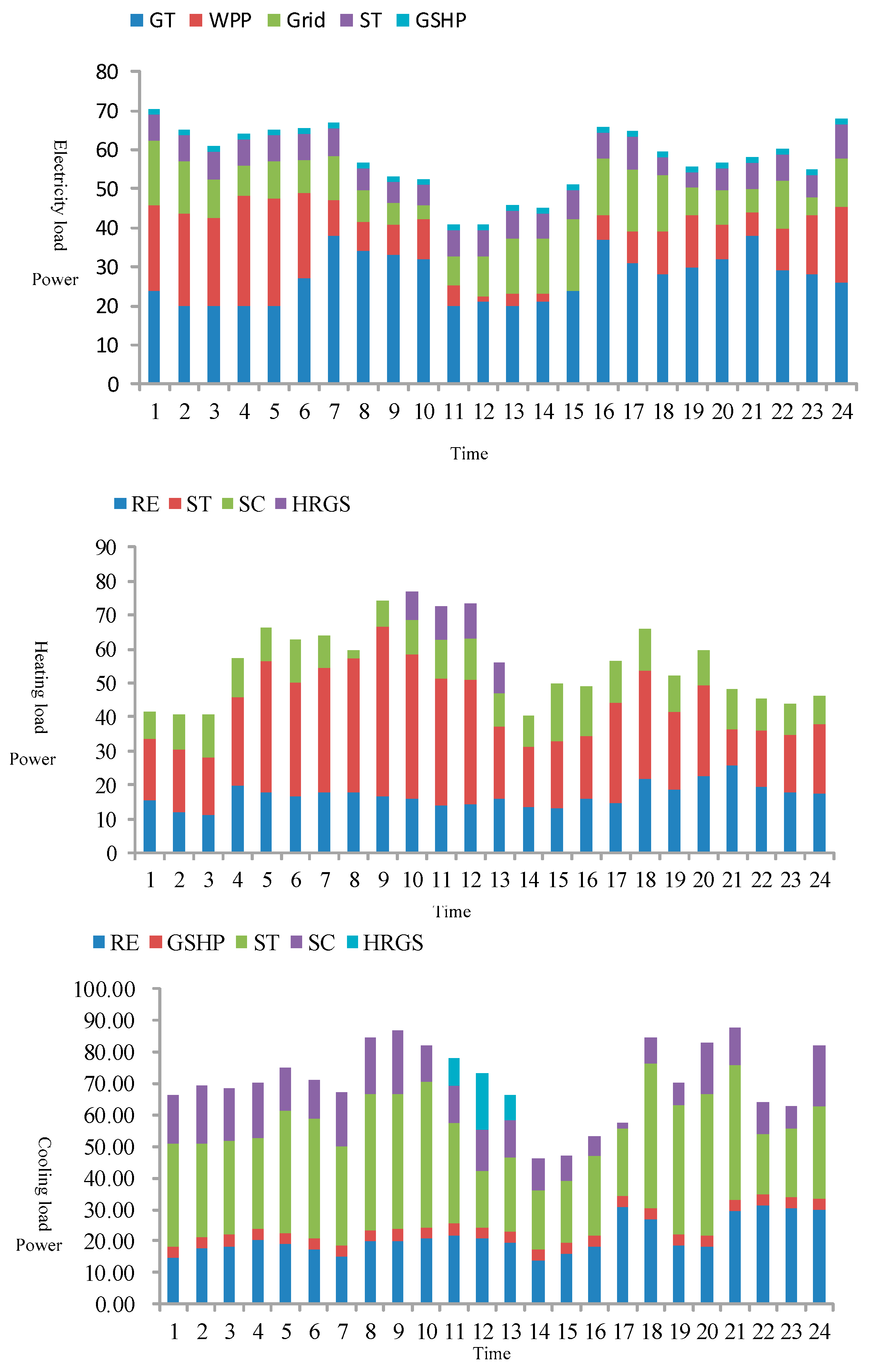
5.2.2. Operation Results in Scenario 2
5.2.3. Operation Results in Scenario 3
5.2.4. Operation Result in Scenario 4
5.2.5. Operation Result in Scenario 5
5.3. Evaluation and Comparison of the Different Scenarios
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| NG | Natural gas |
| The gas generating set produce electrical energy | |
| The energy of absorption heat pump units Consumption | |
| the heat in the storage tank | |
| the energy storage in Ground-Source Heat Pump | |
| the electric refrigeration steam compression refrigeration unit | |
| The smoke from the group of motors | |
| the energy rate of the system | |
| the natural gas input to the system | |
| NSR | the Natural gas (NG) saving rate |
| , , and | The system load of heating, cooling, and power |
| , , , and | The inputs of natural gas, wind power plant (WPP), solar energy, and ground-source heat pump |
| TOC | the total operating cost |
| the system electricity purchased from the grid | |
| the price of the system electricity purchased from the grid | |
| , | the prices of wind power and gas generation |
| the natural gas consumption | |
| the price of natural gas | |
| other operating costs | |
| the discount rate | |
| the index for the period of operation | |
| the total number of years in operation | |
| , | the initial investment costs of the reference system |
| the system’s total operating cost | |
| the carbon emissions of the CCHP system | |
| the carbon dioxide emissions from natural gas combustion | |
| the carbon dioxide emissions per unit power | |
| he system electricity purchased from the grid | |
| the power generation output of the gas turbine at time t | |
| the power generation output of the steam turbine at time t | |
| the wind power output at time t | |
| The station service power consumption ratio of the CCHP system | |
| the electricity for regenerative electric boiler (RE) at time t | |
| the electricity for the electric compression chiller (EC) at time t | |
| the total electricity at time t | |
| the power load required by the buildings at time t | |
| the electricity bought from the grid at time t | |
| the power required by the ground-source heat pump unit | |
| the power required for the hot water heat absorption heat pump unit (AM) | |
| the heat energy generated by ST at time t | |
| the heat energy generated by RE | |
| the heat energy generated by GSHP at time t | |
| the heating energy for the absorption chiller (AC) at time t | |
| the heating energy for heat exchanger (HE) at time t | |
| the heat energy generated by AM at time t | |
| , | the heating energies for AC and HE at time t |
| the heating load provided by HE at time t | |
| the heating energy load required by the buildings at time t | |
| , | The cooling energies generated by EC and AC at time t |
| the cooling energy load required by the buildings at time t | |
| the heat energy generated by HRSGs for ST | |
| the heat energy efficiency of HRSGs | |
| the energy efficiency of the gas turbine unit | |
| the electricity generation efficiency of the gas turbine unit | |
| the heat collected by the flat-plate collector at time t | |
| The heat conversion efficiency of the flat-plate collector at time t | |
| , | the heat energies generated by SC for ST and HE at time t |
| the heat energy stored by ST at time t | |
| , | the heat energies generated by SC and HR for ST at time t |
| the density of the water in the tank | |
| the specific heat at constant pressure | |
| , | the volumes of water in the tank and the tank at time t |
| the temperature function of the water in the tank at time t | |
| the ambient temperature at time t | |
| the heat transporting coefficient of the water tank | |
| the area of the water tank | |
| the capacity stored by RE at time t | |
| the dissipating heat efficiency of RE | |
| the heat energy stored by RE at time t | |
| the heat energy released by RE at time t | |
| the stored heat energy efficiency of RE at time t | |
| the released heat energy efficiency of RE at time t | |
| the electricity generated by WPP for meeting the electricity demand | |
| the output generated by WPP for RE at time t | |
| the electricity generated by WPP for RE at time t | |
| the cool energy generated by the GSHP at time t | |
| the power consumption by the GSHP at time t | |
| the transporting efficiency of the cool energy generated by the GSHP | |
| the heat energy generated by the GSHP at time t | |
| the power consumption by the GSHP at time t | |
| the transporting efficiency of the heat energy generated by the GSHP | |
| the cool energy released by ST | |
| the heat energy released by ST | |
| the heat energy generated by HE at time t | |
| the high-pressure steam provided by HRSGs for HE at time t | |
| , | the heat energy flows generated by SC and other components for HE at time t |
| transporting efficiency of HE at time t | |
| the cooling energy generated by AC at time t | |
| the heat medium water flow provided by HRSGs for AC at time t | |
| other components for AC | |
| the cooling transporting coefficient of AC | |
| the cooling energy generated by EC at time t | |
| the electrical energy for EC at time t | |
| the cooling transporting coefficient of EC | |
| the minimum and maximum output range of wind power at time t | |
| the uncertainty coefficient of wind power output | |
| an arbitrary positive number |
References
- Chen, Q.; Wang, W.; Lu, J.; Ding, J. An overview of the political, technical and economical aspects of gas-fired distributed energy system in China. Appl. Therm. Eng. 2013, 52, 531–537. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, J.J.; Creamer, K.S. Inhibition of anaerobic digestion process: A review. Bioresour. Technol. 2008, 99, 4044–4064. [Google Scholar] [CrossRef] [PubMed]
- Midilli, A.; Dogru, M.; Howarth, C.R.; Ling, M.J.; Ayhan, T. Combustible gas production from sewage sludge with a downdraft gasifiery. Energy Convers. Manag. 2001, 42, 157–172. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Y.; Dor, L.; Yang, W.; Blasiak, W. A thermo dynamic analysis of solid waste gasification in the Plasma Gasification Melting process. Appl. Energy 2013, 112, 405–413. [Google Scholar] [CrossRef]
- Wu, D.W.; Wang, R.Z. Combined cooling, heating and power: A review. Prog. Energy Combust. Sci. 2006, 2, 459–495. [Google Scholar] [CrossRef]
- Cho, H.; Smith, A.D.; Mago, P. Combined cooling, heating and power: A review of performance improvement and optimization. Appl. Energy 2014, 36, 168–185. [Google Scholar] [CrossRef]
- Suamir, I.; Tassou, S. Performance evaluation of integrated trigeneration and CO2 refrigeration systems. Appl. Therm. Eng. 2013, 50, 1487–1495. [Google Scholar] [CrossRef]
- Fumo, N.; Chamra, L.M. Analysis of systems based on source primary energy combined cooling, heating, and power consumption. Appl. Energy 2010, 87, 2023–2030. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhao, P.; Niu, X.Q.; Dai, Y.P. Parametric analysis of a new combined cooling, heating and power system with transcritical CO2 driven by solar energy. Appl. Energy 2012, 94, 58–64. [Google Scholar] [CrossRef]
- Mago, P.J. Performance analysis of CCHP and CHP systems operating following the thermal and electric load. Int. J. Energy Res. 2009, 43, 852–864. [Google Scholar] [CrossRef]
- Maraver, D.; Sin, A.; Royo, J.; Sebastián, F. Assessment of CCHP systems based on biomass combustion for small-scale applications through a review of the technology and analysis of energy efficiency parameters. Appl. Energy 2013, 102, 1303–1313. [Google Scholar] [CrossRef]
- Gao, P.; Li, W.; Cheng, Y.; Tong, Y.W.; Dai, Y.; Wang, R. Thermodynamic performance assessment of CCHP system driven by different composition gas. Appl. Energy 2014, 136, 599–610. [Google Scholar] [CrossRef]
- Li, S.; Sui, J.; Jin, H.; Zheng, J. Full chain energy performance for a combined cooling, heating and power system running with methanol and solar energy. Appl. Energy 2013, 112, 673–681. [Google Scholar] [CrossRef]
- Hu, M.Q. A probability constrained multi-objective optimization model for CCHP system operation decision support. Appl. Energy 2014, 116, 230–242. [Google Scholar] [CrossRef]
- Cardona, E. Optimal design of CHCP plants in the civil sector by thermo-economics. Appl. Energy 2007, 84, 729–748. [Google Scholar] [CrossRef]
- Kong, X.Q.; Wang, R.Z.; Li, Y.; Huang, X.H. Optimal operation of a micro-combined cooling, heating and power system driven by a gas engine. Energy Convers. Manag. 2009, 50, 530–538. [Google Scholar] [CrossRef]
- Ren, H.B. A MILP model for integrated plan and evaluation of distributed energy systems. Appl. Energy 2010, 87, 1001–1014. [Google Scholar] [CrossRef]
- Chua, K.J.; Yang, W.M.; Er, S.S.; Ho, C.A. Sustainable energy systems for a remote island community. Appl. Energy 2014, 113, 1752–1763. [Google Scholar] [CrossRef]
- Flores, R.J. Dynamic distributed generation dispatch strategy for lowering the cost of building energy. Appl. Energy 2014, 132, 196–208. [Google Scholar] [CrossRef]
- Li, H.; Fu, L.; Geng, K.; Jiang, Y. Energy utilization evaluation of CCHP systems. Energy Build. 2006, 38, 253–257. [Google Scholar] [CrossRef]
- Burdett, R.L.; Kozan, E. A multi-criteria approach for hospital capacity analysis. Eur. J. Oper. Res. 2016, 255, 505–521. [Google Scholar] [CrossRef]
- Burdett, R.L. Multi-objective models and techniques for railway capacity analysis. Eur. J. Oper. Res. 2015, 245, 489–505. [Google Scholar] [CrossRef]
- Wang, L. Robust Multi-Objective Operation Optimization for Multi-Energy Complementary Microgrids. Ph.D. Thesis, Shandong University, Jinan, China, 2017; pp. 32–36. [Google Scholar]


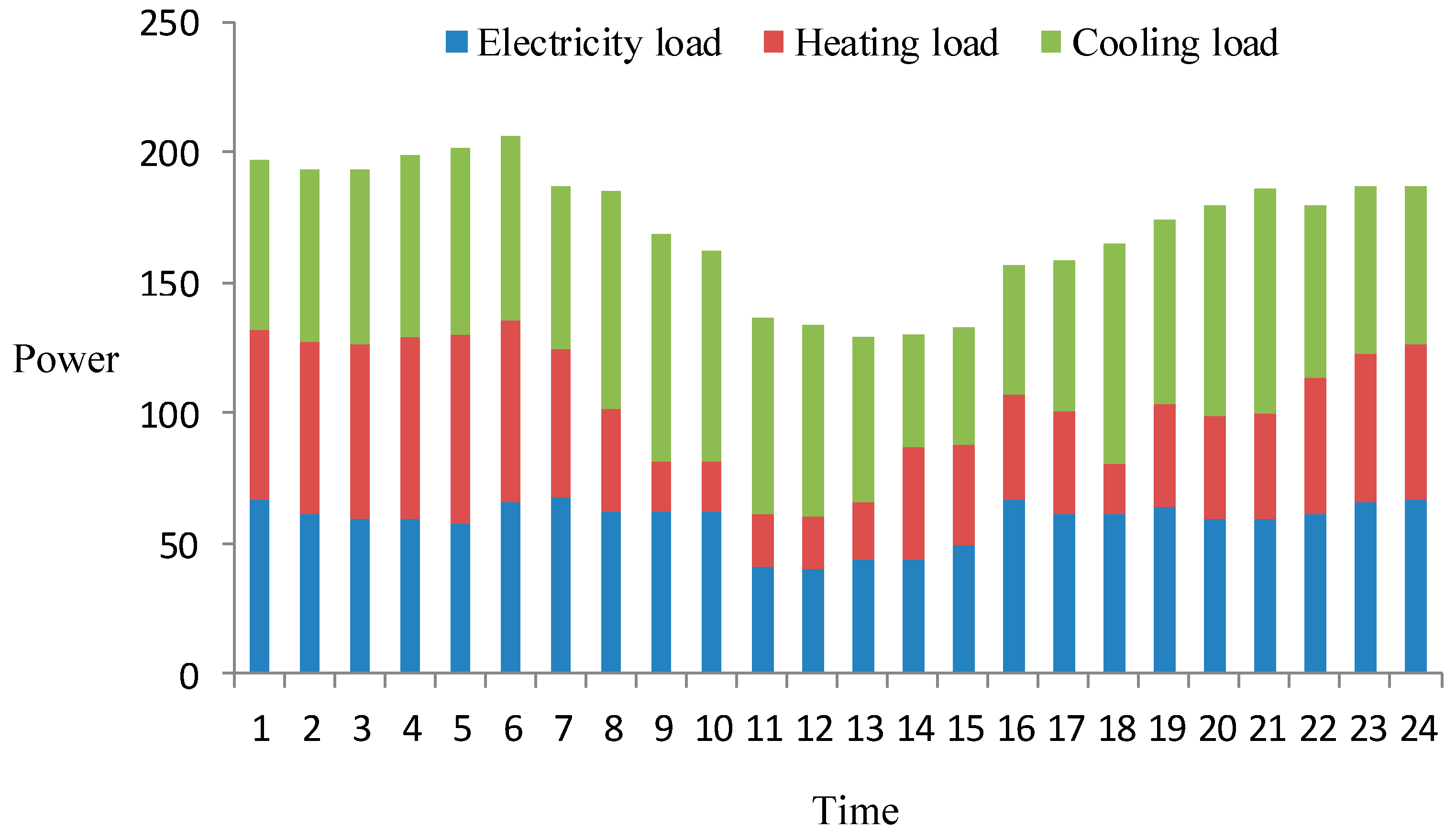

| No. | Amount (10,000 yuan) |
|---|---|
| Engineering fee | 4865 |
| Other expenses | 654 |
| Interest | 125 |
| Type | Price |
|---|---|
| Natural gas | 2.4 yuan/m3 |
| Electricity | 1.2863/0.8293/0.3351 yuan/kW·h |
| Water | 5.6 yuan/ton |
| Scenario | Constraint Violation Probability | |
|---|---|---|
| 1 | 0 | 53.64 |
| 2 | 1 | 50 |
| 3 | 3 | 41.36 |
| 4 | 5 | 33.13 |
| 5 | 12 | 11.5 |
| ER/% | TOC/million yuan | Carbon Dioxide Emission/1000 ton | NPV/million yuan | IRR/% | |
|---|---|---|---|---|---|
| Scenario 1 | 77.9 | 130.369 | 1677.36 | 32.35 | 9.62 |
| Scenario 2 | 58.6 | 121.415 | 1270.48 | 120.94 | 13.75 |
| Scenario 3 | 72.9 | 128.655 | 1803.74 | 49.67 | 10.45 |
| Scenario 4 | 64.5 | 126.123 | 1384.74 | 74.39 | 11.62 |
| Scenario 5 | 63.3 | 156.756 | 1434.63 | 63.25 | 10.53 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Guo, H.; Lin, H.; Tan, Q.; Yang, S.; Gejirifu, D.; Ju, L.; Song, X. Robust Scheduling Optimization Model for Multi-Energy Interdependent System Based on Energy Storage Technology and Ground-Source Heat Pump. Processes 2019, 7, 27. https://doi.org/10.3390/pr7010027
Tan Z, Guo H, Lin H, Tan Q, Yang S, Gejirifu D, Ju L, Song X. Robust Scheduling Optimization Model for Multi-Energy Interdependent System Based on Energy Storage Technology and Ground-Source Heat Pump. Processes. 2019; 7(1):27. https://doi.org/10.3390/pr7010027
Chicago/Turabian StyleTan, Zhongfu, Hongwu Guo, Hongyu Lin, Qingkun Tan, Shenbo Yang, De Gejirifu, Liwei Ju, and Xueying Song. 2019. "Robust Scheduling Optimization Model for Multi-Energy Interdependent System Based on Energy Storage Technology and Ground-Source Heat Pump" Processes 7, no. 1: 27. https://doi.org/10.3390/pr7010027
APA StyleTan, Z., Guo, H., Lin, H., Tan, Q., Yang, S., Gejirifu, D., Ju, L., & Song, X. (2019). Robust Scheduling Optimization Model for Multi-Energy Interdependent System Based on Energy Storage Technology and Ground-Source Heat Pump. Processes, 7(1), 27. https://doi.org/10.3390/pr7010027





