A Model-Based Investigation of Cytokine Dynamics in Immunotherapies
Abstract
1. Introduction
2. Materials and Method
2.1. Clinical Data and a Mathematical Model of CRS
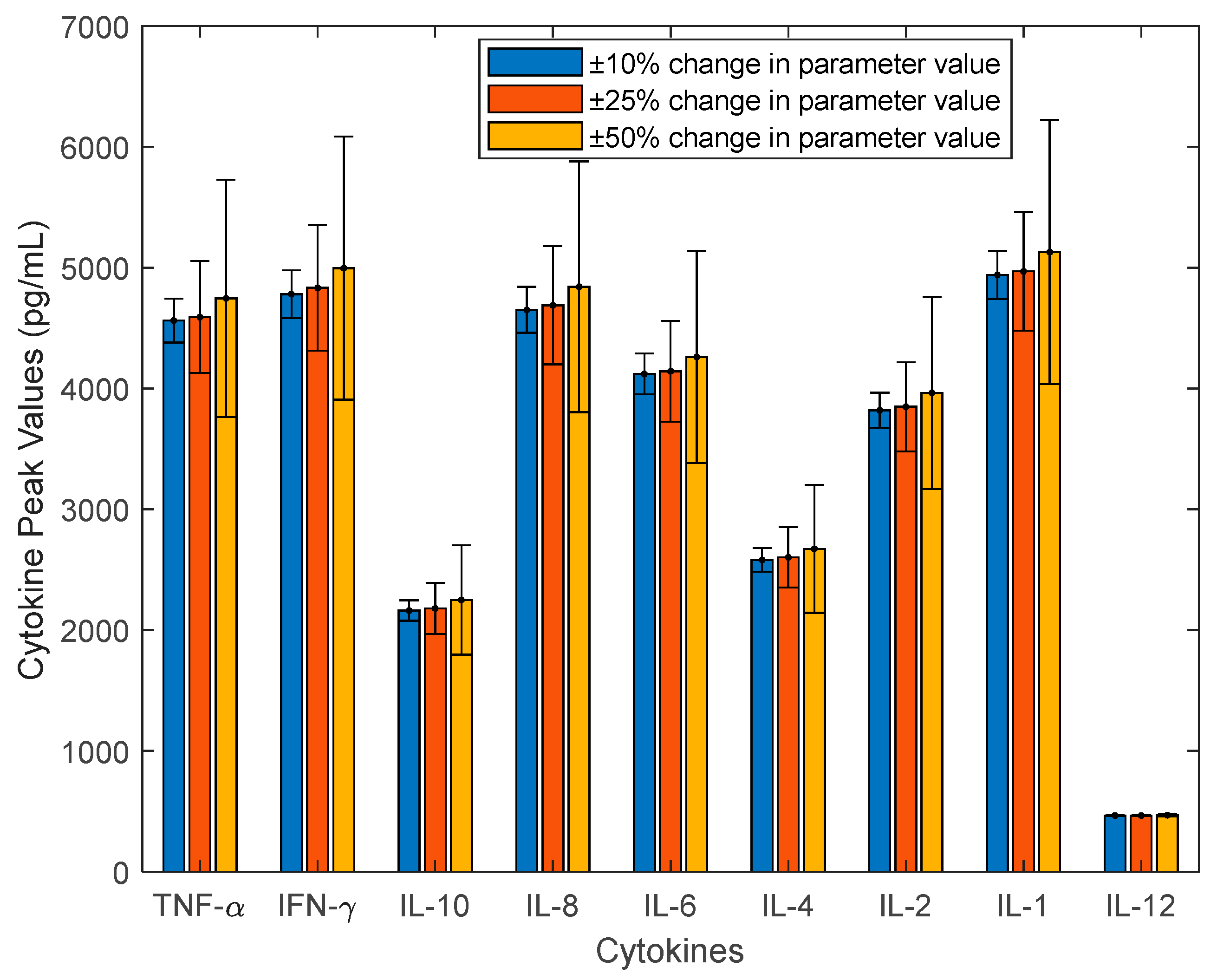
2.2. Investigate the Uncertainty of CRS Using Sensitivity Analysis, Monte Carlo Sampling, and Principal Component Analysis
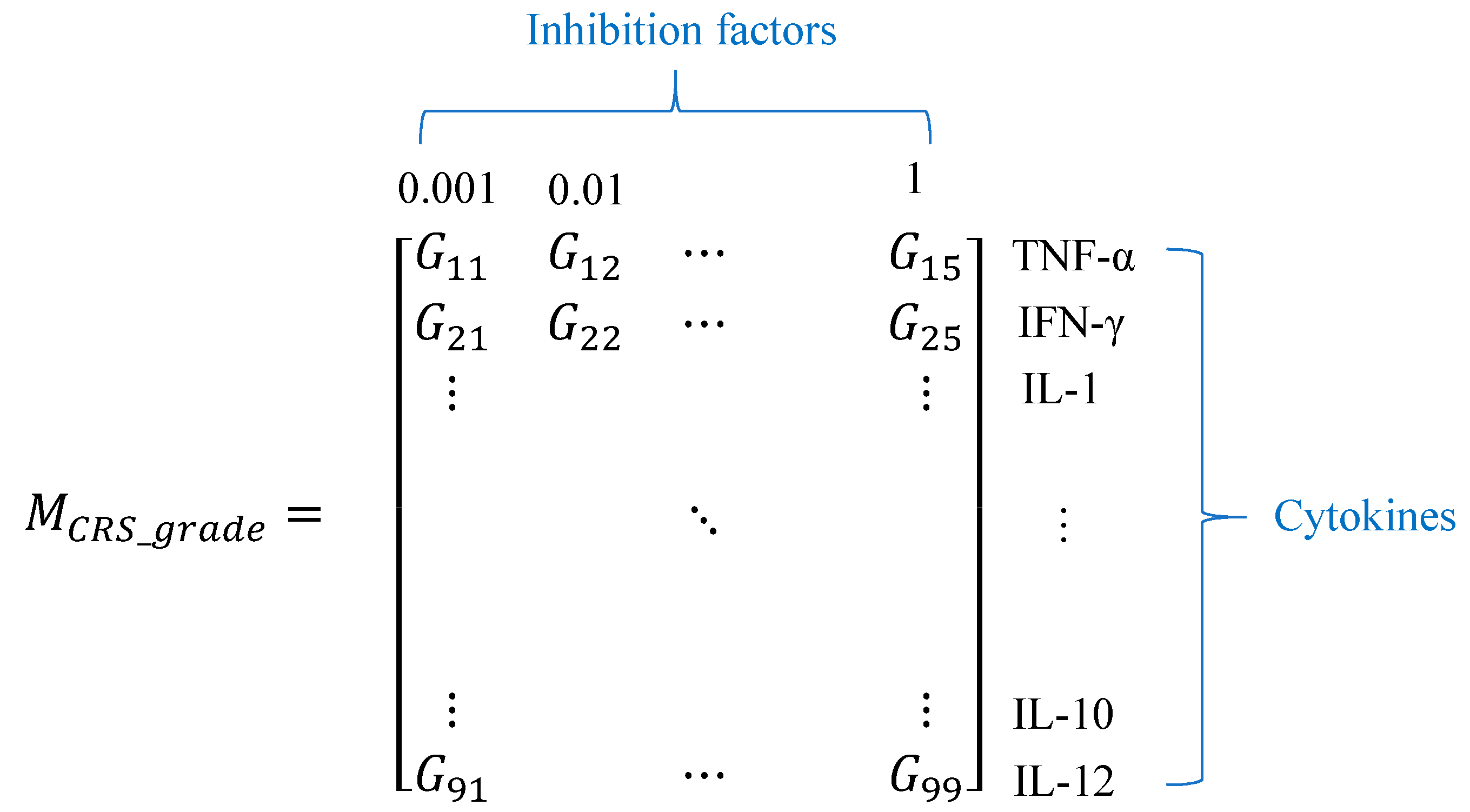
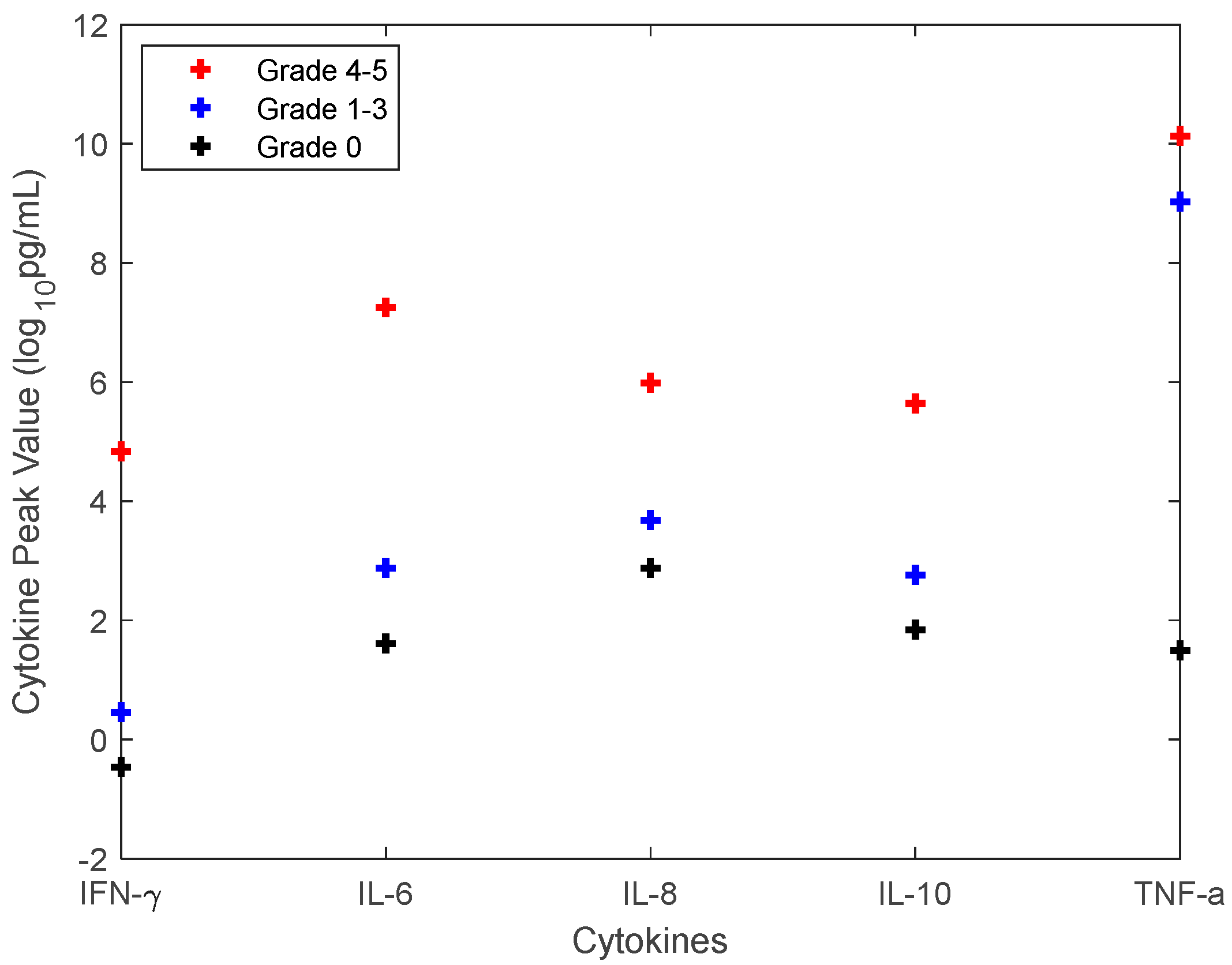
2.3. The Approach to Quantify the CRS Grade
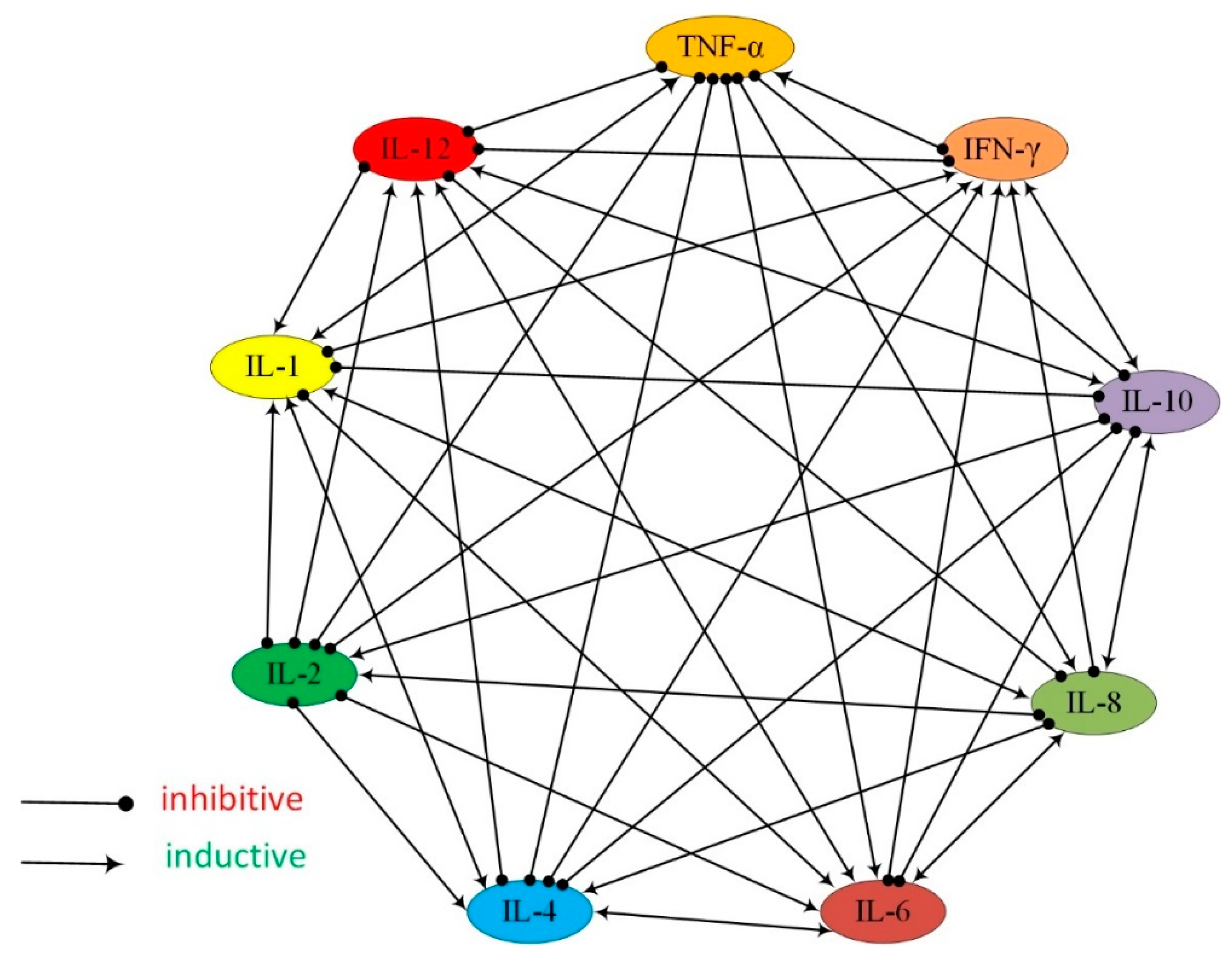
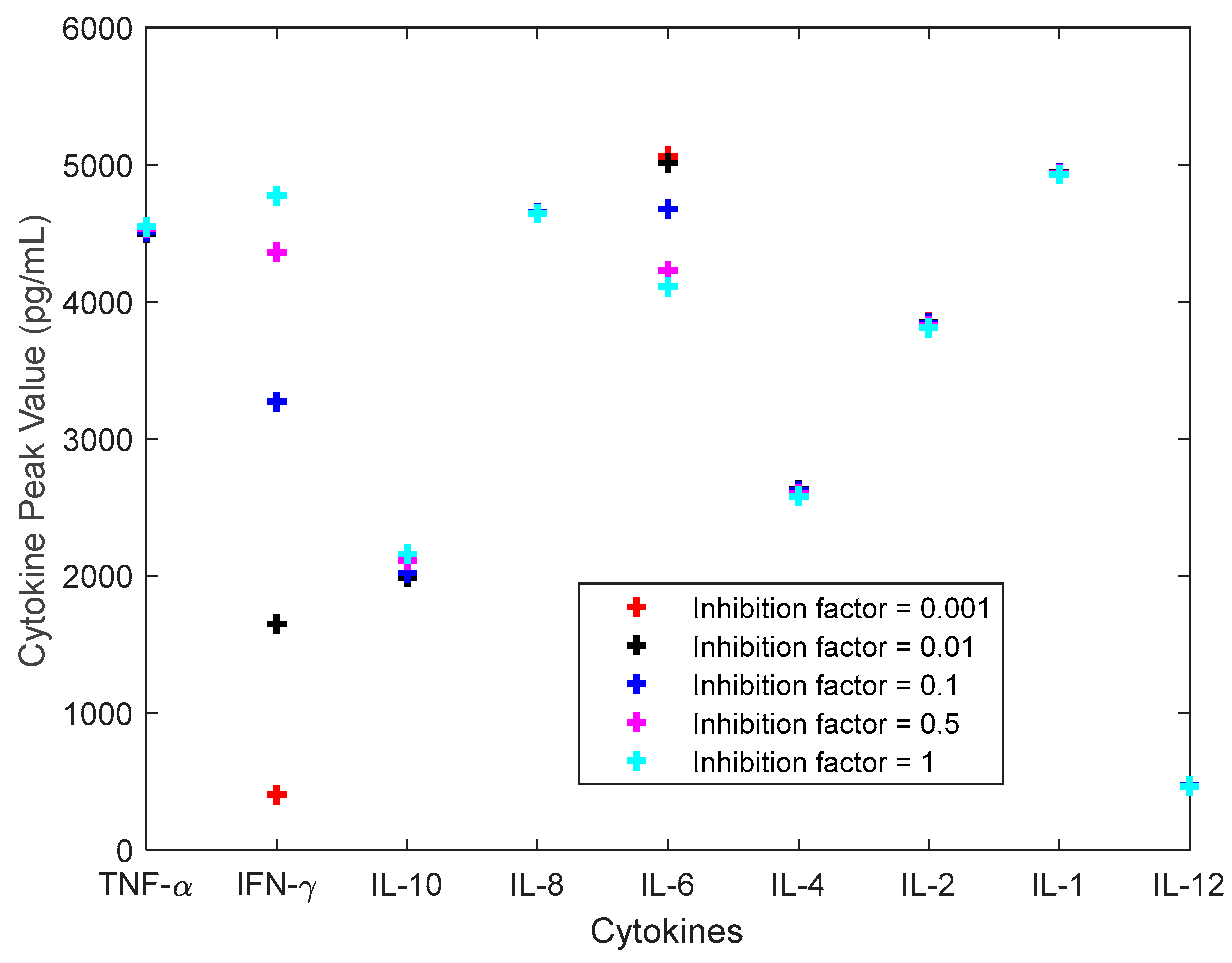
2.4. Investigation of Cytokine Inhibition
3. Results
3.1. Investigation of Uncertainties in CRS
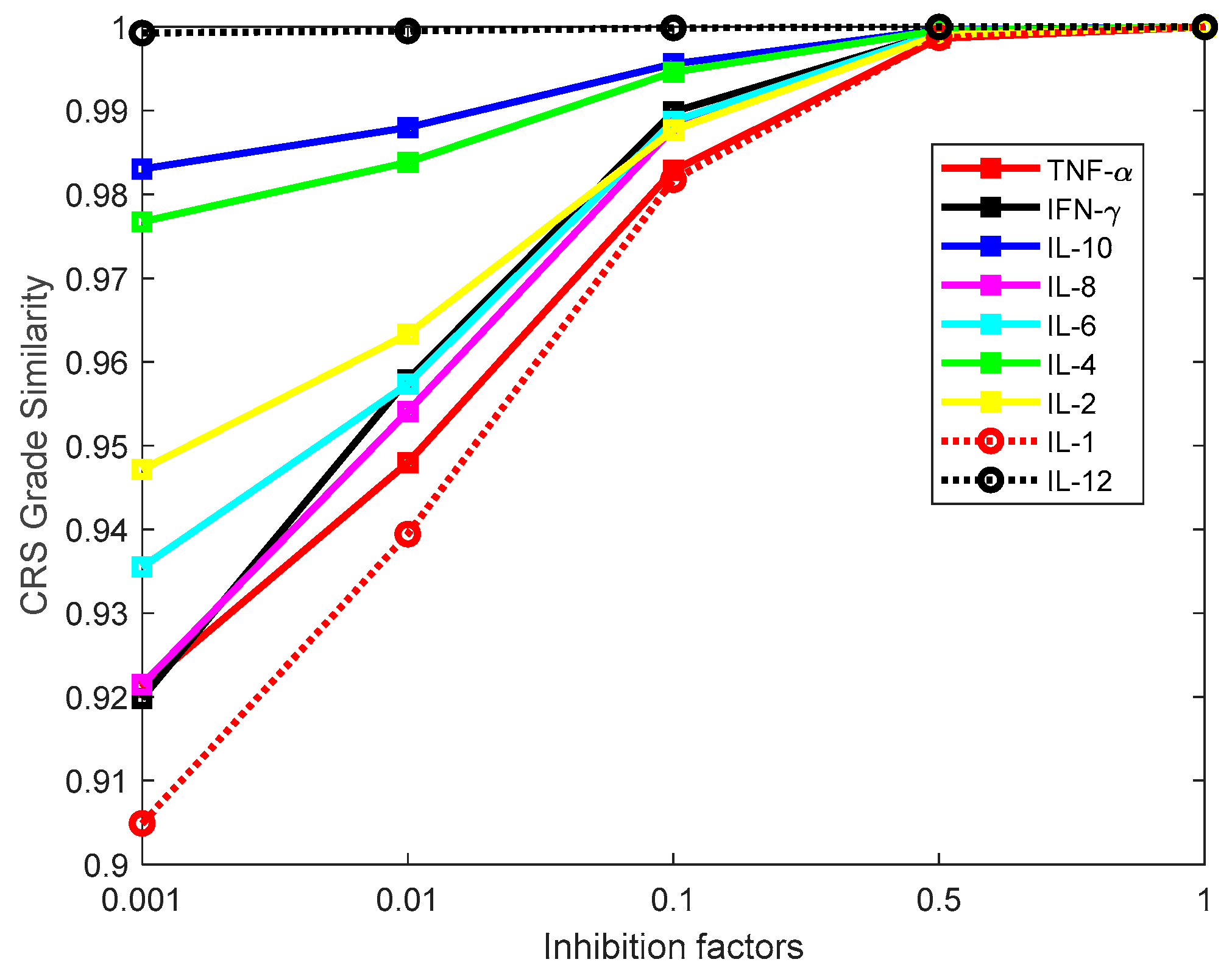
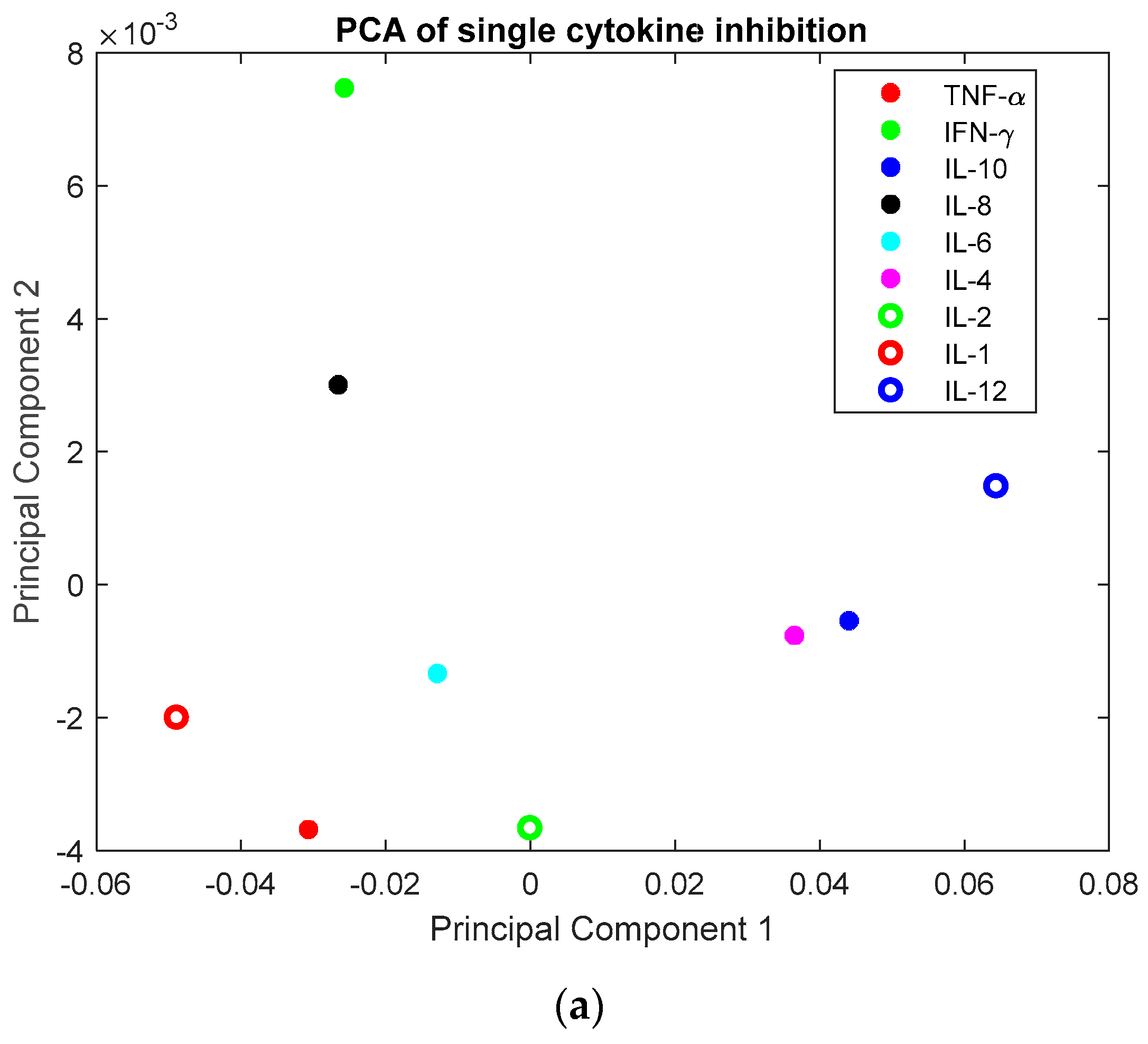
3.2. Investigation of Single Cytokine Inhibition
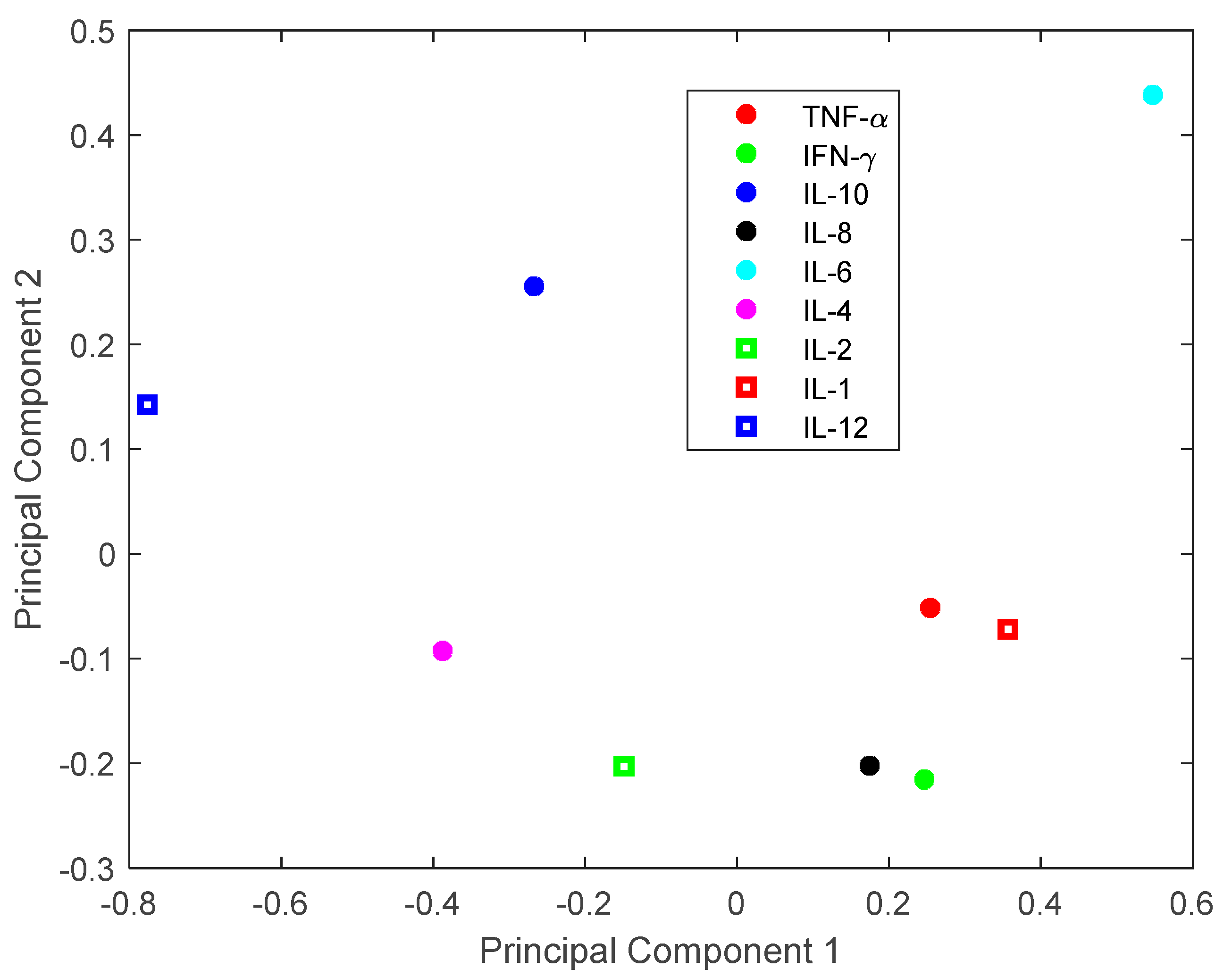
3.3. Investigation of Multiple Cytokine Inhibition
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rosenberg, S.A.; Yang, J.C.; Restifo, N.P. Cancer immunotherapy: Moving beyond current vaccines. Nat. Med. 2004, 10, 909–915. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.W.; Gardner, R.; Porter, D.L.; Louis, C.U.; Ahmed, N.; Jensen, M.; Grupp, S.A.; Mackall, C.L. Current concepts in the diagnosis and management of cytokine release syndrome. Blood 2014, 124, 188–195. [Google Scholar] [CrossRef] [PubMed]
- Almasbak, H.; Aarvak, T.; Vemuri, M.C. CAR T Cell Therapy: A Game Changer in Cancer Treatment. J. Immunol. Res. 2016, 2016, 5474602. [Google Scholar] [CrossRef] [PubMed]
- Adams, G.P.; Weiner, L.M. Monoclonal antibody therapy of cancer. Nat. Biotechnol. 2005, 23, 1147–1157. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Xiang, R.; Qing, K.; Li, X.; Zhang, Y.; Wang, L.; Zhu, H.; Mao, Y.; Xu, Z.; Li, J. The severe cytokine release syndrome in phase I trials of CD19-CAR-T cell therapy: A systematic review. Ann. Hematol. 2018, 97, 1327–1335. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.G.; Han, W.D. Biomarkers of cytokine release syndrome and neurotoxicity related to CAR-T cell therapy. Biomark. Res. 2018, 6, 4. [Google Scholar] [CrossRef] [PubMed]
- Suntharalingam, G.; Perry, M.R.; Ward, S.; Brett, S.J.; Castello-Cortes, A.; Brunner, M.D.; Panoskaltsis, N. Cytokine storm in a phase 1 trial of the anti-CD28 monoclonal antibody TGN1412. N. Engl. J. Med. 2006, 355, 1018–1028. [Google Scholar] [CrossRef] [PubMed]
- Hay, K.A.; Hanafi, L.A.; Li, D.; Gust, J.; Liles, W.C.; Wurfel, M.M.; López, J.A.; Chen, J.; Chung, D.; Harju-Baker, S.; et al. Kinetics and biomarkers of severe cytokine release syndrome after CD19 chimeric antigen receptor-modified T-cell therapy. Blood 2017, 130, 2295–2306. [Google Scholar] [CrossRef] [PubMed]
- Teachey, D.T.; Lacey, S.F.; Shaw, P.A.; Melenhorst, J.J.; Maude, S.L.; Frey, N.; Pequignot, E.; Gonzalez, V.E.; Chen, F.; Finklestein, J.; et al. Identification of Predictive Biomarkers for Cytokine Release Syndrome after Chimeric Antigen Receptor T-cell Therapy for Acute Lymphoblastic Leukemia. Cancer Discov. 2016, 6, 664–679. [Google Scholar] [CrossRef] [PubMed]
- Waito, M.; Walsh, S.R.; Rasiuk, A.; Bridle, B.W.; Willms, A.R. A Mathematical Model of Cytokine Dynamics During a Cytokine Storm; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Yiu, H.H.; Graham, A.L.; Stengel, R.F. Dynamics of a Cytokine Storm. PLoS ONE 2012, 7, e45027. [Google Scholar] [CrossRef] [PubMed]
- Zi, Z. Sensitivity analysis approaches applied to systems biology models. IET Syst. Biol. 2011, 5, 336–346. [Google Scholar] [CrossRef] [PubMed]
- Tomovic, R.; Vukobratovic, M. General Sensitivity Theory; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Eslami, M. Introduction to System Sensitivity Theory—Frank, P.M. IEEE Trans. Syst. Man Cybern. 1980, 10, 337–338. [Google Scholar]
- Van Mourik, S.; Ter Braak, C.; Stigter, H.; Molenaar, J. Prediction uncertainty assessment of a systems biology model requires a sample of the full probability distribution of its parameters. PeerJ 2014, 2, e433. [Google Scholar] [CrossRef] [PubMed]
- Doucet, A.; de Freitas, N.; Gordon, N. An Introduction to Sequential Monte Carlo Methods, in Sequential Monte Carlo Methods in Practice. In Statistics for Engineering and Information Science; Doucet, A., de Freitas, N., Gordon, N., Eds.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Johnson, S.C. Hierarchical Clustering Schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Corpet, F. Multiple Sequence Alignment with Hierarchical-Clustering. Nucleic Acids Res. 1988, 16, 10881–10890. [Google Scholar] [CrossRef] [PubMed]
- Wojdasiewicz, P.; Poniatowski, L.A.; Szukiewicz, D. The Role of Inflammatory and Anti-Inflammatory Cytokines in the Pathogenesis of Osteoarthritis. Med. Inflamm. 2014, 2014, 561459. [Google Scholar] [CrossRef] [PubMed]
- Textor, A.; Schmidt, K.; Kloetzel, P.M.; Weißbrich, B.; Perez, C.; Charo, J.; Anders, K.; Sidney, J.; Sette, A.; Schumacher, T.N.; et al. Preventing tumor escape by targeting a post-proteasomal trimming independent epitope. J. Exp. Med. 2016, 213, 2333–2348. [Google Scholar] [CrossRef] [PubMed]
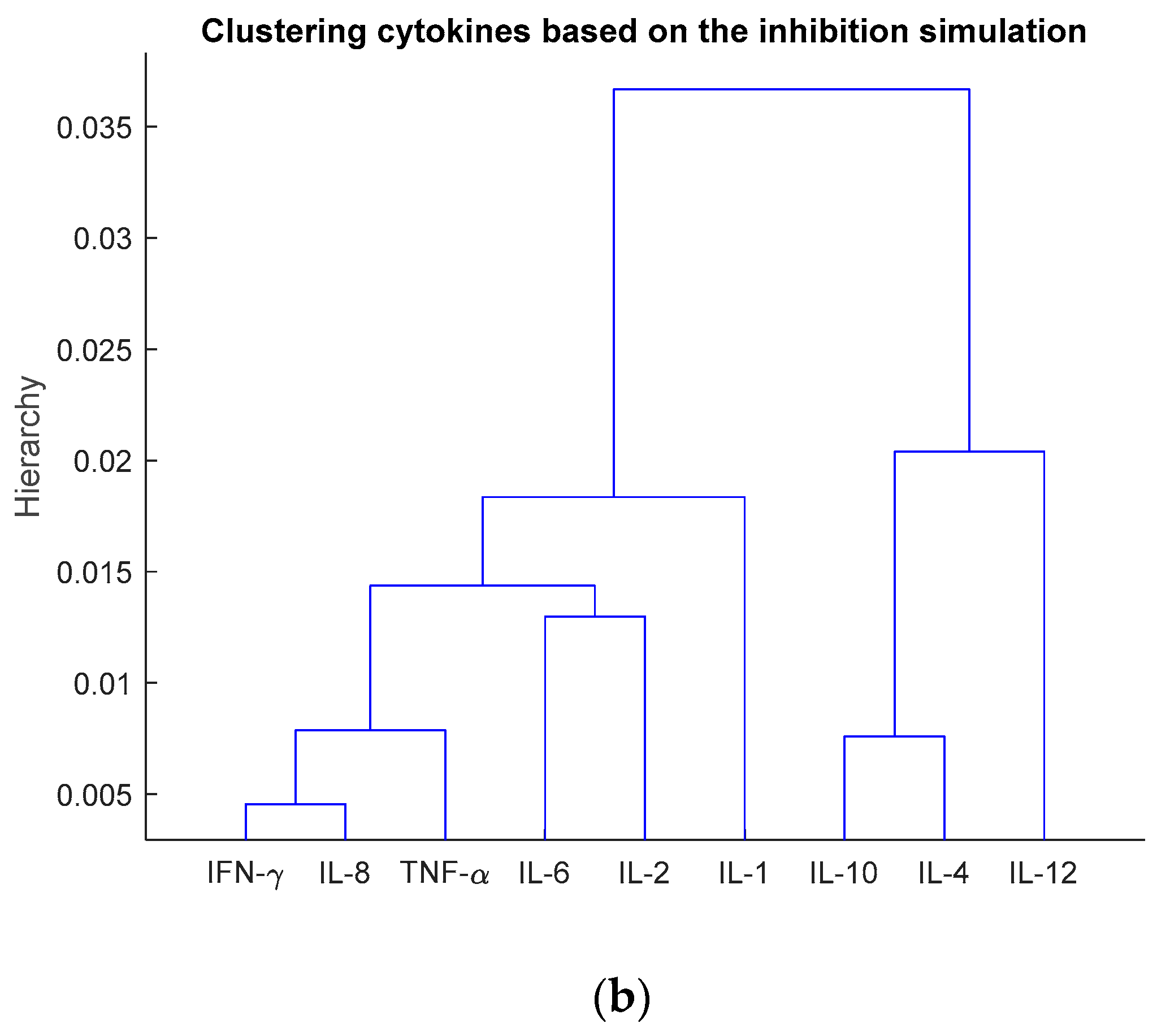
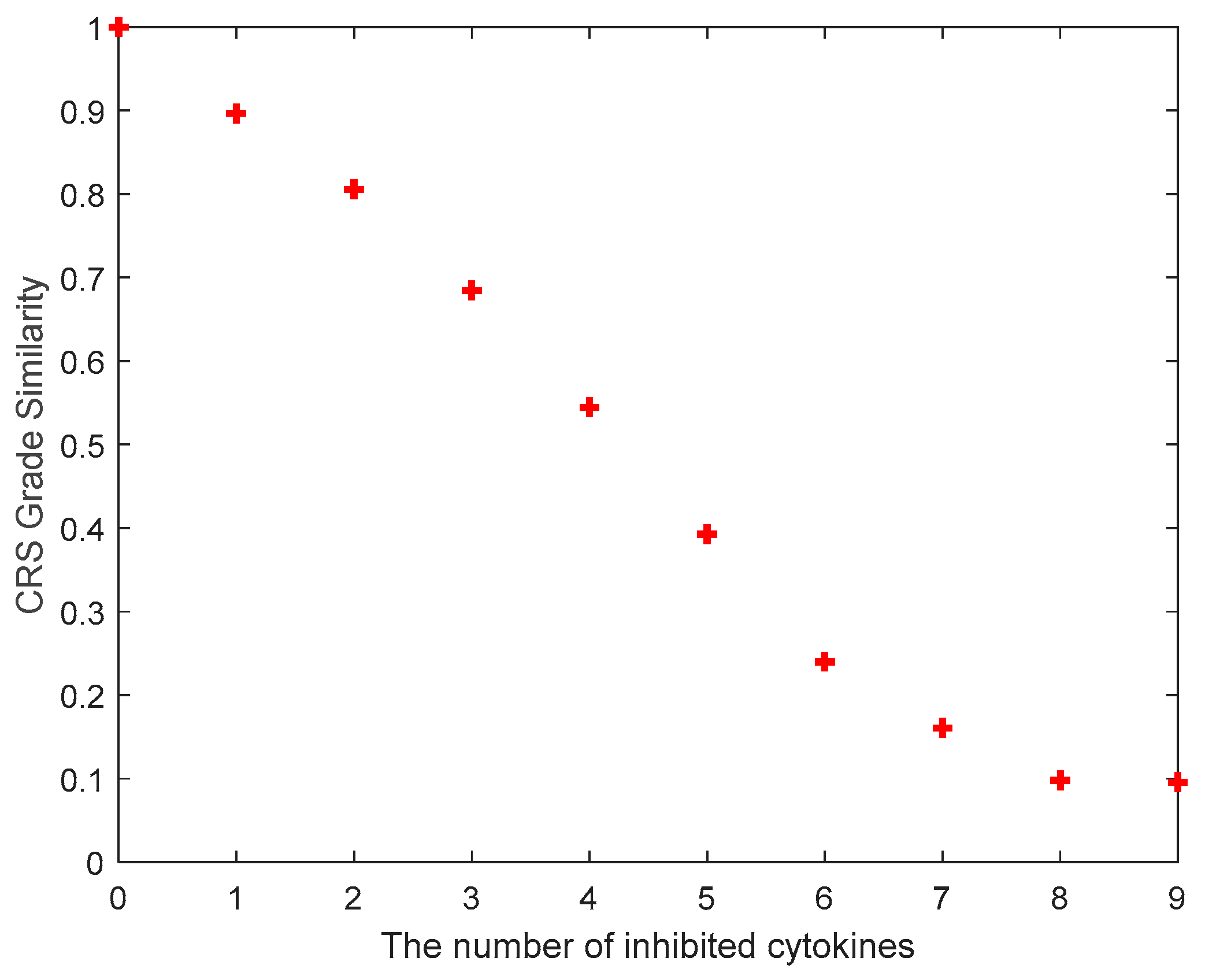
| Number of Cytokines for Inhibition | The Inhibited Cytokines |
|---|---|
| 1 | IL-1 |
| 2 | IL-8, IL-1 |
| 3 | TNF-α, IL-8, IL-1 |
| 4 | INF-γ, TNF-α, IL-8, IL-1 |
| 5 | IL-6, INF-γ, TNF-α, IL-8, IL-1 |
| 6 | IL-2, IL-6, INF-γ, TNF-α, IL-8, IL-1 |
| 7 | IL-4, IL-2, IL-6, INF-γ, TNF-α, IL-8, IL-1 |
| 8 | IL-10, IL-4, IL-2, IL-6, INF-γ, TNF-α, IL-8, IL-1 |
| 9 | IL-12, IL-10, IL-4, IL-2, IL-6, INF-γ, TNF-α, IL-8, IL-1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hopkins, B.; Pan, Y.; Tucker, M.; Huang, Z. A Model-Based Investigation of Cytokine Dynamics in Immunotherapies. Processes 2019, 7, 12. https://doi.org/10.3390/pr7010012
Hopkins B, Pan Y, Tucker M, Huang Z. A Model-Based Investigation of Cytokine Dynamics in Immunotherapies. Processes. 2019; 7(1):12. https://doi.org/10.3390/pr7010012
Chicago/Turabian StyleHopkins, Brooks, Yiming Pan, Matthew Tucker, and Zuyi (Jacky) Huang. 2019. "A Model-Based Investigation of Cytokine Dynamics in Immunotherapies" Processes 7, no. 1: 12. https://doi.org/10.3390/pr7010012
APA StyleHopkins, B., Pan, Y., Tucker, M., & Huang, Z. (2019). A Model-Based Investigation of Cytokine Dynamics in Immunotherapies. Processes, 7(1), 12. https://doi.org/10.3390/pr7010012






