On-Line Optimal Input Design Increases the Efficiency and Accuracy of the Modelling of an Inducible Synthetic Promoter †
Abstract
1. Introduction
2. Results
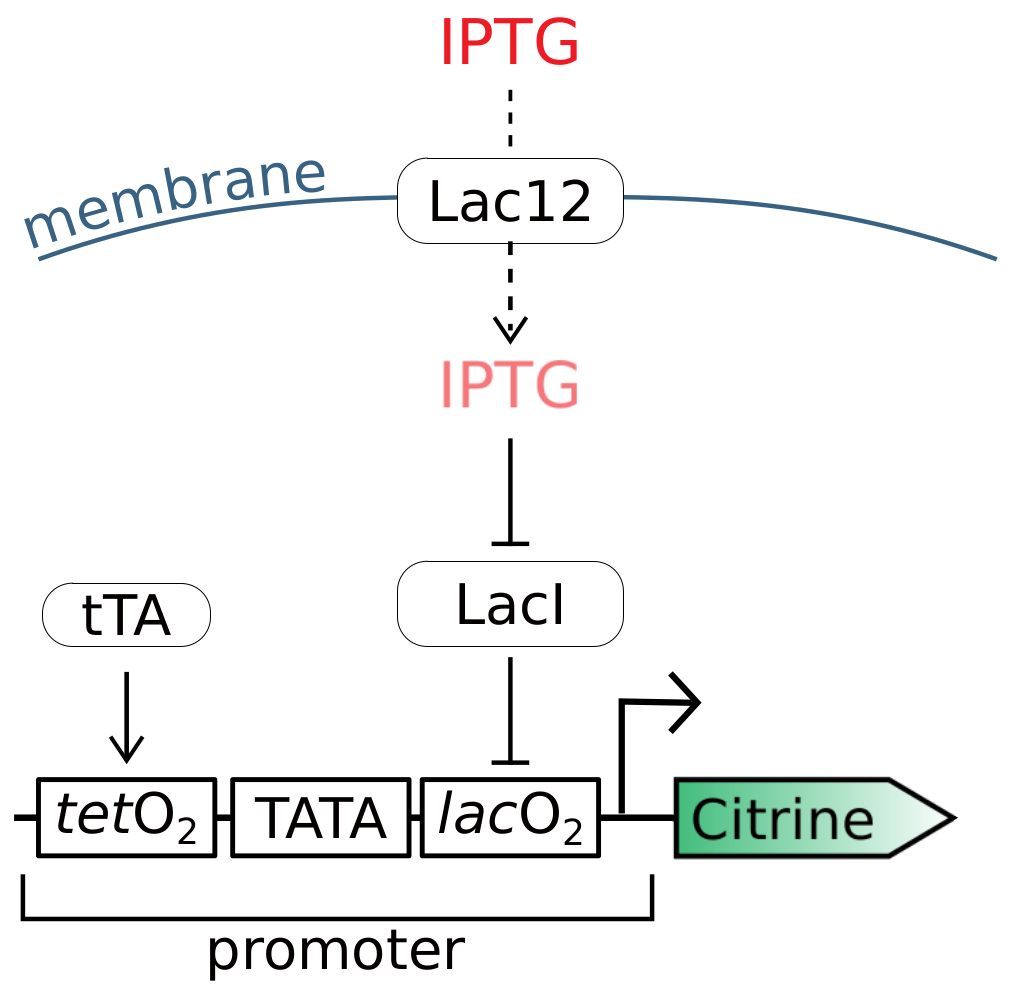
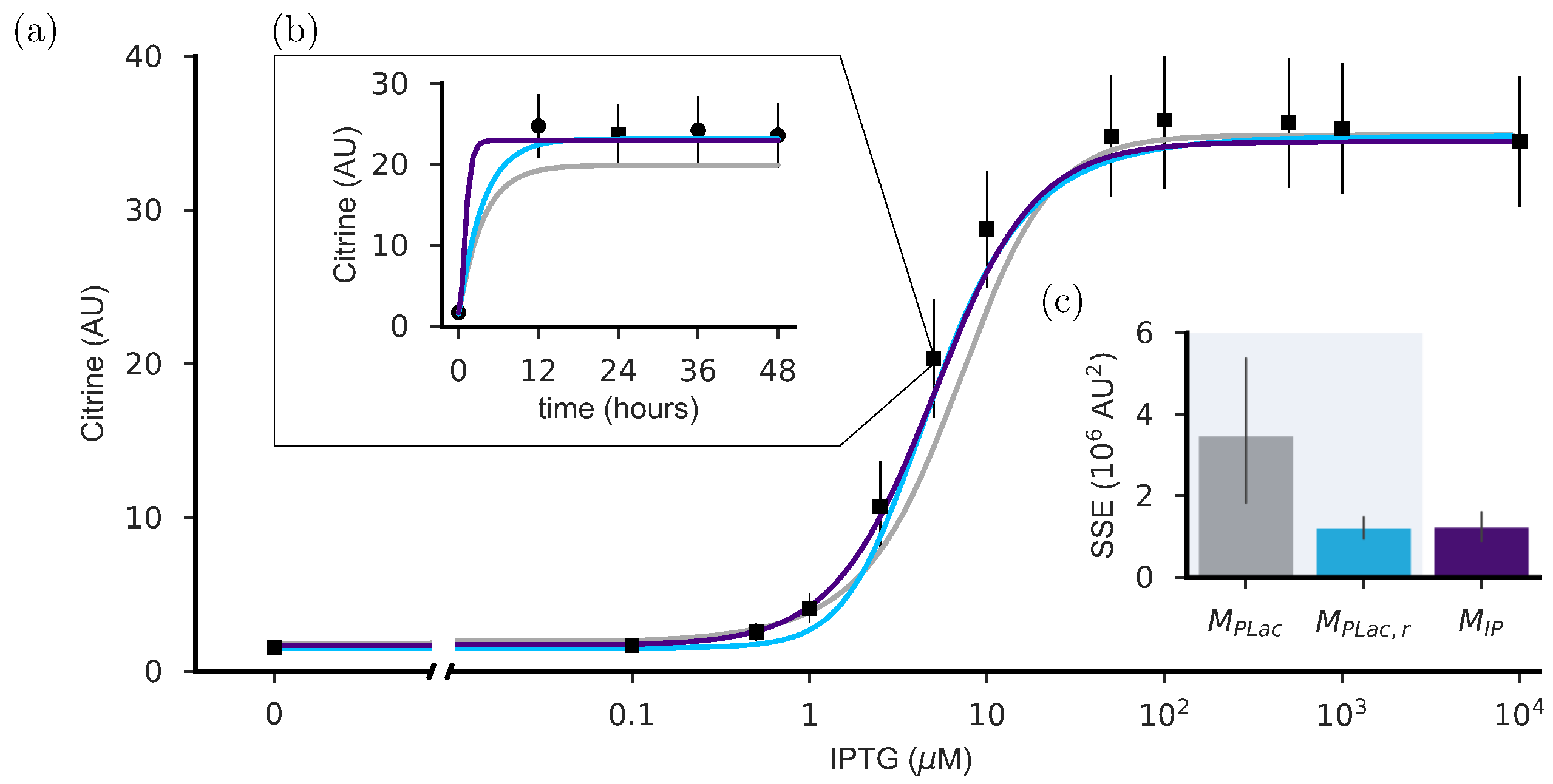
2.1. Refitting Gnügge et al.’s Model
2.2. The Dynamics of the Inducible Promoter Is Captured by a Reduced-Order Model
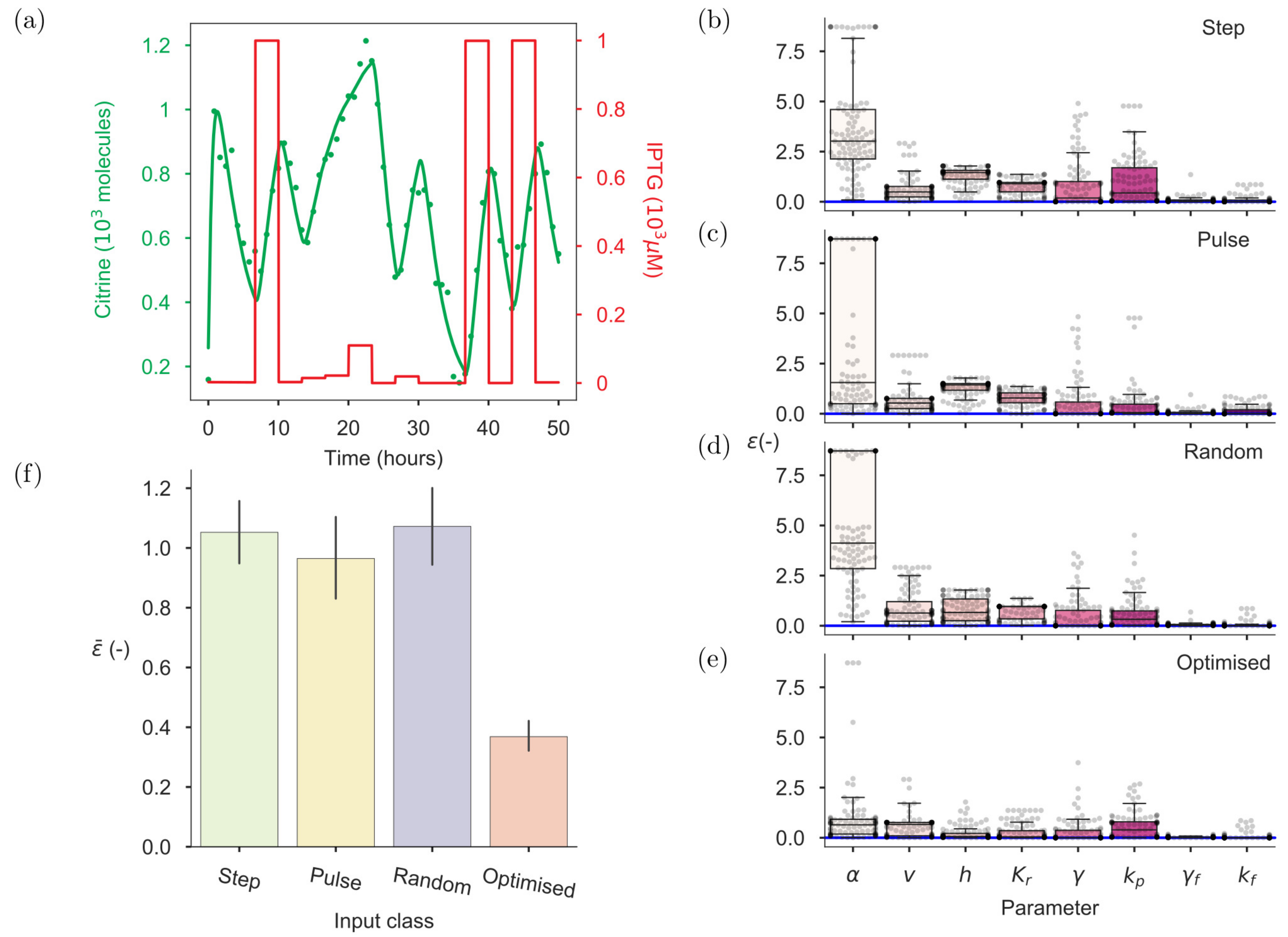
2.3. Intuition-Driven Inputs Are Poorly Informative
2.4. Optimal Input Design (OID) Increases the Accuracy of Model Identification
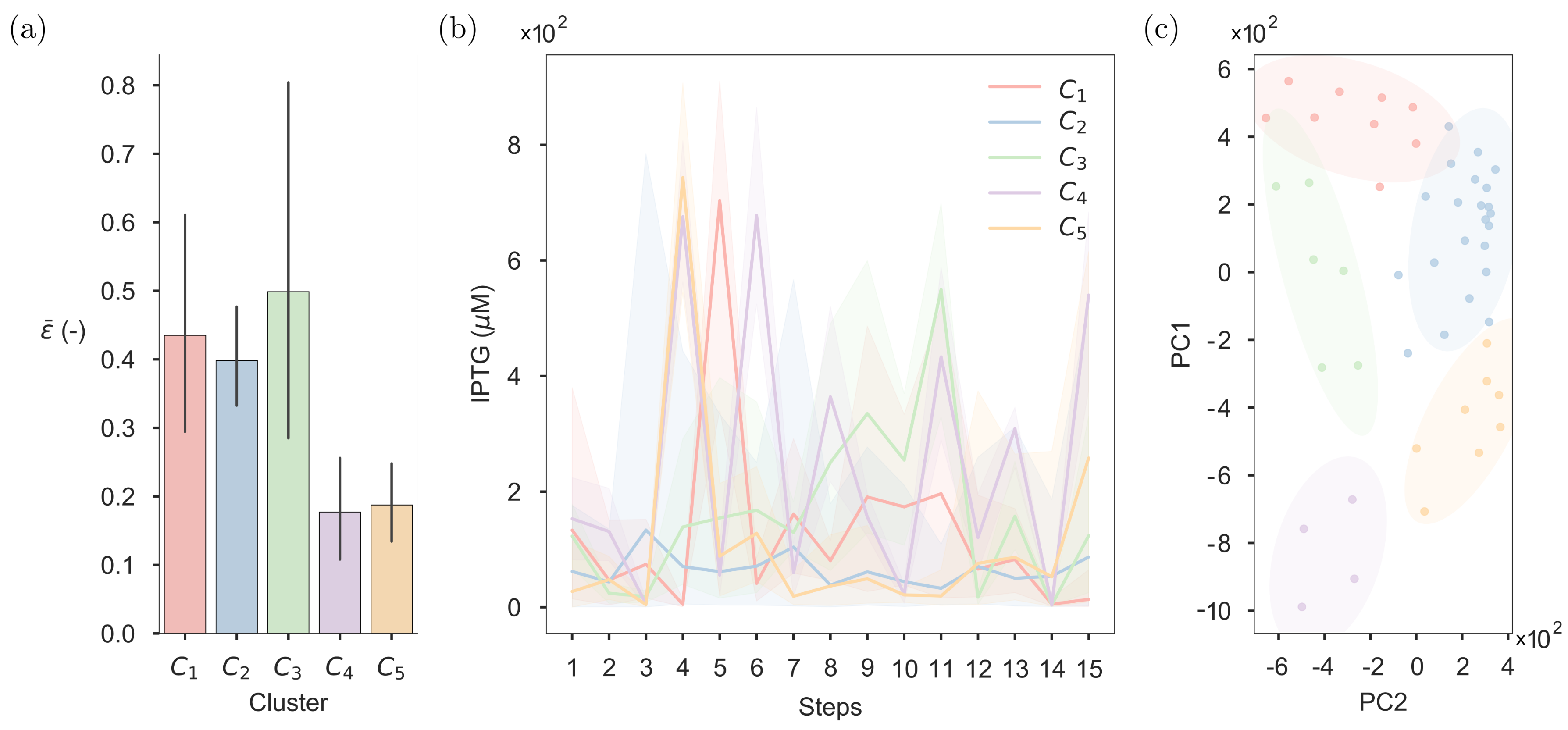
2.5. Clustering of the Optimised Inputs
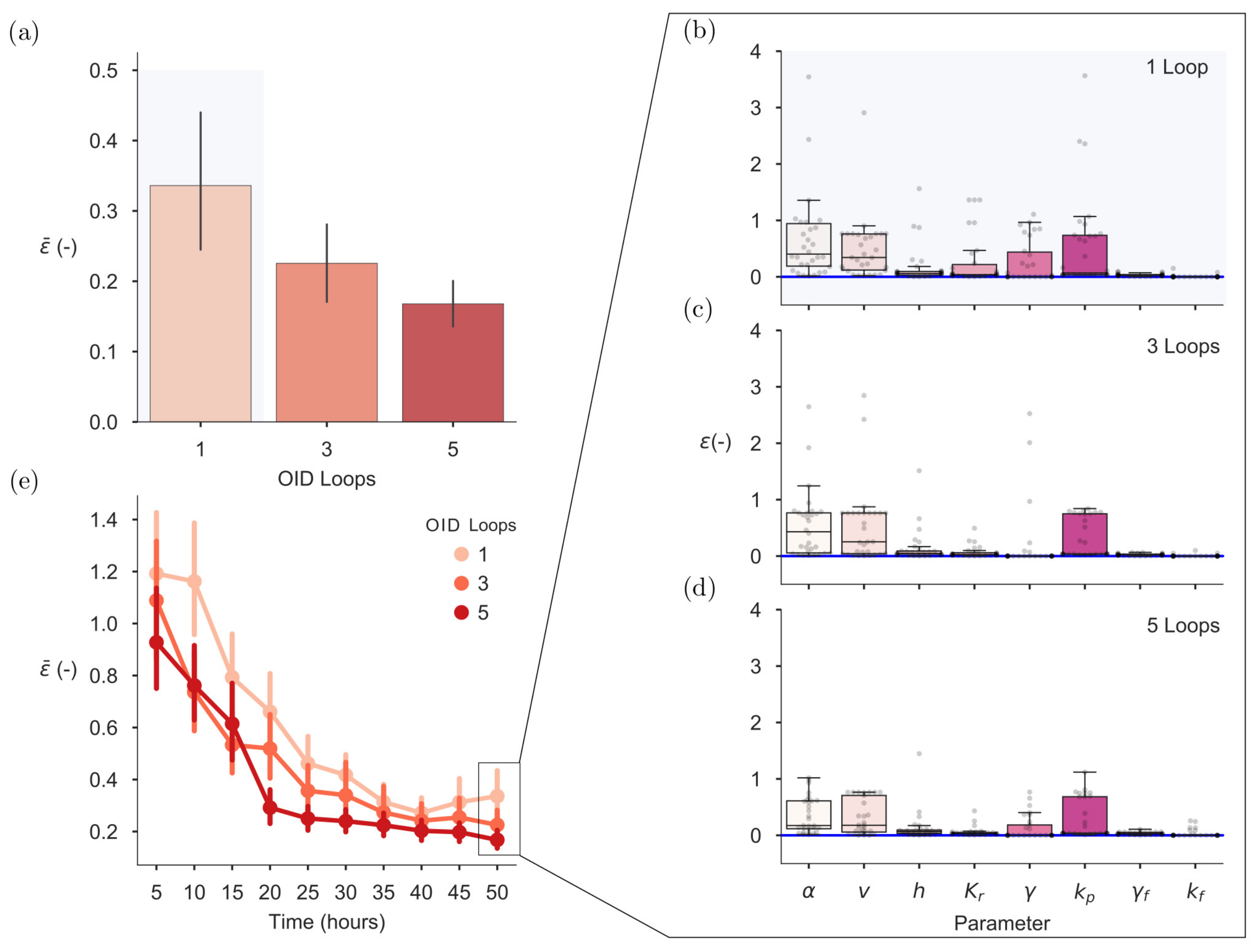
2.6. On-Line OID Supports the Automation of Model Calibration
3. Discussion
4. Methods
4.1. Generating Pseudo Experimental Data for the Identification of
4.2. Generating Pseudo Experimental Data for the Comparison of Input Classes
4.3. Parameter Estimation
4.4. Off-Line Optimal Experimental Design
4.5. Clustering of the Optimised Inputs
4.6. On-Line Optimal Experimental Design
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OED | Optimal Experimental Design |
| MBOED | Model-Based Optimal Experimetal Design |
| OID | Optimal Input Design |
| SOM | Self-Organising Maps |
| PE | Parameter Estimation |
| eSS | enhanced Scatter Search |
| DE | Differential Evolution |
| SSE | Sum of Squared Error of predictions |
| IPTG | isopropyl thiogalactopyranoside |
References
- Cameron, D.E.; Bashor, C.J.; Collins, J.J. A brief history of synthetic biology. Nat. Rev. Microbiol. 2014, 12, 381–390. [Google Scholar] [CrossRef] [PubMed]
- Ellis, T.; Wang, X.; Collins, J.J. Diversity-based, model-guided construction of synthetic gene networks with predicted functions. Nat. Biotechnol. 2009, 27, 465–471. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, A.A.; Der, B.S.; Shin, J.; Vaidyanathan, P.; Paralanov, V.; Strychalski, E.A.; Ross, D.; Densmore, D.; Voigt, C.A. Genetic circuit design automation. Science 2016, 352, aac7341. [Google Scholar] [CrossRef] [PubMed]
- Salis, H.M. The ribosome binding site calculator. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 2011; Volume 498, pp. 19–42. [Google Scholar]
- Borkowski, O.; Ceroni, F.; Stan, G.B.; Ellis, T. Overloaded and stressed: Whole-cell considerations for bacterial synthetic biology. Curr. Opin. Microbiol. 2016, 33, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Ljung, L. System Identification: Theory for the User, Ptr Prentice Hall Information and System Sciences Series; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Bandara, S.; Schlöder, J.P.; Eils, R.; Bock, H.G.; Meyer, T. Optimal experimental design for parameter estimation of a cell signaling model. PLoS Comput. Biol. 2009, 5, e1000558. [Google Scholar] [CrossRef] [PubMed]
- Ruess, J.; Parise, F.; Milias-Argeitis, A.; Khammash, M.; Lygeros, J. Iterative experiment design guides the characterization of a light-inducible gene expression circuit. Proc. Natl. Acad. Sci. USA 2015, 112, 8148–8153. [Google Scholar] [CrossRef] [PubMed]
- Balsa-Canto, E.; Henriques, D.; Gábor, A.; Banga, J.R. AMIGO2, a toolbox for dynamic modeling, optimization and control in systems biology. Bioinformatics 2016, 32, 3357–3359. [Google Scholar] [CrossRef] [PubMed]
- Gnugge, R.; Dharmarajan, L.; Lang, M.; Stelling, J. An Orthogonal Permease–Inducer–Repressor Feedback Loop Shows Bistability. ACS Synth. Biol. 2016, 5, 1098–1107. [Google Scholar] [CrossRef] [PubMed]
- Egea, J.A.; Balsa-Canto, E.; García, M.S.G.; Banga, J.R. Dynamic Optimization of Nonlinear Processes with an Enhanced Scatter Search Method. Ind. Eng. Chem. Res. 2009, 48, 4388–4401. [Google Scholar] [CrossRef]
- Balsa-Canto, E.; Alonso, A.A.; Banga, J.R. Computational procedures for optimal experimental design in biological systems. IET Syst. Biol. 2008, 2, 163–172. [Google Scholar] [CrossRef] [PubMed]
- Walter, E.; Pronzato, L. Identification of Parametric Models from Experimental Data; Springer: Berlin, Germany, 1997. [Google Scholar]
- Kohonen, T.; Maps, S.O. Springer series in information sciences. Self-Organ. Maps 1995, 30, 105–176. [Google Scholar]
- Vesanto, J.; Himberg, J.; Alhoniemi, E.; Parhankangas, J.; Parhankangas, J. Self-organizing map in Matlab: The SOM Toolbox. In Proceedings of the Matlab DSP Conference, Espoo, Finland, 16–17 November 1999; Volume 99, pp. 35–40. [Google Scholar]
- Liu, Y.; Li, Z.; Xiong, H.; Gao, X.; Wu, J. Understanding of internal clustering validation measures. In Proceedings of the 2010 IEEE 10th International Conference on Data Mining (ICDM), Sydney, Australia, 13–17 December 2010; pp. 911–916. [Google Scholar]
- Available online: https://github.com/csynbiosysIBioEUoE/ODidiPAmCSB2018SI (accessed on 29 June 2018).
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Mooers, C.N. Performance evaluation of the self-organizing map for feature extraction. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef]
- Available online: https://datasync.ed.ac.uk/index.php/s/xGL4oSbJMyu91Bt (accessed on 29 June 2018).


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bandiera, L.; Hou, Z.; Kothamachu, V.B.; Balsa-Canto, E.; Swain, P.S.; Menolascina, F. On-Line Optimal Input Design Increases the Efficiency and Accuracy of the Modelling of an Inducible Synthetic Promoter. Processes 2018, 6, 148. https://doi.org/10.3390/pr6090148
Bandiera L, Hou Z, Kothamachu VB, Balsa-Canto E, Swain PS, Menolascina F. On-Line Optimal Input Design Increases the Efficiency and Accuracy of the Modelling of an Inducible Synthetic Promoter. Processes. 2018; 6(9):148. https://doi.org/10.3390/pr6090148
Chicago/Turabian StyleBandiera, Lucia, Zhaozheng Hou, Varun B. Kothamachu, Eva Balsa-Canto, Peter S. Swain, and Filippo Menolascina. 2018. "On-Line Optimal Input Design Increases the Efficiency and Accuracy of the Modelling of an Inducible Synthetic Promoter" Processes 6, no. 9: 148. https://doi.org/10.3390/pr6090148
APA StyleBandiera, L., Hou, Z., Kothamachu, V. B., Balsa-Canto, E., Swain, P. S., & Menolascina, F. (2018). On-Line Optimal Input Design Increases the Efficiency and Accuracy of the Modelling of an Inducible Synthetic Promoter. Processes, 6(9), 148. https://doi.org/10.3390/pr6090148




