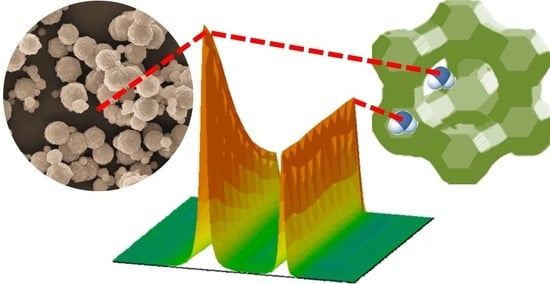
Diffusion in Nanoporous Materials: Novel Insights by Combining MAS and PFG NMR
Abstract
1. Introduction
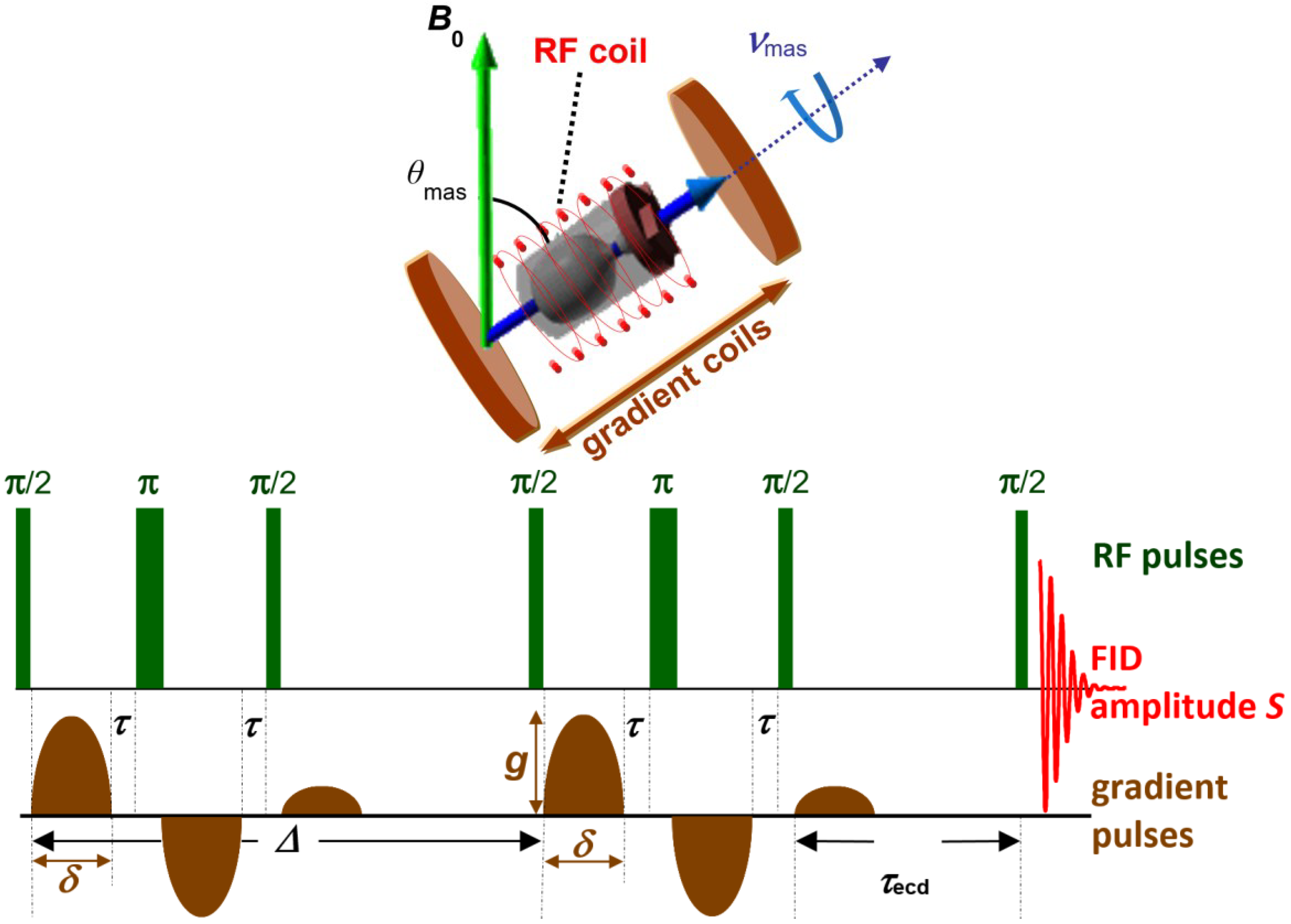
2. Experimental Procedure
3. Diffusion Measurement by MAS PFG NMR
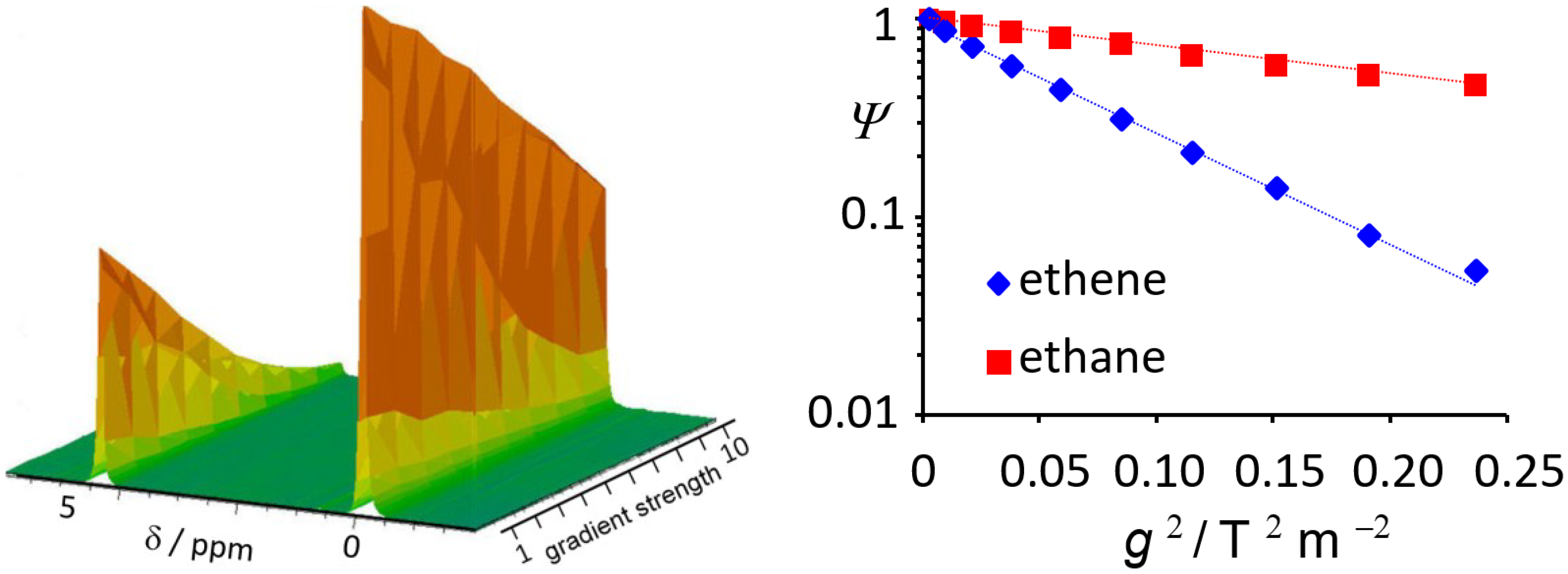
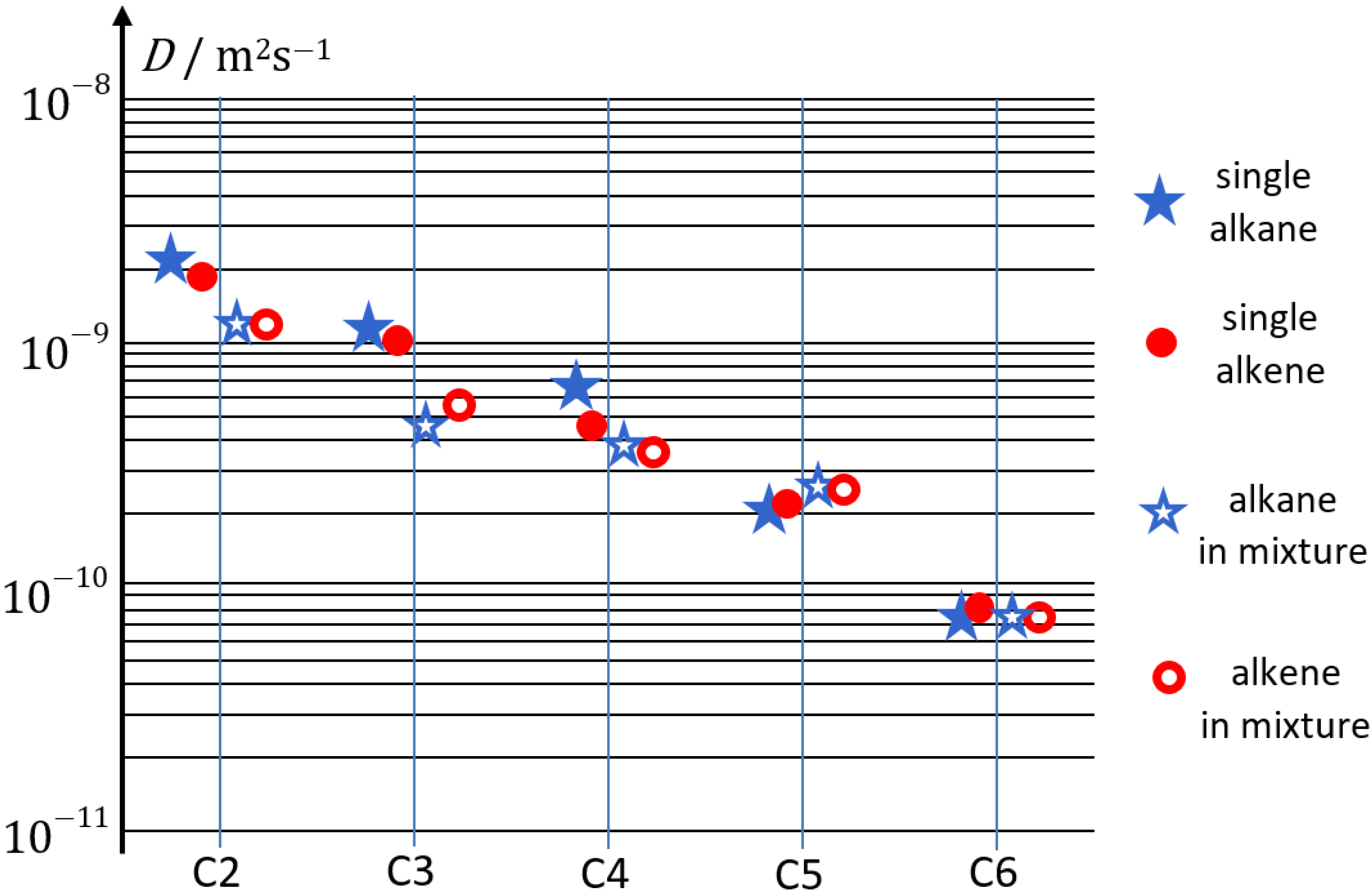
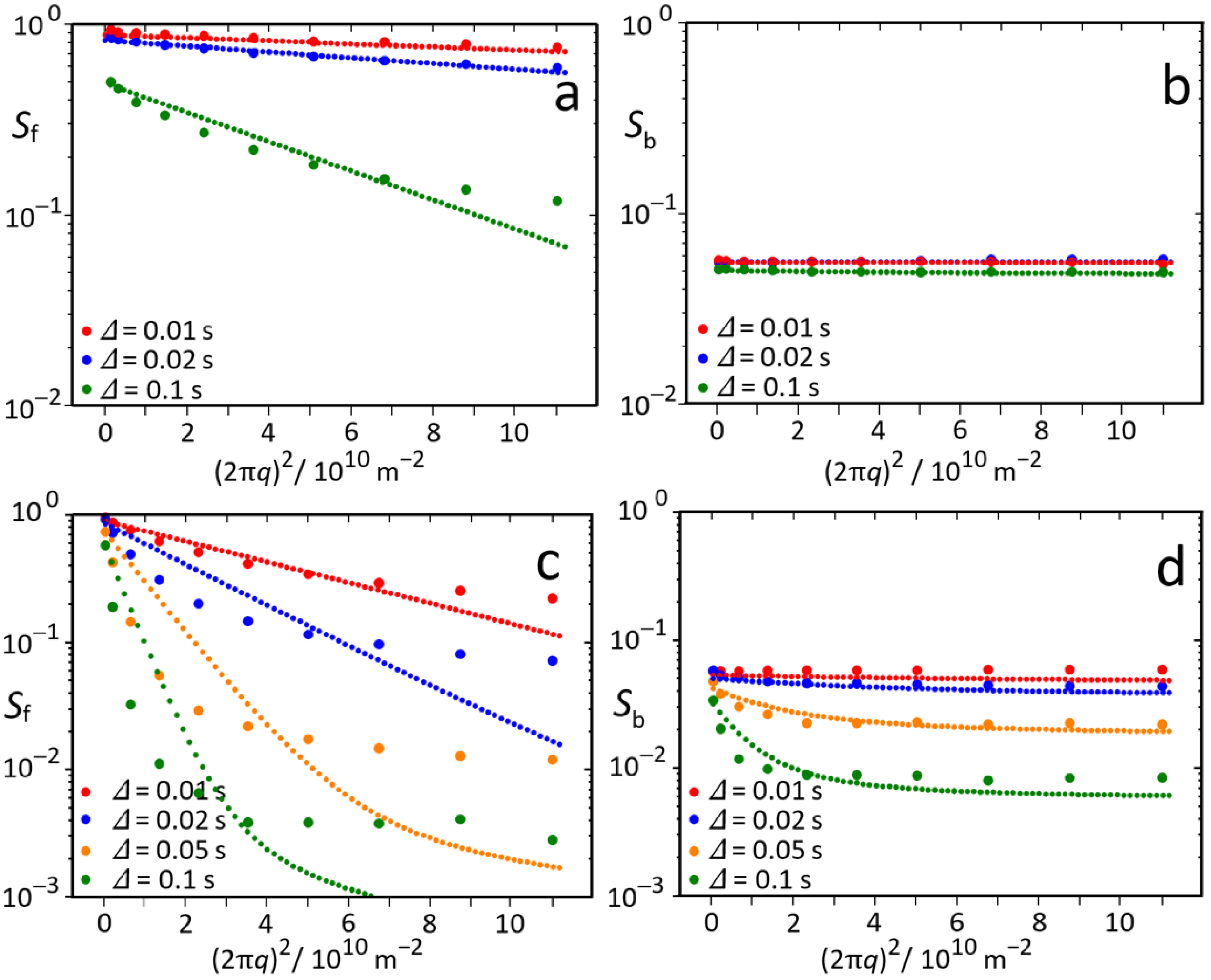
3.1. Mixture Diffusion in Microporous Materials
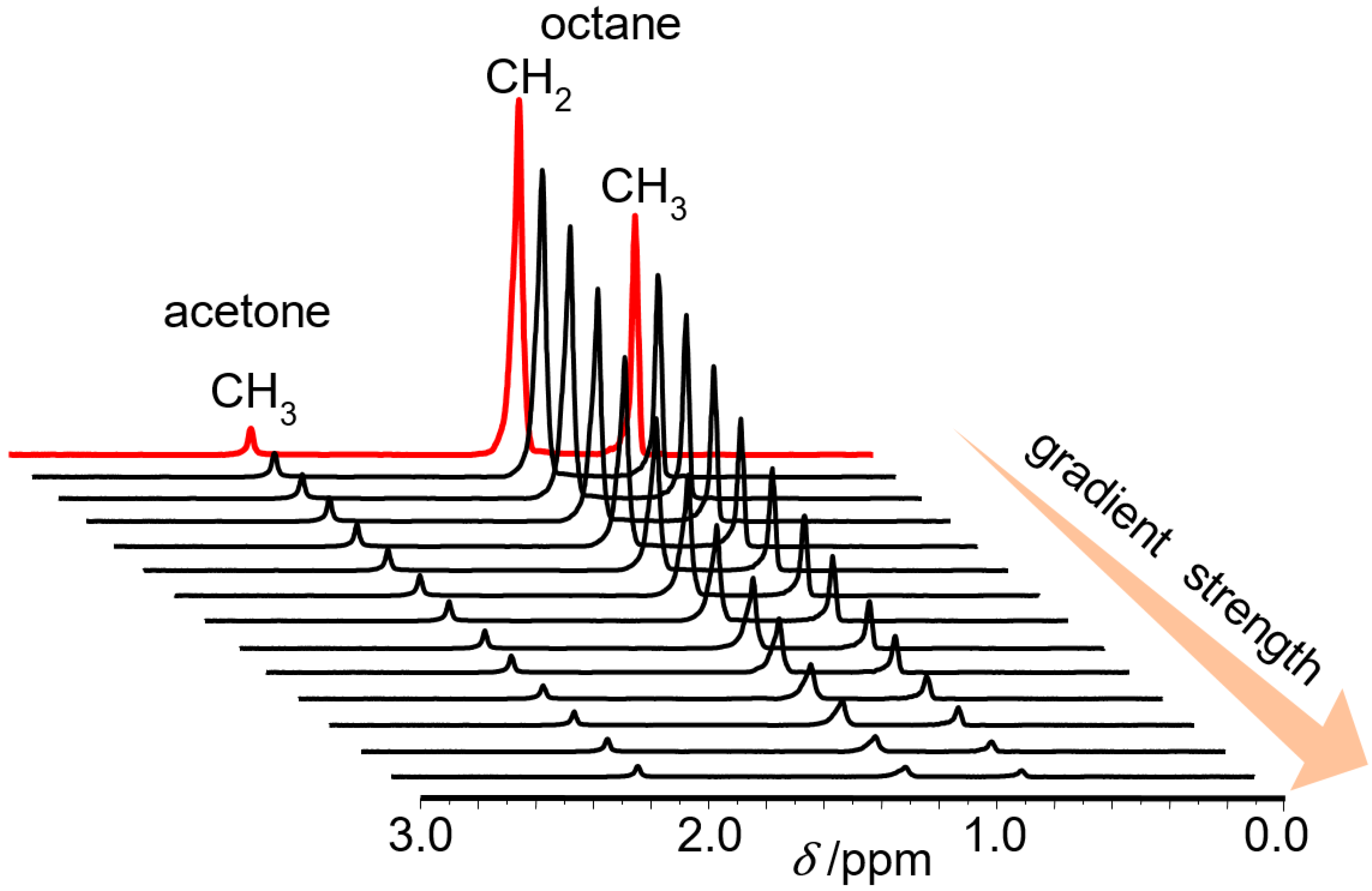
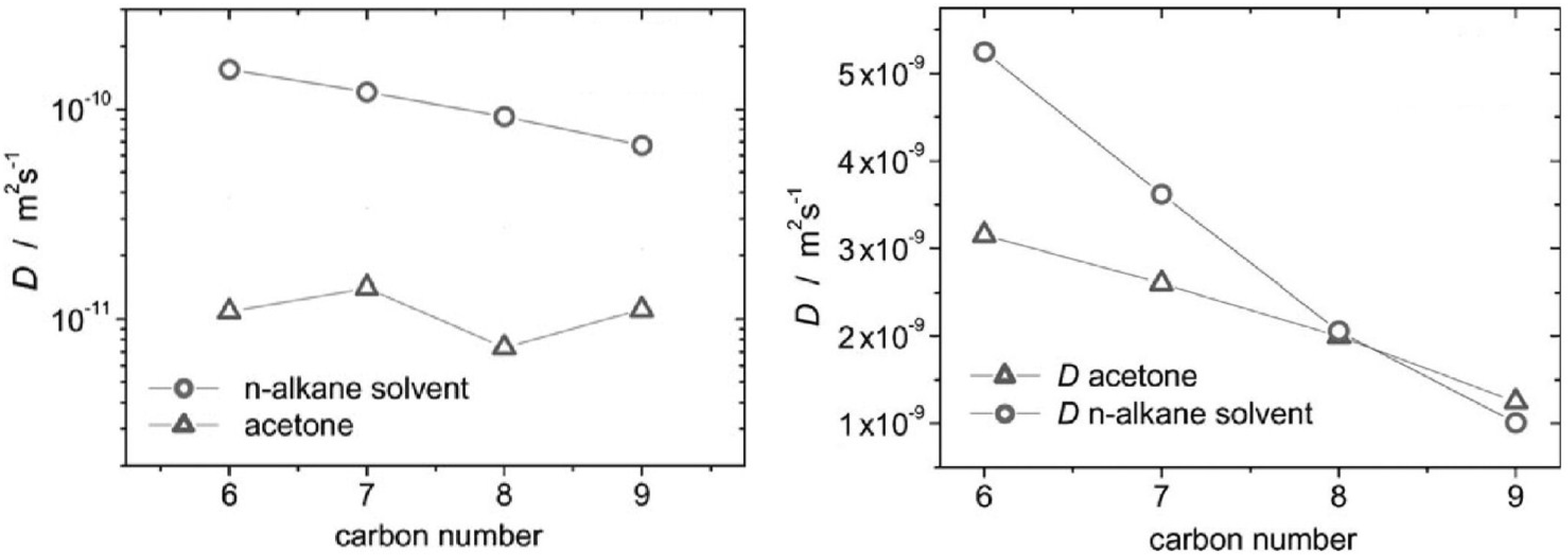
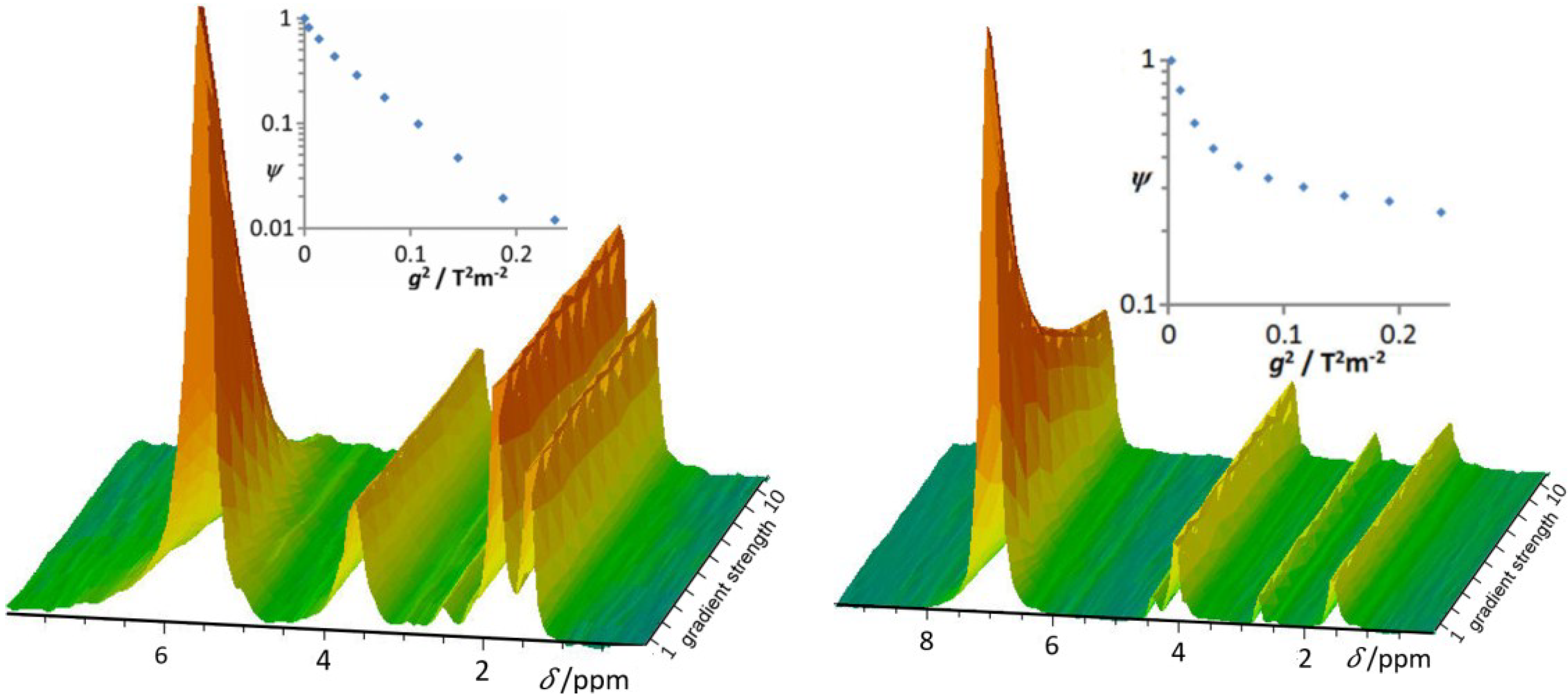
3.2. Complex Formation in Acetone–n-Alkane Mixtures Revealed via MAS PFG NMR
3.3. Diffusion Studies with Nematic Liquid Crystals in Confining Pore Spaces
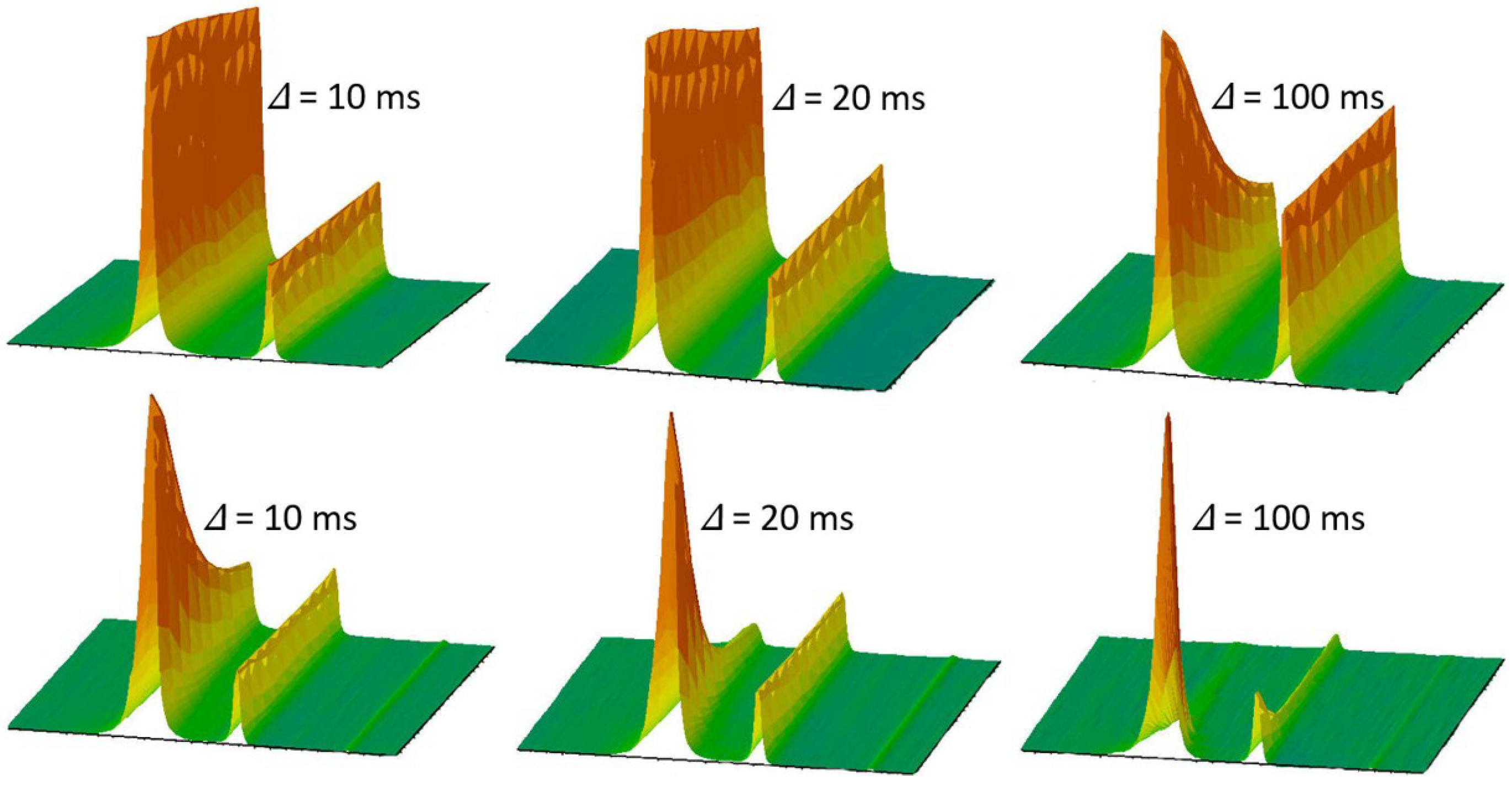
3.4. Water Diffusion in Lithium-Exchanged Low-Silica X-Type Zeolites
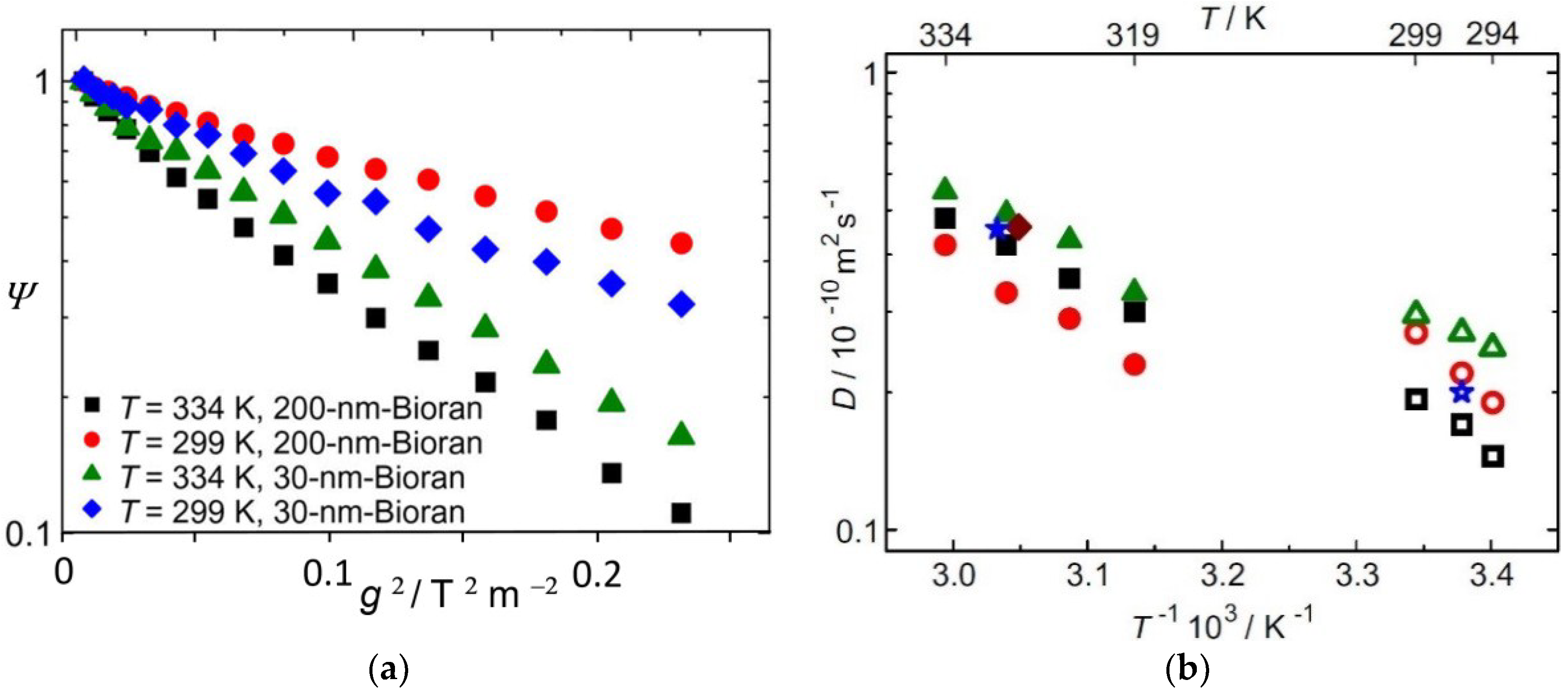
3.5. Proton Mobility in Functionalized Mesoporous Materials
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Bunde, A.; Caro, J.; Kärger, J.; Vogl, G. (Eds.) Diffusive Spreading in Nature, Technology and Society; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Ruthven, D.M.; Farooq, S.; Knaebel, K.S. Pressure Swing Adsorption; VCH: New York, NY, USA, 1994. [Google Scholar]
- Schüth, F.; Sing, K.S.W.; Weitkamp, J. (Eds.) Handbook of Porous Solids; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Ertl, G.; Knözinger, H.; Schüth, F.; Weitkamp, J. (Eds.) Handbook of Heterogeneous Catalysis, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Van de Voorde, M.H.; Sels, B. (Eds.) Nanotechnology in Catalysis: Applications in the Chemical Industry, Energy Development, and Environment Protection; Wiley-VCH: Weinheim, Germany, 2017. [Google Scholar]
- Chen, N.Y.; Degnan, T.F.; Smith, C.M. Molecular Transport and Reaction in Zeolites; VCH: New York, NY, USA, 1994. [Google Scholar]
- Kärger, J.; Freude, D. Mass transfer in micro- and mesoporous materials. Chem. Eng. Technol. 2002, 25, 769–778. [Google Scholar] [CrossRef]
- Kärger, J.; Ruthven, D.M.; Theodorou, D.N. Diffusion in Nanoporous Materials; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Kärger, J. Diffusionsuntersuchung von Wasser an 13X- sowie 4A- und 5A-Zeolithen mit Hilfe der Methode der gepulsten Feldgradienten. Z. Phys. Chem. 1971, 248, 27–41. [Google Scholar] [CrossRef]
- Kärger, J.; Vasenkov, S. Quantitation of diffusion in zeolite catalysts. Microporous Mesoporous Mater. 2005, 85, 195–206. [Google Scholar] [CrossRef]
- Valiullin, R. Diffusion NMR of Confined Systems; Royal Society of Chemistry: Cambridge, UK, 2016. [Google Scholar]
- Kärger, J.; Heink, W. The Propagator Representation of Molecular Transport in Microporous Crystallites. J. Magn. Reson. 1983, 51, 1–7. [Google Scholar] [CrossRef]
- Callaghan, P.T. Principles of NMR Microscopy; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Price, W.S. NMR Studies of Translational Motion; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kärger, J. (Ed.) Leipzig, Einstein, Diffusion, 3rd ed.; Leipziger Universitätsverlag: Leipzig, Germany, 2014. [Google Scholar]
- Zhdanov, S.P.; Khvostchov, S.S.; Feoktistova, N.N. Synthetic Zeolites; Gordon and Breach: New York, NY, USA, 1990. [Google Scholar]
- Kärger, J. Measurement of diffusion in zeolites—A never ending challenge? Adsorption 2003, 9, 29–35. [Google Scholar] [CrossRef]
- Gaede, H.C.; Gawrisch, K. Multi-dimensional pulsed field gradient magic angle spinning NMR experiments on membranes. Magn. Reson. Chem. 2004, 42, 115–122. [Google Scholar] [CrossRef] [PubMed]
- Pampel, A.; Zick, K.; Glauner, H.; Engelke, F. Studying lateral diffusion in lipid bilayers by combining a magic angle spinning NMR probe with a microimaging gradient system. J. Am. Chem. Soc. 2004, 126, 9534–9535. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, M.; Kärger, J.; Freude, D.; Pampel, A.; van Baten, J.M.; Krishna, R. Mixture diffusion in zeolites studied by MAS PFG NMR and molecular simulation. Microporous Mesoporous Mater. 2007, 105, 124–131. [Google Scholar] [CrossRef]
- Romanova, E.E.; Grinberg, F.; Pampel, A.; Karger, J.; Freude, D. Diffusion studies in confined nematic liquid crystals by MAS PFG NMR. J. Magn. Reson. 2009, 196, 110–114. [Google Scholar] [CrossRef] [PubMed]
- Gratz, M.; Hertel, S.; Wehring, M.; Stallmach, F.; Galvosas, P. Mixture diffusion of adsorbed organic compounds in metal-organic frameworks as studied by magic-angle spinning pulsed-field gradient nuclear magnetic resonance. New J. Phys. 2011, 13, 045016. [Google Scholar] [CrossRef]
- Kimmich, R. NMR Tomography, Diffusometry, Relaxometry; Springer: Berlin, Germany, 1997. [Google Scholar]
- Valiullin, R.; Kärger, J. Confined Fluids: NMR Perspectives on Confinements and on Fluid Dynamics. In Diffusion NMR of Confined Systems; Valiullin, R., Ed.; Royal Society of Chemistry: Cambridge, UK, 2016; pp. 390–434. [Google Scholar]
- Harris, R.K.; Becker, E.D.; De Menezes, S.M.C.; Goodfellow, R.; Granger, P. NMR Nomenclature. Nuclear Spin Properties and Conventions for Chemical Shifts–(IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 1795–1818. [Google Scholar] [CrossRef]
- Callaghan, P.T.; Coy, A.; MacGowan, D.; Packer, K.J.; Zelaya, F.O. Diffraction-like effects in NMR diffusion studies of fluids in porous solids. Nature 1991, 351, 467–469. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Rousselot-Pailley, P.; Maux, D.; Wieruszeski, J.M.; Aubagnac, J.L.; Martinez, J.; Lippens, G. Impurity detection in solid-phase organic chemistry: Scope and limits of HR MAS NMR. Tetrahedron 2000, 56, 5163–5167. [Google Scholar] [CrossRef]
- Schröder, H. High resolution magic angle spinning NMR for analyzing small molecules attached to solid support. J. Comb. Chem. 2003, 6, 741–753. [Google Scholar] [CrossRef]
- Pampel, A.; Fernandez, M.; Freude, D.; Kärger, J. New options for measuring molecular diffusion in zeolites by MAS PFG NMR. Chem. Phys. Lett. 2005, 407, 53–57. [Google Scholar] [CrossRef]
- Schlayer, S.; Stallmach, F.; Horch, C.; Splith, T.; Pusch, A.-K.; Pielenz, F.; Peksa, M. Konstruktion und Test eines Gradientensystems für NMR-Diffusionsuntersuchungen in Grenzflächensystemen. Chem. Ing. Tech. 2013, 85, 1755–1760. [Google Scholar] [CrossRef]
- Romanova, E.E.; Scheffler, F.; Freude, D. Crystallization of zeolite MFI under supergravity, studied in situ by 11B MAS NMR spectroscopy. Microporous Mesoporous Mater. 2009, 126, 268–271. [Google Scholar] [CrossRef]
- Dvoyashkina, N.; Freude, D.; Stepanov, A.G.; Böhlmann, W.; Krishna, R.; Kärger, J.; Haase, J. Alkane/alkene mixture diffusion in silicalite-1 studied by MAS PFG NMR. Microporous Mesoporous Mater. 2018, 257, 128–134. [Google Scholar] [CrossRef]
- Mildner, T.; Ernst, H.; Freude, D. 207Pb NMR detection of spinning-induced temperature gradients in MAS rotors. Solid State Nucl. Magn. Reson. 1995, 5, 269–271. [Google Scholar] [CrossRef]
- Ferguson, D.B.; Haw, J.F. Transient methods for in-situ NMR of reactions on solid catalysts using temperature jumps. Anal. Chem. 1995, 67, 3342–3348. [Google Scholar] [CrossRef]
- Neue, G.; Dybowski, C. Determining temperature in a magic-angle spinning probe using the temperature dependence of the isotropic chemical shift of lead nitrate. Solid State Nucl. Magn. Reson. 1997, 7, 333–336. [Google Scholar] [CrossRef]
- Chmelik, C.; Freude, D.; Bux, H.; Haase, J. Ethane/ethene mixture diffusion in the MOF sieve ZIF-8 studied by MAS PFG NMR diffusometry. Microporous Mesoporous Mater. 2012, 147, 135–141. [Google Scholar] [CrossRef]
- Chmelik, C. Characteristic features of molecular transport in MOF ZIF-8 as revealed by IR microimaging. Microporous Mesoporous Mater. 2015, 216, 138–145. [Google Scholar] [CrossRef]
- Park, K.S.; Ni, Z.; Cote, A.P.; Choi, J.Y.; Huang, R.D.; Uribe-Romo, F.J.; Chae, H.K.; O’Keeffe, M.; Yaghi, O.M. Exceptional chemical and thermal stability of zeolitic imidazolate frameworks. Proc. Natl. Acad. Sci. USA 2006, 103, 10186–10191. [Google Scholar] [CrossRef] [PubMed]
- Bux, H.; Liang, F.; Li, Y.; Cravillon, J.; Wiebcke, M.; Caro, J. Zeolitic imidazolate framework membrane with molecular sieving properties by microwave-assisted solvothermal synthesis. J. Am. Chem. Soc. 2009, 131, 16000–16001. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.; Hupp, J.T. Metal-organic frameworks as sensors: A ZIF-8 based Fabry-Pérot device as a selective sensor for chemical vapors and gases. J. Am. Chem. Soc. 2010, 132, 7832–7833. [Google Scholar] [CrossRef] [PubMed]
- Kärger, J.; Binder, T.; Chmelik, C.; Hibbe, F.; Krautscheid, H.; Krishna, R.; Weitkamp, J. Microimaging of transient guest profiles to monitor mass transfer in nanoporous materials. Nat. Mater. 2014, 13, 333–343. [Google Scholar] [CrossRef] [PubMed]
- Gladstone, S.; Laidler, K.J.; Eyring, H. The Theory of Rate Processes; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Ruthven, D.M.; Derrah, R.I. Transition state theory of zeolitic diffusion. J. Chem. Soc. Faraday Trans. I 1972, 68, 2332–2343. [Google Scholar] [CrossRef]
- Kärger, J.; Pfeifer, H.; Haberlandt, R. Application of absolute rate theory to intracrystalline diffusion in zeolites. J. Chem. Soc. Faraday Trans. I 1980, 76, 1569–1575. [Google Scholar] [CrossRef]
- Chmelik, C.; Kärger, J. The predictive power of classical transition state theory revealed in diffusion studies with MOF ZIF-8. Microporous Mesoporous Mater. 2016, 225, 128–132. [Google Scholar] [CrossRef]
- Caro, J.; Bülow, M.; Schirmer, W.; Kärger, J.; Heink, W.; Pfeifer, H.; Zhdanov, S.P. Microdynamics of methane, ethane and propane in ZSM-5 type zeolites. J. Chem. Soc. Faraday Trans. I 1985, 81, 2541–2550. [Google Scholar] [CrossRef]
- Heink, W.; Kärger, J.; Pfeifer, H.; Salverda, P.; Datema, K.P.; Nowak, A.K. High-temperature pulsed field gradient nuclear magnetic resonance self-diffusion measurements of n-Alkanes in MFI-type zeolites. J. Chem. Soc. Faraday Trans. 1992, 88, 3505–3509. [Google Scholar] [CrossRef]
- Jobic, H.; Schmidt, W.; Krause, C.; Kärger, J. PFG NMR and QENS diffusion studies of n-alkane homologues in MFI-type zeolites. Microporous Mesoporous Mater. 2006, 90, 299–306. [Google Scholar] [CrossRef]
- Tsai, H.L.; Sato, S.; Takahashi, R.; Sodesawa, T.; Takenaka, S. Liquid-phase hydrogenation of ketones in the mesopores of nickel catalysts. Phys. Chem. Chem. Phys. 2002, 4, 3537–3542. [Google Scholar] [CrossRef]
- Nguyen, N.Q.; McGann, M.R.; Lacks, D.J. Elastic stability limits of polyethylene and n-alkane crystals from molecular simulation. J. Phys. Chem. B 1999, 103, 10679–10683. [Google Scholar] [CrossRef]
- Kishore, K.; Bharat, S.; Kannan, S. Correlation of Kauzman temperature with odd-even effect in n-alkanes. J. Chem. Phys. 1996, 105, 11364–11365. [Google Scholar] [CrossRef]
- Takahashi, R.; Sato, S.; Sodesawa, T.; Ikeda, T. Diffusion coefficient of ketones in liquid media within mesopores. Phys. Chem. Chem. Phys. 2003, 5, 2476–2480. [Google Scholar] [CrossRef]
- Fernandez, M.; Pampel, A.; Takahashi, R.; Sato, S.; Freude, D.; Kärger, J. Revealing complex-formation in acetone-n-alkane mixtures by MAS PFG NMR diffusion measurement in nanoporous hosts. Phys. Chem. Chem. Phys. 2008, 10, 4165–4171. [Google Scholar] [CrossRef] [PubMed]
- Rincon Bonilla, M.; Bhatia, S.K. Diffusion in Pore Networks: Effective self-diffusivity and the concept of tortuosity. J. Phys. Chem. C 2013, 117, 3343–3357. [Google Scholar] [CrossRef]
- Rincon Bonilla, M.; Titze, T.; Schmidt, F.; Mehlhorn, D.; Chmelik, C.; Valiullin, R.; Bhatia, S.K.; Kaskel, S.; Ryoo, R.; Kärger, J. Diffusion study by IR micro-imaging of molecular uptake and release on mesoporous zeolites of structure type CHA and LTA. Materials 2013, 6, 2662–2688. [Google Scholar] [CrossRef] [PubMed]
- Kärger, J.; Valiullin, R. Mass transfer in mesoporous materials: The benefit of microscopic diffusion measurement. Chem. Soc. Rev. 2013, 42, 4172–4197. [Google Scholar] [CrossRef] [PubMed]
- Mehlhorn, D.; Kondrashova, D.; Küster, C.; Enke, D.; Emmerich, T.; Bunde, A.; Valiullin, R.; Kärger, J. Diffusion in complementary pore spaces. Adsorption 2016, 22, 879–890. [Google Scholar] [CrossRef]
- Stoeckel, D.; Kübel, C.; Hormann, K.; Höltzel, A.; Smarsly, B.M.; Tallarek, U. Morphological analysis of disordered macroporous-mesoporous solids based on physical reconstruction by nanoscale tomography. Langmuir 2014, 30, 9022–9027. [Google Scholar] [CrossRef] [PubMed]
- Kondrashova, D.; Lauerer, A.; Mehlhorn, D.; Jobic, H.; Feldhoff, A.; Thommes, M.; Chakraborty, D.; Gommes, C.; Zecevic, J.; de Jongh, P.; et al. Scale-dependent diffusion anisotropy in nanoporous silicon. Sci. Rep. 2017, 7, 40207. [Google Scholar] [CrossRef] [PubMed]
- Reich, S.-J.; Svidrytski, A.; Höltzel, A.; Florek, J.; Kleitz, F.; Wang, W.; Kübel, C.; Hlushkou, D.; Tallarek, U. Hindered diffusion in ordered mesoporous silicas: Insights from pore-scale simulations in physical reconstructions of SBA-15 and KIT-6 silica. J. Phys. Chem. C 2018, 122, 12350–12361. [Google Scholar] [CrossRef]
- Crawford, G.P.; Vilfan, M.; Doane, J.W.; Vilfan, I. Escaped-radial nematic configuration in submicrometer-size cylindrical cavities: Deuterium nuclear-magnetic-resonance study. Phys. Rev. A 1991, 43, 835–842. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.; Cramer, T.; Arndt, M.; Kremer, F.; Naji, L.; Stannarius, R. NMR and dielectric studies of nano-confined nematic liquid crystals. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 2006, 303, 209–217. [Google Scholar] [CrossRef]
- Gueudré, L.; Milina, M.; Mitchell, S.; Pérez-Ramírez, J. Superior mass transfer properties of technical zeolite bodies with hierarchical porosity. Adv. Funct. Mater. 2014, 24, 209–219. [Google Scholar] [CrossRef]
- Mitchell, S.; Pinar, A.B.; Kenvin, J.; Crivelli, P.; Kärger, J.; Pérez-Ramírez, J. Structural analysis of hierarchically organized zeolites. Nat. Commun. 2015, 6, 8633. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, M.; Schwieger, W. Hierarchically-structured porous materials: From basic understanding to applications. Chem. Soc. Rev. 2016, 45, 3311–3312. [Google Scholar] [CrossRef] [PubMed]
- Coasne, B. Multiscale adsorption and transport in hierarchical porous materials. New J. Chem. 2016, 40, 4078–4094. [Google Scholar] [CrossRef]
- Galarneau, A.; Guenneau, F.; Gedeon, A.; Mereib, D.; Rodriguez, J.; Fajula, F.; Coasne, B. Probing interconnectivity in hierarchical microporous/mesoporous materials using adsorption and nuclear magnetic resonance diffusion. J. Phys. Chem. C 2016, 120, 1562–1569. [Google Scholar] [CrossRef]
- Trogadas, P.; Nigra, M.M.; Coppens, M.-O. Nature-inspired optimization of hierarchical porous media for catalytic and separation processes. New J. Chem. 2016, 40, 4016–4026. [Google Scholar] [CrossRef]
- Coppens, M.O.; Ye, G. Nature-inspired optimization of transport in porous media. In Diffusive Spreading in Nature, Technology and Society; Bunde, A., Caro, J., Kärger, J., Vogl, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 203–232. [Google Scholar]
- Kärger, J. NMR Self-diffusion studies in heterogeneous systems. Adv. Colloid Interface Sci. 1985, 23, 129–148. [Google Scholar] [CrossRef]
- Reginald Waldeck, A.; Hossein Nouri-Sorkhabi, M.; Sullivan, D.R.; Kuchel, P.W. Effects of cholesterol on transmembrane water diffusion in human erythrocytes measured using pulsed field gradient NMR. Biophys. Chem. 1995, 55, 197–208. [Google Scholar] [CrossRef]
- Meier, C.; Dreher, W.; Leibfritz, D. Diffusion in compartmental systems. II. Diffusion weighted measurements of rat brain tissue in vivo and postmortem at very large b-values. Magn. Reson. Med. 2003, 50, 510–514. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, M.; Alerstam, E.; Wirestam, R.; Stahlberg, F.; Brockstedt, S.; Lätt, J. Evaluating the accuracy and precision of a two-compartment Kärger model using Monte Carlo simulations. J. Magn. Res. 2010, 206, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Himmelein, S.; Sporenberg, N.; Schönhoff, M.; Ravoo, B.J. Size-selective permeation of water-soluble polymers through the bilayer membrane of cyclodextrin vesicles investigated by PFG-NMR. Langmuir 2014, 30, 3988–3995. [Google Scholar] [CrossRef] [PubMed]
- Melchior, J.-P.; Majer, G.; Kreuer, K.-D. Why do proton conducting polybenzimidazole phosphoric acid membranes perform well in high-temperature PEM fuel cells? Phys. Chem. Chem. Phys. 2016, 19, 601–612. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.S.D.; Barreiros, S.; Cabrita, E.J. Probing sol-gel matrices microenvironments by PGSE HR-MAS NMR. Magn. Reson. Chem. 2017, 55, 452–463. [Google Scholar] [CrossRef] [PubMed]
- Cabrita, E.J.; Berger, S.; Brauer, P.; Kärger, J. High-resolution DOSY NMR with spins in different chemical surroundings: Influence of particle exchange. J. Magn. Reson. 2002, 157, 124–131. [Google Scholar] [CrossRef] [PubMed]
- Kühl, G.H. Crystallization of low-silica faujasite. Zeolites 1987, 7, 451–457. [Google Scholar] [CrossRef]
- Schneider, D.; Toufar, H.; Samoson, A.; Freude, D. 17O DOR and other solid-state NMR studies concerning the basic properties of zeolites LSX. Solid State Nucl. Magn. Reson. 2009, 35, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Freude, D.; Beckert, S.; Stallmach, F.; Kurzhals, R.; Täschner, D.; Toufar, H.; Kärger, J.; Haase, J. Ion and water mobility in hydrated Li-LSX zeolite studied by 1H, 6Li and 7Li NMR spectroscopy and diffusometry. Microporous Mesoporous Mater. 2013, 172, 174–181. [Google Scholar] [CrossRef]
- Beckert, S.; Stallmach, F.; Toufar, H.; Freude, D.; Kärger, J.; Haase, J. Tracing water and cation diffusion in hydrated zeolites of type Li-LSX by pulsed field gradient NMR. J. Phys. Chem. C 2013, 117, 24866–24872. [Google Scholar] [CrossRef]
- Lauerer, A.; Kurzhals, R.; Toufar, H.; Freude, D.; Kärger, J. Tracing compartment exchange by NMR diffusometry: Water in lithium-exchanged low-silica X zeolites. J. Magn. Reson. 2018, 289, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Laberty-Robert, C.; Vallé, K.; Pereira, F.; Sanchez, C. Design and properties of functional hybrid organic-inorganic membranes for fuel cells. Chem. Soc. Rev. 2011, 40, 961–1005. [Google Scholar] [CrossRef] [PubMed]
- Hickner, M.A.; Ghassemi, H.; Kim, Y.S.; Einsla, B.R.; McGrath, J.E. Alternative polymer systems for proton exchange membranes (PEMs). Chem. Rev. 2004, 104, 4587–4612. [Google Scholar] [CrossRef] [PubMed]
- Kreuer, K.-D.; Paddison, S.J.; Spohr, E.; Schuster, M. Transport in proton conductors for fuel-cell applications: simulations, elementary reactions, and phenomenology. Chem. Rev. 2004, 104, 4637–4678. [Google Scholar] [CrossRef] [PubMed]
- Sharifi, M.; Wark, M.; Freude, D.; Haase, J. Highly proton conducting sulfonic acid functionalized mesoporous materials studied by impedance spectroscopy, MAS NMR spectroscopy and MAS PFG NMR diffusometry. Microporous Mesoporous Mater. 2012, 156, 80–89. [Google Scholar] [CrossRef]
- Dvoyashkina, N.; Seidler, C.F.; Wark, M.; Freude, D.; Haase, J. Proton mobility in sulfonic acid functionalized mesoporous materials studied by MAS PFG NMR diffusometry and impedance spectroscopy. Microporous Mesoporous Mater. 2018, 255, 140–147. [Google Scholar] [CrossRef]
- D’Orazio, F.; Bhattacharja, S.; Halperin, W.P.; Gerhardt, R. Enhanced self-diffusion of water in restricted geometry. Phys. Rev. Lett. 1989, 63, 43–46. [Google Scholar] [CrossRef] [PubMed]
- Kärger, J.; Pfeifer, H.; Riedel, E.; Winkler, H. Self-diffusion measurements of water adsorbed in NaY zeolites by means of NMR pulsed field gradient techniques. J. Colloid Interface Sci. 1973, 44, 187–188. [Google Scholar] [CrossRef]
- Inayat, A.; Knoke, I.; Spieker, E.; Schwieger, W. Assemblies of mesoporous FAU-type zeolite nanosheets. Angew. Chem. Int. Ed. 2012, 51, 1962–1965. [Google Scholar] [CrossRef] [PubMed]
- Na, K.; Choi, M.; Ryoo, R. Recent advances in the synthesis of hierarchically nanoporous zeolites. Microporous Mesoporous Mater. 2013, 166, 3–19. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kärger, J.; Freude, D.; Haase, J. Diffusion in Nanoporous Materials: Novel Insights by Combining MAS and PFG NMR. Processes 2018, 6, 147. https://doi.org/10.3390/pr6090147
Kärger J, Freude D, Haase J. Diffusion in Nanoporous Materials: Novel Insights by Combining MAS and PFG NMR. Processes. 2018; 6(9):147. https://doi.org/10.3390/pr6090147
Chicago/Turabian StyleKärger, Jörg, Dieter Freude, and Jürgen Haase. 2018. "Diffusion in Nanoporous Materials: Novel Insights by Combining MAS and PFG NMR" Processes 6, no. 9: 147. https://doi.org/10.3390/pr6090147
APA StyleKärger, J., Freude, D., & Haase, J. (2018). Diffusion in Nanoporous Materials: Novel Insights by Combining MAS and PFG NMR. Processes, 6(9), 147. https://doi.org/10.3390/pr6090147