A Systems and Treatment Perspective of Models of Influenza Virus-Induced Host Responses
Abstract
1. Introduction
1.1. Immune Modulation for the Treatment of IAV Infection
1.2. Mathematical Models of the Lung Host Response to IAV Infection
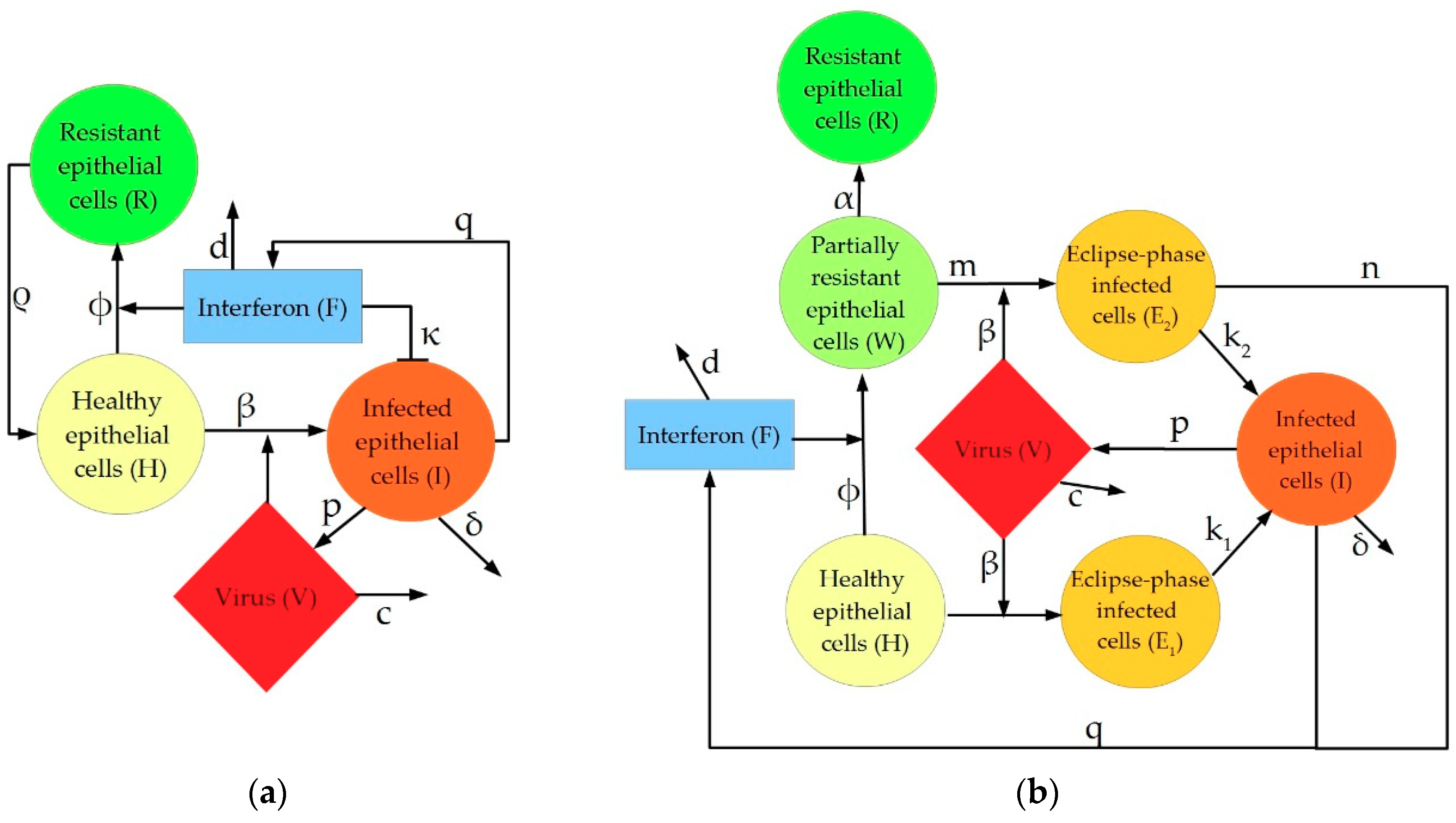
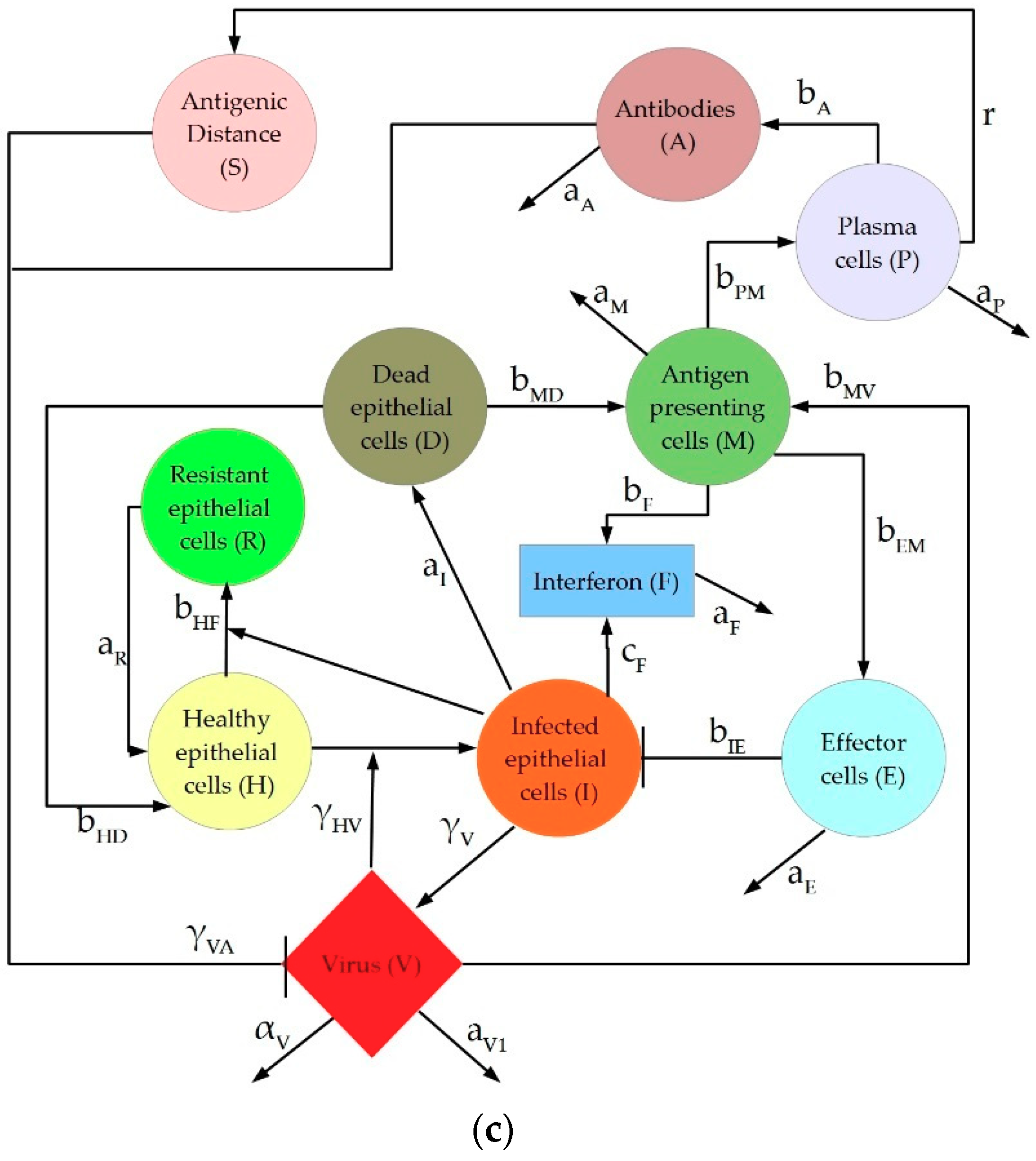
2. Description of IAV Immune Response Models
3. Materials and Methods
4. Results
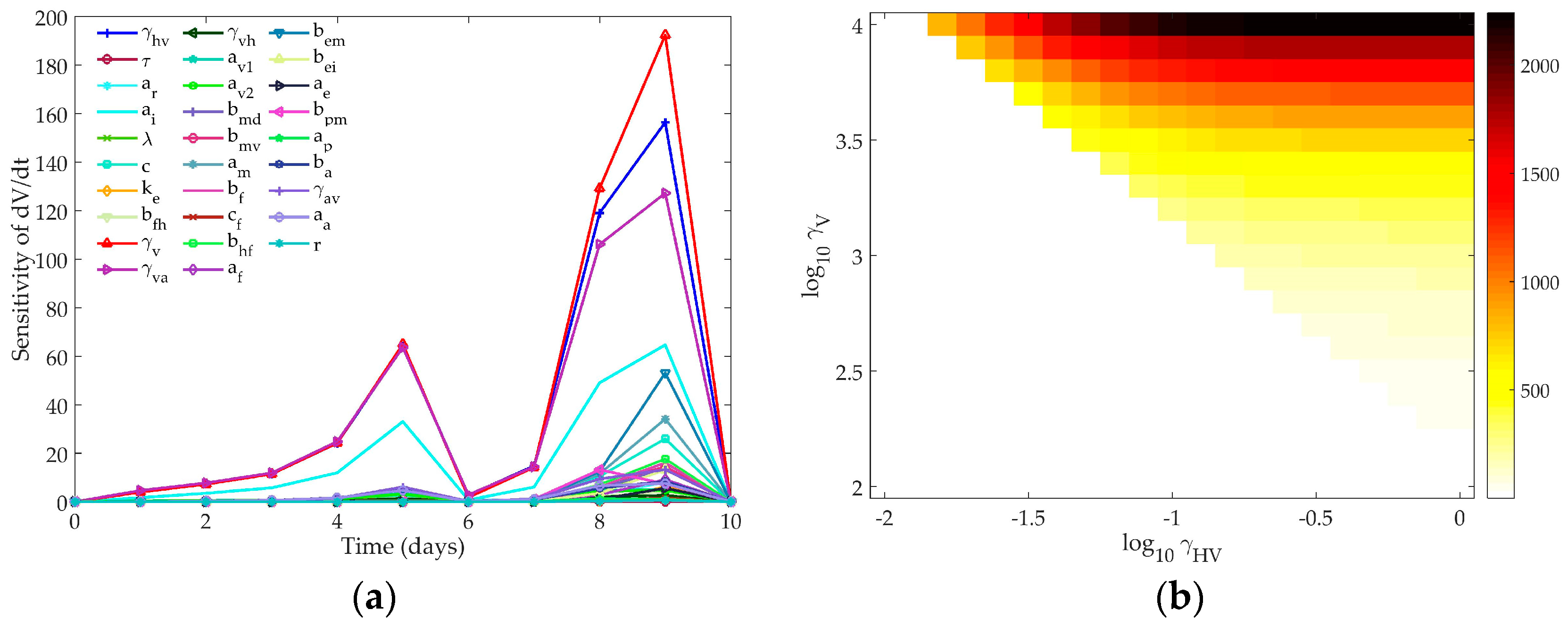
4.1. Sensitivity Analysis
4.1.1. Pawelek Model
4.1.2. Saenz Model
4.1.3. Hancioglu Model
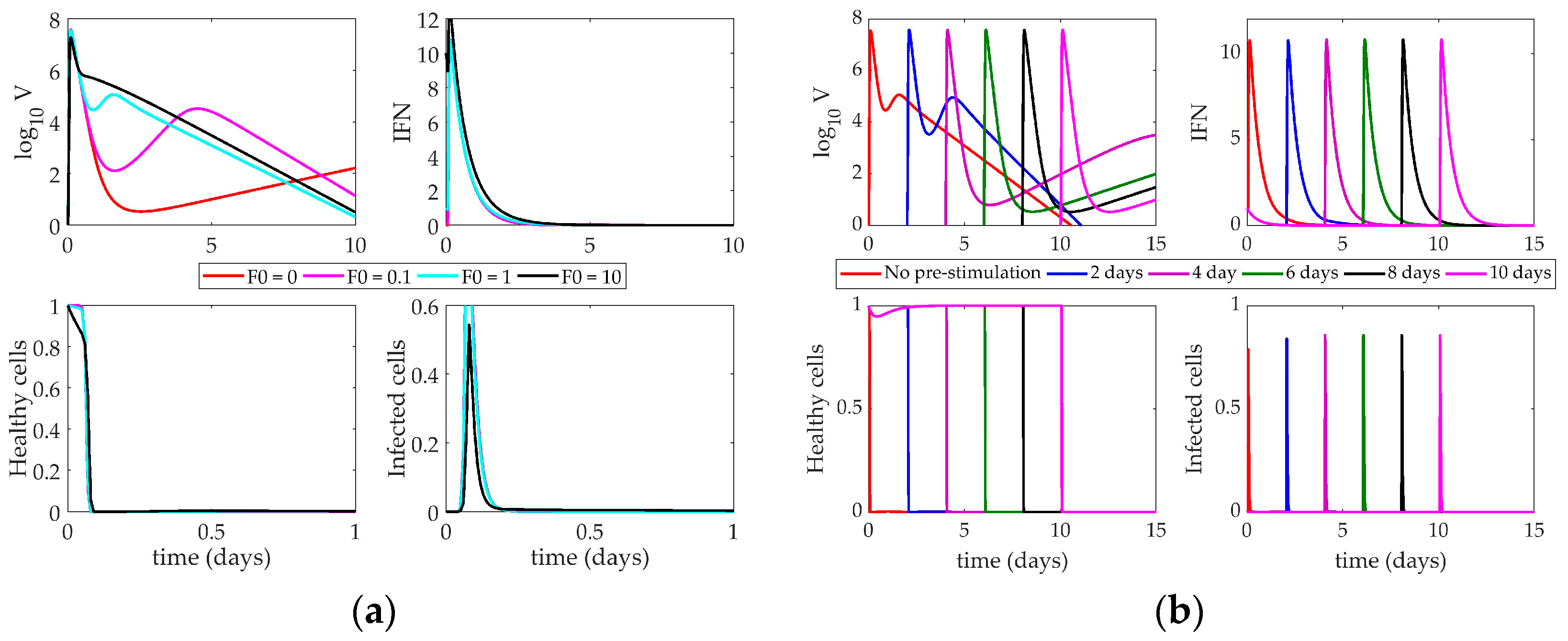
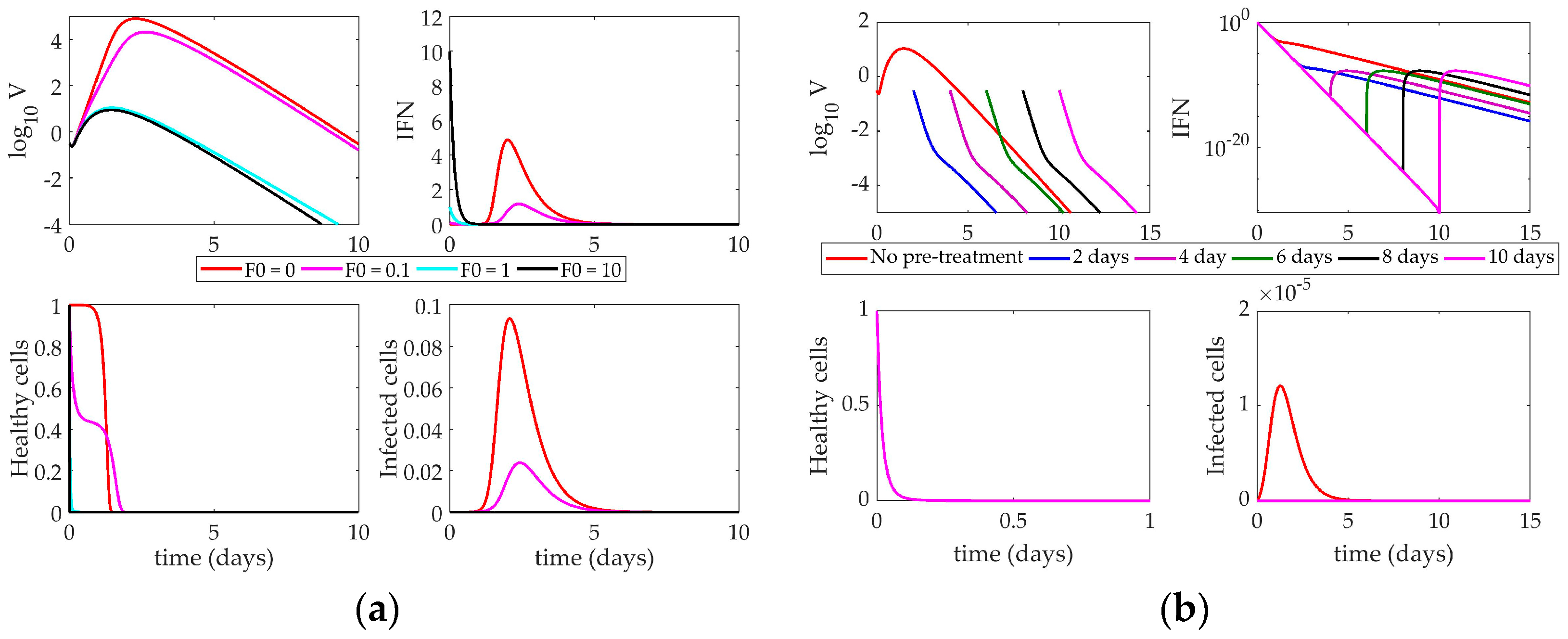
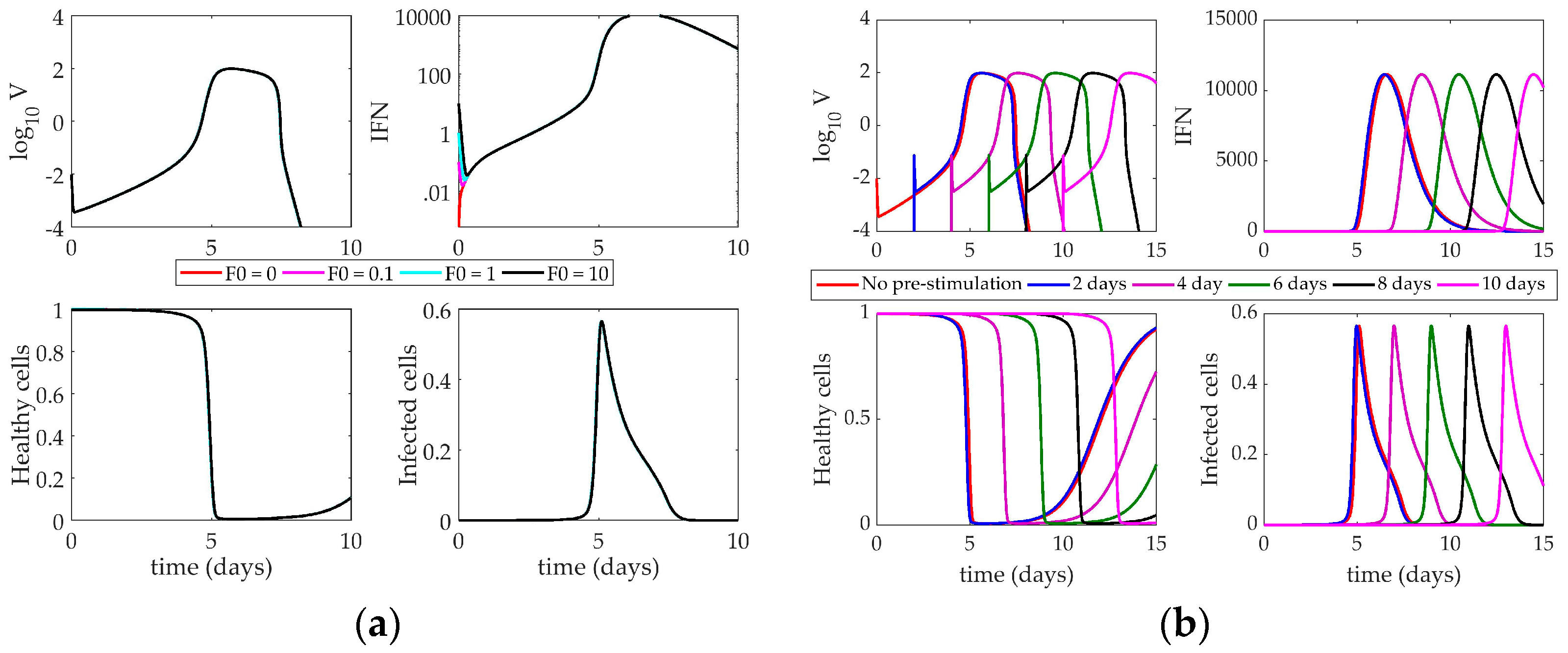
4.2. Models’ Response to Simulated IFN Pre-Stimulation
4.2.1. Pawelek Model Response to IFN Pre-Stimulation
4.2.2. Saenz Model Response to IFN Pre-Stimulation
4.2.3. Hancioglu Model Response to IFN Pre-Stimulation
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameter | Definition | Value | Units |
|---|---|---|---|
| β | Infectivity of virus | 4.7 × 10−5 | (RNA copy)−1 mL NS day−1 |
| φ | Rate of production of virus-resistant epithelial cells | 0.33 | (IFN fold change)−1 day−1 |
| ρ | Rate of loss of resistance in epithelial cells | 2.6 | day−1 |
| δ | Death of infected epithelial cells | 2 | day−1 |
| κ | Rate of infected cell clearance by natural killer cells | 4.2 | (IFN fold change)−1 day−1 |
| p | Replication rate of virus | 5.3 × 10−3 | (RNA copy)−1 day−1 cell−1 |
| c | Clearance of virus by immune system | 16 | day−1 |
| q | Rate of production of interferon by infected cells | 9.6 × 10−10 | (IFN fold change) day−1 cell−1 |
| d | Rate of depletion of interferon | 1.99 | day−1 |
| Parameter | Definition | Value | Units |
|---|---|---|---|
| β | Infectivity of virus | 1.4 × 10−4 | (RNA copy)−1 mL NS day−1 |
| φ | Rate of production of virus-resistant epithelial cells | 56 | (IFN fold change)−1 day−1 |
| k1 | Rate of production of unprotected infected cells | 2 | day−1 |
| δ | Death of infected epithelial cells | 2 | day−1 |
| m | IFN-reduced infectivity | 1 | unitless |
| k2 | Eclipse phase of interferon-protected infected cells | 2 | day−1 |
| α | Rate at which partially-resistant cells become fully resistant | 4 | day−1 |
| p | Replication rate of virus | 1.4 × 10−5 | (RNA copy)−1 day−1 cell−1 |
| c | Clearance of virus by immune system | 5.2 | day−1 |
| q | Rate of production of interferon by infected epithelial cells | 5 × 10−10 | (IFN fold change) day−1 cell−1 |
| d | Rate of depletion of interferon | 6.8 | day−1 |
| n | IFN-reduced production | 1 | unitless |
| Parameter | Definition | Value |
|---|---|---|
| γHV | Rate of epithelial cells infected by virus | 0.34 |
| aR | Loss of resistance to infection | 1 |
| aI | Death of infected cells | 1.5 |
| bHD | Rate of regeneration of epithelial cells | 4 |
| αV | Nonspecific clearance of virus | 1.7 |
| bIE | Clearance of infected cells by effector cells | 0.066 |
| bFH | Rate of binding of IFN to epithelial cells | 17 |
| γV | Rate of virus secretion by infected cells | 510 |
| γVA | Rate of antibody neutralization of virus | 619.2 |
| γVH | Rate of adsorption of virus by infected cells | 1.02 |
| aV1 | Nonspecific clearance of virus | 100 |
| aV2 | Nonspecific clearance of virus | 23,000 |
| bMD | Stimulation of antigen presenting cells by dead cells | 1 |
| bMV | Stimulation of antigen presenting cells by virus | 0.0037 |
| aM | Death of antigen presenting cells | 1 |
| bF | IFN production by antigen presenting ells | 250,000 |
| cF | IFN production by infected cells | 2000 |
| bHF | Rate of production of virus-resistant cells | 0.01 |
| aF | Natural decay of IFN | 8 |
| bEM | Production of effector cells | 8.3 |
| bEI | Death of effector cells through interaction with infected cells | 2.72 |
| aE | Natural death of effector cells | 0.4 |
| bPM | Production of plasma cells | 11.5 |
| aP | Death of plasma cells | 0.4 |
| bA | Production of antibodies by plasma cells | 0.043 |
| γAV | Rate at which antibodies bind to virus | 146.2 |
| aA | Natural decay of antibodies | 0.043 |
| r | Rate of compatibility of antibodies and virus | 3 × 10−5 |
References
- World Health Organization. Influenza (Seasonal). Available online: http://www.who.int/news-room/fact-sheets/detail/influenza-(seasonal) (accessed on 1 June 2018).
- Potter, C.W. A history of influenza. J. Appl. Microbiol. 2001, 91, 572–579. [Google Scholar] [CrossRef] [PubMed]
- Kilbourne, E.D. Influenza pandemics of the 20th centIury. Emerg. Infect. Dis. 2006, 12, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Gill, J.R.; Sheng, Z.M.; Ely, S.F.; Guinee, D.G., Jr.; Beasley, M.B.; Suh, J.; Deshpande, C.; Mollura, D.J.; Morens, D.M.; Bray, M.; et al. Pulmonary pathologic findings of fatal 2009 pandemic influenza A/H1N1 viral infections. Arch. Pathol. Lab. Med. 2010, 134, 235–243. [Google Scholar] [PubMed]
- Chotpitayasunondh, T.; Ungchusak, K.; Hanshaoworakul, W.; Chunsuthiwat, S.; Sawanpanyalert, P.; Kijphati, R.; Lochindarat, S.; Srisan, P.; Suwan, P.; Osotthanakorn, Y.; et al. Human disease from influenza A (H5N1), Thailand, 2004. Emerg. Infect. Dis. 2005, 11, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Hien, T.T.; Liem, N.T.; Dung, N.T.; San, L.T.; Mai, P.P.; Chau, N.v.V.; Suu, P.T.; Dong, V.C.; Mai, L.T.Q.; Thi, N.T.; et al. Avian influenza A (H5N1) in 10 patients in Vietnam. N. Engl. J. Med. 2004, 350, 1179–1188. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Zhou, Y.H.; Yang, Z.Q. The cytokine storm of severe influenza and development of immunomodulatory therapy. Cell. Mol. Immunol. 2016, 13, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Hayden, F.G. Antiviral resistance in influenza viruses—Implications for management and pandemic response. N. Engl. J. Med. 2006, 354, 785–788. [Google Scholar] [CrossRef] [PubMed]
- Beigel, J.H.; Farrar, J.; Han, A.M.; Hayden, F.G.; Hyer, R.; de Jong, M.D.; Lochindarat, S.; Tien, N.T.K.; Hein, N.T. Avian influenza A (H5N1) infection in humans. N. Engl. J. Med. 2005, 353, 1374–1385. [Google Scholar] [PubMed]
- Lee, K.-Y.; Rhim, J.-W.; Kang, J.-H. Hyperactive immune cells (T cells) may be responsible for acute lung injury in influenza virus infections: A need for early immune-modulators for severe cases. Med. Hypotheses 2011, 76, 64–69. [Google Scholar] [CrossRef] [PubMed]
- Peiris, J.S.M.; Cheung, C.Y.; Leung, C.Y.H.; Nicholls, J.M. Innate immune responses to influenza A H5N1: Friend or foe? Trends Immunol. 2009, 30, 574–584. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.-J.; Chan, K.-W.; Lin, Y.-P.; Zhao, G.-Y.; Chan, C.; Zhang, H.-J.; Chen, H.-L.; Wong, S.S.Y.; Lau, S.K.P.; Woo, P.C.Y.; et al. Delayed antiviral plus immunomodulator treatment still reduces mortality in mice infected by high inoculum of influenza A/H5N1 virus. Proc. Natl. Acad. Sci. USA 2008, 105, 8091–8096. [Google Scholar] [CrossRef] [PubMed]
- Cilloniz, C.; Pantin-Jackwood, M.J.; Ni, C.; Goodman, A.G.; Peng, X.; Proll, S.C.; Carter, V.S.; Rosenzweig, E.R.; Szretter, K.J.; Katz, J.M.; et al. Lethal dissemination of H5N1 influenza virus is associated with dysregulation of inflammation and lipoxin signaling in a mouse model of infection. J. Virol. 2010, 84, 7613–7624. [Google Scholar] [CrossRef] [PubMed]
- Menachery, V.D.; Eisfeld, A.J.; Schäfer, A.; Josset, L.; Sims, A.C.; Proll, S.; Fan, S.; Li, C.; Neumann, G.; Tilton, S.C.; et al. Pathogenic influenza viruses and coronaviruses utilize similar and contrasting approaches to control interferon-stimulated gene responses. MBio 2014, 5, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Walsh, K.B.; Teijaro, J.R.; Rosen, H.; Oldstone, M.B.A. Quelling the storm: Utilization of sphingosine-1-phosphate receptor signaling to ameliorate influenza virus-induced cytokine storm. Immunol. Res. 2011, 51, 15–25. [Google Scholar] [CrossRef] [PubMed]
- Snelgrove, R.J.; Godlee, A.; Hussell, T. Airway immune homeostasis and implications for influenza-induced inflammation. Trends Immunol. 2011, 32, 328–334. [Google Scholar] [CrossRef] [PubMed]
- De Jong, M.D.; Simmons, C.P.; Thanh, T.T.; Hien, V.M.; Smith, G.J.D.; Chau, T.N.B.; Hoang, D.M.; Chau, N.V.V.; Khanh, T.H.; Dong, V.C.; et al. Fatal outcome of human influenza A (H5N1) is associated with high viral load and hypercytokinemia. Nat. Med. 2006, 12, 1203–1207. [Google Scholar] [CrossRef] [PubMed]
- Tisoncik, J.R.; Korth, M.J.; Simmons, C.P.; Farrar, J.; Martin, T.R.; Katze, M.G. Into the eye of the cytokine storm. Microbiol. Mol. Biol. Rev. 2012, 76, 16–32. [Google Scholar] [CrossRef] [PubMed]
- Falagas, M.E.; Vouloumanou, E.K.; Baskouta, E.; Rafailidis, P.I.; Polyzos, K.; Rello, J. Treatment options for 2009 H1N1 influenza: Evaluation of the published evidence. Int. J. Antimicrob. Agents 2010, 35, 421–430. [Google Scholar] [CrossRef] [PubMed]
- Carter, M.J. A rationale for using steroids in the treatment of severe cases of H5N1 avian influenza. J. Med. Microbiol. 2007, 56, 875–883. [Google Scholar] [CrossRef] [PubMed]
- Kudo, K.; Takasaki, J.; Manabe, T.; Uryu, H.; Yamada, R.; Kuroda, E.; Kobayashi, N.; Matsushita, T. Systemic corticosteroids and early administration of antiviral agents for pneumonia with acute wheezing due to influenza A(H1N1)pdm09 in Japan. PLoS ONE 2012, 7, e32280. [Google Scholar] [CrossRef] [PubMed]
- Kil, H.-R.; Lee, J.-H.; Lee, K.-Y.; Rhim, J.-W.; Youn, Y.-S.; Kang, J.-H. Early corticosteroid treatment for severe pneumonia caused by 2009 H1N1 influenza virus. Crit. Care 2011, 15, 413. [Google Scholar] [CrossRef] [PubMed]
- Brun-Buisson, C.; Richard, J.-C.M.; Mercat, A.; Thiébaut, A.C.M.; Brochard, L. Early corticosteroids in severe influenza A/H1N1 pneumonia and acute respiratory distress syndrome. Am. J. Respir. Crit. Care Med. 2011, 183, 1200–1206. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-H.; Hong, S.-B.; Yun, S.-C.; Choi, W.-I.; Ahn, J.-J.; Lee, Y.J.; Lee, H.-B.; Lim, C.-M.; Koh, Y. Corticosteroid treatment in critically ill patients with pandemic influenza A / H1N1 2009 infection analytic strategy using propensity scores. Am. J. Respir. Crit. Care Med. 2011, 183, 1207–1214. [Google Scholar] [CrossRef] [PubMed]
- Salomon, R.; Hoffmann, E.; Webster, R.G. Inhibition of the cytokine response does not protect against lethal H5N1 influenza infection. Proc. Natl. Acad. Sci. USA 2007, 104, 12479–12481. [Google Scholar] [CrossRef] [PubMed]
- Shinya, K.; Ito, M.; Makino, A.; Tanaka, M.; Miyake, K.; Eisfeld, A.J.; Kawaoka, Y. The TLR4-TRIF pathway protects against H5N1 influenza virus infection. J. Virol. 2012, 86, 19–24. [Google Scholar] [CrossRef] [PubMed]
- Shinya, K.; Okamura, T.; Sueta, S.; Kasai, N.; Tanaka, M.; Ginting, T.E.; Makino, A.; Eisfeld, A.J.; Kawaoka, Y. Toll-like receptor pre-stimulation protects mice against lethal infection with highly pathogenic influenza viruses. Virol. J. 2011, 8, 97. [Google Scholar] [CrossRef] [PubMed]
- Cluff, C.W.; Baldridge, J.R.; Stöver, A.G.; Evans, T.; Johnson, D.A.; Lacy, M.J.; Valerie, G.; Yorgensen, V.M.; Johnson, C.L.; Mark, T.; et al. Synthetic toll-like receptor 4 agonists stimulate innate resistance to infectious challenge. Infect. Immun. 2005, 73, 3044–3052. [Google Scholar] [CrossRef] [PubMed]
- Isaacs, A.; Lindenmann, J. Virus interference. I. The interferon. Proc. R. Soc. Lond. B. Biol. Sci. 1957, 147, 258–267. [Google Scholar] [CrossRef] [PubMed]
- Trinchieri, G. Type I interferon: Friend or foe? J. Exp. Med. 2010, 207, 2053–2063. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, A.; Nakamura, S.; Seki, M.; Fukudome, K.; Iwanaga, N.; Imamura, Y.; Miyazaki, T.; Izumikawa, K.; Kakeya, H.; Yanagihara, K.; et al. Toll-like receptor 4 agonistic antibody promotes innate immunity against severe pneumonia induced by coinfection with influenza virus and streptococcus pneumoniae. Clin. Vaccine Immunol. 2013, 20, 977–985. [Google Scholar] [CrossRef] [PubMed]
- Wong, J.P.; Christopher, M.E.; Viswanathan, S.; Dai, X.; Salazar, A.M.; Sun, L.Q.; Wang, M. Antiviral role of toll-like receptor-3 agonists against seasonal and avian influenza viruses. Curr. Pharm. Des. 2009, 15, 1269–1274. [Google Scholar] [CrossRef] [PubMed]
- Nagai, T.; Makino, S.; Ikegami, S.; Itoh, H.; Yamada, H. Effects of oral administration of yogurt fermented with Lactobacillus delbrueckii ssp. bulgaricus OLL1073R-1 and its exopolysaccharides against influenza virus infection in mice. Int. Immunopharmacol. 2011, 11, 2246–2250. [Google Scholar] [CrossRef] [PubMed]
- Maeda, N.; Nakamura, R.; Hirose, Y.; Murosaki, S.; Yamamoto, Y.; Kase, T.; Yoshikai, Y. Oral administration of heat-killed Lactobacillus plantarum L-137 enhances protection against influenza virus infection by stimulation of type I interferon production in mice. Int. Immunopharmacol. 2009, 9, 1122–1125. [Google Scholar] [CrossRef] [PubMed]
- Cillóniz, C.; Shinya, K.; Peng, X.; Korth, M.J.; Proll, S.C.; Aicher, L.D.; Carter, V.S.; Chang, J.H.; Kobasa, D.; Feldmann, F.; et al. Lethal influenza virus infection in macaques is associated with early dysregulation of inflammatory related genes. PLoS Pathog. 2009, 5, e1000604. [Google Scholar] [CrossRef] [PubMed]
- Kobasa, D.; Jones, S.M.; Shinya, K.; Kash, J.C.; Copps, J.; Ebihara, H.; Hatta, Y.; Kim, J.H.; Halfmann, P.; Hatta, M.; et al. Aberrant innate immune response in lethal infection of macaques with the 1918 influenza virus. Nature 2007, 445, 319–323. [Google Scholar] [CrossRef] [PubMed]
- Pawelek, K.A.; Huynh, G.T.; Quinlivan, M.; Cullinane, A.; Rong, L.; Perelson, A.S. Modeling within-host dynamics of influenza virus infection including immune responses. PLoS Comput. Biol. 2012, 8, e1002588. [Google Scholar] [CrossRef] [PubMed]
- Saenz, R.A.; Quinlivan, M.; Elton, D.; Macrae, S.; Blunden, A.S.; Mumford, J.A.; Daly, J.M.; Digard, P.; Cullinane, A.; Grenfell, B.T.; et al. Dynamics of influenza virus infection and pathology. J. Virol. 2010, 84, 3974–3983. [Google Scholar] [CrossRef] [PubMed]
- Hancioglu, B.; Swigon, D.; Clermont, G. A dynamical model of human immune response to influenza A virus infection. J. Theor. Biol. 2007, 246, 70–86. [Google Scholar] [CrossRef] [PubMed]
- Baccam, P.; Beauchemin, C.; Macken, C.A.; Hayden, F.G.; Perelson, A.S. Kinetics of influenza A virus infection in humans. J. Virol. 2006, 80, 7590–7599. [Google Scholar] [CrossRef] [PubMed]
- Handel, A.; Longini, I.M.; Antia, R. Towards a quantitative understanding of the within-host dynamics of influenza A infections. J. R. Soc. Interface 2010, 7, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Bocharov, G.A.; Romanyukha, A.A. Numerical treatment of the parameter identification problem for delay-differential systems arising in immune response modelling. Appl. Numer. Math. 1994, 15, 307–326. [Google Scholar] [CrossRef]
- Price, I.; Mochan-Keef, E.D.; Swigon, D.; Ermentrout, G.B.; Lukens, S.; Toapanta, F.R.; Ross, T.M.; Clermont, G. The inflammatory response to influenza A virus (H1N1): An experimental and mathematical study. J. Theor. Biol. 2015, 374, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Bocharov, G.A.; Romanyukha, A.A. Mathematical model of antiviral immune response III. Influenza A virus infection. J. Theor. Biol. 1994, 167, 323–360. [Google Scholar] [CrossRef] [PubMed]
- Nagaraja, S.; Wallqvist, A.; Reifman, J.; Mitrophanov, A.Y. Computational approach to characterize causative factors and molecular indicators of chronic wound inflammation. J. Immunol. 2014, 192, 1824–1834. [Google Scholar] [CrossRef] [PubMed]
- Mifsud, E.J.; Tan, A.C.L.; Jackson, D.C. TLR agonists as modulators of the innate immune response and their potential as agents against infectious disease. Front. Immunol. 2014, 5, 79. [Google Scholar] [CrossRef] [PubMed]
- Tan, A.C.L.; Mifsud, E.J.; Zeng, W.; Edenborough, K.; McVernon, J.; Brown, L.E.; Jackson, D.C. Intranasal administration of the TLR2 agonist pam2Cys provides rapid protection against influenza in mice. Mol. Pharm. 2012, 9, 2710–2718. [Google Scholar] [CrossRef] [PubMed]
- Wong, J.P.; Christopher, M.E.; Viswanathan, S.; Karpoff, N.; Dai, X.; Das, D.; Sun, L.Q.; Wang, M.; Salazar, A.M. Activation of toll-like receptor signaling pathway for protection against influenza virus infection. Vaccine 2009, 27, 3481–3483. [Google Scholar] [CrossRef] [PubMed]
- Lau, Y.F.; Tang, L.H.; Ooi, E.E.; Subbarao, K. Activation of the innate immune system provides broad-spectrum protection against influenza A viruses with pandemic potential in mice. Virology 2010, 406, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Biron, C.A. Role of early cytokines, including alpha and beta interferons (IFN-alpha/beta), in innate and adaptive immune responses to viral infections. Semin. Immunol. 1998, 10, 383–390. [Google Scholar] [CrossRef] [PubMed]
- García-Sastre, A.; Durbin, R.K.; Zheng, H.; Palese, P.; Gertner, R.; Levy, D.E.; Durbin, J.E. The role of interferon in influenza virus tissue tropism. J. Virol. 1998, 72, 8550–8558. [Google Scholar] [PubMed]
- Stark, G.R.; Kerr, I.M.; Williams, B.R.; Silverman, R.H.; Schreiber, R.D. How cells respond to interferons. Annu. Rev. Biochem. 1998, 67, 227–264. [Google Scholar] [CrossRef] [PubMed]
- Van Boxel-Dezaire, A.H.H.; Rani, M.R.S.; Stark, G.R. Complex modulation of cell type-specific signaling in response to type I interferons. Immunity 2006, 25, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Dobrovolny, H.M.; Reddy, M.B.; Kamal, M.A.; Rayner, C.R.; Beauchemin, C.A.A. Assessing mathematical models of influenza infections using features of the immune response. PLoS ONE 2013, 8, e57088. [Google Scholar] [CrossRef] [PubMed]
- Fensterl, V.; Sen, G.C. Interferons and viral infections. Biofactors 2009, 35, 14–20. [Google Scholar] [CrossRef] [PubMed]
- Pestka, S.; Krause, C.D.; Walter, M.R. Interferons, interferon-like cytokines, and their receptors. Immunol. Rev. 2004, 202, 8–32. [Google Scholar] [CrossRef] [PubMed]
- Flammer, J.R.; Dobrovolna, J.; Kennedy, M.A.; Chinenov, Y.; Glass, C.K.; Ivashkiv, L.B.; Rogatsky, I. The type I interferon signaling pathway is a target for glucocorticoid inhibition. Mol. Cell. Biol. 2010, 30, 4564–4574. [Google Scholar] [CrossRef] [PubMed]
- Kandun, I.N.; Wibisono, H.; Sedyaningsih, E.R.; Yusharmen, D.P.H.; Hadisoedarsuno, W.; Purba, W.; Santoso, H.; Septiawati, C.; Tresnaningsih, E. Three Indonesian clusters of H5N1 virus infection in 2005. N. Engl. J. Med. 2006, 355, 2186–2194. [Google Scholar] [CrossRef] [PubMed]
- Yuen, K.Y.; Chan, P.K.S.; Peiris, M.; Tsang, D.N.C.; Que, T.L.; Shortridge, K.F.; Cheung, P.T.; To, W.K.; Ho, E.T.F. Clinical features and rapid viral diagnosis of huamn disease associated with avian influenza A H5N1 virus. Lancet 1998, 351, 467–471. [Google Scholar] [CrossRef]
- Bernard, G. The International Sepsis Forum’s controversies in sepsis: Corticosteroids should not be routinely used to treat septic shock. Crit. Care 2002, 6, 384. [Google Scholar] [CrossRef] [PubMed]
- Annane, D.; Bellisant, E.; Bollaert, P.E.; Briegel, J.; Keh, D.; Kupfer, Y. Corticosteroids for severe sepsis and septic shock: A systematic review and meta-analysis. BMJ 2004, 329, 480. [Google Scholar] [CrossRef] [PubMed]
- Stephen, E.L.; Sammons, M.L.; Pannier, W.L.; Baron, S.; Spertzel, R.O.; Levy, H.B. Effect of a nuclease-resistant derivative of polyriboinosinic-polyribocytidylic acid complex on yellow fever in rhesus monkeys (Macaca mulatta). J. Infect. Dis. 1977, 136, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Seo, S.U.; Lee, K.H.; Byun, Y.H.; Kweon, M.N.; Seong, B.L. Immediate and broad-spectrum protection against heterologous and heterotypic lethal challenge in mice by live influenza vaccine. Vaccine 2007, 25, 8067–8076. [Google Scholar] [CrossRef] [PubMed]
- Abe, T.; Takahashi, H.; Hamazaki, H.; Miyano-Kurosaki, N.; Matsuura, Y.; Takaku, H. Baculovirus Induces an Innate Immune Response and Confers Protection from Lethal Influenza Virus Infection in Mice. J. Immunol. 2003, 171, 1133–1139. [Google Scholar] [CrossRef] [PubMed]

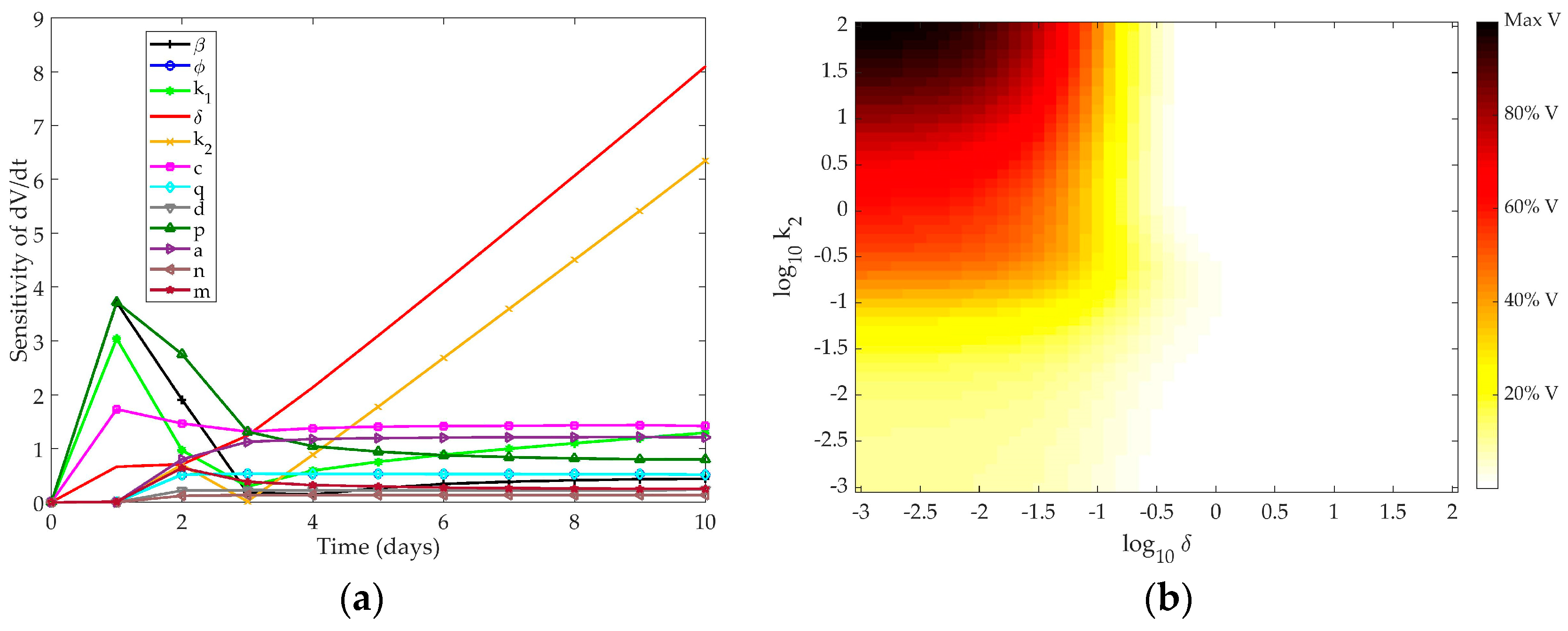
| Parameter | AUC |
|---|---|
| ρ | 36.87 |
| δ | 29.43 |
| d | 24.83 |
| φ | 14.93 |
| β | 8.68 |
| q | 6.59 |
| c | 4.37 |
| κ | 4.01 |
| p | 1.90 |
| Parameter | AUC |
|---|---|
| δ | 38.26 |
| k2 | 24.50 |
| c | 14.43 |
| p | 13.86 |
| a | 10.40 |
| φ | 4.75 |
| q | 4.75 |
| β | 3.35 |
| k1 | 3.07 |
| m | 2.93 |
| d | 2.00 |
| n | 1.18 |
| Parameter | AUC | Parameter | AUC |
|---|---|---|---|
| γV | 225.56 | γAV | 16.24 |
| γHV | 182.04 | aF | 11.65 |
| γVA | 137.81 | aR | 10.69 |
| bEM | 66.00 | kE | 8.67 |
| aI | 64.59 | aA | 8.08 |
| aM | 46.53 | bA | 7.54 |
| c | 31.24 | aE | 6.60 |
| bHF | 24.14 | bFH | 6.24 |
| bMV | 22.02 | aV1 | 4.25 |
| bF | 21.79 | aV2 | 4.00 |
| bPM | 21.75 | γVH | 2.90 |
| bMD | 19.95 | aP | 2.43 |
| λ | 19.53 | cF | 2.35 |
| bEI | 16.91 | r | 0.83 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mochan, E.; Ackerman, E.E.; Shoemaker, J.E. A Systems and Treatment Perspective of Models of Influenza Virus-Induced Host Responses. Processes 2018, 6, 138. https://doi.org/10.3390/pr6090138
Mochan E, Ackerman EE, Shoemaker JE. A Systems and Treatment Perspective of Models of Influenza Virus-Induced Host Responses. Processes. 2018; 6(9):138. https://doi.org/10.3390/pr6090138
Chicago/Turabian StyleMochan, Ericka, Emily E. Ackerman, and Jason E. Shoemaker. 2018. "A Systems and Treatment Perspective of Models of Influenza Virus-Induced Host Responses" Processes 6, no. 9: 138. https://doi.org/10.3390/pr6090138
APA StyleMochan, E., Ackerman, E. E., & Shoemaker, J. E. (2018). A Systems and Treatment Perspective of Models of Influenza Virus-Induced Host Responses. Processes, 6(9), 138. https://doi.org/10.3390/pr6090138






