An Integrated Mathematical Model of Cellular Cholesterol Biosynthesis and Lipoprotein Metabolism
Abstract
1. Introduction
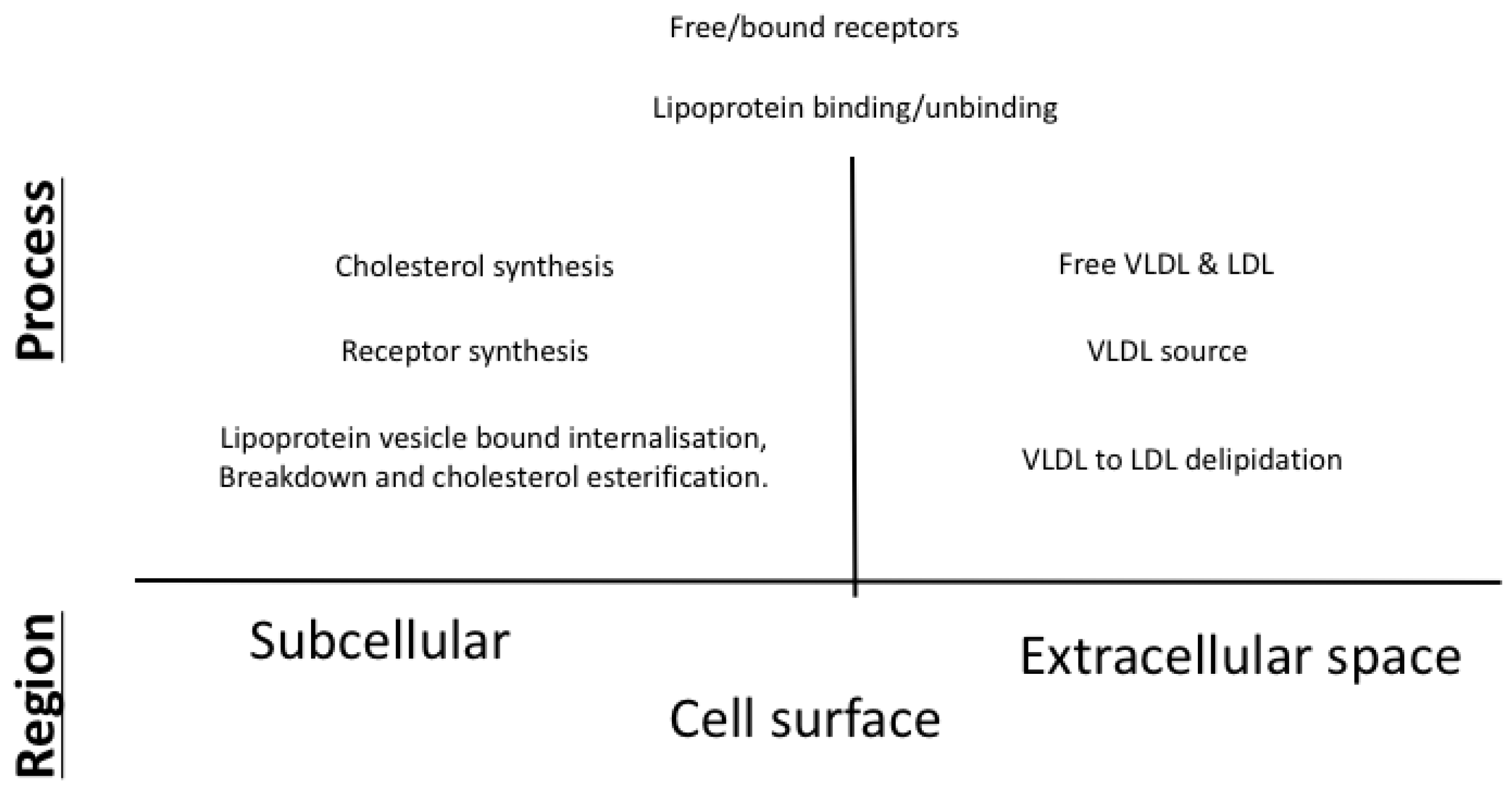
1.1. Cholesterol Biosynthesis and Lipoprotein Metabolism
2. Materials and Methods
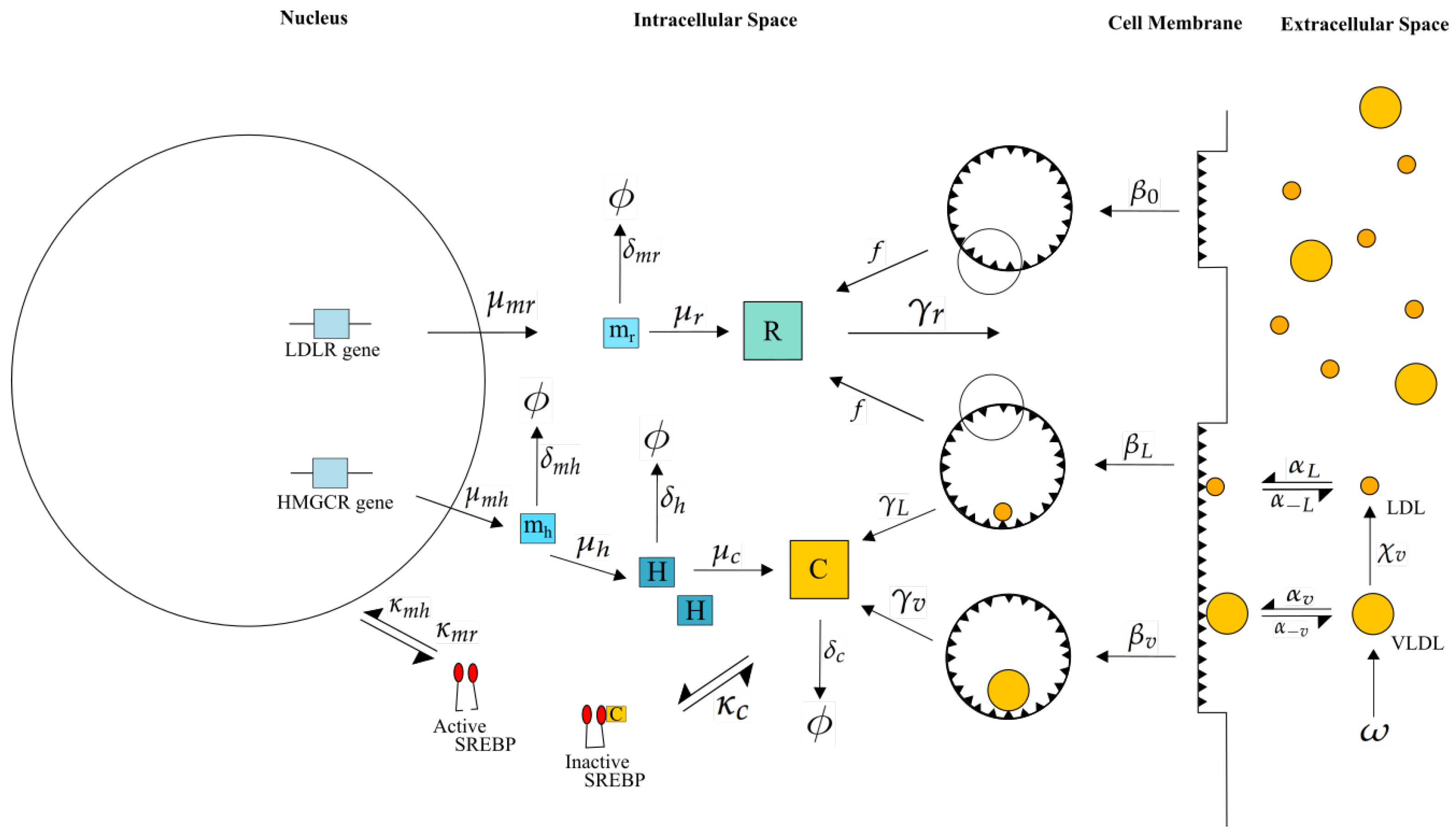
2.1. Mathematical Formulation
2.2. Model Reduction
2.3. Non-Dimensionalisation
2.4. Parameter Estimation
3. Results
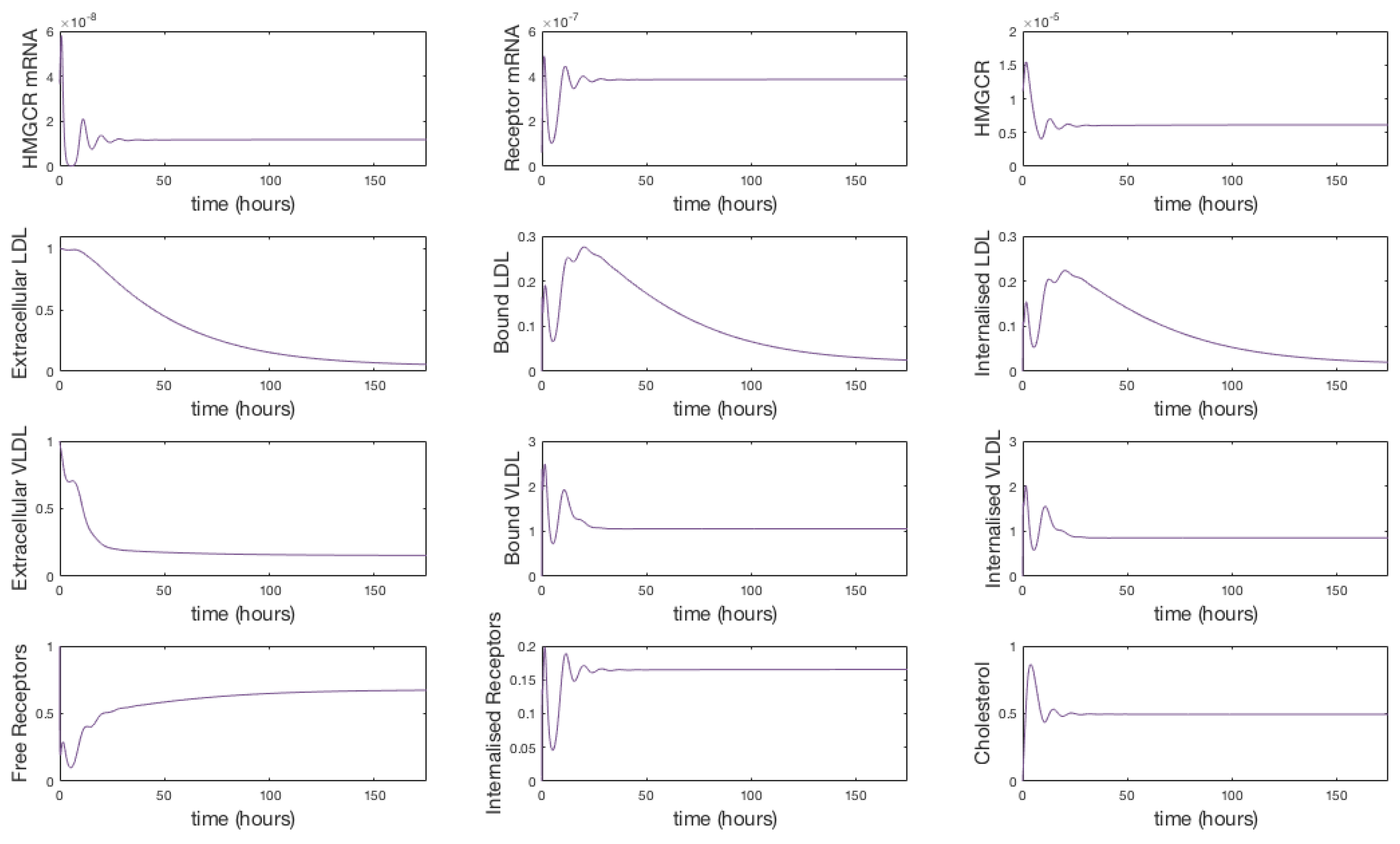
3.1. Numerical Simulations
3.2. Model Analysis
3.2.1. Steady-State Analysis
3.2.2. Sensitivity analysis
3.3. Investigating Familial Hypercholesterolaemia (FH)
3.3.1. Class I FH
3.3.2. Class III FH
3.3.3. Class IV FH
3.3.4. Class V FH
3.3.5. Individual Class FH Summary
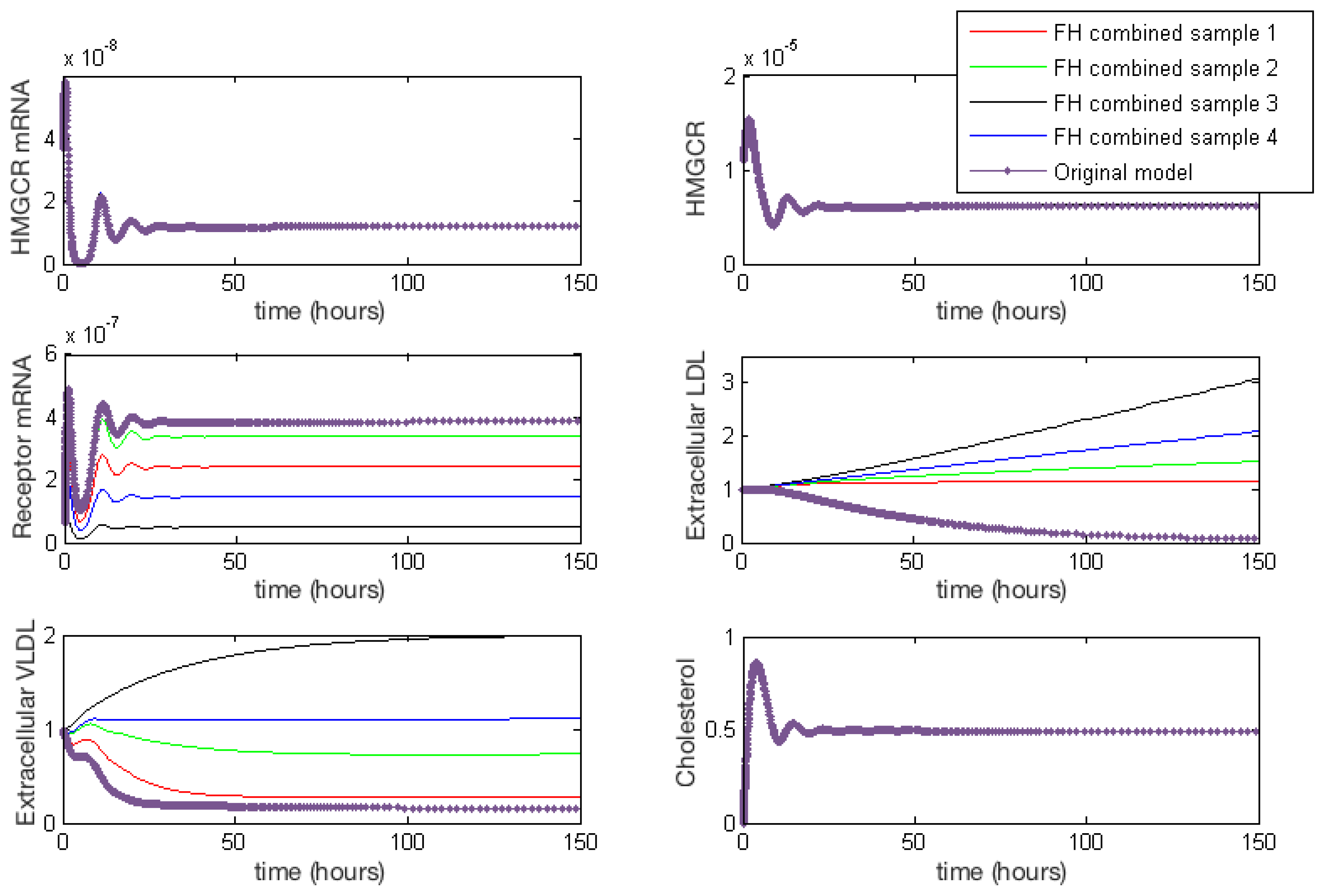
3.3.6. Combined FH
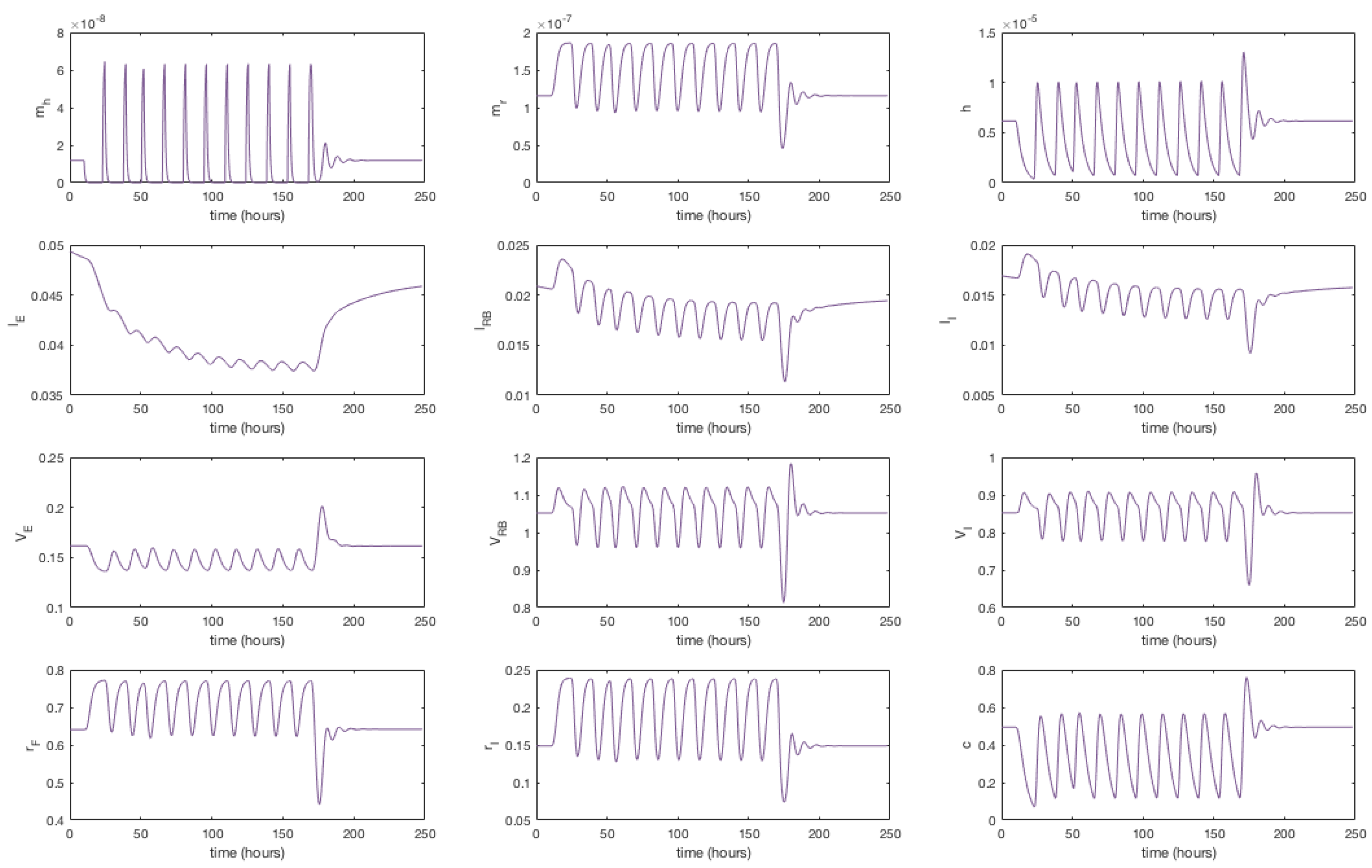
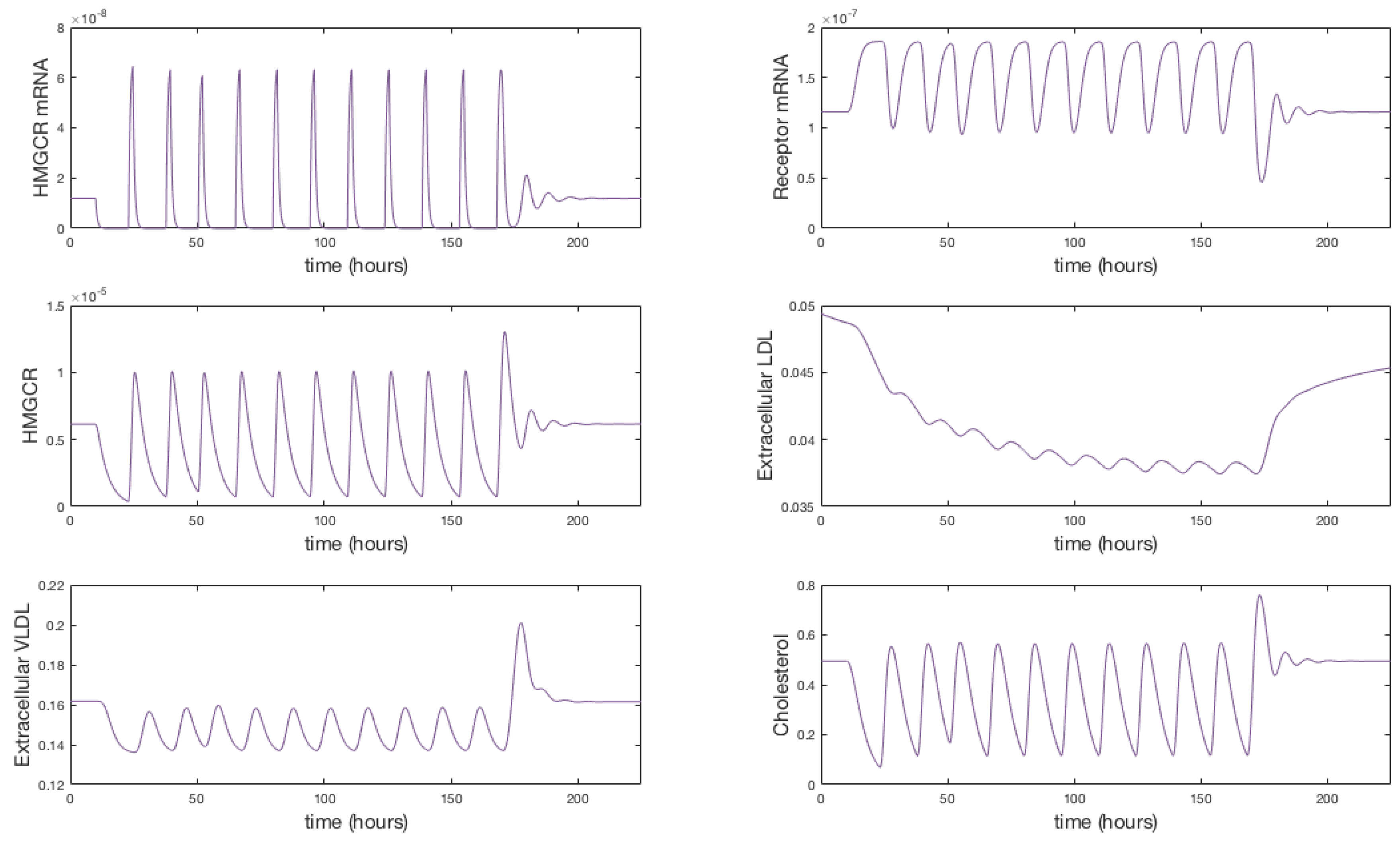
3.4. Modelling Statin Therapy
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Model Reduction
Appendix B. Parameter Estimation
Appendix C. Sensitivity Analysis
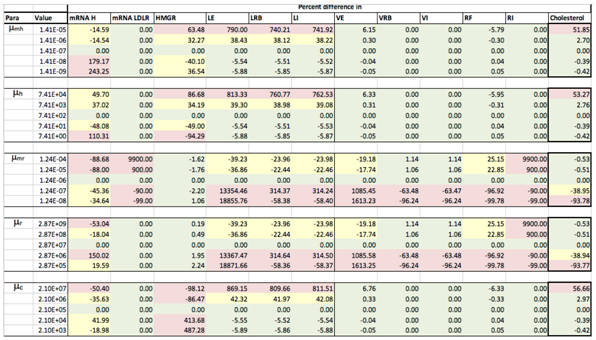
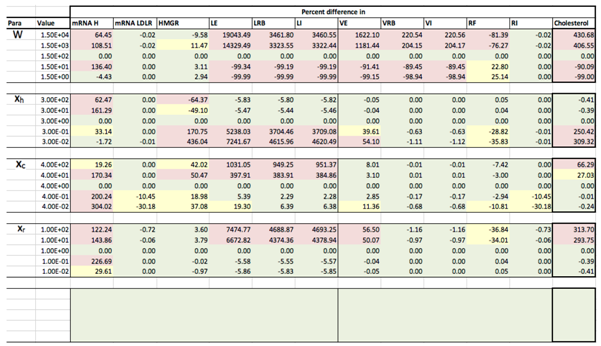
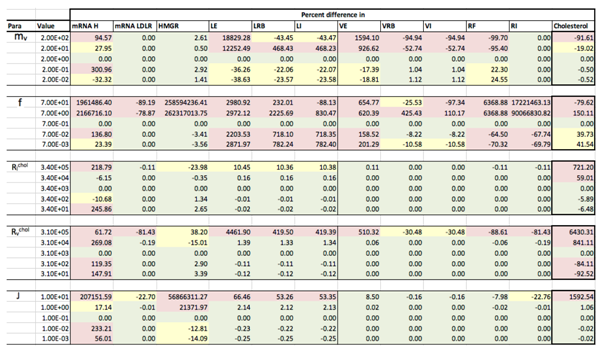
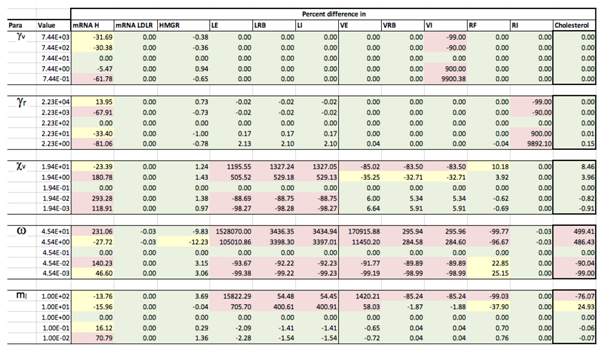
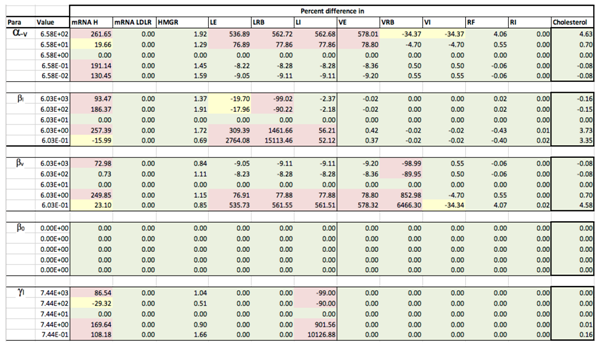
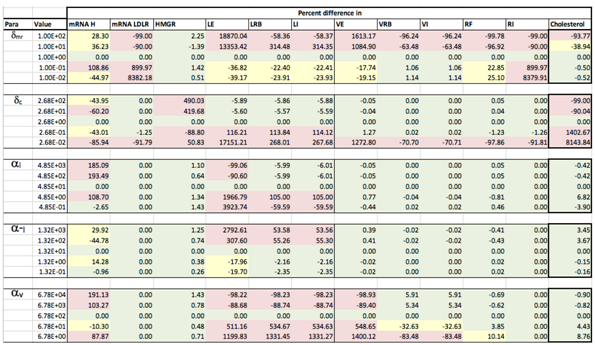
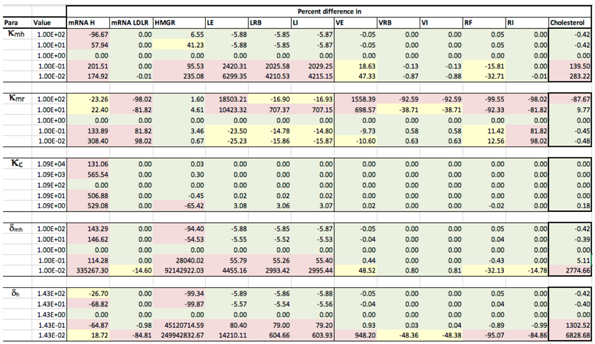
Appendix D. Familial Hypercholesterolaemia Analysis
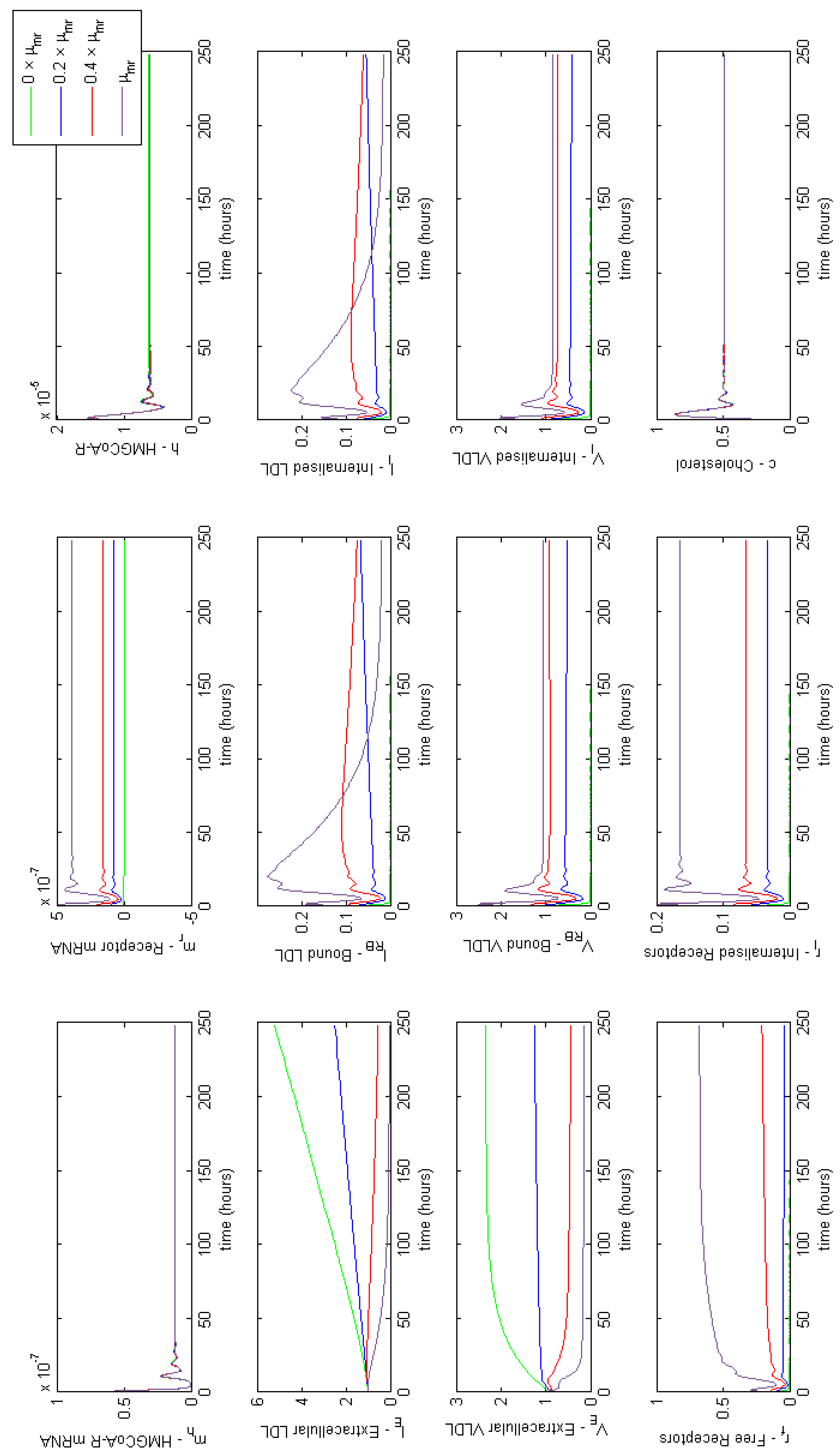
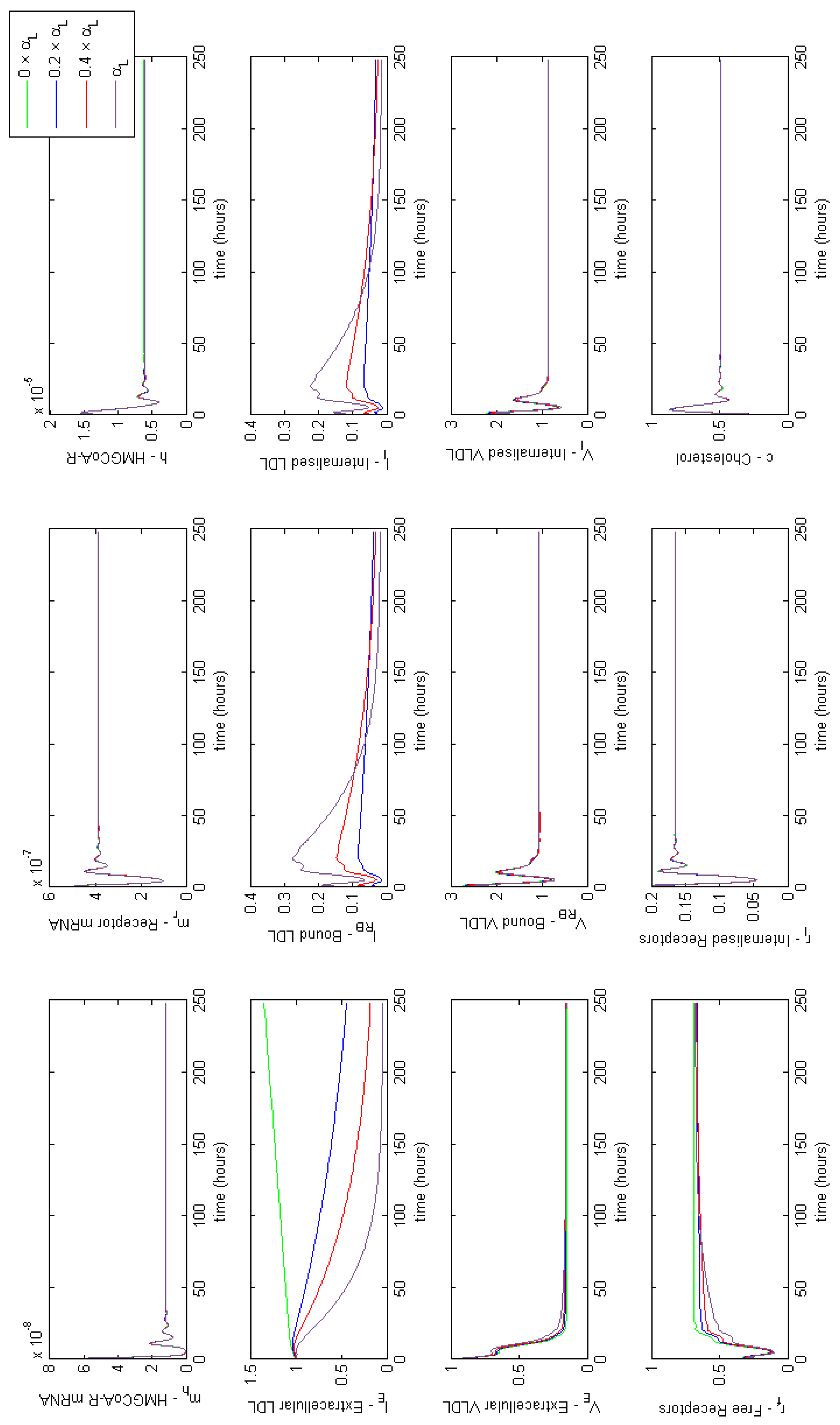
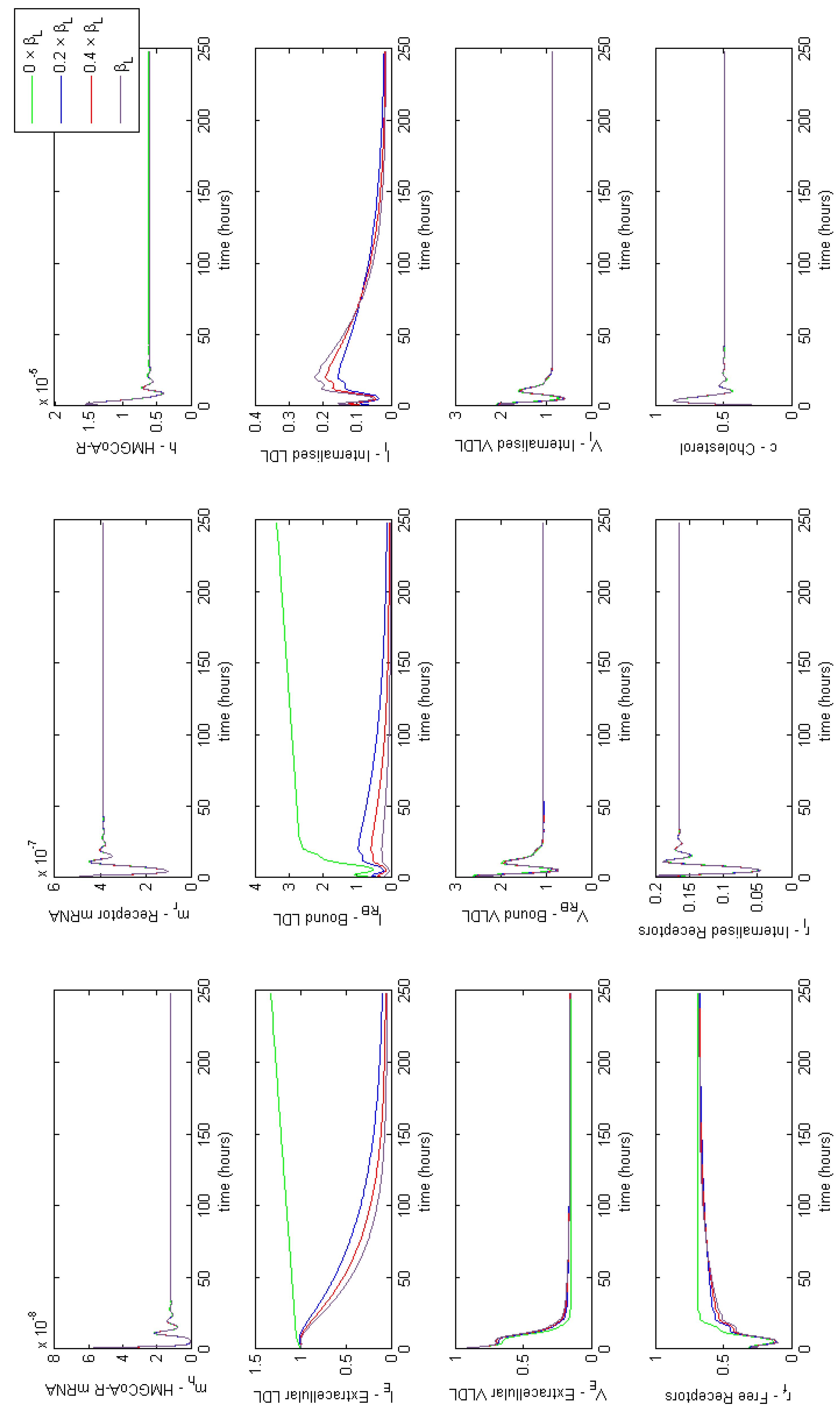
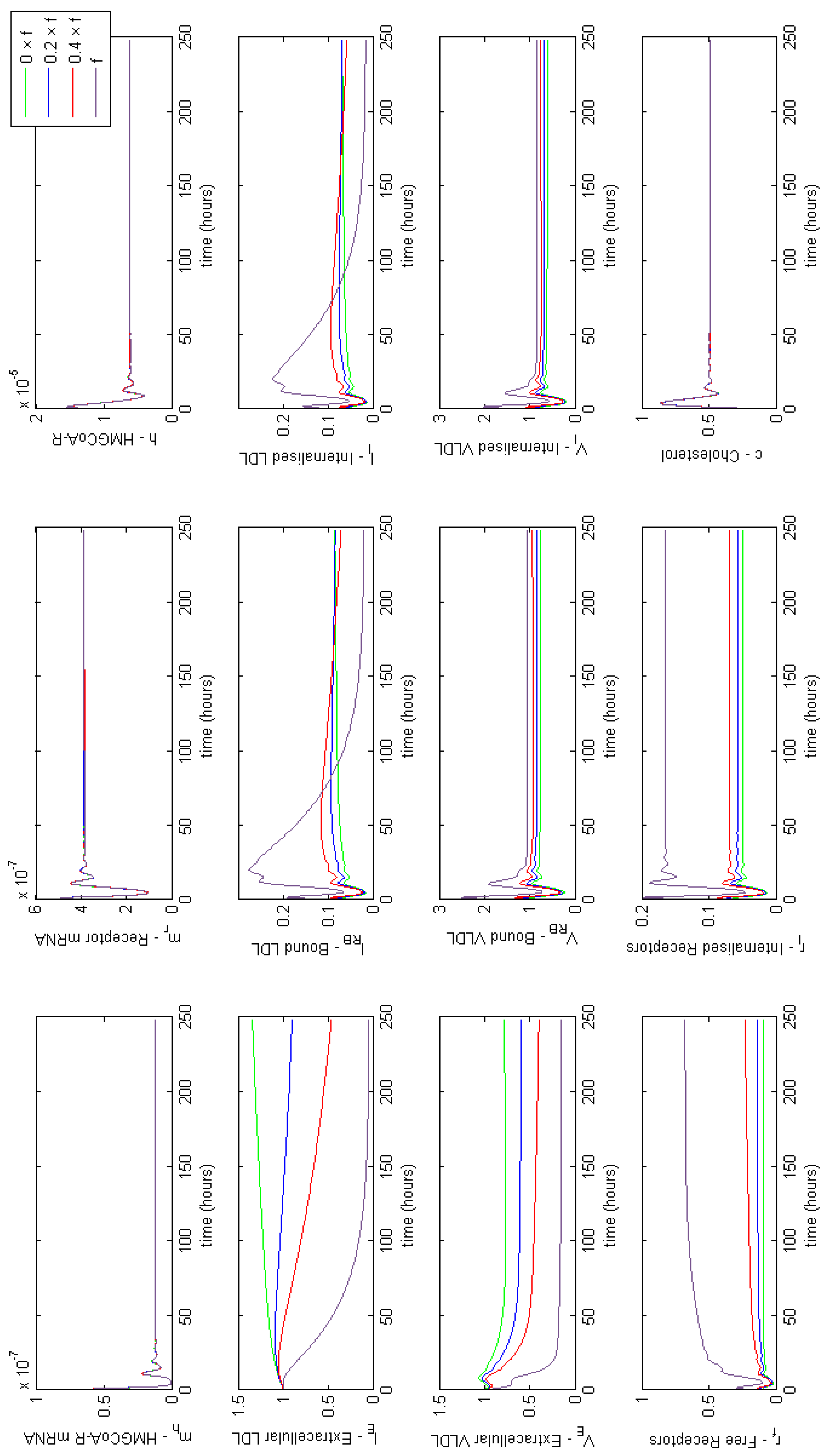
Appendix E. Full Model Results for Combined Cases of Familial Hypercholesterolaemia
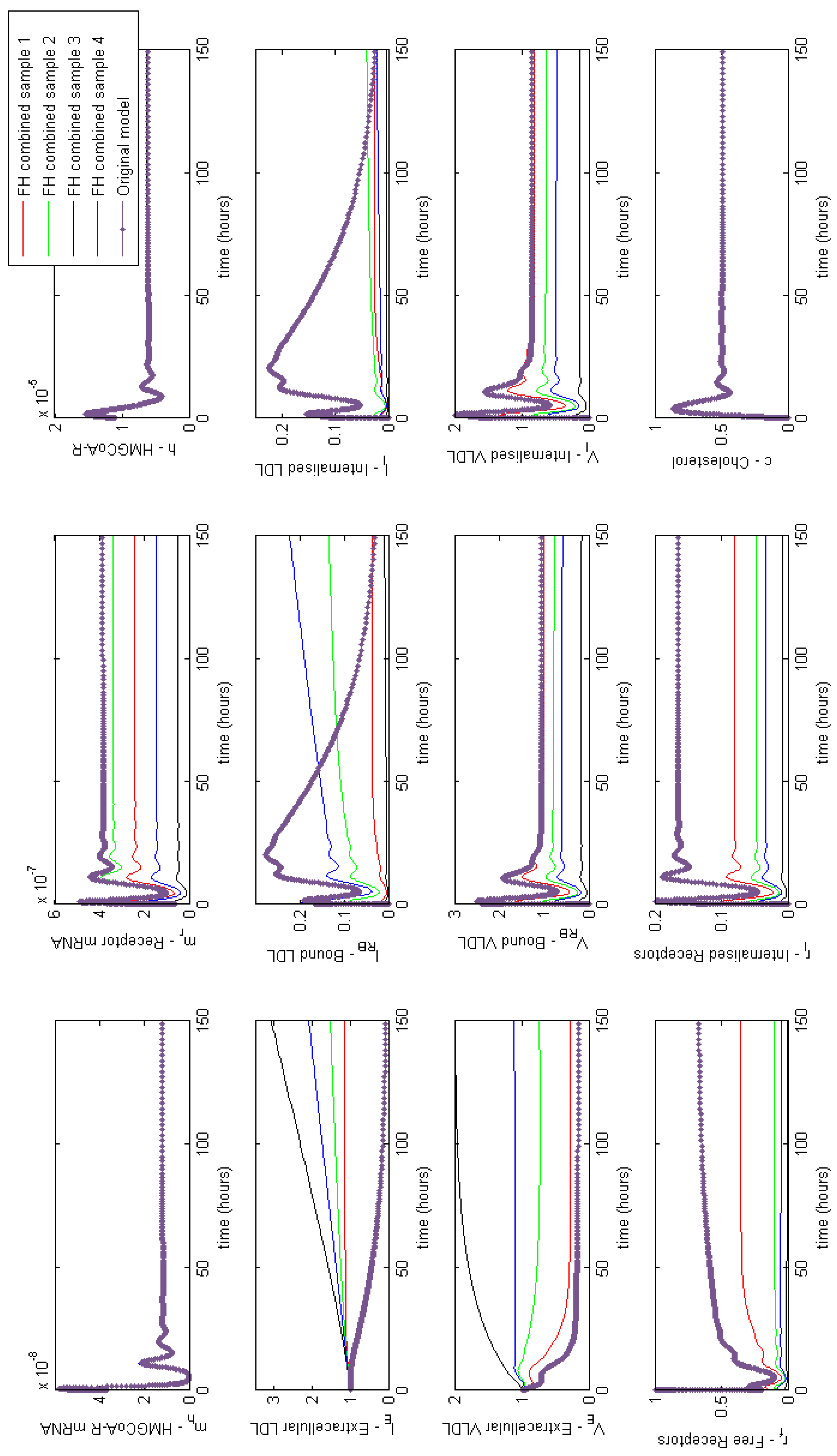
Appendix F. Full Model Results for Statin Application
References
- O’Brien, J.; Sampson, E. Lipid composition of the normal human brain: Gray matter, white matter, and myelin. J. Lipid Res. 1965, 6, 537–544. [Google Scholar] [PubMed]
- Jousilahti, P.; Vartiainen, E.; Tuomilehto, J.; Puska, P. Sex, age, cardiovascular risk factors, and coronary heart disease A prospective follow-up study of 14,786 middle-aged men and women in Finland. Circulation 1999, 99, 1165–1172. [Google Scholar] [CrossRef] [PubMed]
- Turley, S.; Dietschy, J. The intestinal absorption of biliary and dietary cholesterol as a drug target for lowering the plasma cholesterol level. Prev. Cardiol. 2003, 6, 29–64. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, J.; Brown, M.; Anderson, R.; Russell, D.; Schneider, W. Receptor-mediated endocytosis: Concepts emerging from the LDL receptor system. Annu. Rev. Cell Biol. 1985, 1, 1–39. [Google Scholar] [CrossRef] [PubMed]
- Grundy, S. Inflammation, metabolic syndrome, and diet responsiveness. Circulation 2003, 108, 126–128. [Google Scholar] [CrossRef] [PubMed]
- Gowdy, K.; Fessler, M. Emerging roles for cholesterol and lipoproteins in lung disease. Pulm. Pharmacol. Ther. 2013, 26, 430–437. [Google Scholar] [CrossRef] [PubMed]
- Bermudes, A.; de Carvalho, W.; Dietist, P.; Muramoto, G.; Maranhão, R.; Delgado, A. Changes in lipid metabolism in pediatric patients with severe sepsis and septic shock. Nutrition 2018, 47, 104–109. [Google Scholar] [CrossRef] [PubMed]
- Lagrost, G.; Grosjean, S.; Masson, D.; Deckert, V.; Gautier, T.; Debomy, F.; Vinault, S.; Jeannin, A.; Labbé, J.; Bonithon-Kopp, C. Low preoperative cholesterol level is a risk factor of sepsis and poor clinical outcome in patients undergoing cardiac surgery with cardiopulmonary bypass. Crit. Care Med. 2014, 42, 1065–1073. [Google Scholar] [CrossRef] [PubMed]
- Paalvast, Y.; Kuivenhoven, J.; Groen, A. Evaluating computational models of cholesterol metabolism. Biochim. Biophys. Acta 2015, 1851, 1360–1376. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, B.; Sweby, P.; Minihane, A.M.; Jackson, K.; Tindall, M. A mathematical model of the sterol regulatory element binding protein 2 cholesterol biosynthesis pathway. J. Theor. Biol. 2014, 349, 150–162. [Google Scholar] [CrossRef] [PubMed]
- Pool, F.; Currie, R.; Sweby, P.; Salazar, D.; Tindall, M. A mathematical model of the mevalonate cholesterol biosynthesis pathway. J. Theor. Biol. 2018, 443, 157–176. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, B. Mathematical Modelling of Low Density Lipoprotein Metabolism. Intracellular Cholesterol Regulation. Ph.D. Thesis, University of Reading, Reading, UK, 2011. [Google Scholar]
- Wattis, J.; O’Malley, B.; Blackburn, H.; Pickersgill, L.; Panovska, J.; Byrne, H.; Jackson, K. Mathematical model for low density lipoprotein (LDL) endocytosis by hepatocytes. Bull. Math. Biol. 2008, 70, 2303–2333. [Google Scholar] [CrossRef] [PubMed]
- Cromwell, W.; Otvos, J.; Keyes, M.; Pencina, M.; Sullivan, L.; Vasan, R.; Wilson, P.; D’Agostino, R. LDL particle number and risk of future cardiovascular disease in the Framingham Offspring Study implications for LDL management. J. Clin. Lipidol. 2007, 1, 583–592. [Google Scholar] [CrossRef] [PubMed]
- Tindall, M.; Wattis, J.; O’Malley, B.; Pickersgill, L.; Jackson, K. A continuum receptor model of hepatic lipoprotein metabolism. J. Theor. Biol. 2009, 257, 371–384. [Google Scholar] [CrossRef] [PubMed]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. The Cell Cycle. In Molecular Biology of the Cell, 5th ed.; Garland Science: New York, NY, USA, 2008; pp. 1053–1114. [Google Scholar]
- Jackson, K.; Maitin, V.; Leake, D.; Yaqoob, P.; Williams, C. Saturated fat-induced changes in Sf 60–400 particle composition reduces uptake of LDL by HepG2 cells. J. Lipid Res. 2006, 47, 393–403. [Google Scholar] [CrossRef] [PubMed]
- Lange, Y.; Ye, J.; Rigney, M.; Steck, T. Regulation of endoplasmic reticulum cholesterol by plasma membrane cholesterol. J. Lipid Res. 1999, 40, 2264–2270. [Google Scholar] [PubMed]
- Darzacq, X.; Shav-Tal, Y.; de Turris, V.; Brody, Y.; Shenoy, S.; Phair, R.; Singer, R. In vivo dynamics of RNA polymerase II transcription. Nat. Struct. Mol. Biol. 2007, 14, 796–806. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, J.; Brown, M. Progress in understanding the LDL receptor and HMG-CoA reductase, two membrane proteins that regulate the plasma cholesterol. J. Lipid Res. 1984, 25, 1450–1461. [Google Scholar] [PubMed]
- National Center for Biotechnology Information. Genome. 2015. Available online: http://www.ncbi.nlm.nih.gov/genome (accessed on 31 July 2015).
- Trachsel, H. Translation in Eukaryotes; CRC Press: Boca Raton, FL, USA, 1991; pp. 149–176. [Google Scholar]
- Istvan, E.; Palnitkar, M.; Buchanan, S.; Deisenhofer, J. Crystal structure of the catalytic portion of human HMG-CoA reductase: Insights into regulation of activity and catalysis. EMBO J. 2000, 19, 819–830. [Google Scholar] [CrossRef] [PubMed]
- Segal, I. Enzyme Kinetics Behaviour and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems; A Wiley-Interscience Publication; Wiley: New York, NY, USA, 1975; pp. 60–100. [Google Scholar]
- Tanaka, R.; Edwards, P.; Lan, S.; Knöppel, E.; Fogelman, A. Purification of 3-hydroxy-3-methylglutaryl coenzyme A reductase from human liver. J. Lipid Res. 1982, 23, 523–530. [Google Scholar] [PubMed]
- Soutar, A.; Knight, B. Structure and regulation of the LDL-receptor and its gene. Br. Med. Bull. 1990, 46, 891–916. [Google Scholar] [CrossRef] [PubMed]
- Wilson, G.; Deeley, R. An episomal expression vector system for monitoring sequence-specific effects on mRNA stability in human cell lines. Plasmid 1995, 33, 198–207. [Google Scholar] [CrossRef] [PubMed]
- Vargas, N.; Brewer, B.; Rogers, T.; Wilson, G. Protein kinase C activation stabilizes LDL receptor mRNA via the JNK pathway in HepG2 cells. J. Lipid Res. 2009, 50, 386–397. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.; Dana, S.; Goldstein, J. Regulation of 3-Hydroxy-3-methylglutaryl Coenzyme A Reductase Activity in Cultured Human Fibroblasts comparison of cells from a normal subject and from a patient with homozygous familial hypercholesterolemia. J. Biol. Chem. 1974, 249, 789–796. [Google Scholar] [PubMed]
- Harwood, J.R.H.; Pellarin, L. Kinetics of low-density lipoprotein receptor activity in Hep-G2 cells: Derivation and validation of a Briggs–Haldane-based kinetic model for evaluating receptor-mediated endocytotic processes in which receptors recycle. Biochem. J. 1997, 323, 649–659. [Google Scholar] [CrossRef] [PubMed]
- Mahley, R.; Innerarity, T. Lipoprotein receptors and cholesterol homeostasis. Biochim. Biophys. Acta-Rev. Biomembr. 1983, 737, 197–222. [Google Scholar] [CrossRef]
- Goldstein, J.; Anderson, R.; Brown, M. Coated pits, coated vesicles, and receptor-mediated endocytosis. Nature 1979, 279, 679–685. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.; Goldstein, J. Receptor-mediated endocytosis: Insights from the lipoprotein receptor system. Proc. Natl. Acad. Sci. USA 1979, 76, 3330–3337. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Goldstein, J.; Brown, M. Characterization of the low density lipoprotein receptor in membranes prepared from human fibroblasts. J. Biol. Chem. 1978, 253, 3852–3856. [Google Scholar] [PubMed]
- Shearer, K. The Regulation and Uptake of Dietary Fats. Ph.D. Thesis, University of Reading, Reading, UK, 2010. [Google Scholar]
- Dunn, K.; McGraw, T.; Maxfield, F. Iterative fractionation of recycling receptors from lysosomally destined ligands in an early sorting endosome. J. Cell Biol. 1989, 109, 3303–3314. [Google Scholar] [CrossRef] [PubMed]
- Panovska, J.; Tindall, M.; Wattis, J.; Byrne, H. Mathematical models of hepatic lipoprotein metabolism. In Proceedings of the 5th Mathematics in Medicine Study Group, Oxford, UK, 12–16 September 2005. [Google Scholar]
- Rudling, M.; Angelin, B.; Ståhle, L.; Reihnér, E.; Sahlin, S.; Olivecrona, H.; Björkhem, I.; Einarsson, C. Regulation of hepatic low-density lipoprotein receptor, 3-hydroxy-3-methylglutaryl coenzyme A reductase, and cholesterol 7α-hydroxylase mRNAs in human liver. J. Clin. Endocrinol. Metab. 2002, 87, 4307–4313. [Google Scholar] [CrossRef] [PubMed]
- Go, G.; Mani, A. Low-density lipoprotein receptor (LDLR) family orchestrates cholesterol homeostasis. Yale J. Biol. Med. 2012, 85, 19–28. [Google Scholar] [PubMed]
- Foundation, F.H. Familial Hypercholesterolaemia. 2018. Available online: https://thefhfoundation.org (accessed on 6 June 2018).
- Dammerman, M.; Breslow, J. Genetic basis of lipoprotein disorders. Circulation 1995, 91, 505–512. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, H.; Russell, D.; Brown, M.; Goldstein, J. The LDL receptor locus in familial hypercholesterolemia: Mutational analysis of a membrane protein. Annu. Rev. Genet. 1990, 24, 133–170. [Google Scholar] [CrossRef] [PubMed]
- Iman, R. Latin Hypercube Sampling. In Encyclopedia of Quantitative Risk Analysis and Assessment; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Golan, D.; Tashjian, A.; Armstrong, E. Principles of Pharmacology: The Pathophysiologic Basis of Drug Therapy; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2011. [Google Scholar]
- Balasubramaniam, S.; Szanto, A.; Roach, P. Circadian rhythm in hepatic low-density-lipoprotein (LDL)-receptor expression and plasma LDL levels. Biochem. J. 1994, 298, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Lickwar, C.R.; Mueller, F.; Hanlon, S.E.; McNally, J.G.; Lieb, J.D. Genome-wide protein-DNA binding dynamics suggest a molecular clutch for transcription factor function. Nature 2012, 484, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Swartz, J. A filter microplate assay for quantitative analysis of DNA binding proteins using fluorescent DNA. Anal. Biochem. 2011, 415, 168–174. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Description | Dimensional Value | Units | Reference |
|---|---|---|---|---|
| Rate of HMGCR mRNA transcription. | [19,20] | |||
| Rate of receptor mRNA transcription. | [19,21] | |||
| Rate of HMGCR translation. | [20,22] | |||
| Rate of cholesterol production. | [23,24,25] | |||
| Rate of receptor translation. | [26] | |||
| Rate of HMGCR mRNA degradation. | [27] | |||
| Rate of receptor mRNA degradation. | [28] | |||
| Rate of HMGCR degradation. | [29] | |||
| Rate of cholesterol degradation. | This study. | |||
| SREBP-HMGCR gene binding affinity. | This study. | |||
| Cholesterol-SREBP-2 dissociation constant. | This study. | |||
| LDLR gene-SREBP-2 dissociation constant. | This study. | |||
| Rate of LDL-receptor binding. | [30] | |||
| Rate of LDL-receptor unbinding. | [30] | |||
| Rate of VLDL-receptor binding. | [15,17,31] | |||
| Rate of VLDL-receptor unbinding. | [15,17] | |||
| Rate of LDL internalisation. | [30,32,33] | |||
| Rate of VLDL internalisation. | [15] | |||
| Rate of free receptor internalisation. | 0 | [34] | ||
| Rate of LDL to cholesterol conversion. | [33] | |||
| Rate of VLDL to cholesterol conversion. | [15] | |||
| Rate of receptor recycling. | [30] | |||
| Rate of VLDL-LDL delipidation. | [35] | |||
| Receptors covered by bound LDL. | 1 | [32] | ||
| Receptors covered by bound VLDL. | 2 | [15] | ||
| P | Number of receptors per pit. | 180 | [15] | |
| f | Fraction of receptors recycled. | [36] | ||
| Average cholesterol content per LDL. | 3400 | [37] | ||
| Average cholesterol content per VLDL. | 3100 | [17] | ||
| J | Nucleus to cell ratio. | [16] | ||
| W | Cell medium to cell volume ratio. | [15] | ||
| Molec. of cholesterol to inactivate SREBP-2. | 4 | [12] | ||
| Number of binding sites for SREBP-2 on HMGCR gene. | 3 | [12] | ||
| Number of binding sites for SREBP-2 on receptor gene. | 1 | [12] | ||
| Influx of extracellular VLDL. | molec./mL | This study. | ||
| Initial HMGCR mRNA conc. | molec./mL | This study [10] | ||
| Initial LDLR mRNA conc. | molec./mL | [38] | ||
| Initial HMGCR conc. | molec./mL | This study/[10] | ||
| Initial extracellular LDL conc. | molec./mL | [15,17] | ||
| Initial extracellular VLDL conc. | molec./mL | [15,17] | ||
| Initial unbound receptor conc. | molec./mL | [15,30] |
| Parameter | Description | Definition | Non-Dimensional Value |
|---|---|---|---|
| Rate of HMGCR mRNA transcription. | |||
| Rate of receptor mRNA transcription. | |||
| Rate of HMGCR translation. | |||
| Rate of receptor translation. | |||
| Rate of cholesterol synthesis. | |||
| HMGCR DNA-SREBP-2binding affinity. | 1 | ||
| Receptor DNA-SREBP-2binding affinity. | 1 | ||
| SREBP-Cholesterol dissociation constant. | |||
| Rate of HMGCR mRNA degradation. | 1 | ||
| Rate of receptor mRNA degradation. | 1 | ||
| Rate of HMGCR degradation. | |||
| Rate of cholesterol degradation. | |||
| Rate of receptor-LDL binding. | |||
| Rate of receptor-LDL unbinding. | |||
| Rate of receptor-VLDL binding. | |||
| Rate of receptor-VLDL unbinding. | |||
| Rate of LDL internalisation. | |||
| Rate of VLDL internalisation. | |||
| Rate of empty pit internalisation. | 0 | ||
| Rate of LDL-cholesterol conversion. | |||
| Rate of VLDL-cholesterol conversion. | |||
| Rate of receptor recycling. | |||
| Rate of VLDL-LDL breakdown. | |||
| Influx of extracellular VLDL. | |||
| Ratio of initial free receptors to initial extracellular LDL. | |||
| Ratio of initial free receptors to initial extracellular VLDL. | |||
| Ratio of initial extracellular LDL to intracellular cholesterol concentration. | |||
| Ratio of initial extracellular VLDL to to intracellular cholesterol concentration. | |||
| Ratio of extracellular VLDL to LDL concentration. | |||
| Initial HMGCR mRNA concentration. | 3.65 | ||
| Initial LDLR mRNA concentration. | 6.09 | ||
| Initial HMGCR concentration. | |||
| Initial extracellular VLDL concentration | 1 | ||
| Initial free receptor concentration. | 0.999 |
| Class | Description | Parameter Affected |
|---|---|---|
| I | LDLR not synthesised. | |
| II | LDLR not transported to the golgi apparatus. | |
| III | LDL-LDLR binding ineffective. | |
| IV | Bound LDL not internalised properly. | |
| V | Receptors not recycled effectively. | f |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pool, F.; Sweby, P.K.; Tindall, M.J. An Integrated Mathematical Model of Cellular Cholesterol Biosynthesis and Lipoprotein Metabolism. Processes 2018, 6, 134. https://doi.org/10.3390/pr6080134
Pool F, Sweby PK, Tindall MJ. An Integrated Mathematical Model of Cellular Cholesterol Biosynthesis and Lipoprotein Metabolism. Processes. 2018; 6(8):134. https://doi.org/10.3390/pr6080134
Chicago/Turabian StylePool, Frances, Peter K. Sweby, and Marcus J. Tindall. 2018. "An Integrated Mathematical Model of Cellular Cholesterol Biosynthesis and Lipoprotein Metabolism" Processes 6, no. 8: 134. https://doi.org/10.3390/pr6080134
APA StylePool, F., Sweby, P. K., & Tindall, M. J. (2018). An Integrated Mathematical Model of Cellular Cholesterol Biosynthesis and Lipoprotein Metabolism. Processes, 6(8), 134. https://doi.org/10.3390/pr6080134





