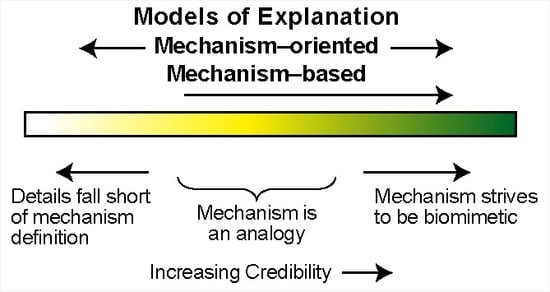
The Spectrum of Mechanism-Oriented Models and Methods for Explanations of Biological Phenomena
Abstract
1. Introduction
2. Background
Framing the Context: Mechanisms as Explanations of Phenomena
- mechanism: (1) a structure, system (e.g., biological, mechanical, chemical, electrical and so on), or process performing a function in virtue of its component parts, component operations and their organization (adapted from [4]), where the function is responsible for the phenomenon to be explained; (2) entities and activities organized in such a way that they are responsible for the phenomenon to be explained (adapted from [5,6])
- phenomenon: (1) an observable fact or event: an item of experience or reality; (2) a fact or event of scientific interest susceptible of scientific description and explanation [7]
- mechanistic: (1) determined by, for example, a mechanical, chemical, and/or electrical mechanism, or executing software; (2) like, for example, a mechanical, chemical, or electrical mechanism in one or more ways; (3) of or relating to using a mechanism as an approach to explaining a biological phenomenon; (4) mechanism-oriented
3. Methodological Complexity
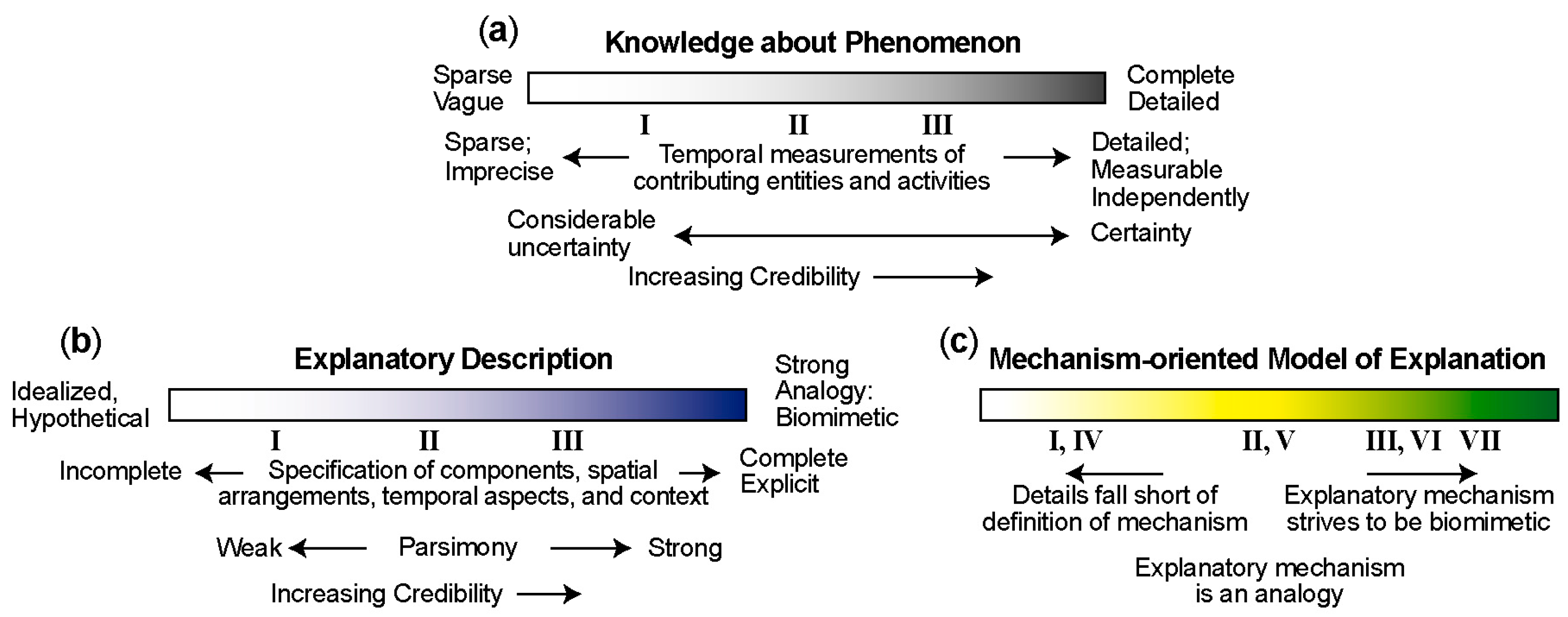
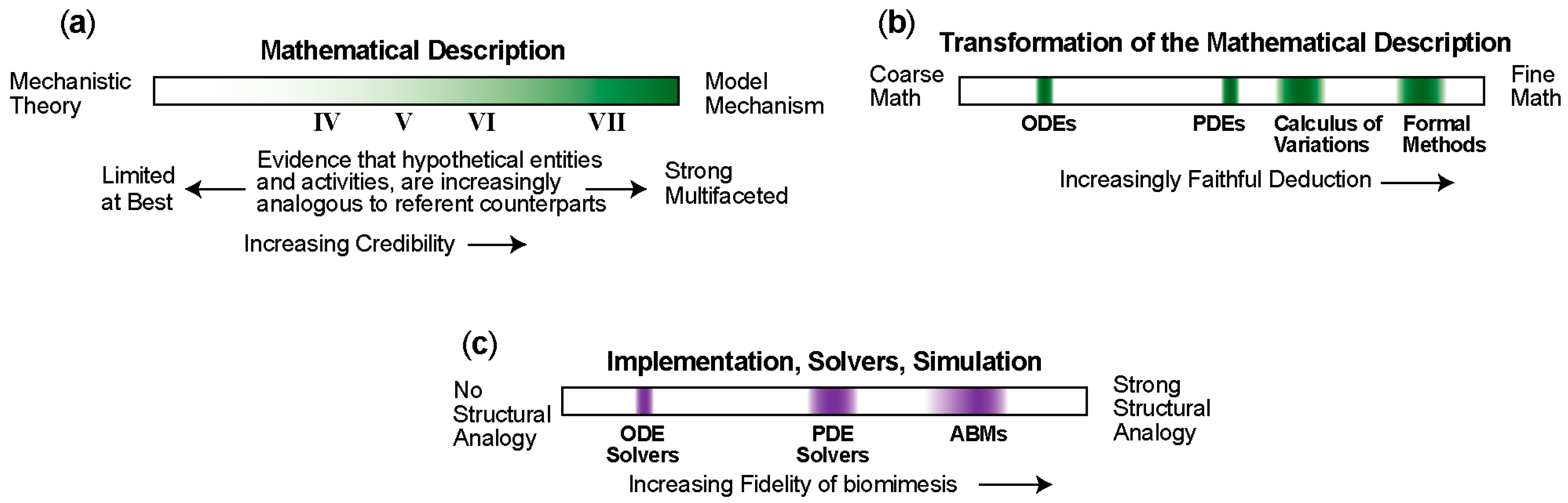
4. Mechanism-Oriented Models of Explanation
5. Three Groups of Models of Explanation
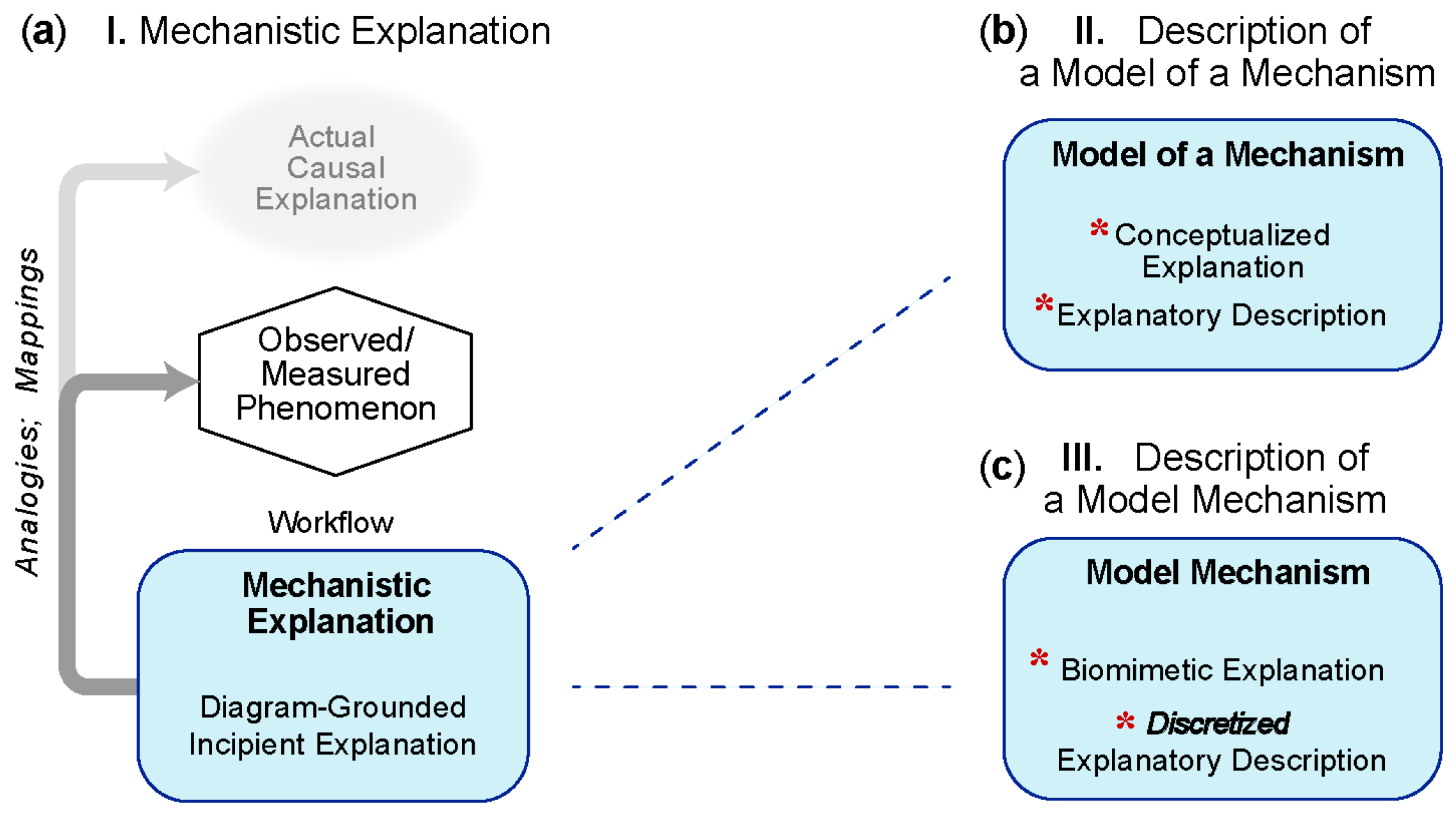
5.1. Group A: Three Types of Mechanism-Oriented Models of Explanation
5.1.1. I—Mechanistic Explanation
Example I.1: The well-known Hodgkin and Huxley model is a Mechanistic Explanation. It is an incomplete how-possibly story that provides preliminary insights into mechanisms responsible for generating and propagating action potentials along axons [13]. The authors make clear that their account is merely an explanatory model, not an actual explanation.
“…certain features of our equations were capable of a physical interpretation but the success of the equations is no evidence in favour of the mechanism of permeability change that we tentatively had in mind when formulating them.”
Example I.2: Russmann et al. [14] offer a three-step Mechanistic Explanation of how hepatocyte death may be caused by drug-induced liver injury. 1) The initial injury results in direct cell stress possibly including mitochondrial impairment. 2) Death receptor-mediated pathways are triggered leading to mitochondrial permeability transition. 3) The result is apoptotic or necrotic cell death.
Example I.3: Bassler et al. [15] sought Mechanistic Explanations for unanticipated clinical side effects and efficacy limitations of integrin αIIbβ3 antagonists. They posited a three-stage Mechanistic Explanation involving paradoxical platelet activation by αIIbβ3 antagonists: a ligand-bound conformation change; receptor clustering; and pre-stimulation of platelets.
5.1.2. II—Analogous-Mechanism Model
Example II.1: The three-element Hill muscle model for estimation of muscle force generation [16] is an idealized Analogous-Mechanism Model (Figure 2b). Such models do not have direct biological counterparts and any contextual location is hypothetical. However, measurements of the idealized mechanism during operation—if it were made real, concrete—are expected to adequately match measurements of the target phenomenon qualitatively and quantitatively.
Example II.2: Some therapeutic proteins such as trastuzumab, which is a monoclonal antibody, bind to pharmacological targets on cells. Efficacy is disrupted when the therapeutic protein binds instead to soluble targets shed from cells. Li et al. [17] describe a minimal physiologically based pharmacokinetic Analogous-mechanism Model intended to represent key features of a plausible mechanism hypothesized to be responsible for reduced efficacy. A computational description of their model in operation was used to simulate efficacy changes.
Example II.3: A demographic collapse of freshwater fish species, such as brown trout, can occur when rates of environmental change exceed the population’s capacity to adapt. Ayllón et al. [18] describe a spatially explicit, multi-attribute, eco-genetic individual-based Analogous-mechanism Model that was used to study possible trout dynamics under three scenarios: (1) climate change-induced warming, (2) warming plus flow reduction resulting from climate and land use change and (3) a baseline of no environmental change.
5.1.3. III—Model Mechanism
Example III.1: An illustrative example is the two-dimensional model mechanism developed by Norton et al. [19] to facilitate achieving two related goals: (1) improve explanatory insight into the generation of the four distinguishable morphologies of ductal carcinoma in situ of the breast. (2) Disentangle the mechanisms involved in tumor progression. Additional examples are included with those provided below under Group C.
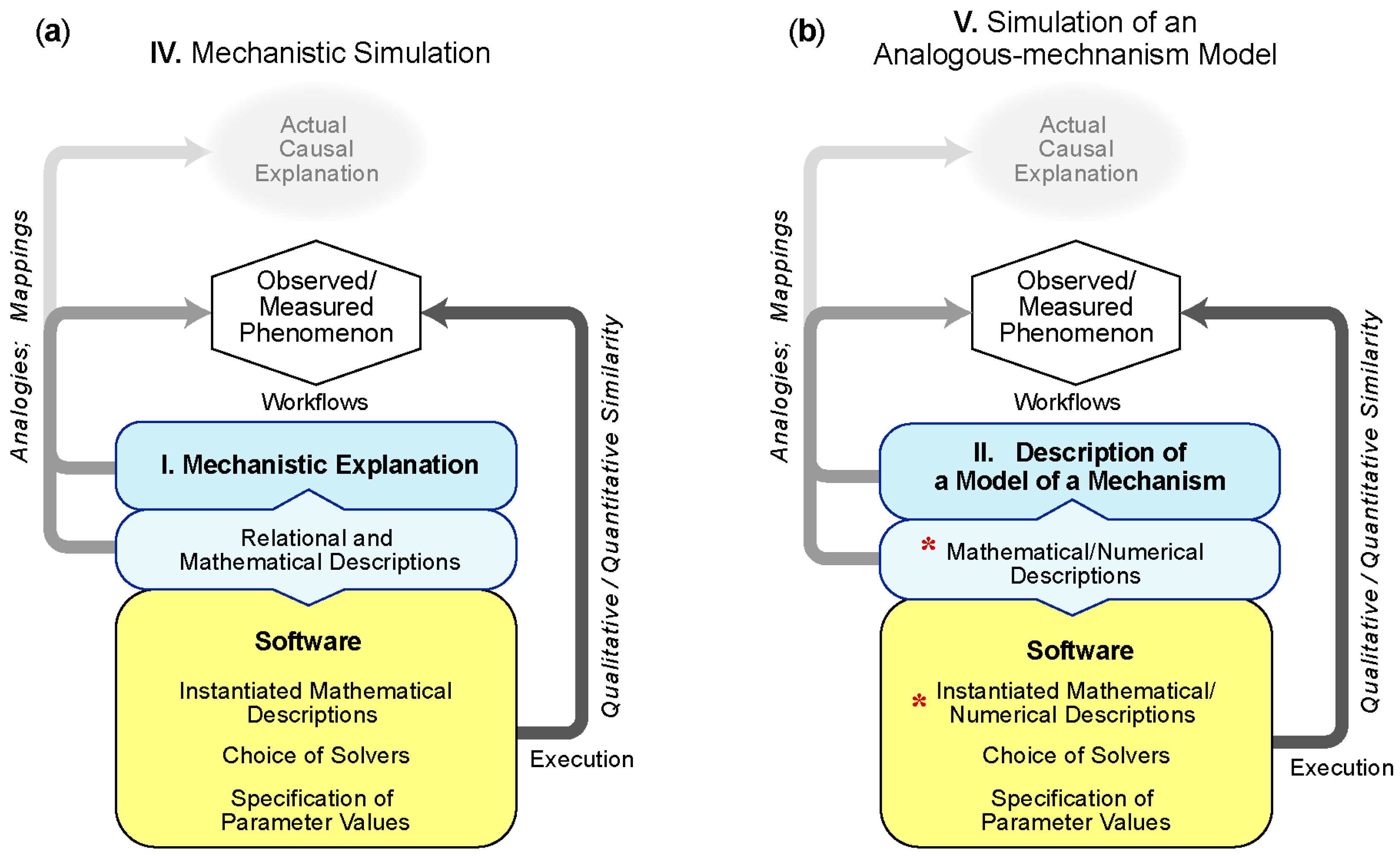
5.2. Group B: Using Simulation to Support and Enhance I and II
5.2.1. IV—Simulation of a Mechanistic Explanation
Example IV.1: The gamma rhythm is one of several characterized oscillations of activity in the brain (brain waves). The alpha rhythm of about 8 Hz is powerful enough that it can be readily detected outside of the head, something discovered in the 1920s by Hans Berger. In contrast to alpha, gamma oscillations are faster (~40 Hz) and more spatially localized, best detected by electrodes placed directly on the brain surface or into the brain parenchyma. A Simulation of a Mechanistic Explanation [22] helped explore how these gamma oscillations could be generated through inhibitory inputs, which were classically thought of as delaying or eliminating neural activity. Wang and Buzsaki demonstrated a mechanistic explanation wherein inhibitory inputs could in some cases paradoxically facilitate activity [23]. The dual roles of inhibition and facilitation allow it to entrain cell activity to a signal originating in inhibitory cells.
Example IV.2: More recent mechanistic explorations of gamma oscillations have focused on their possible role in the genesis of schizophrenia, where abnormalities in gamma oscillations have been demonstrated. Other clues to the biological explanation of schizophrenia have come from analogies with psychotomimetic drugs, such as ketamine. More recently, possible roles of particular molecular abnormalities have been suggested by a genome-wide association study. These many scales of causality were assessed by Neymotin et al. [24] using multiscale simulations of a mechanistic explanations to explore how alterations in one of the neural receptors at molecular scale might produce alterations in gamma oscillations in neuronal receptors at the molecular scale. By using both dynamical and information theoretic measures, simulation suggested how anomalies in neuronal activity might produce disturbances in function—disturbances in information flow. Thus, the model illustrates several levels of mechanistic explanation, connecting molecular anomalies with cellular anomalies, network anomalies and information transmission disturbance. Neurons were modeled with piecewise integrated difference equations, including inputs on the soma and dendrites, representing transmitted as well as background molecules and their receptors. Networks of simulated neurons were composed according to a fixed relationship between three different neuron types. Simulated current injections were used to drive the network to a baseline activity and then tuned to generate baseline theta, gamma and theta-modulated gamma oscillations in a Local Field Potential (LFP) spanning the simulated pyramidal neurons. The LFP oscillations provide the distinguishing phenomena. The simulated intervention mechanism consisted of turning on and off the NMDA (N-methyl-D-aspartate) inputs across 16 different cellular locations. Because the interventions are below the network scale, instantiated by the underlying software and mapped to the derived properties of the LFP oscillations, this model provides an excellent example of Simulation of a Mechanistic Explanation. Further, each neuron is, itself, an example of IV, in that it is a collection of sections (soma and dendrites), each of which is a system of difference equations propagating the inputs. However, the neuronal network is designed using random connectivity, since there are no data on actual cell-to-cell connectivity. Therefore, at this level, the model is only structurally evocative of the referent and thus approaches a Simulation of an Analogous-mechanism model (V). By using the information theoretic measures to relate the external inputs to spike outputs, the authors were able to demonstrate an inverse relation between gamma activity and the ability of the network to transmit information, to demonstrate how gamma oscillation might underlie information processing and how gamma oscillation anomalies could underlie the abnormal information processing in schizophrenia.
5.2.2. V—Simulation of an Analogous-mechanism Model
Example V.1: Based on epidemiological studies, high-density lipoprotein (HDL) is believed to play an important role in lowering the risk of cardiovascular disease by mediating reverse cholesterol transport. Therapies that raise HDL-cholesterol, however, have been unable to confirm this hypothesis and demand a re-examination of the proposed mechanism. It is known that lipid-poor ApoA-I plays a role in initiating reverse cholesterol transport and that the drug RG7232 increases HDL-cholesterol. However, the influence of RG7232 on lipid-poor ApoA-I and reverse cholesterol transport is unclear because their direct measurement during dosing intervals is problematic. Lu et al. [27] developed an Analogous-mechanism Model and corresponding simulation to explore this response. The model is based on two other Analogous-mechanism Models, (1) a model of lipoprotein metabolism and kinetics and (2) a model of RG7232 pharmacokinetics. They are combined into a single simulation. The linked simulation goes further by additionally representing the hypothesis that the affinity of low-density lipoprotein (LDL) particles to LDL receptors are dependent on particle size or density. This hypothesis is implemented as a modified elimination rate. The resulting model describes temporal concentrations in two-compartments as coupled ordinary differential equations that are solved using the SimBiology toolbox of MathWorks. The simulation model is “analogous” in the sense that the proposed density-dependent elimination rate and compartmentalization is an analogy to chemical kinetics and chemical engineering. Parameters are estimated using a Bayesian approach that updates the parameter values from model components using the Matlab Global Optimization toolbox of MathWorks. The implementations simulate output from the linked Analogous-mechanism Model as if it were real.
Example V.2: More than 40% of astronauts who participate in long-duration missions return with ophthalmic changes similar to idiopathic intracranial hypertension. Experts posited that a microgravity-induced cephalic fluid shift elevates intracranial pressure (ICP). Feola et al. [32] hypothesized that elevated ICP would alter the peak strain environment in the optic nerve head (ONH) to cause tissue remodeling that may be contributing to the observed ophthalmic changes. They also suspected that variations in intraocular pressure (IOP) and mean arterial pressure (MAP) would affect the biomechanical strain in the OHN tissues. To explore that explanation, they implemented a finite element Analogous-mechanism Model in which a simulated structural mechanism is strongly analogous to (functions as an analog of) the ocular structure. The geometry of the analog was based on established ocular biomechanics research and it included representing coarse grain features of tissue structures known to play a significant role in the observed ophthalmic changes: sclera, preliminary neural tissue, lamina cribrosa, central retinal vessel, dura mater and pia mater of the optic nerve sheath. Furthermore, an annular ring was incorporated around the scleral canal to account for the circumferential alignment of the scleral collagen fibers around the ONH. The open source package Gmsh (V2.8.3) was used to generate the 3D finite element geometry and mesh and open source FE solver FEBio (V2.0) was used to solve for all simulations. The authors used Latin hypercube sampling of biologically plausible regions of parameter space to simulate biomechanical responses of their analog eye structure to various combinations of simulated ICPs, as well as varying IOP, MAP, and simulated tissue mechanical property conditions. Execution results showed that chronically elevated ICP coupled with interindividual differences in simulated optic nerve head mechanical properties could influence the risk for experiencing extreme optic nerve strains. The authors inferred that individuals with both soft optic nerve or pia mater and elevated ICP would be especially at risk.
Example V.3: Rosiglitazone is a PPARγ agonist, one of several approved insulin sensitizers used to treat diabetes. Despite being on the market for over a decade, the drug continues to be studied in the lab to understand the mechanism of action of this class of molecule. In Goto-Kakizaki rats, which are a rodent model of early-developing, non-obese type-2 diabetes, Gao and Jusko [30] show that rosiglitazone decreases glucose levels. To simulate how the insulin/glucose regulation might work, they built a feedback model—glucose stimulating insulin production and insulin increasing glucose consumption. The model is analogous to other simple feedback systems, without specifying the actual, detailed, biological mechanism (e.g., intermediate steps) for glucose/insulin co-regulation. The model also incorporates two pharmacodynamic effects of rosiglitazone that impact this feedback system: enhancing insulin sensitivity (i.e., increasing the rate of insulin-dependent loss of glucose) and inhibiting glucose production. As with many models of pharmacology, the pharmacokinetic part uses an idealized one-compartment model to fit observed drug absorption and loss. The simulation is implemented using coupled ODEs, plus analytical expressions for some of the molecules. Given its importance to diabetes and the system under study, the component representing the time-dependent body weight of the rats was a key variable being simulated along with the molecular components. Guided by experimental measurements (of drug, glucose and insulin levels over time), the model was parameterized for control, low dose and high dose rosiglitazone cases. The match between simulation output and experiment measurements showed that the Analogous-mechanism Model explained the observations sufficiently well. Using that model, the authors identified drug regimen design principles: specifically, to enhance insulin sensitivity in the long term (>6 weeks), a high-dose drug is needed continuously; neither lower-dose nor shorter-term treatment succeeded in elevating the sensitivity.
Example V.4: Attempts to design and build synthetic cellular memory systems using recombinases have thus far been hindered by a lack of validated computational models of a plausible mechanism representing DNA recombination. The predictive capabilities of such models are needed to reduce the number of iterative cycles required to align experimental results with design performance requirements. Bowyer et al. [31] developed and validated the first Simulation of an Analogous-mechanism Model for how DNA recombination might occur. The models were constructed by extracting verified biological details from an extensive review of the experimental literature and made use of a model analogy with well-established reactions networks common to chemistry and chemical engineering. Three essential biological details for which a consensus was lacking were included/excluded from the simulations. The computational model consisted of a system of ODEs, each representing the concentration of a distinct biological entity and model parameters that were optimized via the use of genetic algorithms to refine parameter values but no details on how the model was implemented were provided. Model predictions were compared to experimental data to determine which set of details might represent the most plausible mechanisms and thus serve as analogs of actual structural details by which DNA recombination works. They found that including unidirectional (versus bidirectional) excision, limiting recombinase directionality factor to monomeric form in solution (versus dimer or tetramer) and integrase monomer (versus dimer) binding to DNA produced the best model match to the data. Referring to Table 1, the contextual location this Analogous-mechanism Model is implied but is not part of the implemented computational model.
5.3. Group C: Using Computation to Support and Enhance Model Mechanisms
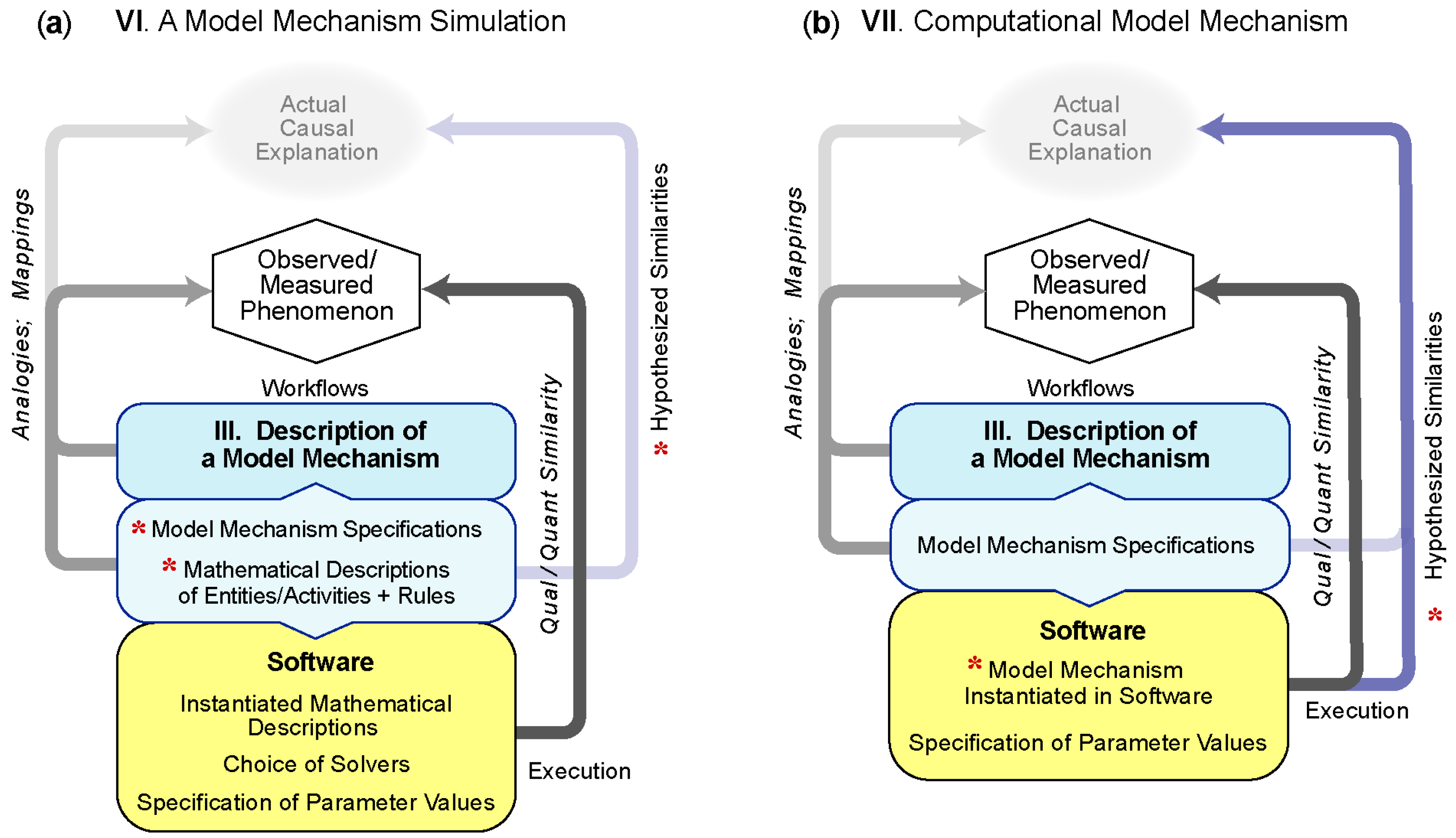
5.3.1. VI—Simulation of a Model Mechanism
Example VI.1: Simulations of Model Mechanisms are being used to help design and improve therapeutic interventions in disease [36,37,38]. For example, they are providing improved insight into possible failure modes of current treatments strategies for Tuberculosis (TB). Building on their multilevel, multi-attribute Model Mechanism of an immune response to TB, Linderman et al. [34] explored simulations of consequences of potential new pharmacological interventions on six different model entities and activities, including simulating immunomodulation by a cytokine; the consequences of oral and inhaled antibiotics; and the effect of vaccination. In line with the features of a biological mechanism (Table 1), their Model Mechanism identifies a phenomenon, the immune response of TB as indicated by granuloma formation and function. Components are represented at different spatial and temporal scales describe, starting with an agent-based analogy of cell behavior (macrophages and T cells) across a cross-section of lung tissue. Through rule-based probabilistic interactions, cell behavior is simulated in response to a bacterial environment. At the lowest levels of simulation hierarchy, ordinary differential equations were solved within each cell agent to simulate receptor/ligand binding, trafficking, and intracellular signaling. Partial differential equations were solved to simulate consequences of molecular diffusion. By linking their Simulation of a Model Mechanism for TB to ordinary differential equation-based pharmacokinetic and pharmacodynamic models, the authors simulated plausible consequences of the Model Mechanism’s behavior during exposure to antibiotics. While simulations rely on some model compartments that are Analogous-mechanism Models, the whole system is arguably a Model Mechanism. It is biomimetic and represents an interconnected biological mechanism of granuloma formation and immune response that extends from molecular to organ levels.
Example VI.2: A decade ago, several laboratories sought improved models of explanation for vascular patterning defects observed in diabetic retinopathy and tumor angiogenesis. Evidence suggested that an explanatory mechanism would involve disruption of (1) Notch-driven specialization of endothelial cells into leading tip cells and following stalk cells and (2) a feedback loop that links VEGF-A tip cell induction with delta-like 4 (Dll4)-notch-mediated lateral inhibition. Bentley et al. [39] constructed a hierarchical Simulation of a Model Mechanism to explore the phenomenon of angiogenesis by connecting Analogous-mechanism Models of these processes into a large biomimetic system. The components included endothelial cell agents and membrane agents with multiple cell agents arranged as a cylindrical capillary with each cell having membrane agents distributed at the periphery. The study explored how different simulated VEGF environments and filopodia dynamics would affect simulations of Notch-mediated selection of tip cells. A staged simulation (temporally and spatially) first relied on a rule-based evaluation of membrane processes for filopodium retraction or extension or notch response to VEGF. In following, the spatial sum of protein levels was calculated and redistributed within the endothelial cells and membrane agents. The modeling paradigm closely follows that of a Model Mechanism, where features reflect those of a biological mechanism (Table 1). An important observation of the simulations was that, by removing information that could influence simulated cell biasing, the simulated Dll4-notch lateral inhibition mechanism could generate an alternating pattern of cell fates characteristic of normal tip cell selection. The authors inferred from simulation results that abnormal patterning could be attributed to the dynamics of this particular sub-system, rather than any uncontrolled bias.
5.3.2. VII—A Computational Model Mechanism
Example VII.1: Enhanced mechanism-based explanations are needed to anticipate, prevent and reverse the liver injury caused by acetaminophen and other drugs. A characteristic acetaminophen phenomenon—the target phenomenon for this example—is that hepatic necrosis begins adjacent to central veins in hepatic lobules and progresses upstream. The prevailing (mechanism-oriented spatiotemporal) explanation (PE) is that location dependent differences in reactive metabolite formation within hepatic lobules (called zonation) are necessary and sufficient requisites to account for the phenomenon. Progress has been stymied because challenging that hypothesis in mice would require sequential intracellular measurements at different lobular locations within the same mouse, which is infeasible. Smith et al. [33] circumvent that impediment by performing experiments on virtual Mouse Analogs, where each is equipped with an in-silico liver that achieved multiple validation targets. Components and spaces at all levels of granularity are written in Java, utilizing the MASON multi-agent simulation toolkit. An accurate causal model of the PE that exhibits all Table 1 features was instantiated and parameterized so that, upon dosing with objects representing acetaminophen, metabolism and pharmacokinetic validation targets were achieved. However, the authors demonstrated that the PE failed to achieve the target phenomenon. Two parsimoniously more complex variants also failed to achieve the target phenomenon but a fourth variant met stringent tests of sufficiency. Execution of that forth Computational Model Mechanism provided a multilevel biomimetic causal explanation of key temporal features of acetaminophen hepatotoxicity in mice including the target phenomenon. The authors argue that the causal explanation provided during execution is strongly analogous to the actual causal mechanism in mice.
Example VII.2: Inflammation is not the result of one cell or molecule acting alone. It is a multicellular process that can be highly localized and yet also have diffuse actions. One of the keys to understanding tissue-level morphogenesis and spatially localized or heterogeneous processes such as inflammation is to explicitly study the spatial component—how the cells are arranged in the tissue and the influences that they have on each other. Thus, to gain insight into the pathogenesis of gastrointestinal inflammatory diseases, Cockrell et al. [41] developed a multi-level, discrete-event Model Mechanism that is used to study scenarios of how simulated cellular and molecular pathways may govern morphogenesis and inflammation in healthy and disease ileal mucosal dynamics. The system includes individual agents representing five different cell types, each with multiple independently acting instantiations at different physical locations. Cell agents have specific behaviors (proliferation, death, anoikis, etc.) and can influence each other’s decision-making process. Inside each agent, there is also a simulated signaling network. The system uses algebraic rules to simulate most of the different components, including a representation of extracellular paracrine signaling between cells (with the addition of a grid-based partial differential equation to simulate consequences of diffusion), the dynamics of the simulated intracellular signaling networks and (using the current values of key intracellular signaling components as a basis) the likelihood of cell agents exhibiting each possible behavior. By simulating cell behavior in a virtual world that is analogous to biological microenvironments, the system can generate measurable phenomena (predictions) at multiple levels. Simulations provide insight into plausible pathological processes, including crosstalk between morphogenesis and inflammation and the effects of cell death on tissue health.
Example VII.3: Changes to savanna ecosystems related to climate change and land use practices are linked to fluctuations in savanna bird community structures, functional traits, and risk of extinction. Better, more insightful models of explanation are needed to support policy changes. However, detailed species-specific data for a given ecosystem are often limited. As a method test case for overcoming such limitations, Scherer et al. [42] used an agent-oriented approach (implemented in NetLogo) that merged trait-based and individual-based simulation methods to predict how different bird functional types might change in response to concurrent alterations to savanna rangeland from a combination of climate change and land use. The entire simulated ecosystem operates during execution as a Model Mechanism. Contained within are all of the features listed in Table 1. The system includes a spatial and stochastically varying set of entities representative of the type of individual, home range, vegetation, landscape, and environment. Each entity was characterized by a set of state variables, examples of which include age and reproductive status, or grasses, shrubs, or trees. Executions advance in uniform steps that map to an interval of up to 100 years and progress by randomly selecting, calculating and updating properties that control the spatial composition and configuration of simulated habitat and animals. Simulation results provided possible explanations for why simulated extinction risks for simulated larger- bodied insectivores, omnivores and small-bodied species were impacted differently by changes in simulated shrub-grass ratio and clumping intensity of shrub patches. Such predictions could prove essential for identifying better policies for conservation management.
6. Relevant Information, Multiple Sources
7. Workflow, Provenance and Hybrid Models
8. Concluding Remarks
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Craver, C.; Tabery, J. Mechanisms in Science. In The Stanford Encyclopedia of Philosophy; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Braillard, P.A.; Malaterre, C. Explanation in Biology: An Enquiry into the Diversity of Explanatory Patterns in the Life Sciences; Braillard, P.A., Malaterre, C., Eds.; Springer: Dordrecht, The Netherland, 2015. [Google Scholar]
- Kaplan, D.M.; Craver, C.F. The explanatory force of dynamical and mathematical models in neuroscience: A mechanistic perspective. Philos. Sci. 2011, 78, 601–627. [Google Scholar] [CrossRef]
- Bechtel, W.; Abrahamsen, A. Explanation: A mechanist alternative. Stud. Hist. Philos. Sci. Part C 2005, 36, 421–441. [Google Scholar] [CrossRef]
- Craver, C.F. Explaining the Brain: Mechanisms and the Mosaic Unity of Neuroscience; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Illari, P.M.; Williamson, J. What is a mechanism? Thinking about mechanisms across the sciences. European. J. Philos. Sci. 2012, 2, 119–135. [Google Scholar] [CrossRef]
- Merriam-Webster Unabridged. Available online: http://unabridged.merriam-webster.com/ (accessed on 2 October 2016).
- Craver, C.F. When mechanistic models explain. Synthese 2006, 153, 355–376. [Google Scholar] [CrossRef]
- Darden, L. Thinking again about biological mechanisms. Philos. Sci. 2009, 75, 958–969. [Google Scholar] [CrossRef]
- Miyakawa, K.; Albee, R.; Letzig, L.G.; Lehner, A.F.; Scott, M.A.; Buchweitz, J.P.; James, L.P.; Ganey, P.E.; Roth, R.A. A Cytochrome P450–independent mechanism of acetaminophen-induced injury in cultured mouse hepatocytes. J. Pharmacol. Exp. Therap. 2015, 354, 230–237. [Google Scholar] [CrossRef] [PubMed]
- Thakore, K.N.; Mehendale, H.M. Role of hepatocellular regeneration in CCl4 autoprotection. Toxicol. Path 1991, 19, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Rudraiah, S.; Rohrer, P.R.; Gurevich, I.; Goedken, M.J.; Rasmussen, T.; Hines, R.N.; Manautou, J.E. Tolerance to acetaminophen hepatotoxicity in the mouse model of autoprotection is associated with induction of flavin-containing monooxygenase-3 (FMO3) in hepatocytes. Toxicol. Sci. 2014, 27, kfu124. [Google Scholar] [CrossRef] [PubMed]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
- Russmann, S.; Kullak-Ublick, G.A.; Grattagliano, I. Current concepts of mechanisms in drug-induced hepatotoxicity. Curr. Med. Chem. 2009, 16, 3041–3053. [Google Scholar] [CrossRef] [PubMed]
- Bassler, N.; Loeffler, C.; Mangin, P.; Yuan, Y.; Schwarz, M.; Hagemeyer, C.E.; Eisenhardt, S.U.; Ahrens, I.; Bode, C.; Jackson, S.P.; et al. A mechanistic model for paradoxical platelet activation by ligand-mimetic αIIbβ3 (GPIIb/IIIa) antagonists. Arterioscl. Thromb. Vasc. Biol. 2007, 27, E9–E15. [Google Scholar] [CrossRef] [PubMed]
- Zajac, F.E. Muscle and tendon Properties models scaling and application to biomechanics and motor. Crit. Rev. Biomed. Eng. 1989, 17, 359–411. [Google Scholar] [PubMed]
- Li, L.; Gardner, I.; Rose, R.; Jamei, M. Incorporating target shedding into a minimal PBPK–TMDD model for monoclonal antibodies. CPT Pharmacomet. Syst. Pharmacol. 2014, 3, e96. [Google Scholar] [CrossRef] [PubMed]
- Ayllón, D.; Railsback, S.F.; Vincenzi, S.; Groeneveld, J.; Almodóvar, A.; Grimm, V. InSTREAM-Gen: Modelling eco-evolutionary dynamics of trout populations under anthropogenic environmental change. Ecol. Mod. 2016, 326, 36–53. [Google Scholar] [CrossRef]
- Norton, K.A.; Wininger, M.; Bhanot, G.; Ganesan, S.; Barnard, N.; Shinbrot, T. A 2D mechanistic model of breast ductal carcinoma in situ (DCIS) morphology and progression. J. Theor. Biol. 2010, 263, 393–406. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Clegg, L.E.; Mac Gabhann, F. Molecular mechanism matters: Benefits of mechanistic computational models for drug development. Pharmacol. Res. 2015, 99, 149–154. [Google Scholar] [CrossRef] [PubMed]
- Bangs, A.; Bowling, K.; Paterson, T. Simulating Patient-Specific Outcomes. US Patent 10/961,523, 7 October 2004. [Google Scholar]
- Lytton, W.W.; Sejnowski, T.J. Simulations of cortical pyramidal neurons synchronized by inhibitory interneurons. J. Neurophysiol. 1991, 66, 1059–1079. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.J.; Buzsáki, G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J. Neurosci. 1996, 16, 6402–6413. [Google Scholar] [CrossRef] [PubMed]
- Neymotin, S.A.; Lazarewicz, M.T.; Sherif, M.; Contreras, D.; Finkel, L.H.; Lytton, W.W. Ketamine disrupts theta modulation of gamma in a computer model of hippocampus. J. Neurosci. 2011, 31, 11733–11743. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Xue, C.; Shtylla, B.; Brown, A. A stochastic multiscale model that explains the segregation of axonal microtubules and neurofilaments in neurological diseases. PLoS Comput. Biol. 2015, 11, e1004406. [Google Scholar] [CrossRef] [PubMed]
- Meier-Schellersheim, M.; Fraser, I.D.; Klauschen, F. Multiscale modeling for biologists. WIREs: Syst. Biol. Med. 2009, 1, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Cleary, Y.; Maugeais, C.; Kiu Weber, C.I.; Mazer, N.A. Analysis of “on/off” kinetics of a CETP inhibitor using a mechanistic model of lipoprotein metabolism and kinetics. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 465–473. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bassingthwaighte, J.B.; Chizeck, H.J.; Atlas, L.E. Strategies and tactics in multiscale modeling of cell-to-organ systems. Proc. IEEE 2006, 94, 819–831. [Google Scholar] [CrossRef] [PubMed]
- Ménochet, K.; Kenworthy, K.E.; Houston, J.B.; Galetin, A. Simultaneous assessment of uptake and metabolism in rat hepatocytes: A comprehensive mechanistic model. J. Pharmacol. Exp. Therap. 2012, 341, 2–15. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Jusko, W.J. Modeling disease progression and rosiglitazone intervention in type 2 diabetic Goto-Kakizaki rats. J. Pharmacol. Exp. Therap. 2012, 341, 617–625. [Google Scholar] [CrossRef] [PubMed]
- Bowyer, J.; Zhao, J.; Rosser, S.; Colloms, S.; Bates, D. Development and experimental validation of a mechanistic model of in vitro DNA recombination. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milano, Italy, 25–29 August 2015. [Google Scholar]
- Feola, A.J.; Myers, J.G.; Raykin, J.; Mulugeta, L.; Nelson, E.S.; Samuels, B.C.; Ethier, C.R. Finite element modeling of factors influencing optic nerve head deformation due to intracranial pressure. Investig. Ophthal. Vis. Sci. 2016, 57, 1901–1911. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.K.; Petersen, B.K.; Ropella, G.E.P.; Kennedy, R.C.; Kaplowitz, N.; Ookhtens, M.; Hunt, C.A. Competing Mechanistic hypotheses of acetaminophen-induced hepatotoxicity challenged by virtual experiments. PLoS Comput. Biol. 2016. [Google Scholar] [CrossRef] [PubMed]
- Linderman, J.J.; Cilfone, N.A.; Pienaar, E.; Gong, C.; Kirschner, D.E. A multi-scale approach to designing therapeutics for tuberculosis. Integr. Biol. 2015, 7, 591–609. [Google Scholar] [CrossRef] [PubMed]
- Issad, T.; Malaterre, C. Are dynamic mechanistic explanations still mechanistic? In Explanation in Biology: An Enquiry into the Diversity of Explanatory Patterns in the Life Sciences; Braillard, P.A., Malaterre, C., Eds.; Dordrecht, The Netherland, 2015; pp. 265–292. [Google Scholar]
- Schoeberl, B.; Pace, E.A.; Fitzgerald, J.B.; Harms, B.D.; Xu, L.; Nie, L.; Linggi, B.; Kalra, A.; Paragas, V.; Bukhalid, R.; et al. Therapeutically targeting ErbB3: A key node in ligand-induced activation of the ErbB receptor-PI3K axis. Sci. Signal 2009, 2, ra31. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, I.; Mac Gabhann, F. Mechanistic Models Predict Efficacy of CCR5-Deficient Stem Cell Transplants in HIV Patient Populations. CPT Pharmacomet. Syst. Pharmacol. 2016, 5, 82–90. [Google Scholar] [CrossRef] [PubMed]
- Moreno, J.D.; Zhu, Z.I.; Yang, P.-C.; Bankston, J.R.; Jeng, M.-T.; Kang, C.; Wang, L.; Bayer, J.D.; Christini, D.J.; Trayanova, N.A.; et al. A computational model to predict the effects of class I anti-arrhythmic drugs on ventricular rhythms. Sci. Transl. Med. 2011, 3, ra83. [Google Scholar] [CrossRef] [PubMed]
- Bentley, K.; Gerhardt, H.; Bates, P.A. Agent-based simulation of notch-mediated tip cell selection in angiogenic sprout initialisation. J. Theor. Biol. 2009, 250, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Hunt, C.A. Identifying the rules of engagement enabling leukocyte rolling, activation, and adhesion. PLoS Comput. Biol. 2010, 6, e1000681. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cockrell, C.; Christley, S.; An, G. Investigation of inflammation and tissue patterning in the gut using a spatially explicit general-purpose model of enteric tissue (SEGMEnT). PLOS Comput. Biol. 2014, 10, e1003507. [Google Scholar] [CrossRef] [PubMed]
- Scherer, C.; Jeltsch, F.; Grimm, V.; Blaum, N. Merging trait-based and individual-based modelling: An animal functional type approach to explore the responses of birds to climatic and land use changes in semi-arid African savannas. Ecol. Mod. 2016, 24, 75–89. [Google Scholar] [CrossRef]
- Weisel, E.W.; Petty, M.D.; Mielke, R.R. Validity of models and classes of models in semantic composability. In Proceedings of the Fall 2003 Simulation Interoperability Workshop, Orlando, FL, USA, 14–19 September 2003. [Google Scholar]
- Yankeelov, T.E.; An, G.; Saut, O.; Luebeck, E.G.; Popel, A.S.; Ribba, B.; Vicini, P.; Zhou, X.; Weis, J.A.; Ye, K.; Genin, G.M. Multi-scale Modeling in Clinical Oncology: Opportunities and Barriers to Success. Ann. Biomed. Eng. 2016, 44, 2626–2641. [Google Scholar] [CrossRef] [PubMed]
- Kazic, T. Ten Simple Rules for Experiments’ Provenance. PLoS Comput. Biol. 2015, 11, e1004384. [Google Scholar] [CrossRef] [PubMed]
- McDougal, R.; Bulanova, A.; Lytton, W. Reproducibility in computational neuroscience models and simulations. IEEE Trans. Biomed. Eng. 2016, 63, 2021–2035. [Google Scholar] [CrossRef] [PubMed]
| Mechanism Features | Examples | Explanations |
|---|---|---|
| Phenomenon | A clearly identified phenomenon is the requisite for specifying the other four features of mechanism and for developing a credible explanation of that phenomenon. | |
| Components | entities, activities, modules, processes, underlying finer details | Working entities act in the mechanism. Activities are producers of change. Some entities and activities can be organized into a module. Inner layer phenomena can be the entities and activities responsible for the outer layer phenomenon. |
| Spatial arrangement of components | localization, structure orientation, connectivity, compartmentalization | Components are typically localized and organized into a structure. A component’s orientation can be a prerequisite for an activity. Producing change requires connectivity. Compartmentalization facilitates spatial arrangement within a structure. |
| Temporal aspects of components | order, rate, duration, frequency | Entities may play their role is a particular order. Some activities have characteristic rates. Activities can occur in stages and/or exhibit temporal organization. An activity and/or stage can repeat or exhibit frequencies. Stages can unfold in a particular order and have duration. |
| Contextual locations | location within a hierarchy and/or within a series | A mechanism is situated in wider context, such as within a hierarchy of mechanism levels or within a temporal series of mechanisms not directly influencing the phenomenon of interest. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hunt, C.A.; Erdemir, A.; Lytton, W.W.; Mac Gabhann, F.; Sander, E.A.; Transtrum, M.K.; Mulugeta, L. The Spectrum of Mechanism-Oriented Models and Methods for Explanations of Biological Phenomena. Processes 2018, 6, 56. https://doi.org/10.3390/pr6050056
Hunt CA, Erdemir A, Lytton WW, Mac Gabhann F, Sander EA, Transtrum MK, Mulugeta L. The Spectrum of Mechanism-Oriented Models and Methods for Explanations of Biological Phenomena. Processes. 2018; 6(5):56. https://doi.org/10.3390/pr6050056
Chicago/Turabian StyleHunt, C. Anthony, Ahmet Erdemir, William W. Lytton, Feilim Mac Gabhann, Edward A. Sander, Mark K. Transtrum, and Lealem Mulugeta. 2018. "The Spectrum of Mechanism-Oriented Models and Methods for Explanations of Biological Phenomena" Processes 6, no. 5: 56. https://doi.org/10.3390/pr6050056
APA StyleHunt, C. A., Erdemir, A., Lytton, W. W., Mac Gabhann, F., Sander, E. A., Transtrum, M. K., & Mulugeta, L. (2018). The Spectrum of Mechanism-Oriented Models and Methods for Explanations of Biological Phenomena. Processes, 6(5), 56. https://doi.org/10.3390/pr6050056