Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages
Abstract
1. Introduction
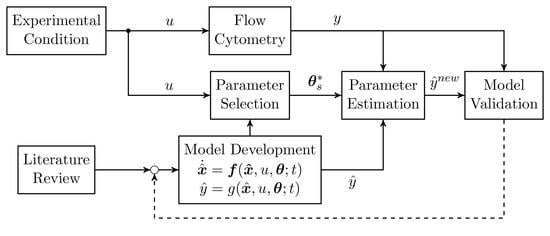
2. Material and Methods
2.1. Materials and Cell Culture
2.2. Flow Cytometry Analysis
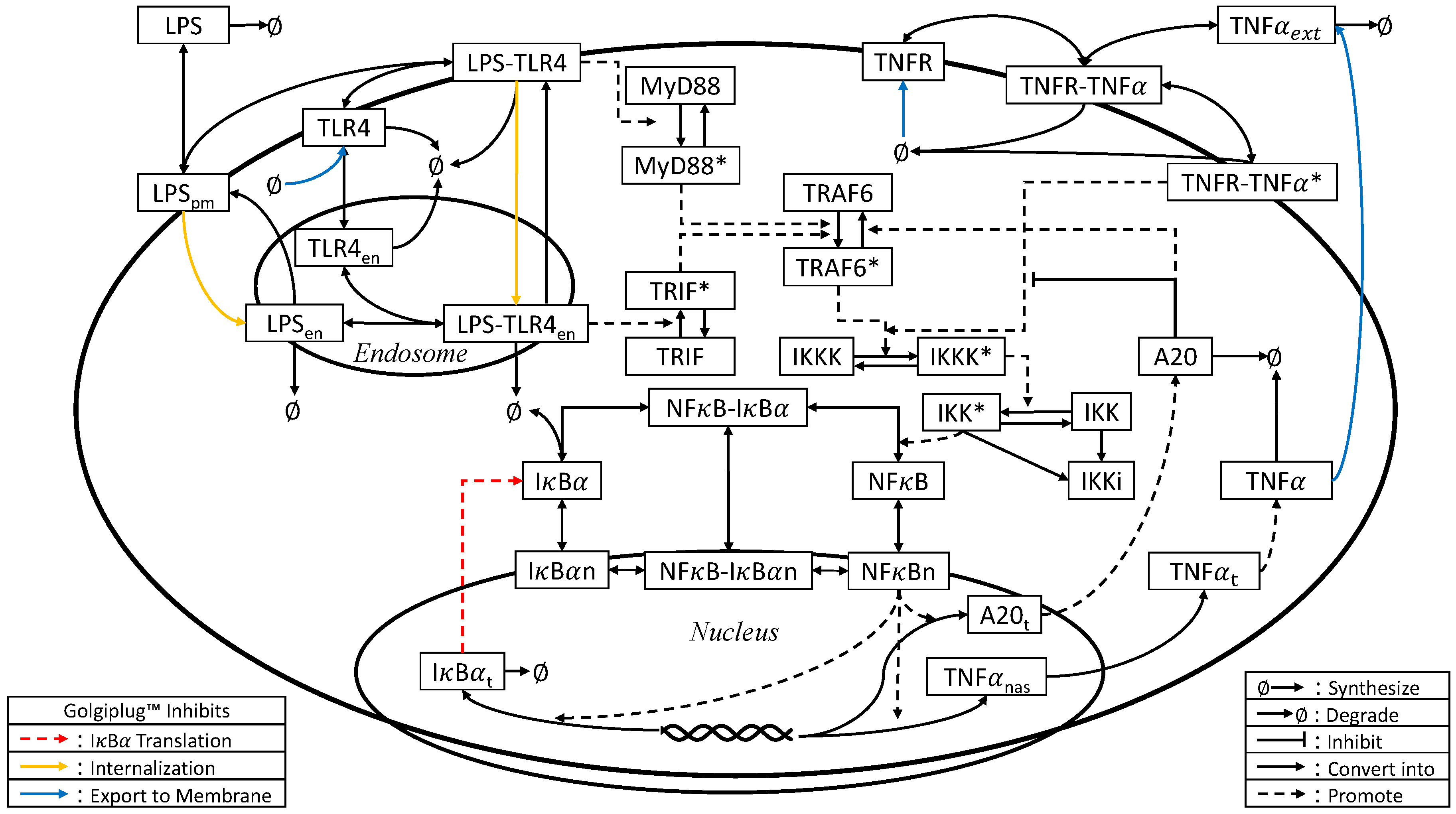
2.3. Model Development
2.4. Parameter Estimation
3. Results
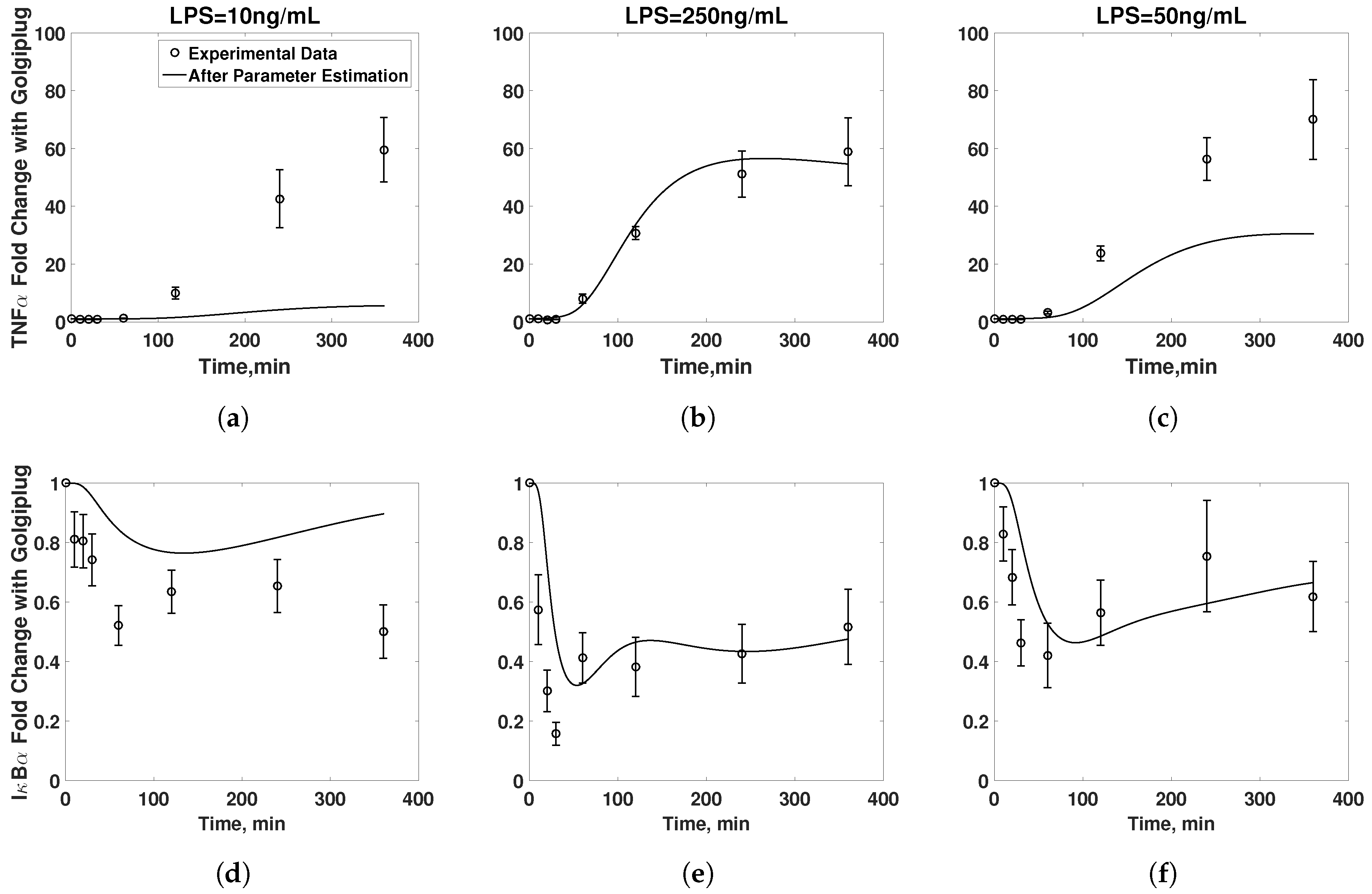
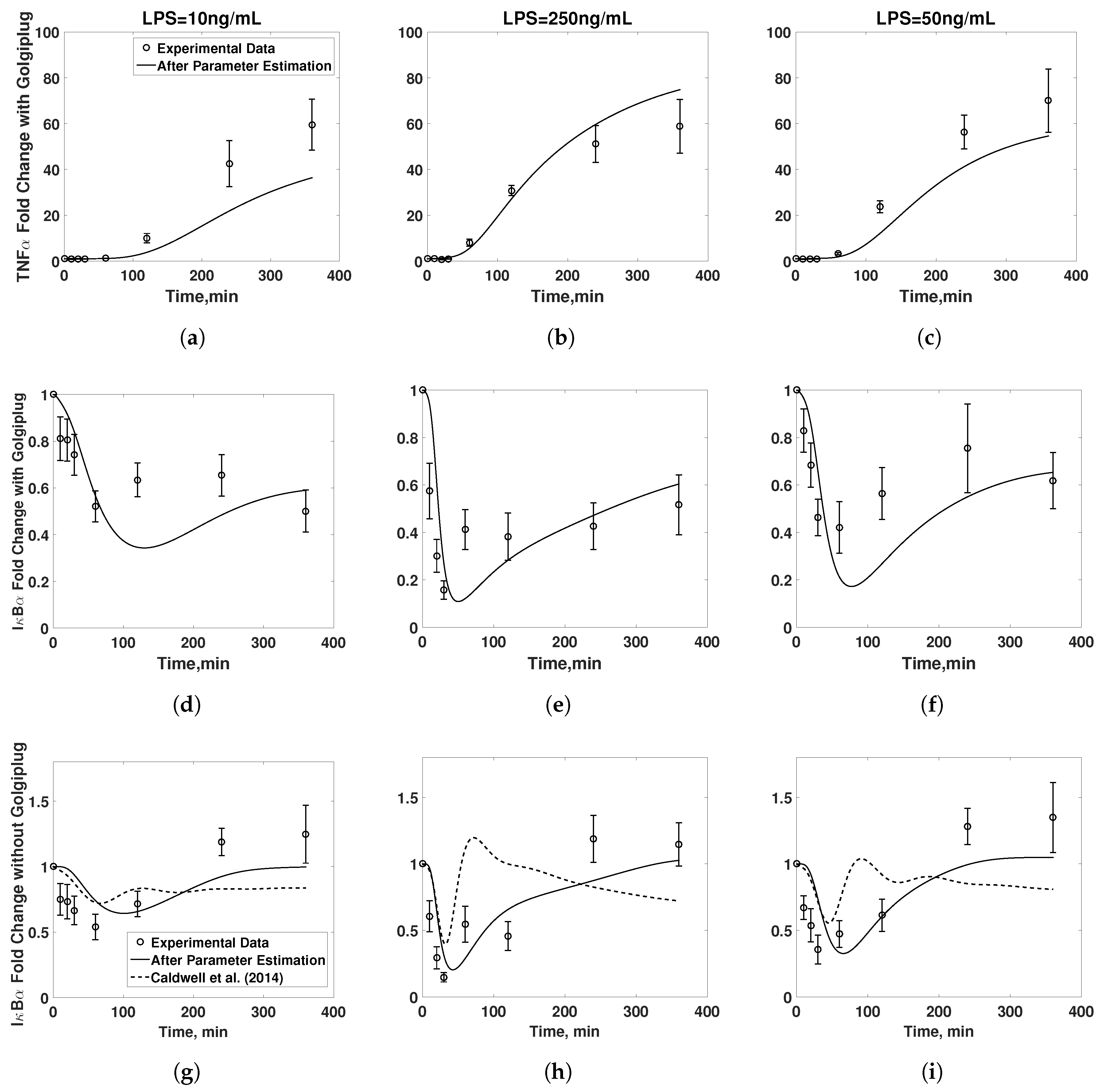
3.1. Model Validation
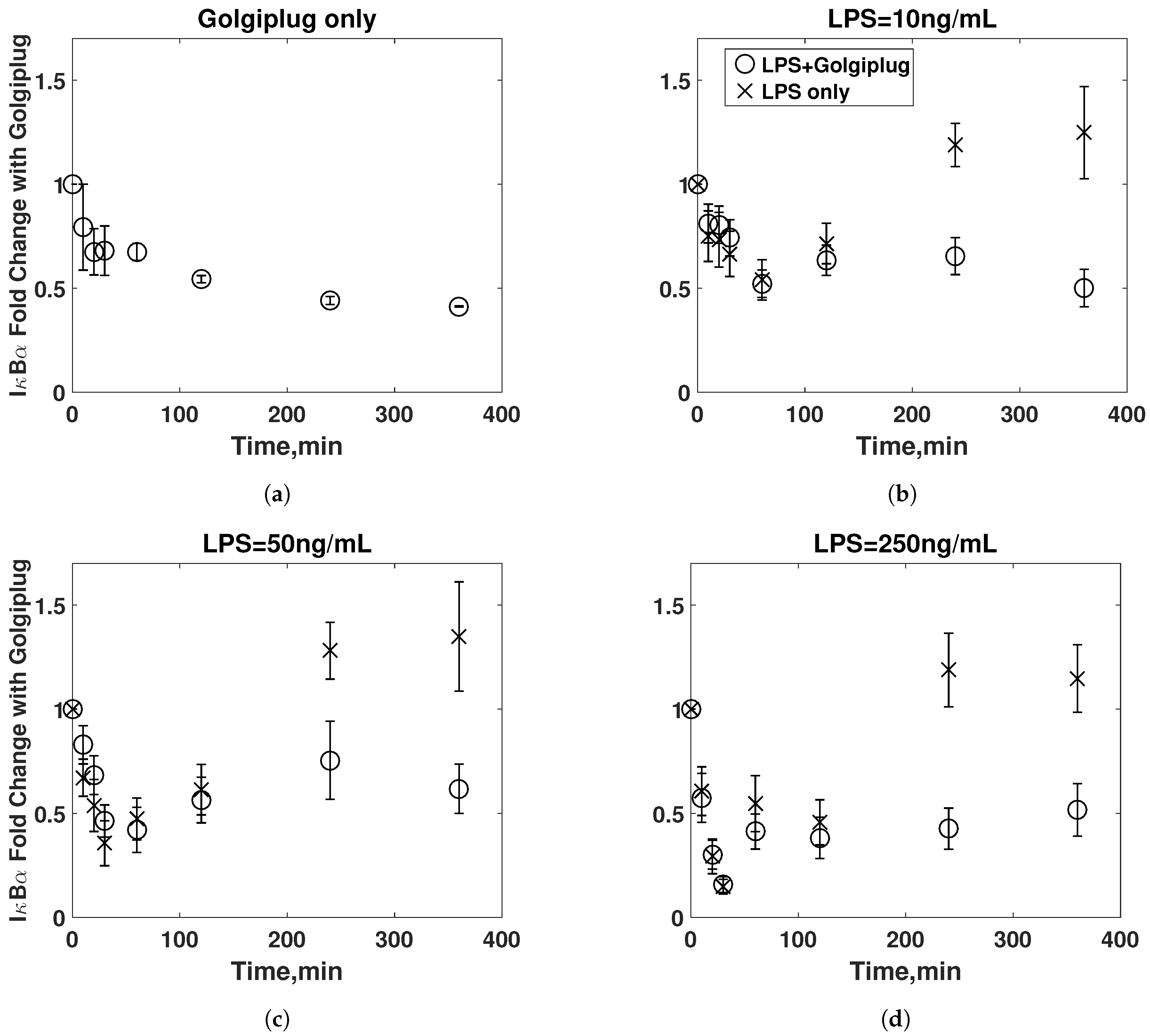
3.2. Golgiplug™-Induced ER Stress
3.3. Model Refinement
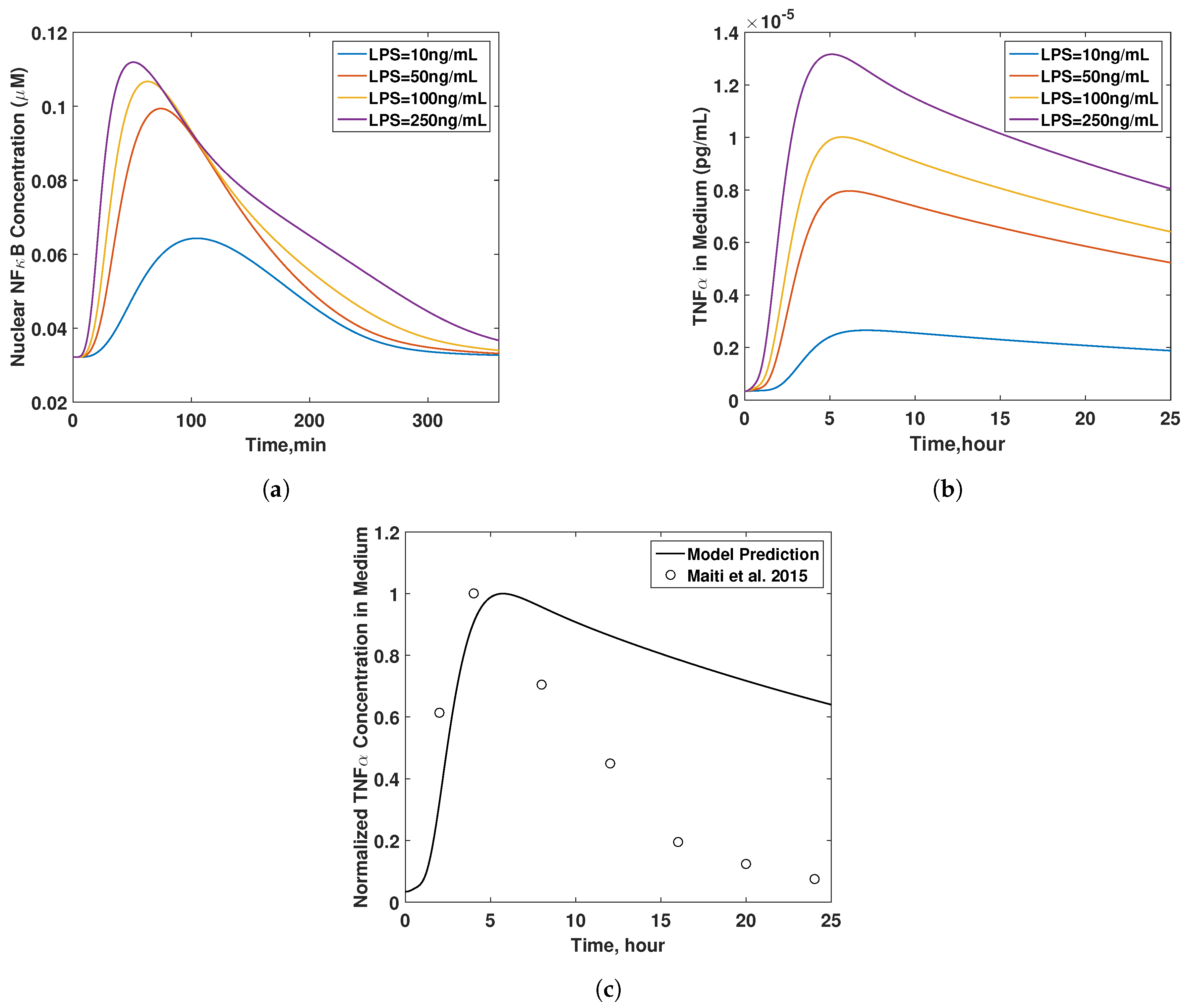
3.4. Final Model Validation
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| LPS | lipopolysaccharide |
| NFB | nuclear factor B |
| TNF | tumor necrosis factor |
| IB | inhibitor of B, |
| TLR4 | Toll-like receptor 4 |
| IKK | IB kinase |
| MyD88 | myeloid differentiation primary response 88 |
| TIR | Toll/interleukin-1 receptor |
| TRIF | TIR-domain-containing adaptor-inducing interferon- |
| TRAF6 | TNF receptor-associated factor 6 |
| IKKK | IKK kinase |
| ER | endoplasmic reticulum |
| TNFR | TNF receptor |
| CD14 | cluster of differentiation 14 |
| MFI | mean fluorescence intensity |
| IB | IB transcript |
| eIF2 | eukaryotic initiation factor 2 -subunit |
| C1 | TNFR complex |
References
- Hughey, J.J.; Lee, T.K.; Covert, M.W. Computational modeling of mammalian signaling networks. Wiley Interdisciplin. Rev. Syst. Biol. Med. 2010, 2, 194–209. [Google Scholar] [CrossRef] [PubMed]
- Handly, L.N.; Yao, J.; Wollman, R. Signal transduction at the single-cell level: Approaches to study the dynamic nature of signaling networks. J. Mol. Biol. 2016, 428, 3669–3682. [Google Scholar] [CrossRef] [PubMed]
- Gaudet, S.; Miller-Jensen, K. Redefining signaling pathways with an expanding single-cell toolbox. Trends Biotechnol. 2016, 34, 458–469. [Google Scholar]
- Cohen, A.A.; Geva-Zatorsky, N.; Eden, E.; Frenkel-Morgenstern, M.; Issaeva, I.; Sigal, A.; Milo, R.; Cohen-Saidon, C.; Liron, Y.; Kam, Z.; et al. Dynamic proteomics of individual cancer cells in response to a drug. Science 2008, 322, 1511–1516. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Taylor, B.; Ourthiague, D.R.; Hoffmann, A. Distinct single-cell signaling characteristics are conferred by the MyD88 and TRIF pathways during TLR4 activation. Sci. Signal. 2015, 8, ra69. [Google Scholar] [CrossRef] [PubMed]
- Hasenauer, J.; Waldherr, S.; Doszczak, M.; Radde, N.; Scheurich, P.; Allgöwer, F. Identification of models of heterogeneous cell populations from population snapshot data. BMC Bioinform. 2011, 12, 125. [Google Scholar] [CrossRef] [PubMed]
- Hasenauer, J.; Waldherr, S.; Doszczak, M.; Scheurich, P.; Radde, N.; Allgöwer, F. Analysis of heterogeneous cell populations: A density-based modeling and identification framework. J. Process Control 2011, 21, 1417–1425. [Google Scholar] [CrossRef]
- Williams, R.A.; Timmis, J.; Qwarnstrom, E.E. Computational models of the NF-κB signalling pathway. Computation 2014, 2, 131–158. [Google Scholar] [CrossRef]
- Gábor, A.; Villaverde, A.F.; Banga, J.R. Parameter identifiability analysis and visualization in large-scale kinetic models of biosystems. BMC Syst. Biol. 2017, 11, 54. [Google Scholar] [CrossRef] [PubMed]
- Kravaris, C.; Hahn, J.; Chu, Y. Advances and selected recent developments in state and parameter estimation. Comput. Chem. Eng. 2013, 51, 111–123. [Google Scholar] [CrossRef]
- Raue, A.; Kreutz, C.; Maiwald, T.; Bachmann, J.; Schilling, M.; Klingmüller, U.; Timmer, J. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 2009, 25, 1923–1929. [Google Scholar] [CrossRef] [PubMed]
- Kravaris, C.; Seinfeld, J.H. Identification of parameters in distributed parameter systems by regularization. SIAM J. Control Optim. 1985, 23, 217–241. [Google Scholar] [CrossRef]
- Xue, Q.; Lu, Y.; Eisele, M.R.; Sulistijo, E.S.; Khan, N.; Fan, R.; Miller-Jensen, K. Analysis of single-cell cytokine secretion reveals a role for paracrine signaling in coordinating macrophage responses to TLR4 stimulation. Sci. Signal. 2015, 8, ra59. [Google Scholar] [CrossRef] [PubMed]
- Tay, S.; Hughey, J.J.; Lee, T.K.; Lipniacki, T.; Quake, S.R.; Covert, M.W. Single-cell NF-κB dynamics reveal digital activation and analogue information processing. Nature 2010, 466, 267. [Google Scholar] [CrossRef] [PubMed]
- Maiti, S.; Dai, W.; Alaniz, R.C.; Hahn, J.; Jayaraman, A. Mathematical modeling of pro- and anti-inflammatory signaling in macrophages. Processes 2015, 3, 1–18. [Google Scholar] [CrossRef]
- Hayden, M.S.; Ghosh, S. NF-κB, the first quarter-century: Remarkable progress and outstanding questions. Genes Dev. 2012, 26, 203–234. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Hahn, J. Parameter set selection via clustering of parameters into pairwise indistinguishable groups of parameters. Ind. Eng. Chem. Res. 2009, 48, 6000–6009. [Google Scholar] [CrossRef]
- Yao, K.Z.; Shaw, B.M.; Kou, B.; McAuley, K.B. Modeling ethylene/butene copolymerization with multi-site catalysts: Parameter estimability and experimental design. Polym. React. Eng. 2003, 3, 563–588. [Google Scholar] [CrossRef]
- Prussin, C. Cytokine flow cytometry: Understanding cytokine biology at the single-cell level. J. Clin. Immunol. 1997, 17, 195. [Google Scholar] [CrossRef] [PubMed]
- Schulz, K.R.; Danna, E.A.; Krutzik, P.O.; Nolan, G.P. Single-cell phospho-protein analysis by flow cytometry. Curr. Protoc. Immunol. 2012, 8–17. [Google Scholar] [CrossRef]
- Caldwell, A.B.; Cheng, Z.; Vargas, J.D.; Birnbaum, H.A.; Hoffmann, A. Network dynamics determine the autocrine and paracrine signaling fucntions of TNF. Genes Dev. 2014, 28, 2120–2133. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, A.; Levchenko, A.; Scott, M.L.; Baltimore, D. The IκB-NF-κB signaling module: Temporal control and selective gene activation. Science 2002, 298, 1241–1245. [Google Scholar] [CrossRef] [PubMed]
- Werner, S.L.; Kearns, J.D.; Zadorozhnaya, V.; Lynch, C.; O’Dea, E.; Boldin, M.P.; Ma, A.; Baltimore, D.; Hoffmann, A. Encoding NF-κB temporal control in response to TNF: Distinct roles for the negative regulators IκBα and A20. Genes Dev. 2008, 22, 2093–2101. [Google Scholar] [CrossRef] [PubMed]
- Junkin, M.; Kaestli, A.J.; Cheng, Z.; Jordi, C.; Albayrak, C.; Hoffmann, A.; Tay, S. High-content quantification of single-cell immune dynamics. Cell Rep. 2016, 15, 411–422. [Google Scholar] [CrossRef] [PubMed]
- Krikos, A.; Laherty, C.D.; Dixit, V.M. Transcriptional activation of the tumor necrosis factor α-inducible zinc finger protein, a20, is mediated by κB elements. J. Biol. Chem. 1992, 267. [Google Scholar]
- Lee, E.G.; Boone, D.L.; Chai, S.; Libby, S.L.; Chien, M.; Lodolce, J.P.; Ma, A. Failure to regulate TNF-induced NF-κB and cell death responses in A20-deficient mice. Science 2000, 289, 2350–2354. [Google Scholar] [CrossRef] [PubMed]
- Boone, D.L.; Turer, E.E.; Lee, E.G.; Ahmad, R.C.; Wheeler, M.T.; Tsui, C.; Hurley, P.; Chien, M.; Chai, S.; Hitotsumatsu, O.; et al. The ubiquitin-modifying enzyme A20 is required for termination of Toll-like receptor responses. Nat. Immunol. 2004, 5, 1052–1060. [Google Scholar] [CrossRef] [PubMed]
- Chardin, P.; McCormick, F. Brefeldin A: The advantage of being uncompetitive. Cell 1999, 97, 153–155. [Google Scholar] [CrossRef]
- Ward, T.H.; Polishchuk, R.S.; Caplan, S.; Hirschberg, K.; Lippincott-Schwartz, J. Maintenance of Golgi structure and function depends on the integrity of ER export. J. Cell Biol. 2001, 155, 557–570. [Google Scholar] [CrossRef] [PubMed]
- Latz, E.; Visintin, A.; Lien, E.; Fitzgerald, K.A.; Monks, B.G.; Kurt-Jones, E.A.; Golenbock, D.T.; Espevik, T. Lipopolysaccharide rapidly traffics to and from the Golgi apparatus with the Toll-like Receptor 4-MD-2-CD14 complex in a process that Is distinct from the initiation of signal transduction. J. Biol. Chem. 2002, 49, 47834–47843. [Google Scholar] [CrossRef] [PubMed]
- Liaunardy-Jopeace, A.; Bryant, C.E.; Gay, N.J. The COPII adaptor protein TMED7 is required to initiate and mediate the anterograde trafficking of Toll-like receptor 4 to the plasma membrane. Sci. Signal. 2014, 7, ra70. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Lou, J.; Ouyang, C.; Chen, W.; Liu, Y.; Liu, X.; Cao, X.; Wanga, J.; Lu, L. Ras-related protein Rab10 facilitates TLR4 signaling by promoting replenishment of TLR4 onto the plasma membrane. Proc. Natl. Acad. Sci. USA 2010, 107, 13806–13811. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.J.; Ledgerwood, E.C.; Prins, J.B.; Galbraith, J.; Johnson, D.R.; Pober, J.S.; Bradley, J.R. TNF recruits TRADD to the plasma membrane but not the trans-Golgi Network, the principal subcellular location of TNF-R1. J. Immunol. 1999, 162, 1042–1048. [Google Scholar] [PubMed]
- Neznanov, N.; Kondratova, A.; Chumakov, K.M.; Angres, B.; Zhumabayeva, B.; Agol, V.I.; Gudkov, A.V. Poliovirus protein 3A inhibits tumor necrosis factor (TNF)-induced apoptosis by eliminating the TNF receptor from the cell surface. J. Virol. 2001, 75, 10409–10420. [Google Scholar] [CrossRef] [PubMed]
- Xaus, J.; Comalada, M.; Valledor, A.F.; Lloberas, J.; López-Soriano, F.; Argilés, J.M.; Bogdan, C.; Celada, A. LPS induces apoptosis in macrophages mostly through the autocrine production of TNF-α. Blood 2000, 95, 3823–3831. [Google Scholar] [PubMed]
- Covert, M.W.; Leung, T.H.; Gaston, J.E.; Baltimore, D. Achieving stability of lipopolysaccharide-induced NF-κB activation. Science 2005, 309, 1854–1857. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, E.; Alvarez-Barrientos, A.; Maroto, B.; Boscà, L.; Knaus, U.G. TLR4-mediated survival of macrophages is MyD88 dependent and requires TNF-α autocrine signalling. J. Immunol. 2007, 178, 3731–3739. [Google Scholar] [CrossRef] [PubMed]
- Zanoni, I.; Ostuni, R.; Marek, L.R.; Barresi, S.; Barbalat, R.; Barton, G.M.; Granucci, F.; Kagan, J.C. CD14 controls the LPS-induced endocytosis of Toll-like Receptor 4. Cell 2011, 147, 868–880. [Google Scholar]
- Tan, Y.; Zanoni, I.; Cullen, T.W.; Goodman, A.L.; Kagan, J.C. Mechanisms of Toll-like receptor 4 endocytosis reveal a common immune-evasion strategy used by pathogenic and commensal bacteria. Immunity 2015, 43, 909–922. [Google Scholar] [CrossRef] [PubMed]
- Rajaiah, R.; Perkins, D.J.; Ireland, D.D.C.; Vogel, S.N. CD14 dependence of TLR4 endocytosis and TRIF signaling displays ligand specificity and is dissociable in endotoxin tolerance. Proc. Natl. Acad. Sci. USA 2013, 112, 8391–8396. [Google Scholar] [CrossRef] [PubMed]
- Kagan, J.C.; Su, T.; Horng, T.; Chow, A.; Akira, S.; Medzhitov, R. TRAM couples endocytosis of Toll-like receptor 4 to the induction of interferon-β. Nat. Immunol. 2008, 9, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Jayaraman, A.; Hahn, J. Parameter sensitivity analysis of IL-6 signaling pathways. IET Syst. Biol. 2007, 1, 342–352. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.C.; Lo, Y.C.; Wu, H. Helical assembly in the MyD88-IRAK4-IRAK2 complex in TLR/IL-1R signalling. Nature 2010, 465, 885–890. [Google Scholar] [CrossRef] [PubMed]
- Bagnall, J.; Boddington, C.; Boyd, J.; Brignall, R.; Rowe, W.; Jones, N.A.; Schmidt, L.; Spiller, D.G.; White, M.R.; Paszek, P. Quantitative dynamic imaging of immune cell signalling using lentiviral gene transfer. Integr. Biol. 2015, 7, 713–725. [Google Scholar] [CrossRef] [PubMed]
- Moya, C.; Huang, Z.; Cheng, P.; Jayaraman, A.; Hahn, J. Investigation of IL-6 and IL-10 signalling via mathematical modelling. IET Syst. Biol. 2011, 5, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Sung, M.H.; Li, N.; Lao, Q.; Gottschalk, R.A.; Hager, G.L.; Fraser, I.D.C. Switching of the relative dominance between feedback mechanisms in lipopolysaccharide-Induced NF-κB signaling. Sci. Signal. 2014, 7, ra6. [Google Scholar] [CrossRef] [PubMed]
- Tsukamoto, H.; Fukudome, K.; Takao, S.; Tsuneyoshi, N.; Kimoto, M. Lipopolysaccharide-binding protein-mediated Toll-like receptor 4 dimerization enables rapid signal transduction against lipopolysaccharide stimulation on membrane-associated CD14-expressing cells. Int. Immunol. 2010, 22, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Sakai, J.; Cammarota, E.; Wright, J.A.; Cicuta, P.; Gottschalk, R.A.; Li, N.; Fraser, I.D.C.; Bryant, C.E. Lipopolysaccharide-induced NF-κB nuclear translocation is primarily dependent on MyD88, but TNFα expression requires TRIF and MyD88. Sci. Rep. 2017, 7, 1428. [Google Scholar] [CrossRef] [PubMed]
- Shao, R.G.; Shimizu, T.; Pommier, Y. Brefeldin A Is a potent inducer of apoptosis in human cancer cells independently of p53. Exp. Cell Res. 1996, 227, 190–196. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.L.; Kim, S.Y.; Shin, S.W.; Park, J.W. Regulation of brefeldin A-induced ER stress and apoptosis by mitochondrial NADP+-dependent isocitrate dehydrogenase. Biochem. Biophys. Res. Commun. 2012, 417, 760–764. [Google Scholar] [CrossRef] [PubMed]
- Cláudio, N.; Dalet, A.; Gatti, E.; Pierre, P. Mapping the crossroads of immune activation and cellular stress response pathways. EMBO J. 2013, 32, 1214–1224. [Google Scholar] [CrossRef] [PubMed]
- Mellor, H.; Kimball, S.R.; Jefferson, L.S. Brefeldin A inhibits protein synthesis through the phosphorylation of the α-subunit of eukaryotic initiation factor-2. FEBS Lett. 1994, 350, 143–146. [Google Scholar] [CrossRef]
- Tam, A.B.; Mercado, E.L.; Hoffmann, A.; Niwa, M. ER stress activates NF-κB by integrating functions of basal IKK activity, IRE1 and PERK. PLoS ONE 2012, 7, e45078. [Google Scholar] [CrossRef] [PubMed]
- Fishman, P.E.; Curran, P.K. Brefeldin A inhibits protein synthesis in cultured cells. FEBS Lett. 1992, 314, 371–374. [Google Scholar] [CrossRef]
- Ando, Y.; Oku, T.; Tsuji, T. Platelet supernatant suppresses LPS-induced nitric oxide production from macrophages accompanied by inhibition of NF-κB signaling and increased Arginase-1 expression. PLoS ONE 2016. [Google Scholar] [CrossRef] [PubMed]
- Selimkhanov, J.; Taylor, B.; Yao, J.; Pilko, A.; Albeck, J.; Hoffmann, A.; Tsimring, L.; Wollman, R. Accurate information transmission through dynamic biochemical signaling networks. Science 2014, 346, 1370–1373. [Google Scholar] [CrossRef] [PubMed]
- Kellogg, R.A.; Tian, C.; Lipniacki, T.; Quake, S.R.; Tay, S. Digital signaling decouples activation probability and population heterogeneity. eLife 2015, 4, e08931. [Google Scholar] [CrossRef] [PubMed]
- Noman, A.S.M.; Koide, N.; Hassan, F.; I.-E.-Khuda, I.; Dagvadorj, J.; Tumurkhuu, G.; Islam, S.; Naiki, Y.; Yoshida, T.; Yokochi, T. Thalidomide inhibits lipopolysaccharide-induced tumor necrosis factor-a production via down-regulation of MyD88 expression. Innate Immun. 2009, 15, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 82, 2340–2361. [Google Scholar]
- Haseltine, E.L.; Rawlings, J.B. Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics. J. Chem. Phys. 2002, 117, 6959–6969. [Google Scholar] [CrossRef]
- Cao, Y.; Petzold, L.R. The numerical stability of leaping methods for stochastic simulation of chemically reacting systems. J. Chem. Phys. 2004, 121, 12169–12178. [Google Scholar] [CrossRef] [PubMed]
- Kwon, J.S.I.; Nayhouse, M.; Christofides, P.D.; Orkoulas, G. Modeling and control of protein crystal shape and size in batch crystallization. AIChE J. 2013, 59, 2317–2327. [Google Scholar] [CrossRef]
- Kwon, J.S.; Nayhouse, M.; Christofides, P.D.; Orkoulas, G. Modeling and control of shape distribution of protein crystal aggregates. Chem. Eng. Sci. 2013, 104, 484–497. [Google Scholar] [CrossRef]
- Lipniacki, T.; Paszek, P.; Brasier, A.R.; Luxon, B.A.; Kimmel, M. Stochastic regulation in early immune response. Biophys. J. 2006, 90, 725–742. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.E.; Ihekwaba, A.E.C.; Elliott, M.; Johnson, J.R.; Gibney, C.A.; Foreman, B.E.G.; Nelson, V.S.; Horton, C.A.; Spiller, D.G.; Edwards, S.W.; et al. Oscillations in TNFα signaling control the dynamics of gene expression. Science 2004, 306, 704–708. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, D.J. Stochastic modelling for quantitative description of heterogeneous biological systems. Nat. Rev. Genet. 2009, 10, 122. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Rawlings, J.B. Comparison of parameter estimation methods in stochastic chemical kinetic models: Examples in systems biology. AIChE J. 2014, 60, 1253–1268. [Google Scholar] [CrossRef] [PubMed]
- Ashyraliyev, M.; Fomekong-Nanfack, Y.; Kaandorp, J.A.; Blom, J.G. Systems biology: Parameter estimation for biochemicalmodels. FEBS J. 2009, 276, 886–902. [Google Scholar] [CrossRef] [PubMed]
- Kiparissides, A.; Koutinas, M.; Kontoravdi, C.; Mantalaris, A.; Pistikopoulos, E.N. ‘Closing the loop’ in biological systems modeling—from the in silico to the in vitro. Automatica 2011, 47, 1147–1155. [Google Scholar] [CrossRef]
- Lamoreaux, L.; Roederer, M.; Koup, R. Intracellular cytokine optimization and standard operating procedure. Nat. Protoc. 2006, 1, 1507–1516. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.K.; Denny, E.M.; Sanghvi, J.C.; Gaston, J.E.; Maynard, N.D.; Hughey, J.J.; Covert, M.W. A noisy paracrine signal determines the cellular NF-κB response to lipopolysaccharide. Sci. Signal. 2009, 2, ra65. [Google Scholar] [CrossRef] [PubMed]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2006, 24, 619–644. [Google Scholar] [CrossRef]
- Misumi, Y.; Yuko Misumi, K.M.; Takatsuki, A.; Tamura, G.; Ikehara, Y. Novel blockade by brefeldin A of intracellular transport of secretory proteins in cultured rat hepatocytes. J. Biol. Chem. 1986, 261, 1139–11403. [Google Scholar]
- Bueno, C.; Almeida, J.; Alguero, M.; Sánchez, M.; Vaquero, J.; Laso, F.; Miguel, J.S.; Escribano, L.; Orf, A. Flow cytometric analysis of cytokine production by normal human peripheral blood dendritic cells and monocytes: Comparative analysis of different stimuli, secretion-blocking agents and incubation periods. Cytometry Part A 2001, 46, 33–40. [Google Scholar] [CrossRef]
- Gottschalk, R.A.; Martins, A.J.; Angermann, B.R.; Dutta, B.; Ng, C.E.; Uderhardt, S.; Tsang, J.S.; Fraser, I.D.C.; Meier-Schellersheim, M.; Germain, R.N. Distinct NF-κB and MAPK activation thresholds uncouple steady-state microbe sensing from anti-pathogen inflammatory responses. Cell Syst. 2016, 2, 378–390. [Google Scholar] [CrossRef] [PubMed]
| Parameter |
|---|
| TLR4 constitutive generation rate |
| IKKK-mediated IKK activation (IKK → IKKa) |
| IB transcript degradation rate |
| Hill coefficient of IB transcription |
| Hill coefficient of IB transcription |
| Hill coefficient of TNF transcription |
| Parameter | New Value |
|---|---|
| Coefficient for eIF2 phosphorylation () | 1.00 |
| A20-mediated C1 deactivation | 9.04 × 10 M min |
| TLR4 constitutive generation rate | 3.75 × 10 M min |
| IKKK-mediated IKK activation | 4.75 × 10 M min |
| Constitutive inactivation of IKK | 2.85 × 10 |
| IB mRNA degradation rate | 5.83 × 10 |
| Hill coefficient of IB transcription | 4.16 |
| Hill coefficient of IB transcription | 5.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Ding, Y.; Jayaraman, A.; Kwon, J.S. Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages. Processes 2018, 6, 21. https://doi.org/10.3390/pr6030021
Lee D, Ding Y, Jayaraman A, Kwon JS. Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages. Processes. 2018; 6(3):21. https://doi.org/10.3390/pr6030021
Chicago/Turabian StyleLee, Dongheon, Yufang Ding, Arul Jayaraman, and Joseph S. Kwon. 2018. "Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages" Processes 6, no. 3: 21. https://doi.org/10.3390/pr6030021
APA StyleLee, D., Ding, Y., Jayaraman, A., & Kwon, J. S. (2018). Mathematical Modeling and Parameter Estimation of Intracellular Signaling Pathway: Application to LPS-induced NFκB Activation and TNFα Production in Macrophages. Processes, 6(3), 21. https://doi.org/10.3390/pr6030021