Modeling the Circular Economy Processes at the EU Level Using an Evaluation Algorithm Based on Shannon Entropy
Abstract
1. Introduction
2. Theory and Methods
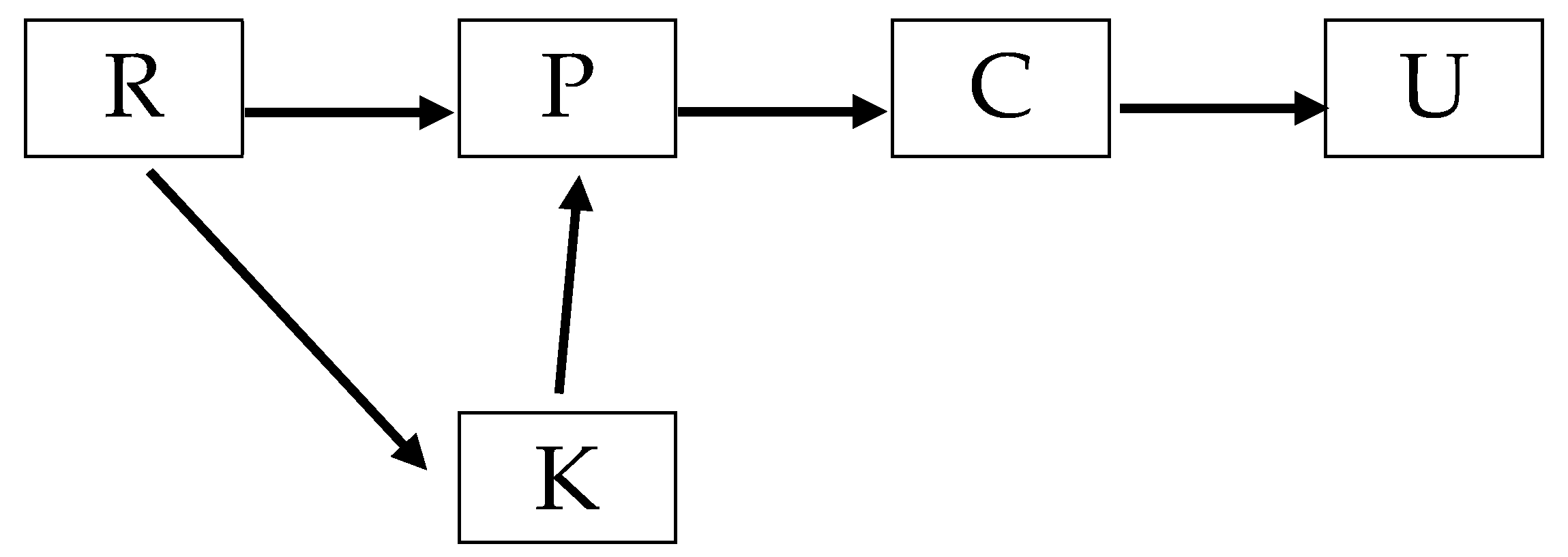
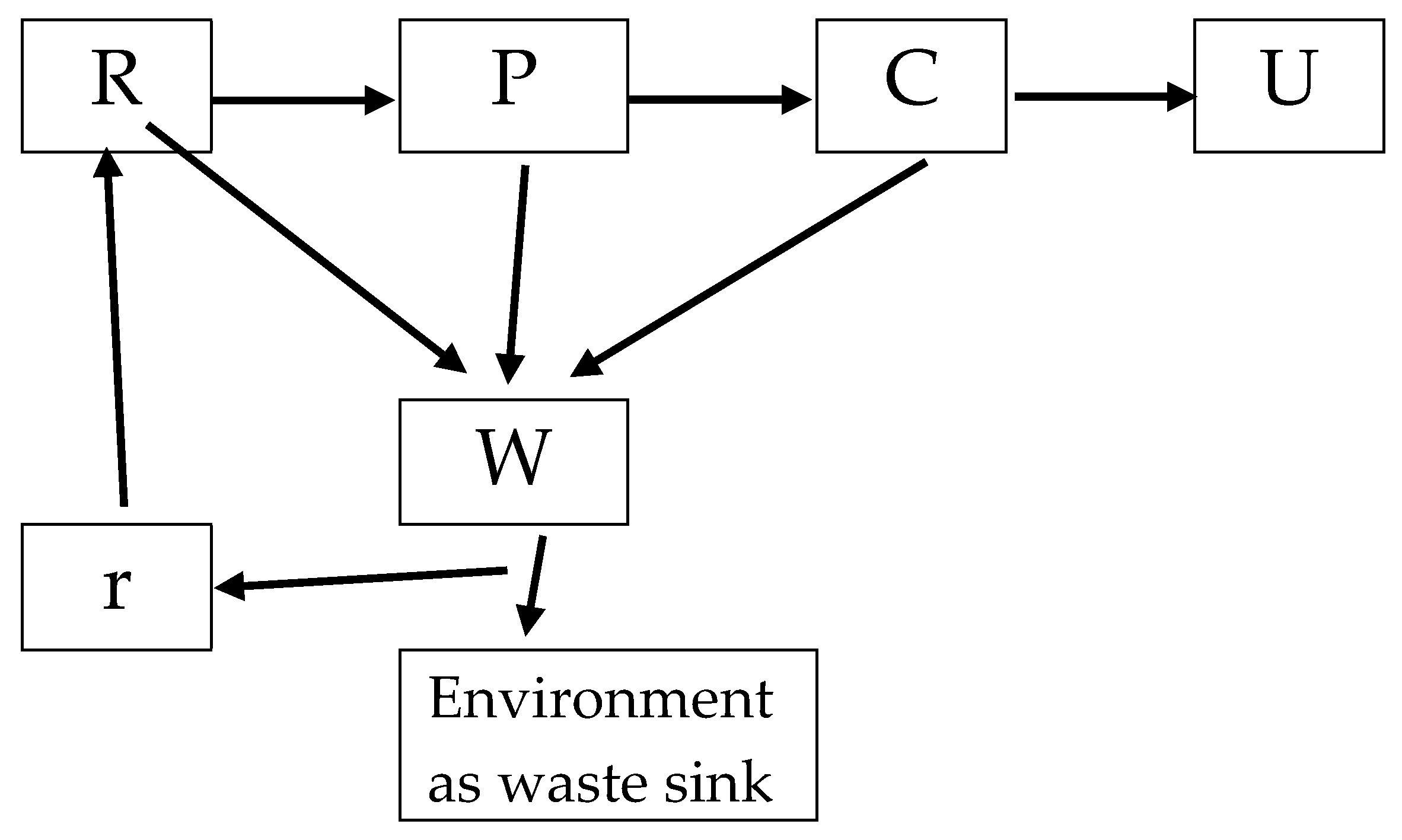
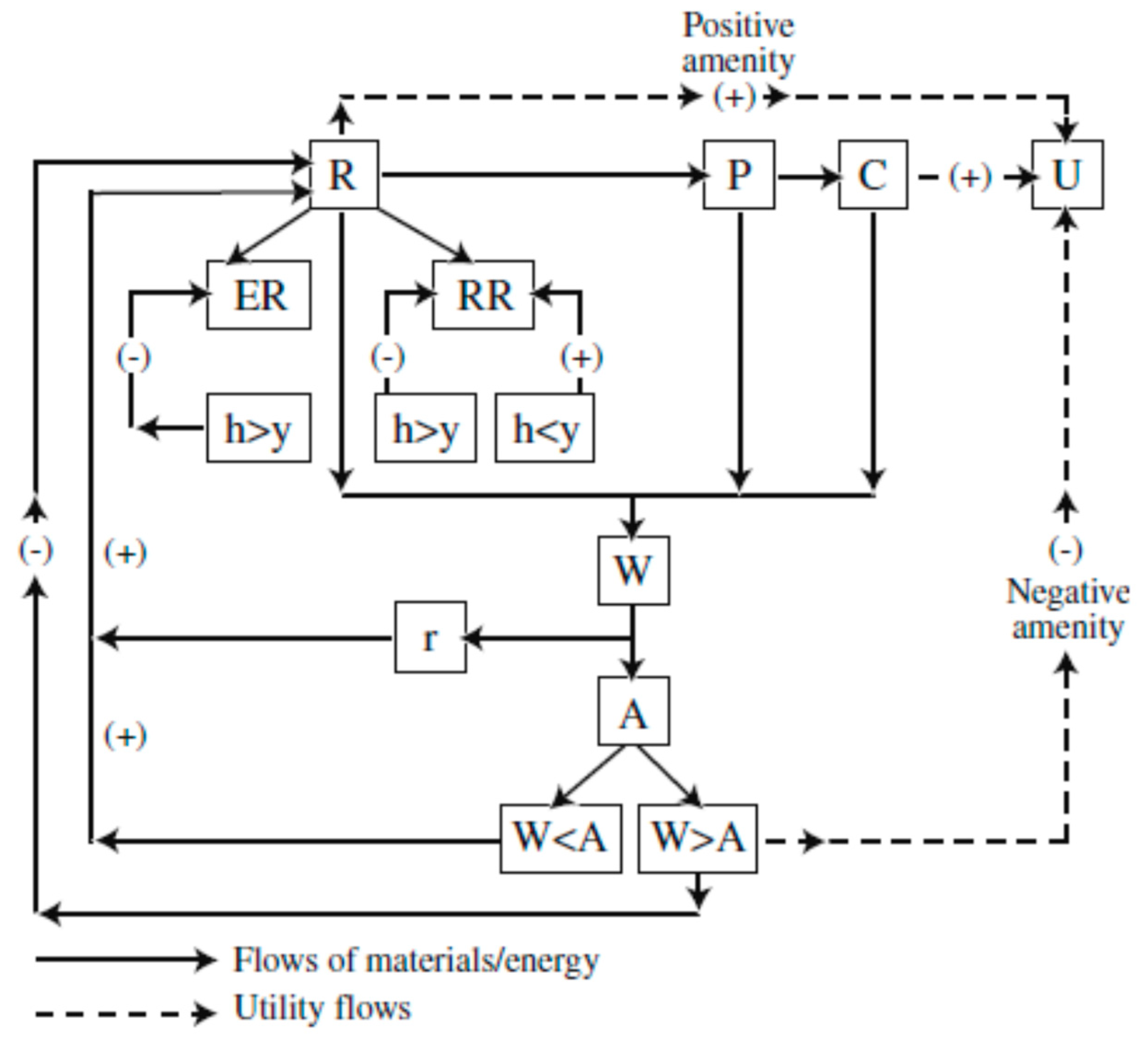
2.1. Circular Economy Processes
2.2. Shannon Entropy Composite Index
- (i).
- H(X) ≥ 0. Equality holds if, and only if,∃such that pi = 1 and pj = 1,∀/{i};
- (ii).
- H(X) ≤ ln(n). Equality holds if, and only if, pi = 1/n,., ∀.
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Shannon Composite Index
References
- Cobo, S.; Dominguez-Ramos, A.; Irabien, A. From linear to circular integrated waste management systems: A review of methodological approaches. Resour. Conserv. Recycl. 2018, 135, 279–295. [Google Scholar] [CrossRef]
- Rada, E.C.; Ragazzi, M.; Torretta, V.; Castagana, G.; Adami, L.; Cioca, L.I. Circular economy and waste to energy. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2018; Volume 1968, p. 030050. [Google Scholar]
- Romero-Hernández, O.; Romero, S. Maximizing the value of waste: From waste management to the circular economy. Thunderbird Int. Bus. Rev. 2018, 60, 757–764. [Google Scholar] [CrossRef]
- Ragazzi, M.; Fedrizzi, S.; Rada, E.C.; Ionescu, G.; Ciudin, R.; Cioca, L.I. Experiencing Urban Mining in an Italian Municipality towards a Circular Economy vision. Energy Procedia 2017, 119, 192–200. [Google Scholar] [CrossRef]
- Stahel, W.R. Analysis of the structure and values of the European Commission’s Circular Economy Package. Proceedings of Institution of Civil Engineers: Waste and Resource Management; Thomas Telford Ltd.: London, UK, 2017; Volume 170, pp. 41–44. [Google Scholar]
- Andersen, M.S. An introductory note on the environmental economics of the circular economy. Sustain. Sci. 2007, 2, 133–140. [Google Scholar] [CrossRef]
- Kronborg, M.T. Optimal Consumption and Investment with Labor Income and European/American Capital Guarantee. Risks 2014, 2, 171–194. [Google Scholar] [CrossRef]
- Núñez-Cacho, P.; Molina-Moreno, V.; Corpas-Iglesias, F.A.; Cortés-García, F.J. Family Businesses Transitioning to a Circular Economy Model: The Case of “Mercadona”. Sustainability 2018, 10, 538. [Google Scholar] [CrossRef]
- Shaheen, S.A.; Mallery, M.A.; Kingsley, K.J. Personal vehicle sharing services in North America. Res. Transp. Bus. Manag. 2012, 3, 71–81. [Google Scholar] [CrossRef]
- Molina-Sánchez, E.; Leyva-Díaz, J.C.; Cortés-García, F.J.; Molina-Moreno, V. Proposal of Sustainability Indicators for the Waste Management from the Paper Industry within the Circular Economy Model. Water 2018, 10, 1014. [Google Scholar] [CrossRef]
- Ljunggren Söderman, M.; Eriksson, O.; Björklund, A.; Östblom, G.; Ekvall, T.; Finnveden, G.; Sundqvist, J.O. Integrated economic and environmental assessment of waste policy instruments. Sustainability 2016, 8, 411. [Google Scholar] [CrossRef]
- Sjöström, M.; Östblom, G. Future Waste Scenarios for Sweden Based on a CGEmodle; Working Paper 109; National Institute of Economic Research: Stockholm, Sweden, 2009; Available online: https://econpapers.repec.org/paper/hhsnierwp/0109.htm (accessed on 11 October 2017).
- Xie, J.; Saltzman, S. Environmental policy analysis: An environmental computable general-equilibrium approach for developing countries. J. Policy Model. 2000, 22, 453–489. [Google Scholar] [CrossRef]
- OECD. Environmental Quality Objectives—A Shared Responsibility, Summary of Government Bill 2004/05:150: OECD Environmental Outlook to 2030; OECD: Paris, France, 2001; ISBN 978-92-64-04048-9. [Google Scholar]
- EU. Regulation (EC) No 2150/2002 of the European Parliament and the Council on Waste Statistics. 2002. Available online: http://www.kluwerlawonline.com/abstract.php?id=EELR2003019 (accessed on 23 August 2018).
- MacArthur, E. Towards the circular economy. J. Ind. Ecol. 2013, 23–44. Available online: https://mvonederland.nl/system/files/media/towards-the-circular-economy.pdf (accessed on 21 October 2017).
- Kopnina, H. Sustainability: New strategic thinking for business. Environ. Dev. Sustain. 2017, 19, 27–43. [Google Scholar] [CrossRef]
- Hussain, M.E.; Haque, M. Impact of Economic Freedom on the Growth Rate: A Panel Data Analysis. Economies 2016, 4, 5. [Google Scholar] [CrossRef]
- Morrison, P.M. Meeting the Environmental Challenge with Technology. In Proceedings of the SPE Digital Energy Conference and Exhibition, The Woodlands, TX, USA, 19–21 April 2011. [Google Scholar]
- Zhao, H.; Guo, S.; Zhao, H. Impacts of GDP, Fossil Fuel Energy Consumption, Energy Consumption Intensity, and Economic Structure on SO2 Emissions: A Multi-Variate Panel Data Model Analysis on Selected Chinese Provinces. Sustainability 2018, 10, 657. [Google Scholar] [CrossRef]
- Liu, Y. Energy Production and Regional Economic Growth in China: A More Comprehensive Analysis Using a Panel Model. Energies 2013, 6, 1409–1420. [Google Scholar] [CrossRef]
- Georgescu-Roegen, N. The Entropy Law and Economic Processes; Harvard University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Lahti, T.; Wincent, J.; Parida, V. A Definition and Theoretical Review of the Circular Economy, Value Creation, and Sustainable Business Models: Where Are We Now and Where Should Research Move in the Future? Sustainability 2018, 10, 2799. [Google Scholar] [CrossRef]
- De Almeida, S.T.; Borsato, M. Assessing the efficiency of End of Life technology in waste treatment—A bibliometric literature review. Resour. Conserv. Recycl. 2019, 140, 189–208. [Google Scholar] [CrossRef]
- Bernstad Saraiva, A.; Souza, R.G.; Mahler, C.F.; Valle, R.A.B. Consequential lifecycle modelling of solid waste management systems—Reviewing choices and exploring their consequences. J. Clean. Prod. 2018, 202, 488–496. [Google Scholar] [CrossRef]
- Tseng, M.L.; Wong, W.P.; Soh, K.L. An overview of the substance of Resource, Conservation and Recycling. Resour. Conserv. Recycl. 2018, 136, 367–375. [Google Scholar] [CrossRef]
- Xiao, S.; Dong, H.; Geng, Y.; Brander, M. An overview of China’s recyclable waste recycling and recommendations for integrated solutions. Resour. Conserv. Recycl. 2018, 134, 112–120. [Google Scholar] [CrossRef]
- Nuñez-Cacho, P.; Górecki, J.; Molina-Moreno, V.; Corpas-Iglesias, F.A. What Gets Measured, Gets Done: Development of a Circular Economy Measurement Scale for Building Industry. Sustainability 2018, 10, 2340. [Google Scholar] [CrossRef]
- Andersen, P. What Is Web 2.0?: Ideas, Technologies and Implications for Education; JISC: Bristol, UK, 2007; Volume 1, pp. 1–64. [Google Scholar]
- Perman, R.; Ma, Y.; McGilvray, J.; Common, M. Natural Resource and Environmental Economics; Pearson Education: London, UK, 2003. [Google Scholar]
- Cleary, J. Life cycle assessments of municipal solid waste management systems: A comparative analysis of selected peer-reviewed literature. Environ. Int. 2009, 35, 1256–1266. [Google Scholar] [CrossRef] [PubMed]
- Pearce, D.; Turner, R.K. Economics of Natural Resources and the Environment; Harvester Wheatsheaf: London, UK, 1990. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Commemorative Edition; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Rényi, A. On Measures of Entropy and Information; Hungarian Academy of Sciences: Budapest, Hungary, 1961. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Tikhomirov, V.M. ε-entropy and ε-capacity of sets in function spaces. Uspekhi Mat. Nauk. 1959, 14, 3–86. [Google Scholar]
- Cannon, W.R.; Zucker, J.D.; Baxter, D.J.; Kumar, N.; Baker, S.E.; Hurley, J.M.; Dunlap, J.C. Prediction of Metabolite Concentrations, Rate Constants and Post-Translational Regulation Using Maximum Entropy-Based Simulations with Application to Central Metabolism of Neurospora crassa. Processes 2018, 6, 63. [Google Scholar] [CrossRef]
- Sherwin, W.B. Entropy, or Information, Unifies Ecology and Evolution and Beyond. Entropy 2018, 20, 727. [Google Scholar] [CrossRef]
- Baravalle, R.; Rosso, O.; Montani, F. Causal Shannon–Fisher Characterization of Motor/Imagery Movements in EEG. Entropy 2018, 20, 660. [Google Scholar] [CrossRef]
- Luo, Z.; Xie, F.; Zhang, B.; Qiu, D. Quantifying the Nonlinear Dynamic Behavior of the DC-DC Converter via Permutation Entropy. Energies 2018, 11, 2747. [Google Scholar] [CrossRef]
- Dai, S.; Niu, D. Comprehensive Evaluation of the Sustainable Development of Power Grid Enterprises Based on the Model of Fuzzy Group Ideal Point Method and Combination Weighting Method with Improved Group Order Relation Method and Entropy Weight Method. Sustainability 2017, 9, 1900. [Google Scholar]
- Huo, W.; Huang, Y.; Pei, J.; Zhang, Q.; Gu, Q.; Yang, J. Ship Detection from Ocean SAR Image Based on Local Contrast Variance Weighted Information Entropy. Sensors 2018, 18, 1196. [Google Scholar] [CrossRef] [PubMed]
- Brock, W.A.; Taylor, M.S. Economic growth and the environment: A review of theory and empirics. In Handbook of Economic Growth; Atlanta, GA, USA, 2005; Volume 1, pp. 1749–1821. Available online: http://www.sciencedirect.com/science/article/pii/S1574068405010282 (accessed on 14 June 2018).
- Lyasnikov, N.V.; Dudin, M.N.; Sekerin, V.D.; Veselovsky, M.Y.; Aleksakhina, V.G. The national innovation system: The conditions of its making and factors in its development. Life Sci. J. 2014, 11, 535–538. [Google Scholar]
- Mankiw, N.G.; Romer, D.; Weil, D.N. A contribution to the empirics of economic growth. Q. J. Econ. 1992, 107, 407–437. [Google Scholar] [CrossRef]
- Schmidheiny, K. Panel Data: Fixed and Random Effects; Basel Universität: Basel, Switzerland, 2016; Available online: http://www.schmidheiny.name/teaching/panel2up.pdf (accessed on 18 May 2018).
- Barro, R.J. Health and economic growth. Ann. Econ. Financ. 2013, 14, 329–366. [Google Scholar]
- Solow, R.M. A Contribution to the Theory of Economic Growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Swan, T.W. Economic growth and capital accumulation. Econ. Rec. 1956, 32, 334–361. [Google Scholar] [CrossRef]
- Busu, M.; Gyorgy, A. Real Convergence, Steps from Adherence to Integration of the Countries from Central and Eastern Europe. Amfiteatru Econ. J. 2016, 18, 303–316. [Google Scholar]
- Pett, M.A.; Lackey, N.R.; Sullivan, J.J. Making Sense of Factor Analysis: The Use of Factor Analysis for Instrument Development in Health Care Research; Sage: Newcastle upon Tyne, UK, 2003. [Google Scholar]
- Weinberg, D.; Carmeli, A. Exploring the antecedents of relationship commitment in an import–export dyad. In New Perspectives in International Business Research; Feldman, M.P., Santangelo, G.D., Eds.; Emerald: Bingley, UK, 2008; pp. 113–136. [Google Scholar]
- Urban, M. The Influence of Blockholders on Agency Costs and Firm Value an Empirical Examination of Blockholder Characteristics and Interrelationships for German Listed Firms; Springer: Berlin, Germany, 2015. [Google Scholar]
- Block, J. Long-Term Orientation of Family Firms: An Investigation of R&D Investments, Downsizing Practices, and Executive Pay; Gabler: Wiesbaden, Germany, 2009. [Google Scholar]
- Puigcerver-Peñalver, M.C. The impact of structural funds policy on European regions’ growth. A theoretical and empirical approach. Eur. J. Comp. Econ. 2007, 4, 179. [Google Scholar]
- Monge, M.A.S.; Vidal, J.M.; Villalba, L.J.G. Entropy-Based Economic Denial of Sustainability Detection. Entropy 2017, 19, 649. [Google Scholar] [CrossRef]
- Ranjbari, M.; Morales-Alonso, G.; Carrasco-Gallego, R. Conceptualizing the Sharing Economy through Presenting a Comprehensive Framework. Sustainability 2018, 10, 2336. [Google Scholar] [CrossRef]
- Su, B.; Heshmati, A.; Geng, Y.; Yu, X. A review of the circular economy in China: Moving from rhetoric to implementation. J. Clean. Prod. 2013, 42, 215–227. [Google Scholar] [CrossRef]
- Ghisellini, P.; Cialani, C.; Ulgiati, S. A review on circular economy: The expected transition to a balanced interplay of environmental and economic systems. J. Clean. Prod. 2016, 114, 11–32. [Google Scholar] [CrossRef]
- Yao, L.; Wu, W.; Kang, Y.; Li, L. Fault Diagnosis and Minimum Rational Entropy Fault Tolerant Control of Stochastic Distribution Collaborative Systems. Entropy 2018, 20, 820. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, Y.; Jiang, H.; Fan, S. Non-Gaussian Systems Control Performance Assessment Based on Rational Entropy. Entropy 2018, 20, 331. [Google Scholar] [CrossRef]
- De Montis, A.; Caschili, S.; Chessa, A. Commuter networks and community detection: A method for planning sub-regional areas. Eur. Phys. J. Spéc. Top. 2013, 215, 75–91. [Google Scholar] [CrossRef]
- Vuţă, M.; Vuţă, M.; Enciu, A.; Cioacă, S.I. Assessment of the Circular Economy's Impact in the EU Economic Growth. Amfiteatru Econ. 2018, 20, 248–261. [Google Scholar]
- Preston, F. A Global Redesign?: Shaping the Circular Economy; Chatham House: London, UK, 2012; Available online: https://www.bitcni.org.uk/wp-content/uploads/2014/11/bp0312_preston.pdf (accessed on 11 October 2017).
- Malecki, E.; Moriset, B. The Digital Economy; Routledge: London, UK, 2008. [Google Scholar]
- World Bank. World Development Report 2017: Governance and the Law; World Bank: Washington, DC, USA, 2017. [Google Scholar]
| Country | Recycling (%) | GDP Per Capita ($) |
|---|---|---|
| Austria | 59.2 | 47,291 |
| Belgium | 54.6 | 43,324 |
| Bulgaria | 19.1 | 8032 |
| Cyprus | 4.2 | 25,234 |
| Czech Republic | 7.4 | 20,368 |
| Denmark | 41.8 | 56,308 |
| Estonia | 17.4 | 19,705 |
| Finland | 33.6 | 45,703 |
| France | 30.6 | 38,477 |
| Germany | 62.1 | 44,470 |
| Greece | 12.8 | 18,613 |
| Hungary | 10.4 | 14,225 |
| Ireland | 33.1 | 69,331 |
| Italy | 19.2 | 31,953 |
| Latvia | 4.5 | 15,594 |
| Lithuania | 1.9 | 16,681 |
| Luxembourg | 43.7 | 104,103 |
| Malta | 13.4 | 26,946 |
| Netherlands | 46.8 | 48,223 |
| Poland | 15.9 | 13,812 |
| Portugal | 15.9 | 21,136 |
| Romania | 1.8 | 10,814 |
| Slovakia | 4.1 | 17,605 |
| Slovenia | 15.4 | 23,597 |
| Spain | 31.2 | 28,157 |
| Sweden | 47.9 | 53,442 |
| UK | 30.3 | 39,720 |
| Country | Y1 | Y2 | Z1 | Z2 | U1 | U2 |
|---|---|---|---|---|---|---|
| Austria | 0.12849 | 0.12849 | 0.12849 | 0.12849 | 0.12849 | 0.12849 |
| Belgium | 0.57259 | 0.65302 | 131.667 | 176.780 | 213.332 | 258.445 |
| Bulgaria | 0.49847 | 0.44311 | 105.081 | 0.93704 | 186.746 | 175.369 |
| Croatia | 0.11464 | 0.10399 | −0.32592 | −0.40509 | 0.49073 | 0.41156 |
| Czech Republic | 0.09085 | 0.08407 | −0.41127 | −0.48393 | 0.40538 | 0.33272 |
| Cyprus | 0.02292 | 0.03152 | −0.65491 | −0.69191 | 0.16174 | 0.12474 |
| Denmark | 0.18883 | 0.16218 | −0.05981 | −0.17479 | 0.75684 | 0.64186 |
| Estonia | 0.12849 | 0.12849 | 0.12849 | 0.12849 | 0.12849 | 0.12849 |
| Finland | 0.57259 | 0.65302 | 78.495 | 176.780 | 160.160 | 92.293 |
| France | 0.49847 | 0.44311 | 51.909 | 0.93705 | 133.574 | 9.217 |
| Germany | 0.11464 | 0.10399 | −0.32592 | −0.40509 | 0.49073 | 0.41156 |
| Greece | 0.09085 | 0.08407 | −0.41127 | −0.48393 | 0.40538 | 0.33272 |
| Hungary | 0.02292 | 0.03152 | −0.65491 | −0.69191 | 0.16174 | 0.12474 |
| Ireland | 0.18883 | 0.16218 | −0.05981 | −0.17479 | 0.75684 | 0.64186 |
| Italy | 0.12849 | 0.12849 | 0.12849 | 0.12849 | 0.12849 | 0.12849 |
| Latvia | 0.57259 | 0.65302 | 25.323 | 176.780 | 106.988 | −73.859 |
| Lithuania | 0.49847 | 0.44311 | −1.263 | 0.93706 | 80.402 | −156.935 |
| Luxembourg | 0.11464 | 0.10399 | −0.32592 | −0.40509 | 0.49073 | 0.41156 |
| Malta | 0.09085 | 0.08407 | −0.41127 | −0.48393 | 0.40538 | 0.33272 |
| Netherlands | 0.02292 | 0.03152 | −0.65491 | −0.69191 | 0.16174 | 0.12474 |
| Poland | 0.18883 | 0.16218 | −0.05981 | −0.17479 | 0.75684 | 0.64186 |
| Portugal | 0.12849 | 0.12849 | 0.12849 | 0.12849 | 0.12849 | 0.12849 |
| Romania | 0.57259 | 0.65302 | 0.21495 | 176.780 | 160.160 | 92.293 |
| Slovakia | 0.49847 | 0.103654 | 0.93705 | 51.909 | 133.574 | 9.217 |
| Slovenia | 0.11464 | 0.10399 | −0.32592 | −0.40509 | 0.49073 | 0.41156 |
| Spain | 0.09085 | 0.08407 | −0.41127 | −0.48393 | 0.40538 | 0.33272 |
| Sweden | 0.02292 | 0.03152 | −0.65491 | −0.69191 | 0.16174 | 0.12474 |
| UK | 0.18883 | 0.16218 | −0.05981 | −0.17479 | 0.75684 | 0.64186 |
| Country | P1 | P2 |
|---|---|---|
| Austria | 0.11464 | 0.10399 |
| Belgium | 0.09085 | 0.08407 |
| Bulgaria | 0.02292 | 0.03152 |
| Croatia | 0.18883 | 0.16218 |
| Czech Republic | 0.12849 | 0.12849 |
| Cyprus | 0.57259 | 0.65302 |
| Denmark | 0.49847 | 0.44311 |
| Estonia | 0.11464 | 0.10399 |
| Finland | 0.09085 | 0.08407 |
| France | 0.09085 | 0.08407 |
| Germany | 0.02292 | 0.03152 |
| Greece | 0.18883 | 0.16218 |
| Hungary | 0.12849 | 0.12849 |
| Ireland | 0.57259 | 0.65302 |
| Italy | 0.49847 | 0.44311 |
| Latvia | 0.11464 | 0.10399 |
| Lithuania | 0.09085 | 0.08407 |
| Luxembourg | 0.02292 | 0.03152 |
| Malta | 0.18883 | 0.16218 |
| Netherlands | 0.49847 | 0.44311 |
| Poland | 0.11464 | 0.10399 |
| Portugal | 0.09085 | 0.08407 |
| Romania | 0.23498 | 0.23587 |
| Slovakia | 0.02292 | 0.03152 |
| Slovenia | 0.45678 | 0.12305 |
| Spain | 0.32976 | 0.21387 |
| Sweden | 0.87142 | 0.16540 |
| UK | 0.01245 | 0.01276 |
| Country | F1 | F2 | Score |
|---|---|---|---|
| Austria | 0.09085 | 0.08407 | 0.17492 |
| Belgium | 0.02292 | 0.03152 | 0.05444 |
| Bulgaria | 0.18883 | 0.16218 | 0.35101 |
| Croatia | 0.11464 | 0.10399 | 0.21863 |
| Czech Republic | 0.09085 | 0.08407 | 0.17492 |
| Cyprus | 0.02292 | 0.03152 | 0.05444 |
| Denmark | 0.18883 | 0.16218 | 0.35101 |
| Estonia | 0.49847 | 0.44311 | 0.94158 |
| Finland | 0.09085 | 0.08407 | 0.17492 |
| France | 0.02292 | 0.03152 | 0.05444 |
| Germany | 0.18883 | 0.16218 | 0.35101 |
| Greece | 0.12849 | 0.12849 | 0.25698 |
| Hungary | 0.57259 | 0.65302 | 122.561 |
| Ireland | 0.09085 | 0.08407 | 0.17492 |
| Italy | 0.02292 | 0.03152 | 0.05444 |
| Latvia | 0.18883 | 0.16218 | 0.35101 |
| Lithuania | 0.12849 | 0.12849 | 0.25698 |
| Luxembourg | 0.57259 | 0.65302 | 122.561 |
| Malta | 0.49847 | 0.44311 | 0.94158 |
| Netherlands | 0.11464 | 0.10399 | 0.21863 |
| Poland | 0.2376 | 0.06534 | 0.30294 |
| Portugal | 0.12765 | 0.54398 | 0.67163 |
| Romania | 0.12673 | 0.07653 | 0.20326 |
| Slovakia | 0.09834 | 0.23476 | 0.33313 |
| Slovenia | 0.10987 | 0.09876 | 0.20863 |
| Spain | 0.1765 | 0.23463 | 0.41113 |
| Sweden | 0.87523 | 0.09823 | 0.97346 |
| UK | 0.10754 | 0.06543 | 0.17297 |
| Country | Outcome |
|---|---|
| Luxembourg | 1 |
| Ireland | 0.77952 |
| Denmark | 0.71611 |
| Sweden | 0.61038 |
| Netherlands | 0.47246 |
| Austria | 0.29624 |
| Finland | 0.24549 |
| Germany | 0.19605 |
| Belgium | 0.15337 |
| UK | 0.13882 |
| France | 0.12903 |
| Italy | 0.12544 |
| Spain | 0.11092 |
| Malta | 0.10964 |
| Cyprus | 0.08766 |
| Slovenia | 0.06607 |
| Portugal | 0.04724 |
| Czech Republic | 0.04724 |
| Estonia | 0.03048 |
| Greece | 0.03558 |
| Slovakia | 0.02696 |
| Lithuania | 0.01522 |
| Latvia | 0.00354 |
| Hungary | 0.00287 |
| Poland | 0.00201 |
| Romania | 0.00132 |
| Bulgaria | 0.00076 |
| Country | Outcome | R&D Investment | Efficiency Index |
|---|---|---|---|
| Austria | 0.2962 | 0.9876 | 0.3000 |
| Belgium | 0.1534 | 0.8112 | 0.1891 |
| Bulgaria | 0.0008 | 0.0089 | 0.0854 |
| Cyprus | 0.0877 | 0.0193 | 4.5420 |
| Czech Republic | 0.0472 | 0.2726 | 0.1733 |
| Denmark | 0.7161 | 1.0365 | 0.6909 |
| Estonia | 0.0305 | 0.0523 | 0.5828 |
| Finland | 0.2455 | 0.6324 | 0.3882 |
| France | 0.1290 | 4.2567 | 0.0303 |
| Germany | 0.1961 | 5.9453 | 0.0330 |
| Greece | 0.0356 | 0.2754 | 0.1292 |
| Hungary | 0.0029 | 0.1126 | 0.0255 |
| Ireland | 0.7795 | 0.3312 | 2.3536 |
| Italy | 0.1254 | 2.7216 | 0.0461 |
| Latvia | 0.0035 | 0.0319 | 0.1110 |
| Lithuania | 0.0152 | 0.0712 | 0.2138 |
| Luxembourg | 1.0000 | 0.1319 | 7.5815 |
| Malta | 0.1096 | 0.0483 | 2.2700 |
| Netherlands | 0.4725 | 1.8995 | 0.2487 |
| Poland | 0.0020 | 0.4312 | 0.0047 |
| Portugal | 0.0472 | 0.4321 | 0.1093 |
| Romania | 0.0013 | 0.0698 | 0.0189 |
| Slovakia | 0.0270 | 0.0812 | 0.3320 |
| Slovenia | 0.0661 | 0.0533 | 1.2396 |
| Spain | 0.1109 | 1.7832 | 0.0622 |
| Sweden | 0.6104 | 1.5282 | 0.3994 |
| UK | 0.1388 | 4.2674 | 0.0325 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Busu, C.; Busu, M. Modeling the Circular Economy Processes at the EU Level Using an Evaluation Algorithm Based on Shannon Entropy. Processes 2018, 6, 225. https://doi.org/10.3390/pr6110225
Busu C, Busu M. Modeling the Circular Economy Processes at the EU Level Using an Evaluation Algorithm Based on Shannon Entropy. Processes. 2018; 6(11):225. https://doi.org/10.3390/pr6110225
Chicago/Turabian StyleBusu, Cristian, and Mihail Busu. 2018. "Modeling the Circular Economy Processes at the EU Level Using an Evaluation Algorithm Based on Shannon Entropy" Processes 6, no. 11: 225. https://doi.org/10.3390/pr6110225
APA StyleBusu, C., & Busu, M. (2018). Modeling the Circular Economy Processes at the EU Level Using an Evaluation Algorithm Based on Shannon Entropy. Processes, 6(11), 225. https://doi.org/10.3390/pr6110225






