Simulation of High Pressure Separator Used in Crude Oil Processing
Abstract
:1. Introduction
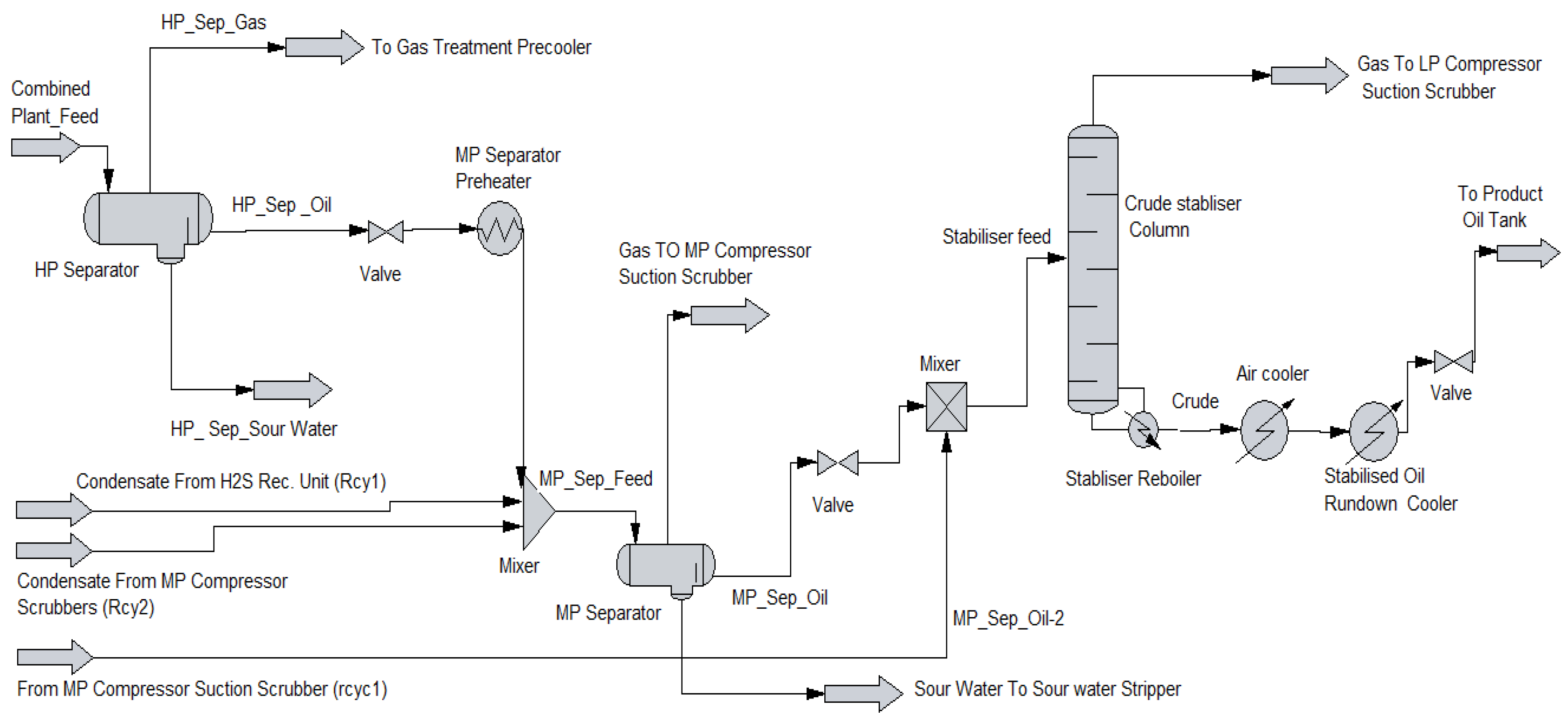
1.1. Separation Vessel Used in Crude Oil Processing
1.2. Simulation Model
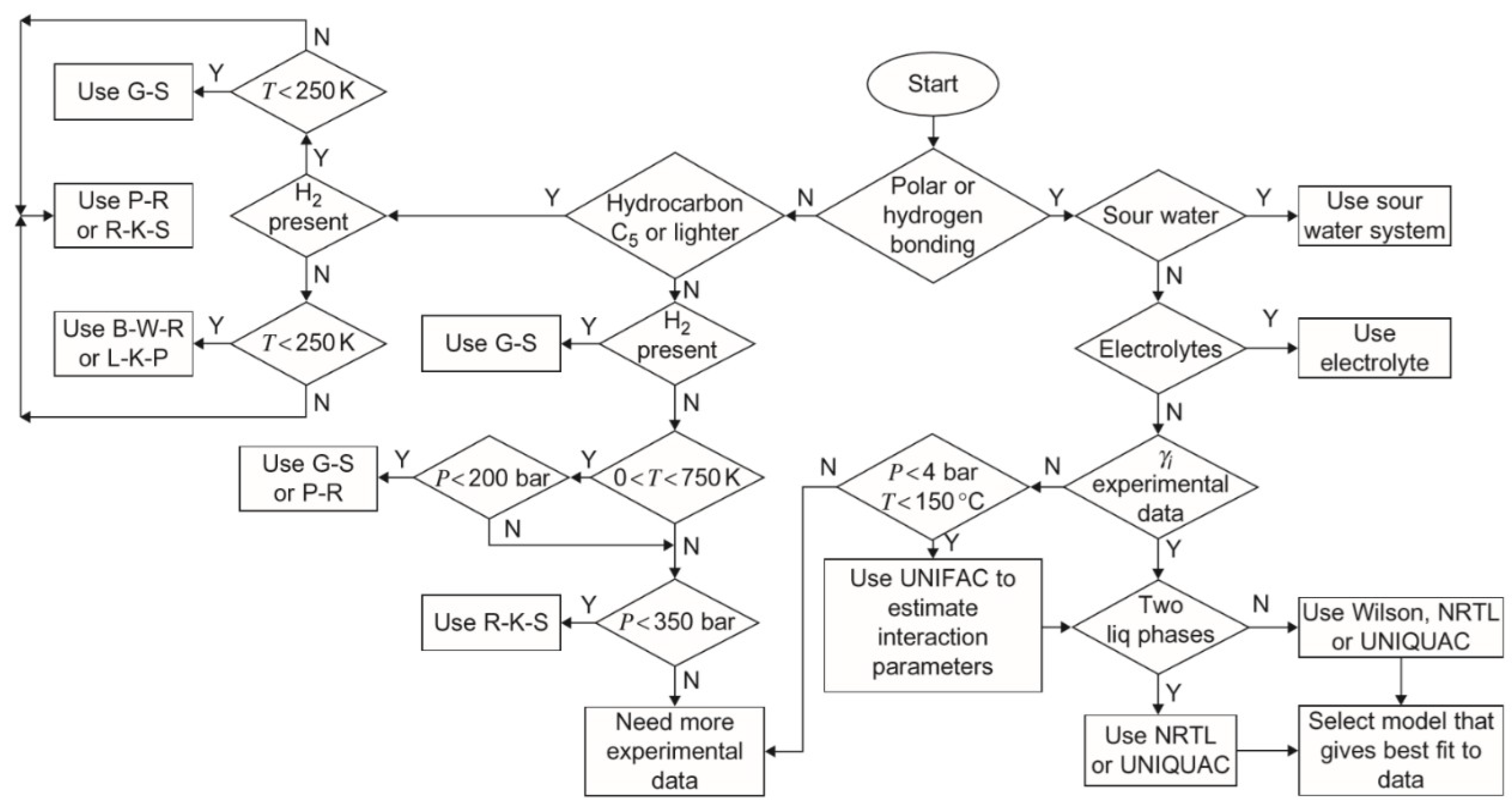
1.3. Simulation and Model Selection
1.4. Research Aim and Outcome
2. Materials and Methods
2.1. Process Simulation
2.2. Thermodynamics Package
2.3. Simulation Conditions
2.4. Sensitivity Study
2.5. Phase Envelope
3. Results and Discussion
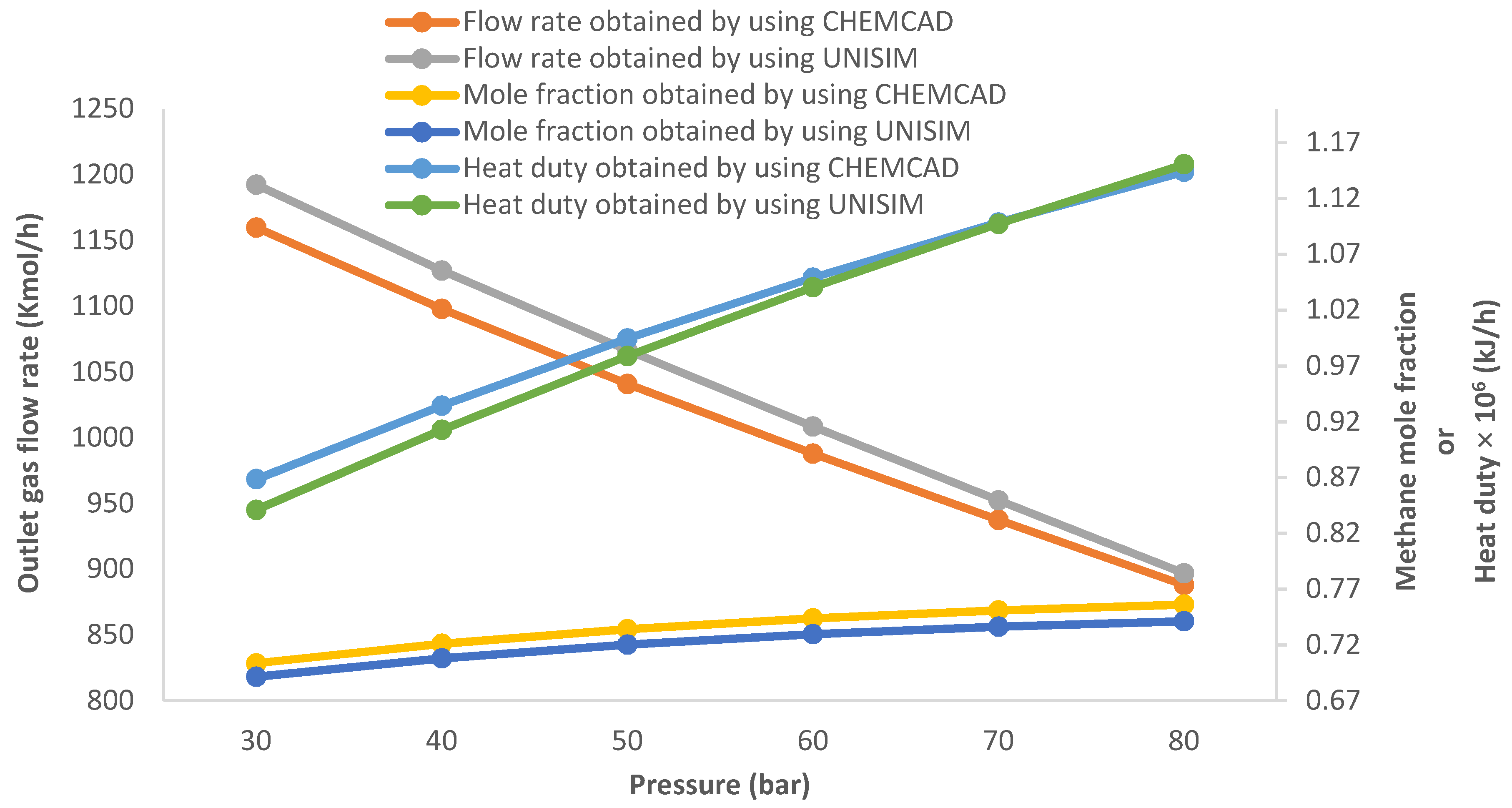
3.1. Effect of Changing the Pressure of the HP Sparator on the Gas Flow Rate, Methane Concentration and Preheater Heating Duty
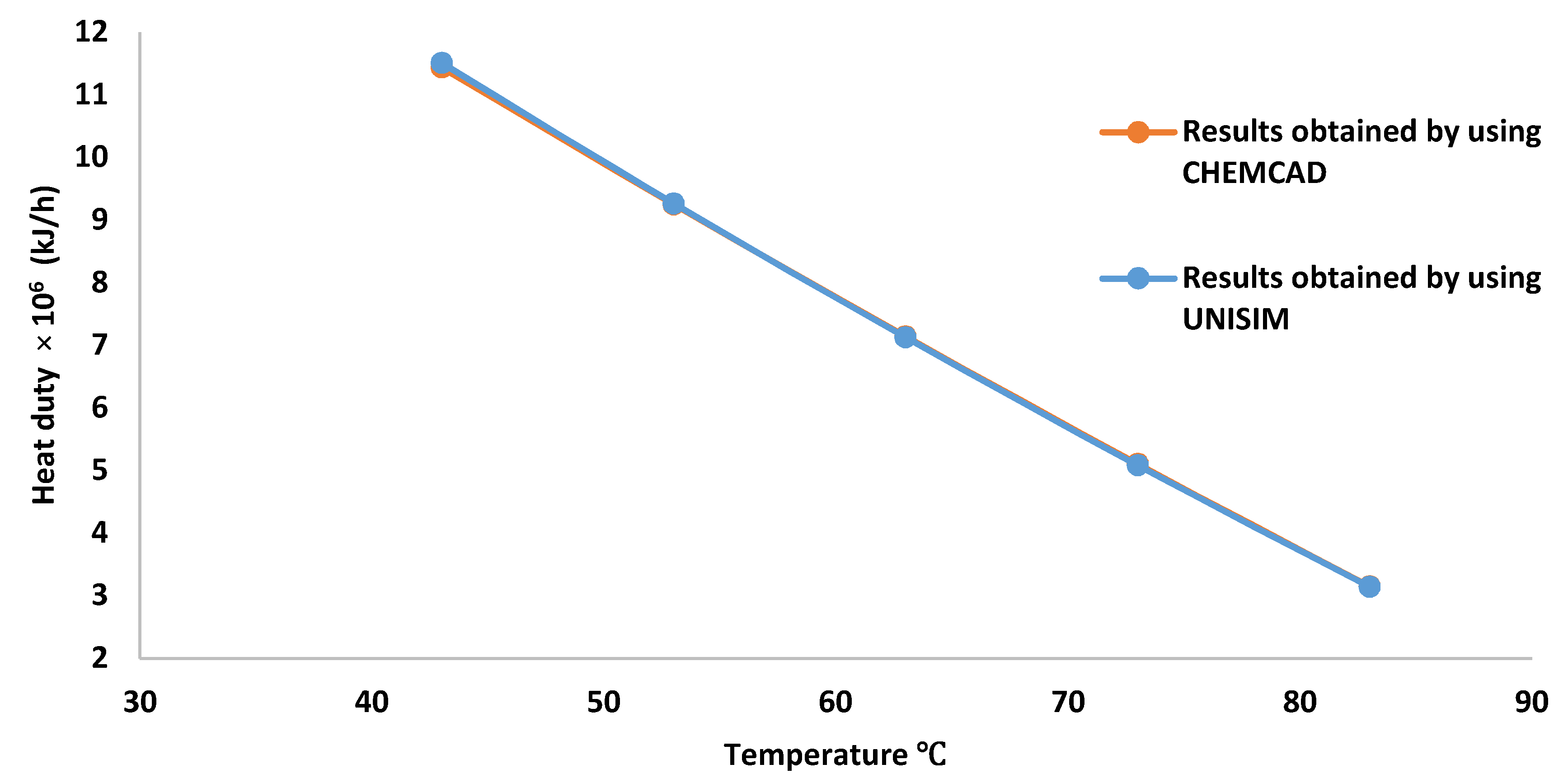
3.2. High Pressure Separator Temperature Effect on the Gas Flow Rate, Methane Concentration and Preheater Heating Duty
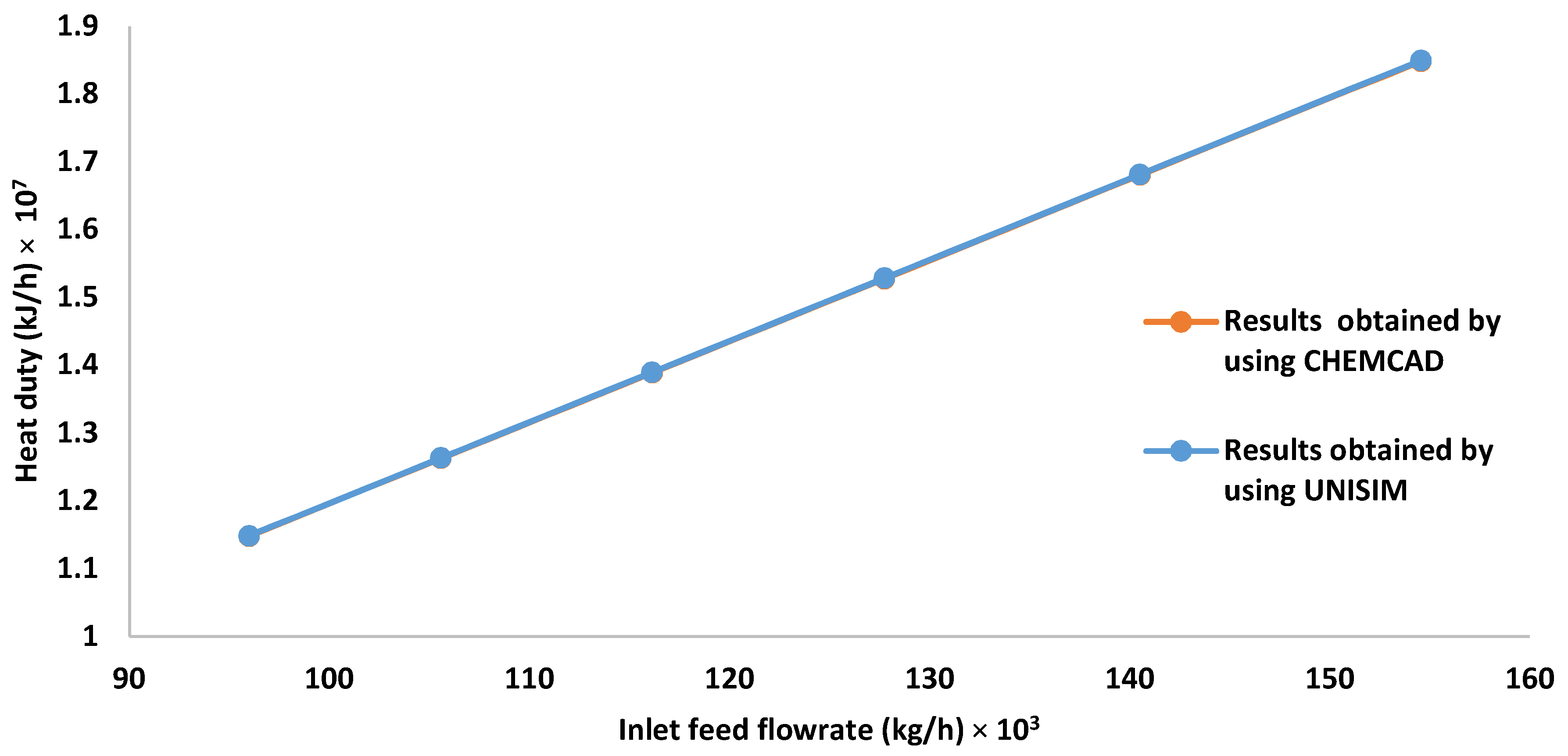
3.3. Effect of Increasing the Inlet HP Separator Feed Flow Rate on the Gas Flow Rate, Methane Mole Fraction, and Heat Required by the Preheater
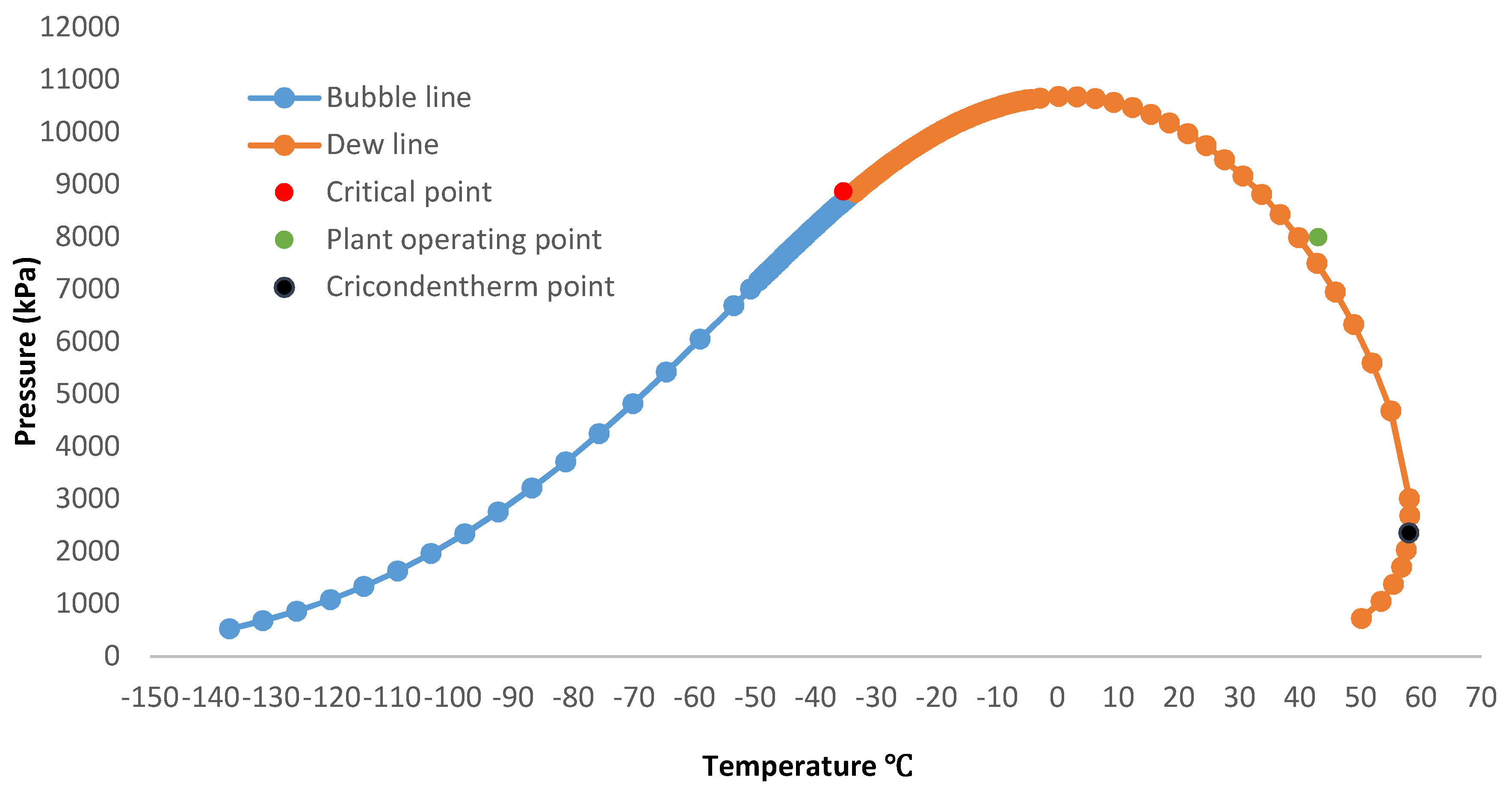
3.4. Phase Envelope
4. Conclusions and Further Work
Conflicts of Interest
Nomenclature
| A | Empirical coefficient, selected by the simulator |
| Empirical coefficient, selected by the simulator | |
| Empirical coefficient, selected by the simulator | |
| Empirical coefficient, selected by the simulator | |
| Attractive parameter in cubic equations of state (J·m3·mol−2) | |
| Empirical coefficient, selected by the simulator | |
| Repulsive parameter in equation of state (m3·mol−1) | |
| Empirical coefficient, selected by the simulator | |
| Empirical coefficient, selected by the simulator | |
| Empirical coefficient, selected by the simulator | |
| K-value of component | |
| Binary interaction parameter in cubic equations of state | |
| Empirical coefficient, selected by the simulator | |
| P | Total pressure (Pa) |
| Pressure of component i at critical point (Pa) | |
| Universal gas constant (J·mol−1·K) | |
| Absolute temperature (K) | |
| Temperature of component i at critical point (K) | |
| Reduced temperature (dimensionless) | |
| V | Volume (m3) |
| Mole fraction of component i in the liquid phase | |
| Mole fraction of component i in the vapor phase | |
| Compressibility factor | |
| Function in cubic equations of state | |
| Fugacity coefficient of component i in liquid phase | |
| Fugacity coefficient of component i in vapor phase | |
| Acentric factor |
References
- Manning, F.S.; Thompson, R.E. Oilfield Processing of Petroleum: Crude Oil; Pennwell Books: Tulsa, OK, USA, 1991; Volume 2. [Google Scholar]
- Mokhatab, S.; Poe, W.A. Handbook of Natural Gas Transmission and Processing; Gulf Professional Publishing: Cambridge, MA, USA, 2012. [Google Scholar]
- Abdel-Aal, H.K.; Aggour, M.A.; Fahim, M.A. Petroleum and Gas Field Processing; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Lieberman, N.P.; Lieberman, E.T. Working Guide to Process Equipment; McGraw-Hill Professional: New York, NY, USA, 2008. [Google Scholar]
- Seader, J.D.; Henley, E.J.; Roper, D.K. Separation Process Principles; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Devold, H. Oil and Gas Production Handbook: An Introduction to Oil and Gas Production; Lulu. com: Morrisville, NC, USA, 2013. [Google Scholar]
- Gudmestad, O.T.; Zolotukhin, A.B.; Jarlsby, E.T. Petroleum Resources with Emphasis on Offshore Fields; WIT Press: Billerica, MA, USA, 2010. [Google Scholar]
- Peng, D.-Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Gmehling, J.; Kolbe, B.; Kleiber, M.; Rarey, J. Chemical Thermodynamics for Process Simulation. Wiley-VCH Verlag &, Co. KGaA: Weinheim, Germany, 2012. [Google Scholar]
- Wei, Y.S.; Sadus, R.J. Equations of state for the calculation of fluid-phase equilibria. AlChE J. 2000, 46, 169–196. [Google Scholar] [CrossRef]
- Gutierrez, J.P.; Benítez, L.A.; Martínez, J.; Ale Ruiz, L.; Erdmann, E. Thermodynamic Properties for the Simulation of Crude Oil Primary Refining. Int. J. Eng. Res. Appl. 2014, 4, 190–194. [Google Scholar]
- Sengers, J.V.; Kayser, R.; Peters, C.; White, H. Equations of State for Fluids and Fluid Mixtures; Elsevier: Amsterdam, The Netherlands, 2000; Volume 5. [Google Scholar]
- Valderrama, J.O. The state of the cubic equations of state. Ind. Eng. Chem. Res. 2003, 42, 1603–1618. [Google Scholar] [CrossRef]
- De Hemptinne, J.C.; Ledanois, J.-M. Select Thermodynamic Models for Process Simulation: A Practical Guide Using a Three Steps Methodology; Editions Technip: Paris, France, 2012. [Google Scholar]
- Chemstations. CHEMCAD Help. 2018. Available online: https://www.chemstations.eu (accessed on 1 October 2018).
- De Hemptinne, J.; Behar, E. Thermodynamic modelling of petroleum fluids. Oil Gas Sci. Technol. Rev. IFP 2006, 61, 303–317. [Google Scholar] [CrossRef]
- Edwards, J.E. Process Modelling Selection of Thermodynamic Methods; P & I Design Ltd.: Thornaby, UK, 2000. [Google Scholar]
- Edwin, M.; Abdulsalam, S.; Muhammad, I.M. Research. Process Simulation and Optimization of Crude Oil Stabilization Scheme Using Aspen-HYSYS Software. Int. J. Recent Trends Eng. Res. 2017, 3. [Google Scholar] [CrossRef]
- Towler, G.; Sinnott, R.K. Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design; Elsevier: Waltham, MA, USA, 2012. [Google Scholar]
- Gil Chaves, I.D.; López, J.R.G.; García Zapata, J.L.; Leguizamón Robayo, A.; Rodríguez Niño, G. Process simulation in chemical engineering. In Process Analysis and Simulation in Chemical Engineering; Springer: Basel, Switzerland, 2016; pp. 1–51. [Google Scholar]
- Michelsen, M.L. Calculation of phase envelopes and critical points for multicomponent mixtures. Fluid Phase Equilib. 1980, 4, 1–10. [Google Scholar] [CrossRef]
| Component | Chemical Formula | Mass Flow Rate (kg/h) |
|---|---|---|
| Hydrogen Sulfide | H2S | 854.1820 |
| Carbon Dioxide | CO2 | 2041.8970 |
| Nitrogen | N2 | 399.9500 |
| Methane | CH4 | 13,924.100 |
| Ethane | C2H6 | 6194.2178 |
| Propane | C3H8 | 6045.8480 |
| I-Butane | C4H10 | 889.7230 |
| N-Butane | C4H10 | 3771.3100 |
| I-Pentane | C5H12 | 1349.6700 |
| N-Pentane | C5H12 | 2748.3030 |
| N-Hexane | C6H14 | 3769.9010 |
| Heptane | C7H16 | 3795.1810 |
| Octane | C8H18 | 4069.6010 |
| Nonane | C9H20 | 3773.9570 |
| Decane | C10H22 | 3366.5690 |
| Undecane | C11H24 | 3173.9910 |
| Dodecane | C12H26 | 2725.6790 |
| Tridecane | C13H28 | 2585.4040 |
| Tetradecane | C14H30 | 2321.1870 |
| Pentadecane | C15H32 | 2065.0300 |
| Hexadecane | C16H34 | 1831.2710 |
| Heptadecane | C17H36 | 1717.1020 |
| Octadecane | C18H38 | 1532.6370 |
| Nonadecane | C19H40 | 1570.9020 |
| Water | H2O | 987.6000 |
| Parameter | Design (Range) | Unit Operating Conditions (Design) | Unit Operating Conditions (Data) | Simulation Data Input |
|---|---|---|---|---|
| Temperature (°C) | −10 to 80 | 20–45 | 43 | 43 |
| Pressure (bar) | Up to 92 | 78–83 | 80 | 80 |
| Feed flow rate (kmol/h) | - | 1215.6480 | 1800.5150 | 1800.5150 |
| Inlet Feed Components | Normalized Inlet Feed Mole Fraction (Provided Data and Simulation) | Normalized Outlet Gas Mole Fraction (Provided Data) | Normalized Outlet Gas Mole Fraction (Simulation) | Normalized Outlet Liquid Phase Stream Product (Provided Data) | Normalized Outlet Liquid Phase Stream Product (Simulation) |
|---|---|---|---|---|---|
| H2S | 0.0143 | 0.0121 | 0.0122 | 0.0175 | 0.0174 |
| CO2 | 0.0264 | 0.0316 | 0.0323 | 0.0224 | 0.0217 |
| Nitrogen | 0.0081 | 0.0139 | 0.0139 | 0.0024 | 0.0023 |
| Methane | 0.4938 | 0.7411 | 0.7560 | 0.2577 | 0.2405 |
| Ethane | 0.1172 | 0.1204 | 0.1126 | 0.1212 | 0.1297 |
| Propane | 0.0780 | 0.0508 | 0.0463 | 0.1125 | 0.1175 |
| i-Butane | 0.0087 | 0.0037 | 0.0034 | 0.0147 | 0.0151 |
| n-Butane | 0.0369 | 0.0133 | 0.0120 | 0.0649 | 0.0663 |
| i-Pentane | 0.0106 | 0.0023 | 0.0022 | 0.0203 | 0.0205 |
| n-Pentane | 0.0217 | 0.0041 | 0.0037 | 0.0421 | 0.0426 |
| n-Hexane | 0.0249 | 0.0024 | 0.0021 | 0.0509 | 0.0512 |
| Heptanes | 0.0215 | 0.0017 | 0.0009 | 0.0444 | 0.0453 |
| Octanes | 0.0203 | 0.0007 | 0.0004 | 0.0428 | 0.0431 |
| Nonanes | 0.0167 | 0.0003 | 0.0002 | 0.0356 | 0.0358 |
| Decanes | 0.0135 | 0.0001 | 0.0001 | 0.0288 | 0.0289 |
| Undecanes | 0.0116 | 0.0001 | 0.0000 | 0.0247 | 0.0248 |
| Dodecanes | 0.0091 | 0.0000 | 0.0000 | 0.0195 | 0.0196 |
| Tridecanes | 0.0080 | 0.0000 | 0.0000 | 0.0171 | 0.0172 |
| Tetradecane | 0.0067 | 0.0000 | 0.0000 | 0.0143 | 0.0143 |
| Pentadecans | 0.0055 | 0.0000 | 0.0000 | 0.0119 | 0.0119 |
| Hexadecanes | 0.0046 | 0.0000 | 0.0000 | 0.0099 | 0.0099 |
| Heptadecane | 0.0041 | 0.0000 | 0.0000 | 0.0087 | 0.0087 |
| Octadecanes | 0.0034 | 0.0000 | 0.0000 | 0.0074 | 0.0074 |
| Nonadecanes | 0.0033 | 0.0000 | 0.0000 | 0.0071 | 0.0072 |
| H2O | 0.0312 | 0.0015 | 0.0015 | 0.0012 | 0.0011 |
| Total | 1 | 1 | 1 | 1 | 1 |
| Separator Temperature (°C) | Gas Flow Rate (kmol/h) | Methane Mole Fraction |
|---|---|---|
| 43 | 871.1500 | 0.7560 |
| 53 | 937.7800 | 0.7399 |
| 63 | 1004.9700 | 0.7241 |
| 73 | 1073.1800 | 0.7086 |
| 83 | 1142.9800 | 0.6934 |
| Separator Temperature (°C) | Gas Flow Rate (kmol/h) | Methane Mole Fraction |
|---|---|---|
| 43 | 896.9400 | 0.7412 |
| 53 | 950.5100 | 0.7248 |
| 63 | 1000.6800 | 0.7089 |
| 73 | 1048.3200 | 0.6935 |
| 83 | 1094.2600 | 0.6783 |
| Inlet Feed Flow Rate × 103 (kg/h) | Outlet Gas Flow Rate × 104 (kmol/h) | Mole Fraction of Methane in the Outlet Gas Stream |
|---|---|---|
| 95.97 | 1.9100 | 0.7560 |
| 105.57 | 2.1009 | 0.7560 |
| 116.12 | 2.3110 | 0.7560 |
| 127.74 | 2.5421 | 0.7560 |
| 140.51 | 2.7964 | 0.7560 |
| 154.56 | 3.0759 | 0.7560 |
| Inlet Feed Flow Rate × 103 (kg/h) | Outlet Gas Flow Rate × 104 (kmol/h) | Mole Fraction of Methane in the Outlet Gas Stream |
|---|---|---|
| 95.97 | 1.9660 | 0.7412 |
| 105.57 | 2.0934 | 0.7412 |
| 116.12 | 2.2302 | 0.7412 |
| 127.74 | 2.3806 | 0.7412 |
| 140.51 | 2.5517 | 0.7412 |
| 154.56 | 2.7562 | 0.7412 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Mhanna, N.M. Simulation of High Pressure Separator Used in Crude Oil Processing. Processes 2018, 6, 219. https://doi.org/10.3390/pr6110219
Al-Mhanna NM. Simulation of High Pressure Separator Used in Crude Oil Processing. Processes. 2018; 6(11):219. https://doi.org/10.3390/pr6110219
Chicago/Turabian StyleAl-Mhanna, Najah M. 2018. "Simulation of High Pressure Separator Used in Crude Oil Processing" Processes 6, no. 11: 219. https://doi.org/10.3390/pr6110219
APA StyleAl-Mhanna, N. M. (2018). Simulation of High Pressure Separator Used in Crude Oil Processing. Processes, 6(11), 219. https://doi.org/10.3390/pr6110219





