Seasonal Operation Strategy Optimization for Integrated Energy Systems with Considering System Cooling Loads Independently
Abstract
:1. Introduction
- (1)
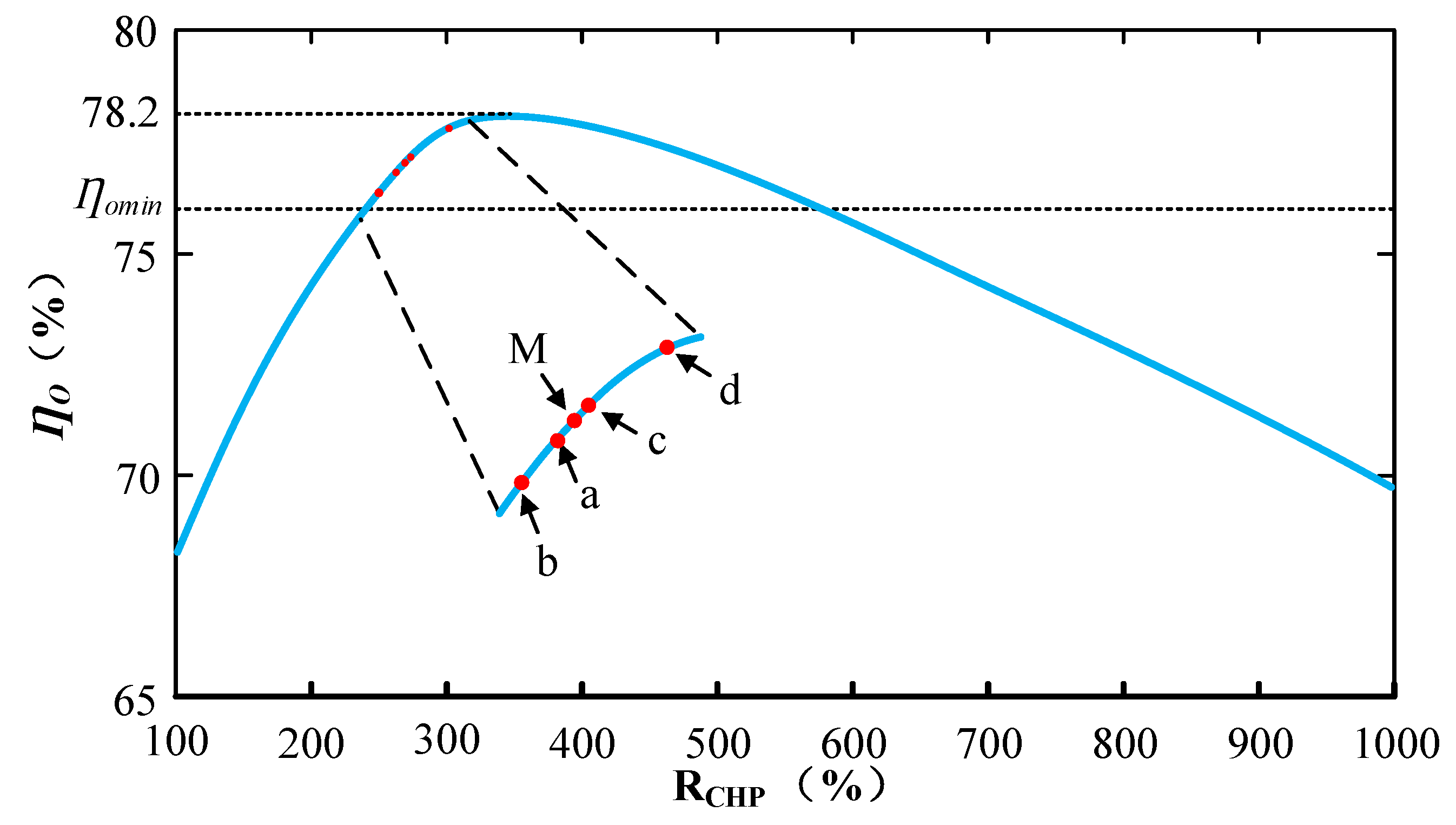
- In most previous studies, the CHP heat to power ratio and energy system heat to power ratio in different seasons were selected as a constant when optimizing CHP operation. In this paper, the state of the art CHP unit with an additionally fired waste heat boiler was introduced to optimize the CHP heat to power ratio in different seasons. The results showed that the average daily fuel costs could be reduced by 5.2% if the CHP heat to power ratio was optimized seasonally.
- (2)
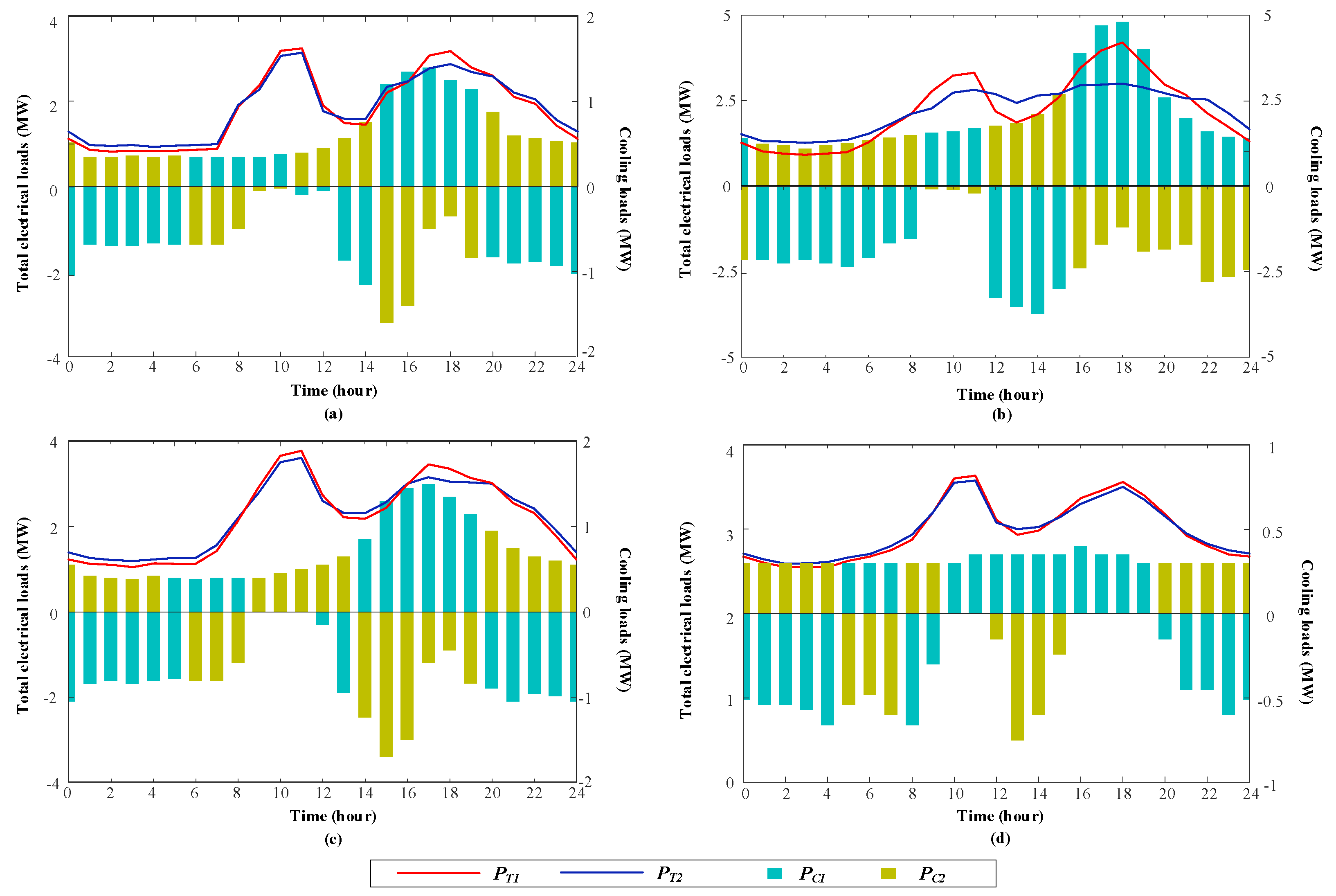
- Compared to the existing literature, system cooling loads were independently considered rather than treated as a part of thermal or electrical loads when optimizing a system operation. Results showed that the peak–valley gap of the power system could be significantly reduced, especially in summer (about 40.7% reduction) if the cooling loads were independently considered.
- (3)
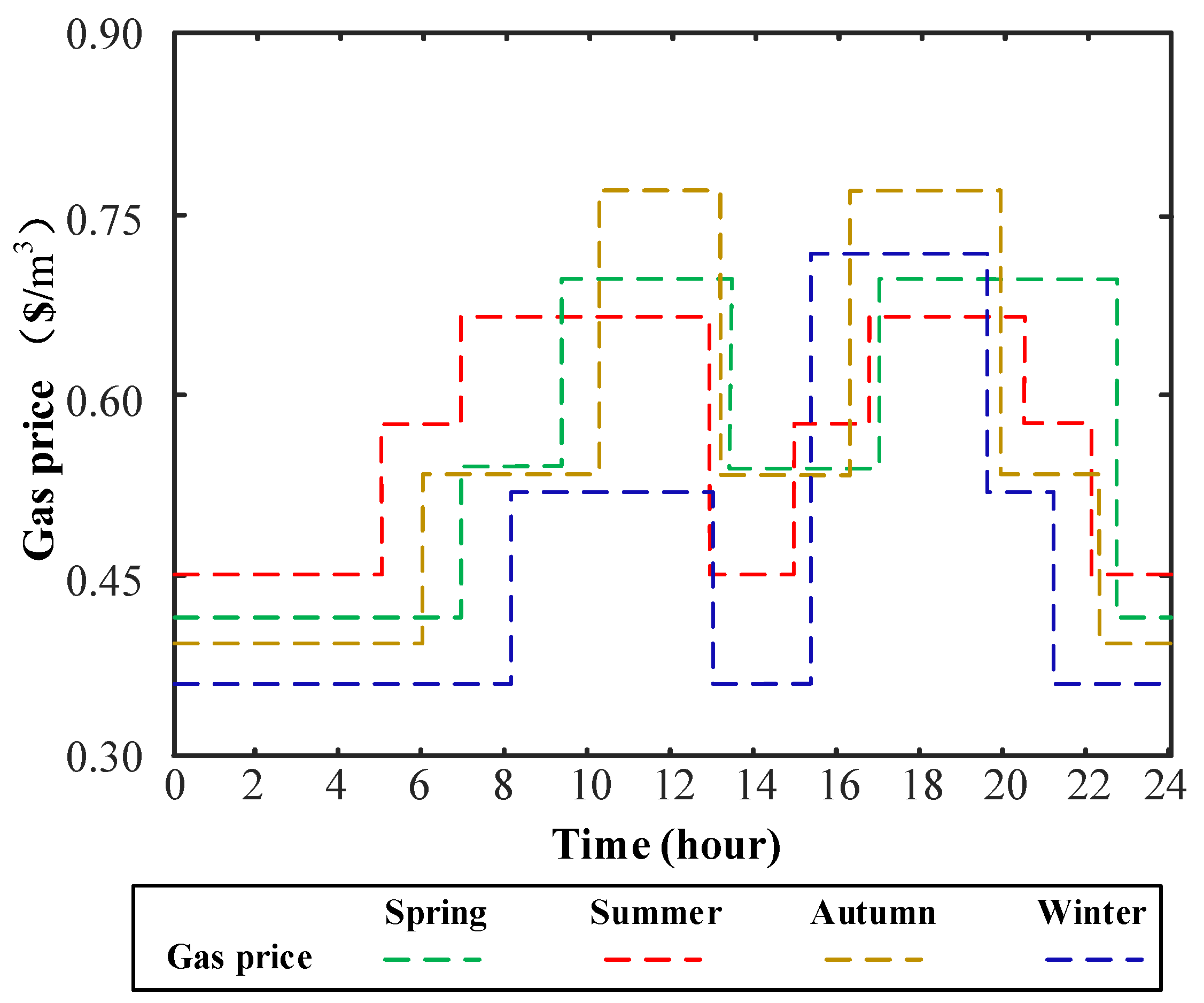
- Different from early research, this paper adopted a time-of-use gas price rather than a constant gas price to optimize the energy system operation. This is because it is believed that the rapid development of CHP and gas boilers can lead to the shortage of natural gas at peak time. Simulation results showed that the average daily thermal production costs could be reduced by 7% when applying the time-of-use gas price. Additionally, adopting time-of-use gas price was conductive to optimizing system configuration.
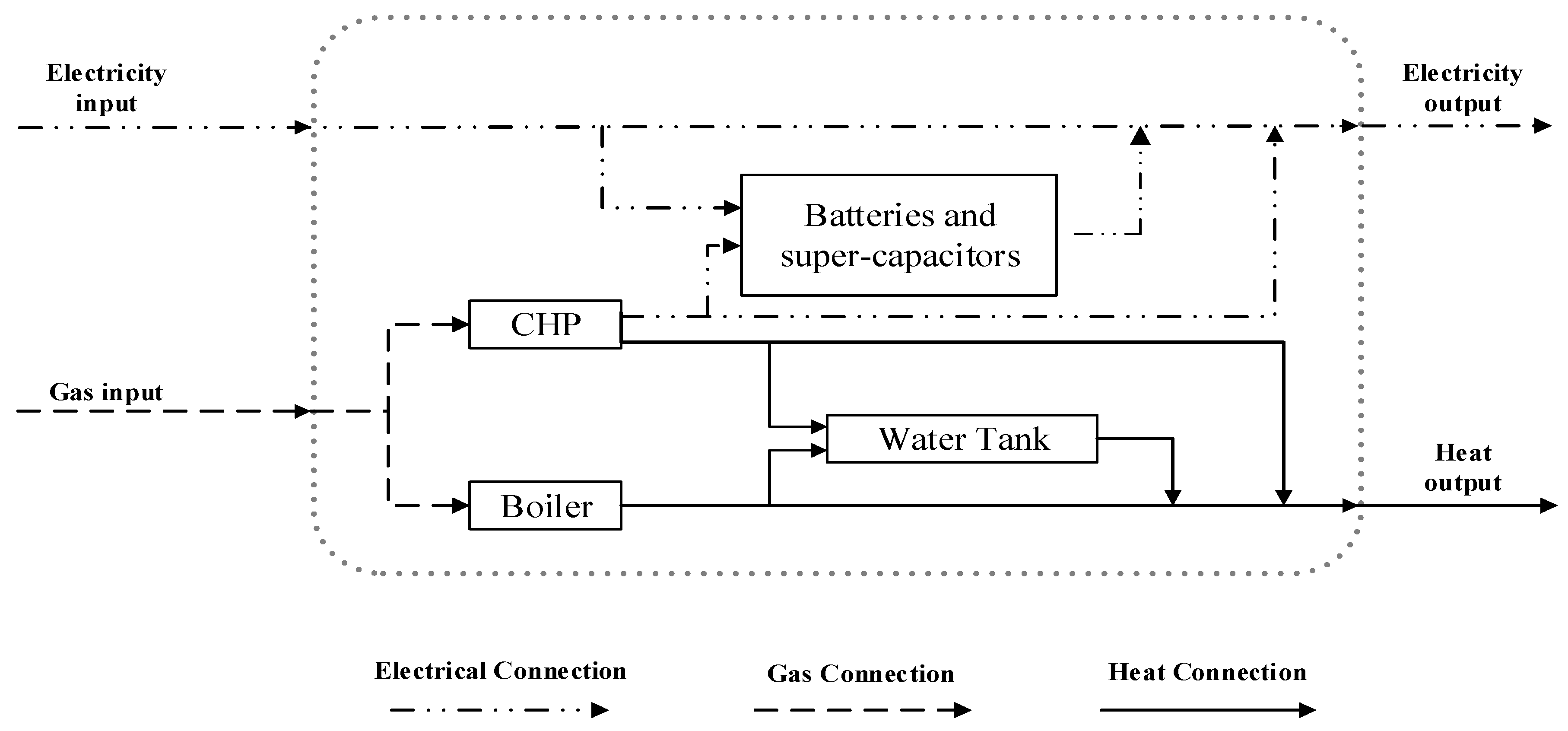
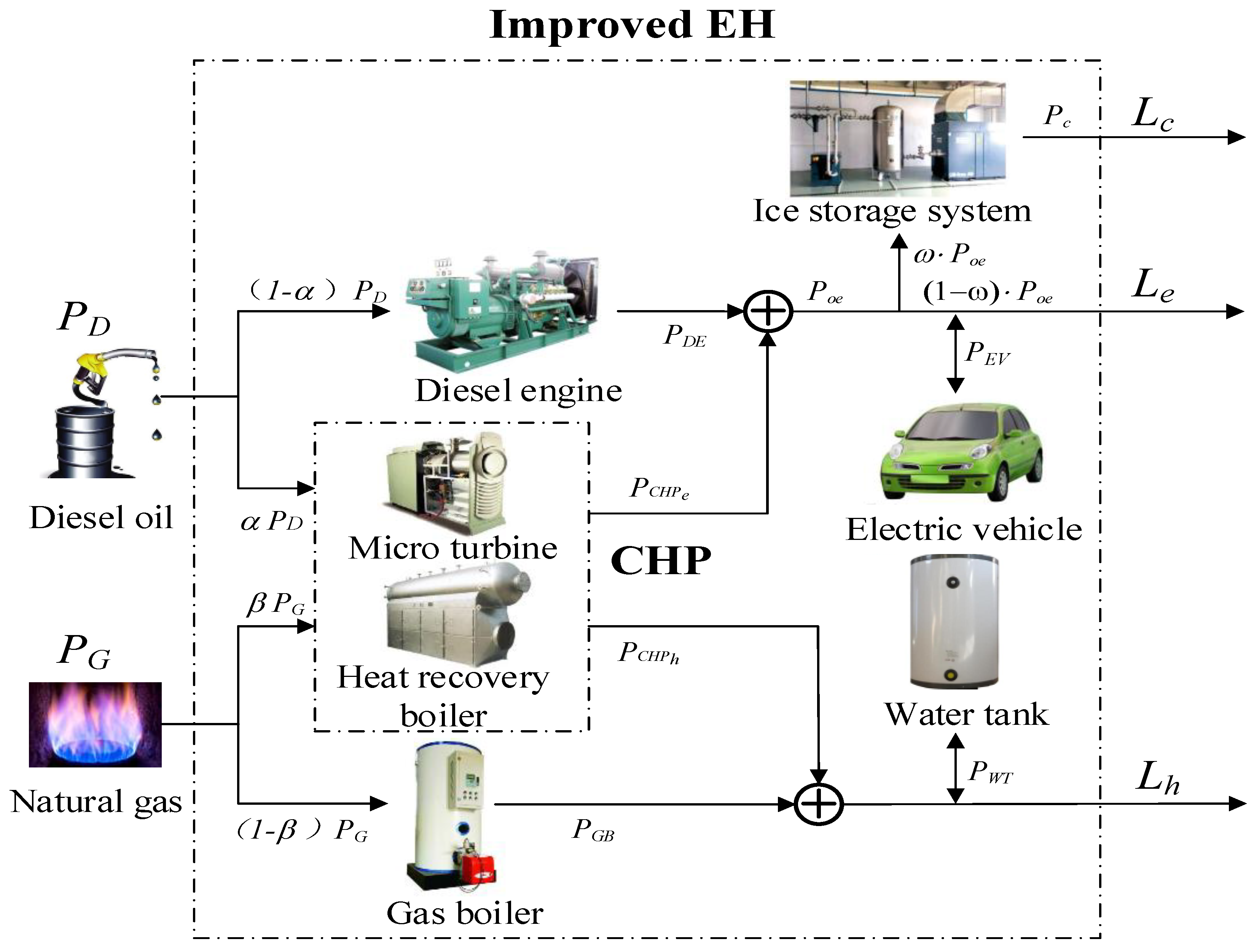
2. Energy Hub Modeling for an Integrated Energy System
2.1. The Energy Hub Model
2.2. Different Energy Carriers’ Output Power Modeling and Operation Constraints
2.2.1. CHP Output Power and Operation Constraints Modeling
2.2.2. Diesel Generator Output Power and Operation Constraints Modeling
2.2.3. Gas Boiler Output Power and Operation Constraints Modeling
2.2.4. Ice Storage System Output Power and Operation Constraints Modeling
2.2.5. Hot Water Tank Output Power and Operation Constraints Modeling
2.2.6. Electric Vehicle Power Exchange Station Output Power and Operation Constraints Modeling
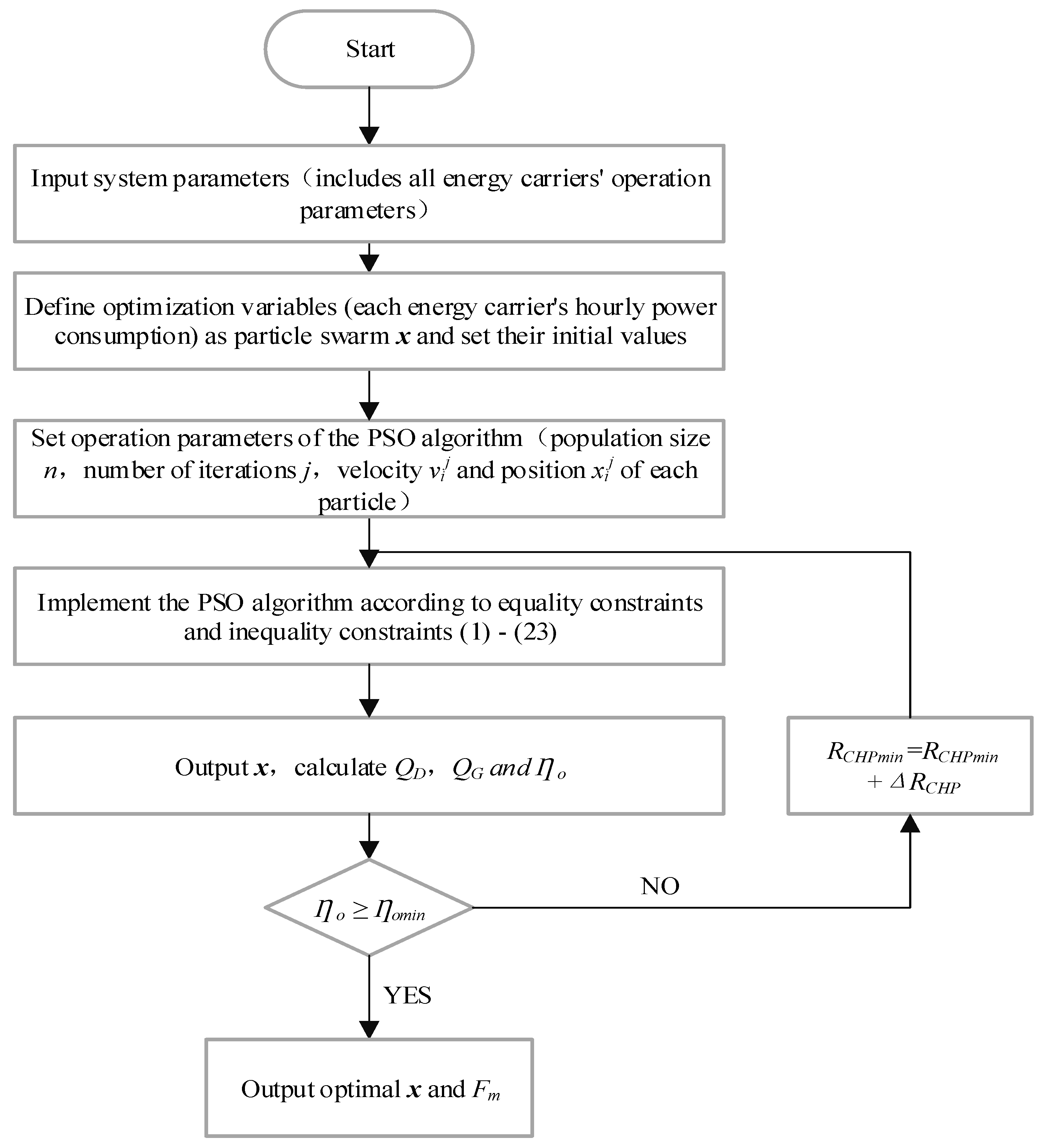
3. System Optimal Operation Strategy
3.1. Objective Function
3.2. Optimization Algorithm
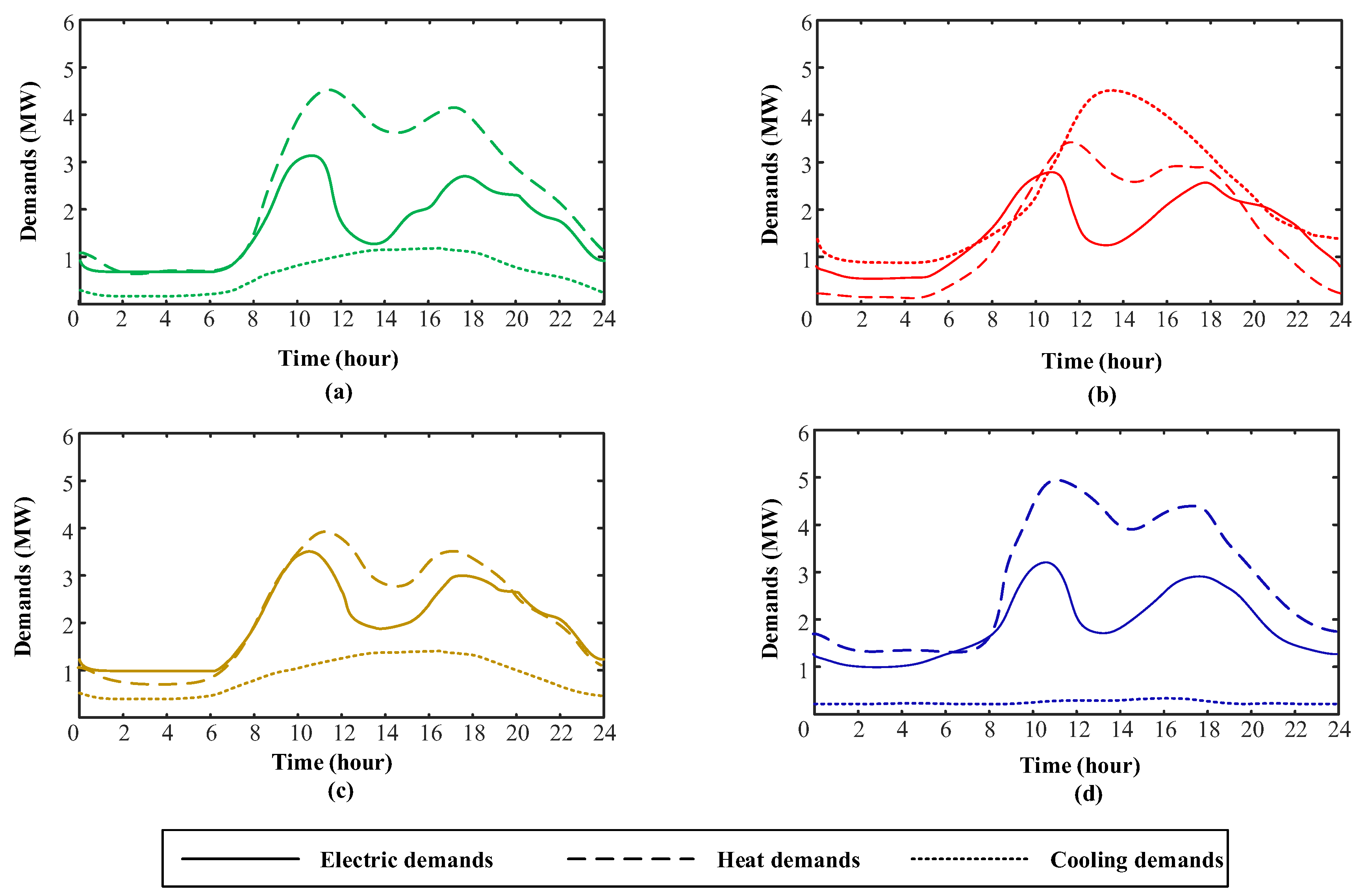
4. Case Study
5. Results and Analysis
5.1. Optimization Results of CHP Heat to Power Ratio
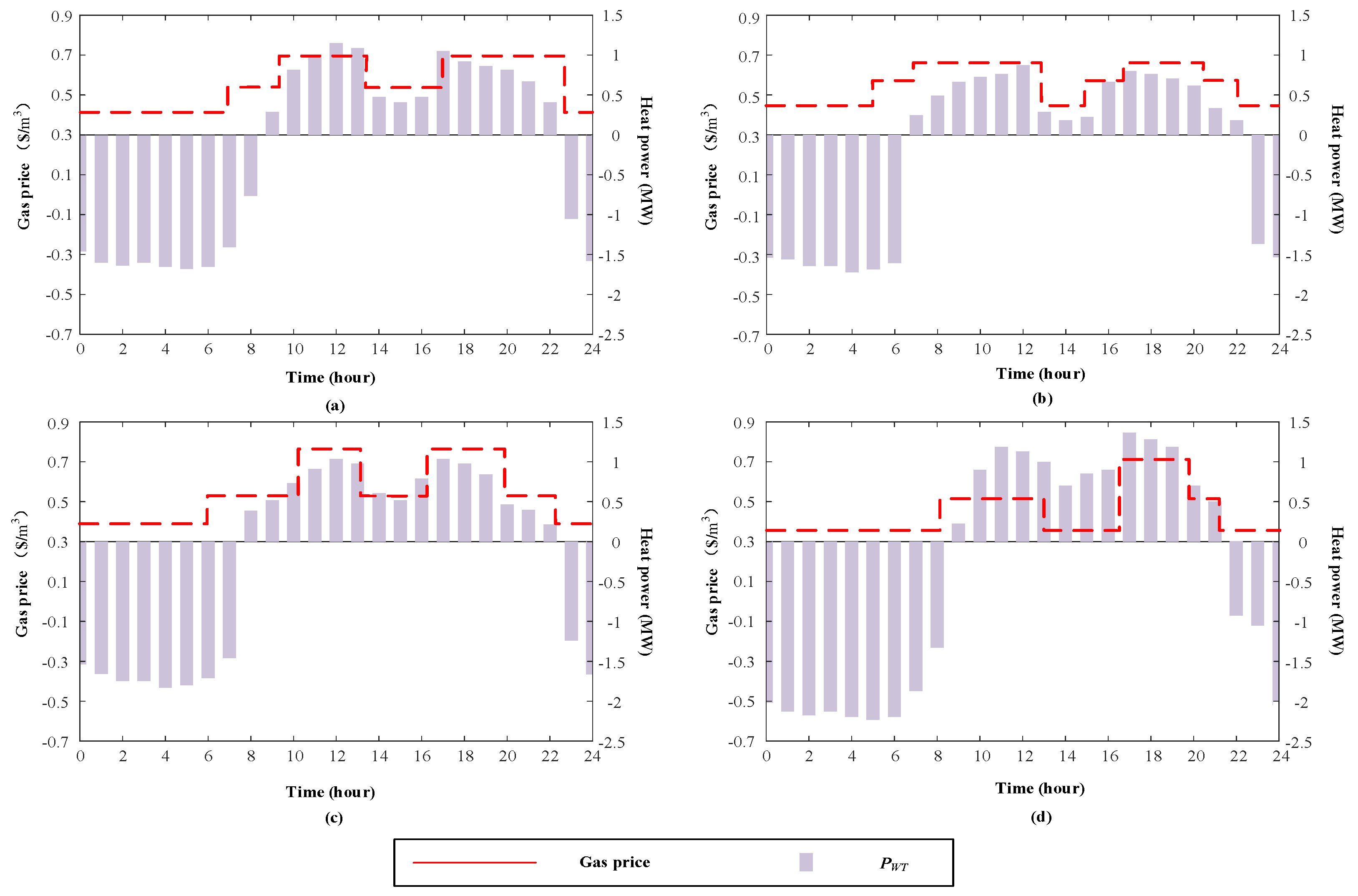
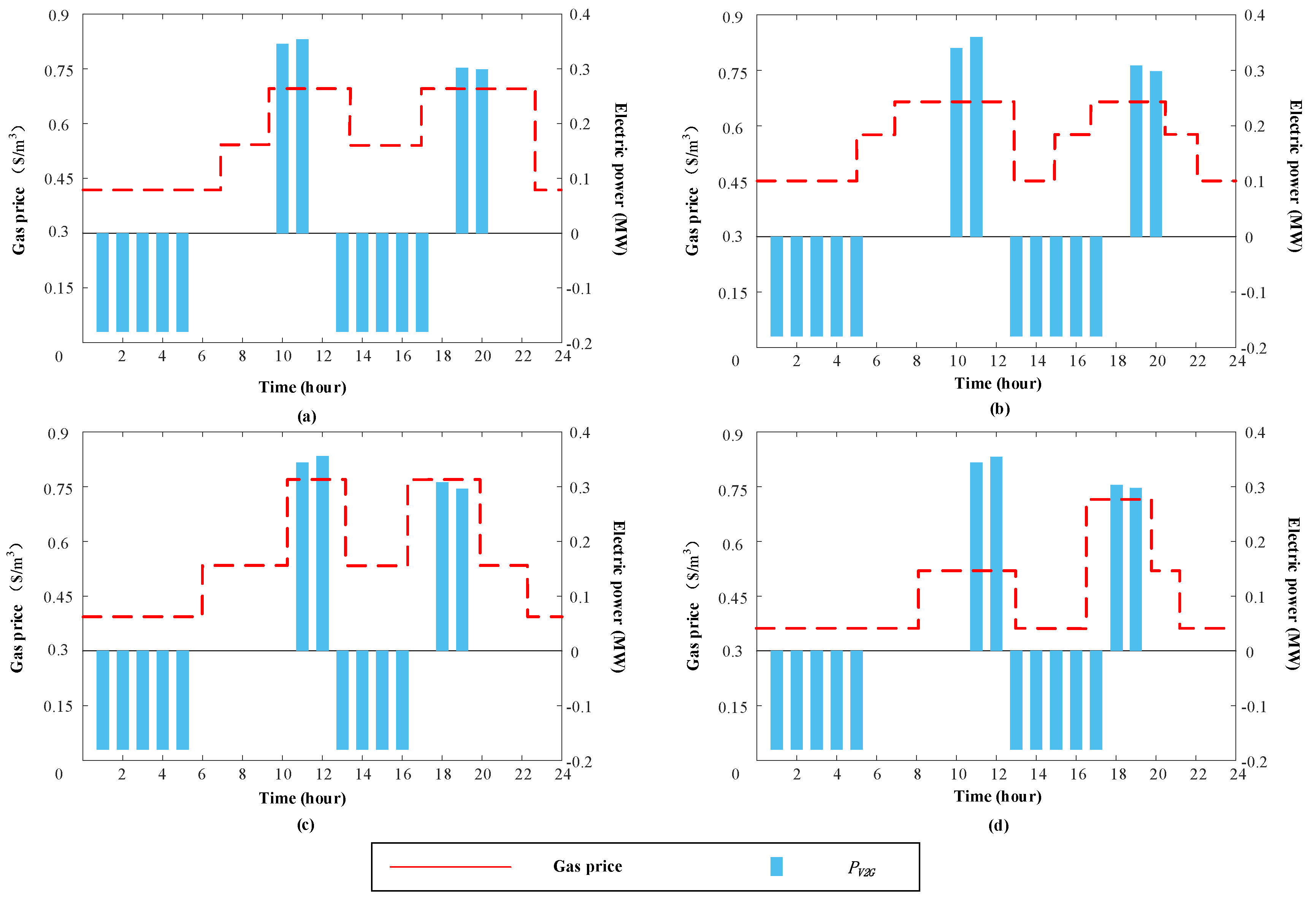
5.2. The Influence of Cooling Loads on System Operation
5.3. System Fuel Costs Optimization under the Time-of-Use Gas Price
6. Conclusions
- (1)
- Taking the seasonal factor into consideration when optimizing the CHP heat to power ratio, the average system fuel costs can be reduced by 5.2% and the CHP heat to power ratio will match up to the system heat to power ratio.
- (2)
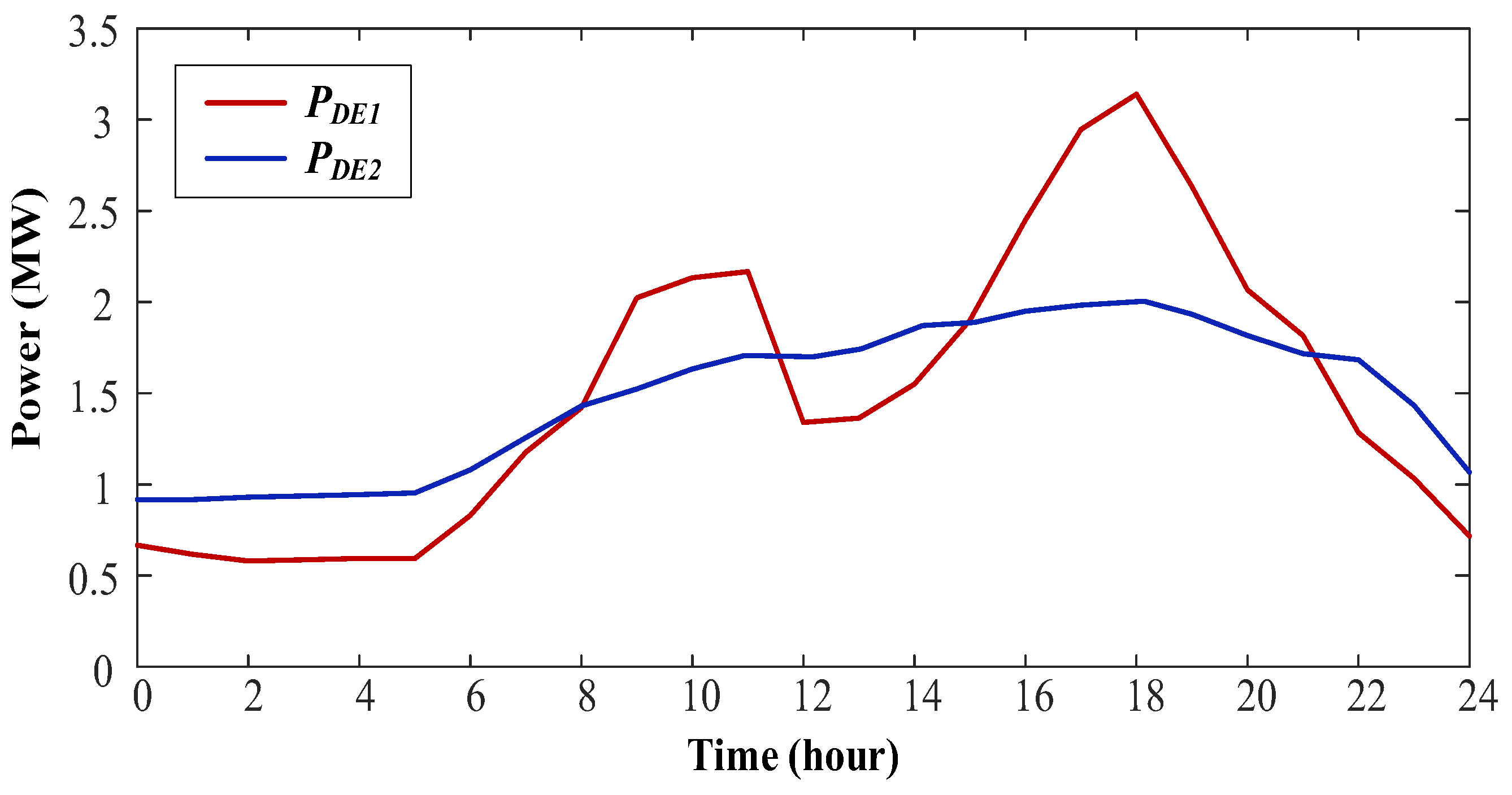
- By considering the cooling loads independently and utilizing the ice storage system to participate in the power system demand response, the system electrical load curve can be regulated in an indirect way. Simulation results also revealed that the peak–valley gap of electrical loads was reduced by 40.7% in summer under the premise of ensuring the cooling loads. Meanwhile, by regulating the system electrical load curve, the installation capacity of the diesel generator can be fully utilized.
- (3)
- The proposed optimal operation strategy makes full use of the load shifting capability of the hot water tank to improve system stability and to respond to the time-of-use gas price simultaneously. However, due to the limited battery installation capacity, the load shifting capability of the electric vehicle power exchange station is constrained.
Author Contributions
Funding
Conflicts of Interest
Appendix A. List of Symbols
| Nomenclature | Meaning | Nomenclature | Meaning |
| Le | Electrical loads | Lh | Thermal loads |
| Lc | Cooling loads | ω | Ratio of power consumed by ice storage system to total power consumption |
| α | Ratio of diesel consumed by diesel generator to total diesel consumption | β | Ratio of natural gas consumed by CHP to total natural gas consumption |
| ηDE | Diesel generator output efficiency | ηCHPe | CHP output electricity efficiency |
| ηCHPh | CHP output heat efficiency | ηGB | Gas boiler generator efficiency |
| PD | Inputs of diesel | PG | Inputs of natural gas |
| PEV | Discharge power of electric vehicle power exchange station | PWT | Discharge power of hot water tank |
| PC | Ice storage system ice making power | RCHP | Heat to power ratio of CHP |
| PCHPh | Thermal output power of a CHP unit | PCHPe | Electrical output power of a CHP unit |
| PCHPin | Input power of CHP | Ka1, Ka2, Kb1 ,Kb2 | Boost factors of CHP heat to power ratio |
| P0 (t) | Supplementary volume of diesel oil at time t | PDE | Diesel generator output power |
| PDEin | Input power of a diesel generator | PDEmax | Maximum operating power of a diesel generator |
| PDEmin | Minimum starting power of a diesel generator | PGB | Gas boiler output power |
| PGBin | Input power of a gas boiler | a1 | Exhaust smoke heat loss |
| a2 | Incomplete combustion loss | a3 | Heat dissipation loss |
| QGB_H (t) | Operation capacity of a gas boiler | QGB_Hmin | Minimum operation capacity of a gas boiler |
| QGB_Hmax | Maximum operation capacity of a gas boiler | TGB_ON (t) | Accumulated operation time of the gas boiler at time t |
| TGB_OFF (t) | Accumulated turn-off time of the gas boiler at time t | TGB_ONmin | Minimum accumulated operation time of the gas boiler |
| TGB_OFFmin | Minimum accumulated turn-off time of the gas boiler | PCout | Output refrigerating power of the ice storage system |
| PCin | Input electrical power of the ice storage system | EER | Energy efficiency ratio of the ice storage system |
| QCice | Ice making capacity of the ice storage tank | QCicemin | Minimum ice making capacity of the ice storage tank |
| QCicemax | Maximum ice making capacity of the ice storage tank | QCw | Ice melting capacity of the ice storage tank |
| QCwmin | Minimum ice melting capacity of the ice storage tank | QCwmax | Maximum ice melting capacity of the ice storage tank |
| MC_ICE (t) | Ice making mode | MC_W (t) | Ice melting mode |
| QWT (t) | Total thermal energy stored in the hot water tank at time t | εWT | Self discharge rate of a hot water tank |
| QWTh (t) | Thermal energy stored in the hot water tank at time t | QWTr (t) | Thermal energy released by the hot water tank at time t |
| QWTmin | Minimum amount of thermal energy that can be stored in the hot water tank | QWTmax | Maximum amount of thermal energy that can be stored in the hot water tank |
| QWThmin | Minimum amount of thermal energy that can flow in the hot water tank within a certain time period | QWThmax | Maximum amount of thermal energy that can flow in the hot water tank within a certain time period |
| QWTrmin | Minimum amount of thermal energy that can release by the hot water time within a certain time period | QWTrmax | Maximum amount of thermal energy that can release by the hot water time within a certain time period |
| tSC | Starting time of charging battery | tc1 | Starting time of low power demand |
| tc2 | Ending time of low power demand | tchg | Total charging time |
| Tg | Period of low demand time | tSD | Starting time of discharging battery |
| td1 | Starting time of peak power demand | td2 | Ending time of peak power demand |
| tchd | Total discharging time | Tf | Period of peak demand time |
| k | Random number between 0 and 1 | QEV (t) | Electrical energy stored in electric vehicle power exchange station at time t |
| LEV | Electric vehicles’ daily energy consumption | SOC | State of Charge |
| SOCmin | Minimum state of Charge | SOCmax | Maximum state of Charge |
| QEV | Rated energy storage capacity of electric vehicle power exchange station | F | Total fuel costs of the system |
| QG (t) | Amount of natural gas (in cubic meter) consumed by the system at time t | QD (t) | Amount of diesel (in liter) consumed by the system at time t |
| CG (t) | Real time natural gas price (in US $/cubic meter) at time t | CD (t) | Real time diesel price (in US $/liter) at time t |
| ηo | Overall efficiency of CHP | RCHPmin | Minimum CHP heat to power ratio |
| Qe | Total electrical energy generated by CHP | Qh | Total thermal energy generated by CHP |
| Qin | Sum of the calorific value of diesel and natural gas consumed by CHP | - | - |
References
- Gu, W.; Wu, Z.; Bo, R.; Liu, W.; Zhou, G.; Chen, W.; Wu, Z. Modeling, planning and optimal energy management of combined cooling, heating and power microgrid: A review. Int. J. Electr. Power Energy Syst. 2014, 54, 26–37. [Google Scholar] [CrossRef]
- Gu, W.; Wang, Z.; Wu, Z.; Luo, Z.; Tang, Y.; Wang, J. An Online Optimal Dispatch Schedule for CCHP Microgrids Based on Model Predictive Control. IEEE Trans. Smart Grid 2016, 8, 2332–2342. [Google Scholar] [CrossRef]
- Stanislav, P.; Bryan, K.; Tihomir, M. Smart Grids better with integrated energy system. In Proceedings of the 2009 IEEE Electrical Power & Energy Conference (EPEC), Montreal, QC, Canada, 22–23 October 2009; pp. 1–8. [Google Scholar]
- Li, D.; Xu, X.; Yu, D.; Dong, M.; Liu, H. Rule Based Coordinated Control of Domestic Combined Micro-CHP and Energy Storage System for Optimal Daily Cost. Appl. Sci. 2018, 8, 8. [Google Scholar] [CrossRef]
- Bartnik, R.; Buryn, Z.; Hnydiuk-Stefan, A.; Juszczak, A. Methodology and a Continuous Time Mathematical Model for Selecting the Optimum Capacity of a Heat Accumulator Integrated with a CHP Plant. Energies 2018, 11, 1240. [Google Scholar] [CrossRef]
- Franco, A.; Bellina, F. Methods for optimized design and management of CHP systems for district heating networks (DHN). Energy Convers. Manag. 2018, 172, 21–31. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Gu, C.; Li, F. Optimal design and operation of CHPs and energy hub with multi objectives for a local energy system. Energy Procedia 2017, 142, 1615–1621. [Google Scholar] [CrossRef]
- Nistor, M.; Antunes, C.H. Integrated Management of Energy Resources in Residential Buildings—A Markovian Approach. IEEE Trans. Smart Grid 2017, 9, 240–251. [Google Scholar] [CrossRef]
- Wang, C.; Lv, C.; Li, P.; Song, G.; Li, S.; Xu, X.; Wu, J. Modeling and optimal operation of community integrated energy systems: A case study from China. Appl. Energy 2018, 230, 1242–1254. [Google Scholar] [CrossRef]
- Liu, J.; Wang, A.; Qu, Y.; Wang, W. Coordinated Operation of Multi-Integrated Energy System Based on Linear Weighted Sum and Grasshopper Optimization Algorithm. IEEE Access 2018, 6, 2169–3536. [Google Scholar] [CrossRef]
- Hu, K.; Chen, L.; Chen, Q.; Wang, X.; Qi, J.; Xu, F.; Min, Y. Phase-change heat storage installation in combined heat and power plants for integration of renewable energy sources into power system. Energy 2017, 124, 640–651. [Google Scholar] [CrossRef]
- Stelt, S.V.D.; AlSkaif, T.; Sark, W.V. Techno-economic analysis of household and community energy storage for residential prosumers with smart appliances. Appl. Energy 2018, 209, 266–276. [Google Scholar] [CrossRef]
- Yu, D.; Liu, H.; Yan, G.; Jiang, J.; Le Blond, S. Optimization of Hybrid Energy Storage Systems at the Building Level with Combined Heat and Power Generation. Energies 2017, 10, 606. [Google Scholar] [CrossRef]
- Farzin, H.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M. Reliability Studies of Distribution Systems Integrated with Electric Vehicles Under Battery-Exchange Mode. IEEE Trans. Power Deliv. 2016, 31, 2473–2482. [Google Scholar] [CrossRef]
- Geidl, M.; Koeppel, G.; Favre-Perrod, P. Klockl, B.; Andersson, G.; Klaus, F. Energy hubs for the future. IEEE Power Energy Mag. 2007, 5, 24–30. [Google Scholar] [CrossRef]
- Hast, A.; Rinne, S.; Syri, S.; Kiviluoma, J. The role of heat storages in facilitating the adaptation of district heating systems to large amount of variable renewable electricity. Energy 2017, 137, 775–788. [Google Scholar] [CrossRef]
- Das, B.K.; Al-Abdeli, Y.M. Optimisation of stand-alone hybrid CHP systems meeting electric and heating loads. Energy Convers. Manag. 2017, 153, 391–408. [Google Scholar] [CrossRef]
- Shi, J.; Xu, J.; Zeng, B.; Zhang, J. A Bi-Level optimal operation for energy hub based on regulating heat-to-electric ratio mode. Power Syst. Technol. 2016, 40, 2959–2966. [Google Scholar]
- Ganesan, P.; Rajakarunakaran, S.; Thirugnanasambandam, M.; Devaraj, D. Artificial neural network model to predict the diesel electric generator performance and exhaust emissions. Energy 2015, 83, 115–124. [Google Scholar] [CrossRef]
- Noguera, A.L.G.; Lora, E.E.S.; Cobas, V.R.M.; Cobas, V.R.M. Optimum design of a hybrid diesel-ORC/photovoltaic system using PSO: Case study for the city of Cujubim, Brazil. Energy 2018, 142, 33–45. [Google Scholar] [CrossRef]
- Sun, F.; Zhao, J.; Fu, L.; Sun, J.; Zhang, S. New district heating system based on natural gas-fired boilers with absorption heat exchangers. Energy 2017, 138, 405–418. [Google Scholar] [CrossRef]
- Chen, W.; Shi, W.; Wang, B.; Shang, S.; Li, X. A deep heat recovery device between flue gas and supply air of gas-fired boiler by using non-contact total heat exchanger. Appl. Energy 2017, 105, 4976–4982. [Google Scholar] [CrossRef]
- Shirazi, A.; Najafi, B.; Aminyavari, M.; Rinaldi, F.; Taylor, R.A. Thermal–economic–environmental analysis and multi-objective optimization of an ice thermal energy storage system for gas turbine cycle inlet air cooling. Energy 2014, 69, 212–226. [Google Scholar] [CrossRef]
- Du, Y.; Gai, W.; Jin, L.; Sheng, W. Thermal comfort model analysis and optimization performance evaluation of a multifunctional ice storage air conditioning system in a confined mine refuge chamber. Energy 2017, 141, 964–974. [Google Scholar] [CrossRef]
- Lin, C.; Yao, C.; Jin, L.; Singh, C. Power system reliability assessment with electric vehicle integration using battery exchange mode. IEEE Trans. Sustain. Energy 2013, 4, 1034–1042. [Google Scholar]
- Delgarm, N.; Sajadi, B.; Kowsary, F.; Delgarm, S. Multi-objective optimization of the building energy performance: A simulation-based approach by means of particle swarm optimization (PSO). Appl. Energy 2016, 170, 293–303. [Google Scholar] [CrossRef]
- Chen, P.; Wang, J. Observer-based estimation of air-fractions for a diesel engine coupled with aftertreatment systems. IEEE Trans. Control Syst. Technol. 2013, 21, 2239–2250. [Google Scholar] [CrossRef]
- Dahl, C.A. Measuring global gasoline and diesel price and income elasticities. Energy Policy 2012, 41, 2–13. [Google Scholar] [CrossRef]
- Zhao, B.; Conejo, A.J.; Sioshansi, R. Unit commitment under gas-supply uncertainty and gas-price variability. IEEE Trans. Power Syst. 2017, 32, 2394–2405. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Yan, H.; He, G.; Zhu, C.; Liu, K.; Liu, Y. Seasonal Operation Strategy Optimization for Integrated Energy Systems with Considering System Cooling Loads Independently. Processes 2018, 6, 202. https://doi.org/10.3390/pr6100202
Li K, Yan H, He G, Zhu C, Liu K, Liu Y. Seasonal Operation Strategy Optimization for Integrated Energy Systems with Considering System Cooling Loads Independently. Processes. 2018; 6(10):202. https://doi.org/10.3390/pr6100202
Chicago/Turabian StyleLi, Kecheng, Huaguang Yan, Guixiong He, Chengzhi Zhu, Kaicheng Liu, and Yuting Liu. 2018. "Seasonal Operation Strategy Optimization for Integrated Energy Systems with Considering System Cooling Loads Independently" Processes 6, no. 10: 202. https://doi.org/10.3390/pr6100202
APA StyleLi, K., Yan, H., He, G., Zhu, C., Liu, K., & Liu, Y. (2018). Seasonal Operation Strategy Optimization for Integrated Energy Systems with Considering System Cooling Loads Independently. Processes, 6(10), 202. https://doi.org/10.3390/pr6100202




