Interactive Tool for Frequency Domain Tuning of PID Controllers
Abstract
1. Introduction
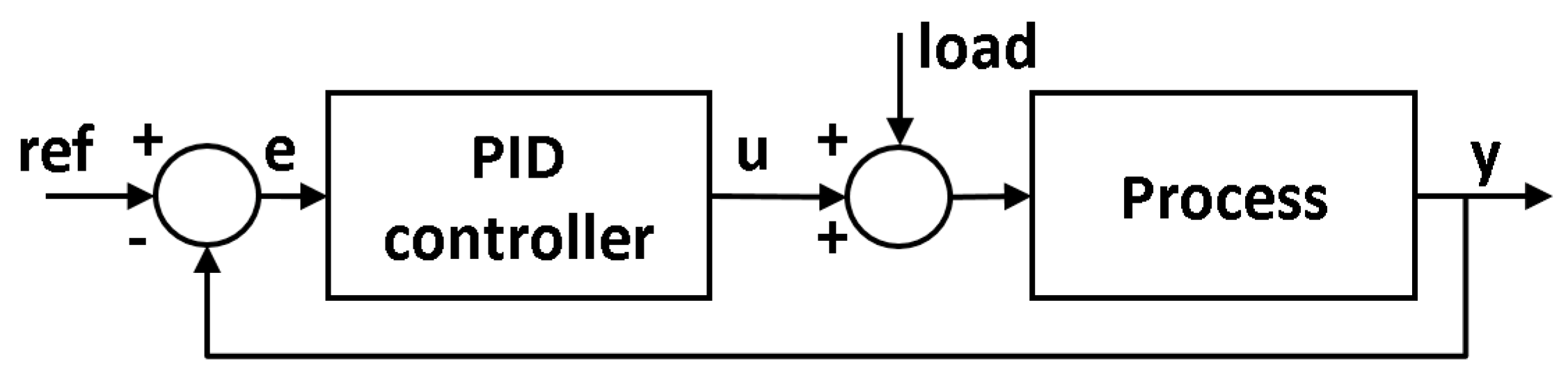
2. Tuning of PID Controllers in the Frequency Domain
2.1. Stability Regions
- PI: Where KD = 0.
- PD: Where KI = 0.
- PIDα: Where the ratio of the derivative and integral time constants α = TD/TI remains constant. This is equal to fix KD = α·(KP)2/KI.
- PIDKD: Where KD is set to a fixed value.
- PIDKI: Where KI is set to a fixed value.
AI(s) = s·A(s) + KI·B(s); BI(s) = s·B(s).
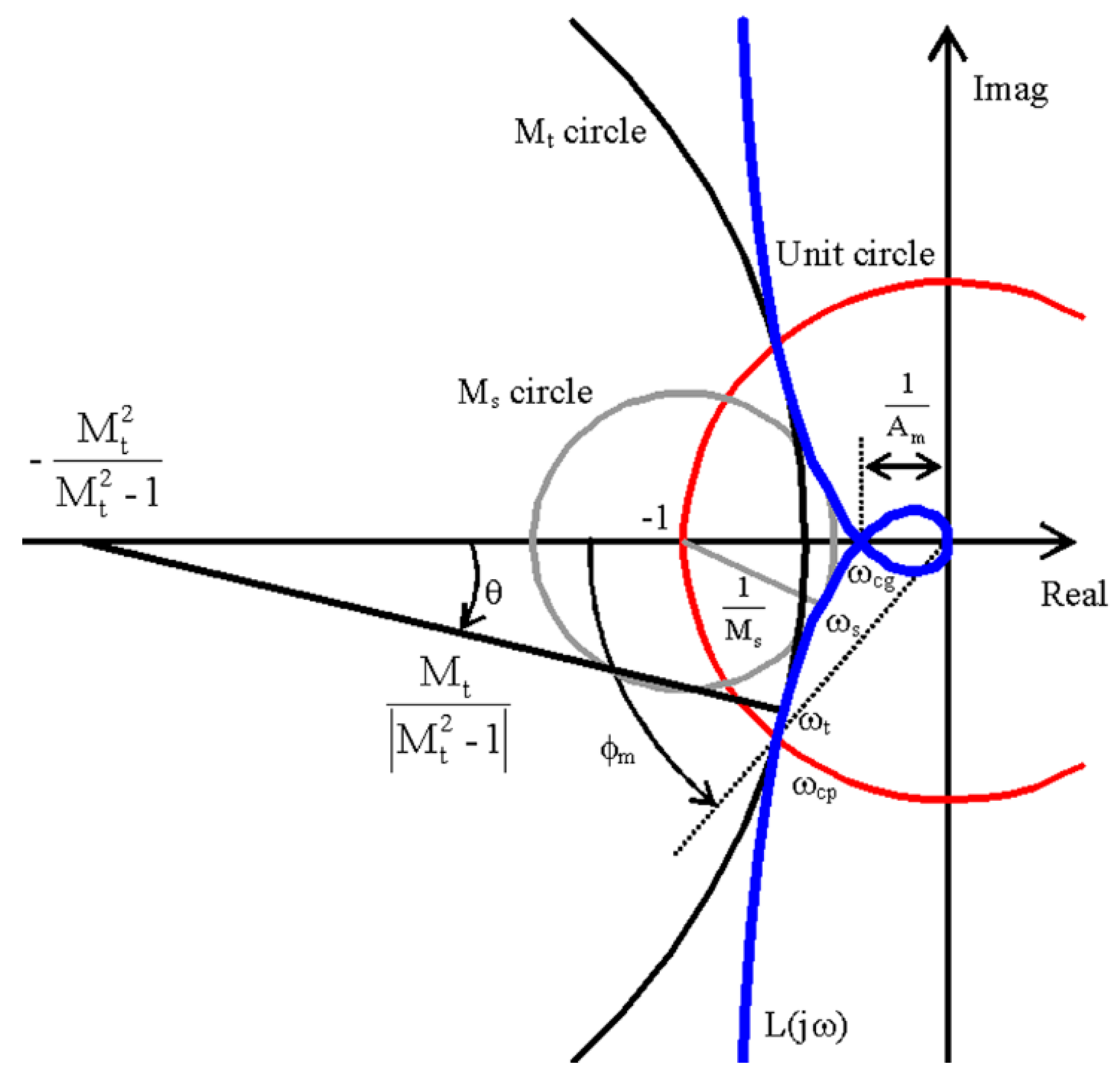
2.2. Specification Boundary Curves
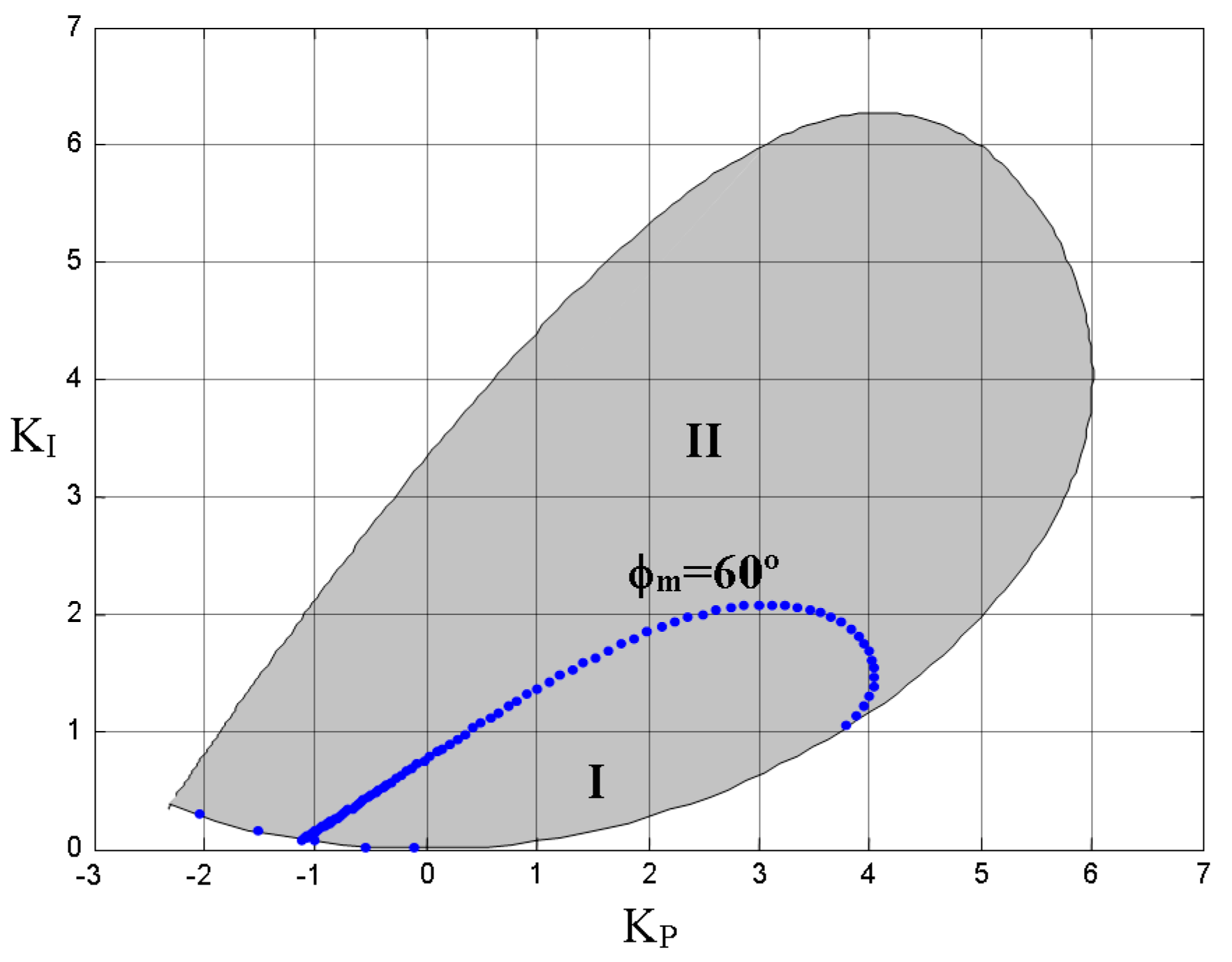
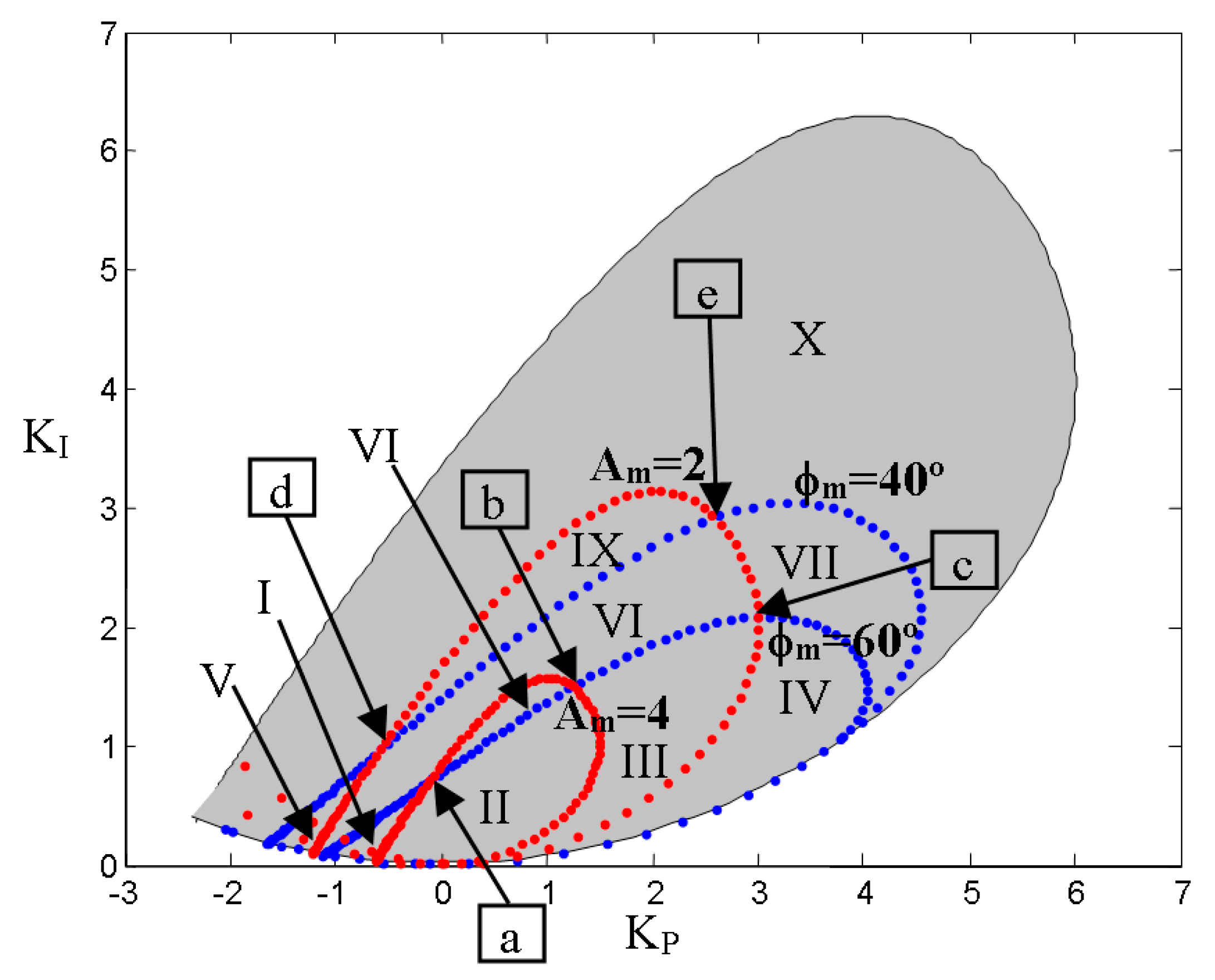
- Zone I: ϕm = 60°, 2 ≤ Am ≤ 4
- Zone II: ϕm = 60°, Am = 4
- Zone III: ϕm = 60°, 2 ≤ Am ≤ 4
- Zone IV: ϕm = 60°, Am ≤ 2
- Zone V: 40° ≤ ϕm ≤ 60°, Am ≤ 2
- Zone VI: 40° ≤ ϕm ≤ 60°, 2 ≤ Am ≤ 4
- Zone VII: 40° ≤ ϕm ≤ 60°, Am = 4
- Zone VIII: 40° ≤ ϕm ≤ 60°, Am ≤ 2
- Zone IX: ϕm ≤ 40°, 2 ≤ Am ≤ 4
- Zone X: ϕm ≤ 40°, Am ≤ 2
- Point a: ϕm = 60°, Am = 4
- Point b: ϕm = 60°, Am = 4
- Point c: ϕm = 60°, Am = 2
- Point d: ϕm = 40°, Am = 2
- Point e: ϕm = 40°, Am = 2
2.3. Discrete Implementation and Practical Considerations
3. Graphical User Interface
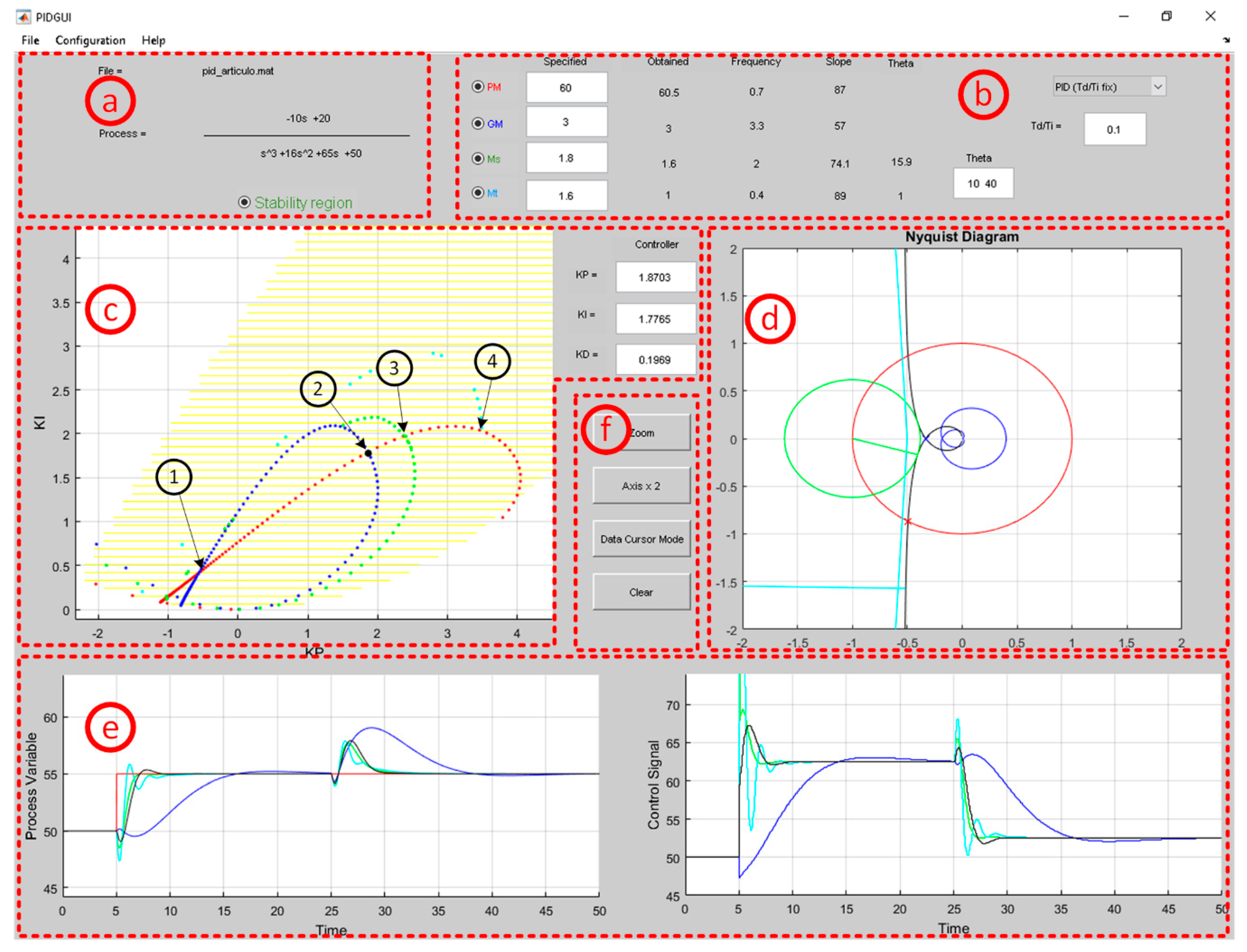
- Process transfer function (a). The transfer function of the process is shown in the upper left corner. Its numerator and denominator coefficients can be specified in the sub-menu Process in the Configuration menu.
- Frequency domain specifications and PID type (b). The kind of controller (PI, PD, PIDα, PIDKD, and PIDKI) is chosen by means of a pop-up menu located in the upper right corner. The design specifications in the frequency domain can be selected by means of radio-buttons located in the upper zone of Figure 7: Phase margin (PM), gain margin (GM), maximum sensitivity (Ms), and maximum complementary sensitivity (Mt). These requirements are specified by single values, or a range of two values, in the corresponding four text fields of the Specified column. On the right side, the truly obtained specification values for the current controller parameters are shown together with the corresponding frequencies. There is also a text field to edit the desired range of the angle θ for Ms and Mt specifications. The slope of the loop Nyquist plot in each of these frequencies, and the obtained angles θ for Ms and Mt, are also shown.
- Controller parameter space (c). This plot shows the KP-KI parameter space for the PI, PIDα, and PIDKD controllers, or the KP-KD parameter space for the PD and PIDKI controllers, according to Table 1. The boundary curves fulfilling the specified frequency requirements are plotted in different colors: Red (PM), blue (GM), green (Ms), and cyan (Mt). These curves can be displayed or hidden using the requirement radio-buttons. The values of the current control parameters (KP, KI, and KD) are visible in the three text fields placed on the right of this plot, and they are also depicted by a black point in the parameter space. The user can change the PID parameters either by dragging the aforementioned black point or by editing the corresponding text fields. Every time the controller changes, the frequency response features, Nyquist plot, and time response are updated. In addition, when the Stability region radio-button is enabled, the plot shows the set of controller parameters that stabilize the specified feedback system, delimiting this region by a set of yellow lines. If the model process is changed, this stability region is automatically updated.
- Nyquist plot (d). In this figure, the Nyquist diagram of the process P(s) is shown in blue, and the Nyquist curve of the compensated open loop L(s) is depicted in black. The unit circle and the circles for Ms and Mt are also depicted in red, green, and cyan, respectively. This information is very important to determine if the Nyquist plot shape is adequate [11]. It is updated when the controller parameters are modified.
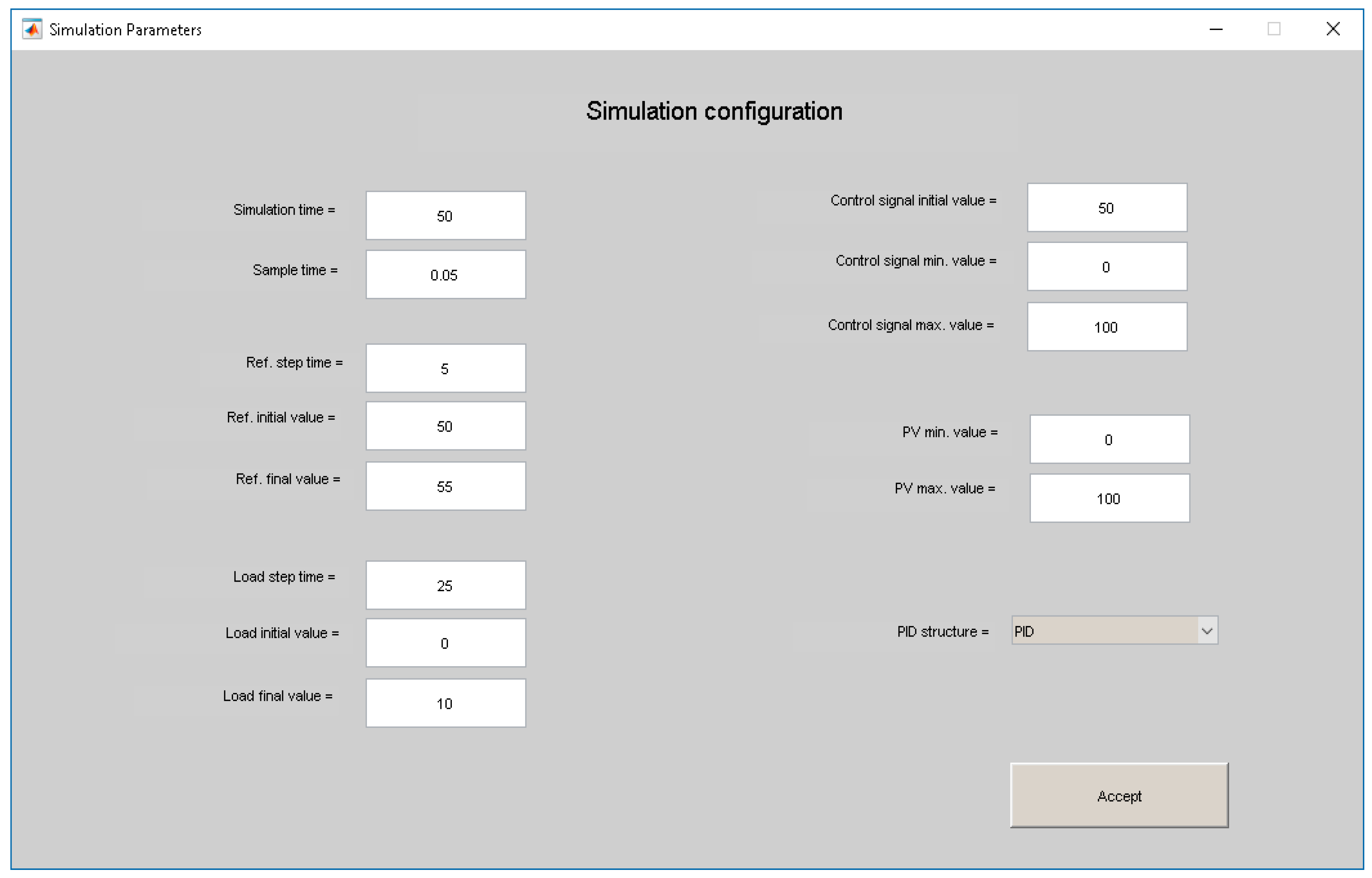
- Time response simulation (e). These plots show the temporal response of the controlled variable and control signal of the specified feedback system. Several temporal responses can be displayed. This is useful to compare different designs. This procedure can be carried out by dragging and releasing the black point of the controller parameter space to other points, or by editing the corresponding text fields. A step change in the reference signal as well as in the load disturbance can be specified for the simulation, as shown in the simulation configuration window (Figure 8), where the initial and final values are defined for both the reference and the load disturbance. This window is accessible from the sub-menu Simulation of the Configuration menu, and it also provides other text fields to specify the minimum and maximum control signal values, and process variable values, initial control signal value, simulation time, and the controller sample time. In addition, the PID structure (PID, PI-D, or I-PD) can be selected using a pop-up menu.
- Figure controls (f). This section covers a set of four buttons related with the figures. There are two toggle-buttons to enable or disable the zoom mode and the data cursor mode in all figures. The Axis x 2 button increases the axis scaling of the controller parameter space. The Clear button removes the time response simulations.
- Possibility to configure the simulation parameters.
- Possibility of modifying the model parameters of the plant and controller.
- Frequency response (Nyquist diagram) of the system.
- Closed-loop temporal response of the controlled variable and the control signal.
- Interactive zooming in the figures.
- Stability region in the parameter space of the KP-KI or KP-KD controller. This feature allows the selection of the controller parameters interactively. Along with it, curves of robustness specifications can also be shown, facilitating the previous task. In addition, this region is useful to compare PID designs.
- The tool allows you to analyze practical aspects, such as the choice of the sampling period and saturations of the control signals.
Educational or Training Uses
- Tuning by trial and error inside the stabilizing region. The tool shows the stabilizing region in the KP-KI or KP-KD parameter space. Moving the black point in different areas of this space, the user can test the stability and closed-loop response for choosing the controller parameters.
- Comparison of PID designs. The tool offers several frequency domain specifications for PID tuning, so the user can easily compare the performance achieved with different specifications, or those obtained with the same specification at different frequencies.
- Effects of practical considerations. Practical aspects of PID controllers have been considered in the tool. Although the controller design is performed in the continuous domain, time response simulations are carried out using a discrete implementation of the controller. In addition to the effects of a bad choice of the PID controller parameters, the user can verify how a bad selection of the sampling period deteriorates the closed-loop time response. In the same way, the effects of process input saturations can be easily visualized with the tool.
4. Illustrative Example
- Process specification: First, the coefficients of the process numerator and denominator are introduced in the Configuration/Process window in the respective textboxes.
- Controller type selection: By default, the last controller type is maintained, so PIDα type must be selected in the corresponding pop-up menu, and Td/Ti must be fixed to 0.1. Immediately, the stabilizing region in the KP-KI space for this system is calculated.
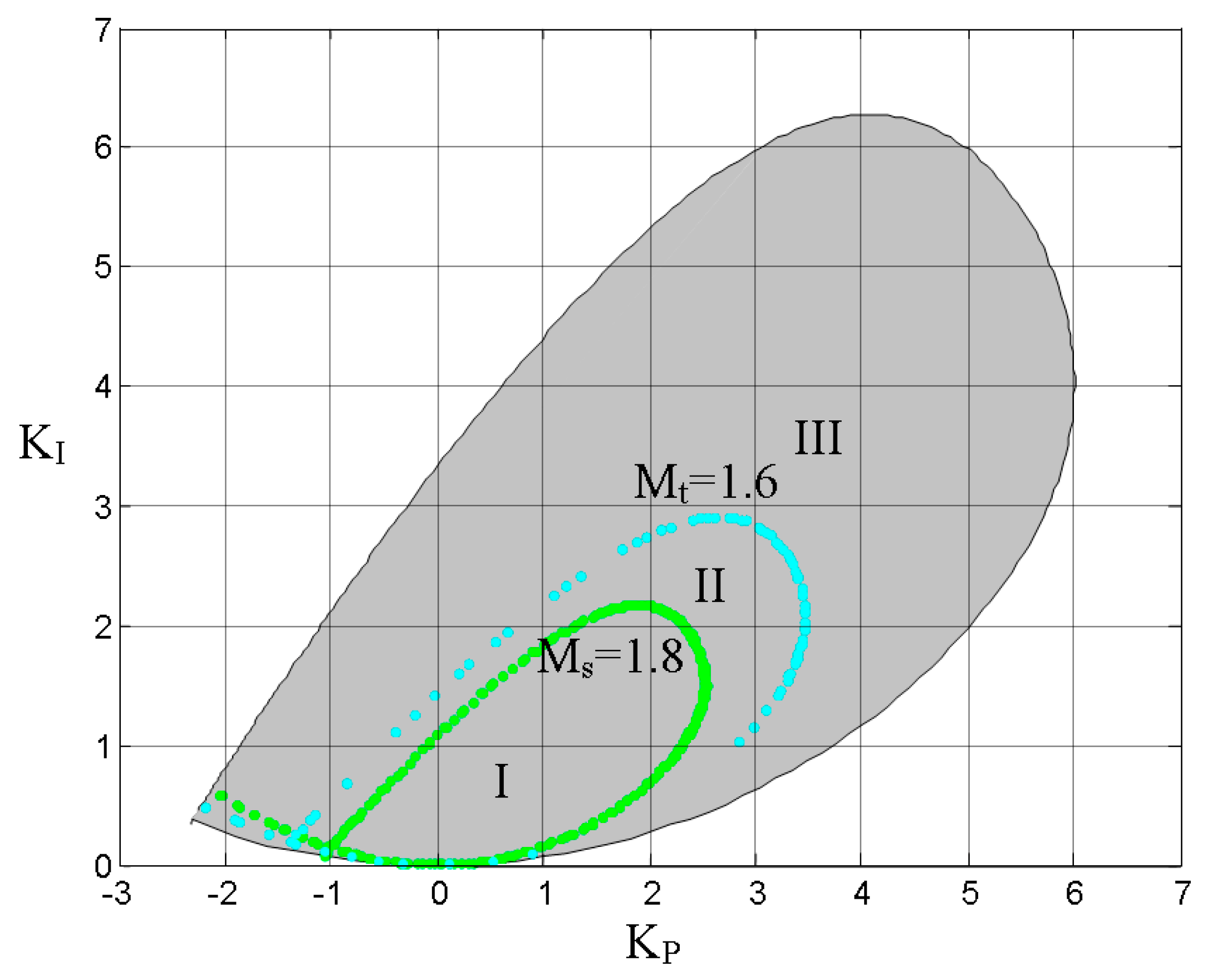
- Defining the desired frequency domain specifications: PM = 60°, GM = 3, Ms = 1.8, and Mt = 1.6. The corresponding boundary curves are depicted when they are enabled using the respective radio-buttons. Figure 7 shows the main window of this example.
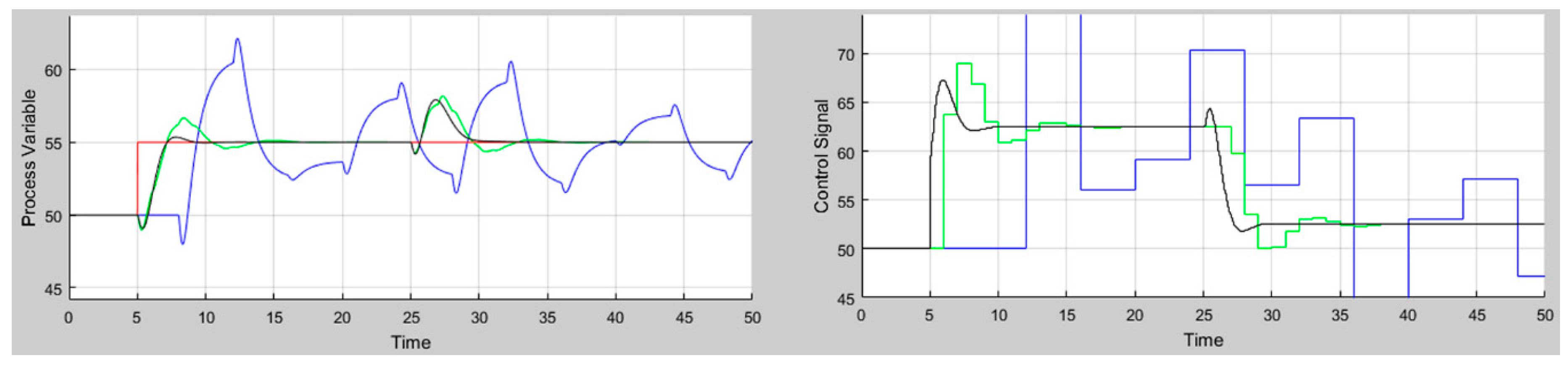
- Simulation configuration: To perform the simulations, the parameters given in Figure 8 are configured. The range of the output and input process variables is from 0 to 100, and their initial values are 50. Step changes are applied from 50 to 55 in the set-point, and from 0 to 10 in the load disturbance, at times t = 5 s and t = 25 s, respectively. The total simulation time is 50 s, and the controller sample time is 0.05 s with PID structure.
- Comparing different designs: In this example, four PID designs are compared dragging the black point in the controller parameter space. All these points are above the 60° phase margin curve (red curve) and the intersections with other specifications curves. Point 1 represents the first curve intersection of PM = 60° and GM = 3 (blue curve). Point 2 is the second intersection of these boundary curves. Point 3 is located in the intersection with curve Ms = 1.8 (green curve), and point 4 with curve Mt = 1.6 (cyan curve). The corresponding PID parameters are collected in Table 5. These can also be identified in the KP-KI space in Figure 7. Their closed-loop responses are depicted in the bottom corner of Figure 7 (design 1 in blue, 2 in black, 3 in green, and 4 in cyan), and the achieved frequency performance indices and their associated frequencies are gathered in Table 5. Designs 2 and 3 obtain similar responses. Design 3 does not show overshoot; however, it has a higher inverse response and a more aggressive control signal. Design 4 achieves a greater oscillatory response and worse robustness, with the lowest gain margin and higher Ms. Design 1 shows the slowest response for tracking and disturbance rejection. Although designs 1 and 2 have practically the same frequency specifications, design 1 achieves them at very low frequencies, and consequently it has a slower response. Additionally, design 2 has a higher KI than that corresponding to design 1, which is advantageous for faster disturbance rejection. It also shows a good control signal response.
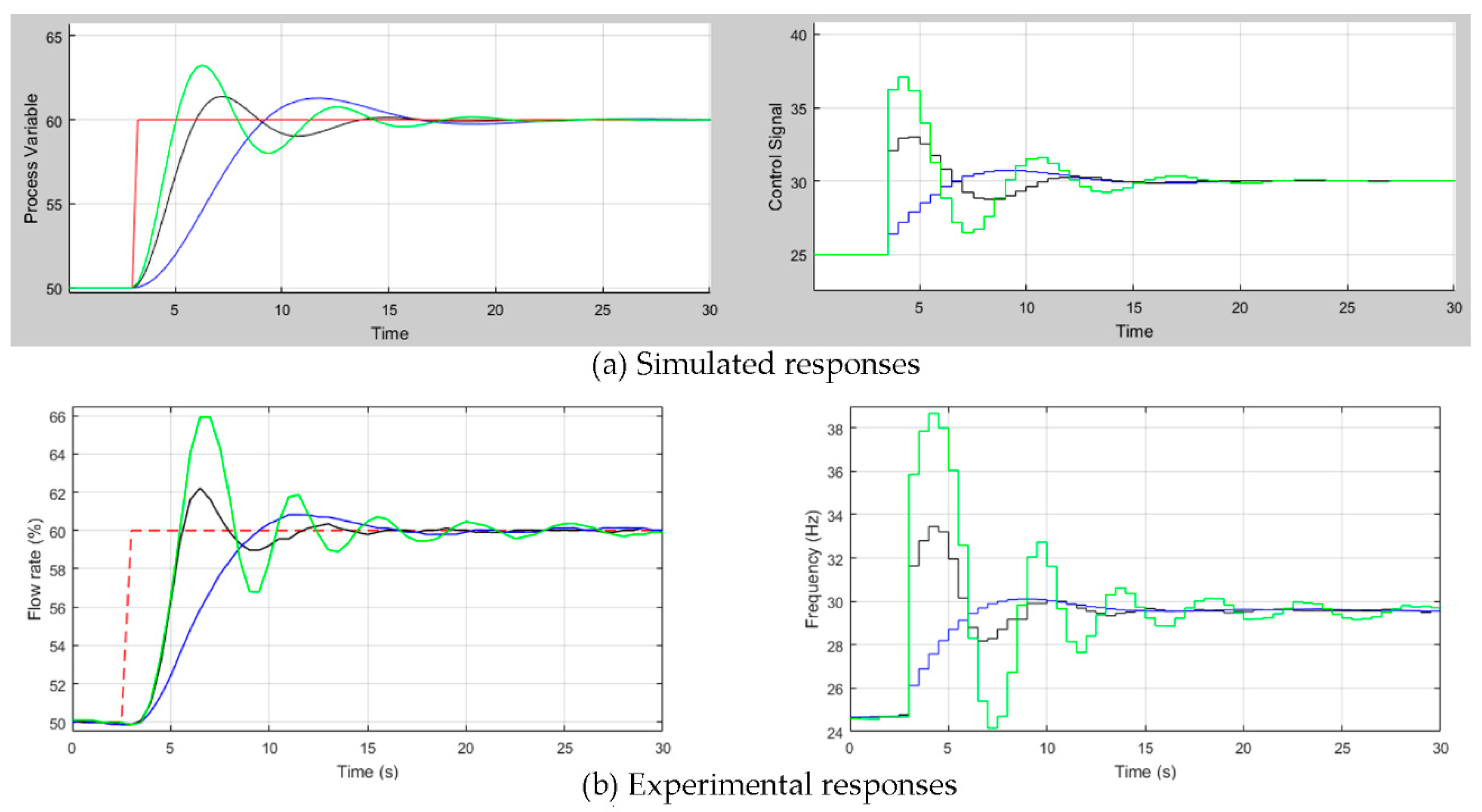
- Considering practical aspects: Assuming that design 2 is the preferred one, Figure 9 shows the closed loop time responses obtained with different controller sample times: 0.05 s (black line), 1 s (green line), and 4 s (blue line). For a sample time of 1 s, the closed-loop response is acceptable and a bit more oscillatory than that obtained with a sample time of 0.05 s. Nevertheless, the response is considerably deteriorated with a sample time of 4 s.
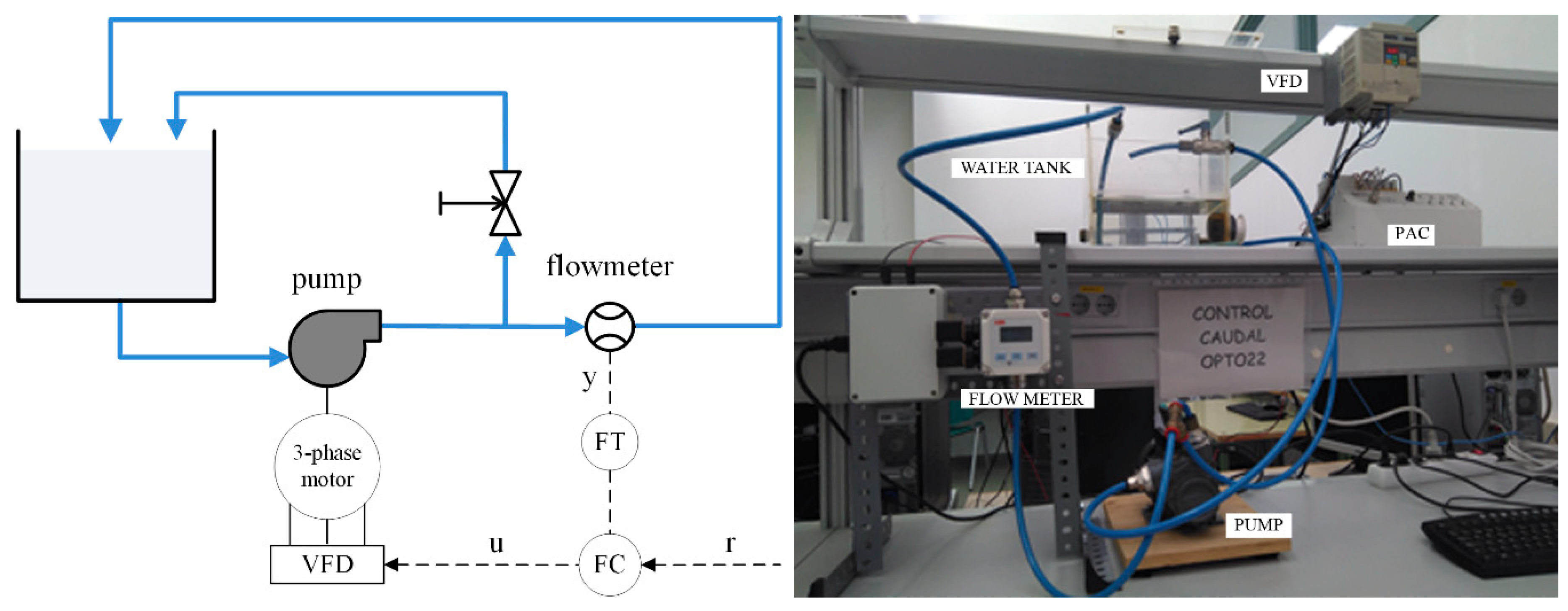
Practical Laboratory Process
5. Assessment and Evaluation
5.1. Student Survey
- Theoretical ideas: Engineering students can consolidate basic concepts in process control, such as robustness specifications in the frequency domain or the design of PID controllers for stable systems comparing the final closed-loop response for several robustness margins.
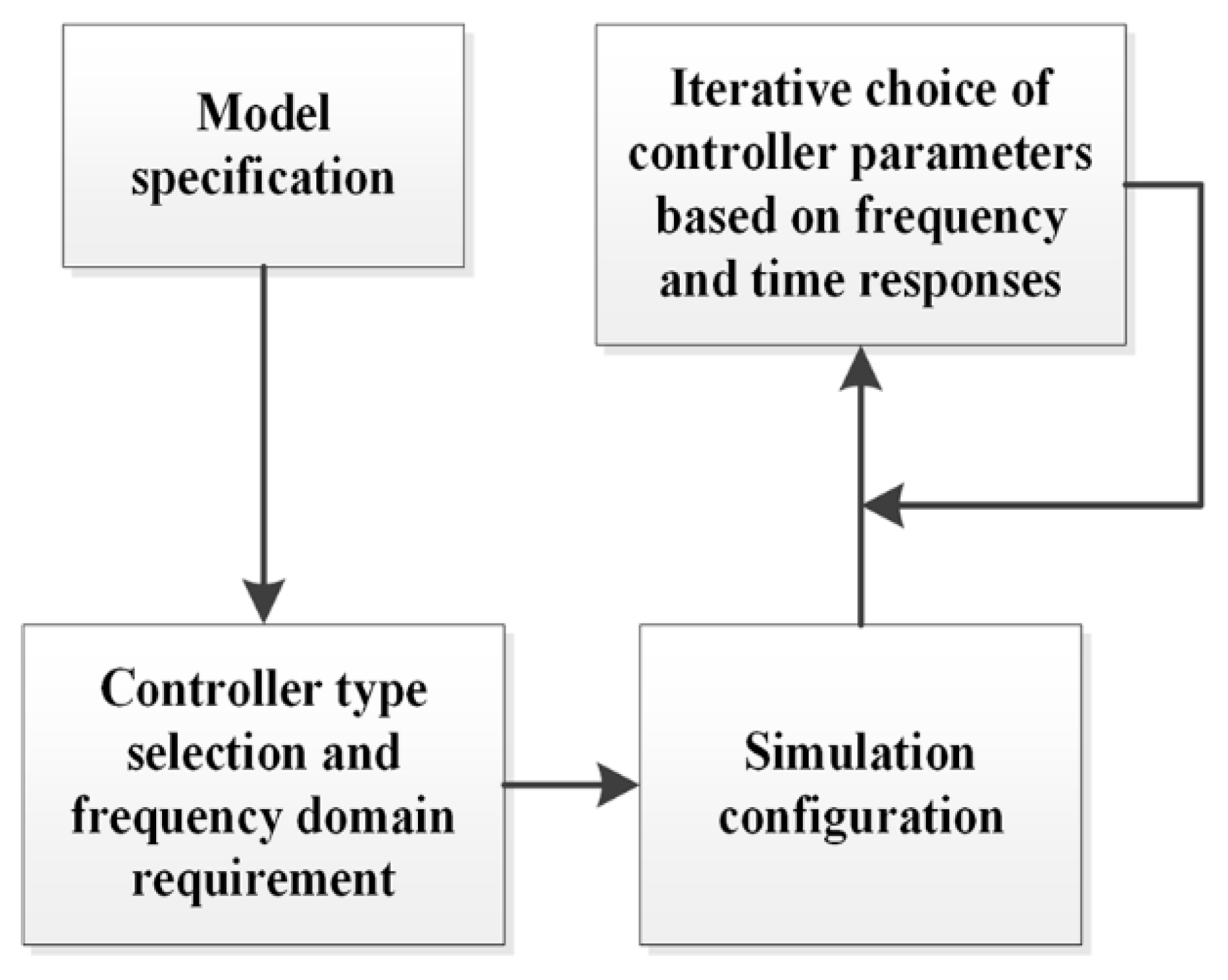
- Easy to understand and use: The GUI has been designed to be user-friendly. Nevertheless, the students are guided in using the tool by the professor, who will describe the state flow shown in Figure 8.
- Real-life problem: After achieving a satisfactory tuning of PID controller parameters, it is necessary to implement the control strategy, which it is mostly performed in a discrete way. In this sense, the tool allows simulations with a discrete implementation of the PID controller, considering practical problems such as sample time effect, or process input constraints implementing an anti-windup mechanism.
- Visual sensation: The GUI is structured coherently. The information shown in the main window was reduced as much as possible to make the navigation easier. It is developed to be interactive and responsive for the user, which is a compulsory feature in the current digitalized era.
- -
- Learning value covers questions to analyze students’ perceptions of how effective the developed tool is to learn about PID control concepts, robustness margins, and its applicability.
- -
- Value added is aimed at assessing the use of the tool in the sense of a theoretical lecture complement.
- -
- Design usability and easy understanding of the tool evaluates students’ perceptions of the ease and clarity to navigate through the GUI.
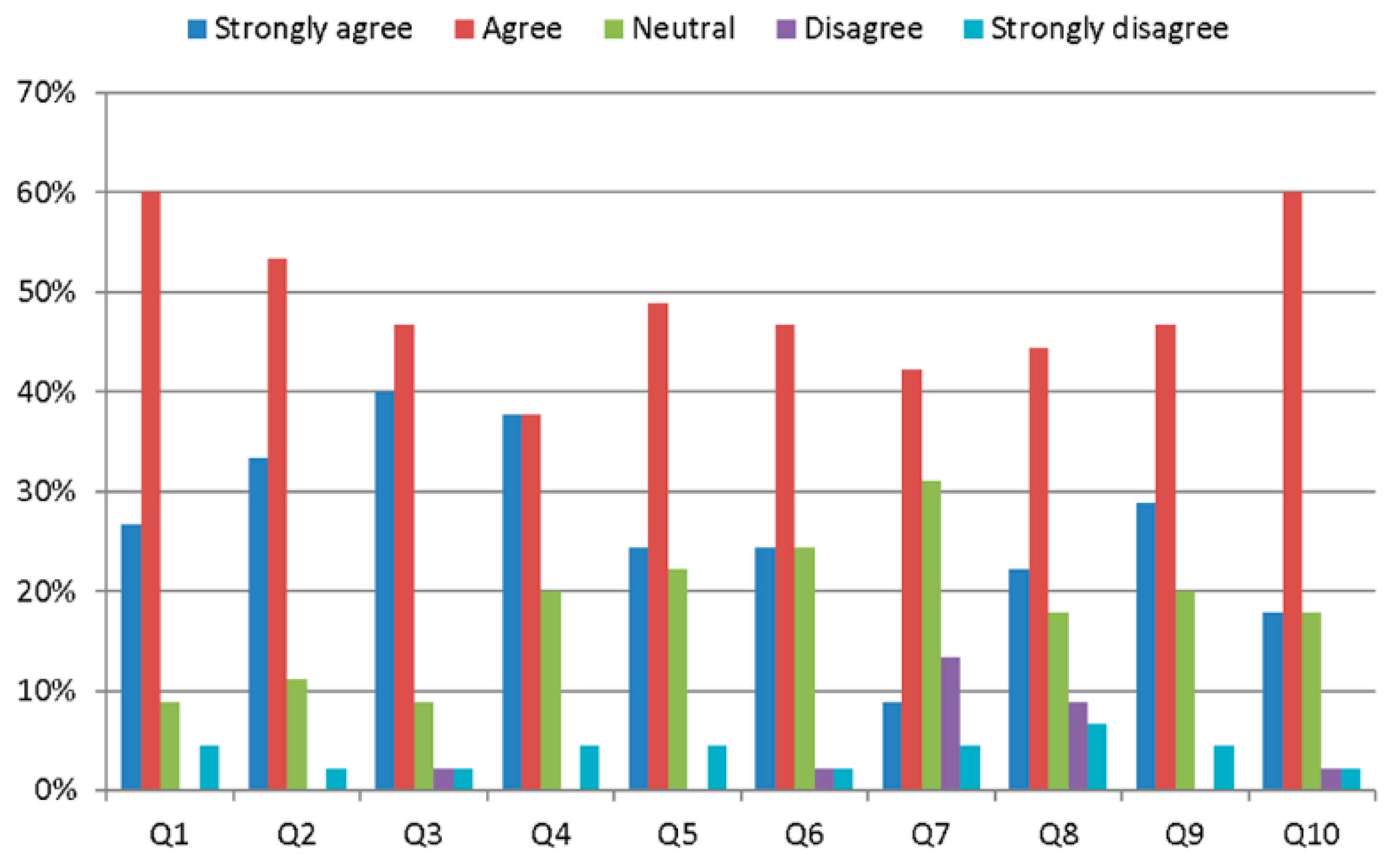
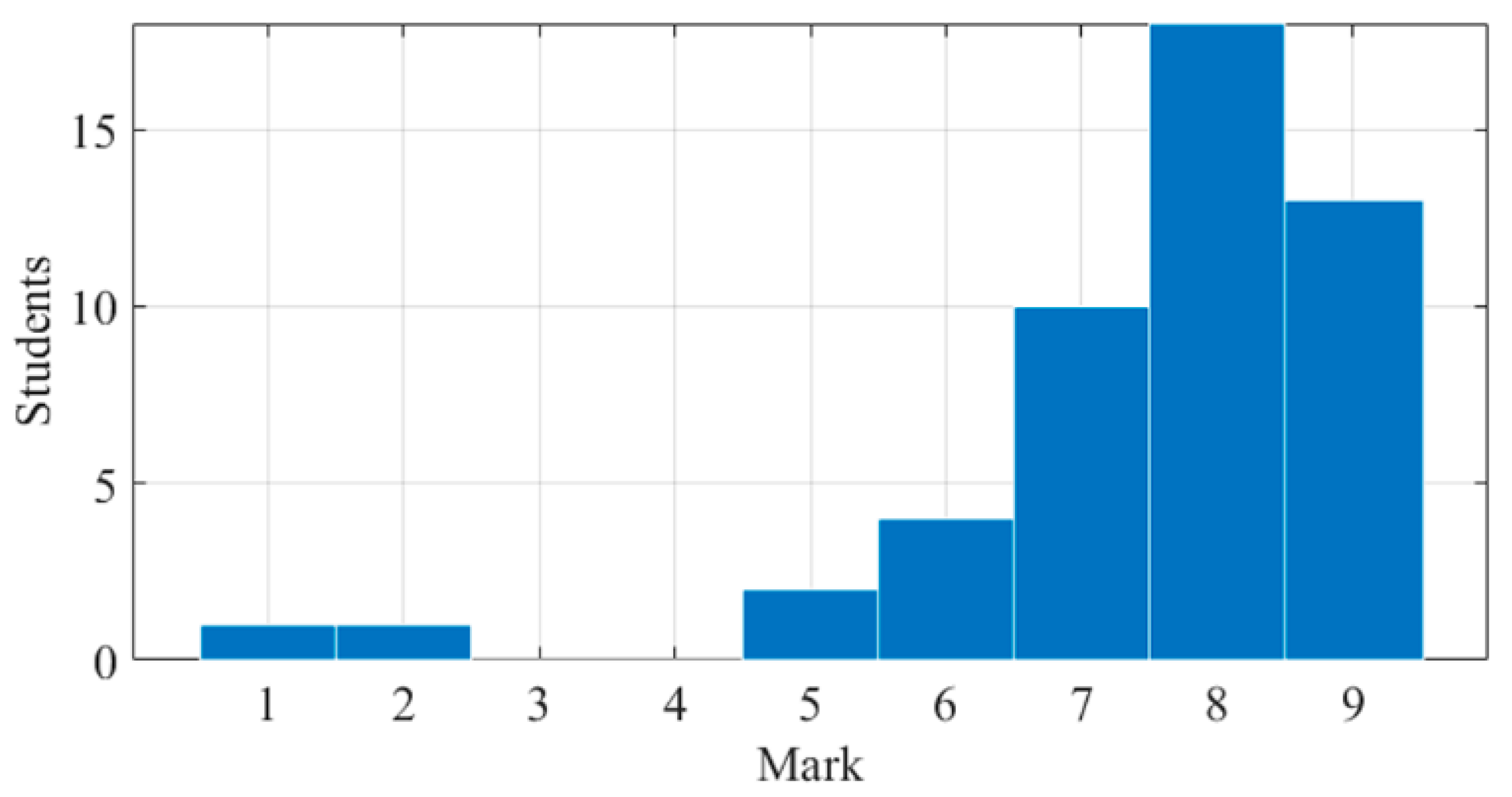
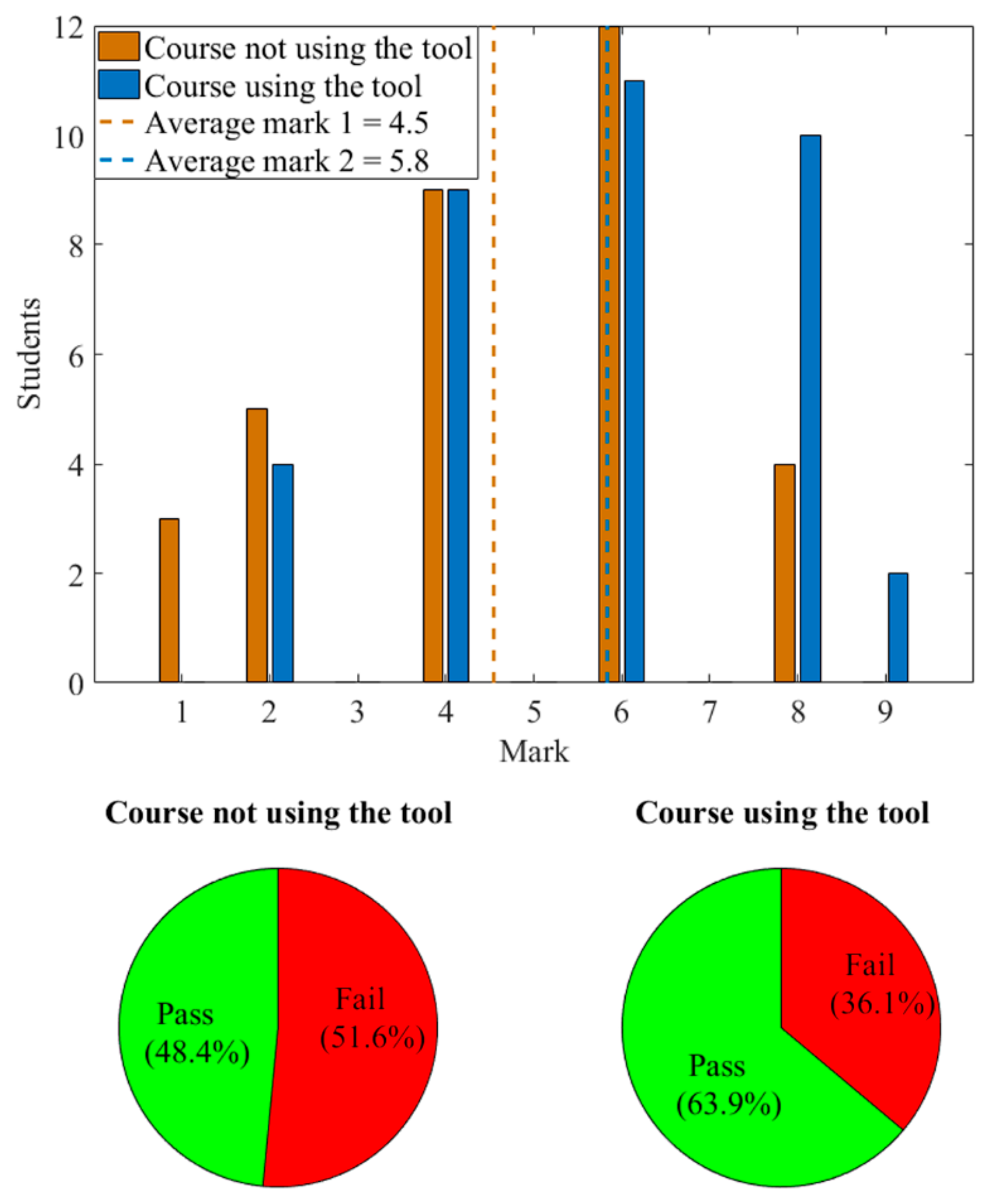
5.2. Student Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Srivastava, S.; Pandit, V.S. A PI/PID controller for time delay systems with desired closed loop time response and guaranteed gain and phase margins. J. Process Control 2016, 37, 70–77. [Google Scholar] [CrossRef]
- Vilanova, R.; Alfaro, V.M. Control PID robusto: Una visión panorámica. Rev. Iberoam. Autom. Inf. Ind. RIAI 2011, 8, 141–158. [Google Scholar] [CrossRef]
- Hägglund, T.; Åström, K.J. Advanced PID Control; ISA—Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 2006; ISBN 1556179421. [Google Scholar]
- Bialkowski, W.L. Control Handbook; Levine, W.S., Ed.; CRC/IEEE Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Alcántara, S.; Vilanova, R.; Pedret, C. PID control in terms of robustness/performance and servo/regulator trade-offs: A unifying approach to balanced autotuning. J. Process Control 2013, 23, 527–542. [Google Scholar] [CrossRef]
- Van Overschee, P.; Moons, C.; Van Brempt, W.; Vanvuchelen, P.; De Moor, B. RaPID: The end of heuristic PID tuning. In Proceedings of the PID ’00: IFAC Workshop on Digital Control, Terrasa, Spain, 4–7 April 2000; pp. 687–692. [Google Scholar]
- O’dwyer, A. Handbook of PI and PID Controller Tuning Rules, 2nd ed.; Imperial College Press: London, UK, 2006; Volume 26, ISBN 978-1-84816-242-6. [Google Scholar]
- Leva, A.; Maggion, M. Model-Based PI(D) Autotuning. In PID Control in the Third Millenium; Springer: London, UK, 2012; pp. 45–73. [Google Scholar]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–768. [Google Scholar] [CrossRef]
- Awouda, A.E.A.; Bin Mamat, R. Refine PID tuning rule using ITAE criteria. In Proceedings of the 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; Volume 5, pp. 171–176. [Google Scholar]
- Åström, K.J.; Hägglund, T. Revisiting the Ziegler–Nichols step response method for PID control. J. Process Control 2004, 14, 635–650. [Google Scholar] [CrossRef]
- Tavakoli, S.; Safaei, M. Analytical PID control design in time domain with performance-robustness trade-off. Electron. Lett. 2018, 54, 815–817. [Google Scholar] [CrossRef]
- Arrieta, O.; Vilanova, R. Simple PID tuning rules with guaranteed Ms robustness achievement. IFAC Proc. Vol. 2011, 44, 12042–12047. [Google Scholar] [CrossRef]
- Alfaro, V.M.; Vilanova, R. Optimal robust tuning for 1DoF PI/PID control unifying FOPDT/SOPDT models. IFAC Proc. Vol. 2012, 2, 572–577. [Google Scholar] [CrossRef]
- Morilla, F.S.D. Methodologies for the Tuning of PID Controllers in the Frequency Domain. IFAC Proc. Vol. 2000, 147–152. [Google Scholar] [CrossRef]
- Morilla, F.; Vázquez, F.; Hernández, R. PID control design with guaranteed stability. IFAC Proc. Vol. 2006, 7, 13–18. [Google Scholar] [CrossRef]
- Mathworks Home Page. Available online: http://www.mathworks.com (accessed on 2 August 2018).
- Ruiz, Á.; Jiménez, J.E.; Sánchez, J.; Dormido, S. Design of event-based PI-P controllers using interactive tools. Control Eng. Pract. 2014, 32, 183–202. [Google Scholar] [CrossRef]
- Morales, D.C.; Jiménez-Hornero, J.E.; Vázquez, F.; Morilla, F. Educational tool for optimal controller tuning using evolutionary strategies. IEEE Trans. Educ. 2012, 55, 48–57. [Google Scholar] [CrossRef]
- Guzmán, J.L.; Aström, K.J.; Dormido, S.; Hägglund, T.; Berenguel, M.; Piguet, Y. Interactive learning modules for PID control. IEEE Control Syst. Mag. 2008, 28, 118–134. [Google Scholar] [CrossRef]
- Guzmán, J.L.; Dormido, S.; Berenguel, M. Interactivity in education: An experience in the automatic control field. Comput. Appl. Eng. Educ. 2013, 21, 360–371. [Google Scholar] [CrossRef]
- Aliane, N. A matlab/simulink-based interactive module for servo systems learning. IEEE Trans. Educ. 2010, 53, 265–271. [Google Scholar] [CrossRef]
- Schlegel, M.; Mertl, J. Stability regions for PI/PID controller and Matlab program. In Proceedings of the 5th International Carpathian Control Conference, Zakopane, Poland, 25–28 May 2004; AGH-UST: Krakow, Poland, 2004; pp. 1–6. [Google Scholar]
- Barmish, B.R. New tools for robustness analysis. In Proceedings of the 27th IEEE Conference on Decision and Control, Austin, TX, USA, 7–9 December 1988; pp. 1–6. [Google Scholar] [CrossRef]
- Ackermann, J. Parameter space design of robust control systems. IEEE Trans. Autom. Contr. 1980, 25, 1058–1072. [Google Scholar] [CrossRef]
- Dormido, S.; Morilla, F. Tuning of PID controllers based on sensitivity margin specification. In Proceedings of the 2004 5th Asian Control Conference (IEEE Cat. No.04EX904), Melbourne, Victoria, Australia, 20–23 July 2004; Volume 1, pp. 486–491. [Google Scholar]
- Balchen, J.G.; Handlykken, M.; Tysso, A. The need for better laboratory experiments in control engineering education. IFAC Proc. Vol. 1981, 14, 3363–3368. [Google Scholar] [CrossRef]
- Ruz, M.L.; Garrido, J.; Vázquez, F. Educational tool for the learning of thermal comfort control based on PMV-PPD indices. Comput. Appl. Eng. Educ. 2018. [Google Scholar] [CrossRef]
- Fragoso, S.; Ruz, M.L.; Garrido, J.; Vázquez, F.; Morilla, F. Educational software tool for decoupling control in wind turbines applied to a lab-scale system. Comput. Appl. Eng. Educ. 2016, 24, 400–411. [Google Scholar] [CrossRef]
- Sánchez, J.; Dormido, S.; Pastor, R.; Morilla, F. A Java/Matlab-Based Environment for Remote Control System Laboratories: Illustrated with an Inverted Pendulum. IEEE Trans. Educ. 2004, 47, 321–329. [Google Scholar] [CrossRef]
- Moodle Home Page. Available online: https://moodle.org/ (accessed on 2 August 2018).
| Control | Plane | Characteristic Equation |
|---|---|---|
| PI | KP-KI | fPI(s; KP, KI) = s A(s) + s KP B(s) + KI B(s) = 0 |
| PD | KP-KD | fPD(s; KP, KD) = A(s) + s KD B(s) + KP B(s) = 0 |
| PIDα | KP-KI | fα(s; KP, KI) = s KI A(s) + s2KP2α B(s) + s KP KI B(s) + KI2B(s) = 0 |
| PIDKD | KP-KI | fKD(s; KP, KI) = s AD(s) + s KP BD(s) + KI BD(s) = 0 |
| PIDKI | KP-KD | fKI(s; KP, KD) = AI(s) + s KD BI(s) + KP BI(s) = 0 |
| Specification | Target Point |
|---|---|
| PM (ϕm) | ϕB = ϕm; rB = 1 |
| GM (Am) | ϕB = 0°; rB = 1/Am |
| Ms (Ms, θ) c = −1 R = 1/MS | |
| Mt (Mt, θ) |
| Control | Boundary Curve |
|---|---|
| PIDα | |
| PIDKD | |
| PIDKI |
| Discrete PID Controller |
|---|
| Design | KP | KI | KD | PM (ωcp) | GM (ωcg) | Ms (ωs) | Mt (ωt) |
|---|---|---|---|---|---|---|---|
| 1 | –0.55 | 0.4 | 0.074 | 60 (0.2) | 3 (0.5) | 1.6 (0.4) | 1 (0.1) |
| 2 | 1.87 | 1.78 | 0.196 | 60.5 (0.7) | 3 (3.3) | 1.6 (2) | 1 (0.4) |
| 3 | 2.37 | 1.96 | 0.29 | 60 (0.9) | 2.5 (3.7) | 1.8 (2.6) | 1 (1.3) |
| 4 | 3.48 | 2.03 | 0.6 | 60 (1.3) | 1.7 (4.8) | 2.5 (4) | 1.6 (3.6) |
| Design | KP | KI | PM (ωcp) | Ms (ωs) |
|---|---|---|---|---|
| PI 1 | 0.103 | 0.155 | 60 (0.3) | 1.5 (0.5) |
| PI 2 | 0.62 | 0.26 | 60 (0.6) | 1.5 (1) |
| PI 3 | 1 | 0.42 | 45 (0.9) | 1.7 (1.1) |
| Learning Value | |
| Q1 | Did the tool help you to visualize new concepts related to PID control design in the frequency domain? |
| Q2 | Do you think you will remember the concepts taught with the tool better than if you had only lecture classes? |
| Q3 | Do you think that the tool motivates learning and is useful as a complement to lecture explanations? |
| Value added | |
| Q4 | Were you satisfied with the simulations performed with the tool? |
| Q5 | Did the tool help you to improve your theoretical knowledge of PID tuning and robustness specifications in the frequency domain? |
| Q6 | Were you able to understand practical problems and implementation issues such as sample time choice or control signal limitations? |
| Q7 | Was the level of interactivity in the tool adequate? |
| Design usability and easy understanding of the tool | |
| Q8 | Do you think that the graphical user interface is user-friendly? |
| Q9 | Was the tool easy to understand and use? |
| Q10 | Were concepts with the tool clearly presented and easy to follow? |
| Group Items | Strongly Agree | Agree | Neutral | Disagree | Strongly Disagree |
|---|---|---|---|---|---|
| Learning value (Q1, Q2, Q3) | 33% | 53% | 10% | 1% | 3% |
| Value added (Q4, Q5, Q6, Q7) | 24% | 44% | 24% | 4% | 4% |
| Design usability and easy understanding of the tool (Q8, Q9, Q10) | 23% | 50% | 19% | 4% | 4% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garrido, J.; Ruz, M.L.; Morilla, F.; Vázquez, F. Interactive Tool for Frequency Domain Tuning of PID Controllers. Processes 2018, 6, 197. https://doi.org/10.3390/pr6100197
Garrido J, Ruz ML, Morilla F, Vázquez F. Interactive Tool for Frequency Domain Tuning of PID Controllers. Processes. 2018; 6(10):197. https://doi.org/10.3390/pr6100197
Chicago/Turabian StyleGarrido, Juan, Mario L. Ruz, Fernando Morilla, and Francisco Vázquez. 2018. "Interactive Tool for Frequency Domain Tuning of PID Controllers" Processes 6, no. 10: 197. https://doi.org/10.3390/pr6100197
APA StyleGarrido, J., Ruz, M. L., Morilla, F., & Vázquez, F. (2018). Interactive Tool for Frequency Domain Tuning of PID Controllers. Processes, 6(10), 197. https://doi.org/10.3390/pr6100197








