Rheological Behavior and Modeling of a Crushed Sandstone-Mudstone Particle Mixture
Abstract
1. Introduction
2. Test Materials and Testing Methods
2.1. Tested Materials
2.2. Confined Uniaxial Compression Tests
2.3. Testing Method
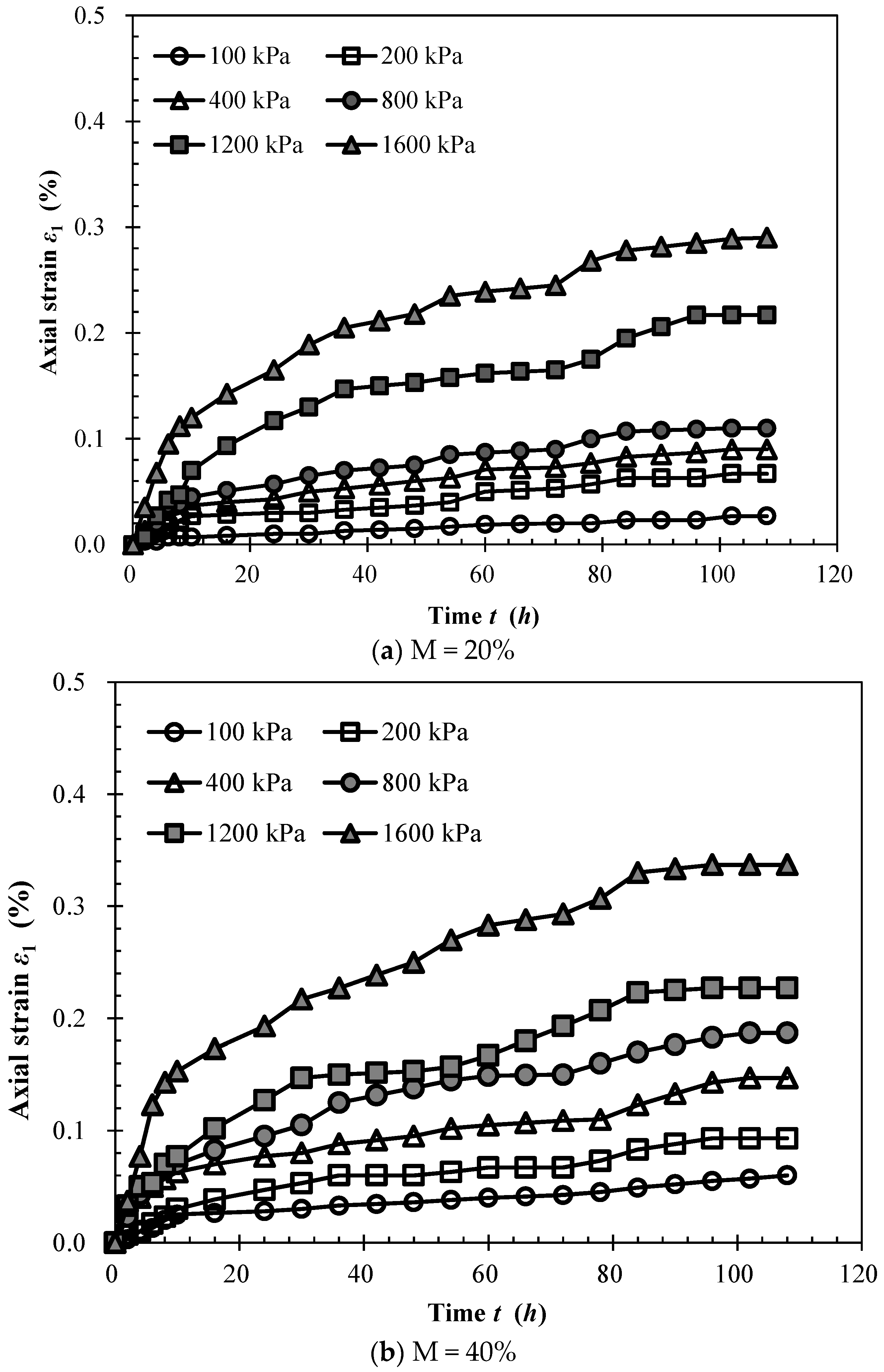
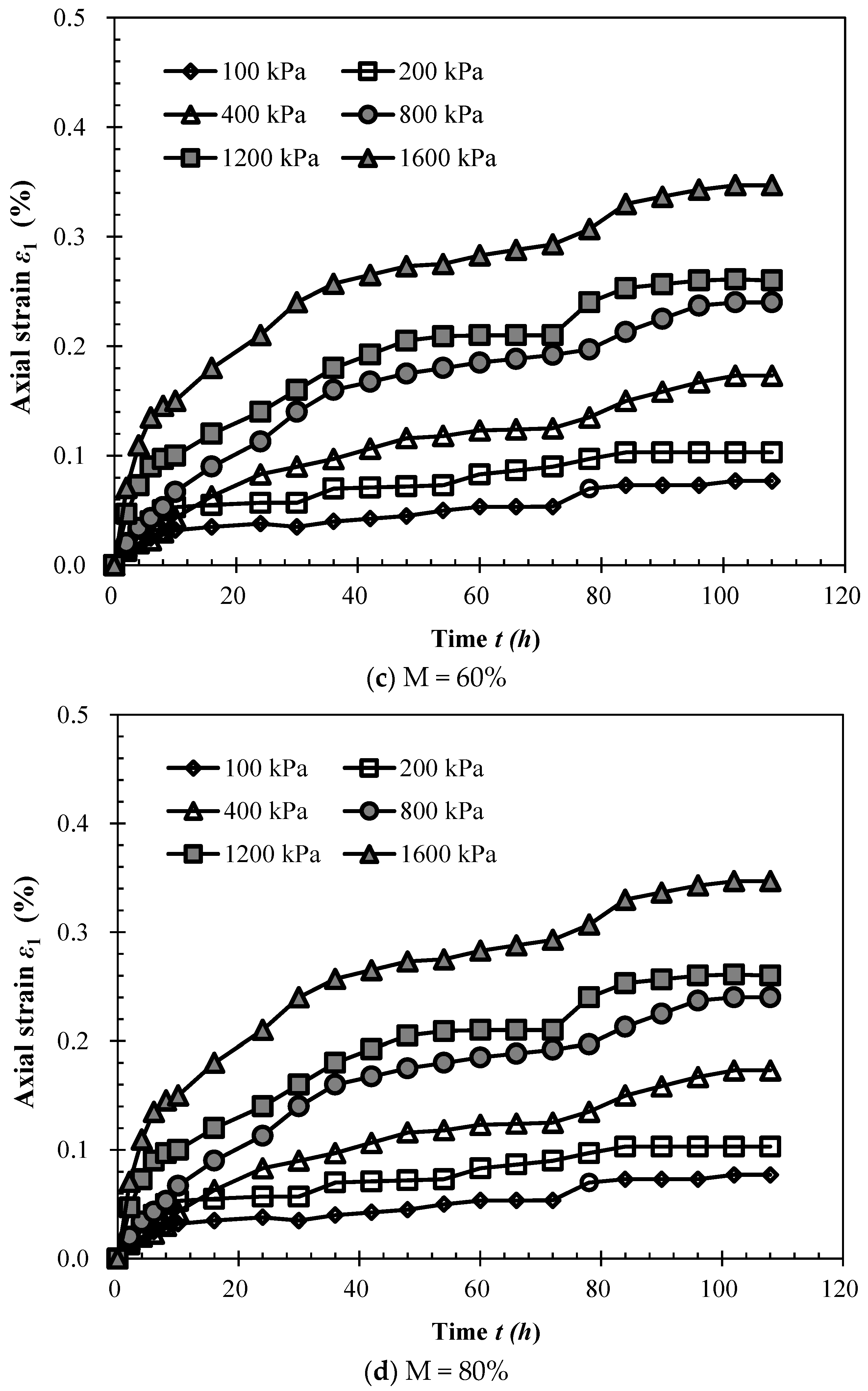
3. Test Results
3.1. Results of the Rheological Tests
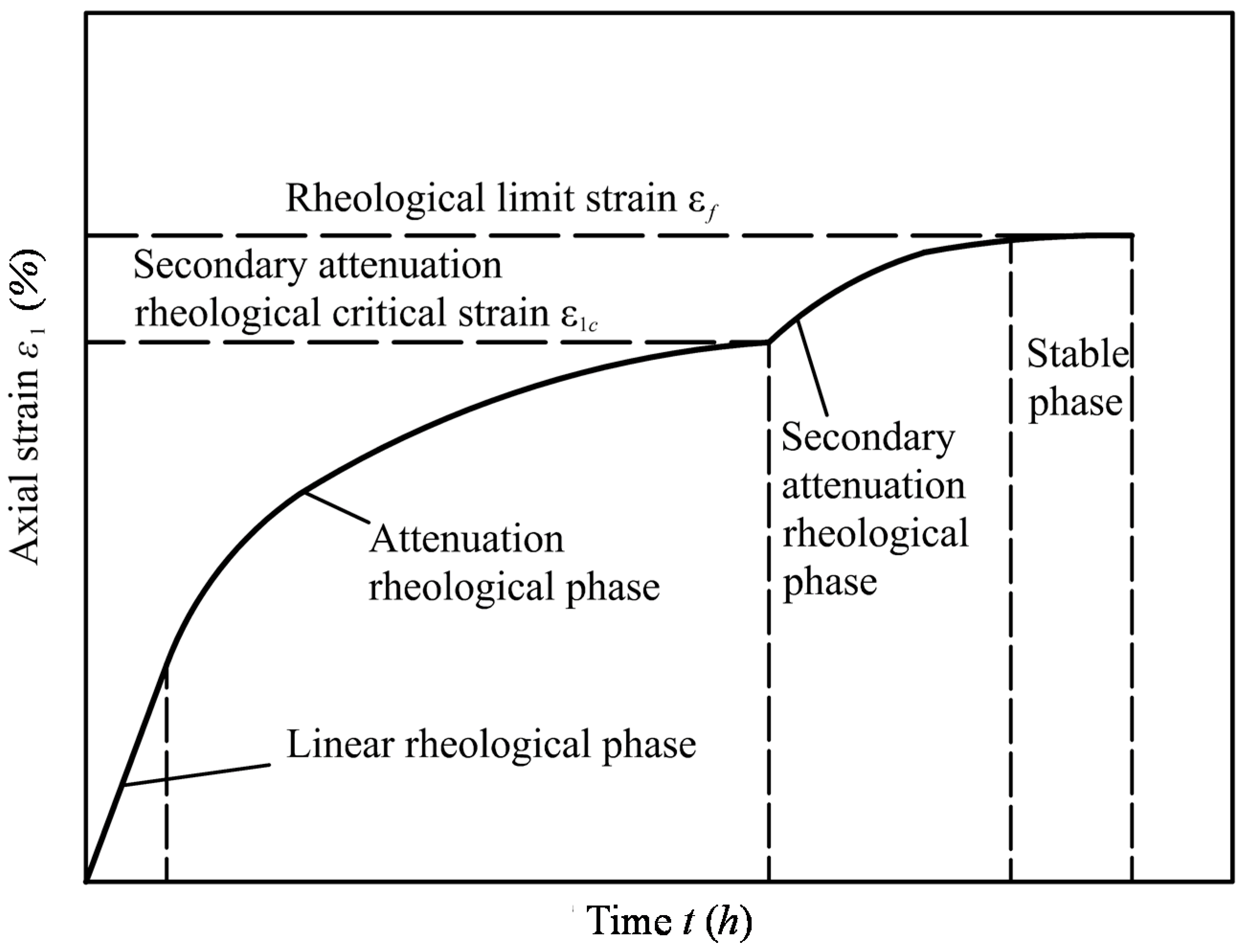
3.2. Four-Phase Rheological Process
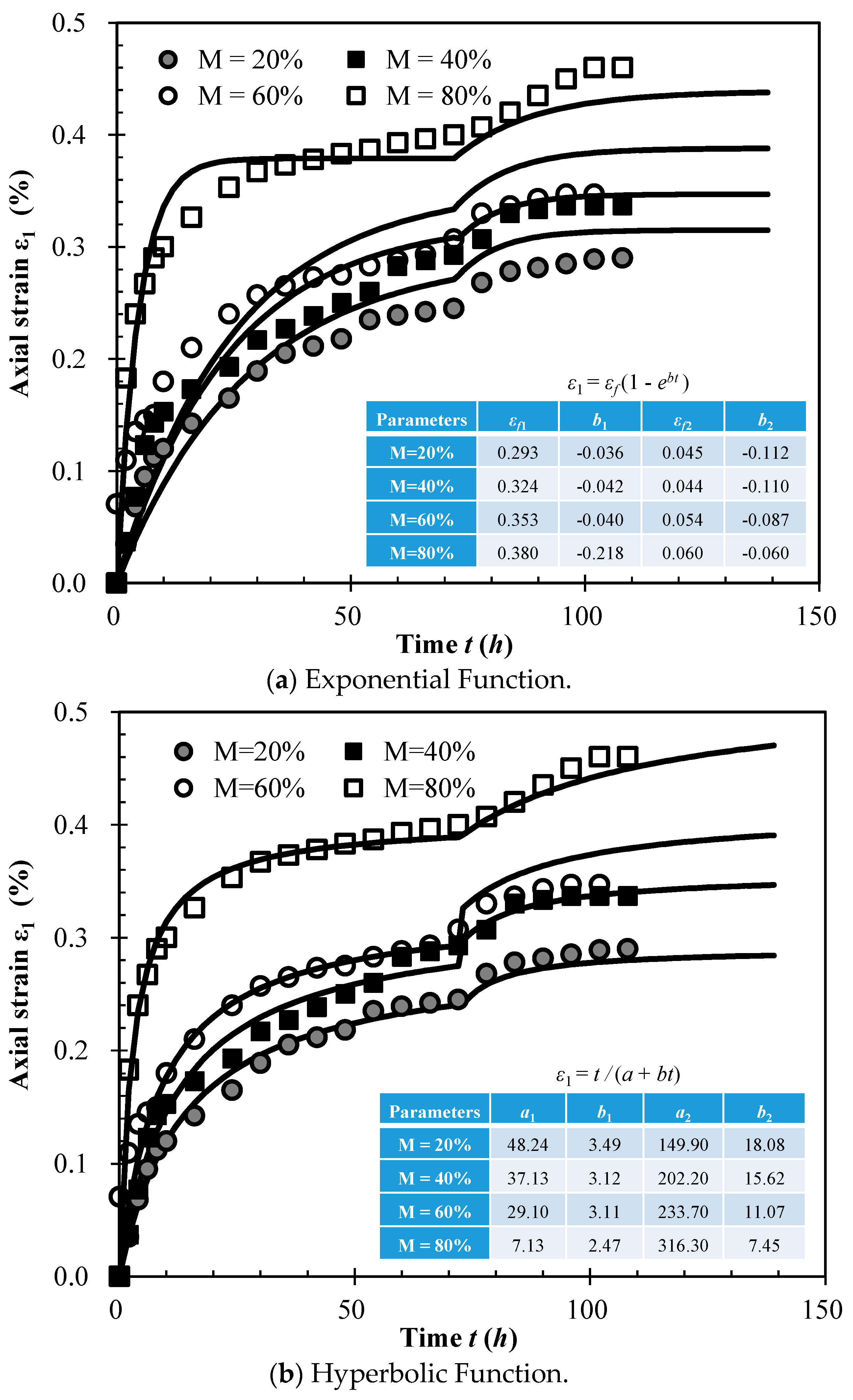
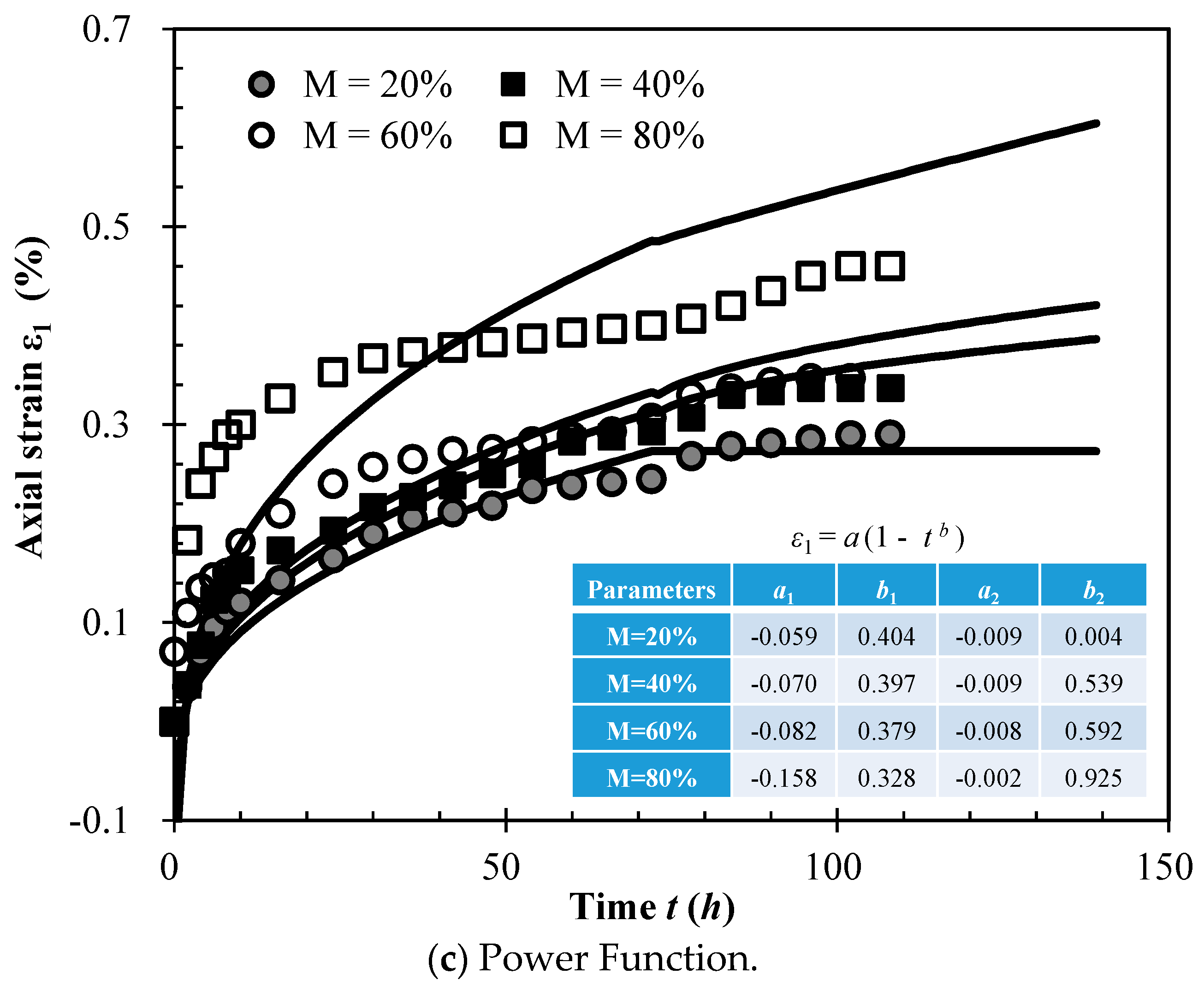
4. Segmented Rheological Model for SMPM
4.1. Segmented Rheological Model
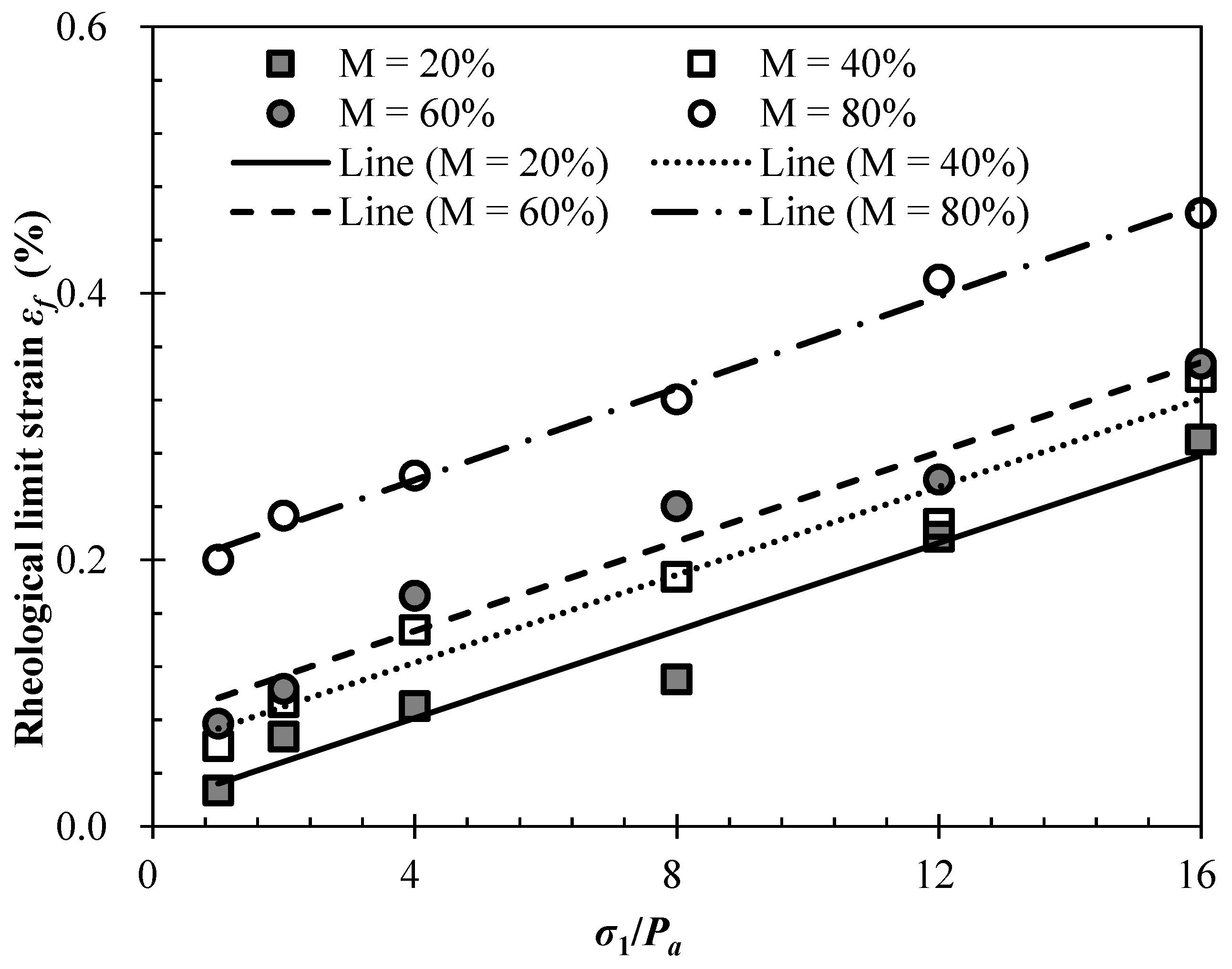
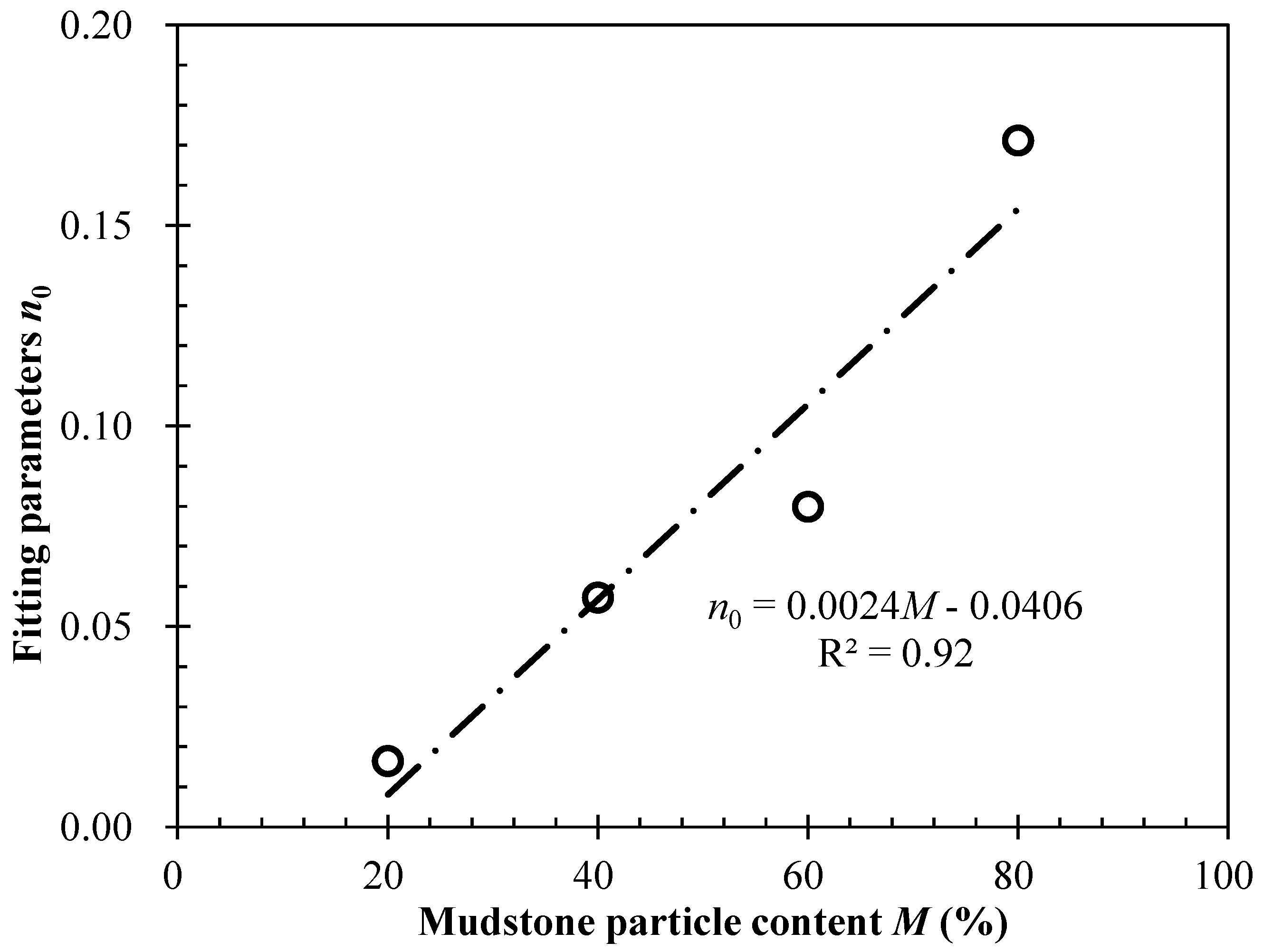
4.2. Rheological Limit Strain εf
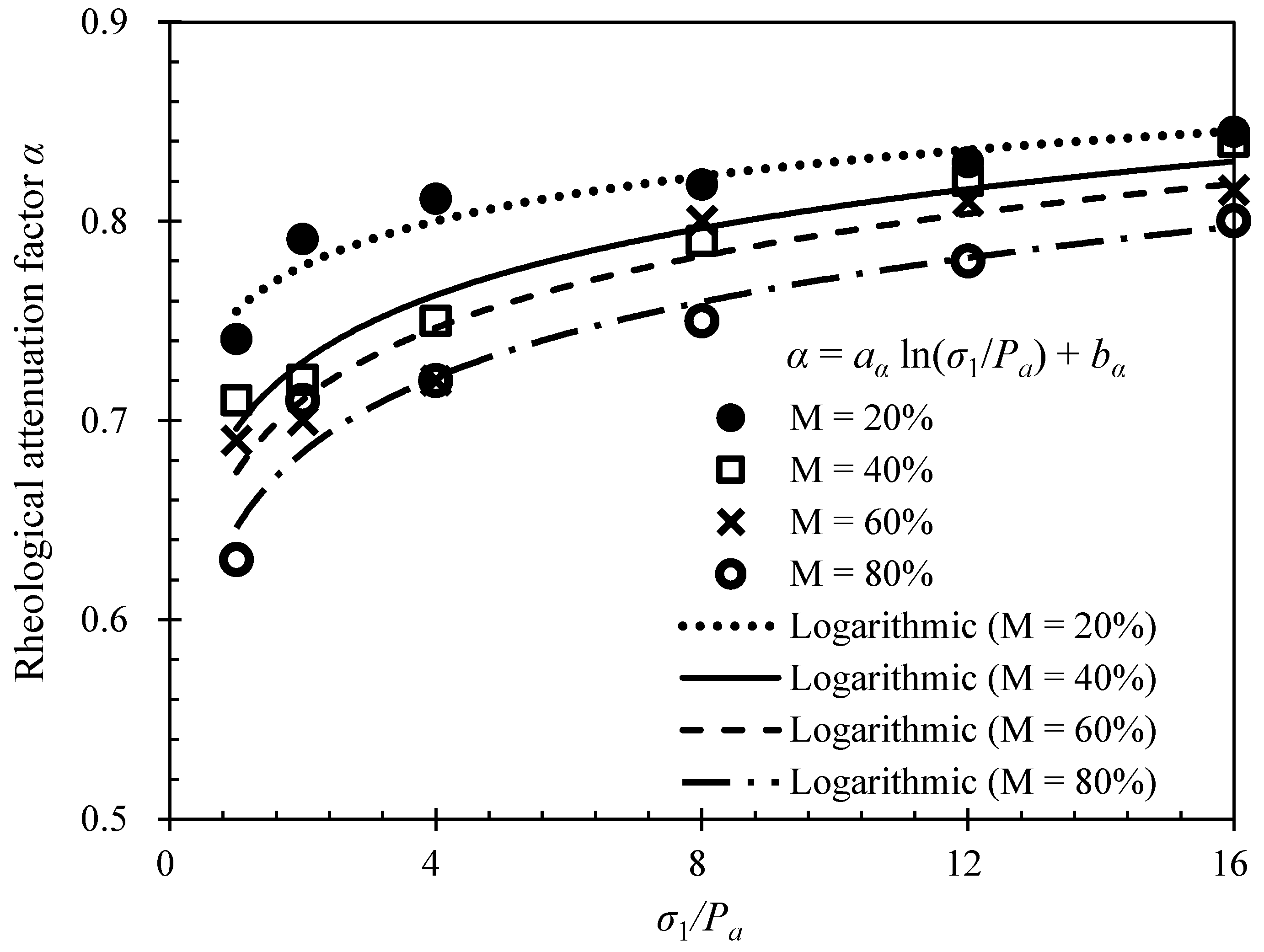
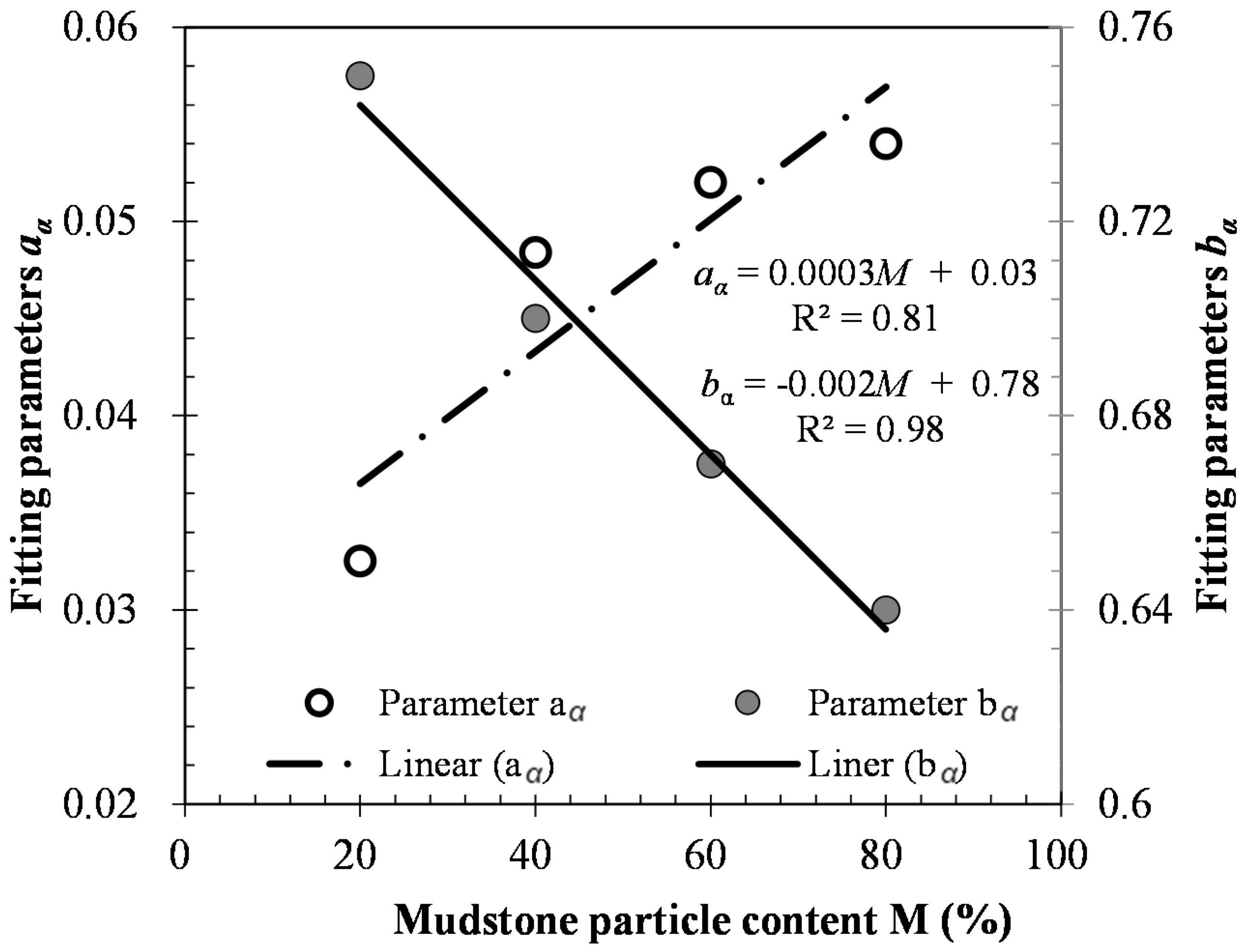
4.3. Rheological Attenuation Factor
5. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chongqing Geological and Mineral Resource Exploration and Development Corporation (CGMREDC). Chongqing Geological Map (Scale 1:500,000); Chongqing Yangtze River Map Printing Factory: Chongqing, China, 2002. [Google Scholar]
- Wang, J.J.; Zhang, H.P.; Deng, D.P. Effects of compaction effort on compaction behavior and particle crushing of a crushed sandstone-mudstone particle mixture. Soil Mech. Found. Eng. 2014, 51, 67–71. [Google Scholar] [CrossRef]
- Wang, J.-J.; Cheng, Y.-Z.; Zhang, H.-P.; Deng, D.-P. Effects of particle size on compaction behavior and particle crushing of crushed sandstone-mudstone particle mixture. Environ. Earth Sci. 2015, 73, 8053–8059. [Google Scholar] [CrossRef]
- Qiu, Z.F. Triaxial Deformation Behavior and Damage Model under Wet-Dry Cycling of a Sandstone-Mudstone Mixture. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2016. (In Chinese). [Google Scholar]
- Wang, J.J.; Fang, X.S.; Qiu, Z.-F. Engineering Properties of a Sandstone-Mudstone Particle Mixture; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Wang, J.J.; Qiu, Z.F.; Deng, W.J.; Zhang, H.P. Effects of mudstone particle content on shear strength of a crushed sandstone-mudstone particle mixture. Mar. Georesour. Geotechnol. 2016, 34, 395–402. [Google Scholar] [CrossRef]
- Qiu, Z.F.; Wang, J.J.; Huang, S.Y.; Bai, J.P. Wetting-induced axial and volumetric strains of a sandstone mudstone particle mixture. Mar. Georesour. Geotechnol. 2018. [Google Scholar] [CrossRef]
- Wang, J.J.; Qiu, Z.F.; Bai, J.P.; Yu, C.; Liu, M.W. Deformation of a sandstone–mudstone particle mixture induced by periodic saturation. Mar. Georesour. Geotechnol. 2018, 36, 494–503. [Google Scholar] [CrossRef]
- Jiang, J.S.; Cheng, Z.L.; Zuo, Y.Z.; Ding, H.S. CT triaxial rheological test on coarse-grained soils. Rock Soil Mech. 2014, 35, 2507–2514. [Google Scholar]
- Indraratna, B.; Thakur, P.K.; Vinod, J.S.; Salim, W. Semi empirical cyclic densification model for ballast incorporating particle breakage. Int. J. Geomech. 2012, 12, 260–271. [Google Scholar] [CrossRef]
- Indraratna, B.; Ngo, N.; Rujikiatkamjorn, C.; Vinod, J.S. Behavior of fresh and fouled railway ballast subjected to direct shear testing: Discrete element simulation. Int. J. Geomech. 2014, 14, 34–44. [Google Scholar] [CrossRef]
- Kong, X.J.; Zhou, Y.; Xu, B.; Zou, D.G. Analysis on Seismic Failure Mechanism of Zipingpu Dam and Several Reflections of Aseismic Design for High Rock-Fill Dam; The Workshop on Biennial International Conference on Engineering; ASCE: Reston, VA, USA, 2010; pp. 3177–3189. [Google Scholar]
- Xiao, Y.; Sun, Y.F.; Hanif, K.F. A particle-breakage critical state model for rockfill material. Sci. China Technol. Sci. 2015, 58, 1125–1136. [Google Scholar] [CrossRef]
- Zhang, B.Y.; Sun, G.L.; Zhang, Z.L. Degrading deformation of rockfill materials and its constitutive model. Chin. J. Geotech. Eng. 2010, 32, 98–103. [Google Scholar]
- Jia, Y.; Xu, B.; Chi, S.; Xiang, B.; Zhou, Y.; Jia, Y. Research on the particle breakage of rockfill materials during triaxial tests. Int. J. Geomech. 2017, 17, 04017085. [Google Scholar] [CrossRef]
- Carrier, B.; Vandamme, M.; Pellenq RJ, M.; Van Damme, H. Creep of clay: Numerical results at the scale of a layer and experimental results at the scale of thin self-standing films. In Proceedings of the 10th International Conference on Mechanics and Physics of Creep, Shrinkage, and Durability of Concrete and Concrete Structures, Vienna, Austria, 21–23 September 2015; pp. 531–536. [Google Scholar]
- Wang, Y.; Yin, Z.Z. Rheology model of rockfill used in the rheology analysis of concrete face rockfill dam. Rock Soil Mech. 2000, 21, 227–230. [Google Scholar]
- Chen, X.B.; Zhang, J.S.; Feng, Z.P. Experimental study on rheological engineering properties of coarsely granular red sandstone soil. Chin. J. Rock Mech. Eng. 2007, 26, 601–607. [Google Scholar]
- Wang, L.Z.; Yin, Z.Y. Stress dilatancy of natural soft clay under an undrained creep condition. Int. J. Geomech. 2014, 15, A4014002. [Google Scholar] [CrossRef]
- Cheng, Z.L.; Ding, H.S. Creep test for rockfill. Chin. J. Geotech. Eng. 2004, 26, 473–476. [Google Scholar]
- Zhang, B.Y.; Chen, T.; Peng, C.; Qian, X.X.; Jie, Y.; Zhang, B. Experimental study on loading-creep coupling effect in rockfill material. Int. J. Geomech. 2017, 17, 04017059. [Google Scholar] [CrossRef]
- Yang, C.; Wen, C.P. Study of nonlinear rheology of improved expansive soil based on model theory and genetic creep theory. Rock Soil Mech. 2016, S2, 75–82. [Google Scholar]
- Zhang, B.Y.; Zhang, J.H.; Sun, G.L. Deformation and shear strength of rockfill materials composed of soft siltstones subjected to stress, cyclical drying/wetting and temperature variations. Eng. Geol. 2015, 190, 87–97. [Google Scholar] [CrossRef]
- Trade Standard of P. R. China SL237-015. Standard method for one-dimensional consolidation properties of soils. In Specification of Soil Test; The Ministry of Water Resources of P.R. China: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Wang, Z.J.; Liu, S.H.; Wang, Y.S.; Kong, W.Y. Analysis on microstructure of granular materials under different stress paths. J. Hydraul. Eng. 2013, 44, 772–778. [Google Scholar]
- Shen, Z.J.; Zhao, K.Z. Back analysis of creep deformation of rockfill dams. J. Hydraul. Eng. 1988, 6, 1–6. [Google Scholar]
- Liang, J.; Liu, H.L. Creep test for rockfill of CFRD. Chin. J. Geotech. Eng. 2004, 24, 257–259. [Google Scholar]
- Feda, J. Creep of Soils and Related Phenomena; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Cao, G.X. Study on Post-Construction Settlement of High Fill Foundation in Mountainous Airport. Ph.D. Thesis, Tsinghua University, Beijing, China, 2011. (In Chinese). [Google Scholar]
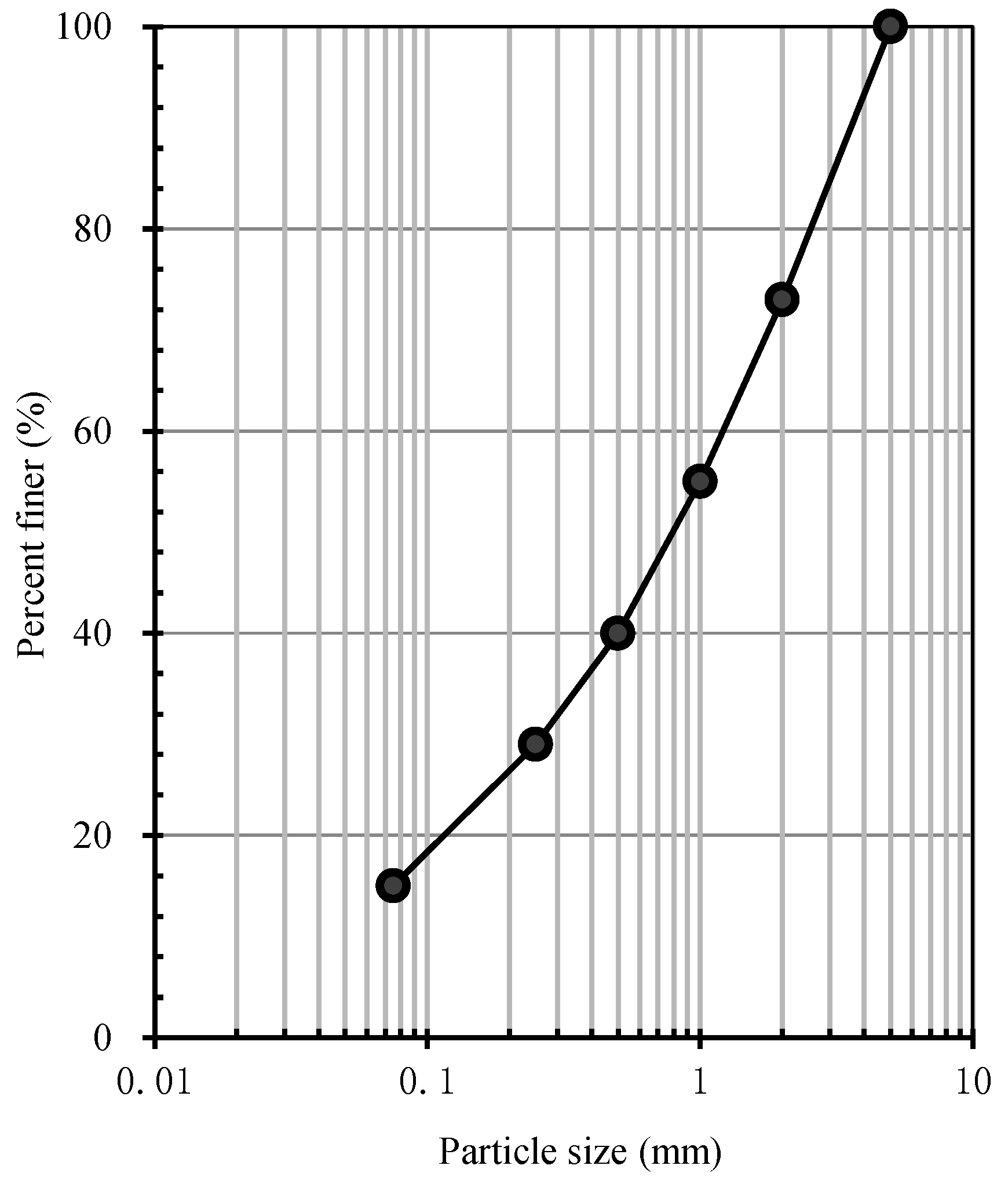

| Particle size (mm) | 5–2 | 2–1 | 1–0.5 | 0.5–0.25 | 0.25–0.075 | <0.075 |
| Content (%) | 27 | 18 | 15 | 11 | 14 | 15 |
| Mudstone Particles Content (%) | m | n | R2 |
|---|---|---|---|
| 20 | 0.0163 | 0.0164 | 0.96 |
| 40 | 0.0165 | 0.0571 | 0.96 |
| 60 | 0.0168 | 0.0798 | 0.96 |
| 80 | 0.0172 | 0.1711 | 0.99 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Z.; Cao, T.; Li, Y.; Wang, J.; Chen, Y. Rheological Behavior and Modeling of a Crushed Sandstone-Mudstone Particle Mixture. Processes 2018, 6, 192. https://doi.org/10.3390/pr6100192
Qiu Z, Cao T, Li Y, Wang J, Chen Y. Rheological Behavior and Modeling of a Crushed Sandstone-Mudstone Particle Mixture. Processes. 2018; 6(10):192. https://doi.org/10.3390/pr6100192
Chicago/Turabian StyleQiu, Zhenfeng, Ting Cao, Yongsuo Li, Junjie Wang, and Yulong Chen. 2018. "Rheological Behavior and Modeling of a Crushed Sandstone-Mudstone Particle Mixture" Processes 6, no. 10: 192. https://doi.org/10.3390/pr6100192
APA StyleQiu, Z., Cao, T., Li, Y., Wang, J., & Chen, Y. (2018). Rheological Behavior and Modeling of a Crushed Sandstone-Mudstone Particle Mixture. Processes, 6(10), 192. https://doi.org/10.3390/pr6100192






