Numerical Simulation of a New Porous Medium Burner with Two Sections and Double Decks
Abstract
:1. Introduction
2. Mechanism of Gas Combustion in a Porous Medium
3. Methodology
3.1. Numerical Model
3.2. Fundamentals
3.3. Boundary Condition
3.4. Numerical Scheme
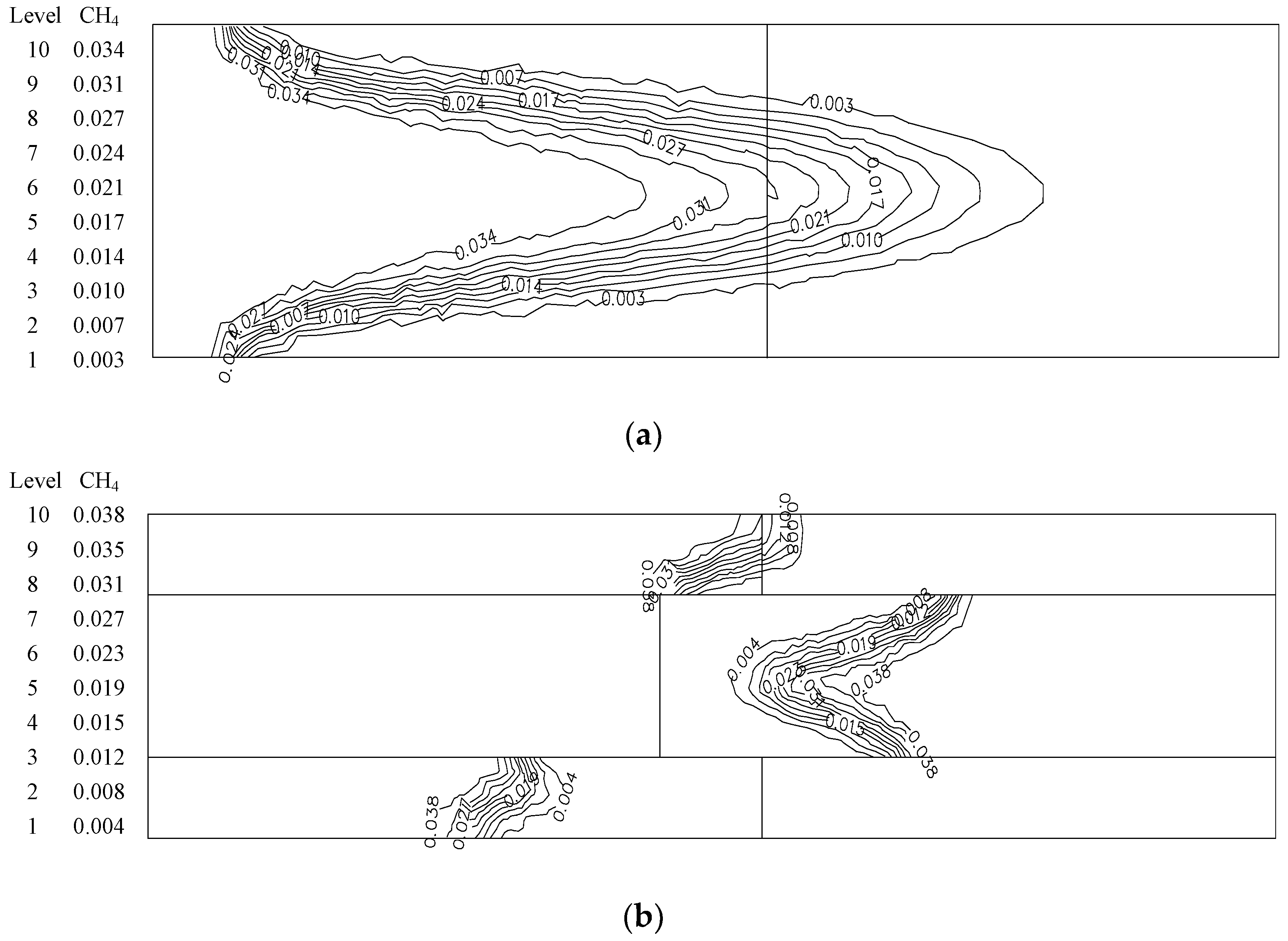
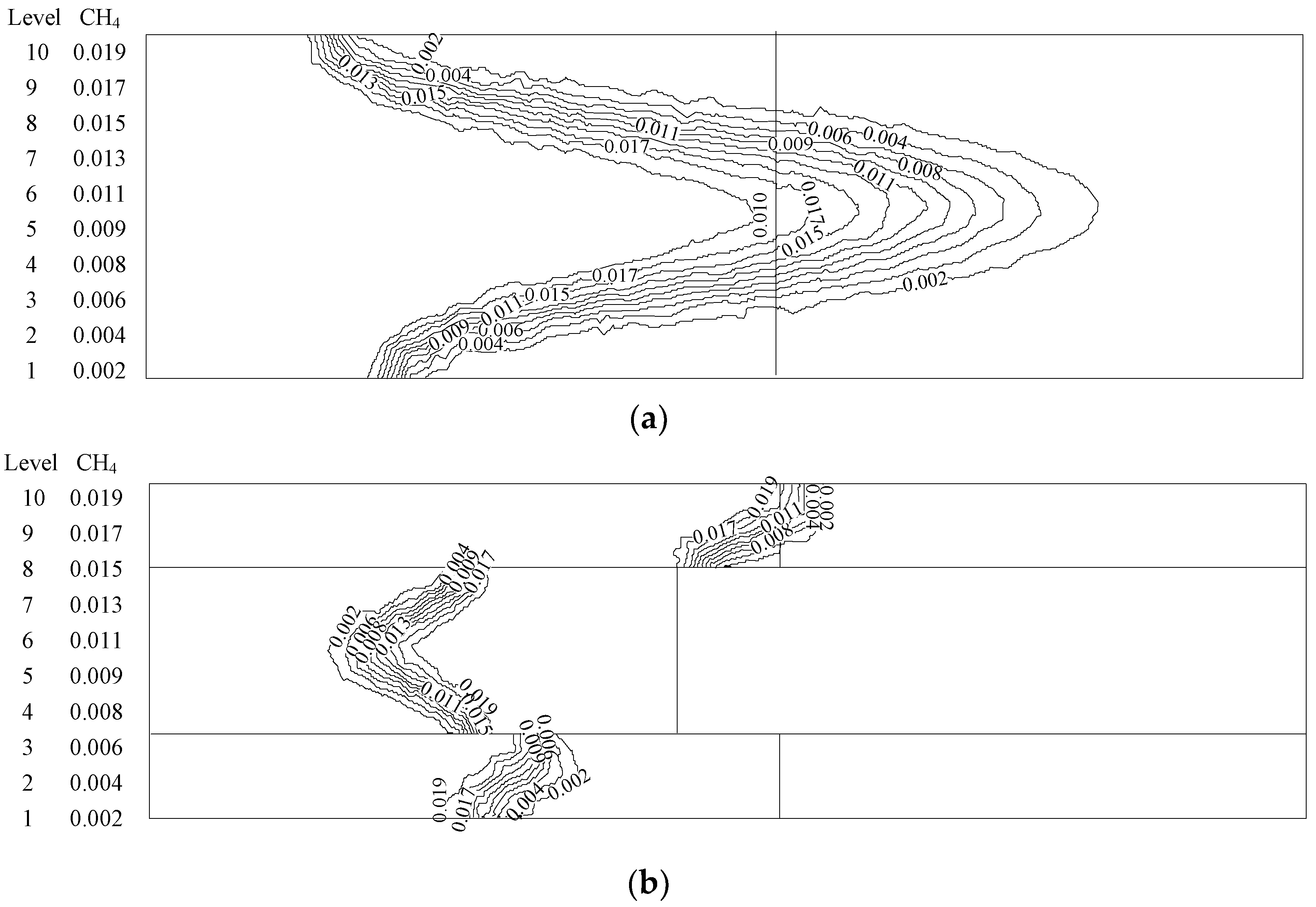
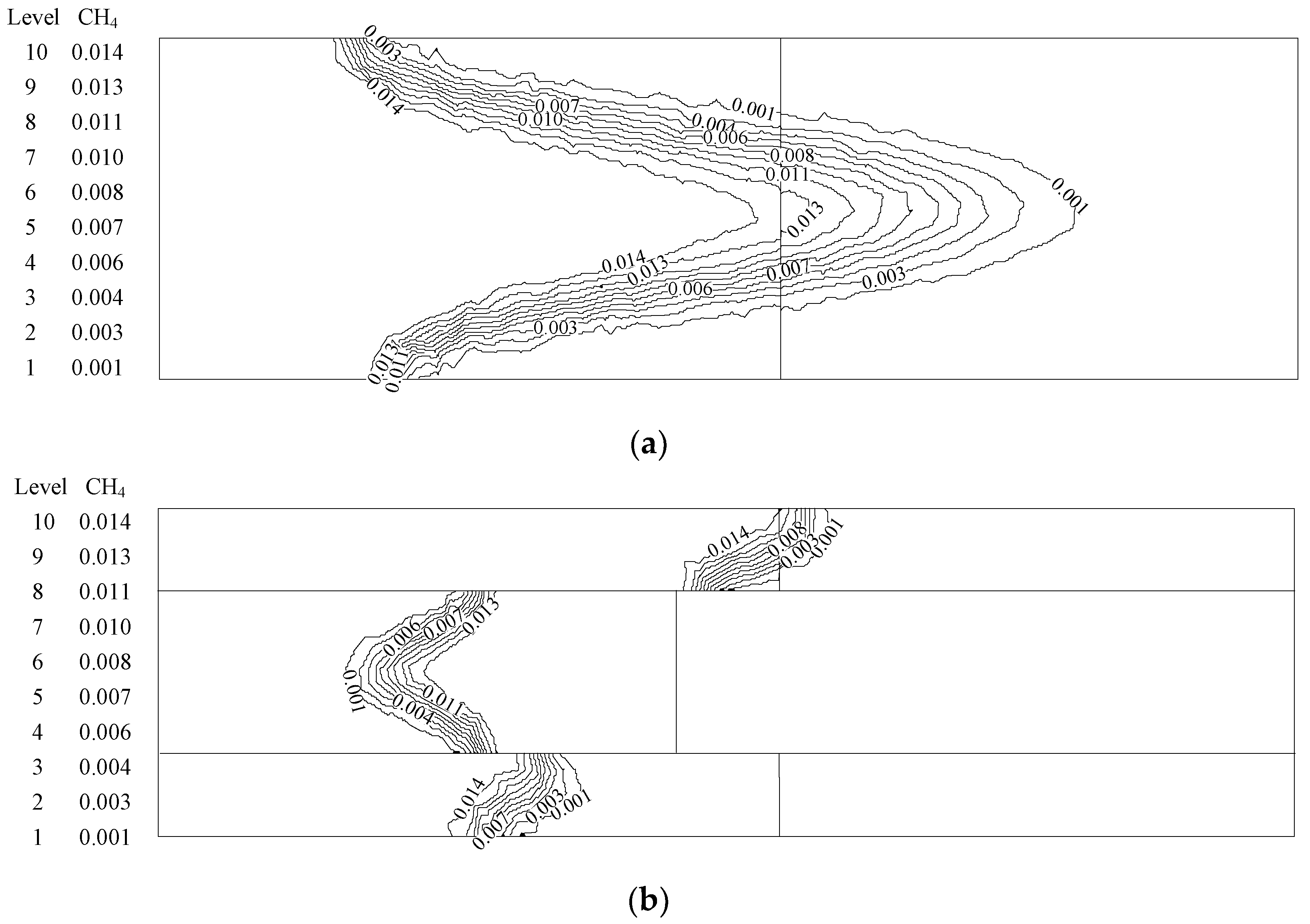
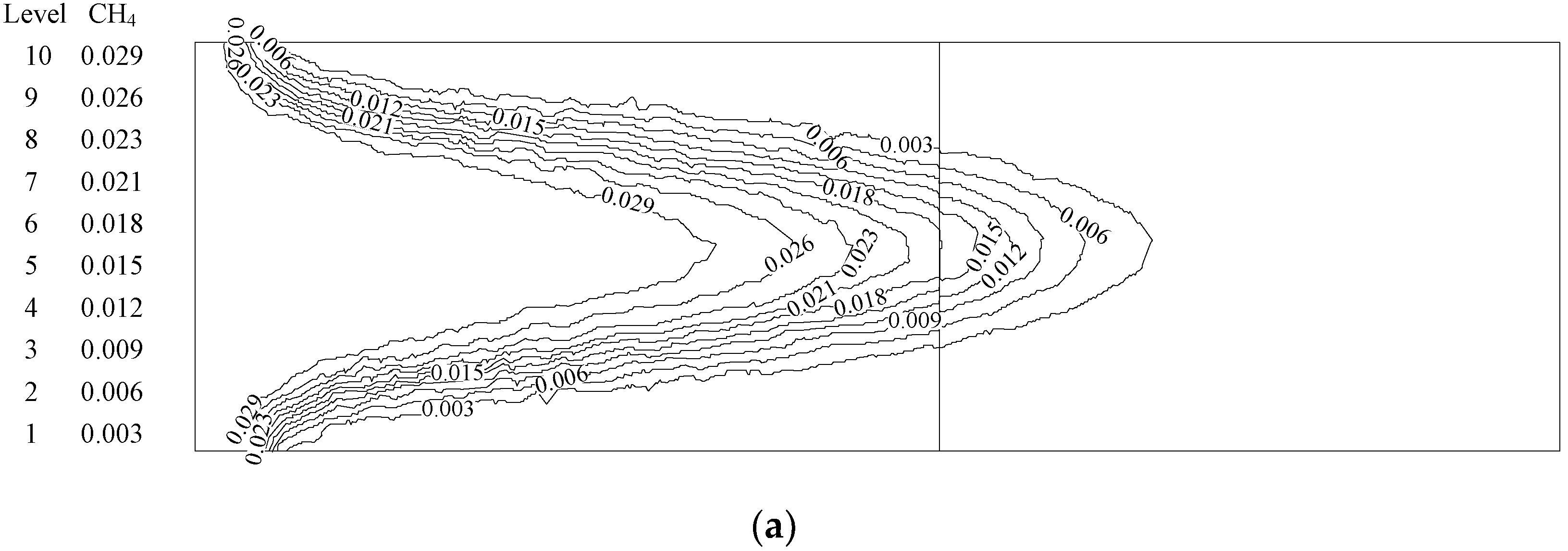
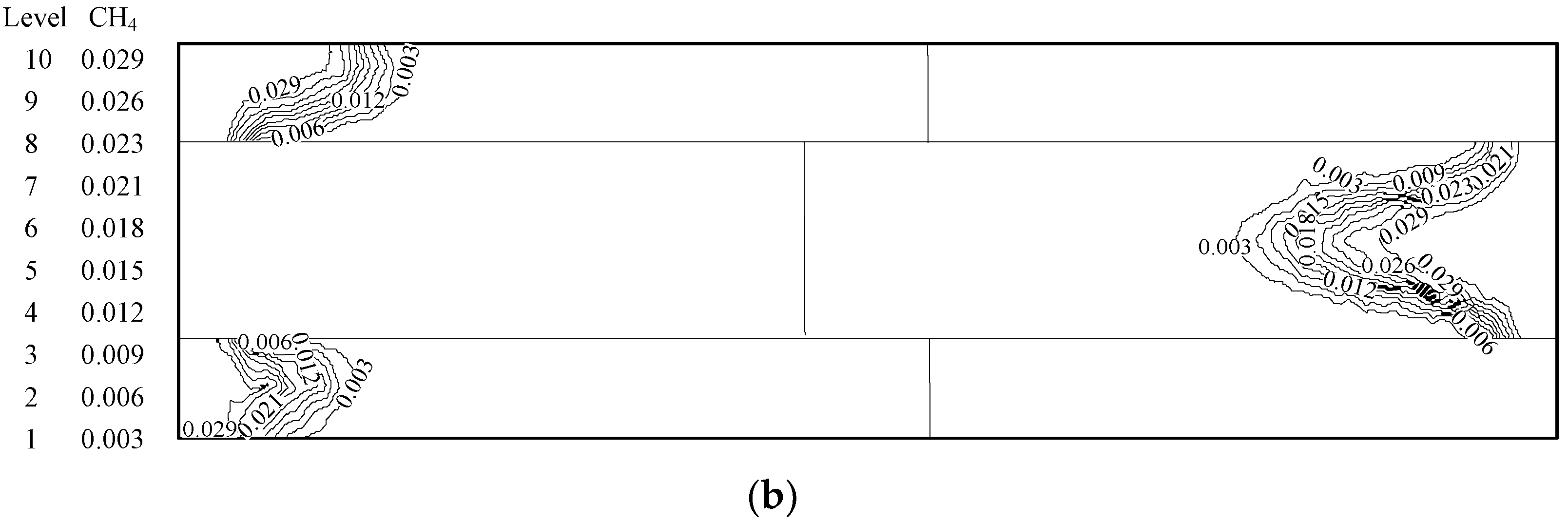
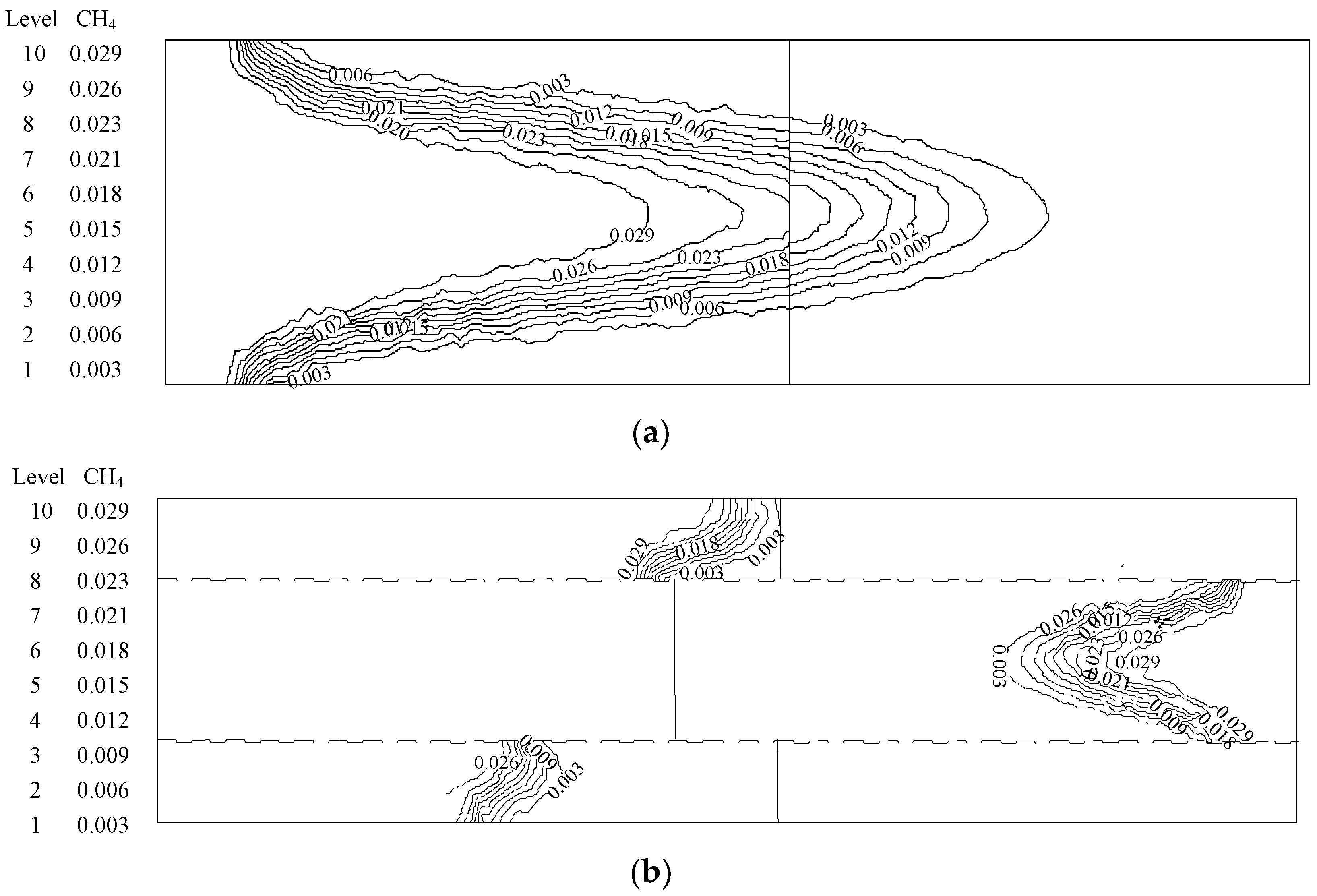
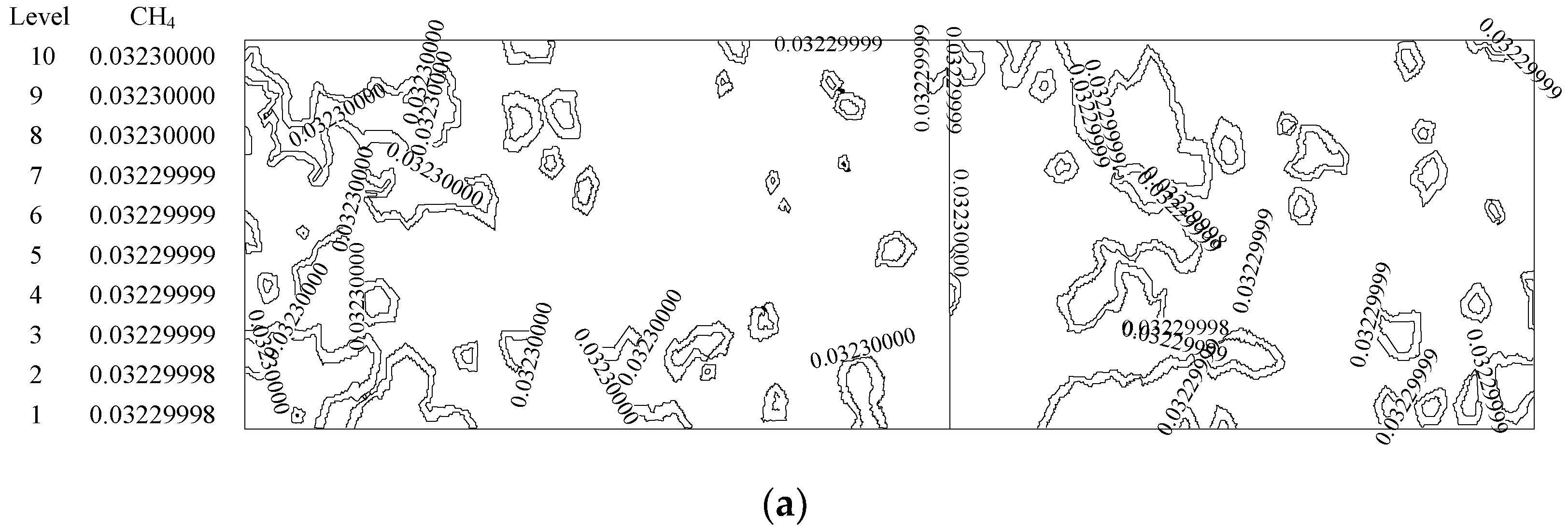
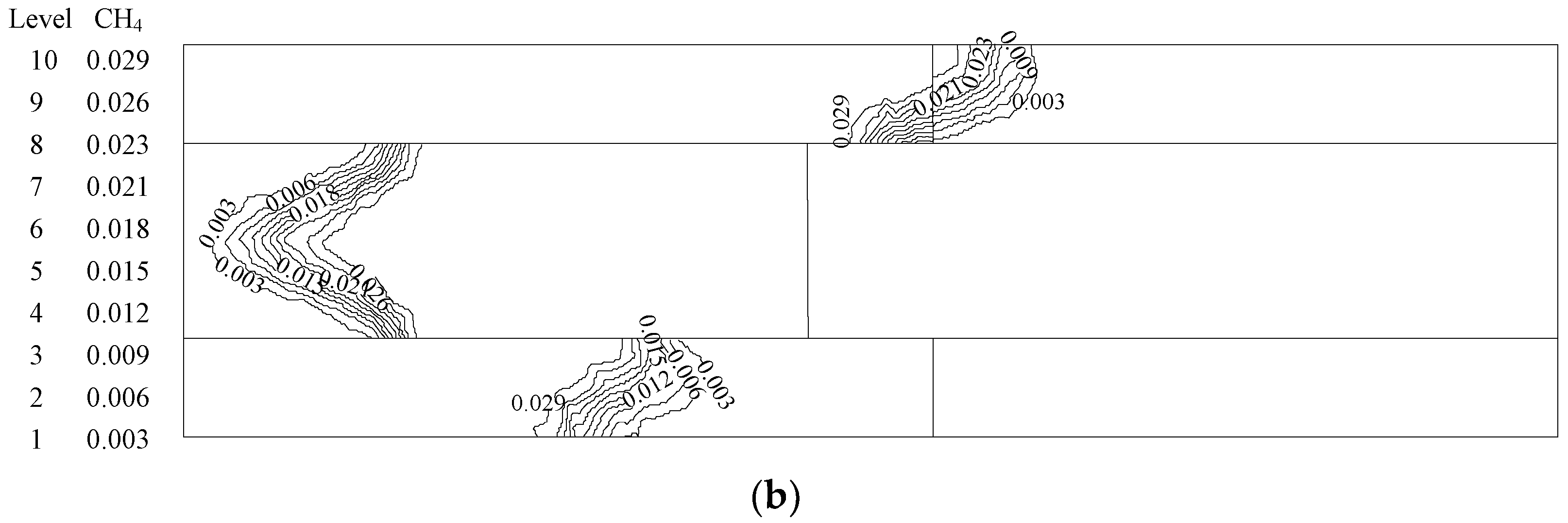
4. Results and Discussion
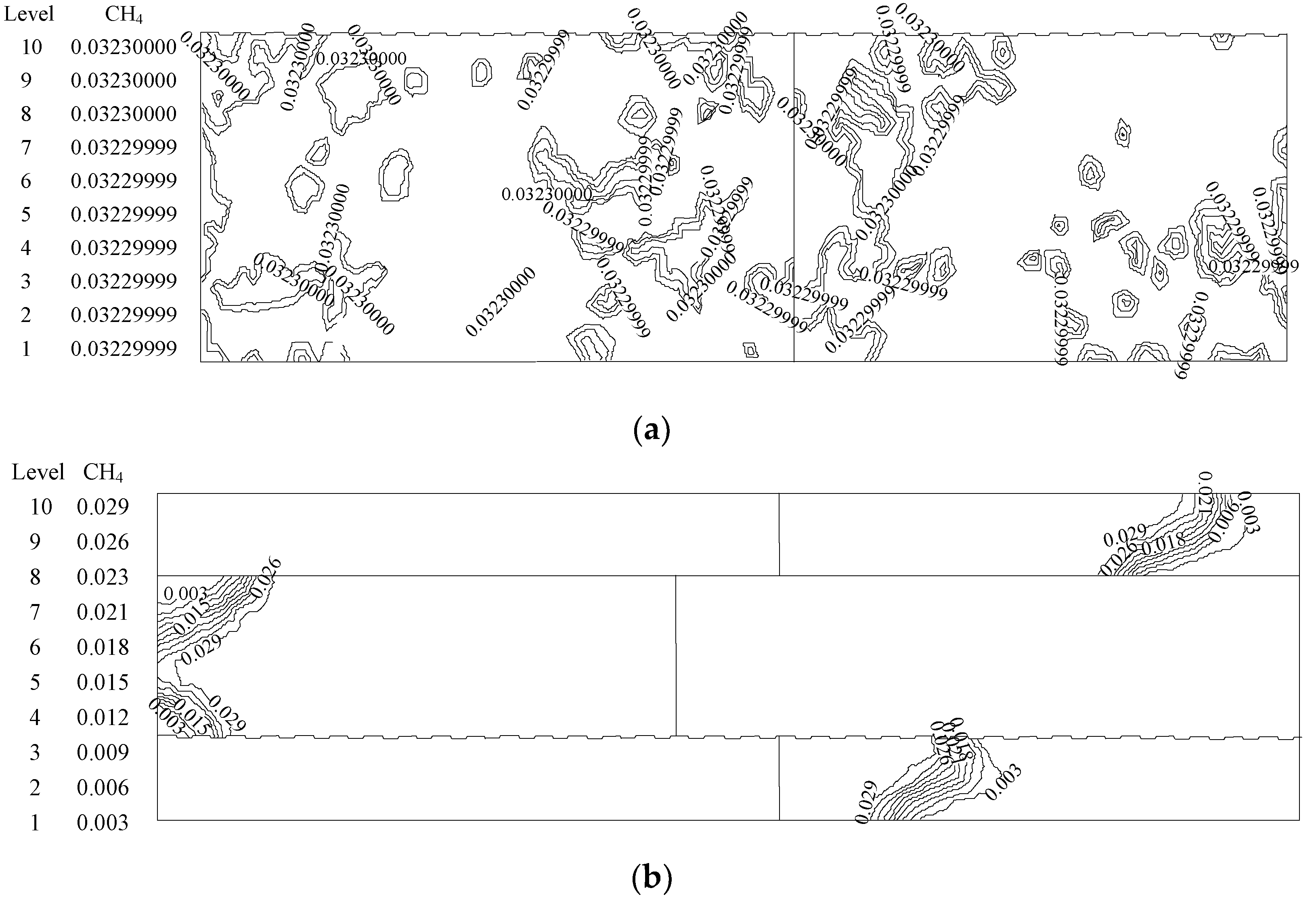
4.1. Analysis of the Effect of the Premixed Gas Combustion
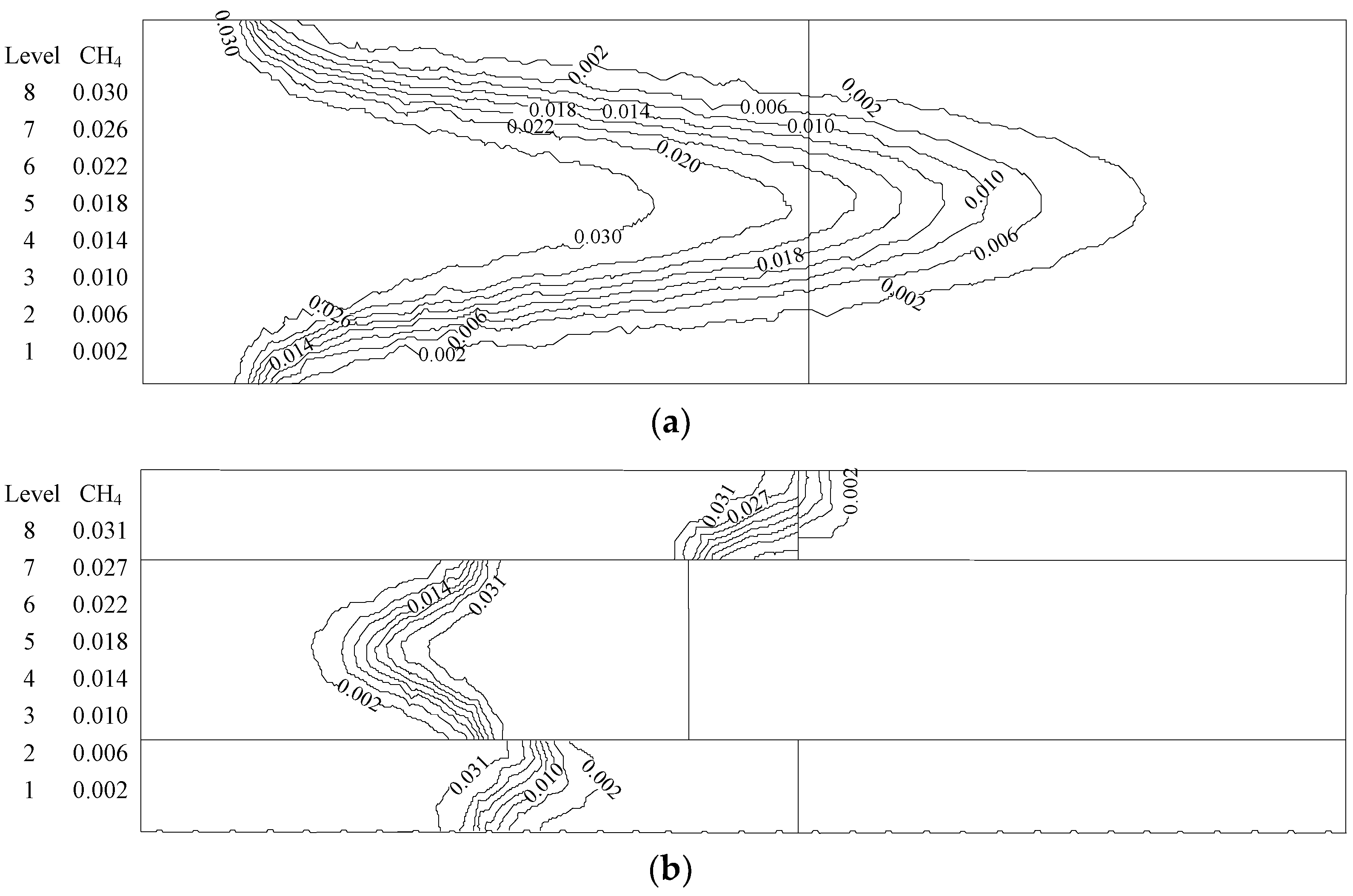
4.1.1. Influence of the Equivalence Ratio of Premixed Gas on Combustion Degree
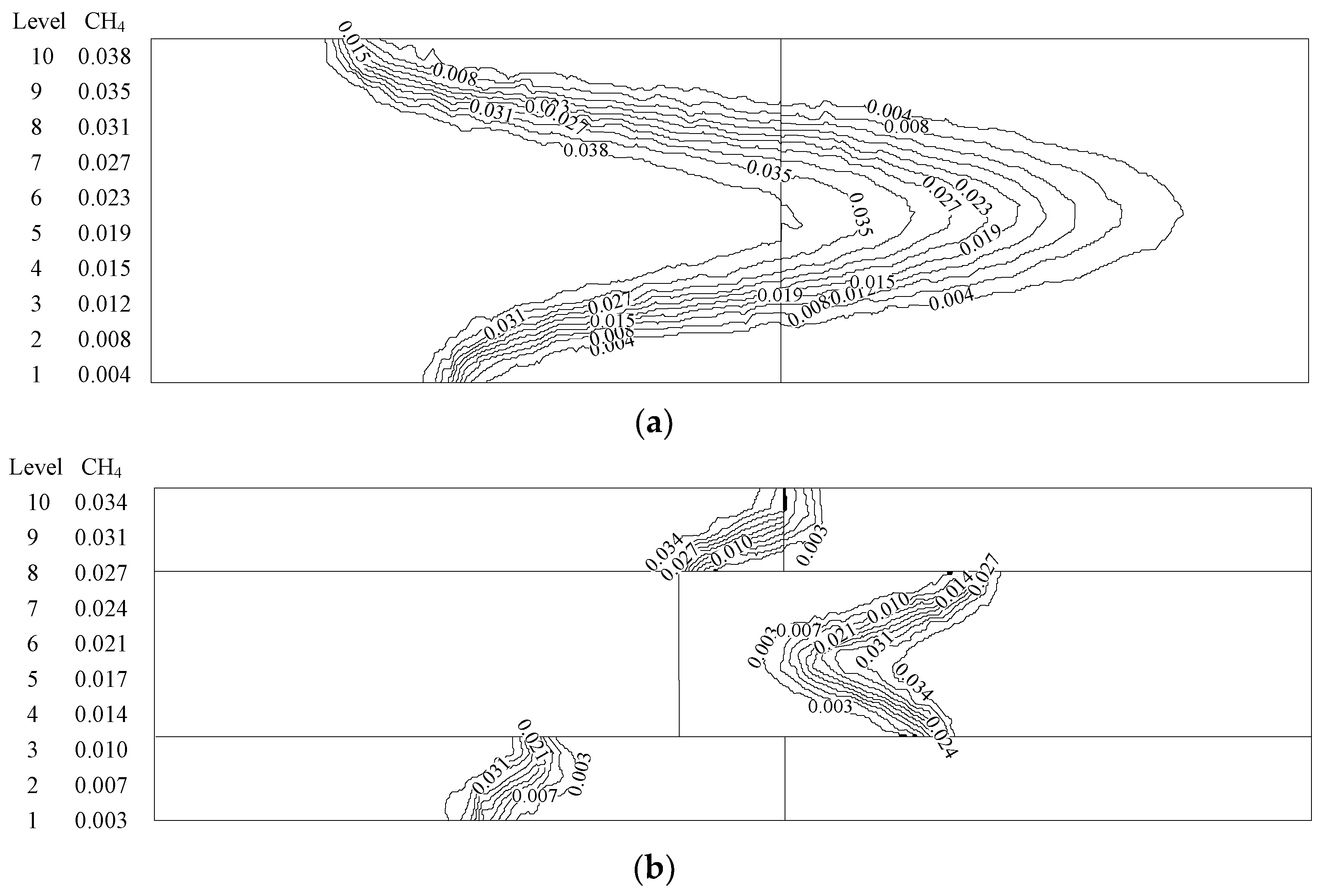
4.1.2. Influence of the Inlet Flow Velocity of Premixed Gas on Combustion Intensity
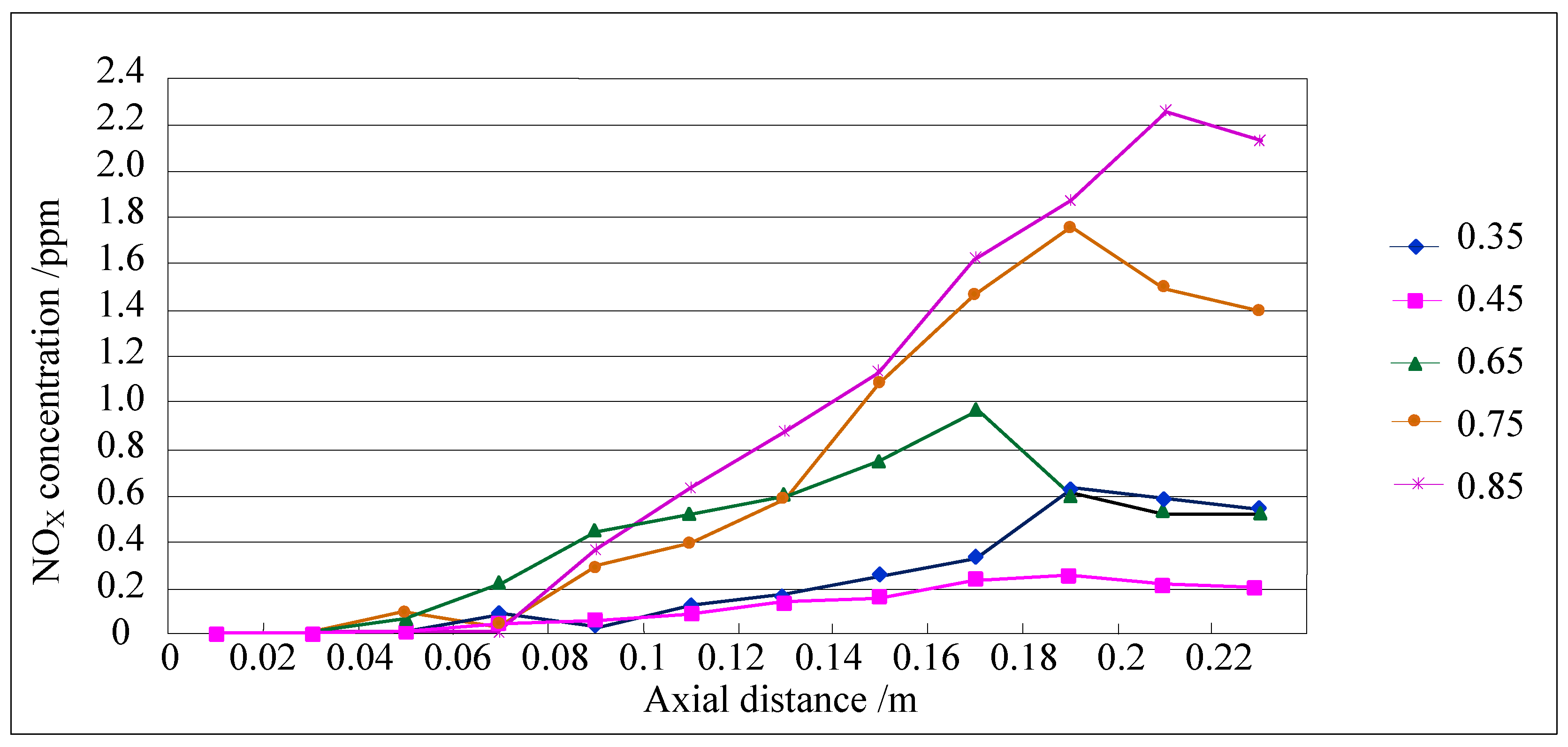
4.2. NOXEmission Characteristics of Different Equivalence Ratios in the New Burner
5. Conclusions
- (1)
- Compared with the ordinary porous medium burner, the new burner can gather heat more effectively, thereby promoting gas combustion. As a result, the gas temperature in the new burner is much higher than that in the ordinary one.
- (2)
- At higher flow velocity, the short preheating time results in poor reaction of the premixed gas in the porous medium of the ordinary burner. On the contrary, under the condition of high flow velocity, the gas concentration contour gradually fades along the gas flow direction in the new burner. The combustion state is good, and the combustion heat is large.
- (3)
- The change of flow velocity of the premixed gas in the inlet exerts an important influence on the combustion in the porous medium. In the case of low flow velocity, the temperature in the inlet increases significantly. In contrast, the temperature in the outlet increases dramatically in the case of high flow velocity. The inlet flow velocity should be set within a reasonable range to ensure the safety and normal operation of the burner.
- (4)
- The emission concentration of major pollutants (NOX) from the new burner is much lower than the minimum standard ((100 ppm) in Beijing, China).
- (5)
- The radiation attenuation coefficient of the small-pore medium in the new burner increases, but the radiation attenuation coefficient of the big-pore medium in the new burner remains unchanged, which increases the stable operating range of the burner.
- (6)
- The thermal conductivity coefficient of the small-pore medium in the new burner increases, but the thermal conductivity coefficient of the big-pore medium in the new burner remains unchanged or reduces slightly, which increases the temperature peak and the stable operating range. The aperture of the porous medium should not be too large. A reasonable range of aperture size can maintain the stability of flame front and obtain the ideal temperature.
- (7)
- Compared with the traditional burner, the new porous medium burner has advantages in improving combustion efficiency, expanding flammability limits, and improving environmental friendliness. Therefore, the application prospects of the new porous medium burner are very broad. The influences of various factors on the combustion process of the new porous medium burner were simulated by CFD (computational fluid dynamics) and the basic characteristics were mastered. The numerical results can provide a theoretical basis and data support for the design of the new porous medium burner. If the design and manufacturing process of the new porous medium burner can be further strengthened, better application value will surely be attained.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Lu, C.; Li, T. A Practical Countercurrent Fluid Catalytic Cracking Regenerator Model for in Situ Operation Optimization. AICHE J. 2012, 58, 2810–2819. [Google Scholar] [CrossRef]
- Jia, Z.; Feng, T. Gas Explosion Characteristics and Its Control Measures in Closed Fire Zone. Comput. Modell. New Technol. 2014, 18, 21–25. [Google Scholar]
- Kamal, M.M.; Mohamad, A.A. Combustion in Porous Media. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 220, 487–508. [Google Scholar] [CrossRef]
- Valerio, G.; Rajnish, N.S.; Robert, R.R. Premixed Combustion of Methane-Air Mixture Stabilized over Porous Medium: A 2-D Numerical Study. Chem. Eng. Sci 2016, 152, 591–605. [Google Scholar]
- Mujeebu, M.A.; Abdullah, M.Z.; Bakar, M.A.; Mohamad, A.A.; Abdullah, M.K. Applications of Porous Media Combustion Technology Review. Appl. Energy 2009, 86, 1365–1375. [Google Scholar] [CrossRef]
- Wood, S.; Harris, A.T. Porous Burners for Lean-Burn Applications. Prog. Energy Combust. Sci. 2008, 34, 667–684. [Google Scholar] [CrossRef]
- Slimane, R.B.; Lau, F.S.; Khinkis, M.; Bingue, J.P.; Saveliev, A.V.; Kennedy, L.A. Conversion of Hydrogen Sulphide to Hydrogen by Super Adiabatic Partial Oxidation: Thermodynamic Consideration. Int. J. Hydrogen Energy 2004, 29, 1471–1477. [Google Scholar] [CrossRef]
- Min, D.K.; Shin, E.D. Laminar Premixed Flame Stabilized inside a Honeycomb Ceramic. Int. J. Heat Mass Transf. 1991, 34, 341–356. [Google Scholar]
- Hayashi, T.C.; Malico, I.; Pereira, J.C.F. Three-dimensional Modeling of Two-Layer Porous Burner for Household Application. Comput. Struct. 2004, 82, 1543–1550. [Google Scholar] [CrossRef]
- Kotani, Y.; Takeno, T. An Experimental Study of Stability and Combustion Characteristics of an Excess Enthalpy Flame. Symp. (Int.) Combust. 1982, 19, 1503–1509. [Google Scholar] [CrossRef]
- Pereira, F.M.; Oliveira, A.A.M. Analysis of the Combustion with Excess Enthalpy in Porous Media. In Proceeding of the European Combustion Meeting, Orléans, France, 2003; pp. 388–392. [Google Scholar]
- Mital, R.; Gore, J.P.; Viskanta, R. A Study of the Structure of Submerged Reaction Zones in Porous Ceramics Radiant Burners. Combust. Flame 1997, 111, 175–184. [Google Scholar] [CrossRef]
- Sathe, S.B.; Kulkarni, M.R.; Peck, R.E.; Tong, T.W. An Experimental and Theoretical Study of Porous Radiant Burner Performance. Symp. (Int.) Combust. 1990, 23, 1011–1018. [Google Scholar] [CrossRef]
- Chen, Y.K.; Matthews, R.D.; Howell, J.R. The Effect of Radiation on the Structure of Premixed Flame within a Highly Porous Inert Medium; American Society of Mechanical Engineers, Heat Transfer Division, (Publication) HTD: Boston, MA, USA, 1987; pp. 35–41. [Google Scholar]
- Wang, E.; Chen, L.; Wu, J. Application and Existing Problems of Porous Ceramics in the Combustion Field. Foshan Ceram. 2005, 100, 35–39. [Google Scholar]
- Chu, J. Study and Development of a Gradually-varied Porous Media Burner. Master’s Thesis, Zhejiang University, Hangzhou, China, 2005. [Google Scholar]
- Du, L.; Xie, M. Numerical Investigation on Effects of Porous Media in Premixed Combustion. J. Dalian Univ. Technol. 2004, 1, 70–75. [Google Scholar]
- Du, L. Investigation on Super-adiabatic Combustion of Lean Premixed Gases in Porous Media. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2003. [Google Scholar]
- Liu, H. Experimental Study and Numerical Simulation of Premixed Gas Combustion in Porous Media. Ph.D. Thesis, Northeastern University, Shengyang, China, 2010. [Google Scholar]
- Liu, H.; Dong, S.; Xing, N.; Li, B. Numerical Simulation of the Influence of Porous Medium Characteristics on Combustion Temperature and Pressure. Appl. Energy Technol. 2009, 10, 31–37. [Google Scholar]
- Barra, A.J.; Diepvens, G.; Ellzey, J.L.; Henneke, M.R. Numerical Study of the Effects of Material Properties on Flame Stabilization in a Porous Burner. Combust. Flame 2003, 134, 369–379. [Google Scholar] [CrossRef]
- Wang, H. Industrial Application and Numerical Simulation of Premixed Gas Combustion in Porous Media. Master’s Thesis, Northeastern University, Shengyang, China, 2009. [Google Scholar]
- Lee, D.K.; Noh, D.S. Experimental and Theoretical Study of Excess Enthalpy Flames Stabilized in a Radial Multi-Channel as a Model Cylindrical Porous Medium Burner. Combust. Flame 2016, 170, 79–90. [Google Scholar] [CrossRef]
- Mendes, M.A.A.; Pereira, J.M.C.; Pereira, J.C.F. A Numerical Study of the Stability of One-Dimensional Laminar Premixed Flame in Inert Porous Media. Combust. Flame 2008, 153, 525–539. [Google Scholar] [CrossRef]
- Afsharvahid, S.; Ashman, P.J.; Dally, B.B. Investigation of NOx Conversion Characteristics in a Porous Medium. Combust. Flame 2008, 152, 604–615. [Google Scholar] [CrossRef]
- Zhao, P. Study on Premixed Combustion in Inert Porous Media. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2007. [Google Scholar]
- Huang, R. Combustion Characteristics of Multi-Species Low Calorific Gaseous Fuels in a Two-Layer Porous Burner. Master’s Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Dong, S. Preliminary Experimental and Numerical Study of Premixed Combustion in Porous Inert Media. Master’s Thesis, Northeastern University, Shengyang, China, 2008. [Google Scholar]
- Zheng, Z. Numerical Study of Natural Gas Premixed Combustion in Porous Inert Media. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2007. [Google Scholar]
- Jia, Z.; Lin, B.; Ye, Q. Analysis of Influencing Factors and Flame Acceleration Mechanism of Gas Explosion Propagation in Tube. Min. Eng. Res. 2009, 24, 57–62. [Google Scholar]
- Gao, Z.; Cui, G.; Zuo, D. Discussion on the Reaction Mechanism of Carbon Combustion. J. Shandong Polytech. Univ. 2002, 16, 39–42. [Google Scholar]
- Yang, S.; Tao, W. Heat Transfer, 3rd ed.; Higher Education Press: Beijing, China, 1998. [Google Scholar]
- Han, Z. Fuel and Combustion; Metallurgical Industry Press: Beijing, China, 2007. [Google Scholar]
- Wang, P. Theoretical and Experimental Study on Gas Thermal Counter Current Oxidation of Low Concentration Methane in Coal Mine. Ph.D. Thesis, Central South University, Changsha, China, 2012. [Google Scholar]
- Dhamrat, R.S.; Ellzey, J.L. Numerical and Experimental Study of the Conversion of Methane to Hydrogen in a Porous Media Reactor. Combust. Flame 2006, 144, 698–709. [Google Scholar] [CrossRef]
- Mohammadi, I.; Hossainpour, S. The Effects of Chemical Kinetics and Wall Temperature Performance of Porous Media Burners. Heat Mass Transf. 2013, 49, 869–877. [Google Scholar] [CrossRef]
- Younis, L.B.; Viskanta, R. Experimental Determination of the Volumetric Heat Transfer Coefficient between Stream of Air and Ceramic Foam. Int. J. Heat Mass Transf. 1993, 36, 1425–1434. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Y. Fire Engineering; China University of Mining and Technology Press: Xuzhou, China, 2002. [Google Scholar]
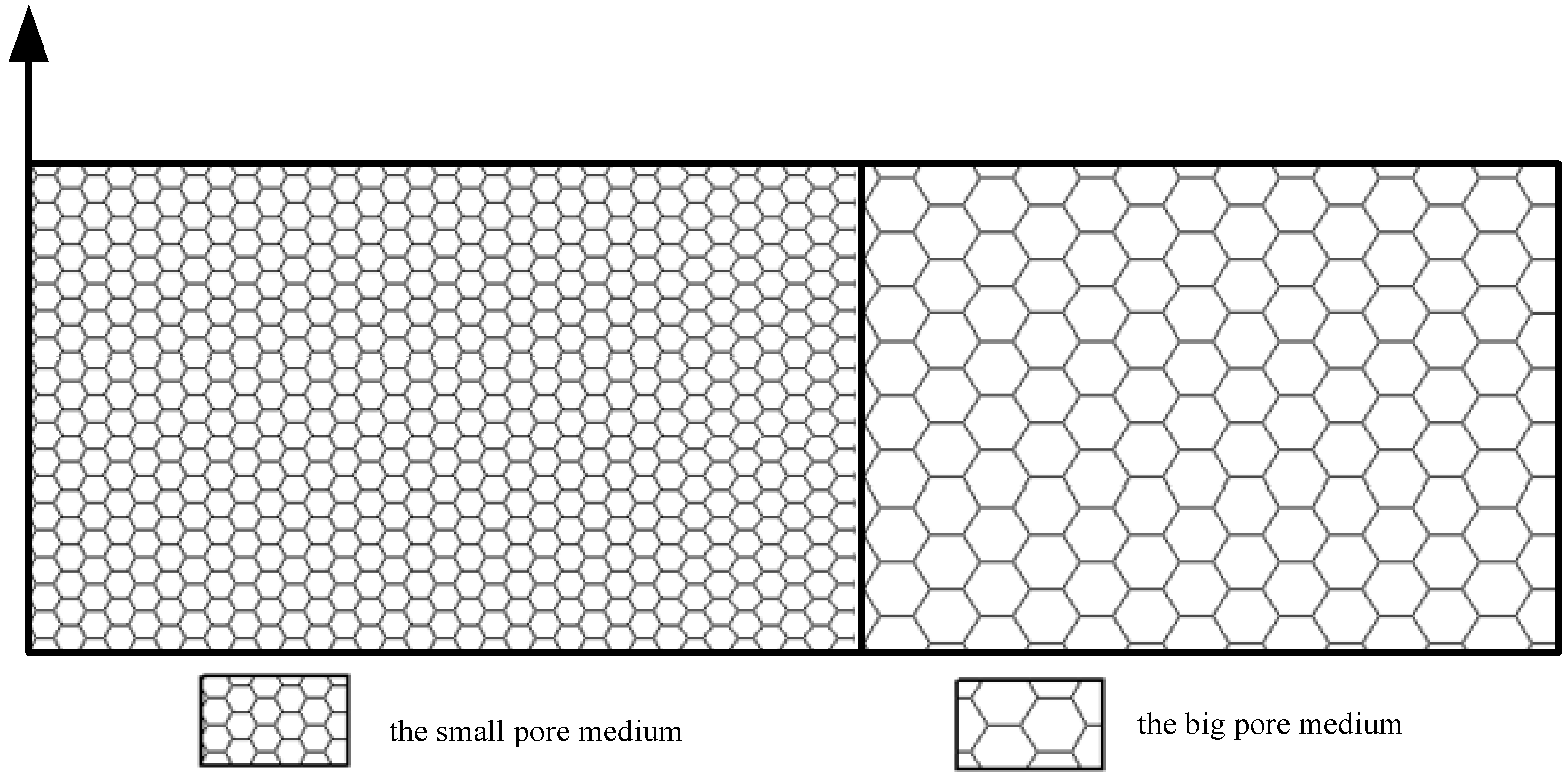
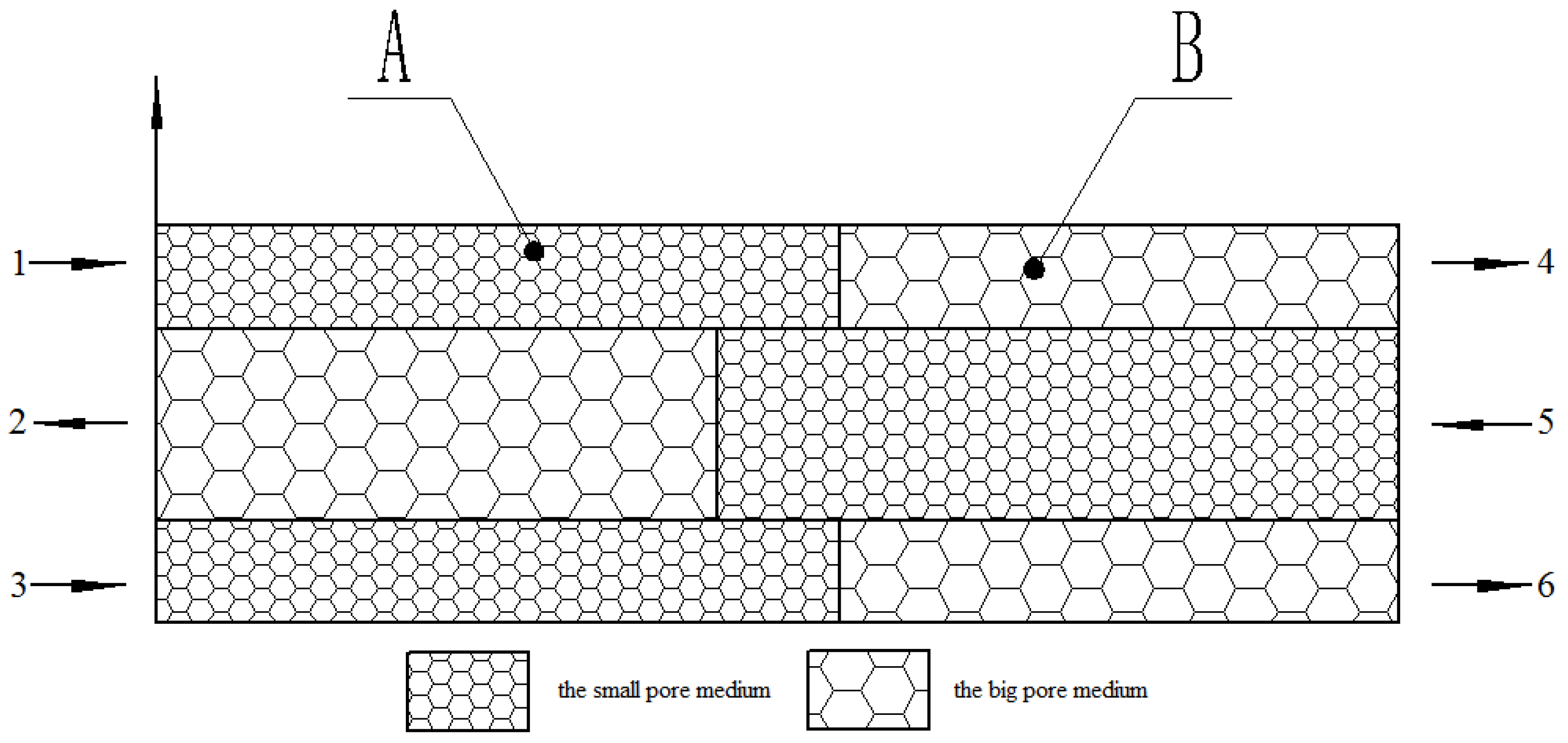









| Medium with Small Pores (Upstream) | Medium with Big Pores (Downstream) | |
|---|---|---|
| Length (m) | 0.12 | 0.1 |
| Pore diameter (PPcm) | 25.6 | 3.9 |
| Porosity | 0.835 | 0.87 |
| Thermal conductivity (W/m·k) | 0.2 | 0.1 |
| Radiation attenuation coefficient (m−1) | 1707 | 257 |
| Scattering albedo | 0.8 | 0.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Z.; Ye, Q.; Wang, H.; Li, H.; Shi, S. Numerical Simulation of a New Porous Medium Burner with Two Sections and Double Decks. Processes 2018, 6, 185. https://doi.org/10.3390/pr6100185
Jia Z, Ye Q, Wang H, Li H, Shi S. Numerical Simulation of a New Porous Medium Burner with Two Sections and Double Decks. Processes. 2018; 6(10):185. https://doi.org/10.3390/pr6100185
Chicago/Turabian StyleJia, Zhenzhen, Qing Ye, Haizhen Wang, He Li, and Shiliang Shi. 2018. "Numerical Simulation of a New Porous Medium Burner with Two Sections and Double Decks" Processes 6, no. 10: 185. https://doi.org/10.3390/pr6100185
APA StyleJia, Z., Ye, Q., Wang, H., Li, H., & Shi, S. (2018). Numerical Simulation of a New Porous Medium Burner with Two Sections and Double Decks. Processes, 6(10), 185. https://doi.org/10.3390/pr6100185






