A Validated Model for Design and Evaluation of Control Architectures for a Continuous Tablet Compaction Process
Abstract
:1. Introduction
2. Continuous Pharmaceutical Tablet Manufacturing Process
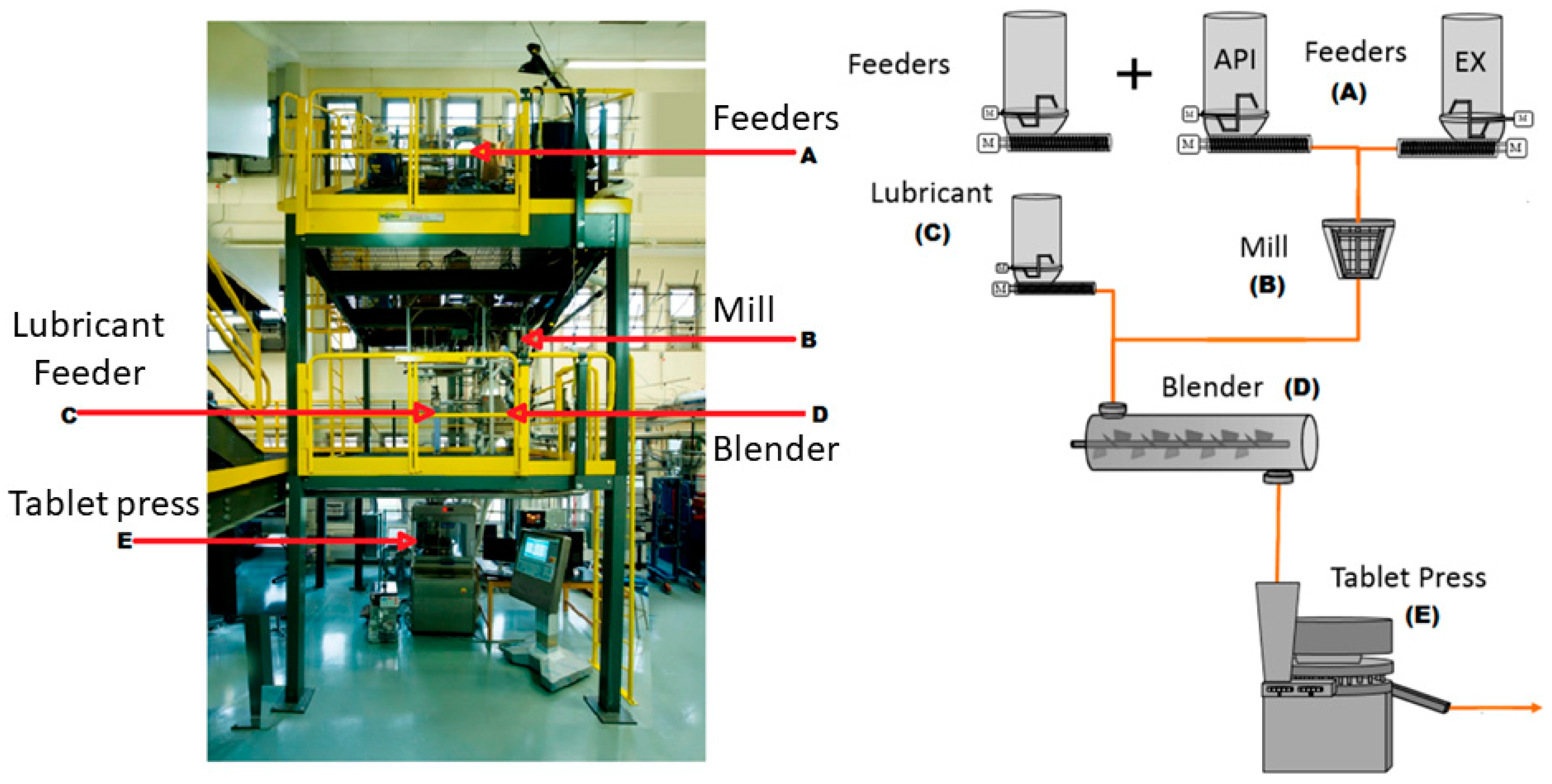
2.1. Pilot-Plant
2.2. Compaction Process
3. Materials and Methods
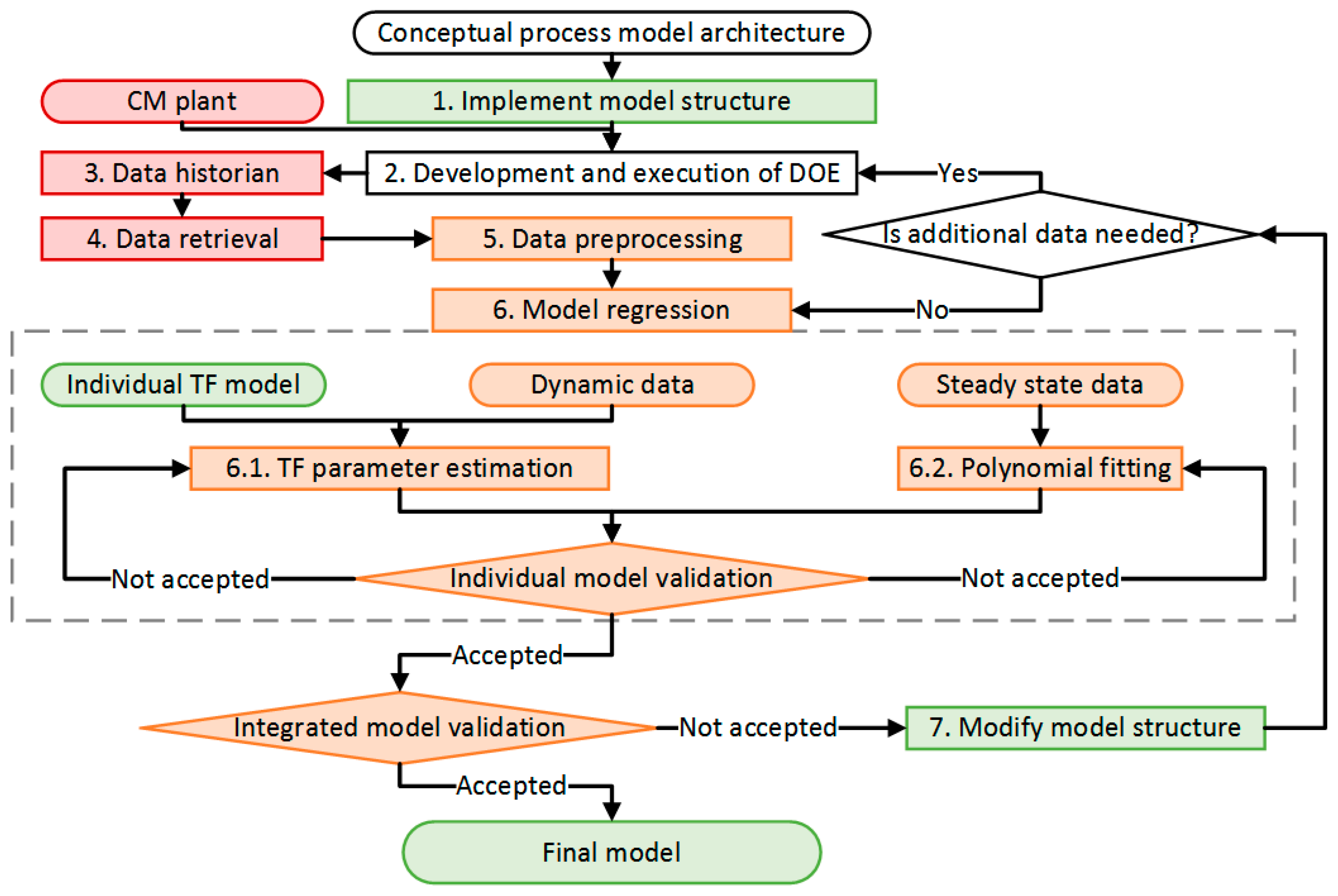
4. Model Development and Validation
4.1. Systematic Modelling Framework for Pharmaceutical Process Control System Design
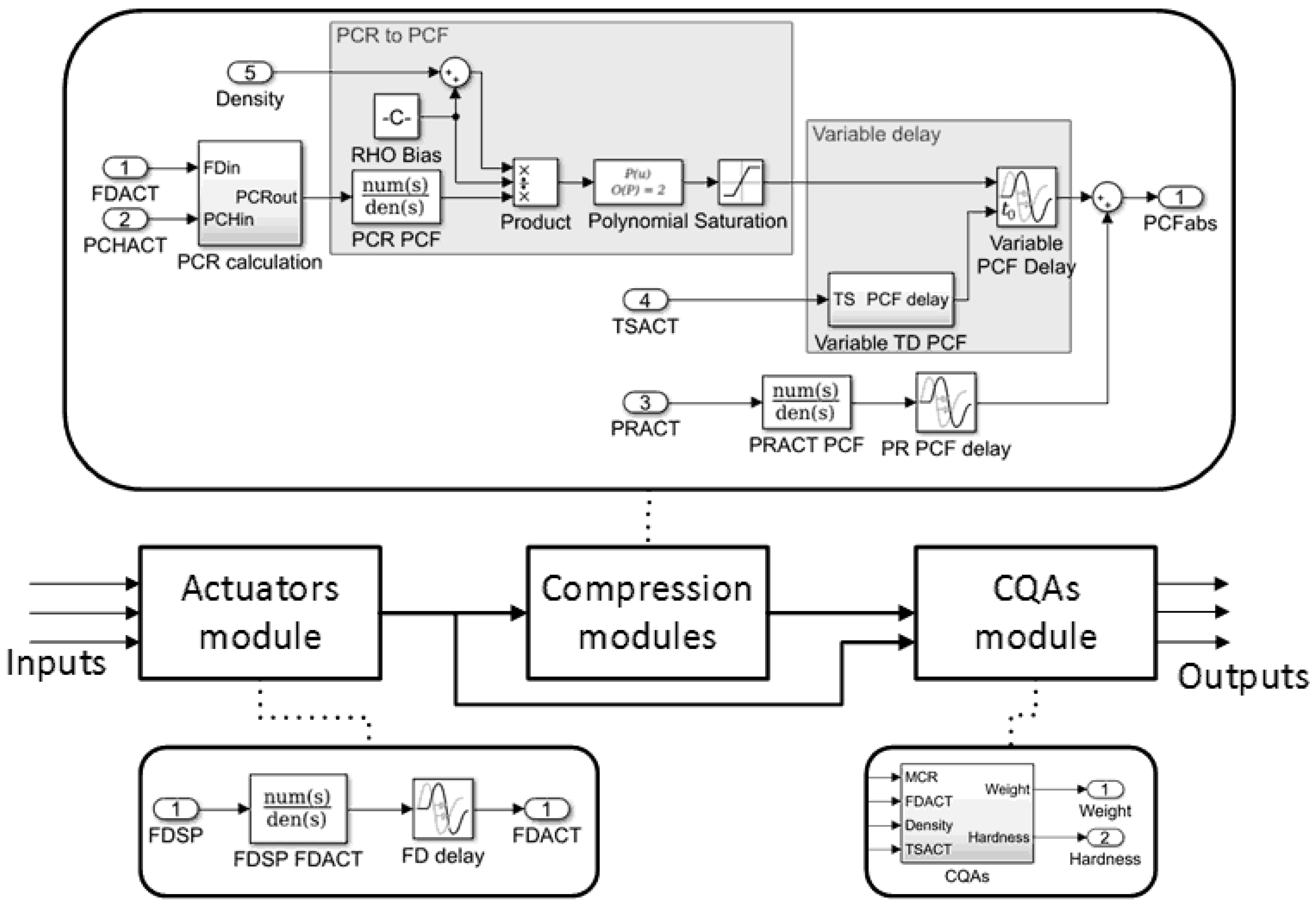
4.2. Model Structure
4.2.1. Transfer Functions
4.2.2. Variable Transport Delays
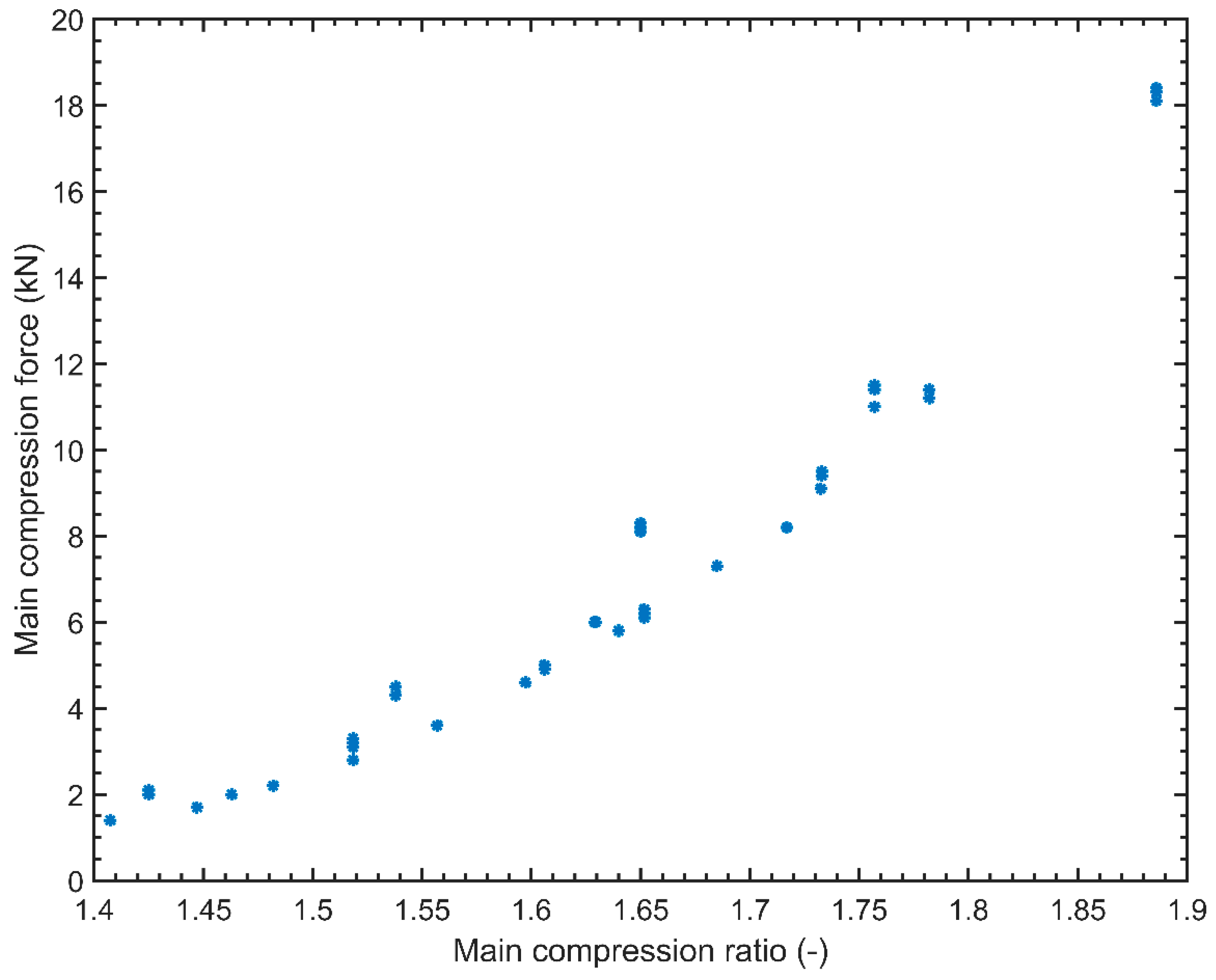
4.3. Nonlinear Force Behavior
4.4. Model Regression
4.4.1. Linear Models
4.4.2. Nonlinear Models
4.5. Model Implementation
4.5.1. Actuators Module
4.5.2. Compression Force Modules
4.5.3. Critical Quality Attributes Module
4.5.4. Tablet Rejection Module
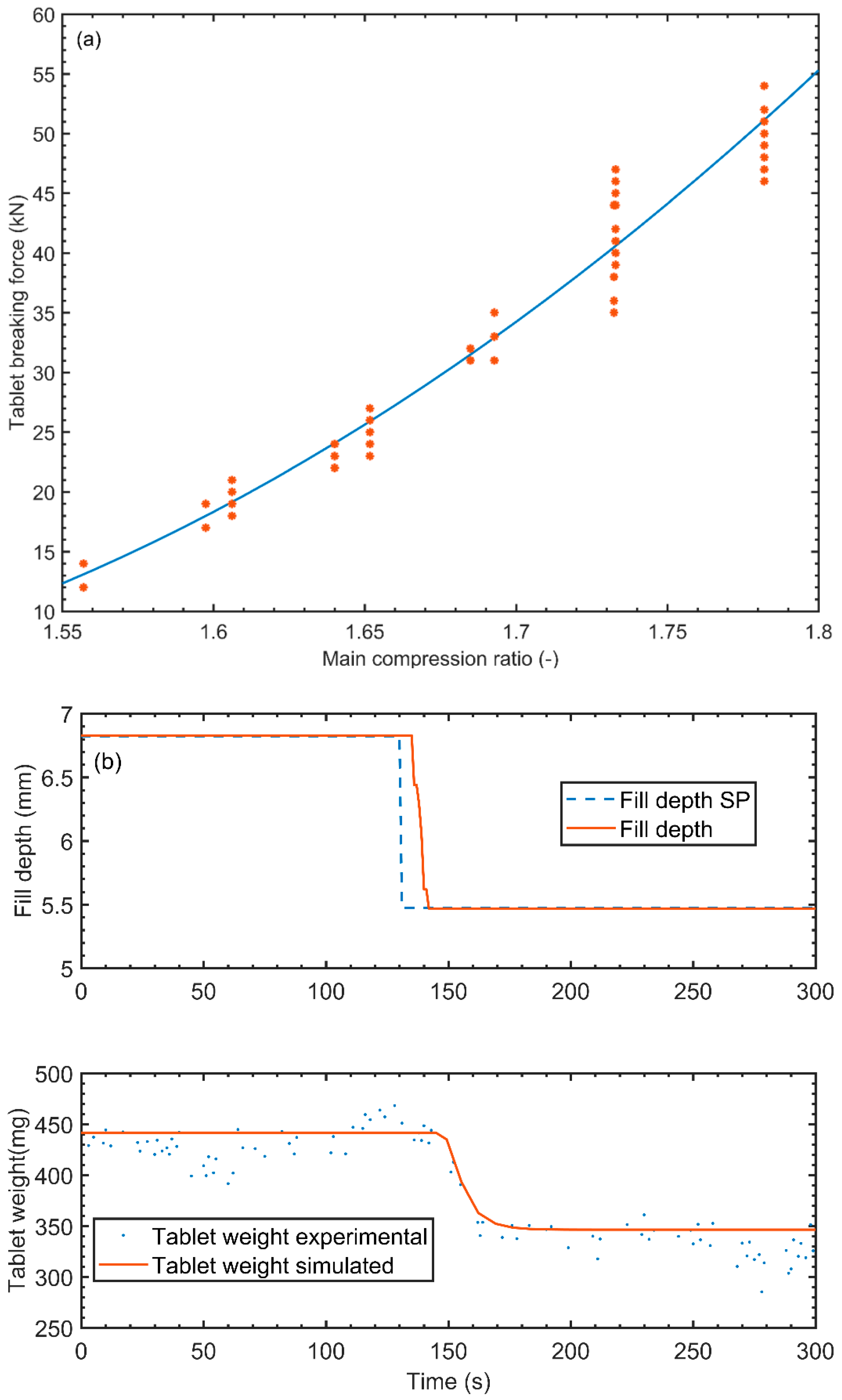
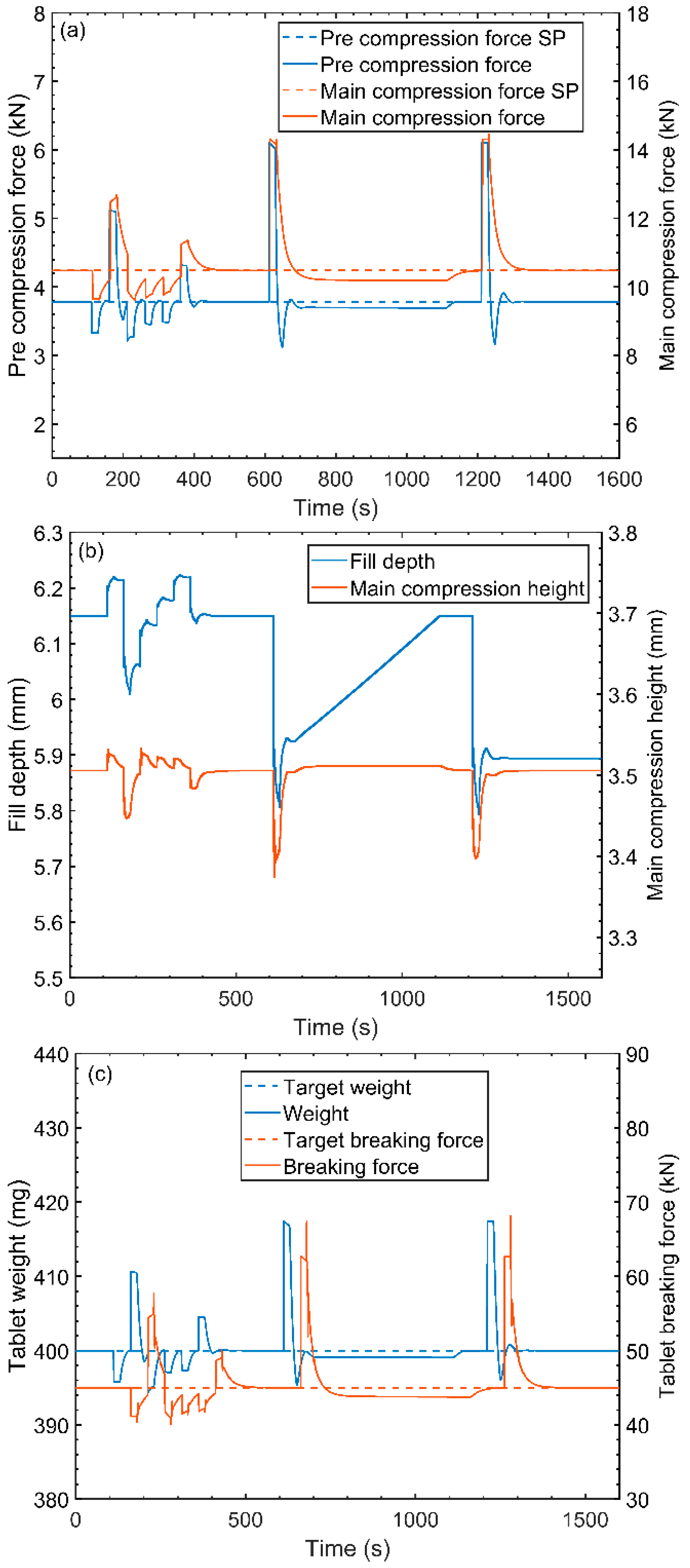
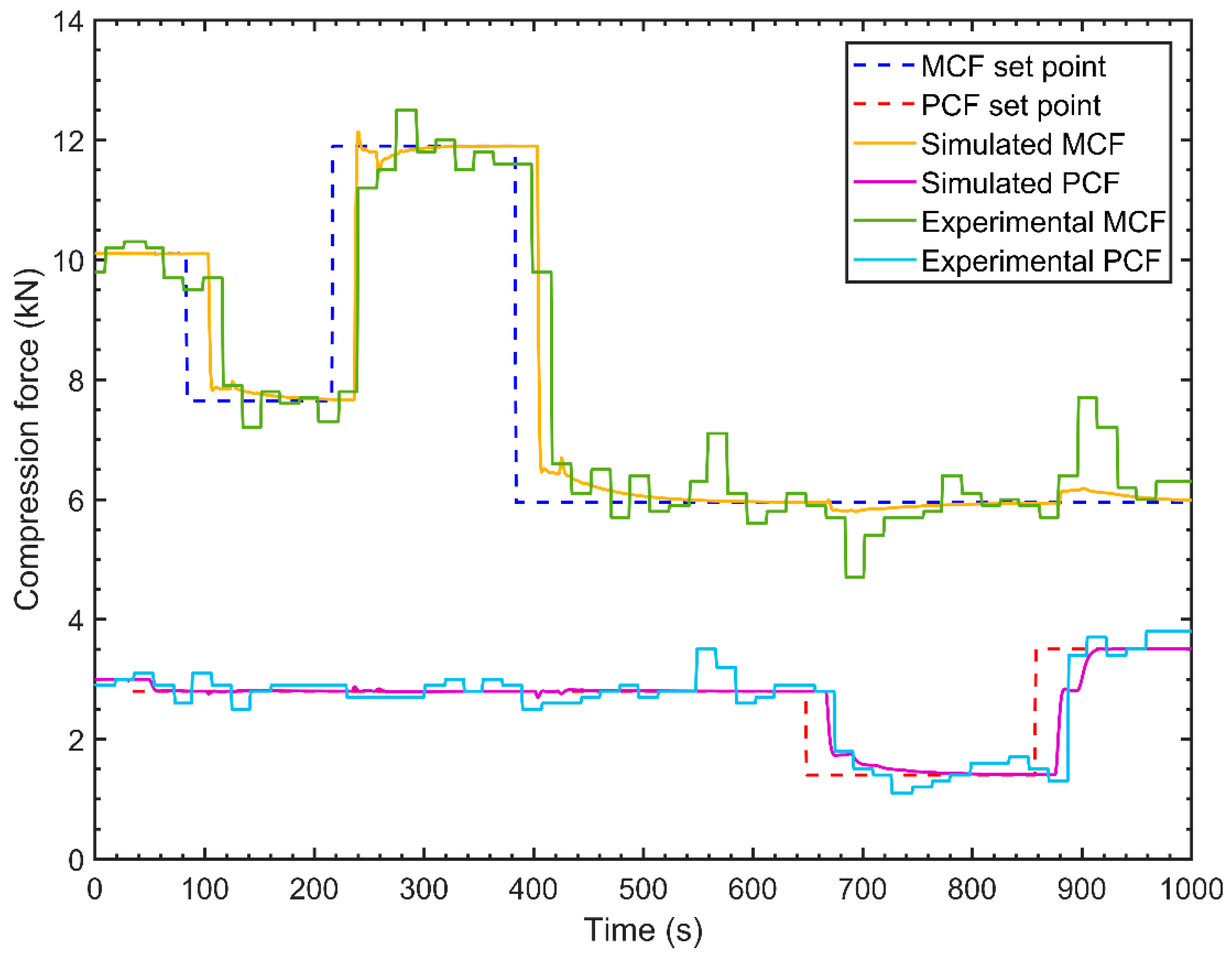
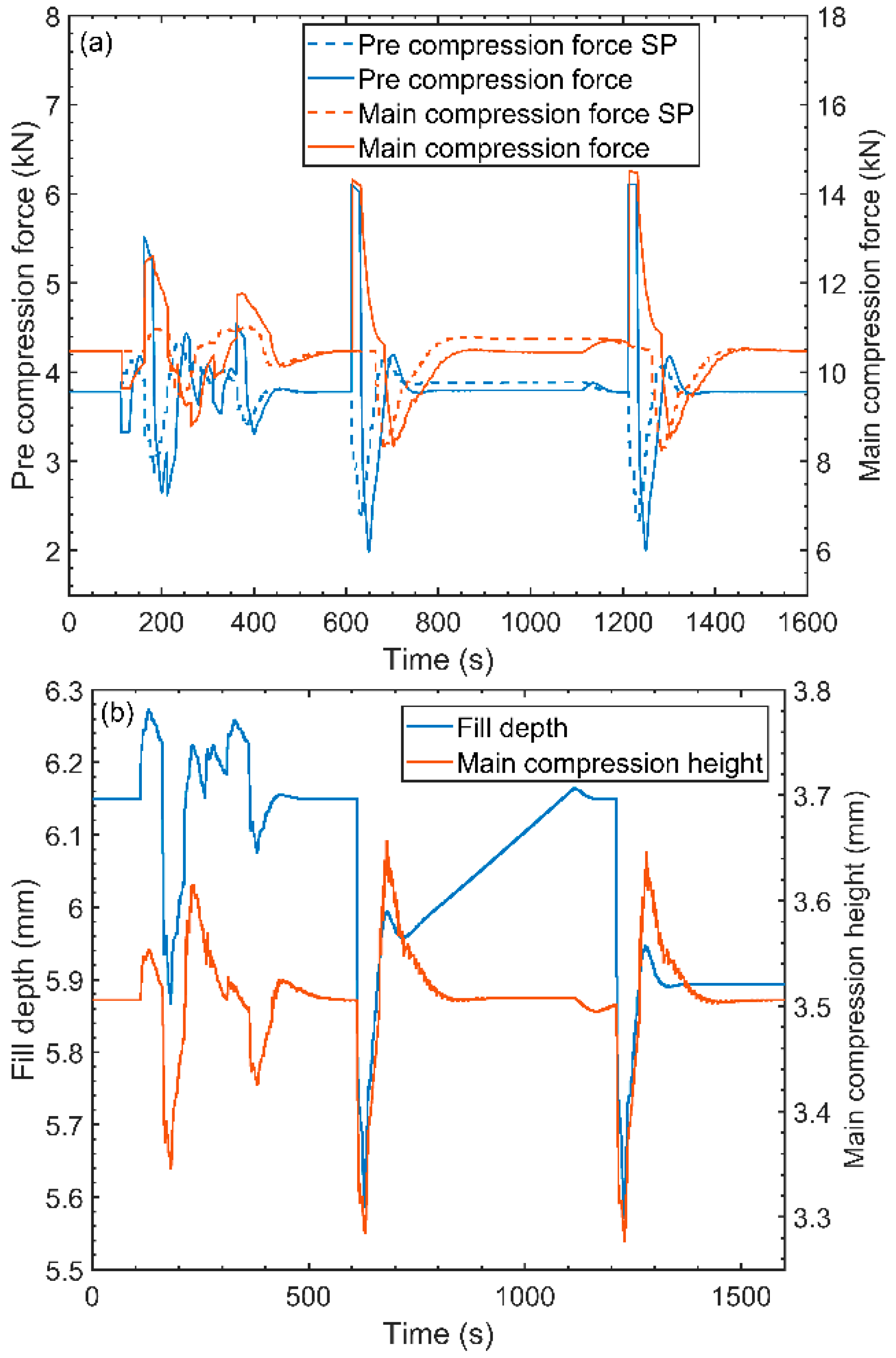
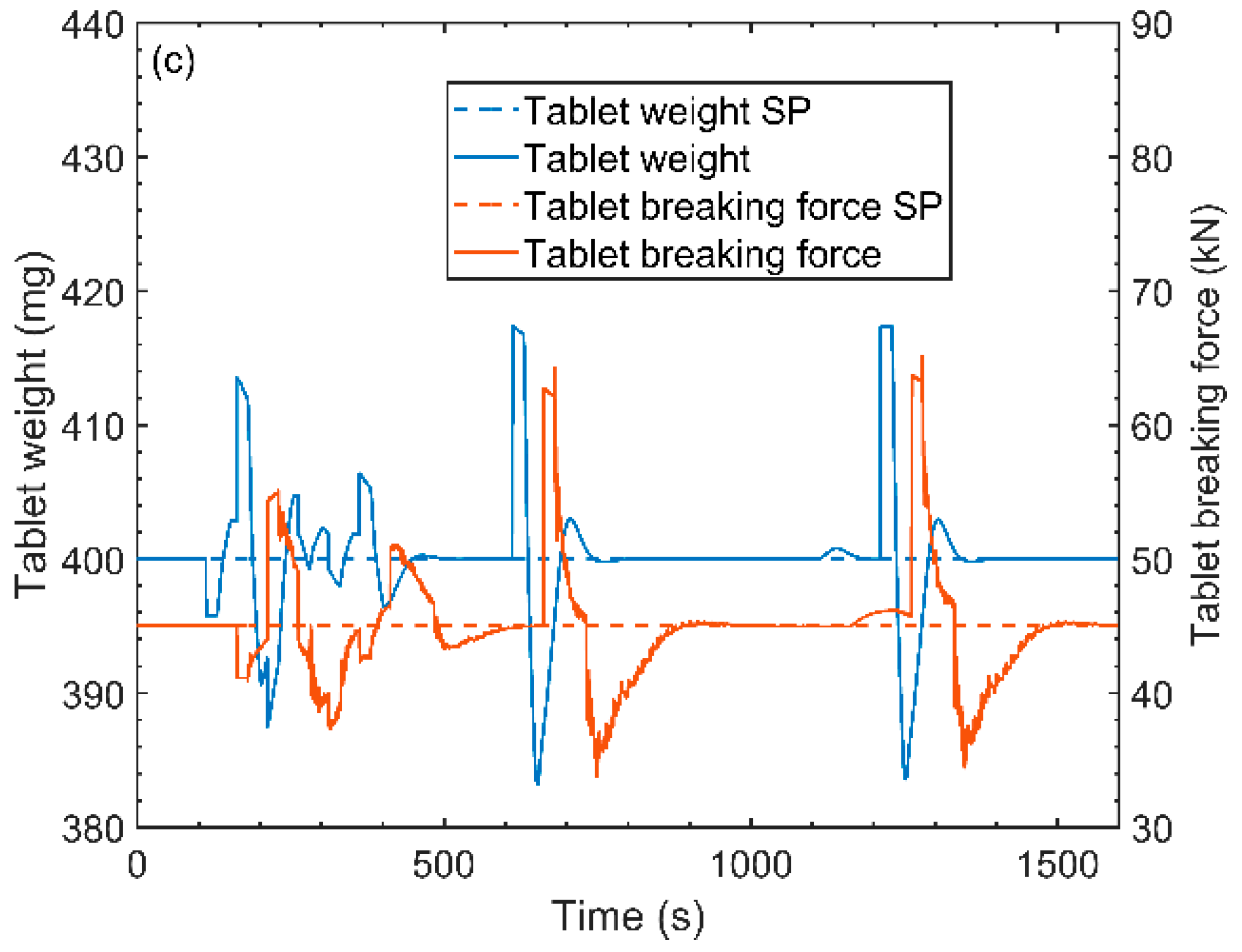
4.6. Model Validation
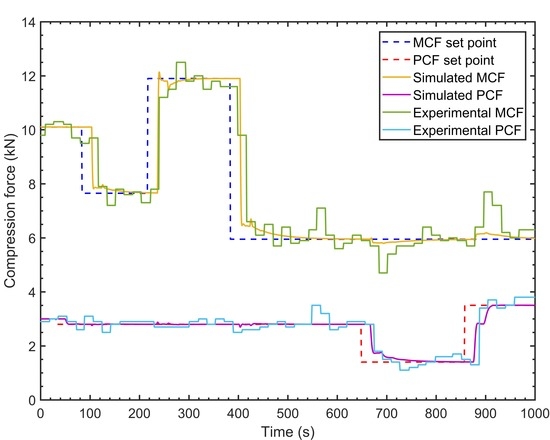
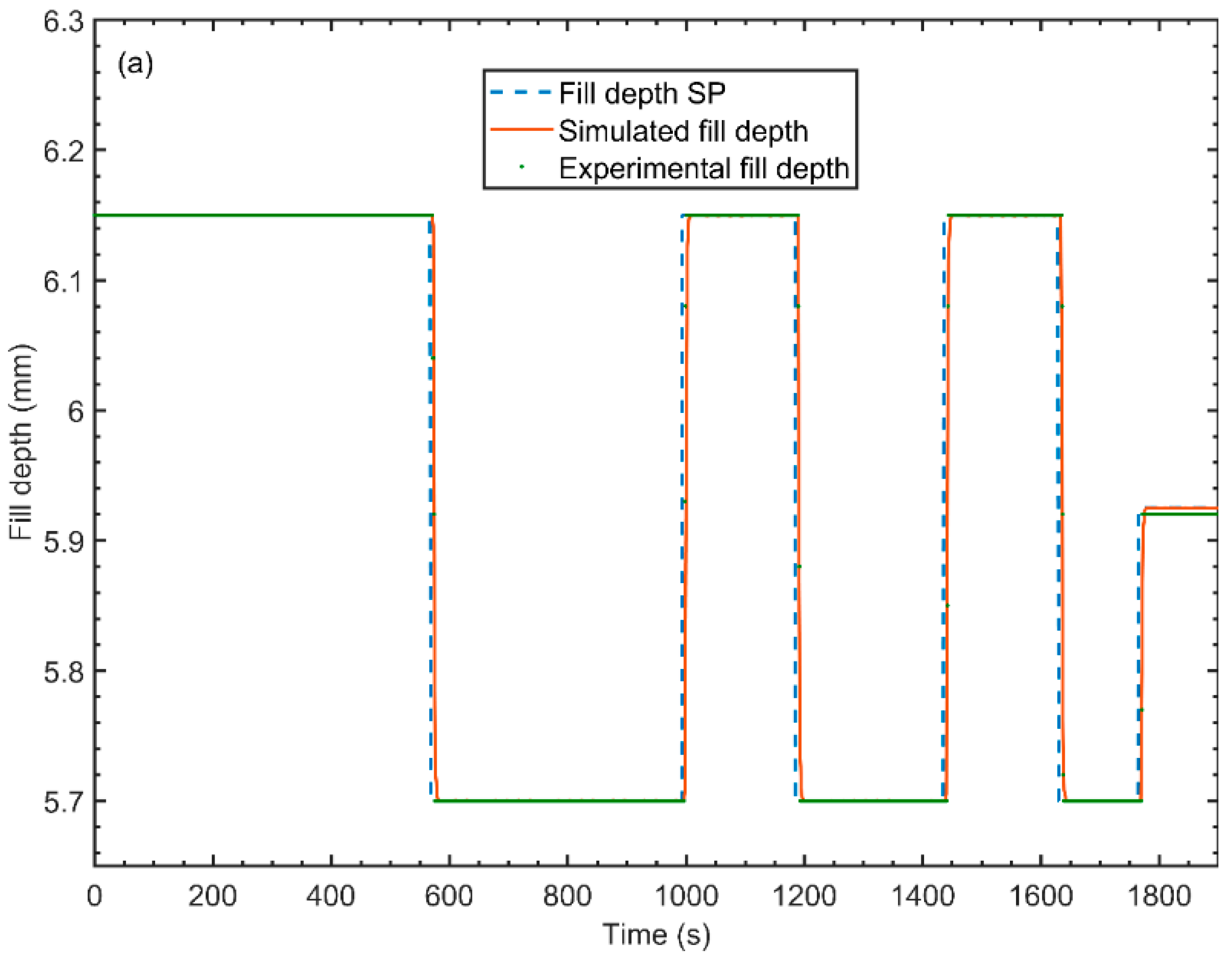
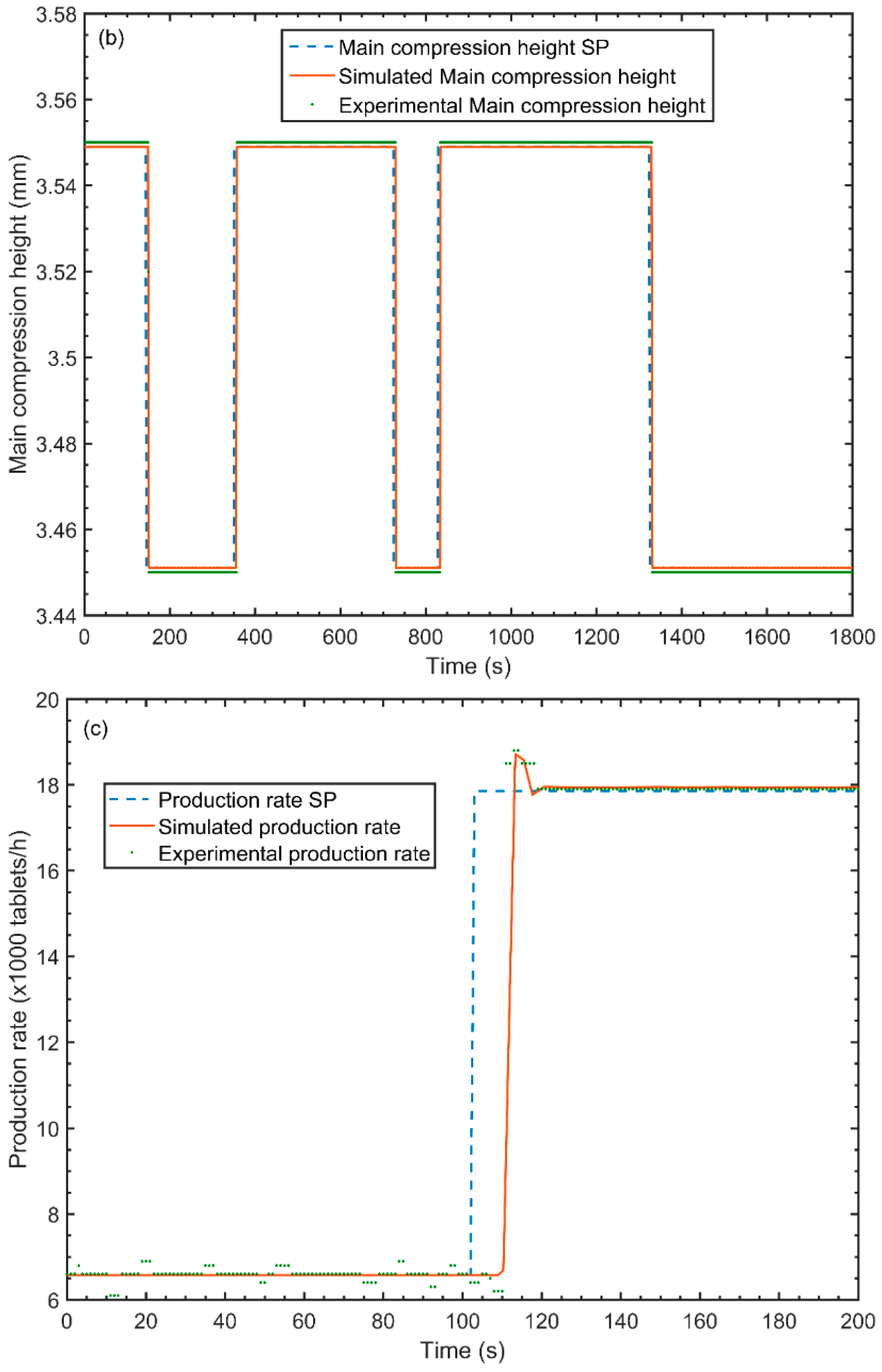
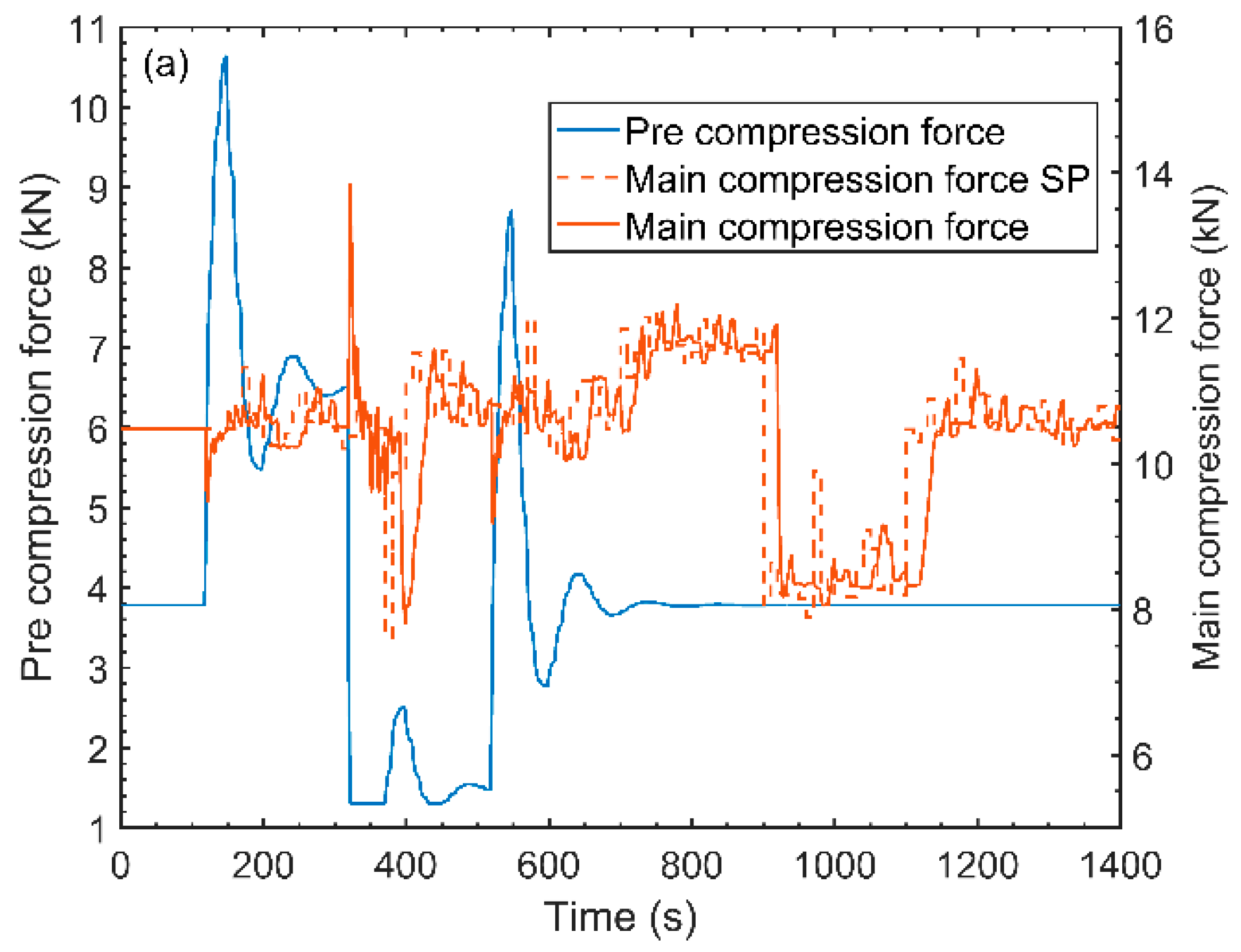
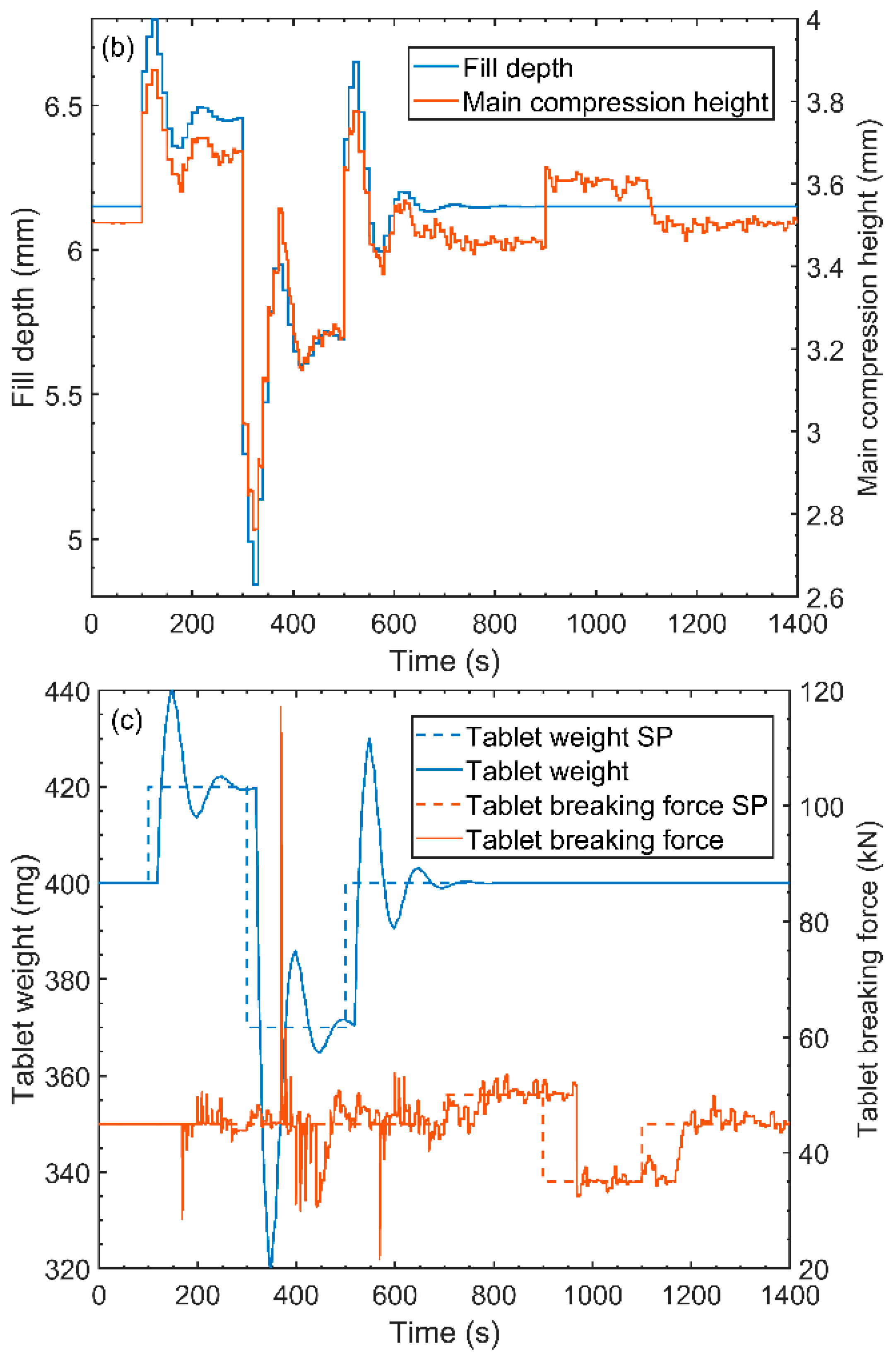
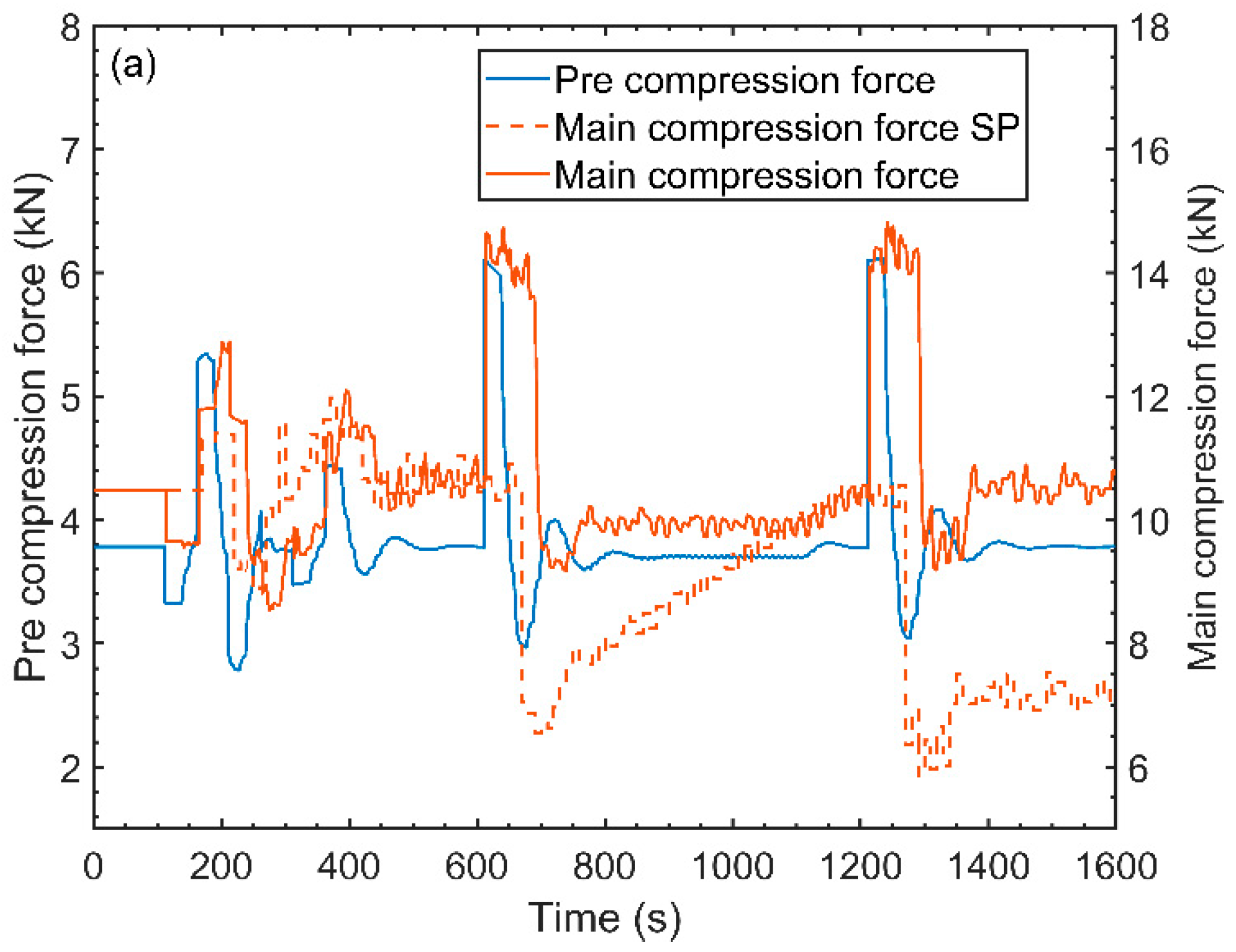
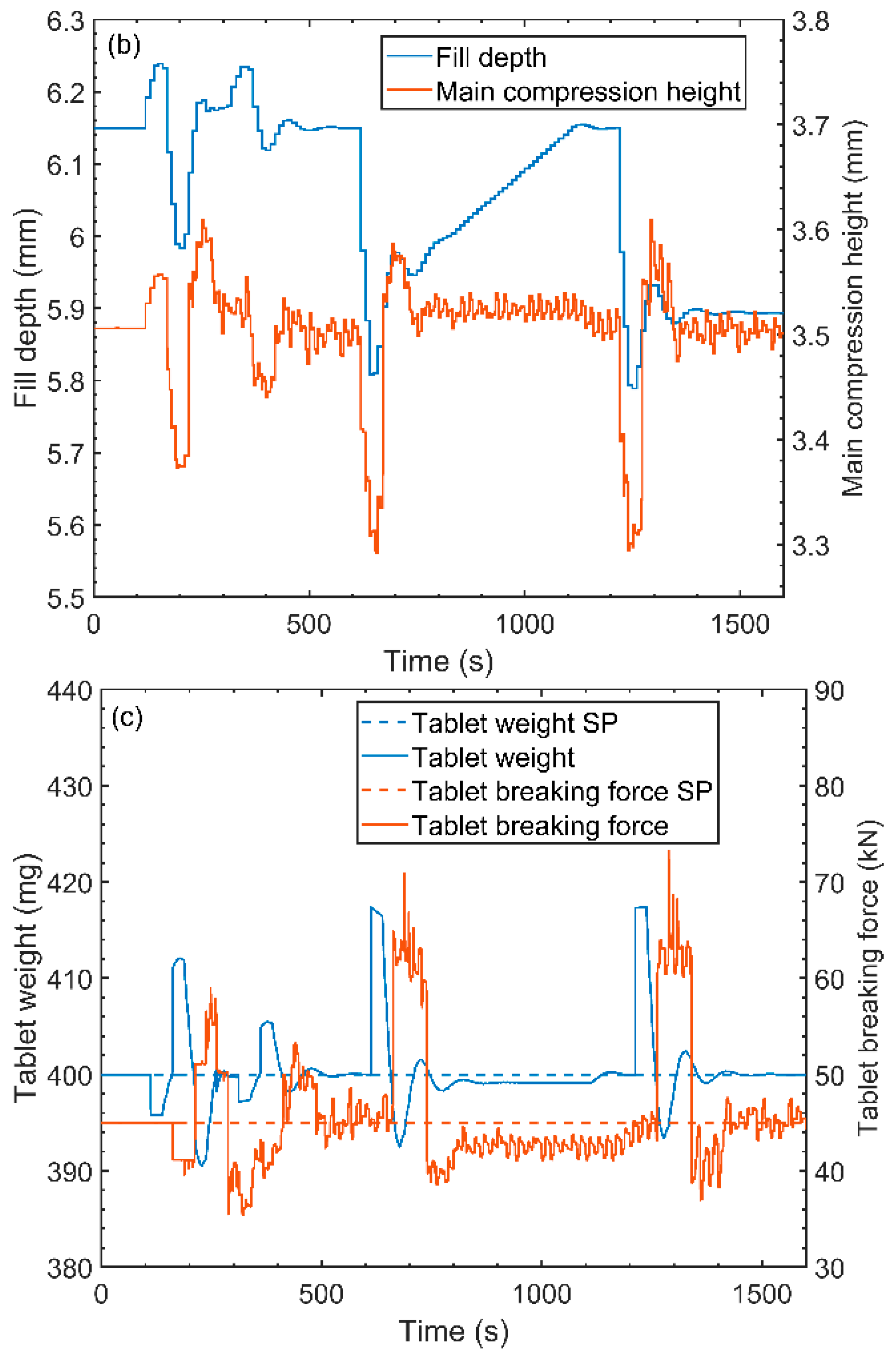
4.6.1. Set Point and Actual Response Dynamics
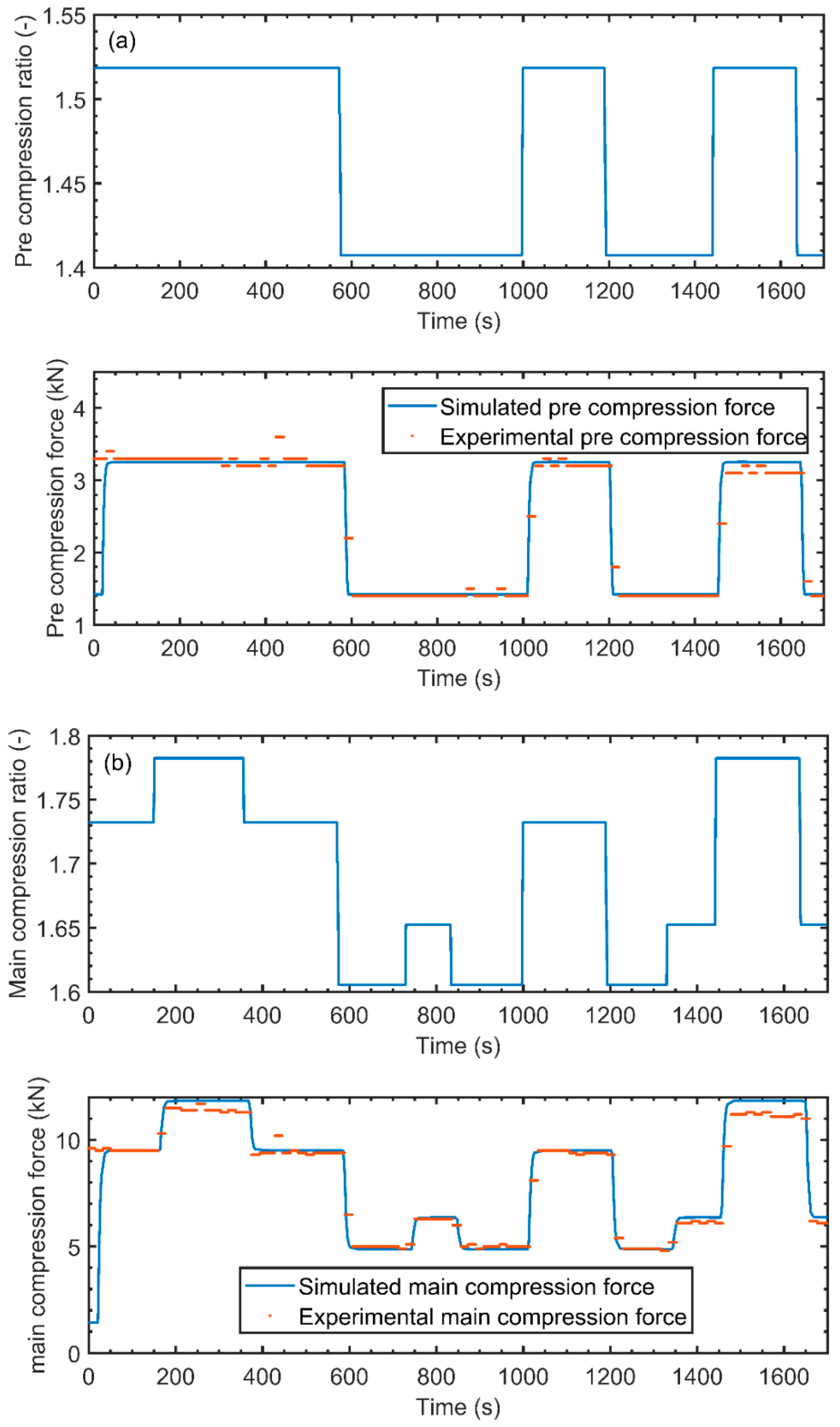
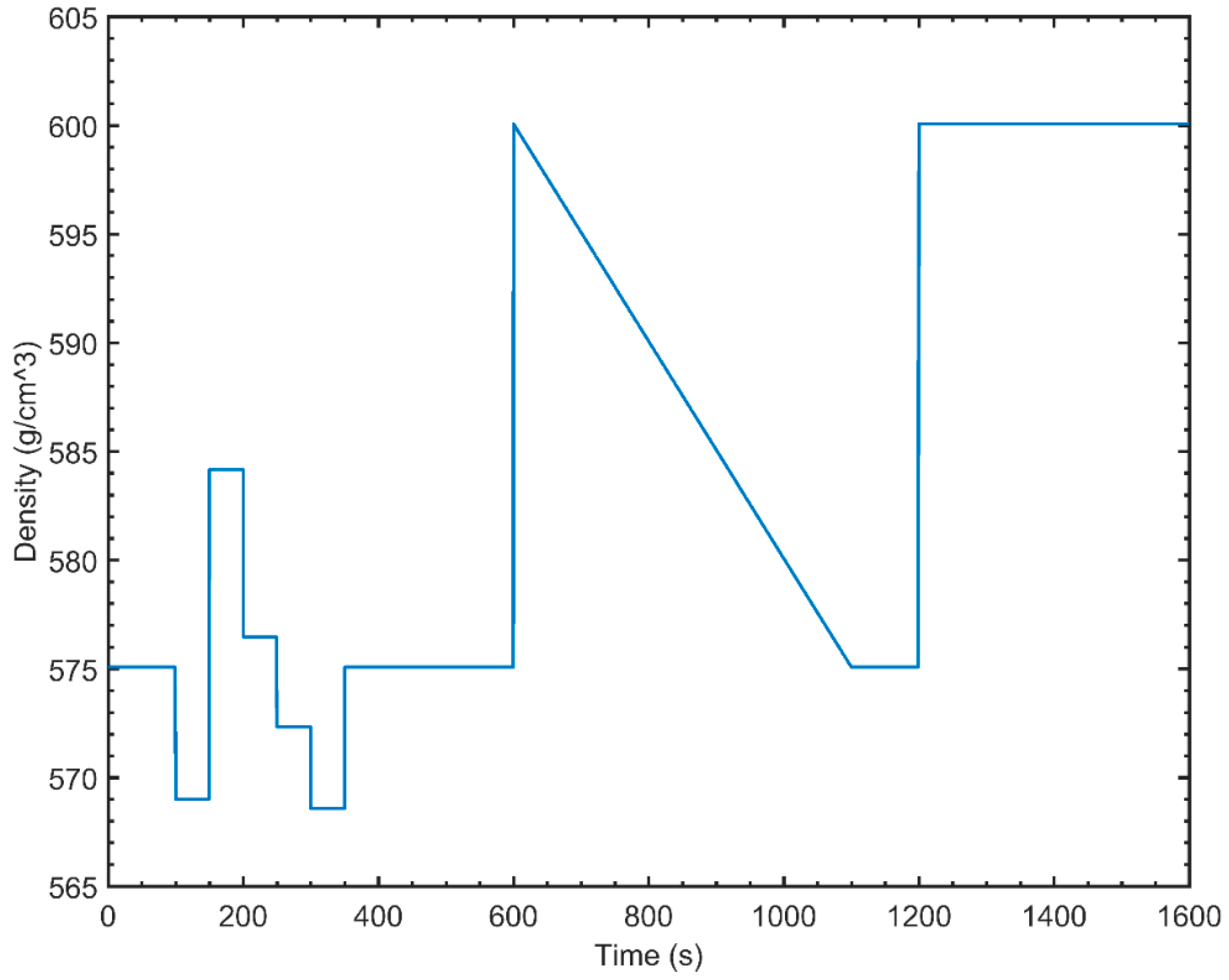
4.6.2. Critical Process Parameter Interaction
4.6.3. Critical Quality Attributes
5. Application of the Developed Model for Design and Evaluation of Control Systems
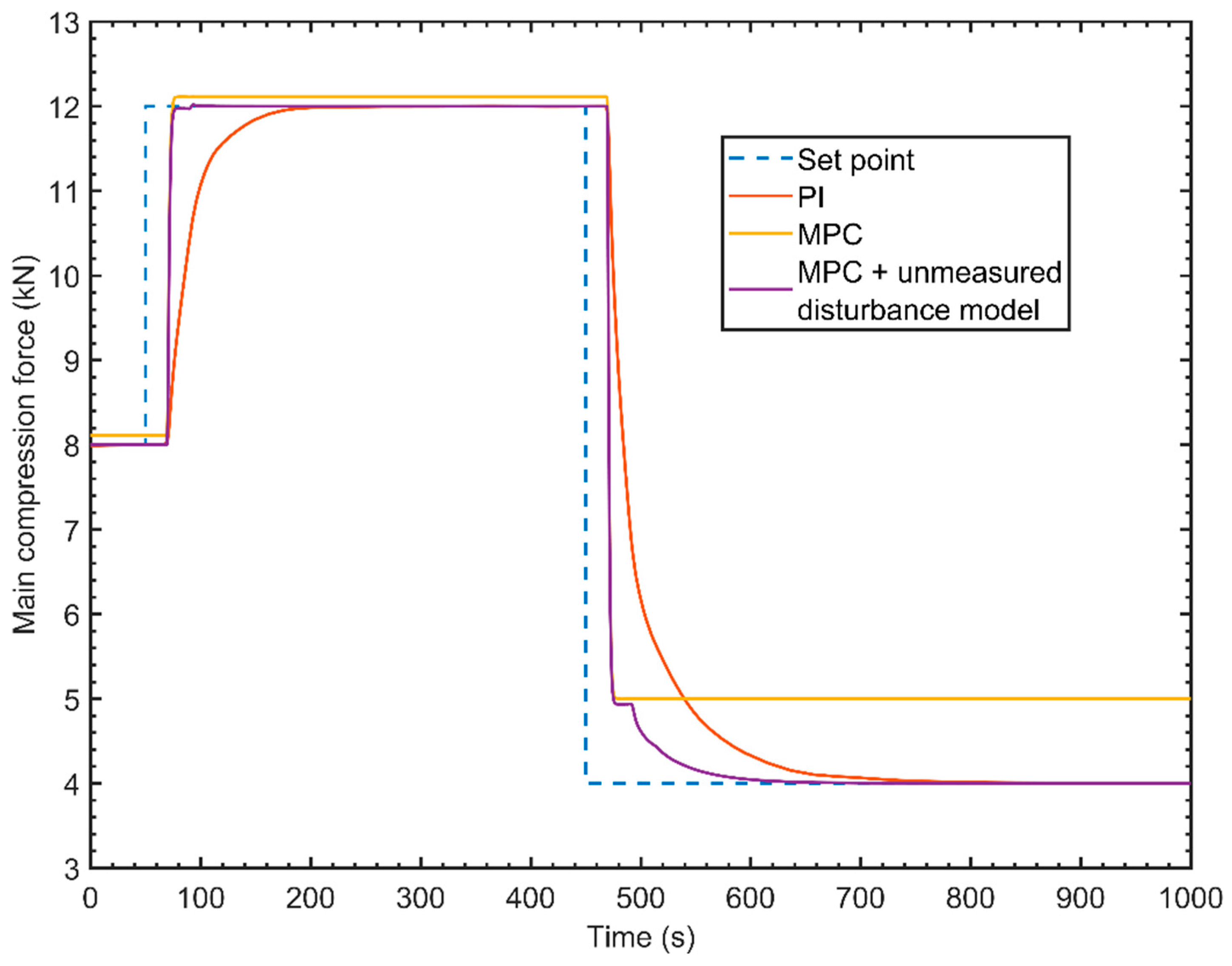
5.1. Control Algorithm Comparison
5.2. Control Strategy Development and Closed Loop Simulation
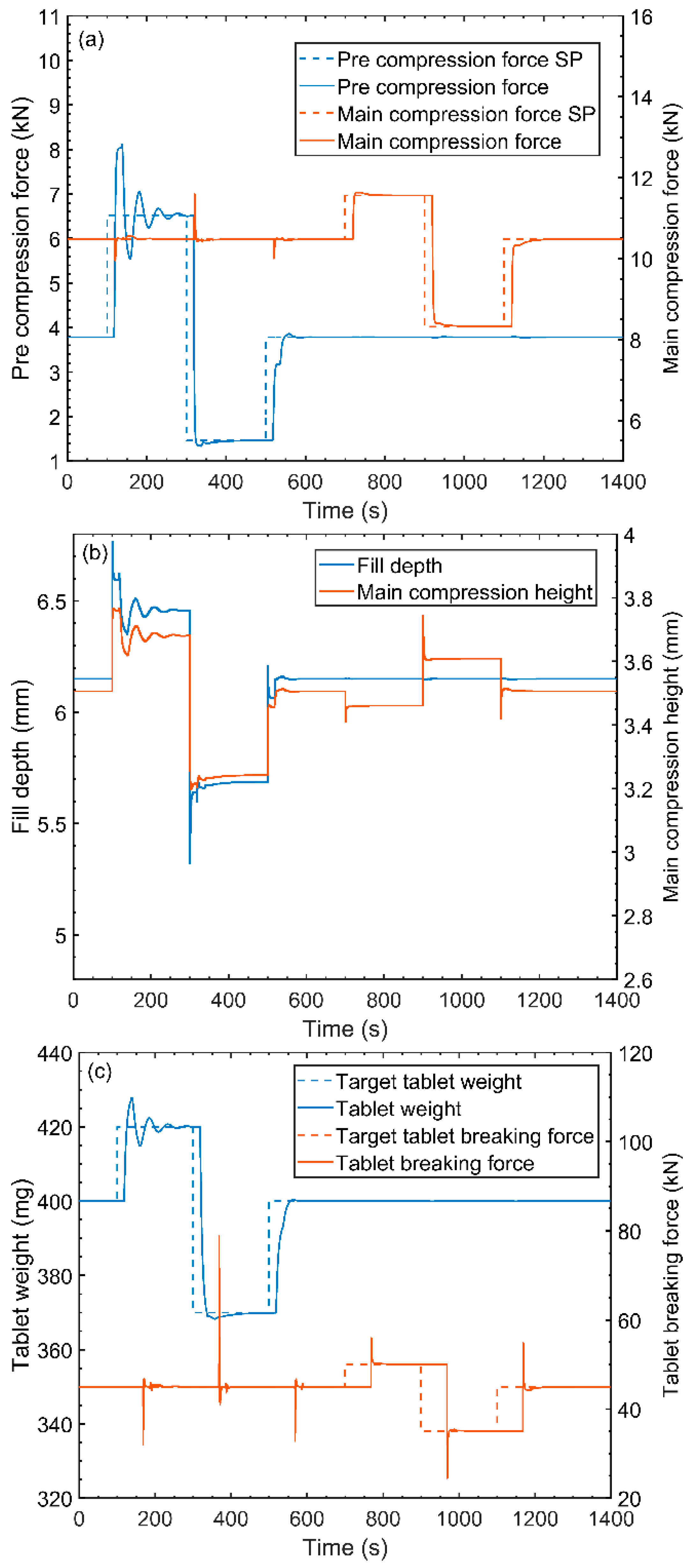
5.2.1. Strategy 1—Simultaneous Control of Pre- and Main Compression Forces
5.2.2. Strategy 2—Cascade Control of Weight and Breaking Force
5.2.3. Strategy 3—Direct Control of Tablet Weight and Cascade Tablet Breaking Force
6. Controller Tuning and Implementation
6.1. PI Controller
6.1.1. Tuning Procedure
6.1.2. Implementation of PI Controller
6.2. MPC
6.2.1. Tuning Procedure
6.2.2. Implementation of MPC
7. Results
7.1. Control Algorithm Performance Analysis
7.2. Control Strategy Evaluation
7.2.1. Strategy 1—Simultaneous Control of Pre- and Main Compression Forces
7.2.2. Strategy 2—Cascade Control of Weight and Breaking Force
7.2.3. Strategy 3—Direct Control of Tablet Weight and Cascade Tablet Breaking Force Control
8. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- U.S. Department of Health and Human Services Food and Drug Administration Guidance for Industry: ICH Q8(R2) Pharmaceutical Development. Work. Qual. Des. Pharm. 2009, 8, 28.
- International conference on harmonisation of technical requirements for registration of pharmaceuticals for human use Pharmaceutical Development Q8(R2). In Proceedings of the ICH Harmonised Tripartite Guideline, Kuala Lumpur, Malaysia, 26–28 July 2010; pp. 1–28.
- Mesbah, A.; Paulson, J.A.; Lakerveld, R.; Braatz, R.D. Model Predictive Control of an Integrated Continuous Pharmaceutical Manufacturing Pilot Plant. Org. Process Res. Dev. 2017, 21, 844–854. [Google Scholar] [CrossRef]
- Sen, M.; Chaudhury, A.; Singh, R.; John, J.; Ramachandran, R. Multi-scale flowsheet simulation of an integrated continuous purification-downstream pharmaceutical manufacturing process. Int. J. Pharm. 2013, 445, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Boukouvala, F.; Niotis, V.; Ramachandran, R.; Muzzio, F.J.; Ierapetritou, M.G. An integrated approach for dynamic flowsheet modeling and sensitivity analysis of a continuous tablet manufacturing process. Comput. Chem. Eng. 2012, 42, 30–47. [Google Scholar] [CrossRef]
- Jain, S. Mechanical properties of powders for compaction and tableting: An overview. Pharm. Sci. Technol. Today 1999, 2, 20–31. [Google Scholar] [CrossRef]
- Michaut, F.; Busignies, V.; Fouquereau, C.; Huet de Barochez, E.; Leclerc, B.; Tchoreloff, P. Evaluation of a Rotary Tablet Press Simulator as a Tool for the Characterization of Compaction Properties of Pharmaceutical Products. J. Pharm. Sci. 2010, 99, 2874–2885. [Google Scholar] [CrossRef] [PubMed]
- Sinka, I.C.; Cunningham, J.C.; Zavaliangos, A. The effect of wall friction in the compaction of pharmaceutical tablets with curved faces: A validation study of the Drucker-Prager Cap model. Powder Technol. 2003, 133, 33–43. [Google Scholar] [CrossRef]
- Mendez, R.; Muzzio, F.; Velazquez, C. Study of the effects of feed frames on powder blend properties during the filling of tablet press dies. Powder Technol. 2010, 200, 105–116. [Google Scholar] [CrossRef]
- Akande, O.F.; Rubinstein, M.H.; Ford, J.L. Examination of the compaction properties of a 1:1 acetaminophen:Microcrystalline cellulose mixture using precompression and main compression. J. Pharm. Sci. 1997, 86, 900–907. [Google Scholar] [CrossRef] [PubMed]
- Gonnissen, Y.; Gonçalves, S.I.V.; De Geest, B.G.; Remon, J.P.; Vervaet, C. Process design applied to optimise a directly compressible powder produced via a continuous manufacturing process. Eur. J. Pharm. Biopharm. 2008, 68, 760–770. [Google Scholar] [CrossRef] [PubMed]
- Haware, R.V.; Tho, I.; Bauer-Brandl, A. Application of multivariate methods to compression behavior evaluation of directly compressible materials. Eur. J. Pharm. Biopharm. 2009, 72, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Seitz, J.A.; Flessland, G.M. Evaluation of the Physical Properties of Compressed Tablets I: Tablet Hardness and Friability. J. Pharm. Sci. 1965, 54, 1353–1357. [Google Scholar] [CrossRef] [PubMed]
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Di Cairano, S. An Industry perspective on MPC in large volumes applications: Potential benefits and open challenges. IFAC Proc. Vol. 2012, 45, 52–59. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Zagrobelny, M.A. MPC Performance Monitoring and Disturbance Model Identification, University of Winsconsin-Madison. Diss. Theses Gradworks 2014. Available online: http://jbrwww.che.wisc.edu/theses/zagrobelny.pdf (accessed 30 November 2017).
- Mayne, D.Q.; Raković, S.V.; Findeisen, R.; Allgöwer, F. Robust output feedback model predictive control of constrained linear systems. Automatica 2006, 42, 1217–1222. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Streif, S.; Kögel, M.; Bäthge, T.; Findeisen, R. Robust Nonlinear Model Predictive Control with Constraint Satisfaction: A Relaxation-based Approach. FAC World Congr. 2014, 47, 11073–11079. [Google Scholar] [CrossRef]
- Maiworm, M.; Bäthge, T.; Findeisen, R. Scenario-based Model Predictive Control: Recursive feasibility and stability. IFAC PapersOnLine 2015, 28, 50–56. [Google Scholar] [CrossRef]
- Allgöwer, F.; Findeisen, R.; Ebenbauer, C. Nonlinear model predictive control. In Control Systems, Robotics and Automation; Birkhäuser: Basel, Basel-Stadt, Switzerland, 2009; Volume XI. [Google Scholar]
- Su, Q.; Moreno, M.; Giridhar, A.; Reklaitis, G.V.; Nagy, Z.K. A Systematic Framework for Process Control Design and Risk Analysis in Continuous Pharmaceutical Solid-Dosage Manufacturing. J. Pharm. Innov. 2017, 12, 1–20. [Google Scholar] [CrossRef]
- Singh, R.; Ierapetritou, M.; Ramachandran, R. System-wide hybrid MPC–PID control of a continuous pharmaceutical tablet manufacturing process via direct compaction. Eur. J. Pharm. Biopharm. 2013, 85, 1164–1182. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Ierapetritou, M.; Ramachandran, R. An engineering study on the enhanced control and operation of continuous manufacturing of pharmaceutical tablets via roller compaction. Int. J. Pharm. 2012. [Google Scholar] [CrossRef] [PubMed]
- Rehrl, J.; Kruisz, J.; Sacher, S.; Khinast, J.; Horn, M. Optimized continuous pharmaceutical manufacturing via model-predictive control. Int. J. Pharm. 2016, 510, 100–115. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.J.; Gatumel, C.; Dirion, J.L.; Berthiaux, H.; Cabassud, M. Implementation of a control loop for a continuous powder mixing process. In Proceedings of the AIChE 2013 Annual Meeting, San Francisco, CA, USA, 6 November 2013. [Google Scholar]
- Singh, R.; Román-Ospino, A.D.; Romañach, R.J.; Ierapetritou, M.; Ramachandran, R. Real time monitoring of powder blend bulk density for coupled feed-forward/feed-back control of a continuous direct compaction tablet manufacturing process. Int. J. Pharm. 2015, 495, 612–625. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Muzzio, F.; Ierapetritou, M.; Ramachandran, R. A Combined Feed-Forward/Feed-Back Control System for a QbD-Based Continuous Tablet Manufacturing Process. Processes 2015, 3, 339–356. [Google Scholar] [CrossRef]
- Singh, R.; Sahay, A.; Karry, K.M.; Muzzio, F.; Ierapetritou, M.; Ramachandran, R. Implementation of an advanced hybrid MPC-PID control system using PAT tools into a direct compaction continuous pharmaceutical tablet manufacturing pilot plant. Int. J. Pharm. 2014, 473, 38–54. [Google Scholar] [CrossRef] [PubMed]
- Sen, M.; Singh, R.; Ramachandran, R. A Hybrid MPC-PID Control System Design for the Continuous Purification and Processing of Active Pharmaceutical Ingredients. Processes 2014, 2, 392–418. [Google Scholar] [CrossRef]
- Bhaskar, A.; Barros, F.N.; Singh, R. Development and implementation of an advanced model predictive control system into continuous pharmaceutical tablet compaction process. Int. J. Pharm. 2017, 534, 159–178. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Sahay, A.; Muzzio, F.; Ierapetritou, M.; Ramachandran, R. A systematic framework for onsite design and implementation of a control system in a continuous tablet manufacturing process. Comput. Chem. Eng. 2014, 66, 186–200. [Google Scholar] [CrossRef]
- Sarkar, S.; Ooi, S.M.; Liew, C.V.; Heng, P.W.S. Influence of Rate of Force Application during Compression on Tablet Capping. J. Pharm. Sci. 2015, 104, 1319–1327. [Google Scholar] [CrossRef] [PubMed]
- Seborg, D.; Edgar, T.; Mellichamp, D. Process Dynamics and Control, 2nd ed.; Wiley: Hoboken, NJ, USA, 2004; ISBN 0-471-00077-9. [Google Scholar]
- Patel, S.; Kaushal, A.M.; Bansal, A.K. Compression Physics in the Formulation Development of Tablets. Crit. Rev. Ther. Drug Carr. Syst. 2006, 23, 1–66. [Google Scholar] [CrossRef]
- Kawakita, K.; Lüdde, K.H. Some considerations on powder compression equations. Powder Technol. 1971, 4, 61–68. [Google Scholar] [CrossRef]


| Model Inputs | Model Outputs | Model Details | |||||
|---|---|---|---|---|---|---|---|
| Order | τ1 (s) | τ2 (s) | θ (s) | Gain | R2 | ||
| Fill depth SP | Fill depth | 1 | 1.0694 | - | 5.4986 | 1 | 0.9966 |
| Main compression height SP | Main compression height | 1 | 0.1658 | - | 5.3616 | 1 | 0.9973 |
| Pre-compression height SP | Pre-compression height | 1 | 0.1658 | - | 5.3616 | 1 | 0.9973 |
| Production rate SP | Production rate | 2 | 0.9 | 0.9968 | 8 | 1 | 0.9824 |
| Model Inputs | Model Outputs | Model Details | |||||
|---|---|---|---|---|---|---|---|
| Order | τ1(s) | τ2(s) | Θmax(s) | Gain | R2 | ||
| Pre-compression ratio | Pre-compression force | 1 | 2.5058 | - | 12.5 | 1 | 0.9680 |
| Main compression ratio | Main compression force | 1 | 3.4244 | - | 15 | 1 | 0.9659 |
| Polynomial Constants | Pre-Compression Force (−) | Main Compression Force (−) |
|---|---|---|
| a1 | 80.92 | 55.97 |
| a2 | −219.40 | −150.34 |
| a3 | 149.83 | 101.98 |
| Controller | Ts (s) | P (Samples) | M (Samples) | Output Weight | Input Rate Weight | ||
|---|---|---|---|---|---|---|---|
| CV 1 (-) | CV 2 (-) | MV 1 (-) | MV 2 (-) | ||||
| MCF | 1 | 40 | 2 | 1 | - | 0.1 | - |
| Strategy 1 | 1 | 25 | 2 | 0.135 | 0.135 | 0.739 | 0.739 |
| Strategy 2—Master | 4 | 20 | 2 | 1 | 1 | 0.1 | 0.1 |
| Strategy 2—Slave | 1 | 25 | 2 | 0.135 | 0.135 | 0.739 | 0.739 |
| Strategy 3—Master | 4 | 20 | 2 | 1 | 1 | 0.1 | 0.1 |
| Strategy 3—Slave | 4 | 20 | 2 | 1 | - | 0.1 | - |
| Strategy | IAE (kN s) | ITAE (kN s) | ISE (kN s) | Rise Time (s) | Settling Time (s) | Overshoot (%) | Steady State Error (%) |
|---|---|---|---|---|---|---|---|
| Experimental PI | 289.95 | 18506 | 693.45 | 121 | 211 | 0 | 0 |
| Simulated PI | 204.00 | 6596.2 | 626.48 | 64 | 120 | 6.11 | 0 |
| Experimental MPC | 180.50 | 5688.6 | 564.33 | 46 | 153 | 0 | −7.50 |
| Simulated MPC | 111.65 | 5216.2 | 317.78 | 23 | 24 | 0 | 2.788 |
| Simulated MPC with disturbance model | 86.830 | 954.490 | 333.68 | 23 | 25 | 0.448 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunes de Barros, F.; Bhaskar, A.; Singh, R. A Validated Model for Design and Evaluation of Control Architectures for a Continuous Tablet Compaction Process. Processes 2017, 5, 76. https://doi.org/10.3390/pr5040076
Nunes de Barros F, Bhaskar A, Singh R. A Validated Model for Design and Evaluation of Control Architectures for a Continuous Tablet Compaction Process. Processes. 2017; 5(4):76. https://doi.org/10.3390/pr5040076
Chicago/Turabian StyleNunes de Barros, Fernando, Aparajith Bhaskar, and Ravendra Singh. 2017. "A Validated Model for Design and Evaluation of Control Architectures for a Continuous Tablet Compaction Process" Processes 5, no. 4: 76. https://doi.org/10.3390/pr5040076
APA StyleNunes de Barros, F., Bhaskar, A., & Singh, R. (2017). A Validated Model for Design and Evaluation of Control Architectures for a Continuous Tablet Compaction Process. Processes, 5(4), 76. https://doi.org/10.3390/pr5040076