Minimizing the Effect of Substantial Perturbations in Military Water Systems for Increased Resilience and Efficiency
Abstract
:1. Introduction
1.1. Motivation and Scope
1.2. Literature Review
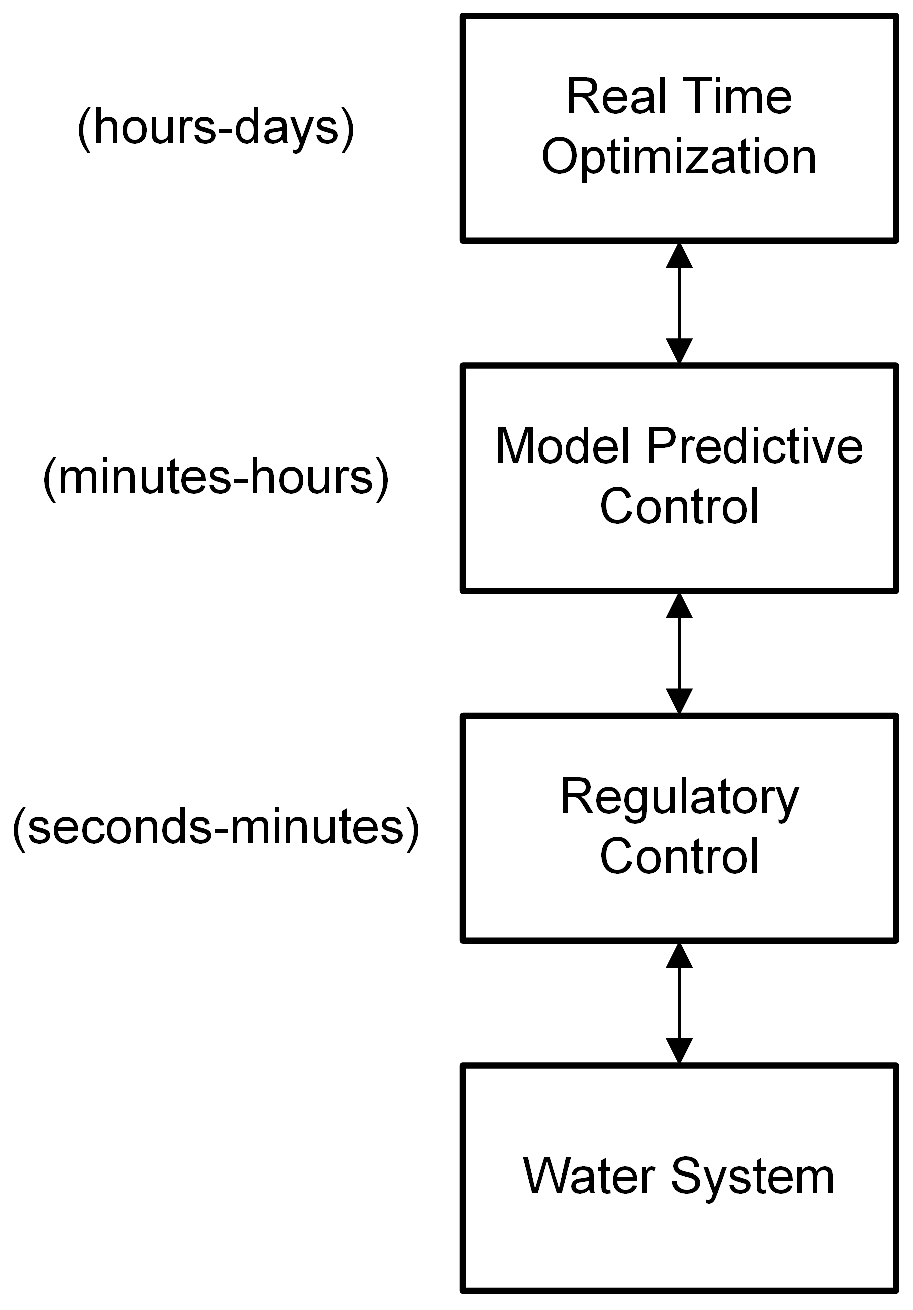
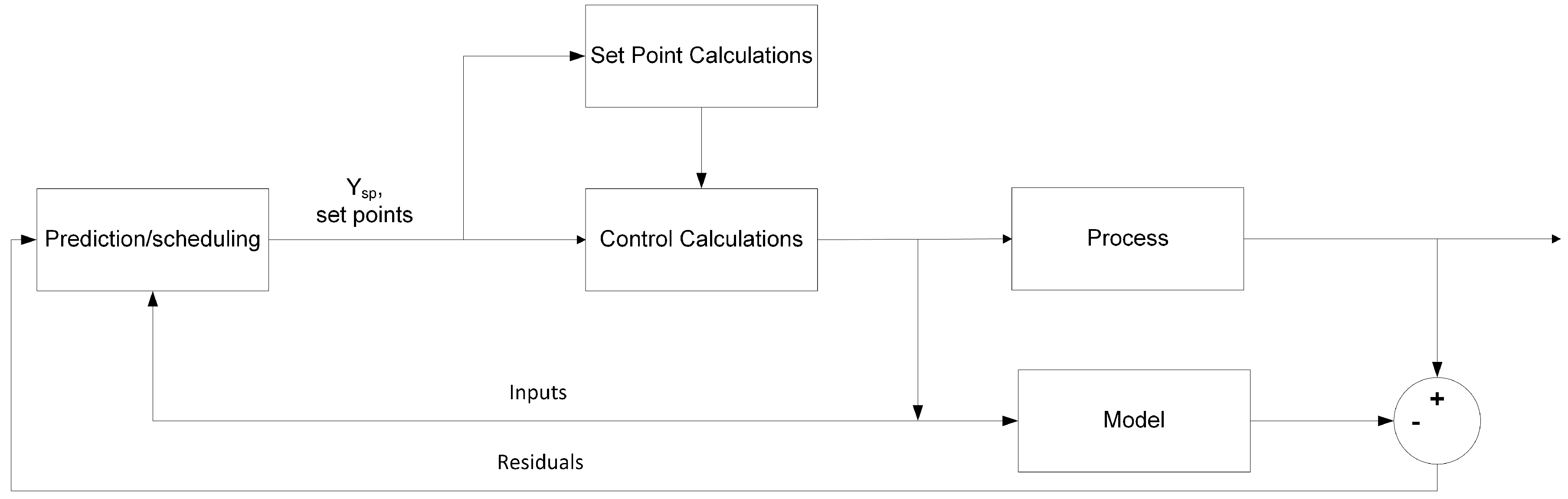
2. Research Methods
2.1. System Identification
2.2. Nonlinear Disturbance Controller Development
3. Results
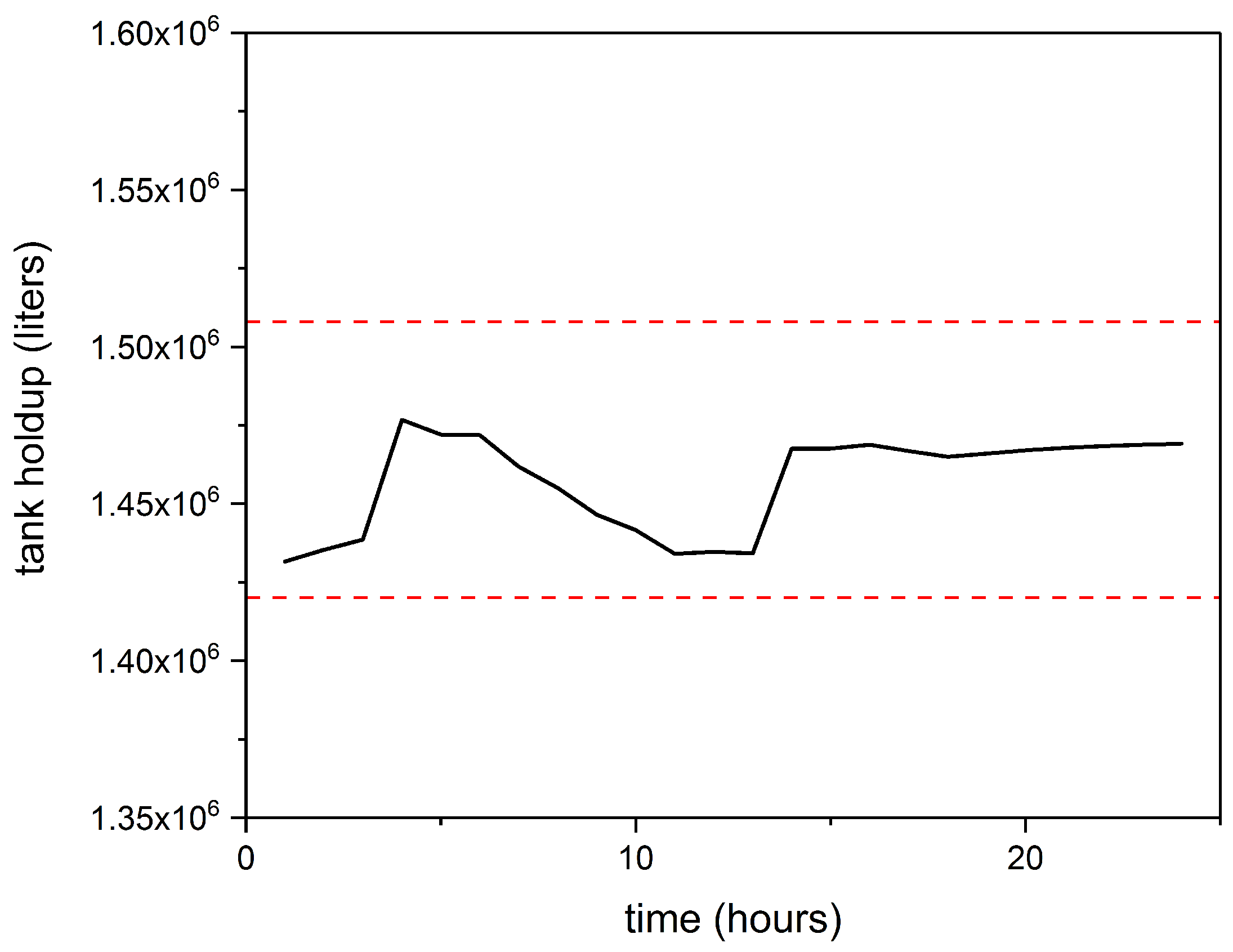
3.1. Averaging Level Control
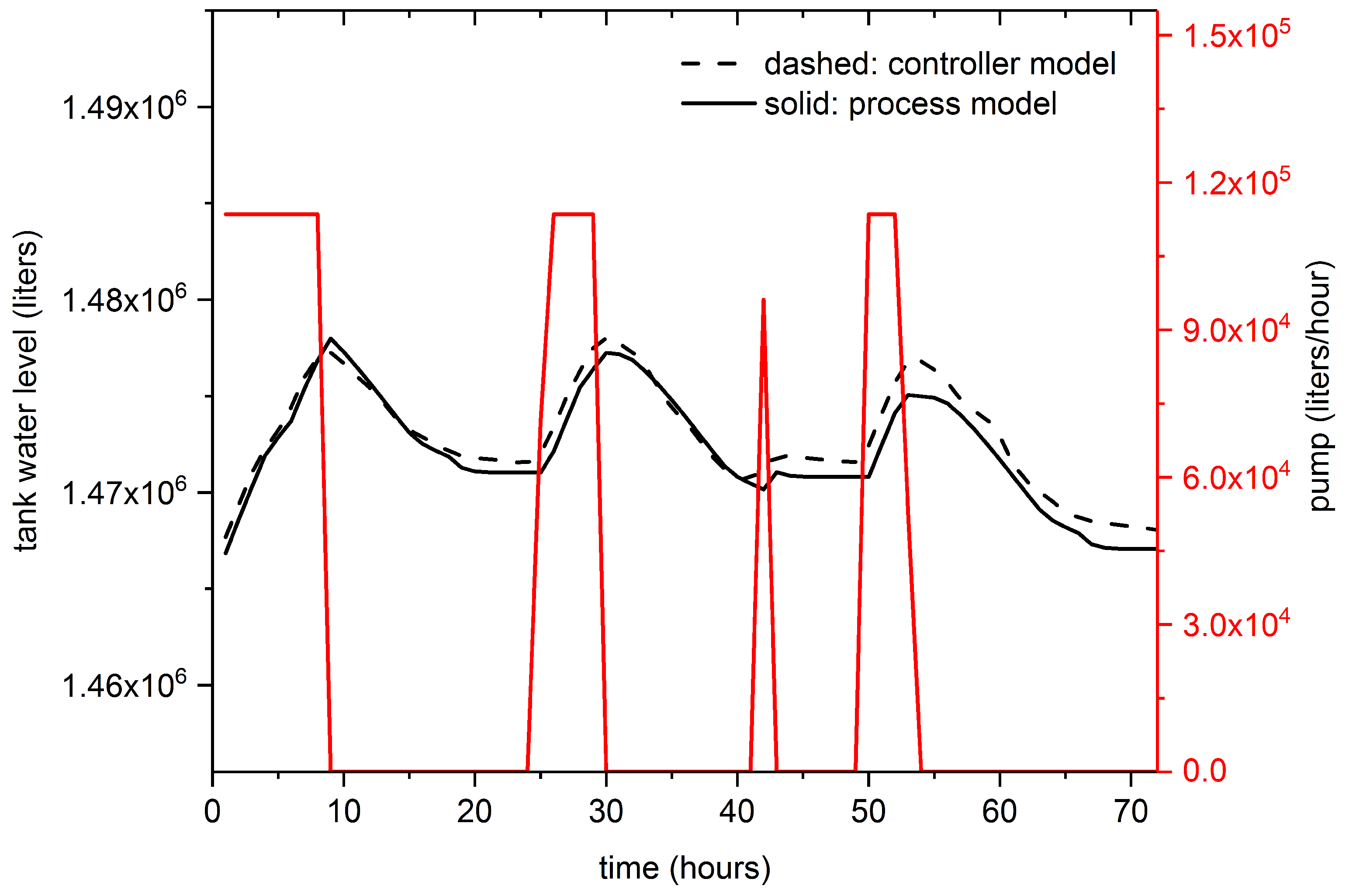
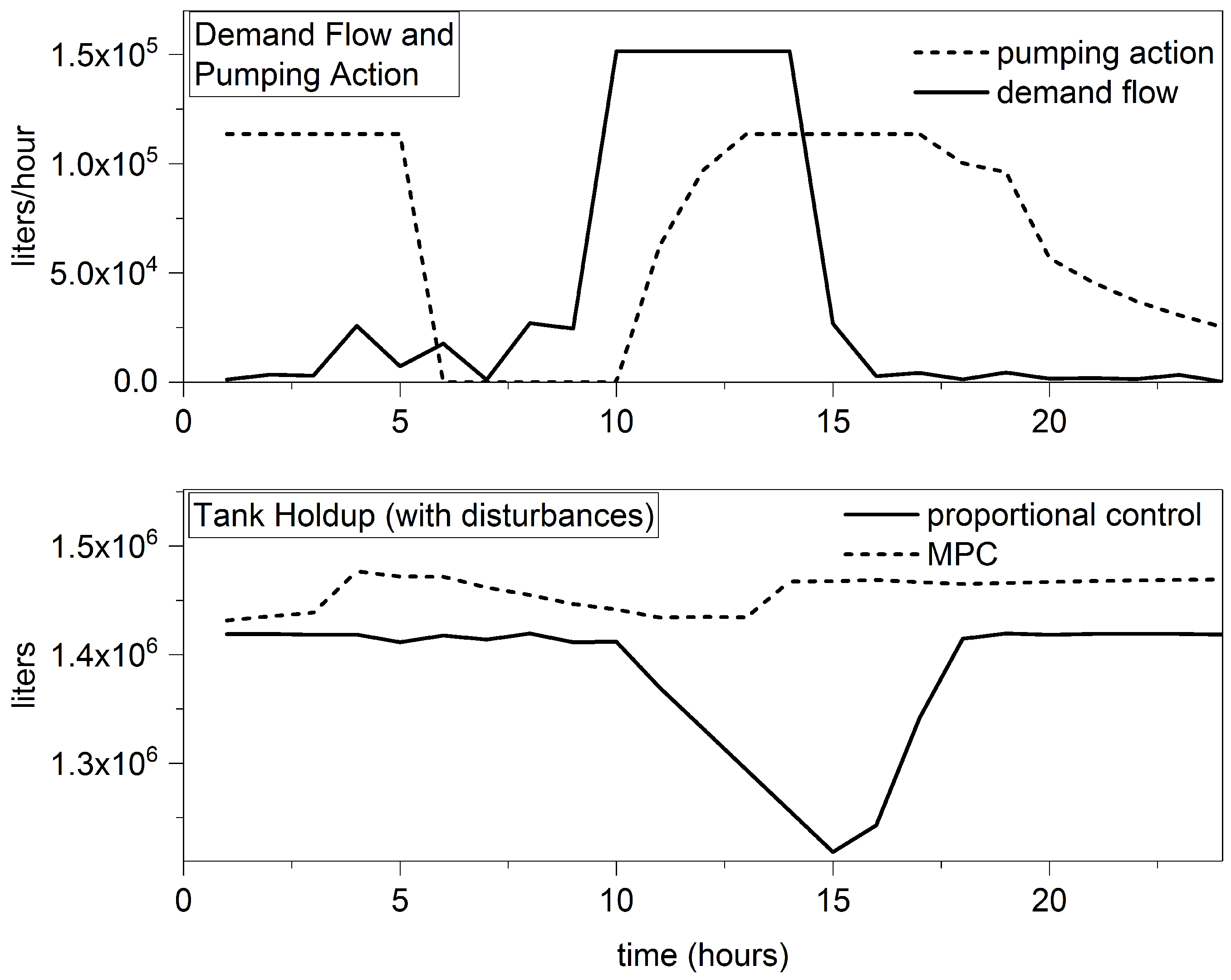
3.2. Closed Loop Controller Response
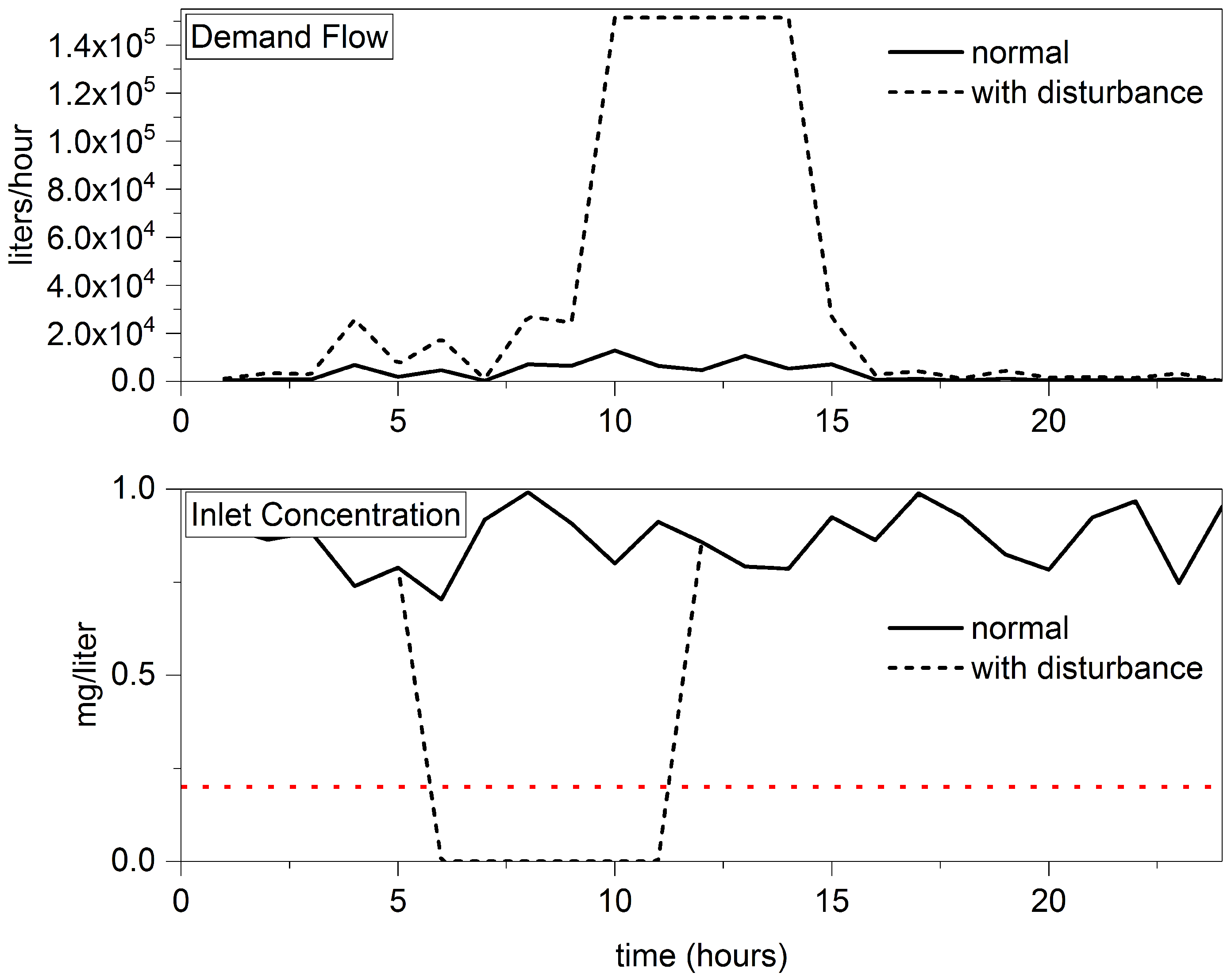
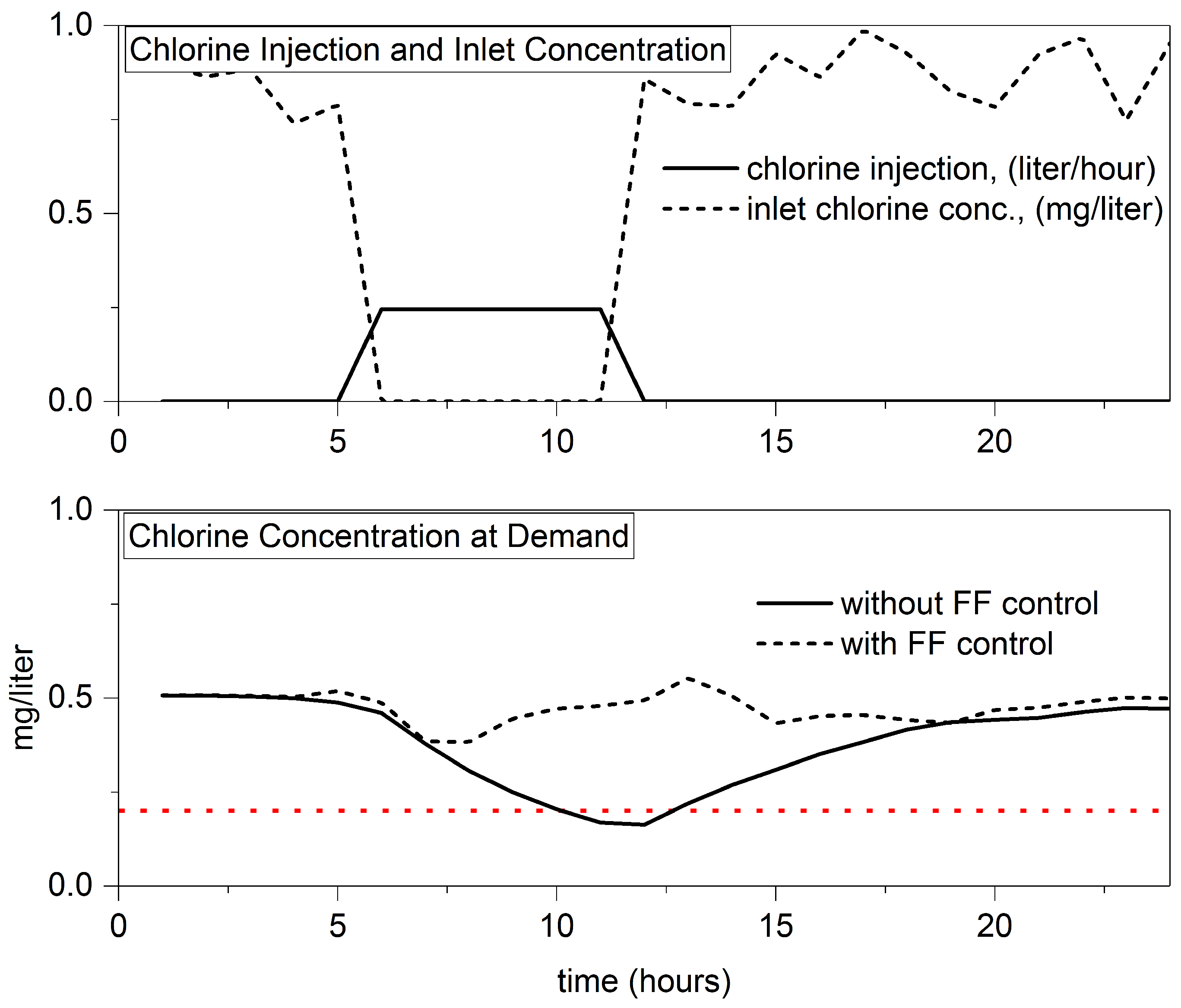
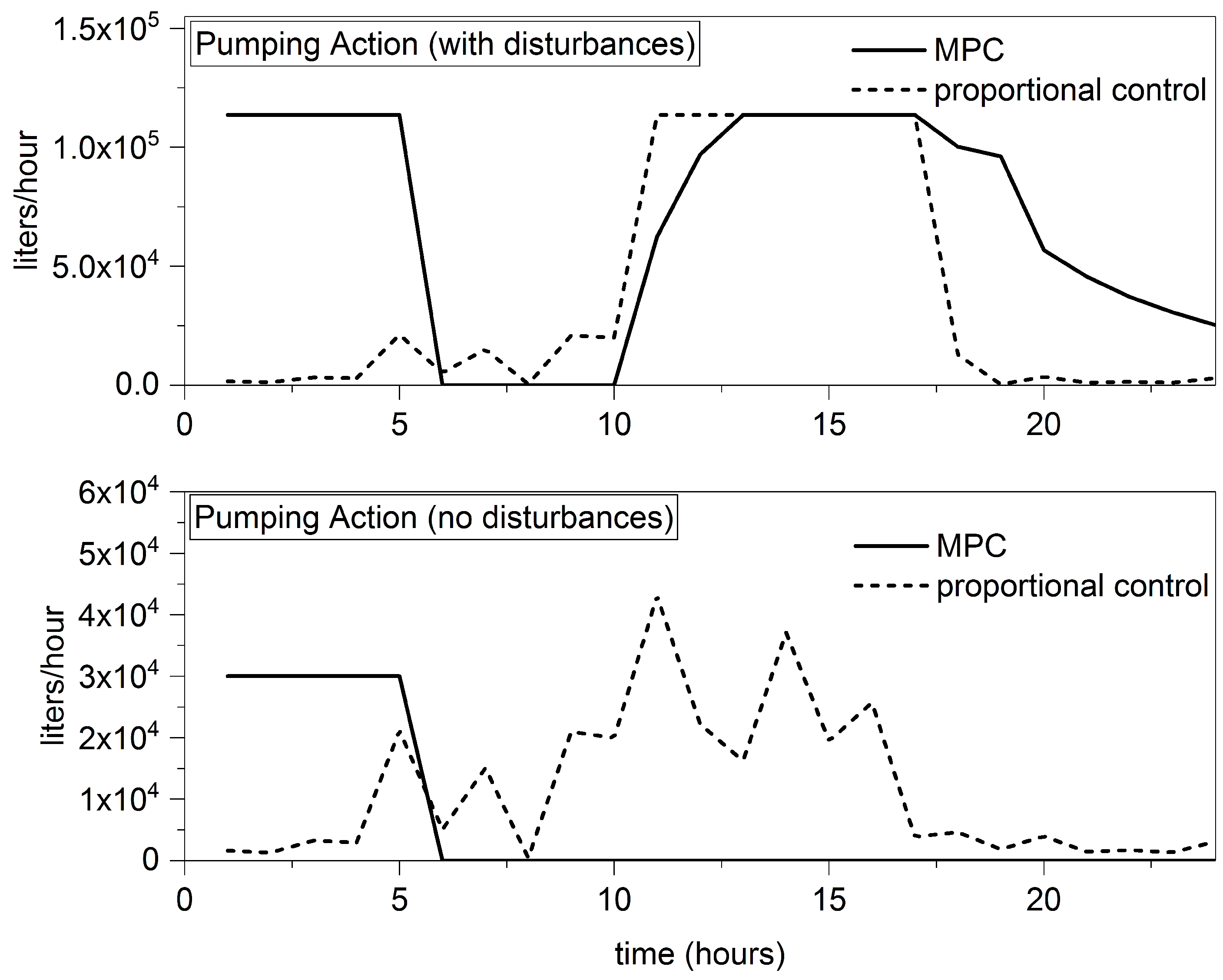
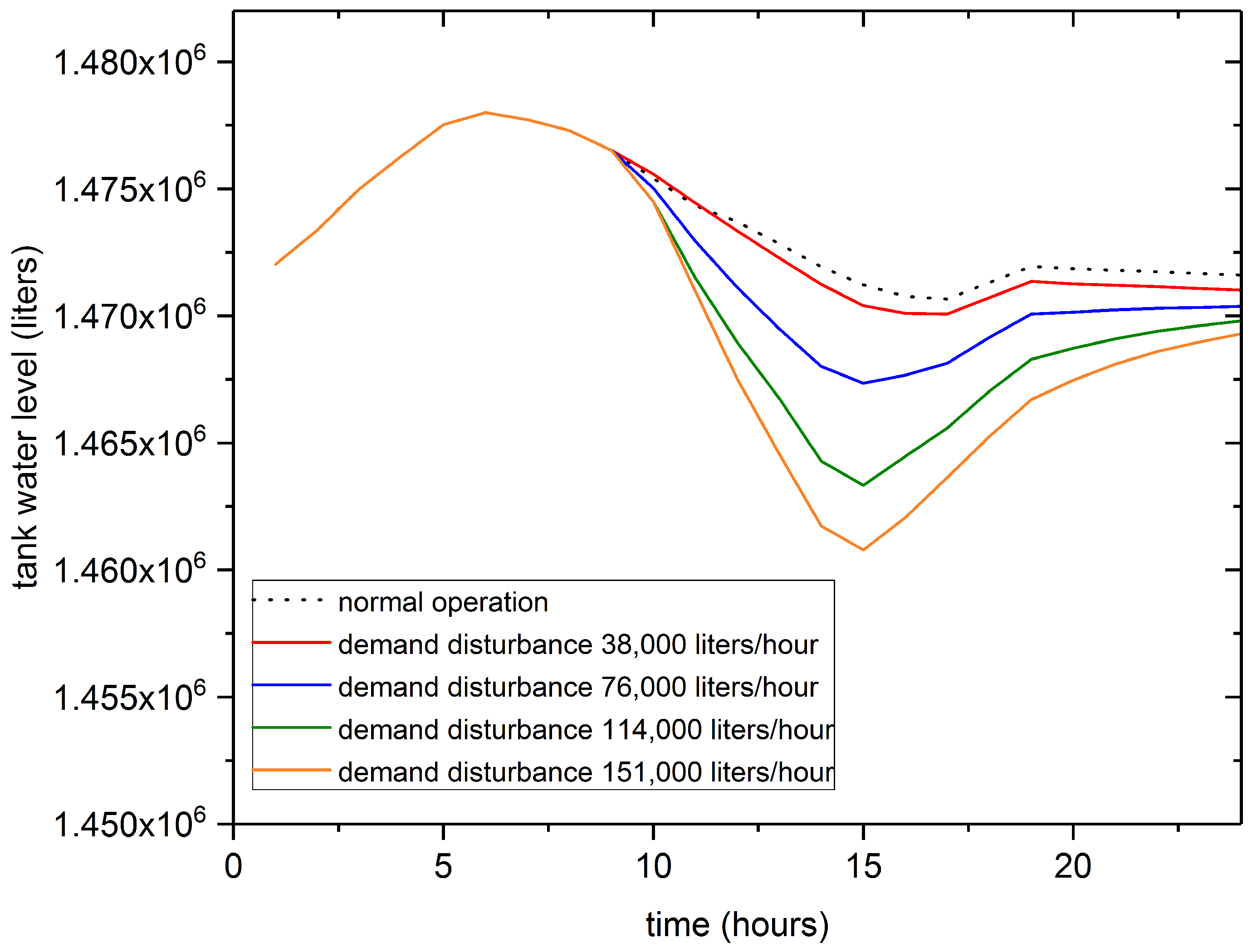
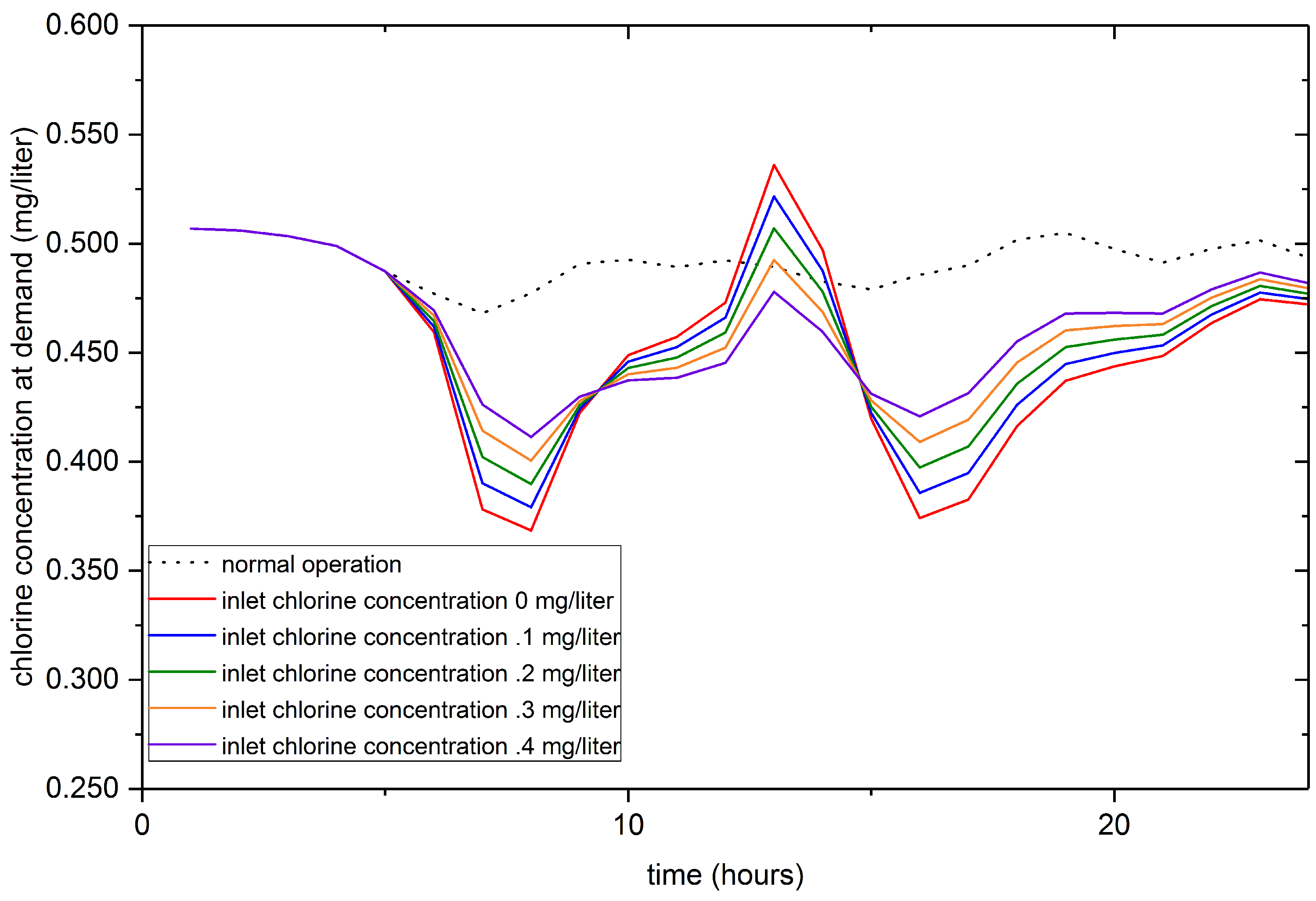
3.3. Robustness Analysis
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Rossman, L.A.; Clark, R.M.; Grayman, W.M. Modeling chlorine residuals in drinking-water distribution systems. J. Environ. Eng. 1994, 120, 803–820. [Google Scholar] [CrossRef]
- James, C. Reducing the Cost of Operational Water on Military Bases Through Modeling, Optimization, and Control. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2017. [Google Scholar]
- Seborg, D.E.; Mellichamp, D.A.; Edgar, T.F.; Doyle, F.J., III. Process Dynamics and Control; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Ormsbee, L.; Reddy, L.; Chase, D. Comparison of Three Nonlinear Control Algorithms for the Optimal Operation of Water Supply Pumping Systems; Integrated Computer Applications in Water Supply (Vol. 1); John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1994; pp. 259–271. [Google Scholar]
- Ormsbee, L.E.; Lansey, K.E. Optimal control of water supply pumping systems. J. Water Resour. Plan. Manag. 1994, 120. [Google Scholar] [CrossRef]
- Van Staden, A.J.; Zhang, J.; Xia, X. A model predictive control strategy for load shifting in a water pumping scheme with maximum demand charges. Appl. Energy 2011, 88, 4785–4794. [Google Scholar] [CrossRef]
- Yu, G.; Powell, R.; Sterling, M. Optimized pump scheduling in water distribution systems. J. Optim. Theory Appl. 1994, 83, 463–488. [Google Scholar] [CrossRef]
- Duzinkiewicz, K.; Brdys, M.; Chang, T. Hierarchical model predictive control of integrated quality and quantity in drinking water distribution systems. Urban Water J. 2005, 2, 125–137. [Google Scholar] [CrossRef]
- Brdys, M.A.; Chang, T.; Duzinkiewicz, K.; Chotkowski, W. Hierarchical control of integrated quality and quantity in water distribution systems. In Proceedings of the ASCE 2000 Joint Conference on Water Resources Engineering and Water Resources Planning and Management, Minneapolis, MN, USA, 30 July–2 August 2000. [Google Scholar]
- Chang, T.; Brdys, M.; Duzinkiewicz, K. Decentralized robust model predictive control of chlorine residuals in drinking water distribution systems. In Proceedings of the World Water and Environmental Resources Congress, World Water and Environmental Resources Congress and Related Symposia, Philadelphi, PA, USA, 23–26 June 2004; pp. 23–26. [Google Scholar]
- Wang, J.; Brdys, M.A. Optimal operation of water distribution systems under full range of operating scenarios. In Proceedings of the 6th UKACC International Control Conference, Glasgow, UK, 30 August–1 September 2006. [Google Scholar]
- Drewa, M.; Brdys, M.; Ciminski, A. Model predictive control of integrated quantity and quality in drinking water distribution systems. In Proceedings of the 8th International IFAC Symposium on Dynamics and Control of Process Systems, Cancún, Mexico, 6–8 June 2007. [Google Scholar]
- Brdys, M.; Chang, T.; Duzinkiewicz, K. Intelligent model predictive control of chlorine residuals in water distribution systems. In Proceedings of the ASCE Water Resource Engineering and Water Resources Planning and Management, Orlando, FL, USA, 20–24 May 2001; pp. 391–401. [Google Scholar]
- Polycarpou, M.M.; Uber, J.G.; Wang, Z.; Shang, F.; Brdys, M. Feedback control of water quality. IEEE Control Syst. 2002, 22, 68–87. [Google Scholar] [CrossRef]
- Trawicki, D.; Duzinkiewicz, K.; Brdys, M. Optimising model predictive controller for hierarchical control of integrated quality and quantity in drinking water distribution systems. In Proceedings of the IFAC I International Conference on Technology, Automation and Control of Wastewater Systems-TiASWiK’02, Gdansk-Sobieszewo, Poland, 19–21 June 2002; pp. 19–21. [Google Scholar]
- Chang, T.; Brdys, M.; Duzinkiewicz, K. Quantifying uncertainties for chlorine residual control in drinking water distribution systems. Proc. ASCE World Water Environm. Resour. 2003, 64, 28–37. [Google Scholar]
- Wang, Y.; Puig, V.; Cembrano, G. Non-linear economic model predictive control of water distribution networks. J. Process Control 2017, 56, 23–34. [Google Scholar] [CrossRef]
- Sandison, J. Controlling chlorination in drinking water: Water and waste water. IMIESA 2006, 31, 32–37. [Google Scholar]
- Brosilow, C.; Joseph, B. Techniques of Model-Based Control; Prentice Hall Professional: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Shinskey, F.G. Process Control Systems: Application, Design and Tuning; McGraw-Hill, Inc.: London, UK, 1990. [Google Scholar]
- Touretzky, C.R.; Baldea, M. Nonlinear model predictive control of energy-integrated process systems. Syst. Control Lett. 2013, 62, 723–731. [Google Scholar]
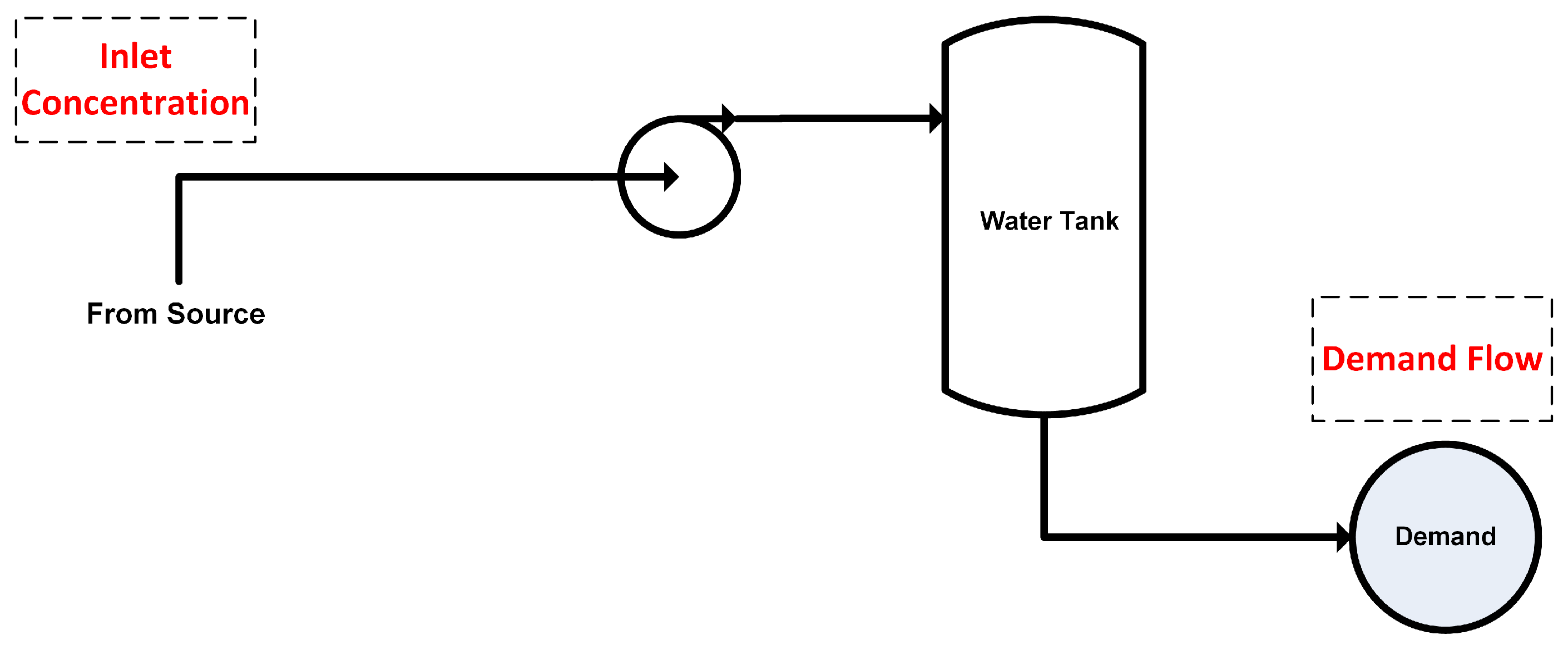
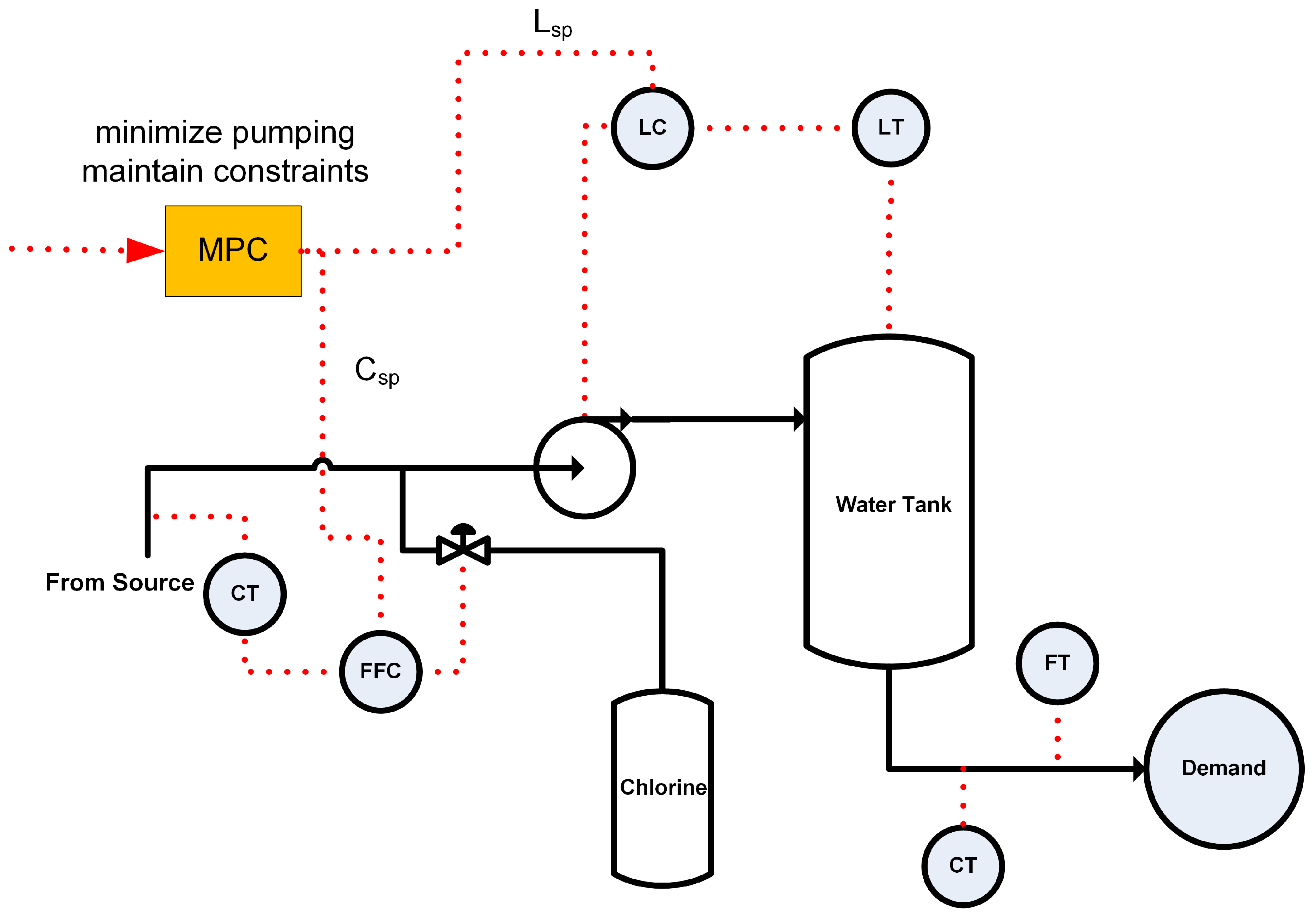
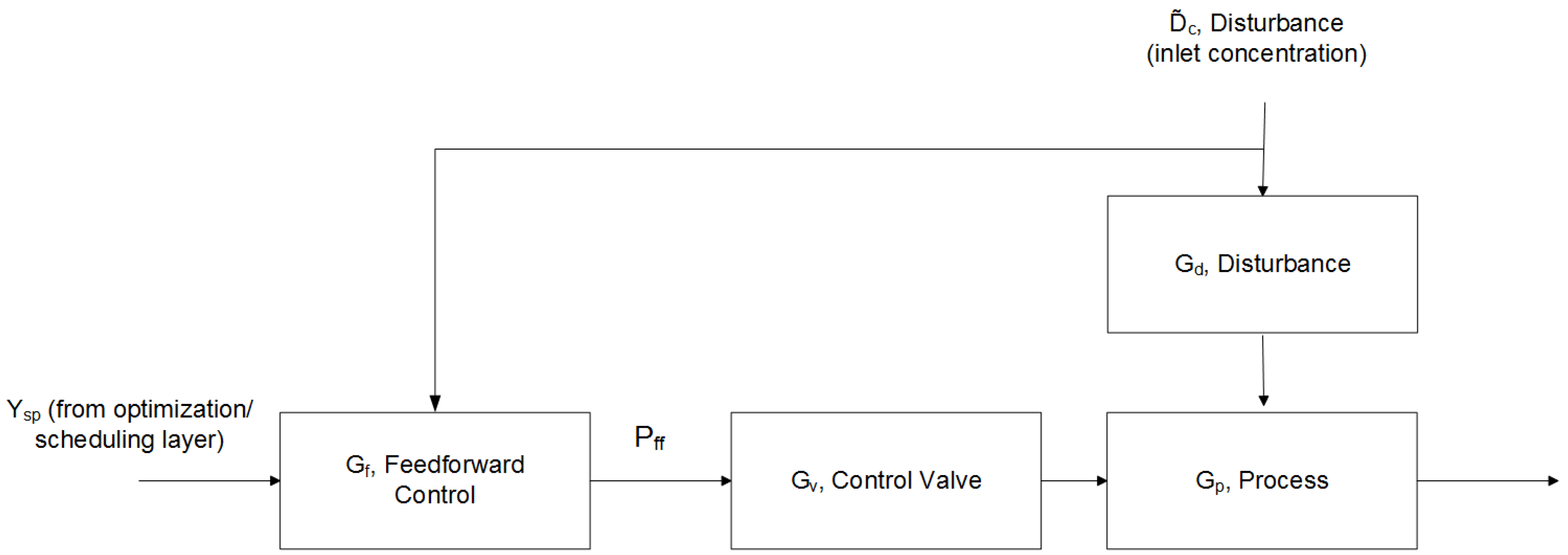
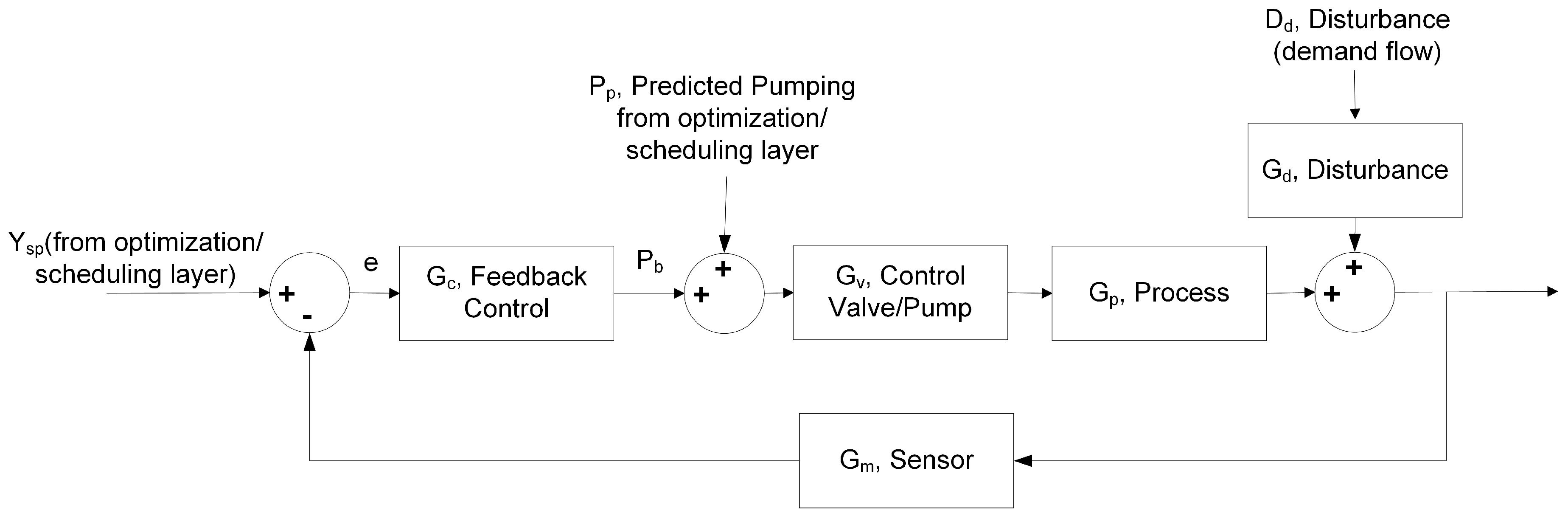

| Tank Holdup, CV | Demand Chlorine Concentration, CV | |
|---|---|---|
| Pump, MV | ||
| Chlorine Injection, MV | ||
| Demand, DV | ||
| Initial Concentration, DV |
| Parameter | Value | Units |
|---|---|---|
| M | 5 | h |
| P | 24 | h |
| 1 | ||
| 0 | L/h | |
| 3.79 | L/h | |
| 0 | L/h | |
| 113,562 | L/h | |
| −0.35 | mg/L2 | |
| 15 | h |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
James, C.M.; Webber, M.E.; Edgar, T.F. Minimizing the Effect of Substantial Perturbations in Military Water Systems for Increased Resilience and Efficiency. Processes 2017, 5, 60. https://doi.org/10.3390/pr5040060
James CM, Webber ME, Edgar TF. Minimizing the Effect of Substantial Perturbations in Military Water Systems for Increased Resilience and Efficiency. Processes. 2017; 5(4):60. https://doi.org/10.3390/pr5040060
Chicago/Turabian StyleJames, Corey M., Michael E. Webber, and Thomas F. Edgar. 2017. "Minimizing the Effect of Substantial Perturbations in Military Water Systems for Increased Resilience and Efficiency" Processes 5, no. 4: 60. https://doi.org/10.3390/pr5040060
APA StyleJames, C. M., Webber, M. E., & Edgar, T. F. (2017). Minimizing the Effect of Substantial Perturbations in Military Water Systems for Increased Resilience and Efficiency. Processes, 5(4), 60. https://doi.org/10.3390/pr5040060




