Reduction of Dust Emission by Monodisperse System Technology for Ammonium Nitrate Manufacturing
Abstract
:1. Introduction
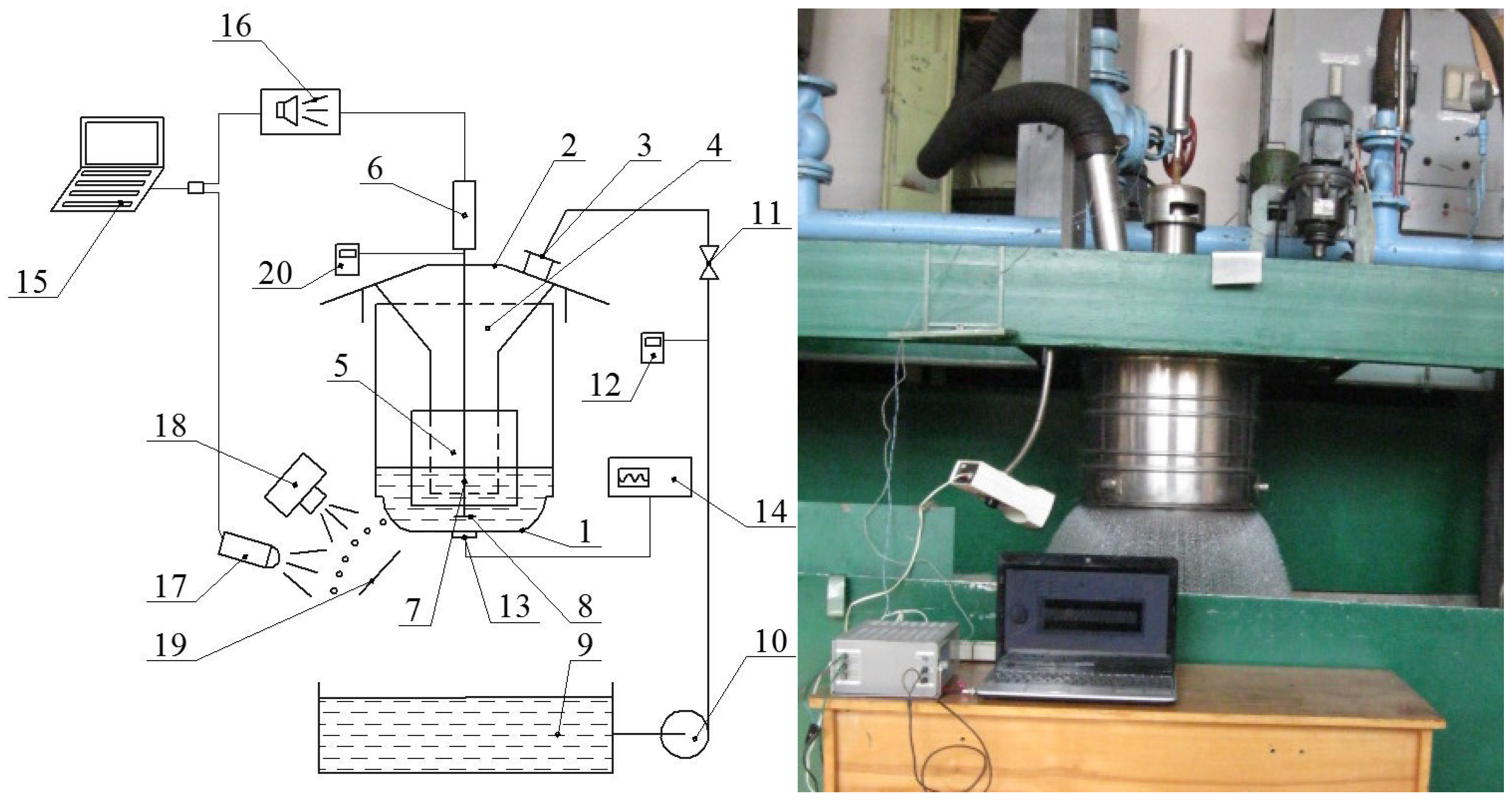
2. Experimental Setup and Methods
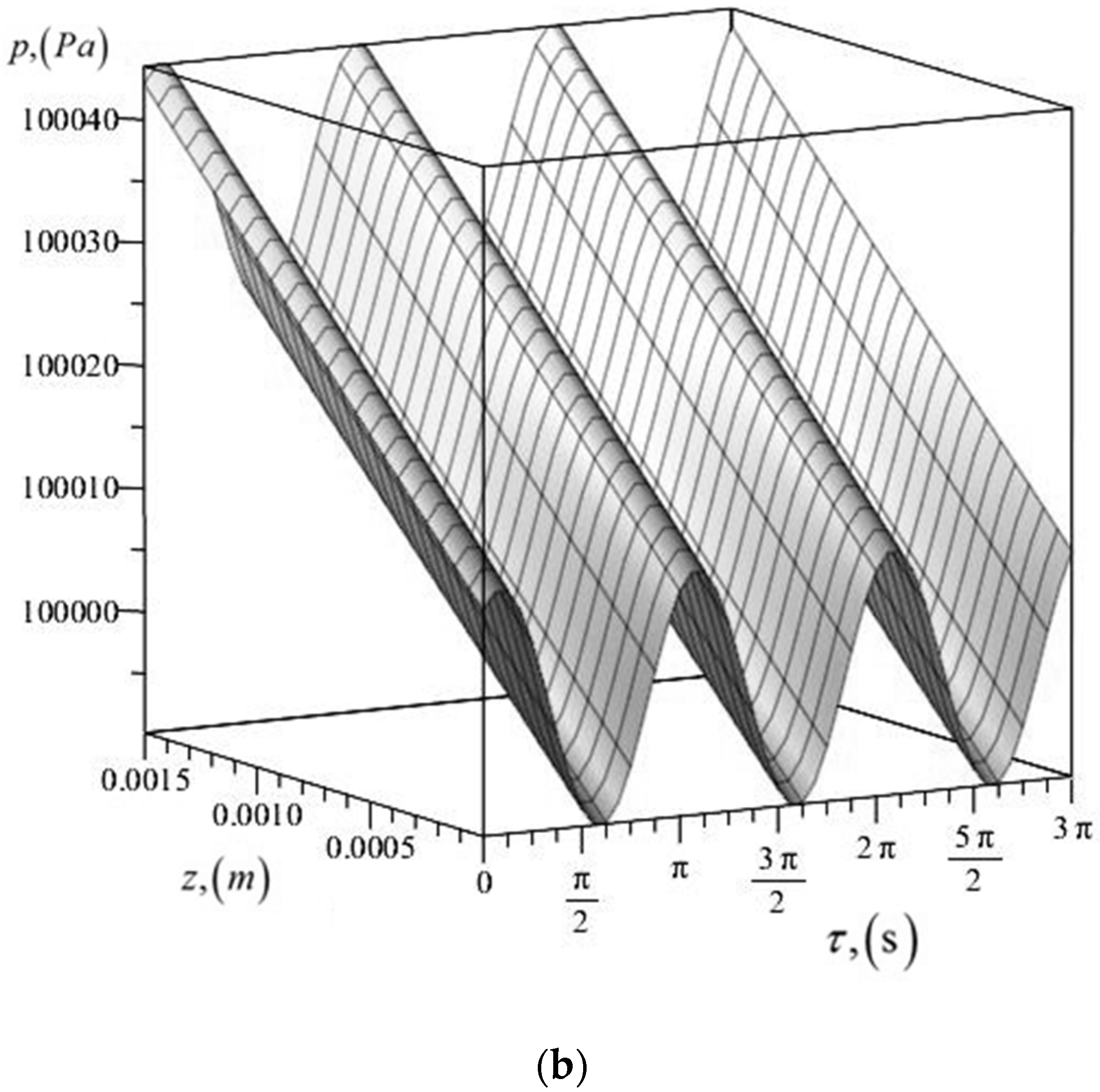
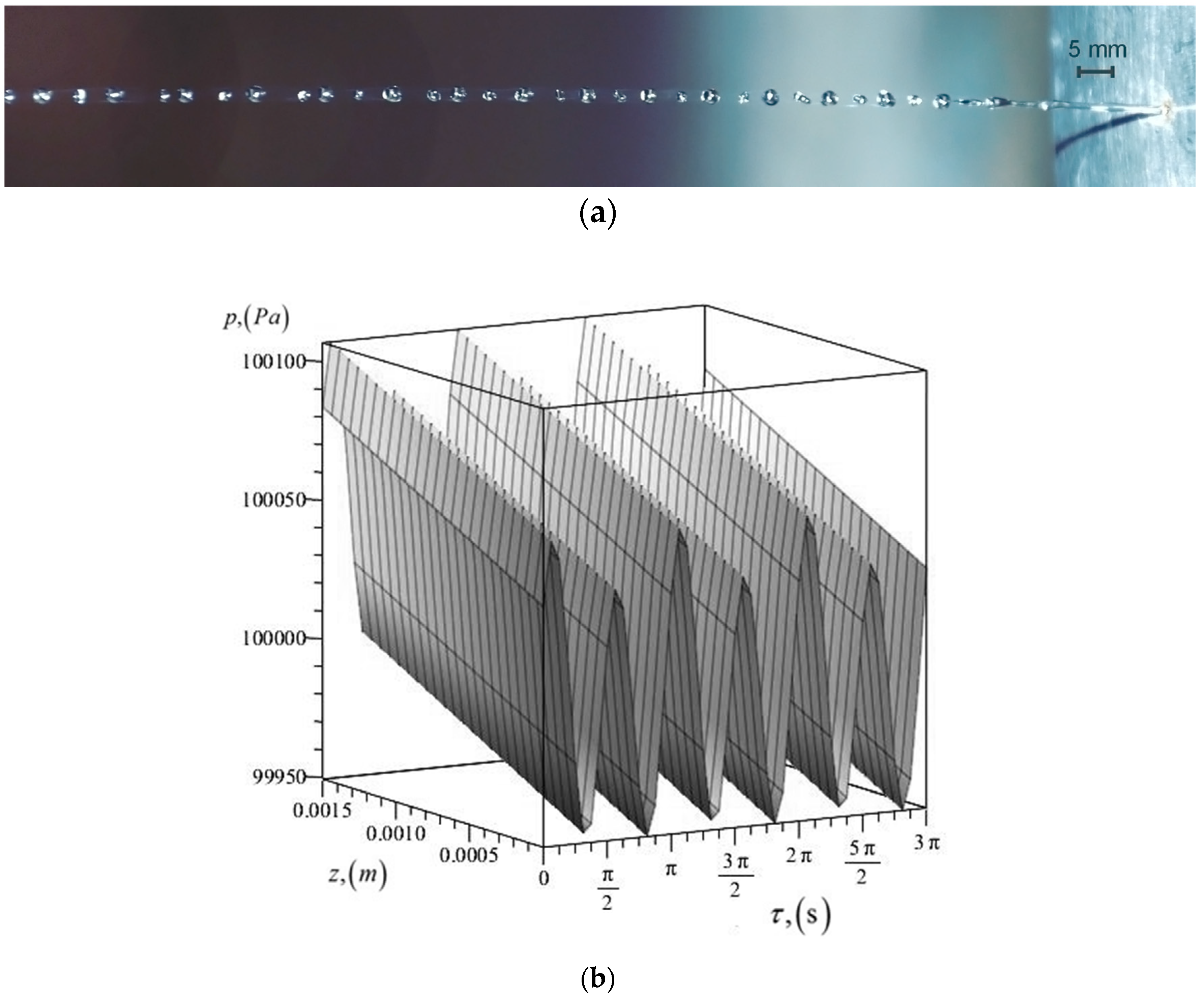
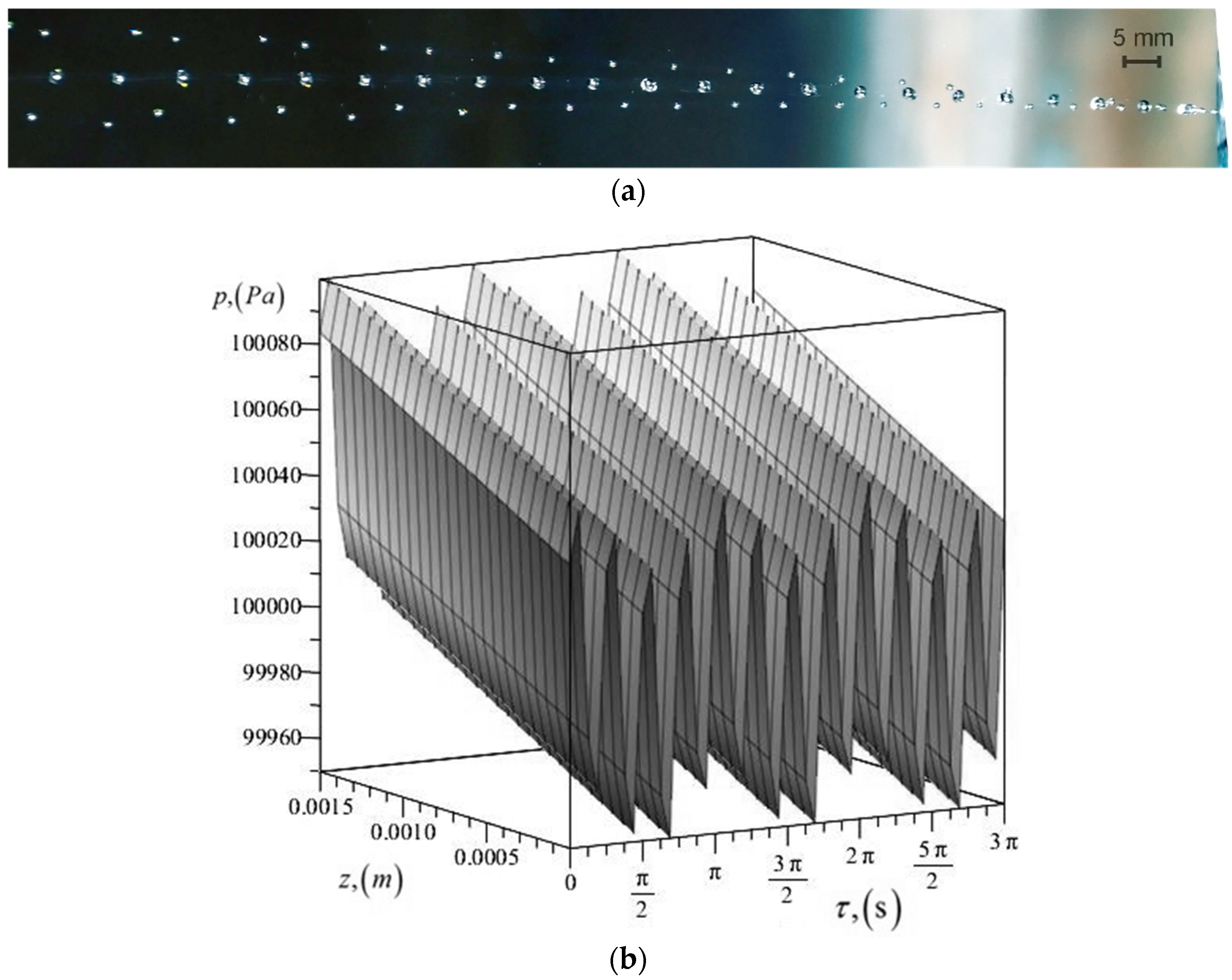
3. Mathematical Model
4. Results and Discussion
5. Industrial Test
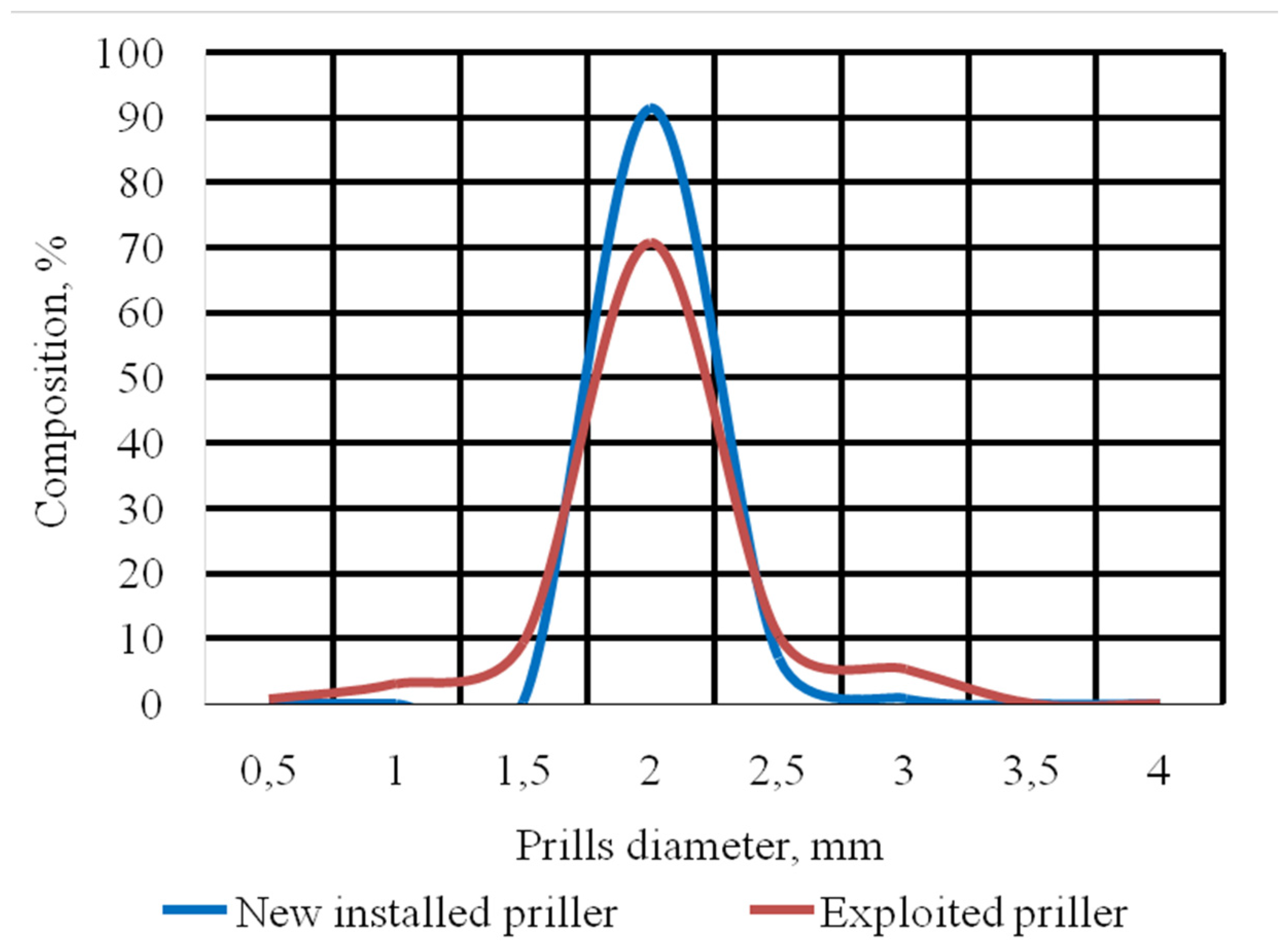
- Samples of ammonium nitrate were taken from the bottom of the tower after passing the “fluidized-bed” cooler in a steady-state condition. Size distribution of the ammonium nitrate particles was determined.
- After sampling ammonium nitrate, the operation parameters of the granulator were changed, namely, the frequency of granulator housing rotation and the forced signal frequency.
- Samples were taken at each condition at steady-state operation and the size distribution was determined for each one.
- Exhaust air samples were taken at steady-state condition for determination of ammonium nitrate dust concentration.
6. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| amplitude (m) | |
| variables, depending on the physical and chemical properties of the liquid | |
| phase shift of the system vibrations (rad) | |
| disc-oscillator diameter (m) | |
| outflowing jet diameter (m) | |
| formed drops diameter (m) | |
| hole diameter (m) | |
| disc vibration frequency (Hz) | |
| quantity of liquid (kg) | |
| distance that the disc runs in one turn (m) | |
| pressure in the jet (Pa) | |
| radial distance (m) | |
| disc speed (m/s) | |
| radial component of the velocity (m/s) | |
| axial component of the velocity (m/s) | |
| axial distance (m) | |
| Greek letters | |
| time (s) | |
| liquid density (kg/m3) | |
| kinematic fluid viscosity (m2/s) | |
| cyclic frequency (rad/s) |
References
- Food and Agriculture Organization of the United Nations. World Fertilizer Trends and Outlook to 2018; FAO: Rome, Italy, 2015. [Google Scholar]
- Bruynseels, J.P. Fluid Bed Granulation of Ammonium Nitrate and Calcium Ammonium Nitrate; Proc. of the Fertiliser Society, 1985; No. 235. [Google Scholar]
- Schoemaker, I.R.; Smit, A.C.M. Criteria for a Choice between Various Granulation and Prilling Technologies for Fertilisers, 1981; Paper read before the Fertiliser Society of London.
- Ammonium Nitrate: A Comparative Analysis of Factors Affecting Global Trade; United States International Trade Commission: Washington, DC, USA, 1998; Investigation No. 332–393.
- Laurent, B. Straight ammonium nitrate fertiliser granule-prillstabilisation: Theoretical possibilities. In Proceedings of the International Fertiliser Association Technical Conference, Chennai, India, 24–27 September 2002. [Google Scholar]
- Gezerman, A.O.; Corbacioglu, B.D. A New Approach to Cooling and Prilling during Fertilizer Manufacture. Int. J. Chem. 2011, 3, 158–168. [Google Scholar] [CrossRef]
- Mehrez, A.; Ali, A.H.H.; Zahra, W.K.; Ookawara, S.; Suzuki, M. Study on Heat and Mass Transfer During Urea Prilling Process. Int. J. Chem. Eng. Appl. 2012, 3, 347–353. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, C.; Zhou, Y. An Innovated Tower-fluidized Bed Prilling Process. Chin. J. Chem. Eng. 2007, 15, 424–428. [Google Scholar] [CrossRef]
- Rahmanian, N.; Homayoonfard, M.; Alamdari, A. Simulation of urea prilling process: An industrial case study. Chem. Eng. Commun. 2013, 200, 1–19. [Google Scholar] [CrossRef]
- Muhammad, A.; Pendyala, R.; Rahmanian, N. CFD Simulation of Droplet Formation Under Various Parameters in Prilling Process. Appl. Mech. Mater. 2014, 625, 394–397. [Google Scholar] [CrossRef]
- Kjaergaard, O.G. Multiple-core encapsulation: Prilling. In Microencapsulation of Food Ingredients; Vilstrup, P., Ed.; Leatherhead Publishing: Surrey, UK, 2001; pp. 197–214. [Google Scholar]
- Kozlov, V.V.; Grek, G.R.; Litvinenko, M.A.; Litvinenko, Y.A.; Kozlov, G.V. Round jet in a transverse shear flow. Vestnik NSU Ser. Phys. 2010, 5, 9–28. (In Russian) [Google Scholar]
- Renardy, Y.; Renardy, M.; Assighaou, S.; Benyahia, L. Numerical simulation of drop retraction after a strain jump. Phys. Rev. E 2009, 79, 046323. [Google Scholar] [CrossRef] [PubMed]
- Chernyshev, A.K.; Levin, B.V.; Tugolukov, A.V. Ammonium Nitrate: Properties, Manufacturing, Usage; Moscow, “INFOCHIM”, Russia, 2009. (In Russian) [Google Scholar]
- Gezerman, A.O. A practical solution to abate emission of ammonium nitrate and ammonia during prilling and granulation processes. Int. J. Mod. Chem. 2012, 2, 57–63. [Google Scholar]
- Muhammad, A.; Pendyala, R.; Rahmanian, N. Analysis of flow of urea in a perforated rotating bucket: Single orifice case. J. Appl. Sci. 2014, 14, 1252–1258. [Google Scholar]
- Hashemi, N.; Nourai, F. Study on pollution prevention through an integrated process-environmental mode in a urea prilling tower. Environ. Model. Assess. 2006, 11, 243–250. [Google Scholar] [CrossRef]
- Saleh, S.N.; Barghi, S. Reduction of fine particle emission from prilling tower using CFD simulation. Chem. Eng. Res. Des. 2016, 109, 171–179. [Google Scholar] [CrossRef]
- Daborh, E.K. Production of mondisperse sprays. Rev. Sci. Instrum. 1967, 38, 502–506. [Google Scholar] [CrossRef]
- Van Hoeve, W.; Gekle, S.; Snoeijer, J.H.; Versluis, M.; Brenner, M.P.; Lohse, D. Breakup of diminutive Rayleigh jets. Phys. Fluids 2010, 22, 122003. [Google Scholar] [CrossRef]
- Vassalo, P.; Ashgriz, N. Satellite formation and merging in liquid jet breakup. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1991, 433, 269–286. [Google Scholar] [CrossRef]
- Eggers, J.; Villermaux, E. Physics of Liquid Jet. Rep. Prog. Phys. 2008, 71, 036601. [Google Scholar] [CrossRef]
- Eggers, J. Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 1997, 69, 865–930. [Google Scholar] [CrossRef]
- Gezerman, A.O.; Corbacioglu, B.D. New approach for obtaining uniform- sized granules by prilling process. Chem. Eng. Elixir Chem. Eng. 2011, 40, 5225–5228. [Google Scholar]
- Lee, T.; Chen, J.W.; Lee, H.L.; Lin, T.Y.; Tsai, Y.C.; Cheng, S.L.; Lee, S.W.; Hu, J.C.; Chen, L.T. Stabilization and spheroidization of ammonium nitrate: Co-crystallization with crown ethers and spherical crystallization by solvent screening. Chem. Eng. J. 2013, 225, 809–817. [Google Scholar] [CrossRef]
- Hjhg Cholin, B.G. Influence of the regular perturbations form of the liquid jet surface on its disintegration into droplets. Proc. USSR Acad. Sci. 1970, 194, 305–308. (In Russian) [Google Scholar]
- Cholin, B.G.; Segal, R.B.; Haysinskiy, Y.F. Long-wave monodisperse disintegration of a liquid jet. Proc. USSR Acad. Sci. 1980, 253, 1074–1076. (In Russian) [Google Scholar]
- Cholin, B.G. Centrifugal granulators and quality of ammonium nitrate granules. Chem. Ind. 1971, 2, 53–56. (In Russian) [Google Scholar]
- Cholin, B.G. Vibratory granulator for obtaining the granulated ammonium nitrate and carbamide. Chem. Ind. 1970, 3, 40–41. (In Russian) [Google Scholar]
- Hahn, B.; Valentine, D. Essential Matlab for Engineers and Scientists; Academic Press: Butterworth-Heinemann:, Italy, 2010. [Google Scholar]
- Crowe, C.T. Multiphase Flow Handbook; Taylor & Francis Group, LLC: New York, NY, USA, 2006. [Google Scholar]
- Kochin, N.E.; Kibel, I.A.; Rose, N.V. Theoretical Hydromechanics; Fizmatgiz, 1963; p. 2. (In Russian) [Google Scholar]
- Saleh, S.N.; Ahmed, S.M.; Al-mosuli, D.; Barghi, S. Basic design methodology for a prilling tower. Can. J. Chem. Eng. 2015, 93, 1403–1409. [Google Scholar] [CrossRef]
- Muhammad, A.; Rahmanian, N.; Pendyala, R. Flow analysis of melted urea in a perforated rotating bucket. Appl. Mech. Mater. 2013, 372, 340–345. [Google Scholar] [CrossRef]
- Wong, D.C.Y.; Simmons, M.J.H.; Decent, S.P.; Pǎrǎu, E.; King, A.C. Break-up dynamics and drop size distributions created from spiralling liquid jets. Int. J. Multiph. Flow 2004, 30, 499–520. [Google Scholar] [CrossRef]



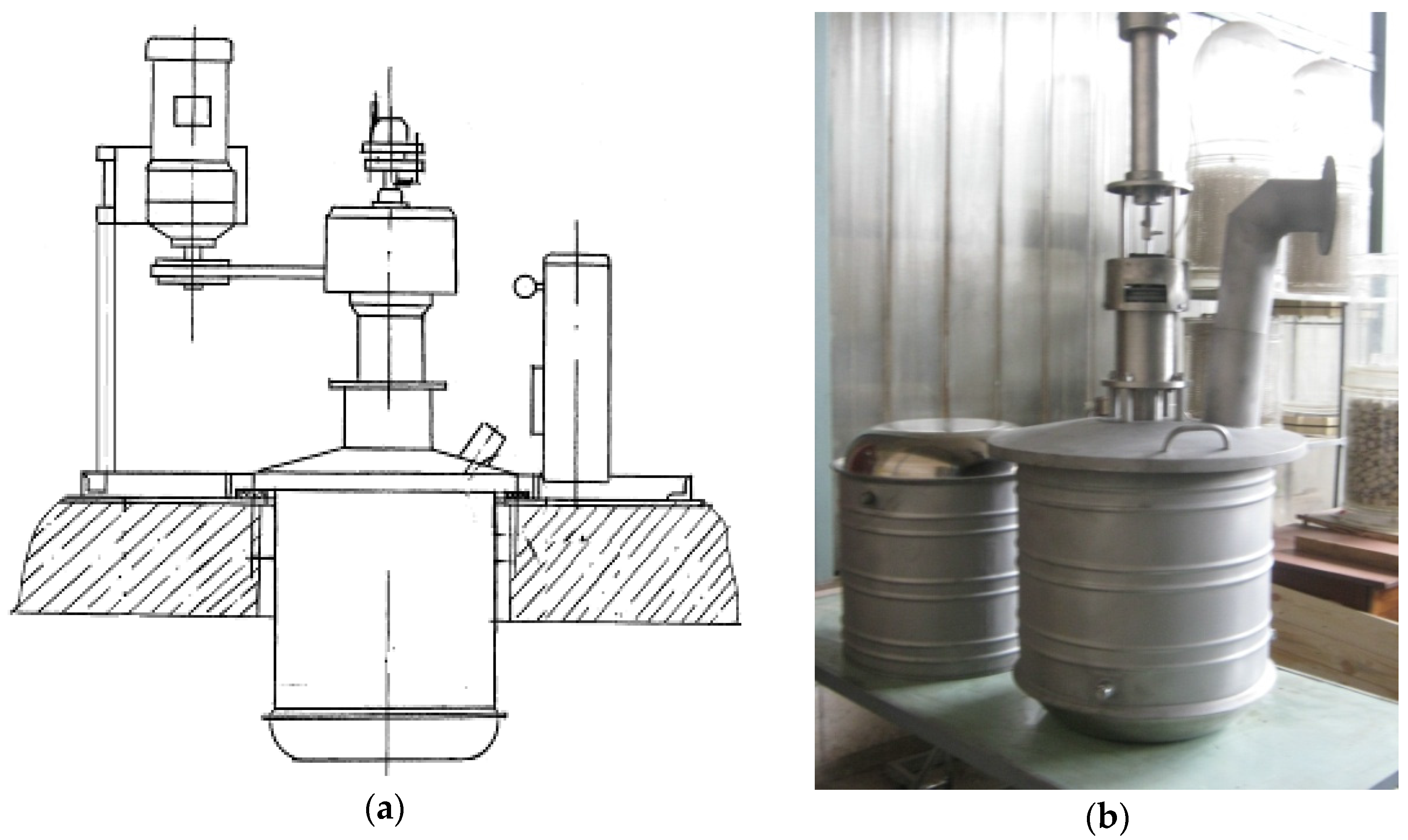

| Operating Condition and Physical Properties of Liquid Feed (Water) | Feed inlet temperature, °C | 20 |
| Ambient Air temperature, °C | 20 | |
| Feed density, kg/m3 | 998 | |
| Feed Dynamic Viscosity, kg/(s·m) | 1.002 × 10−3 | |
| Feed surface tension, N/m | 72.75 × 10−3 | |
| Vibration Specification | Liquid level, mm | 280; 380 |
| Frequency, Hz | 220; 380; 800 | |
| Amplitude, µm | 50; 100 | |
| Hole Specification | Hole diameter, mm | 1.1 |
| Hole length, mm | 1 | |
| Hole material, steel | 321H (AISI) or 1.4878 (EN) |
| Operation Conditions: | |
| Feed inlet temperature, °C; | 180 |
| Prill temperature at the tower base cones, °C; | 110–120 |
| Max. air inlet temperature, °C; | 35 |
| Air outlet temperature, °C; | 45–50 |
| No. of exhaust fans, pcs | 4 |
| Air flow rate, m3/h; | 300,000–500,000 |
| Air velocity, m/s | 0.4–0.7 |
| There is fluidized bed at the tower base, yes | |
| Ammonium nitrate from its concentrated, wt.% | 99,5 |
| Tower dimensions: | |
| Effective tower height, m; | 30 |
| Tower diameter, m; | 16 |
| Rotor priller: | |
| Diameter of the priller, m; | 0.5 |
| Number of prillers, pcs | 1 |
| Number of holes in a priller, pcs | 2300 |
| Hole diameter, mm; | 1 |
| Hole length, mm; | 2 |
| Rotational speed of the priller, rpm; | 28–60 |
| Productivity of the priller, t/h; | 22–30 |
| There is a fusion filter before priller-yes. |
| No. | Rotational Speed of Granulator | Productivity | Frequency | Size Range of Prills, % | Static Pressure | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| rpm | kg/h | Hz | <1 mm | 1.0–2.0 mm | 2.0–2.83 mm | 2.83–3.15 mm | 3.15–4.0 mm | 4.0–6.0 mm | 2.0–4.0 mm | kPa | |
| 1 | 33 | 25,000 | 0 | 3.8 | 13.35 | 75.2 | 6.8 | 0.45 | 0.4 | 82.45 | 3.1 |
| 2 | 33 | 25,000 | 0 | 0.9 | 9.85 | 86.0 | 2.5 | 0.75 | 0 | 89.25 | 3.2 |
| 3 | 33 | 24,000 | 0 | 1.2 | 11.8 | 83.45 | 2.75 | 0.8 | 0 | 87.0 | 3.1 |
| 4 | 33 | 20,000 | 0 | 2.8 | 11.75 | 80.45 | 4.5 | 0.5 | 0 | 85.45 | 1.2 |
| 5 | 33 | 20,000 | 0 | 2.5 | 14.55 | 78.2 | 3.9 | 0.85 | 0 | 82.95 | 1.1 |
| 6 | 33 | 20,000 | 0 | 2.2 | 17.75 | 75.55 | 3.75 | 0.75 | 0 | 80.05 | 1.1 |
| 7 | 33 | 21,000 | 0 | 2.2 | 9.55 | 84.4 | 3.2 | 0.65 | 0 | 88.25 | 1.1 |
| 8 | 33 | 21,000 | 0 | 2.55 | 9.75 | 82.6 | 3.5 | 1.25 | 0.25 | 87.45 | 1.2 |
| 9 | 33 | 20,000 | 0 | 2.6 | 12.1 | 80.65 | 4.25 | 0.4 | 0 | 85.30 | 1.3 |
| 10 | 33 | 22,000 | 0 | 1.95 | 4.2 | 86.9 | 5.55 | 1.4 | 0 | 93.85 | 1.5 |
| 11 | 33 | 23,000 | 320 | 1.9 | 8.4 | 80.0 | 8.25 | 1.45 | 0 | 89.70 | 2.0 |
| 12 | 48 | 23,000 | 340 | 0.85 | 3.95 | 94.35 | 0.85 | 0 | 0 | 94.20 | 2.5 |
| 13 | 60 | 24,000 | 340 | 1.4 | 5.65 | 92.1 | 0.85 | 0 | 0 | 92.95 | 2.5 |
| 14 | 60 | 24,000 | 400 | 0.0 | 8.4 | 91.30 | 0.3 | 0.0 | 0.0 | 91.60 | 2.5 |
| 15 | 60 | 23,000 | 400 | 0.45 | 27.1 | 71.85 | 0.6 | 0 | 0 | 72.45 | 2.5 |
| 16 | 60 | 23,000 | 440 | 0.5 | 40.45 | 57.65 | 0.85 | 0.55 | 0 | 59.05 | 2.5 |
| 17 | 60 | 23,000 | 460 | 0.5 | 50.6 | 47.8 | 0.9 | 0.2 | 0 | 48.90 | 2.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skydanenko, M.; Sklabinskyi, V.; Saleh, S.; Barghi, S. Reduction of Dust Emission by Monodisperse System Technology for Ammonium Nitrate Manufacturing. Processes 2017, 5, 37. https://doi.org/10.3390/pr5030037
Skydanenko M, Sklabinskyi V, Saleh S, Barghi S. Reduction of Dust Emission by Monodisperse System Technology for Ammonium Nitrate Manufacturing. Processes. 2017; 5(3):37. https://doi.org/10.3390/pr5030037
Chicago/Turabian StyleSkydanenko, Maksym, Vsevolod Sklabinskyi, Saad Saleh, and Shahzad Barghi. 2017. "Reduction of Dust Emission by Monodisperse System Technology for Ammonium Nitrate Manufacturing" Processes 5, no. 3: 37. https://doi.org/10.3390/pr5030037
APA StyleSkydanenko, M., Sklabinskyi, V., Saleh, S., & Barghi, S. (2017). Reduction of Dust Emission by Monodisperse System Technology for Ammonium Nitrate Manufacturing. Processes, 5(3), 37. https://doi.org/10.3390/pr5030037







