Abstract
We provide a critical outlook of the evolution of Industrial Process Monitoring (IPM) since its introduction almost 100 years ago. Several evolution trends that have been structuring IPM developments over this extended period of time are briefly referred, with more focus on data-driven approaches. We also argue that, besides such trends, the research focus has also evolved. The initial period was centred on optimizing IPM detection performance. More recently, root cause analysis and diagnosis gained importance and a variety of approaches were proposed to expand IPM with this new and important monitoring dimension. We believe that, in the future, the emphasis will be to bring yet another dimension to IPM: prognosis. Some perspectives are put forward in this regard, including the strong interplay of the Process and Maintenance departments, hitherto managed as separated silos.
1. Introduction: Old and New Trends in Industrial Process Monitoring
With the emergence of Industry 4.0 and the Big Data movement gaining momentum, industry is now presented with unique opportunities in terms of key enablers for boosting its performance to a new level. Performance is here taken in the widest sense, from operational, economic and market-related aspects to process safety and environmental. The key enablers are [1]: (i) data; (ii) technology and (iii) analytics (Figure 1). In fact, data abounds now more than ever, and the speed at which they accumulate is accelerating: according to IBM, 1.6 zetabytes (1021 bytes) of digital data are now available, and this number is increasing [2]. This data deluge is possible because of the development of better, faster and more informative sensing technology, able to collect information from multiple sources, in order to store it in integrated databases and to make it available anywhere at any time. Technology also provides the computational resources (high performance computing, cloud services, distributed and parallel computing, etc.) required to process large amounts of data using advanced analytics platforms (the third enabler), turning them into actionable information, in useful time.
Figure 1.
The key enablers underlying the Big Data movement.
The pressure to take advantage of the key enablers in every function and at any organizational level is rapidly building up [3]. Hitherto, this has happened more visibly in large companies [4], but small and medium enterprises may—and should—also engage in this endeavour [5]. The capacity of organizations to learn and adapt is now under test, and the race for turning the three key enablers into effective sources of competitive advantage is on.
As most core functions in an industrial enterprise, Process Monitoring must inevitably follow this path and address the challenges of synergistically combining the triplet data/technology/analytics, with all knowledge and practices developed and acquired over almost 100 years, since the pioneering work of Walter A. Shewhart in the early 1920s [6]. Industrial Process Monitoring (IPM) is an activity of central importance in companies around the world, allowing them to achieve higher levels of safety, efficiency, quality, profitability and environmental management performances [7,8,9]. A retrospective analysis of the evolution of IPM since its introduction clearly demonstrates the constant struggle undertaken to adapt to new and more demanding application scenarios, characterized by harder-to-handle data structures arising from increasingly complex processes. In the next subsections, some of the easy (and not so easy) identifiable trends of the 10 decades of existence of IPM are shortly referred, including the more recent ones that may guide the evolution of IPM in the near future.
1.1. From Univariate, to Multivariate, to High-Dimensional (“Mega-Variate”)
As a response to the increasing availability of sensors and data acquisition systems collecting information from process units and streams (e.g., temperature, flow rate, pressure, pH, conductivity, etc.), the initially developed univariate approaches [6,10,11] quickly evolve to multivariate methodologies [12,13] and then to high-dimensional frameworks [14,15,16,17,18], able to cope not only with the size, but also with the highly collinear (quite often also rank-deficient) nature of typical data-rich scenarios. This is an old and well-established trend of IPM, which requires no further introduction, since it has been widely addressed and discussed in research and review articles over the last 20 years [8,9,14,15,18,19,20,21,22].
1.2. From Homogeneous Data Tables to Heterogeneous Datasets
The development of metrology and sensing technology led to new types of “variables” to be handled, such as spectra, hyperspectral images, hyphenated data, chromatograms, granulometric curves, particle size distributions, profilometric data, etc. [23,24,25,26,27]. This already motivated the development of dedicated solutions and the emergence of Profile Monitoring as a new field in IPM [24,25,28,29]. The homogeneous data sources prevailing in most of the history of IPM, which were composed mainly of process sensors and univariate quality measurements, all of them collecting scalar values at each sampling time (the so called scalar sensors), are now being upgraded with a rich variety of data structures, consisting of higher order tensors, such as spectra (1st order tensors), grey-level images (2nd order tensors), hyperspectral images (3rd order tensors), hyphenated measurements (nth order tensors, with n ≥ 2, known as tensorial sensors). This heterogeneous character of current industrial data is just the reflex of the Variety dimension of Big Data, in the scope of IPM.
1.3. From Static, to Dynamic, to Non-Stationary
The inertial characteristics of industrial phenomena associated with the high sampling rates provided by modern instrumentation lead to the appearance of autocorrelation patterns in the collected data. The traditional process monitoring methods that were designed to operate under the assumptions of independent and identical distributed random variables (i.i.d.) characteristic of static stationary processes, including all Shewhart-like control charts and its multivariate generalizations, such as the Hotelling’s T2 control chart and Multivariate Statistical Process Control based on Principal Components Analysis (PCA-MSPC), have to be upgraded to include process dynamics [30]. Several types of solutions were proposed to handle the presence of autocorrelation in continuous production systems, namely: (i) adjusting the control limits of the monitoring charts—a solution essentially restricted to univariate processes with very simple dynamics (such as univariate first order autoregressive processes) [31,32,33]; (ii) monitoring the one-step-ahead prediction residuals using a dynamic model structure estimated from normal operation data, such as; time-series [30,34], state-space (e.g., through Canonical Variate Analysis) [35,36,37,38] or dynamic latent variable models [39,40,41]; (iii) implement a variable transformation that diagonalizes the autocorrelation matrix, as happens in multiscale statistical process control; this approach also allows one to handle the presence of multiscale dynamics and complex disturbances [42,43,44,45].
More recently, the need to address non-stationary dynamics has grown in importance, as batch processes are now claiming the attention they deserve given their ubiquitous presence in industrial systems (from semiconductors, to chemicals, pharmaceutical, food, etc.). These processes are intrinsically non-stationary and may present several stages, characteristics that raise important challenges for their monitoring. Solutions developed for this important class of processes include two-way [46,47] and three-way multivariate approaches [48,49,50], dynamic methods [51,52,53] and feature-oriented approaches [54,55].
1.4. From Monitoring the Mean, to Dispersion, to Correlation
The univariate approaches for process monitoring pay close attention to changes in the mean and dispersion of the quantitative process variables under monitoring. However, when moving to multivariate and high-dimensional applications, the focus becomes increasingly centred on the analysis of the processes mean levels. Examples include the Hotelling’s T2 control chart as well as the latent variable approaches for high-dimensional monitoring. In fact, even though PCA-MSPC is often considered to be capable of detecting changes in the variables correlation structure, namely through the Q or SPE (squared prediction error) statistic, and a closer look reveals that such sensitivity can be indeed quite low [56,57,58], and the main strength of this approach is really on monitoring the process levels. On the other hand, a common property of modern industrial processes is the existence of control loops and advanced supervision platforms distributed across all units and organized in several regulation layers through cascading schemes. Such regulating machinery continuously strives to push the target variables to their set points, compensating for the existence of uncontrollable variation sources in some of the input variables (known as load variables in the control community). When a fault occurs, control loops strive to maintain the variable levels at their targets, masking the existence of process upsets. Therefore, in practice, variable levels are not so strongly affected by the existence of process faults, due to the effective action of control loops. However, the correlation between variables does change significantly, as the interplay between process measurements is perturbed by the occurrence of the fault. In these conditions, there are good reasons to expect and believe that monitoring the process correlation structure and, in particular, the fine-grained correlation structure (partial correlations), will bring added sensitivity to the detection of process upsets and also to improve the diagnosis capability of monitoring methods. This line of research was followed by Rato and Reis [57,59]; see also Huwang, et al. [60], Sullivan, et al. [61] and references therein.
1.5. From Unstructured to Structured Process Monitoring
Underlying any process monitoring activity is a model of the normal operating conditions (NOC). Classical NOC models include the Gaussian, Binomial, Poisson, Latent Variable, depending on the object of supervision. Non-parametric approaches are also employed to cope with less conventional NOC regions [62,63,64,65]. Parameters from these approaches are estimated using NOC data, from which control limits are established. However, process data is not the only source of information regarding the system under monitoring. Background knowledge about the process, the existence of accurate mechanistic models built from first principles for some of the process units, process flowsheets, etc., constitute additional sources of available information with which any process operating under NOC must comply. In other words, they represent constraints for the process operating under normal conditions. By including such constraints in the monitoring procedure, one is incorporating more of the systems’ reality in the NOC description. This may have two interesting consequences: (i) as a more complete description of the NOC behaviour is available, it should be possible to detect finer deviations from it, i.e., to increase the monitoring sensitivity; (ii) the use of such additional information will also increase the effectiveness of process diagnosis and troubleshooting activities, beyond what is possible to achieve with the mere use of NOC data. The latter consequence deserves a more detailed inspection. A closer analysis of the nature of NOC data reveals that it is non-causal (or acausal). In fact, data collected and used for process monitoring only reflects normal operation conditions—using Fisher’s terminology, it consists of “happenstance” data and is therefore non-causal in nature. Models built from this data, such as Principal Component Analysis (PCA) or Partial Least Squares (PLS) for high-dimensional processes, will therefore be restricted to the description of non-causal relationships. They do not contain the key ingredient for full diagnosis and fault isolability: causality. This is why, when “inquired” about which variables are mostly contributing to a given change in the monitoring statistics (the purpose of contribution plot analysis), these methods are bound to put forward the set of variables that are correlated with the fault origin without distinguishing which variables are the cause of the fault and which variables are the result, leading to the well-known smearing-out effect; see more in references [8,66,67,68,69,70]. This is a limiting feature of traditional “unstructured” approaches that can be circumvented by incorporating more causal-oriented structure or a priori process knowledge in IPM methodologies.
1.6. Summary of the Article Content and Contributions
The trends presented in the previous sections underline the increasingly complex contexts regarding collected data and the underlying generating mechanisms (processes) that IPM has been facing throughout its history. Traditional monitoring methodologies are no longer able to cope with most of the current application scenarios, and several challenges remain to be addressed, such as: dealing with the increasing volume of data, incorporating multiscale and non-stationary dynamics, fusing heterogeneous data structures, integrating process knowledge with data, monitoring the correlation structure, etc. This is the current context of IPM that makes it one of the most interesting fields in industrial operations, given the number and the relevancy of the challenges, for which suitable solutions need to be found in the short term.
However, a strategic change is also happening in terms of research focus in IPM. The earlier times where characterized for a high, almost entire, dedication to reduce the time between the occurrence of a fault and its detection. For many years, this was the dominating concern of process monitoring, and many methods are still proposed to improve the detection performance, especially its speed. Currently, either because this problem is well covered for a large number of situations, or because of a growing awareness for the effectiveness of the whole IPM cycle instead of just its first stage, this situation is changing. In fact, looking to the typical IPM cycle in practice, one can easily notice that the difference between a good method and the best method, in terms of their detection speed, is typically of the order of seconds, maximum minutes. However, the subsequent stage of the IPM cycle after detection, which is diagnosis, may typically take hours to days, to be successfully completed. Therefore, the process downtime is strongly dominated by the diagnosis stage, and the detection phase is usually only a minor part of it. Consequently, efforts for reducing process and equipment downtime may be more effective if applied on improving fault diagnosis rather than on reducing the detection time by the same relative amount. These facts are currently redirecting more attention to fault diagnosis, and more IPM contributions are appearing in this area.
This is the present. However, we envisage that, with the rising standards of process efficiency, safety, environment performance and economical turnover, together with the new technology resources including those enabled by Manufacture 4.0, IPM will not stop there. Furthermore, the next natural step will be, we believe, the development of predictive capabilities and tools for system failure and malfunction: fault prognosis. Of course, there will always be room for activity at all the three major stages of IPM (detection, diagnosis and prognosis). This is a necessary condition to keep up with the pace of challenges raised by the continuous evolution of industrial processes. However, the state of the art of Diagnosis and Prognosis methods is expected to experience a strong (“inflationary”) expansion in the immediate (present) and near future, respectively, which happened with Detection in the past.
2. Research Focus—The Past: Detection
As referred to in the introductory section, IPM has undergone several trends that reflect the need to adapt to increasingly complex scenarios of processes to be monitored and data to be handled. The prevailing focus in this endeavour has been to achieve the best detection performance possible, as the challenges become more demanding. This includes the mainstream of univariate and multivariate statistical process monitoring methods, which are based on the adoption of a certain probabilistic model structure that is flexible enough for describing the NOC behaviour for a wide class of industrial processes. These general purpose approaches typically do not require specific information about the process structure, other than the parameter estimates of the NOC model that are obtained from process data during Phase 1 analysis [71,72]. Examples include the celebrated Shewhart, Exponentially Weighted Moving Average (EWMA) and Cumulative Sum (CUSUM) control charts based on the univariate i.i.d. Gaussian model [6,10,11], which can be leveraged to a large class of static processes upon the use of sample means, as a consequence of the Central Limit Theorem. Also included are their multivariate extensions that consider NOC behaviours consistent with an m-dimensional i.i.d. Gaussian process, namely the Hotelling’s T2 chart [12], the Multivariate Exponentially Weighted Moving Average chart (MEWMA) [13] and Multivariate Cumulative Sum chart (MCUSUM) [73], as well as the high-dimensional methodologies based on PCA and PLS [14,15,16,17]. These last two approaches belong to the class of latent variable monitoring approaches, and have achieved high levels of success and acceptance in both academia and industry. Their model structures present elements more consistent with the nature of industrial processes operating under normal conditions. Figure 2 presents the model structures implicitly considered in multivariate and latent variable process monitoring approaches, where their acausal nature and assumed distinct inner mechanisms become clear. In particular, multivariate methods tacitly consider the variability drivers to be observable, presenting different levels of correlation. On the other hand, latent variable frameworks assume that the observed variability in the collected measurements is driven by a few underlying and unobservable quantities, which are responsible for their variation (raw materials, environmental conditions, machines, operators, etc.). The last description resonates well with what happens in industrial units operating under NOC scenarios, which motivates the adoption of latent variable tools to handle problems in these settings.
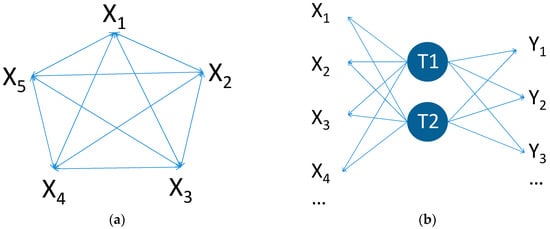
Figure 2.
Graphical illustration of the model structures underlying: (a) classical multivariate approaches and (b) latent variable approaches.
Many other statistical process monitoring methodologies for variables [71,74] and attributes [75,76] belong to this category, as well as other more advanced techniques developed to handle the dynamic [30,34,35,36,37,39,40,41,53,77], multiscale [42,43,44,78], non-Gaussian [79,80,81,82] and nonlinear [81,82,83,84] nature of industrial processes, but it is beyond the scope of this paper to provide an exhaustive presentation of them all (see also [8,9,85]).
All of the methods referred to above were developed to accommodate the increasing complexity of processes and data, and their performance was essentially characterized in terms of detection metrics, which confirms the focus of IPM in the past. The major detection performance dimensions are: detection speed and detection strength.
Detection speed regards the promptness or celerity in signaling an abnormality after it occurs. It is usually assessed through the number of observations it takes to, on average, signal an abnormal event of a given type and with a given magnitude. The figures of merit typically used for characterizing detection speed, are the Average Run Length (ARL) or the related quantity Average Time to Signal (ATS) [43,57,71,86,87,88]. More recently, other measures have also been proposed, such as the Conditional Expected Delay (CED), which represents the average detection delay under the condition that no false alarms have been issued until the moment where the fault occurs [88,89].
Detection strength is related with the ability to correctly detect abnormal situations without incurring in excessive false alarms [90]. The figure of merit commonly adopted is the True Positive Rate, TPR, also referred as True Detection Rate, TDR [43,56,91]. The missed detection rate (a.k.a, overall type II error) is also used sometimes (MDR = 1 − TPR), especially when the aim is to highlight the missed faults [92]. TPR is also known as the method’s sensitivity. Its computation depends on the significance level used to establish the monitoring control limits. The significance level corresponds to the False Positive Rate (FPR, a.k.a., False Alarm Rate, FAR or overall type I error). Therefore, when computing TPR, the FPR must be fixed and clearly specified. Moreover, a comparison of methods based on their TPR is valid only if their (observed) FPR are controlled to be identical.
Achieving good levels of detection speed and strength has been the main focus of IPM research in the past. This is a necessary step when handling new processes, but there is an increasing pressure not to stop the development of advanced monitoring at this stage, and to move on to the often more challenging activity of finding out what the root cause for the abnormality is: process diagnosis.
3. Research Focus—The Present: Diagnosis
The NOC models used in the IPM approaches referred in the previous section contain interesting features for fault detection, namely robustness, good power (sensitivity) and simplicity. However, when addressing the next stage of IPM, Diagnosis, some of their limitations emerge.
One of the limitations is a direct consequence of their intrinsic acausal (or non-causal) nature. The acausal characteristics of the NOC models for the IPM approaches presented in Section 2 do not constitute a major problem when the goal is fault detection: it is usually sufficient to assess whether new observations fall inside the NOC envelope. This envelope contains the NOC variability, and can be derived just attending to the average variables’ levels and main associations among them. However, diagnosis requires more information in order to be properly executed. This activity demands knowledge about the causal directionality of the propagation of effects in the system. Only with this information available is it possible to back-track and figure out which variables may be connected with the origin of the observed abnormal effect. Such causal structure is absent from methods focused on detection, and may lead to ambiguous diagnosis when they are used for that purpose: the smearing-out effect in contribution plots in the scope of PCA-MSPC is a direct consequence of the acausal nature of PCA; see [8,66,67]).
To circumvent this limitation of classical detection-oriented approaches, several methodologies have been developed recently, incorporating more about the process’ causal connectivity in IPM, not only to improve detection but mainly to address fault diagnosis. These “structured” approaches (named this way because they incorporate process-specific structure in their formulations) can be classified as either knowledge-based or data-driven according to the origin of the information on causality.
Knowledge-based structured approaches exploit pre-existing knowledge or information about the causal connectivity of the processes. This a priori knowledge can be translated into qualitative or semi-quantitative NOC models, which bring process-specific causal information to IPM, based on which diagnosis and troubleshooting can be conducted. For instance, one piece of knowledge commonly available in virtually all industrial processes is the compendium of process flowsheets and flow diagrams of the several processing units that constitute the plant. These diagrams show all the relevant pieces of equipment, pipes connecting them, and how information flows from transducers to controllers to actuators [93]. From the analysis of such process maps, causality directions can be readily established and translated into computational code to be integrated in IPM. One approach for codifying this information is through Causal Maps [94,95,96,97]. Other qualitative and semi-quantitative descriptions for incorporating the process causal structure include bond graphs [98,99], signed digraphs (SGDs) [100,101,102,103], parity relations [104], gray-box models [105] and Bayesian Networks [98,106,107].
Data-driven structured approaches, on the other hand, extract the process-specific information for fault diagnosis directly from the immensity of historical records available in process databases. In the era of Big Data and Industry 4.0, this type of structured IPM approaches finds a particularly favourable context to expand their application scope and to grow in diversity and importance. For this reason, we will dedicate some more attention to this category of structured IPM methods, by referring, in the next two subsections, distinct perspectives for conducting process diagnosis using process-specific information, namely:
- Network inference structured approaches (NISA),
- Classification-based approaches (CBA).
3.1. Data-Driven Structured Approaches for Process Diagnosis: Network Inference Structured Approaches (NISA)
This category of data-driven structured methods only requires access to the available NOC data. For example, Bauer, et al. [108] used transfer entropy to identify the directionality of the fault’s propagation path, based on which the root cause of process upsets can be better isolated. Alternatively, time delay analysis can also be applied to the same purpose [109]. On the other hand, Yuan and Qin [110] combined Granger causality with PCA to perform feature selection for faults with oscillatory characteristics and identified the modules that, with high probability, may contain the root cause of the fault.
Partial correlations also constitute a viable solution to extract the network of direct relationships linking the observed variables [111,112,113]. Therefore, they present the potential to be incorporated in effective data-driven structured IPM approaches. In this context, Rato and Reis developed the class of Sensitivity Enhancing Transformations (SET), a solution based on the use of partial correlations that was already successfully applied to process monitoring. Applications include static, dynamic [114] and multiscale processes [115], both offline and online, and for detection [57] as well as for diagnosis [59]. In brief terms, this approach pre-processes the set of monitored variables using a decorrelating transformation that is established taking into account the causal associations between the observed variables. These causal associations stem from a network inference algorithm, which is based on the use of partial correlations and time-series analysis. The transformation essentially consists of building a predictive regression model for each variable as a function of its causal parents, which is then used to compute the variable residuals. Any remaining associations are further removed with resorting to an additional Cholesky transformation. The decorrelated variables can then be monitored using conventional monitoring statistics, such as the Hotelling’s T2 [116].
3.2. Data-Driven Structured Approaches for Process Diagnosis: Classification-Based Approaches (CBA)
Classification-based approaches (CBA) are more demanding in terms of requirements imposed to the data resources: they assume the existence of a labelled dataset of process faults, rather than just access to NOC data, as happens with NISA methods. Therefore, NISA and CBA represent two distinct ways of performing data-driven fault diagnosis: NISA inferring causality from NOC data; CBA using data from previous faults to assist the diagnosis of future upsets. In this context, an obvious limitation of CBA methods is the availability of such labelled dataset of abnormal occurrences. However, with the increasing accumulation of data, situations where this requirement is met tend to increase, turning it into a viable alternative for processes that are in operation for some time. Furthermore, classification approaches can be adapted to recognize previously unseen process upsets. In this case, fault identification can be delegated to process experts. Once a sufficient amount of examples of a new upset have been collected, the CBA model can be expanded or retrained to recognize the new type of process disturbances.
The main motivation for developing this class of methodologies is also rooted in the limitations found in popular tools for conducting fault diagnosis in multivariate scenarios. For instance, the use of contribution plots [47,67,117] is a common way to conduct fault identification in a PCA-based process monitoring approach. They indicate which variables exhibit different behavior from normal operation without requiring any prior information [8]. The final stage of linking signalled variables to an underlying root cause is left to the process expert [8]. However, this is a complicated task, especially for complex processes [118], and, in addition, fault smearing is inherently present in all types of contributions [66] and can lead to incorrect diagnosis [8,67]. In this context, if a historical database of known process faults is available, fault identification can be translated into a classification problem and several machine learning methodologies can be used to facilitate root cause analysis [119]. The idea is simple: a classification model is trained to distinguish between all possible fault types based on each fault’s fingerprint pattern of faulty sensors and actuators; then, during monitoring, the classifier assesses each detected abnormality against this reference library and assigns it to the class it most closely resembles.
In basic process monitoring, fault detection and identification are conducted sequentially: process disturbances are first detected, after which their root cause is identified. This approach is typically followed by researchers stemming from classical statistical process monitoring. However, fault classification models enable the simultaneous detection and identification of process upsets, simply by including “normal operation” as an extra class in the classifier. This approach is more common in research teams with machine learning backgrounds, being adopted, for example, by Yu [120], Lazzaretti et al. [121], and Jing and Hou [122].
However, this apparently simpler methodology also raises some practical issues that need to be addressed. A first issue faced by simultaneous fault detection and identification is that a large data imbalance typically exists between the normal operation class and one or more fault classes, as faulty examples are difficult to obtain [123,124,125]. This presents a significant challenge for most multi-class classifier types [126,127,128,129]. One-class classifiers, which characterize each data class with a separate model, are more tolerant towards class imbalance because they only consider one class at a time, but density-based methods (Gaussian Mixture Models, Parzen models, etc.) still need a sufficient amount of samples to correctly estimate the sample density [130] and to construct meaningful boundaries for each class.
A second issue is that classifiers assign equal weights to each misclassification. In applications where fault diagnosis systems support operator actions and are not (yet) used to directly control the process (e.g., in the chemical or pharmaceutical industry), correct fault detection might be much more important than correct classification. Classifiers for simultaneous detection and identification require class-specific parameters (e.g., different misclassification costs per fault class) to deal with these asymmetric performance requirements [131]. As more parameters are introduced, identification of the fault classification model becomes more complex, and the simplicity in the mathematical formulation of simultaneous fault detection and identification is lost. A solution for this problem was provided by Gins et al. [132]. In contrast, the sequential approach inherently allows for a different emphasis between fault detection and fault identification.
We argue that the sequential fault detection and identification methodology exhibits significant advantages over a simultaneous approach in many situations. However, the exact difference in performance between simultaneous and sequential fault detection and identification has never been thoroughly quantified in an extensive series of benchmarks.
Another class of fault diagnosis approaches based on a classification framework is the one based on variable selection methodologies. The underlying principle is that, when a fault occurs, not all variables change simultaneously. Only a subset of the process variables experiment a significant change. Therefore, by isolating this set of variables, it is possible to reduce the search space of possible faults and speed up the troubleshooting process. The selection of variables is done by implementing a classification methodology before and after the fault is detected and analysing the most discriminating variables for separating these two classes. More information about this class of methodologies can be found in the works of Wang and Jiang [133] and Zou et al. [134].
4. Research Focus—The Future: Prognosis
Once the solutions and methodologies for detection and diagnosis become stabilized and accessible to process owners, the next logical stage in the evolution of IPM (the future) will be, from our perspective, the integration of a predictive dimension: fault prognosis. Knowledge about the evolution of operational risk along time is a highly valuable and strategic asset, as it would allow for a better planning of maintenance and shutdown operations, minimizing production losses, while securing the safety of people and equipment. Economic benefits would simultaneously arise from a better management of process targets and operational risk, but how could it be accomplished in practice? Some opportunities lie ahead that can make this endeavour a reality. Below, we share some ideas on possible routes for addressing this challenge.
With the emergence of Industry 4.0 and Big Data, structured and unstructured data will become increasingly available from all points of the process. Process and product quality databases have been integrated in the past to develop predictive approaches for process monitoring, control and optimization. Soft sensors and inferential models are examples of tools used in this context [135,136,137,138,139,140]. However, quite strangely, there is one database that has been largely overlooked and ignored by most process-oriented developers: the maintenance department database. This resource accumulates faults from all equipment in the plant, and a reasonable conjecture in this context would be that the equipment failure behaviour can be related to the conditions they were subjected to during service. Therefore, by crossing process and maintenance databases, critical information will be obtained about the effect of operation conditions on systems reliability, which can finally bring insights for process improvement and a predictive dimension to operational risk management.
Prognosis may look like a contradiction when analysed under the frame of Shewhart’s “common cause”/“special cause” systematization of variation, where special causes are unpredictable by nature. Shewhart’s perspective, as well as that of the mainstream Statistical Process Control (SPC)/Industrial Process Monitoring (IPM) community, is focused on “Process Health” (as expected—note the presence of the term “Process” in both designations). However, prognosis is closely related to “Equipment Health”—the evolution of the equipment performance over time—based on which inferences that can be made regarding operational effectiveness and failure rate. Thus, prognosis will benefit from an approximation of IPM and disciplines like Reliability and Maintenance (R&M), an interaction that we believe still has much to offer in the forthcoming times.
The aforementioned integration of IPM/R&M will be beneficial not only from the process monitoring perspective, but also (and very importantly) from the standpoint of creating the conditions to make a global optimization of process units, taking into account process-oriented targets (production throughput, selectivity, product quality) and reliability metrics (service time, down-time, time between failures, failure rate). Both have a decisive impact in the global performance of the company, and cannot (should not!) be handled as separates silos (as done in the past), with non-overlapping and independent analysis workflows.
5. Discussion and Final Remarks
In this article, we have made a critical overview of several trends that have been structuring the evolution of IPM since its appearance as an industrial activity almost 100 years ago, as well as the changing research focus in this extended period, from detection, passing by diagnosis, towards prognosis. Section 2 pointed out the strong focus of early works on statistical process monitoring towards the early detection of process upsets (the past). Metrics like the Average Run Length (ARL) and Average Time to Signal (ATS) were the preferred performance criteria, despite their limitations [86,88].
However, the ultimate goal of monitoring is to secure a safe operation for people and assets and to minimize the total downtime of the process, of which the detection time is usually only a small fraction. More significant in this regard is the time spent in diagnosing and troubleshooting activities, until the root cause of the problem is isolated and criticality assessed, based on which a decision is made regarding the continuation of the operation or its immediate shutdown. In this context, several tools and procedures have been proposed to facilitate and narrow down the quest for the underlying root cause. This was the scope of Section 3 (the present), where methodologies, such as the T2 decomposition proposed by Mason et al. [141], in the context of multivariate statistical process monitoring and the contribution plot approach in the context of high-dimensional process monitoring using Principal Components Analysis (PCA) and Partial Least Squares (PLS) models [15,67], are well-known examples of the importance given to fault diagnosis. The former approach is limited by the scope of application of the Hotelling’s T2 methodology, usually restricted to less than 10–15 process variables and involving an undesirably combinatorial complexity that scales unfavourably with the number of variables under monitoring. The latter approach, on the other hand, is indeed quite fast and simple, and often brings up useful information about the problem. However, it also presents some undesirable features, such as the “smearing-out effect”, i.e., a fault in one variable will have an impact on the contributions reported for all the variables correlated with it, reducing the effectiveness of the diagnosis process [66]. These limitations can be properly addressed by IPM methodologies that are able to incorporate more of the process-specific causality structure in their formulations, as described in Section 1.5.
Section 4 addresses what we believe will be the next wave of interest in IPM: Prognosis. With it, IPM will acquire a predictive capability that allows for a better management of processes and their critical assets. Several non-stationary phenomena that previously were just assumed to exist but not handled will be explicitly modelled and integrated in IPM procedures. This includes equipment wearing, fouling, deactivation, corrosion, ageing, etc. Approaches can either be data-driven, model-based, or both (grey/hybrid models). Process and Reliability and Maintenance will necessarily increasingly interact, with mutual benefits for each individual operation, but, most importantly, for the good of the overall system, the entire plant.
This article reflects our personal views, grounded on our experience in this field and on a careful analysis of the rich and diverse technical literature published over the years. We believe the proper integration of the three dimensions of IPM—detection, diagnosis and prognosis—shall make this activity even more effective and important for the companies’ operations in the future.
Acknowledgements
Marco S. Reis acknowledges financial support through project 016658 (references PTDC/QEQ-EPS/1323/2014, POCI-01-0145-FEDER-016658) financed by Project 3599-PPCDT (Promover a Produção Científica e Desenvolvimento Tecnológico e a Constituição de Redes Temáticas) and co-financed by the European Union’s FEDER.
Author Contributions
Marco Reis drafted the document with exception of Section 3.2. Geert Gins drafted Section 3.2 and contributed with improvements in the remaining sections. Marco Reis and Geert Gins revised and edited the entire document during all the revision stages.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reis, M.S.; Braatz, R.D.; Chiang, L.H. Big data-challenges and future research directions. Chem. Eng. Prog. 2016, 46–50. [Google Scholar] [CrossRef]
- Ebbers, M. 5 Things to Know about Big Data in Motion. Available online: https://www.ibm.com/developerworks/community/blogs/5things/entry/5_things_to_know_about_big_data_in_motion?lang=en (accessed on 1 May 2017).
- White, D. Big data-what is it? Chem. Eng. Prog. 2016, 32–35. Available online: https://www.aiche.org/resources/publications/cep/2016/march/big-data-what-it (accessed on 30 June 2017).
- Colegrove, L.F.; Seasholtz, M.B.; Khare, C. Big data-getting started on the journey. Chem. Eng. Prog. 2016, 41–45. Available online: https://www.aiche.org/resources/publications/cep/2016/march/big-data-getting-started-on-journey (accessed on 30 June 2017).
- Manco, G.; Coleman, S.; Goeb, R.; Pievatolo, A.; Tort-Martorell, X.; Reis, M.S. How can smes benefit from big data? Challenges and a path forward. Qual. Reliab. Eng. Int. 2016, 32, 2151–2164. [Google Scholar]
- Shewhart, W.A. Economic Control of Quality of Manufactured Product; D. Van Nostrand Company, Inc.: New York, NY, USA, 1931. [Google Scholar]
- Weese, M.; Martinez, W.; Megahed, F.M.; Jones-Farmer, L.A. Statistical learning methods applied to process monitoring: An overview and perspective. J. Qual. Technol. 2016, 48, 4–27. [Google Scholar]
- Qin, S.J. Survey on data-driven industrial process monitoring and diagnosis. Annu. Rev. Control 2012, 36, 220–234. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Gao, F. Review of recent research on data-based process monitoring. Ind. Eng. Chem. Res. 2013, 52, 3543–3562. [Google Scholar] [CrossRef]
- Page, E.S. Continuous inspection schemes. Biometrics 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Roberts, S.W. Control charts tests based on geometric moving averages. Technometrics 1959, 1, 239–250. [Google Scholar] [CrossRef]
- Hotelling, H. Multivariate quality control, illustrated by the air testing of sample bombsights. In Selected Techniques of Statistical Analysis; Eisenhart, C., Hastay, M.W., Wallis, W.A., Eds.; McGraw-Hill: New York, NY, USA, 1947. [Google Scholar]
- Lowry, C.A.; Woodall, W.H.; Champ, C.W.; Rigdon, C.E. A multivariate exponentially weighted moving average control chart. Technometrics 1992, 34, 46–53. [Google Scholar] [CrossRef]
- Kresta, J.V.; MacGregor, J.F.; Marlin, T.E. Multivariate statistical monitoring of process operating performance. Can. J. Chem. Eng. 1991, 69, 35–47. [Google Scholar] [CrossRef]
- Kourti, T.; MacGregor, J.F. Process analysis, monitoring and diagnosis, using multivariate projection methods. Chemom. Intell. Lab. Syst. 1995, 28, 3–21. [Google Scholar] [CrossRef]
- Jackson, J.E. Quality control methods for several related variables. Technometrics 1959, 1, 359–377. [Google Scholar] [CrossRef]
- Jackson, J.E.; Mudholkar, G.S. Control procedures for residuals associated with principal component analysis. Technometrics 1979, 21, 341–349. [Google Scholar] [CrossRef]
- Kourti, T.; MacGregor, J.F. Multivariate SPC methods for process and product monitoring. J. Qual. Technol. 1996, 28, 409–428. [Google Scholar]
- Kourti, T. Application of latent variable methods to process control and multivariate statistical process control in industry. Int. J. Adapt. Control Signal Process. 2005, 19, 213–246. [Google Scholar] [CrossRef]
- MacGregor, J.F.; Jaeckle, C.; Kiparissides, C.; Koutoudi, M. Process monitoring and diagnosis by multiblock PLS methods. AIChE J. 1994, 40. [Google Scholar] [CrossRef]
- MacGregor, J.F.; Kourti, T. Statistical process control of multivariate processes. Control Eng. Pract. 1995, 3, 403–414. [Google Scholar] [CrossRef]
- Chen, Z.; Lovett, D.; Morris, J. Process analytical technologies and real time process control a review of some spectroscopic issues and challenges. J. Process Control 2011, 21, 1467–1482. [Google Scholar] [CrossRef]
- Reis, M.S.; Saraiva, P.M. Prediction of profiles in the process industries. Ind. Eng. Chem. Res. 2012, 51, 4254–4266. [Google Scholar] [CrossRef]
- Reis, M.S.; Saraiva, P.M. Multiscale statistical process control of paper surface profiles. Qual. Technol. Quant. Manag. 2006, 3, 263–282. [Google Scholar] [CrossRef]
- Woodall, W.H.; Spitzner, D.J.; Montgomery, D.C.; Gupta, S. Using control charts to monitor process and product quality profiles. J. Qual. Technol. 2004, 36, 309–320. [Google Scholar]
- Duchesne, C.; Liu, J.J.; MacGregor, J.F. Multivariate image analysis in the process industries: A review. Chemom. Intell. Lab. Syst. 2012, 117, 116–128. [Google Scholar] [CrossRef]
- Prats-Montalbán, J.M.; de Juan, A.; Ferrer, A. Multivariate image analysis: A review with applications. Chemom. Intell. Lab. Syst. 2011, 107, 1–23. [Google Scholar]
- Kim, K.; Mahmoud, M.A.; Woodall, W.H. On the monitoring of linear profiles. J. Qual. Technol. 2003, 35, 317–328. [Google Scholar]
- Reis, M.S.; Bauer, A. Wavelet texture analysis of on-line acquired images for paper formation assessment and monitoring. Chemom. Intell. Lab. Syst. 2009, 95, 129–137. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Mastrangelo, C.M. Some statistical process control methods for autocorrelated data. J. Qual. Technol. 1991, 23, 179–193. [Google Scholar]
- Vasilopoulos, A.V.; Stamboulis, A.P. Modification of control chart limits in the presence of data correlation. J. Qual. Technol. 1978, 10, 20–30. [Google Scholar]
- Lu, C.-W.; Reynolds, M.R., Jr. Cusum charts for monitoring an autocorrelated process. J. Qual. Technol. 2001, 33, 316–334. [Google Scholar]
- Vermaat, M.B.; Does, R.J.M.M.; Bisgaard, S. EWMA control chart limits for first- and second-order autoregressive processes. Qual. Reliab. Eng. Int. 2008, 24, 573–584. [Google Scholar] [CrossRef]
- Harris, T.J.; Ross, W.H. Statistical process control procedures for correlated observations. Can. J. Chem. Eng. 1991, 69, 48–57. [Google Scholar] [CrossRef]
- Negiz, A.; Çinar, A. Statistical monitoring of multivariable dynamic processes with state-space models. AIChE J. 1997, 43, 2002–2020. [Google Scholar] [CrossRef]
- Simoglou, A.; Martin, E.B.; Morris, A.J. Dynamic multivariable statistical process control using partial least squares and canonical variate analysis. Comput. Chem. Eng. 1999, 23, S277–S280. [Google Scholar] [CrossRef]
- Treasure, R.J.; Kruger, U.; Cooper, J.E. Dynamic multivariate statistical process control using subspace identification. J. Process Control 2004, 14, 279–292. [Google Scholar] [CrossRef]
- Russell, E.L.; Chiang, L.H.; Braatz, R.D. Fault detection in industrial processes using canonical variate analysis and dynamic principal component analysis. Chemom. Intell. Lab. Syst. 2000, 51, 81–93. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. Fault detection in the Tennessee Eastman process using dynamic principal components analysis with decorrelated residuals (DPCA-dr). Chemom. Intell. Lab. Syst. 2013, 125, 101–108. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. Advantage of using decorrelated residuals in dynamic principal component analysis for monitoring large-scale systems. Ind. Eng. Chem. Res. 2013, 52, 13685–13698. [Google Scholar] [CrossRef]
- Ku, W.; Storer, R.H.; Georgakis, C. Disturbance detection and isolation by dynamic principal component analysis. Chemom. Intell. Lab. Syst. 1995, 30, 179–196. [Google Scholar] [CrossRef]
- Bakshi, B.R. Multiscale PCA with application to multivariate statistical process control. AIChE J. 1998, 44, 1596–1610. [Google Scholar] [CrossRef]
- Reis, M.S.; Bakshi, B.R.; Saraiva, P.M. Multiscale statistical process control using wavelet packets. AIChE J. 2008, 54, 2366–2378. [Google Scholar] [CrossRef]
- Reis, M.S.; Saraiva, P.M. Multiscale statistical process control with multiresolution data. AIChE J. 2006, 52, 2107–2119. [Google Scholar] [CrossRef]
- Morris, J. Multiscale multivariate statistical process control. In Encyclopedia of Systems and Control; Baillieul, J., Samad, T., Eds.; Springer: London, UK, 2014; pp. 1–7. [Google Scholar]
- Nomikos, P.; MacGregor, J.F. Monitoring batch processes using multiway principal component analysis. AIChE J. 1994, 40, 1361–1375. [Google Scholar] [CrossRef]
- Nomikos, P.; MacGregor, J.F. Multivariate SPC charts for monitoring batch processes. Technometrics 1995, 37, 41–59. [Google Scholar] [CrossRef]
- Westerhuis, J.A.; Kourti, T.; MacGregor, J.F. Analysis of multiblock and hierarchical PCA and PLS models. J. Chemom. 1998, 12, 301–321. [Google Scholar] [CrossRef]
- Westerhuis, J.A.; Kourti, T.; MacGregor, J.F. Comparing alternative approaches for multivariate statistical analysis of batch process data. J. Chemom. 1999, 13, 397–413. [Google Scholar] [CrossRef]
- Meng, X.; Morris, A.J.; Martin, E.B. On-line monitoring of batch processes using a parafac representation. J. Chemom. 2003, 17, 65–81. [Google Scholar] [CrossRef]
- Van den Kerkhof, P.; Vanlaer, J.; Gins, G.; Van Impe, J.F.M. Dynamic model-based fault diagnosis for (bio)chemical batch processes. Comput. Chem. Eng. 2012, 40, 12–21. [Google Scholar] [CrossRef]
- Chen, J.; Yen, J.-H. Three-way data analysis with time lagged window for on-line batch process monitoring. Korean J. Chem. Eng. 2003, 20, 1000–1011. [Google Scholar] [CrossRef]
- Choi, S.W.; Morris, J.; Lee, I.-B. Dynamic model-based batch process monitoring. Chem. Eng. Sci. 2008, 63, 622–636. [Google Scholar] [CrossRef]
- He, Q.P.; Wang, J. Statistics pattern analysis: A new process monitoring framework and its application to semiconductor batch processes. AIChE J. 2011, 57, 107–121. [Google Scholar] [CrossRef]
- Rato, T.J.; Blue, J.; Pinaton, J.; Reis, M.S. Translation invariant multiscale energy-based PCA (TIME-PCA) for monitoring batch processes in semiconductor manufacturing. IEEE Trans. Autom. Sci. Eng. 2017, 14, 894–904. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. Non-causal data-driven monitoring of the process correlation structure: A comparison study with new methods. Comput. Chem. Eng. 2014, 71, 307–322. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. On-line process monitoring using local measures of association. Part I: Detection performance. Chemom. Intell. Lab. Syst. 2015, 142, 255–264. [Google Scholar] [CrossRef]
- Wang, J.; He, Q.P. Multivariate statistical process monitoring based on statistics pattern analysis. Ind. Eng. Chem. Res. 2010, 49, 7858–7869. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. On-line process monitoring using local measures of association. Part II: Design issues and fault diagnosis. Chemom. Intell. Lab. Syst. 2015, 142, 265–275. [Google Scholar] [CrossRef]
- Huwang, L.; Yeh, A.B.; Wu, C. Monitoring multivariate process variability for individual observations. J. Qual. Technol. 2007, 39, 258–278. [Google Scholar]
- Sullivan, J.H.; Stoumbos, Z.G.; Mason, R.L.; Young, J.C. Step-down analysis for changes in the covariance matrix and other parameters. J. Qual. Technol. 2007, 39, 66–84. [Google Scholar]
- Qiu, P. Distribition-free multivariate process control based on log-linear modeling. IIE Trans. 2008, 40, 664–677. [Google Scholar] [CrossRef]
- Zou, C.; Tsung, F. Likelihood ratio-based distribution-free EWMA control charts. J. Qual. Technol. 2010, 42, 174–196. [Google Scholar]
- Chakraborti, S.; Van der Lan, P.; Bakir, S.T. Nonparametric control charts: An overview and some results. J. Qual. Technol. 2001, 33, 304–315. [Google Scholar]
- Martin, E.B.; Morris, A.J. Non-parametric confidence bounds for process performance monitoring charts. J. Process Control 1996, 6, 349–358. [Google Scholar] [CrossRef]
- Van den Kerkhof, P.; Vanlaer, J.; Gins, G.; Van Impe, J.F.M. Analysis of smearing-out in contribution plot based fault isolation for statistical process control. Chem. Eng. Sci. 2013, 104, 285–293. [Google Scholar] [CrossRef]
- Westerhuis, J.A.; Gurden, S.P.; Smilde, A.K. Generalized contribution plots in multivariate statistical process monitoring. Chemom. Intell. Lab. Syst. 2000, 51, 95–114. [Google Scholar] [CrossRef]
- Yue, H.H.; Qin, S.J. Reconstruction-based fault identification using a combined index. Ind. Eng. Chem. Res. 2001, 40, 4403–4414. [Google Scholar] [CrossRef]
- Kuang, T.-H.; Yan, Z.; Yao, Y. Multivariate fault isolation via variable selection in discriminant analysis. J. Process Control 2015, 35, 30–40. [Google Scholar] [CrossRef]
- Yan, Z.; Yao, Y. Variable selection method for fault isolation using least absolute shrinkage and selection operator (LASSO). Chemom. Intell. Lab. Syst. 2015, 146, 136–146. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control, 4th ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Woodall, W.H.; Montgomery, D.C. Some current directions in the theory and application of statistical process monitoring. J. Qual. Technol. 2014, 46, 78–94. [Google Scholar]
- Crosier, R.B. Multivariate generalizations of cumulative sum quality-control schemes. Technometrics 1988, 30, 291–303. [Google Scholar] [CrossRef]
- Kenett, R.S.; Zacks, S. Modern Industrial Statistics: With Applications in R, Minitab and JMP, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Woodall, W.H. Control charts based o attribute data: Bibliography and review. J. Qual. Technol. 1997, 29, 172–183. [Google Scholar]
- Grant, E.L.; Leavenworth, R.S. Statistical Quality Control, 7th ed.; McGraw-Hill: Boston, MA, USA, 1999. [Google Scholar]
- Komulainen, T.; Sourander, M.; Jämsä-Jounela, S.L. An online application of dynamical PLS to a dearomatization process. Comput. Chem. Eng. 2004, 28, 2611–2619. [Google Scholar] [CrossRef]
- Alawi, A.; Morris, A.J.; Martin, E.B. ESCAPE-15, European Symposium on Computer Aided Process Engineering. In Statistical Performance Monitoring Using State Space Modelling and Wavelet Analysis; Puigjaner, L., Espuña, A., Eds.; Elsevier: Barcelona, Spain, 2005; pp. 1459–1464. [Google Scholar]
- Tian, X.M.; Zhang, X.L.; Deng, X.G.; Chen, S. Multiway kernel independent component analysis based on feature samples for batch process monitoring. Neurocomputing 2009, 72, 1584–1596. [Google Scholar] [CrossRef]
- Yoo, C.K.; Lee, J.-M.; Vanrolleghem, P.A.; Lee, I.-B. On-line monitoring of batch processes using multiway independent component analysis. Chemom. Intell. Lab. Syst. 2004, 71, 151–163. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Qin, S.J. Fault detection of non-linear processes using multiway kernel independent analysis. Ind. Eng. Chem. Res. 2007, 46, 7780–7787. [Google Scholar] [CrossRef]
- Zhao, C.H.; Gao, F.R.; Wang, F.L. Nonlinear batch process monitoring using phase-based kernel independent component analysis-principal component analysis. Ind. Eng. Chem. Res. 2009, 48, 9163–9174. [Google Scholar] [CrossRef]
- Choi, S.W.; Lee, I.-B. Nonlinear dynamic process monitoring based on dynamic kernel PCA. Chem. Eng. Sci. 2004, 59, 5897–5908. [Google Scholar] [CrossRef]
- Lee, J.-M.; Yoo, C.; Lee, I.-B. Fault detection of batch processes using multiway kernel principal component analysis. Comput. Chem. Eng. 2004, 28, 1837–1847. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Yin, R.R.K.; Kavuri, S.N. A review of process fault detection and diagnosis. Part I–III. Comput. Chem. Eng. 2003, 27, 293–311, 313–326, 327–346. [Google Scholar] [CrossRef]
- Woodall, W.H. Controversies and contradictions in statistical process control. J. Qual. Technol. 2000, 32, 341–350. [Google Scholar]
- Ramaker, H.-J.; van Sprang, E.N.; Westerhuis, J.A.; Smilde, A.K. Fault detection properties of global, local and time evolving models for batch process monitoring. J. Process Control 2005, 15, 799–805. [Google Scholar] [CrossRef]
- Kenett, R.S.; Pollak, M. On assessing the performance of sequential procedures for detecting a change. Qual. Reliab. Eng. Int. 2012, 28, 500–507. [Google Scholar] [CrossRef]
- Frisén, M. On multivariate control charts. Production 2011, 21, 235–241. [Google Scholar]
- Rato, T.J.; Rendall, R.; Gomes, V.; Chin, S.-T.; Chiang, A.P.; Saraiva, P.; Reis, M.S. A systematic methodology for comparing batch process monitoring methods: Part I—Assessing detection strength. Ind. Eng. Chem. Res. 2016, 55, 5342–5358. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- Chiang, L.H.; Russel, E.L.; Braatz, R.D. Fault Detection and Diagnosis in Industrial Systems; Springer-Verlag: London, UK, 2001. [Google Scholar]
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineerings’ Handbook, 8th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Chiang, L.H.; Braatz, R.D. Process monitoring using causal map and multivariate statistics: Fault detection and identification. Chemom. Intell. Lab. Syst. 2003, 65, 159–178. [Google Scholar] [CrossRef]
- Thambirajah, J.; Benabbas, L.; Bauer, M.; Thornhill, N.F. Cause-and-effect analysis in chemical processes utilizing XML, plant connectivity and quantitative process history. Comput. Chem. Eng. 2009, 33, 503–512. [Google Scholar] [CrossRef]
- Cheng, H.; Nikus, M.; Jämsä-Jounela, S.-L. Fault diagnosis of the paper machine short circulation process using novel dynamic causal digraph reasoning. J. Process Control 2008, 18, 676–691. [Google Scholar] [CrossRef]
- Chiang, L.H.; Jiang, B.; Zhu, X.; Huang, D.; Braatz, R.D. Diagnosis of multiple and unknown faults using the causal map and multivariate statistics. J. Process Control 2015, 28, 27–39. [Google Scholar] [CrossRef]
- Zhang, X.; Hoo, K.A. Effective fault detection an isolation using the bond graph-based domain decomposition. Comput. Chem. Eng. 2011, 35, 132–148. [Google Scholar] [CrossRef]
- Ould-Bouamama, B.; El Harabi, R.; Abdelkrim, M.N.; Ben Gayed, M.K. Bond graphs for the diagnosis of chemical processes. Comput. Chem. Eng. 2012, 36, 301–324. [Google Scholar] [CrossRef]
- Vedam, H.; Venkatasubramanian, V. PCA-SDG based process monitoring and fault diagnosis. Control Eng. Pract. 1999, 7, 903–917. [Google Scholar] [CrossRef]
- He, B.; Chen, T.; Yang, X. Root cause analysis in multivariate statistical process monitoring: Integrating reconstruction-based multivariate contribution analysis with fuzzy-signed directed graphs. Comput. Chem. Eng. 2014, 64, 167–177. [Google Scholar] [CrossRef]
- Wan, Y.; Yang, F.; Lu, N.; Xu, H.; Ye, H.; Li, W.; Xu, P.; Song, L.; Usadi, A.K. Statistical root cause analysis of novel faults based on digraph models. Chem. Eng. Res. Des. 2013, 91, 89–99. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N. A review of process fault detection and diagnosis. Part II: Qualitative models and search strategies. Comput. Chem. Eng. 2003, 27, 313–326. [Google Scholar] [CrossRef]
- Yoon, S.; MacGregor, J.F. Statistical and causal model-based approaches to fault detection and isolation. AIChE J. 2000, 46, 1813–1824. [Google Scholar] [CrossRef]
- Van Sprang, E.N.M.; Ramaker, H.-J.; Westerhuis, J.A.; Smilde, A.K. Statistical batch process monitoring using gray models. AIChE J. 2005, 51, 931–945. [Google Scholar] [CrossRef]
- Weidl, G.; Madsen, A.L.; Israelson, S. Applications of object-oriented bayesian networks for condition monitoring, root cause analysis and decision support on operation of complex continuous processes. Comput. Chem. Eng. 2005, 29, 1996–2009. [Google Scholar] [CrossRef]
- Yu, J.; Rashid, M.M. A novel dynamic bayesian network-based networked process monitoring approach for fault detection, propagation, identification, and root cause diagnosis. AIChE J. 2013, 59, 2348–2365. [Google Scholar] [CrossRef]
- Bauer, M.; Cox, J.W.; Caveness, M.H.; Downs, J.J.; Thornhill, N.F. Finding the direction of disturbance propagation in a chemical process using transfer entropy. IEEE Trans. Control Syst. Technol. 2007, 15, 12–21. [Google Scholar] [CrossRef]
- Bauer, M.; Thornhill, N.F. A practical method for identifying the propagation path of plant-wide disturbances. J. Process Control 2008, 18, 707–719. [Google Scholar] [CrossRef]
- Yuan, T.; Qin, S.J. International Symposium on Advanced Control of Chemical Processes. In Root Cause Diagnosis of Plant-Wide Oscillations Using Granger Causality, 8th ed.; IFAC: Singapore, 2012; pp. 160–165. [Google Scholar]
- Pellet, J.-P.; Elisseeff, A.A. Partial correlation-based algorithm for causal structure discovery with continuous variables. In Proceedings of the 7th International Conference on Intelligent Data Analysis, Ljubljana, Slovenia, 6–8 September 2007; Springer-Verlag: Ljubljana, Slovenia, 2007; pp. 229–239. [Google Scholar]
- Fuente, A.D.L.; Bing, N.; Hoeschele, I.; Mendes, P. Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics 2004, 20, 3565–3574. [Google Scholar] [CrossRef] [PubMed]
- Kalisch, M.; Bühlmann, P. Robustification of the PC-algorithm for directed acyclic graphs. J. Comput. Graph. Stat. 2008, 17, 773–789. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. Sensitivity enhancing transformations for monitoring the process correlation structure. J. Process Control 2014, 24, 905–915. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. Multiscale and megavariate monitoring of the process networked structure: M2NET. J. Chemom. 2015, 29, 309–322. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. Markovian and non-markovian sensitivity enhancing transformations for process monitoring. Chem. Eng. Sci. 2017, 163, 223–233. [Google Scholar] [CrossRef]
- Alcala, C.F.; Qin, S.J. Reconstruction-based contribution for process monitoring. Automatica 2009, 45, 1593–1600. [Google Scholar] [CrossRef]
- MacGregor, J.; Cinar, A. Monitoring, fault diagnosis, fault-tolerant control and optimization: Data driven methods. Comput. Chem. Eng. 2012, 47, 111–120. [Google Scholar] [CrossRef]
- Cinar, A.; Palazoglu, A.; Kayihan, F. Chemical Process Performance Evaluation; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Yu, J. Localized fisher discriminant analysis based complex chemical process monitoring. AIChE J. 2011, 57, 1817–1828. [Google Scholar] [CrossRef]
- Lazzaretti, A.E.; Ferreira, V.H.; Neto, H.V.; Toledo, L.F.R.B.; Pinto, C.L.S. A New Approach for Event Classification and Novelty Detection in Power Distribution Networks. In Proceedings of the 2013 IEEE Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Jing, C.; Hou, J. SVM and PCA based fault classification approaches for complicated industrial processes. Neurocomputing 2015, 167, 636–642. [Google Scholar] [CrossRef]
- Monroy, I.; Villez, K.; Graells, M.; Venkatasubramanian, V. Fault diagnosis of a benchmark fermentation process: A comparative study of feature extraction and classification techniques. Bioprocess Biosyst. Eng. 2012, 35, 689–704. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.X. Data-driven design of monitoring and diagnosis systems for dynamic processes: A review of subspace technique based schemes and some recent results. J. Process Control 2014, 24, 431–449. [Google Scholar] [CrossRef]
- Gins, G.; Van den Kerkhof, P.; Vanlaer, J.; Van Impe, J. Improving classification-based diagnosis of batch processes through data selection and appropriate pretreatment. J. Process Control 2015, 26, 90–101. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41. [Google Scholar] [CrossRef]
- Ganganwar, V. An overview of classification algorithms for imbalanced dataset. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 42–47. [Google Scholar]
- Liu, Y.; Pan, Y.; Wang, Q.; Huang, D. Statistical process monitoring with integration of data projection and one-class classification. Chemom. Intell. Lab. Syst. 2015, 149, 1–11. [Google Scholar] [CrossRef]
- Lazzaretti, A.E.; Tax, D.M.J.; Neto, H.V.; Ferreira, V.H. Novelty detection and multi-class classification in power distribution voltage waveforms. Expert Syst. Appl. 2016, 45, 322–330. [Google Scholar] [CrossRef]
- Pooyan, N.; Shahbazian, M.; Salahshoor, K.; Hadian, M. Simultaneous fault diagnosis using multi-class support vector machine in a dew point process. J. Nat. Gas Sci. Eng. 2015, 23, 373–379. [Google Scholar] [CrossRef]
- Gins, G.; Wuyts, S.; Van den Zegel, S.; Van Impe, J. Extending process monitoring to simultaneous false alarm rejection and fault identification (FARFI). Lect. Notes Comput. Sci. 2016. [Google Scholar] [CrossRef]
- Wang, K.; Jiang, W. High-dimensional process monitoring and fault isolation via variable selection. J. Qual. Technol. 2009, 41, 247–258. [Google Scholar]
- Zou, C.; Jiang, W.; Tsung, F. A LASSO-based diagnostic framework for multivariate statistical process control. Technometrics 2011, 53, 297–309. [Google Scholar] [CrossRef]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven soft sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef]
- Kaneko, H.; Funatsu, K. A soft sensor method based on values predicted from multiple intervals of time difference for improvement and estimation of prediction accuracy. Chemom. Intell. Lab. Syst. 2011, 109, 197–206. [Google Scholar] [CrossRef]
- Lin, B.; Jørgensen, S.B. Soft sensor design by multivariate fusion of image features and process measurements. J. Process Control 2011, 21, 547–553. [Google Scholar] [CrossRef]
- Shang, C.; Huang, X.; Suykens, J.A.K.; Huang, D. Enhancing dynamic soft sensors based on DPLS: A temporal smoothness regularization approach. J. Process Control 2015, 28, 17–26. [Google Scholar] [CrossRef]
- Sharmin, R.; Sundararaj, U.; Shah, S.; Griend, L.V.; Sun, Y.J. Inferential sensors for estimation of polymer quality parameters: Industrial application of a PLS-based soft-sensor for a ldpe plant. Chem. Eng. Sci. 2006, 61, 6372–6384. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. Multiresolution soft sensors (MR-SS): A new class of model structures for handling multiresolution data. Ind. Eng. Chem. Res. 2017, 56, 3640–3654. [Google Scholar] [CrossRef]
- Mason, R.L.; Tracy, N.D.; Young, J.C. Decomposition of T2 for multivariate control chart interpretation. J. Qual. Technol. 1995, 27, 99–108. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).