On the Use of Multivariate Methods for Analysis of Data from Biological Networks
Abstract
:1. Introduction
2. Preliminary Information
2.1. Univariate Statistical Analysis
2.2. Multivariate Statistical Analysis
3. Advantages of Multivariate Approaches for Biological Network Analysis
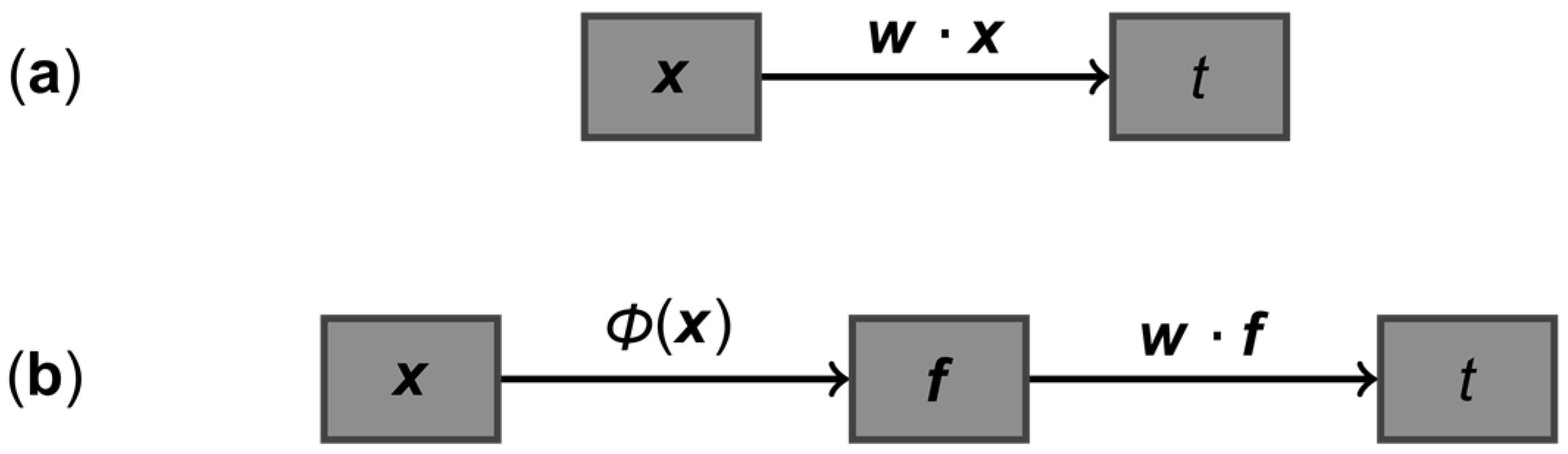
3.1. Advantages of Using Multiple Correlated Measurements for Diagnosis: A General Case
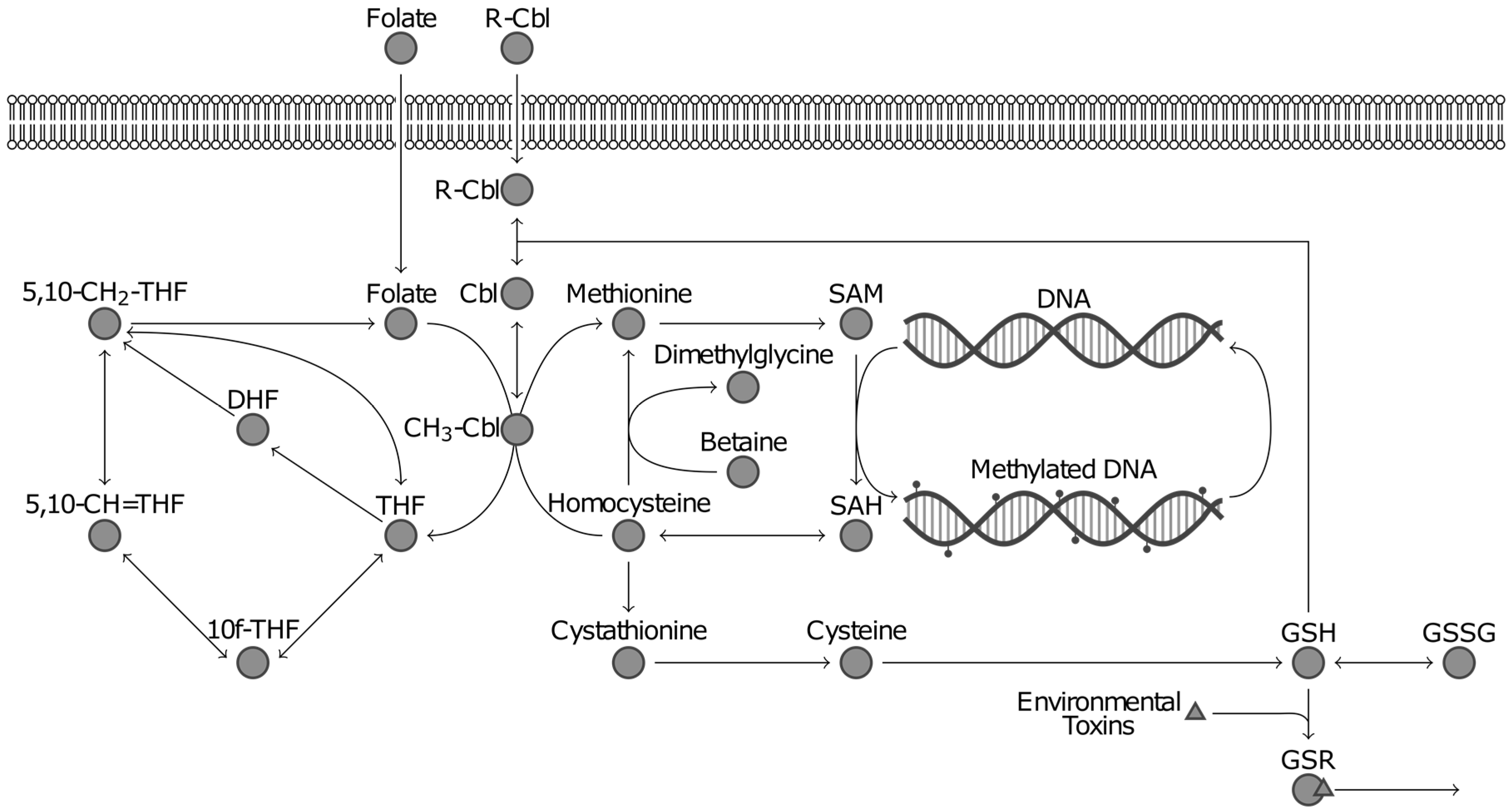
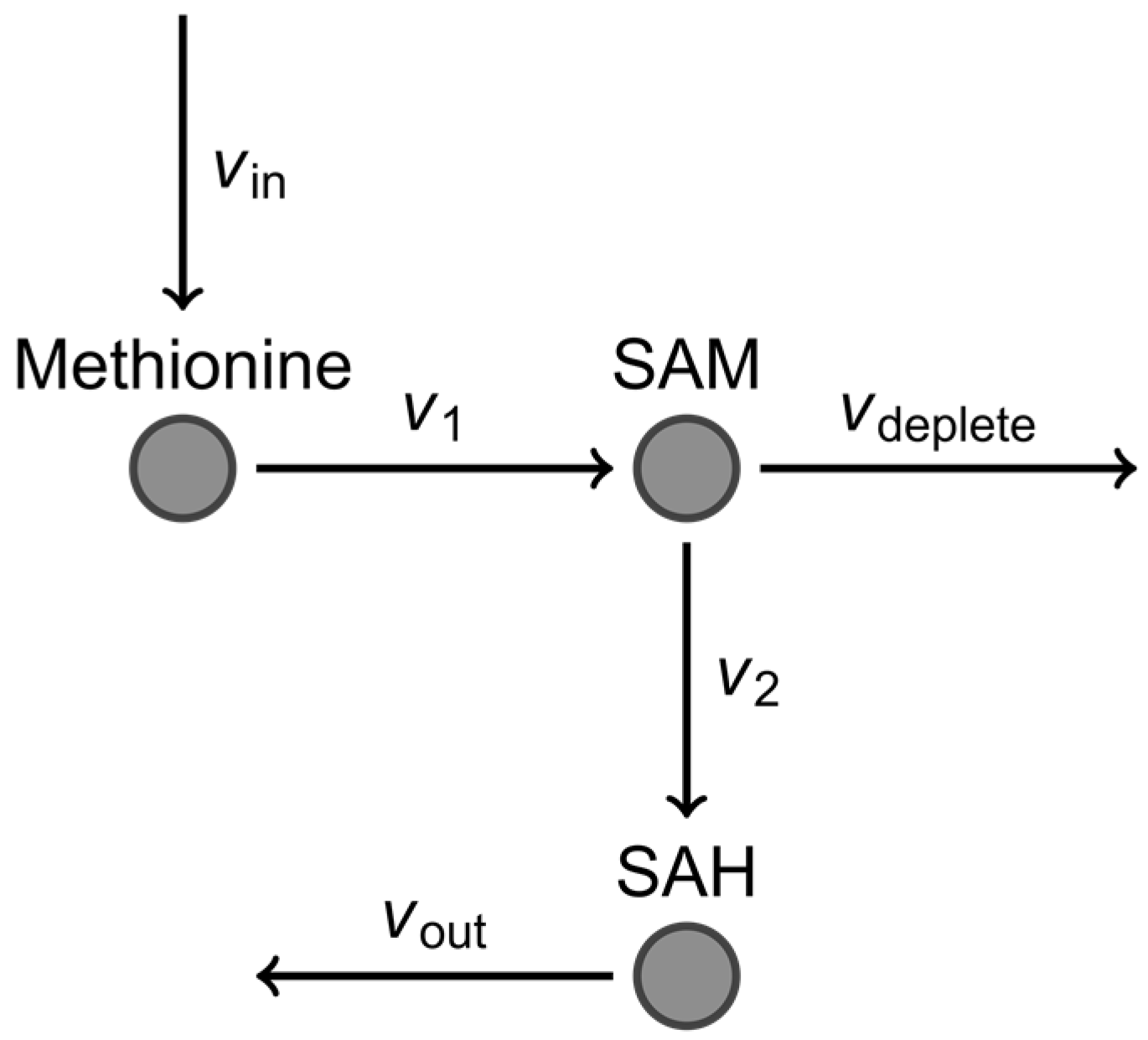
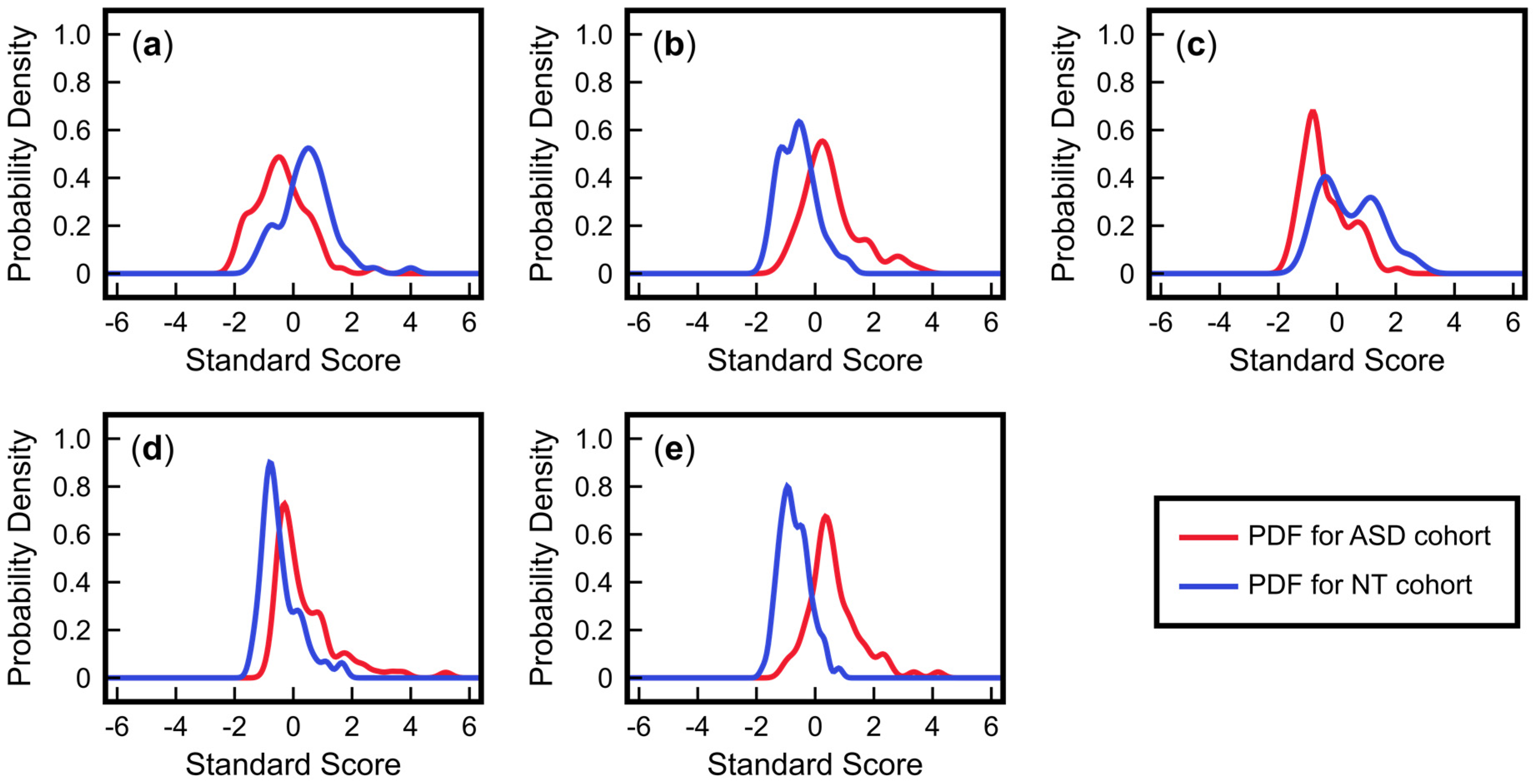
3.2. Advantages of Using Multivariate Approaches over Univariate Approaches: Application to ASD Classification Using Clinical Measurements of FOCM/TS Metabolites
3.3. Advantages of Nonlinear Approaches over Linear Approaches: Application to ASD Classification Using Clinical Measurements of Urine Toxic Metals
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Frye, R.E.; James, S.J. Metabolic pathology of autism in relation to redox metabolism. Biomark. Med. 2014, 8, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Morgan, D.B.; Carver, M.E.; Payne, R.B. Plasma creatinine and urea: Creatinine ratio in patients with raised plasma urea. Br. Med. J. 1977, 2, 929–932. [Google Scholar] [CrossRef] [PubMed]
- Lemieux, I.; Lamarche, B.; Couillard, C.; Pascot, A.; Cantin, B.; Bergeron, J.; Dagenais, G.R.; Després, J.-P. Total cholesterol/HDL cholesterol ratio vs LDL cholesterol/HDL cholesterol ratio as indices of ischemic heart disease risk in men: The Quebec Cardiovascular Study. Arch. Intern. Med. 2001, 161, 2685–2692. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Mika, S.; Ratsch, G.; Weston, J.; Scholkopf, B.; Mullers, K.R. Fisher discriminant analysis with kernels. In Proceedings of the 1999 IEEE Neural Networks for Signal Processing IX Workshop, Madison, WI, USA, 23–25 August 1999; pp. 41–48. [Google Scholar]
- Ruxton, G.D. The unequal variance t-test is an underused alternative to Student’s t-test and the Mann–Whitney U test. Behav. Ecol. 2006, 17, 688–690. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Scheffé, H. The Analysis of Variance; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Johnson, S.C. Hierarchical clustering schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Appling, D.R. Compartmentation of folate-mediated one-carbon metabolism in eukaryotes. FASEB J. 1991, 5, 2645–2651. [Google Scholar] [PubMed]
- Anderson, O.S.; Sant, K.E.; Dolinoy, D.C. Nutrition and epigenetics: An interplay of dietary methyl donors, one-carbon metabolism and DNA methylation. J. Nutr. Biochem. 2012, 23, 853–859. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, J.D.; Martin, J.J. Homocysteine. Int. J. Biochem. Cell Biol. 2000, 32, 385–389. [Google Scholar] [CrossRef]
- Vitvitsky, V.; Thomas, M.; Ghorpade, A.; Gendelman, H.E.; Banerjee, R. A functional transsulfuration pathway in the brain links to glutathione homeostasis. J. Biol. Chem. 2006, 281, 35785–35793. [Google Scholar] [CrossRef] [PubMed]
- Deth, R.; Muratore, C.; Benzecry, J.; Power-Charnitsky, V.-A.; Waly, M. How environmental and genetic factors combine to cause autism: A redox/methylation hypothesis. NeuroToxicology 2008, 29, 190–201. [Google Scholar] [CrossRef] [PubMed]
- James, S.J.; Melnyk, S.; Jernigan, S.; Cleves, M.A.; Halsted, C.H.; Wong, D.H.; Cutler, P.; Bock, K.; Boris, M.; Bradstreet, J.J.; et al. Metabolic endophenotype and related genotypes are associated with oxidative stress in children with autism. Am. J. Med. Genet. B Neuropsychiatr. Genet. 2006, 141, 947–956. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.B.; Audhya, T.; McDonough-Means, S.; Rubin, R.A.; Quig, D.; Geis, E.; Gehn, E.; Loresto, M.; Mitchell, J.; Atwood, S.; et al. Nutritional and metabolic status of children with autism vs. neurotypical children, and the association with autism severity. Nutr. Metab. 2011, 8, 34. [Google Scholar] [CrossRef] [PubMed]
- Melnyk, S.; Fuchs, G.J.; Schulz, E.; Lopez, M.; Kahler, S.G.; Fussell, J.J.; Bellando, J.; Pavliv, O.; Rose, S.; Seidel, L.; et al. Metabolic imbalance associated with methylation dysregulation and oxidative damage in children with autism. J. Autism Dev. Disord. 2012, 42, 367–377. [Google Scholar] [CrossRef] [PubMed]
- Yi, P.; Melnyk, S.; Pogribna, M.; Pogribny, I.P.; Hine, R.J.; James, S.J. Increase in plasma homocysteine associated with parallel increases in plasma S-adenosylhomocysteine and lymphocyte DNA hypomethylation. J. Biol. Chem. 2000, 275, 29318–29323. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.P. Redox potential of GSH/GSSG couple: Assay and biological significance. Methods Enzymol. 2002, 348, 93–112. [Google Scholar] [PubMed]
- Vargason, T.; Howsmon, D.P.; Melnyk, S.; James, S.J.; Hahn, J. Mathematical modeling of the methionine cycle and transsulfuration pathway in individuals with autism spectrum disorder. J. Theor. Biol. 2017, 416, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Howsmon, D.P.; Kruger, U.; Melnyk, S.; James, S.J.; Hahn, J. Classification and adaptive behavior prediction of children with autism spectrum disorder based upon multivariate data analysis of markers of oxidative stress and DNA methylation. PLoS Comput. Biol. 2017, 13, e1005385. [Google Scholar] [CrossRef] [PubMed]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; Volume 2, pp. 1137–1143. [Google Scholar]
- Adams, J.B.; Howsmon, D.P.; Kruger, U.; Geis, E.; Gehn, E.; Fimbres, V.; Pollard, E.; Mitchell, J.; Ingram, J.; Hellmers, R.; et al. Significant association of urinary toxic metals and autism-related symptoms—A nonlinear statistical analysis with cross validation. PLoS ONE 2017, 12, e0169526. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.B.; Audhya, T.; McDonough-Means, S.; Rubin, R.A.; Quig, D.; Geis, E.; Gehn, E.; Loresto, M.; Mitchell, J.; Atwood, S.; et al. Toxicological status of children with autism vs. neurotypical children and the association with autism severity. Biol. Trace Elem. Res. 2012, 151, 171–180. [Google Scholar] [CrossRef] [PubMed]
- Rossignol, D.A.; Genuis, S.J.; Frye, R.E. Environmental toxicants and autism spectrum disorders: A systematic review. Transl. Psychiatry 2014, 4, e360. [Google Scholar] [CrossRef] [PubMed]
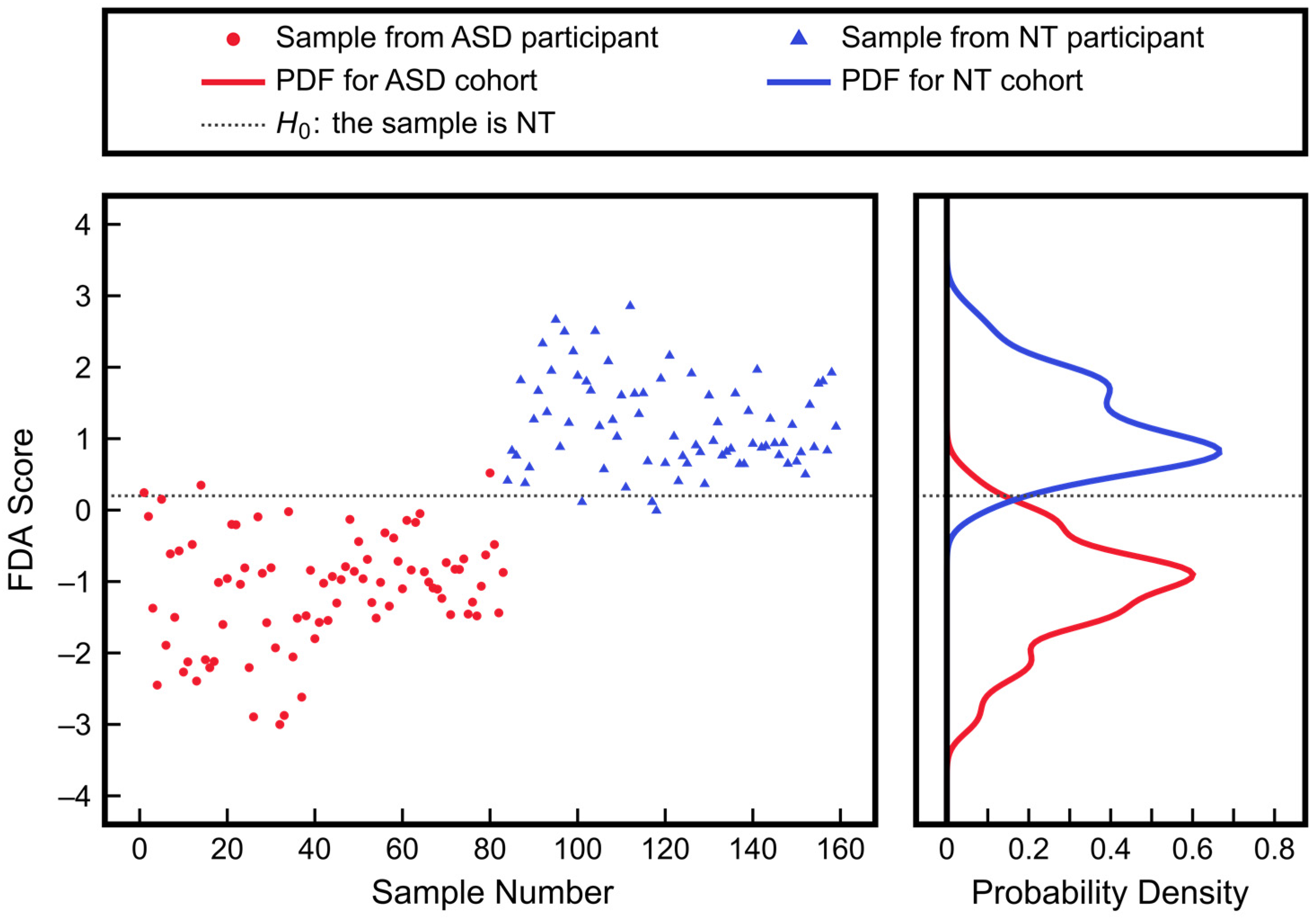
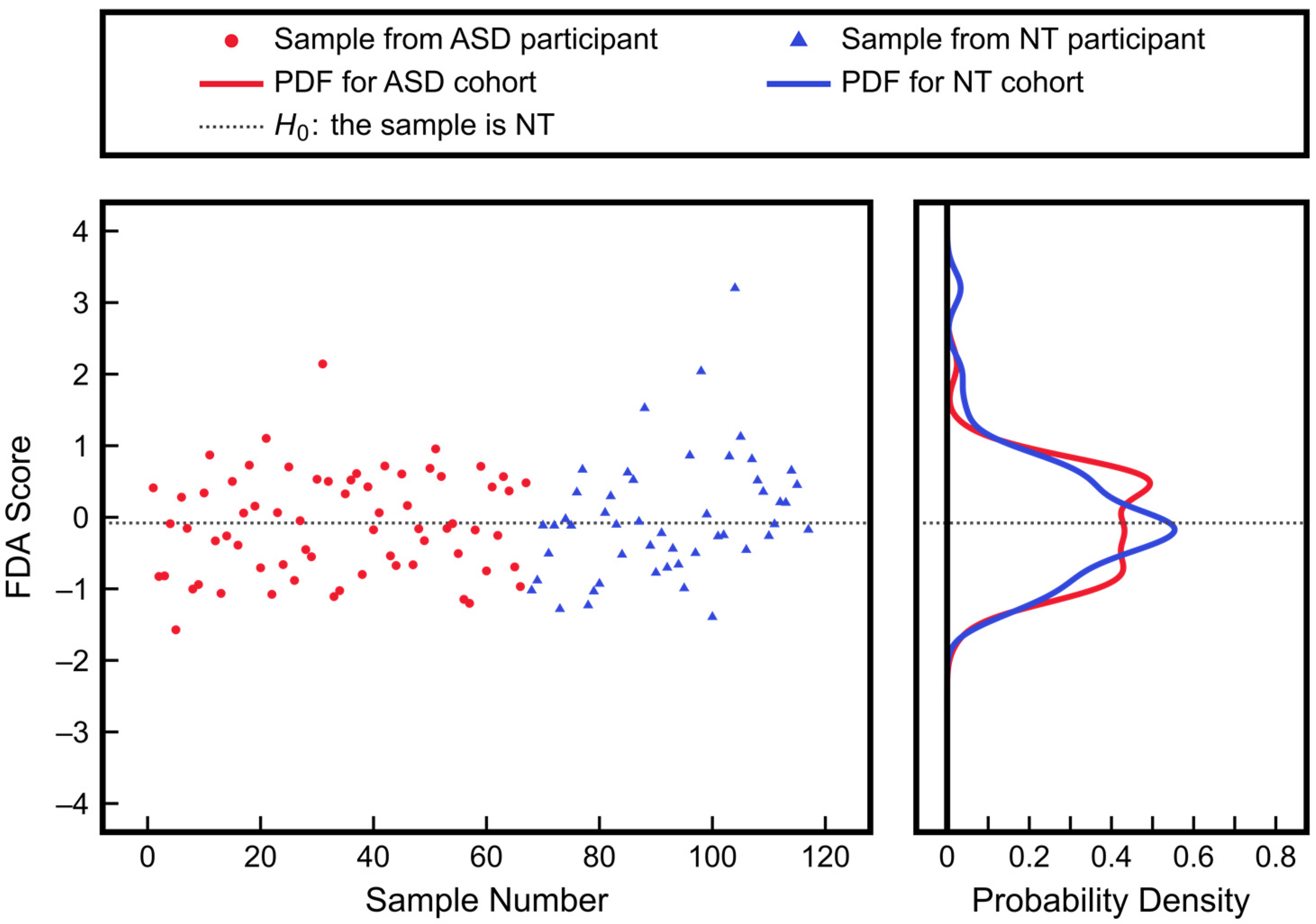
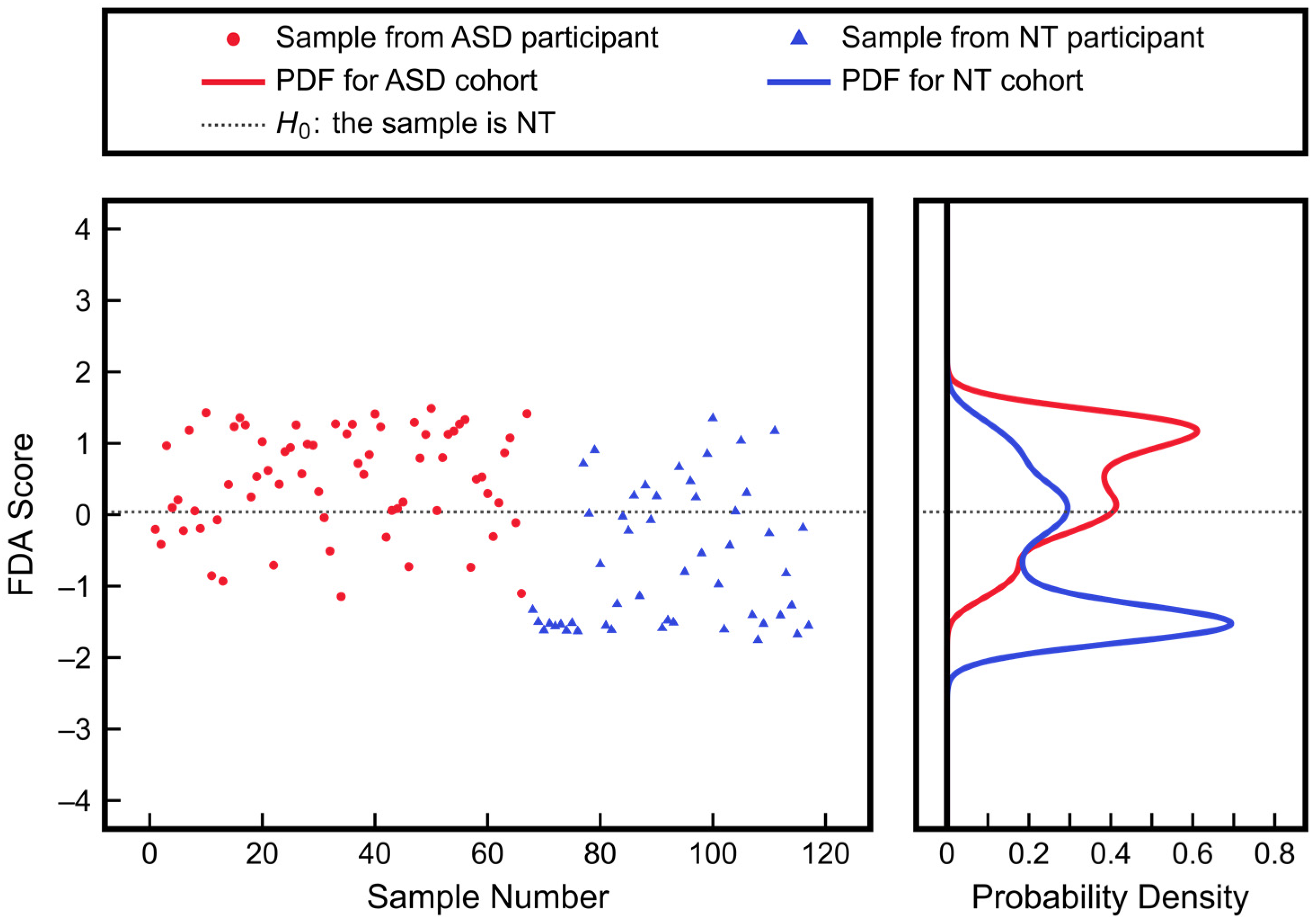
| Measurement | ASD Mean ± SD | NT Mean ± SD | p-Value |
|---|---|---|---|
| n = 83 | n = 76 | ||
| % DNA methylation | 3.37 ± 0.87 | 4.26 ± 0.90 | <0.001 |
| 8-hydroxyguanosine (pmol/mg DNA) | 89.2 ± 27.9 | 56.7 ± 17.9 | <0.001 |
| glutamylcysteine (µM) | 1.87 ± 0.46 | 2.37 ± 0.59 | <0.001 |
| free cystine/free cysteine | 1.51 ± 0.58 | 1.06 ± 0.35 | <0.001 |
| % oxidized glutathione | 0.22 ± 0.07 | 0.12 ± 0.04 | <0.001 |
| Measurement | ASD Mean ± SD | NT Mean ± SD | p-Value |
|---|---|---|---|
| n = 67 | n = 50 | ||
| Aluminum | 9.03 ± 6.55 | 8.55 ± 11.15 | n.s. |
| Cesium | 4.03 ± 1.92 | 3.74 ± 1.75 | n.s. |
| Tungsten | 0.29 ± 0.25 | 0.29 ± 0.21 | n.s. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargason, T.; Howsmon, D.P.; McGuinness, D.L.; Hahn, J. On the Use of Multivariate Methods for Analysis of Data from Biological Networks. Processes 2017, 5, 36. https://doi.org/10.3390/pr5030036
Vargason T, Howsmon DP, McGuinness DL, Hahn J. On the Use of Multivariate Methods for Analysis of Data from Biological Networks. Processes. 2017; 5(3):36. https://doi.org/10.3390/pr5030036
Chicago/Turabian StyleVargason, Troy, Daniel P. Howsmon, Deborah L. McGuinness, and Juergen Hahn. 2017. "On the Use of Multivariate Methods for Analysis of Data from Biological Networks" Processes 5, no. 3: 36. https://doi.org/10.3390/pr5030036
APA StyleVargason, T., Howsmon, D. P., McGuinness, D. L., & Hahn, J. (2017). On the Use of Multivariate Methods for Analysis of Data from Biological Networks. Processes, 5(3), 36. https://doi.org/10.3390/pr5030036







