Abstract
This paper presents a review of history matching and oil field development optimization techniques with a focus on optimization algorithms. History matching algorithms are reviewed as a precursor to production optimization algorithms. Techniques for history matching and production optimization are reviewed including global and local methods. Well placement, well control, and combined well placement-control optimization using both secondary and tertiary oil production techniques are considered. Secondary and tertiary recovery techniques are commonly referred to as waterflooding and enhanced oil recovery (EOR), respectively. Benchmark models for comparison of methods are summarized while other applications of methods are discussed throughout. No single optimization method is found to be universally superior. Key areas of future work are combining optimization methods and integrating multiple optimization processes. Current challenges and future research opportunities for improved model validation and large scale optimization algorithms are also discussed.
1. Introduction
Researchers and practitioners are investigating methods to increase production yield from existing reservoirs. Currently, the majority of reservoirs economically produce at most 60% of the original in place volumes throughout the life of the reservoir using enhanced oil recovery techniques [1]. With optimized waterflooding and enhanced oil recovery methods, there is potential to increase the amount of petroleum that can be economically produced from these reserves.
Enhanced Oil Recovery (EOR) is the practice of using various techniques to increase the amount of oil and gas that can be extracted from existing resources. Many different techniques have been developed for this purpose such as steam flooding [2,3,4,5,6], polymer flooding [2,7,8,9,10,11,12,13], and gas injection [2,14,15], among others. In this paper, EOR is defined as the injection of gas, steam, surfactants, or other chemicals into the reservoir to improve reservoir productivity. EOR is considered a tertiary production technique usually following primary and secondary production phases. In primary production natural forces within the reservoir (fluid expansion, rock expansion, aquifer influx, etc.) provide adequate energy to allow for the extraction of oil and gas. Secondary production is also called waterflooding. In this phase of production water is injected into the reservoir to increase production. Different waterflooding and EOR strategies may be chosen based on reservoir properties and the current production stage of the reservoir. Often these strategies are chosen in order to maximize total oil production or net present value (NPV). Reservoir and production engineers often use trial and error via computer simulations to determine the allocation of production resources. However, this method reduces the probability of finding the optimal field development and production scheme as relatively few scenarios can be considered. This inability to run large numbers of simulations leads to suboptimal reservoir planning and reduced production. In addition to computational limitations, other significant challenges are frequently faced when trying to optimize reservoir development. Some of these include lack of adequate historical data to calibrate reservoir models, large uncertainty in physical properties, and unpredictable oil and gas prices among others. Finding the optimal field development and production scheme increases the productivity of the reservoir. To achieve this, in light of aforementioned challenges, it is necessary to make use of computer-aided optimization techniques to more fully assess reservoirs and make improved field development and production plans. The algorithms for typical field development numerical optimization are shown in Figure 1. The reservoir system (top box) is composed of several injectors and producers. Adjusting the system inputs (i.e., number of new production wells, number new of injection wells, location of new wells, injection flow rate, injection composition, production flow rate, etc.) over the operating life of the reservoir leads to changes in the instantaneous outputs (i.e., flow rate, total recovered oil, produced water, etc.). Noise due to measurement or actuator inaccuracy is introduced into the process as inputs or outputs to the reservoir thereby increasing the uncertainty. Sensor data is fed to history matching algorithms that seek to adjust parameters of the simulated reservoir system to match the actual reservoir. This history matching process is the first optimization method discussed in this review paper. Once a sufficiently accurate representation of the reservoir is achieved, the system model or a simplified version of the model is optimized and new field development and operation strategies are calculated. These strategies are then implemented with the actual reservoir for maximized economics or other objectives related to waterflooding or EOR [16]. Throughout this paper optimization dealing with the variation of well operation parameters for either production or injection wells (i.e., production rate, injection rate, injection composition, etc.) is referred to as well control optimization.
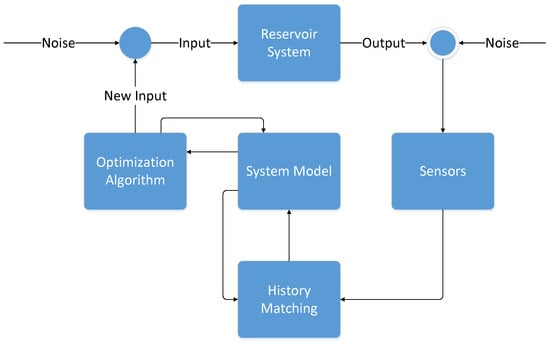
Figure 1.
Model based optimization of multiphase flow in oil reservoirs.
The research on field development optimization is extensive. It is impractical to review every facet of production optimization in a single review paper. Therefore, this review focuses on two key areas related to production optimization: history matching and optimization algorithms. Specifically, these key areas are explored as they pertain to the optimization of waterflood, EOR, and well placement. A contribution of this work is the combined review of history matching and production optimization as tightly linked in practice but rarely reviewed as a holistic process of increasing NPV. This review examines the state of the art in production optimization algorithms and finds that there is no one optimization method in use that is universally superior to others. Combined well placement and well control optimization techniques are also thoroughly reviewed. The current benchmark models for applications of waterflood and EOR optimization are also discussed. Future work recommendations in optimization methods and applications are made. Where a specific topic is too broad to cover in this review, related review papers [17,18,19,20,21,22,23,24] provide further detail for the interested reader. In particular, one area of active research related to production optimization is the quantification of uncertainty, this is reviewed by Oliver and Chen [22]. Future reviews could include an assessment of recent work in this area.
History matching is a data reconciliation process where reservoir data (production, injection, geological, etc.) is used to to tune uncertain reservoir model parameters. The resulting reservoir model is then used in field development and production optimization to determine how a reservoir should be developed and operated to maximize relevant production objectives, such as project profitability. Various optimization algorithms are used in both the history matching data reconciliation process (finding optimum values of uncertain parameters) and the production optimization process (determining optimum development and operation strategies). A general mathematical expression of both data reconciliation and production optimization is given by the spatially discretized Equation (1) and is developed further in subsequent sections.
In this case, are the measured or optimized states (outputs); are the state variables; are a set of unknown or uncertain parameters; and are a set of inputs (i.e., injector flow rates, compositions, locations, etc.). Reservoir dynamic expressions , equations that relate reservoir states to measurements , and inequality constraints compose the general set of equations that are solved in history matching or production optimization. The scalar objective or multi-objective function takes a different form whether the goal is to match measured values or maximize the economics of the reservoir. Continuous (i.e., valve position between 0–100%) or discrete (i.e., pump on or off) variables are either input into the model or else determined by the optimizer. Algebraic, ordinary differential, and partial differential equations are permitted in the general form of Equation (1) [25,26,27,28,29].
Section 2 reviews history matching techniques as applied to enhanced oil recovery and waterflooding. Section 3 surveys current state-of-the-art optimization techniques that are under development or applied in practice. Various methods and their applications are considered in each section. The concluding remarks cover the current state of the field as well as future areas of research.
2. History Matching for Waterflood and Enhanced Oil Recovery
History matching is an essential step of a typical reservoir optimization process. In history matching, geological parameters from lab studies and geological models, such as permeability and porosity, along with fluid properties are fed into a reservoir simulator or model in an attempt to recreate historical data. If the model output doesn’t match the true data then model parameters are changed using a history matching algorithm and the model is run again. The overall objective is to minimize the difference between the model output and the true historical data, as shown in Equation (2). Here is the norm for the minimization (i.e., is the 1-norm), is a weighting on measurement error, and is a penalty on deviation from prior parameter values. Note that the form of the model Equations (2b)–(2d) depends on choice of physics-based, empirical, or reduced order model form [30].
Once this difference between predicted () and measured () values is minimized, it is assumed that the model can be used to predict the future performance of the reservoir. The main difficulty with history matching is that it is an inverse problem and is ill-posed, meaning that there are many sets of parameters that could give a similar quality of match, with no method to distinguish between sets for accuracy without independent test sets that were not used as part of the fitting process. Figure 2 shows the flow of data in a history matching process.
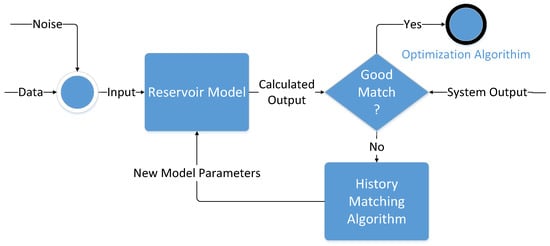
Figure 2.
History matching flowchart with the iterative process to refine model predictions for optimization.
The reservoir model represented in Figure 2 is typically created as a physics-based mathematical representation of the reservoir. The physics-based model is derived from conserved quantities such as mass, species, momentum, and energy to create balance equations [31]. These balance equations are continuous partial differential and algebraic equations that are then discretized into regular or irregular blocks or cells. Coarsely discretized models typically solve faster but have less resolution in the final solution. Vapor-liquid equilibrium (VLE), liquid-liquid equilibrium (LLE), and Equations of State (EOS) predict multi-phase behavior of fluids through the reservoir [32]. Species balances are also used to determine quantities such as water-oil split and the multi-component properties of reservoir fluids [33]. The material properties of each reservoir block such as porosity, permeability, and fluid properties are determined in the history matching process [34]. These models are often referred to as high fidelity or physics-based models. In addition to rigorous physics-based models, empirical or reduced order models are also used [35,36,37,38,39,40,41,42]. The form of some empirical models are determined solely from data while others are structured sets of equations with unknown or uncertain parameters. Whether the reservoir is modeled with a physics-based form or an empirical form, the history matching process is the alignment of measurements to predicted model outputs.
History matching may be performed manually or with computer assistance. Before computer based optimization methods were widely available, history matches were done manually; in other words, an engineer would select the parameters based on a geologic model, run a simulation, and check the quality of fit. Then, the entire process would be repeated with different parameters selected to improve the fit. Such calculations were extremely time-consuming, with some simulations requiring up to months of clock time. Automatic or assisted history matching, however, is now commonplace. In automatic history matching, an optimization algorithm is used to rapidly run several simulations while changing the parameters to find the best fit. There are many different optimization algorithms that are commonly used and they can be broadly categorized into global or local algorithms. Local algorithms find one candidate solution to the optimization problem that depends on the starting initial guess and may not be the global optimum. Global algorithms may find several local solutions or the global solution [43]. This section gives a brief overview of applications and common methods of assisted history matching since 2010 and reviews the application of history matching applied to EOR. For further discussion, the reader is referred to the review by [22,44].
Stochastic methods vary uncertain input parameters from a probability distribution function to create an ensemble of model predictions or optimization results [45,46]. The predictions that most closely align with the measurements are selected to find an optimal solution to the history matching problem. Assisted history matching with stochastic methods may use evolutionary, particle swarm, or simulated annealing algorithms. Stochastic methods search the solution space with some degree of randomness and gradually refine the history match to greater accuracy. Most current research developments involve modifications on these algorithms to improve accuracy, reliability, or computation time. Rahmati et al. [47]. enhanced the differential evolution optimization algorithm to improve convergence rates and robustness. This algorithm was compared to a gradient-based method and a Genetic Algorithm (GA). In the study, the gradient-based method was only able to find local minima due to proximity to the initial guess. The differential algorithm was found to converge with nearly half the simulations of the GA [47]. Park et al. [48] extended a Pareto-based, Multi-Objective Evolutionary Genetic Algorithm (MOEGA) developed by Deb et al. [49] to handle conflicting multiple objectives to history matching [48]. This algorithm is significant because there are generally several sets of data that are to be matched, such as production data, time-lapse seismic data, etc., each with a unique objective function. Generally, these several objectives are lumped into one weighted-sum function that is used for the history match. This can lead to incomplete solutions as the optimization of one objective may increase the error of another. A Multi-Objective Evolutionary Algorithm (MOEA) is able to create a set of solutions that deal with each objective separately and then works to find the best combination. By creating a set of solutions using MOEA, the uncertainty can be measured to some degree. Hajizadeh et al. [50] applied ant colony optimization (ACO) for history matching and uncertainty quantification to both a simple and a complex reservoir model. They found that ACO converged well and was able to perform better than a neighborhood algorithm in their tests.
A common objective in recent studies is to compare two or more methods using the same reservoir data in order to find the best history matching algorithm. ACO, differential evolution (DE), particle swarm optimization (PSO), and the neighborhood algorithm (NA) are all directly compared by Hajizadeh et al. [51]. For a small, simple reservoir with one producing well, the history match of PSO and NA were the best, with PSO achieving slightly better results. On a large synthetic reservoir with complex geology and multiple wells, DE achieved the best history match, and NA was unable to find a satisfactory match [51]. Three stochastic algorithms for joint history matching of production and 4D seismic data were compared by Jin et al. [52]. The methods were Very Fast Simulated Annealing (VFSA), PSO, and NA. In two test fields, the researchers found that PSO, while being slightly more computationally expensive, had good convergence characteristics and was more effective than the other two methods. They also found that VFSA has certain advantages, but requires more iterations and thus is generally more useful when more computational power is available [52]. Currently, there is no method that clearly and consistently outperforms other methods for all reservoirs. While a single best solution for a reservoirs is unlikely, future research should be performed to determine the optimal algorithm for different types of reservoirs and recovery methods.
An Ensemble Kalman Filter (EnKF) updates and predicts states and parameters of the model. Much of the history matching research in recent years has been focused on the use of the EnKF. The EnKF is “a sequential filter method, which means that the model is integrated forward in time and, whenever measurements are available, these are used to reinitialize the model before the integration continues” [53]. The greatest advantages of using EnKF for history matching are the ease of implementation and ability to handle nonlinear systems. EnKF is also easily parallelizable, however the computational cost is high compared to other filter methods. Aanonsen et al. [18] reviewed the use of the EnKF in reservoir engineering from its inception in 1994 to 2009.
Most current developments in the use of EnKF deal with decreasing computation time, ensuring geological consistency, or accurately matching strongly nonlinear reservoirs. A reduced order flow model, in this case Trajectory Piecewise Linearization (TPWL) form, is used in order to increase the ensemble size for the EnKF at low computational cost [54]. This avoids possible issues of ensemble collapse while improving computation time. They demonstrated that using the EnKF on 50 full-fidelity simulations and 150 TPWL simulations gave comparable results to using 200 full-fidelity simulations and resulted in a better history match than using only 50 full-fidelity simulations. Heidari et al. [55] combined the EnKF with pilot points and gradual deformation in order to prevent the EnKF from departing from prior information and to prevent petrophysical properties from reaching non-physical values. Elsheikh et al. [56] proposed an alternative to the EnKF called the iterative stochastic ensemble method (ISEM). ISEM estimates gradients stochastically using an ensemble of gradients. Agbalaka et al. [57] implemented a two-stage ensemble-based history matching technique that allows the EnKF to history match problems that have strong nonlinearities and have multimodal probability distribution functions. Their approach consisted of one EnKF to assimilate all production data followed by a second EnKF that resamples the model variables around a mode. Using their approach, they were able to greatly increase the accuracy of the history match. Emerick and Reynolds [58] created a study using nine recently developed ensemble-based methods to compare quality of the data match, uncertainty quantification, and computation time. The study was performed on a small nonlinear reservoir model. They found that the ensemble smoother with multiple data assimilations and the ensemble random maximum likelihood (EnRML) methods gave the best quality of match. The ensemble smoother with multiple data assimilations also gave the best quantification of uncertainty. The regular ensemble smoother had the lowest computation time, followed by deterministic EnKF and then the normal EnKF. They also found that several EnKF methods were unable to find an acceptable match, showing one of the major drawbacks of the EnKF. Adjusting the EnKF to allow accurate matches for highly nonlinear reservoir models will likely be a main area for future research.
Another group of commonly used methods can be classified as gradient-based as opposed to derivative-free methods. These methods rely on calculating derivatives of the model equations in order to find the optimal set of parameters. They are generally very computationally efficient, but often difficult to implement because implementation requires access to simulator source code. Gradient-based methods often do not find the global solution. Common objectives for research on gradient-based history matching in recent years include combining aspects of gradient-based history matching with other techniques in order to improve accuracy and make implementation easier. Ding [59] developed a data partition technique for gradient-based history matching. Using this technique, they separated the objective function into local components, each of which depends on fewer parameters, and then computed all the derivatives of these objective functions. This greatly assists in the history match of very large fields. Kaleta et al. [60] proposed an approach to gradient-based history matching that uses model reduction instead of a full adjoint-based approach. This was shown to reduce the computational efficiency slightly but greatly simplify the implementation. Bhark et al. [61] used gradient-based optimization within a framework of adaptively scaled frequency-domain parameterization. This method reduces the number of parameters through cosine parameterization and uses gradient-based minimization on the data misfit. Then, the model is gradually refined to include more parameters and the minimization is repeated. This whole process continues until no further improvements occur. The advantage of this method is that it avoids local minima while maintaining stability.
2.1. History Matching as Precursor to Production Optimization
This section is a review of history matching benchmarks for waterflooding and EOR optimization. In 2008, the Brugge benchmark project was created to test various methods of waterflood optimization. Nine groups participated in the project and used a variety of methods for history matching. As summarized by Peters et al. [62] participants were provided with production data, inverted time-lapse seismic data, and other other necessary information to perform history matching. These data sets were obtained from a synthetic truth model. Participants then estimated reservoir permeability, porosity, and net-to gross- (NTG) thickness. With the models obtained from history matching teams developed optimized waterflooding strategies. Their strategies were then implemented on the truth model and production results were compared to the optimum truth production case (obtained using the truth model for production optimization). The highest net present value (NPV) of the project was only 3% below the optimum production [62]. The most popular method that three of the groups (IRIS, SIEP, and Tulsa) used is the EnKF [63,64,65,66]. OU/Chevron used the EnRML method which is an iterative EnKF approach [67]. Two of the groups that used the EnKF and the group that used the EnRML method calculated the three highest NPVs of the project. Halliburton used a global optimization method and an artificial neural network (ANN) as shown in [68]. Roxar used their EnABLE software which ensures that the history match follows the geologic model [69]. Stanford and Chevron used minimization of a misfit function using numerical gradients [70] and then a derivative-free method known as the Hooke-Jeeves direct search [71,72]. Texas A&M University used a streamline-based generalized travel time inversion [73].
Since the Brugge benchmark project, several researchers have applied new and improved methods to the same data in order to compare the performance with other methods [74]. One such study was performed by [75], who developed forms of the iterative ensemble smoother using the Levenberg-Marquardt method to increase computational efficiency and improve the quality of the history match. They applied this technique to the Brugge benchmark case and found that compared to the standard ensemble smoother, ensemble-based Gauss-Newton formulation, and the multiple data assimilation method, the Levenberg-Marquardt method gave the best results.
Several studies on history matching have been performed using real fields undergoing some type of waterflood or EOR. Raniolo et al. [76] used an EnKF to history match a mature field for a polymer flood. The result of their work is a set of alternative models that match historical data to be used for the optimization of polymer injection planning. They showed that EnKF is an efficient and effective way to perform history matching in this case. Douma et al. [77] used the adjoint method for a full-field history match for chemical flooding. They found that the adjoint history match was computationally efficient and helped them understand the reservoir better. When model parameter updates were unrealistic, this information was used to identify shortcomings in the geological reservoir model (e.g., missing faults or aquifer locations). The results of their study also indicate that reduced order modeling may over simplify local reservoir behavior that is important when determining the economic viability of EOR situations [77]. Kaleta et al. [60] proposed the use of gradient-based history matching that uses a linear reduced order model instead of a full adjoint model as described earlier. When applied to a waterflood they found that their approach gave comparable results to a full adjoint based method. Xu et al. [78] applied a modified GA for the history matching of a Vapor Extraction (VAPEX) heavy oil recovery process. They found that their modified approach increased computational efficiency while achieving an excellent match. Studies have been performed on fields undergoing waterflood or EOR using most, if not all, common history matching algorithms.
Table 1 provides a comparison of the different history matching algorithms [22]. There is not one algorithm that clearly outperforms others when history matching in waterflood or EOR situations.

Table 1.
Comparison of history matching techniques. A (+) indicates a benefit or positive feature and a (−) indicates a drawback or limitation of each method.
For fields under waterflood or EOR, where reliable geologic data is difficult to obtain, reduced order proxy modeling presents a method for determining the relationship between controllable reservoir system inputs and oil production. Various data driven models have been applied to the history matching problem including finite impulse response [79], autoregressive models, [36,37,42], and the capacitance resistance model [38,39,40,41]. These models have been coupled with various history matching algorithms including gradient based methods [38] and EKF [80]. One of the major advantages of using reduced order proxy models is the reduced computation time. These models can also quickly provide an understanding of well interactions, and may even be used to infer some geologic structures. However these models lack the ability to incorporate geologic data into the model, and may have difficulty modeling very nonlinear reservoirs, making them less robust than larger, more complex models.
The top down or hierarchical approach to history matching has been applied with success to various reservoirs. The top down approach uses the simplest model necessary for the business decision at hand. Williams et al. [81] describe an algorithm for performing manual history matching that uses a top down approach, first matching reservoir pressure and flow rates followed by tuning of the individual reservoir layers and wells, in a structured manner. This idea of a top down approach was extended to automatic history matching in [82]. The top down approach allows for various global matches to subsequently be matched on the local level, providing a good understanding of uncertainty when compared to building a single detailed model for which to perform history matching. This method has been applied to various real fields with success [82,83,84]. While the top down approach allows for easier understanding of reservoir uncertainties, solving the global and local problems separately may not reveal all possible history matches.
3. Production Optimization for Waterflood and Enhanced Oil Recovery
The optimization objective for fields undergoing waterflood or EOR is to maximize expected NPV or expected cumulative oil production of the reservoir. These objectives are maximized through proper well placement and optimal well control. While well placement and well control optimization are often performed separately, there is increasing interest in performing coupled optimization of both decision variables as shown in Equation (3) where is a scaler weighting on maintaining desired target values such as total production rate, is a penalty on well control changes, has a negative multiplier to maximize production, and has a positive multiplier to minimize operational costs such as injector fluid consumption. The values of k and refer to an index of time steps in the prediction time horizon for the production optimization.
This section examines well placement, well control, and coupled well placement-well control optimization. These types of optimization problems are often referred to as production optimization. The solution methods include stochastic and adjoint techniques. Common stochastic methods include GA, ensemble based optimization (EnOpt), particle swarm optimization (PSO), simulated annealing (SA), and to a lesser extent harmony search methods. A gradient based adjoint method is common as well.
3.1. Well Placement Optimization
A common reservoir optimization problem is injection and production well placement. Due to the significant investment required for drilling and completions, having optimal well configuration is of prime importance. Various parameters must be considered to determine optimal location. These include but are not limited to permeability, porosity, and oil saturation [85]. Well location optimization algorithms often run all iterations within commercial high fidelity reservoir simulators, although use of proxy modeling is becoming more prominent. Independent well placement optimization is often determined after specifying the total number of wells and the operational variables, such as injection rate or bottom hole pressure for the lifetime of the reservoir, and then applying an optimization algorithm [86]. Well placement optimization performed independently of well control optimization tends to lead to a lower NPV [87], nevertheless well placement optimization is more easily implemented when performed independently of well control optimization.
The adjoint optimization method is gaining interest in well placement optimization due to its ability to quickly converge to solutions and allow for utilization of a gradient that can be easily evaluated to find extrema. Zandvliet et al. [88] propose surrounding wells whose location must be optimized with pseudo-wells. The pseudo-wells are modeled to produce or inject at a very low rate so as to not have a noticeable effect on NPV. The adjoint method is used to compute the gradient of NPV over the lifetime of the reservoir in regards to flow rates of the pseudo-wells. The computed gradients are used to decide the directions that wells (producer or injector) must be moved in order to maximize NPV. This method determines which direction to move wells to improve NPV after only one forward (reservoir) and one backward (adjoint) simulation. This is in contrast to many simulations as is the case for many stochastic or finite difference methods. Several researchers advocate the use of continuous variables versus discrete variables so as to be able to more easily implement an adjoint method to find optimal locations for wells [89,90,91,92]. This allows for wells to initially be placed in each grid block and non-optimal well locations to be removed more readily [92]. Zhang et al. [92] further focus on adjoint optimization for increasing overall NPV during waterflood. Large time steps (days or weeks) are used to optimize the location of a specified number of water injection wells. When compared to most stochastic methods fewer simulation runs are needed for this adjoint well placement method, as only a forward and a reverse or adjoint simulation are required. In addition to adjoint optimization, automatic differentiation poses a potential for improvements in reservoir history matching and optimization [93,94]. Automatic differentiation is generally more accurate than numerical methods and can more easily compute higher deviates and partial derivatives with respect to many inputs in gradient based optimization algorithms.
Stochastic methods such as GA, PSO, SA, and harmony search have found use in the well placement problem as their derivative free techniques allow for easy use of discrete information common in well placement problems. While the adjoint method is generally more efficient at finding optimums, it is difficult to implement and cannot be straightforwardly applied for discrete variables such as well locations in a reservoir grid.
Evolutionary algorithms, which are perhaps the most common and well known stochastic optimization algorithm group, have found merit in well placement optimization. Montes et al. [95] propose that the nonlinearity and non-continuity common in well placement optimization limit traditional simplex or gradient methods, and suggest GAs to effectively find optimal well locations. Generally, binary GAs are used in well placement optimization, however continuous GAs are being advocated by Farshi [96], Bukhamsin et al. [97] as they allow for smoother computation of optimal well placement. Farshi [96] also expands the use of GAs by implementing a minimum Euclidian distance between individuals within the population. Thus exploiting engineering intuition such as requiring a minimum distance between wells. The inclusion of curved well placement in addition to straight wells is also considered. Bukhamsin et al. [97] use continuous GAs to optimize the development of a real field located in the Middle East and consider complicated well geometry such as multilateral wells (MLWs) and maximum reservoir contact (MRC) wells. Ariadji et al. [85] use GAs in a commercial simulator with varying well drainage radii and find this is a superior method to traditional guess and check. Emerick et al. [98] utilize the Genocop III algorithm (GA for Numerical Optimization of Constrained Problems) to handle the well placement constraints. The constraints include grid size, maximum length of wells, minimum distance between wells, inactive grid cells, as well as user defined regions of non-uniform shape where well placement is forbidden. The method applied by Emerick et al. [98] does not utilize a proxy model and in some cases involves more than 100 decision variables and thousands of reservoir simulation runs, possibly limiting the utility of the method. Bouzarkouna et al. [99] propose optimal well location can be found through the use of a covariance matrix adaptation evolution strategy that uses adaptive penalization with rejection to deal with constraints. This method is used in conjunction with a meta-model that utilizes an approximate stochastic ranking procedure to rank the fitness of individual wells.
Another stochastic technique employed for optimal well placement is PSO. PSO is a stochastic optimization method based on the behavior of birds that sends particles throughout the solution space. Every particles follows the optimum particle until the swarm of particles arrives at a solution [100]. Onwunalu and Durlofsky [101] apply PSO for determining well location and well type (vertical, horizontal, deviated, multilateral, injector or producer). In this method, particles represent individual wells with a random neighborhood topology being utilized and updated after each iteration with an absorb technique to handle infeasible particles. In the special case of invalid deviated or multilateral well configurations, such as intersecting wells, these problems are resolved through assignment to a negative objective function and use of a penalty method. Cheng et al. [102] use a niche particle swarm algorithm developed by [103] to optimize the well placement of production wells. The niche particle swarm method divides the swarm into smaller subgroups, which then search for the optimal solution of that subgroup. This method increase diversity of the swarm and improves the probability of finding a global maximum when compared to PSO. Nwankwor et al. [104] advocate use of a hybrid differential evolution and particle swarm algorithm to find optimal well locations for a specified number of wells and maintain that the hybrid method employed is more efficient than an evolutionary or PSO performed separately. Ding et al. [105] investigate the use of different PSOs for the optimal well placement problem. The different PSOs utilized include modified PSO, standard PSO, centered-progressive PSO, and modified PSO and quality map method. This study shows that the modified PSO and quality map method are better able to optimally place wells than the other three methods, while modified PSO outperforms simple PSO and center-progressive PSO methods.
Genetic algorithms (GA) are also applied to well placement optimization. Min et al. [106] find the optimal location and number of waterflood injection wells through the use of a multi-objective GA. This multi-objective GA is based on non-dominated sorting and crowding distance sorting, which allows for costs to be minimized and revenue maximized. Hybrid GAs are finding merit in reservoir optimization. Like GAs, Simulated Annealing (SA) has been applied in well placement optimization. SA is modeled after the annealing of metals, where the material is heated and then allowed to slowly cool. Similarly, in SA solutions are selected that lower the objective function while a certain probability of higher solutions are chosen as well. This prevents the algorithm from falling into local minimum. Beckner and Xong [107] present well placement and scheduling as a traveling salesman problem and propose the idea that the ability of SA to deduce non-uniform well spacings makes it a viable optimization technique. Results indicate that non uniform well spacing is optimal and that optimal well spacing results in significant increases in field development profitability [107]. A variant of SA known as VFSA is also finding use in the well placement problem [108]. VFSA constrains the search space as the algorithm progresses, thereby making the algorithm more likely to accept steps that reduce the objective function. Bangerth et al. [109] find that in two different test cases VFSA performs best at finding the global optimum in the well placement problem when compared to simultaneous perturbation stochastic approximation, finite difference gradient, the Nelder-Mead simplex, and a GA, although VFSA often requires more function evaluations than the simultaneous perturbation stochastic approximation method.
To a small extent harmony search is used in the well placement problem. Afshari et al. [110] propose a method for well placement optimization using streamline simulation with an improved harmony search (IHS) algorithm. The IHS method employed is a simple method with few parameters that performs well when compared to other stochastic algorithms [110].
3.2. Well Control Optimization
Well control optimization is commonly performed via stochastic and adjoint methods. In well control optimization, optimum well control strategies for a specified number of wells at specific locations are obtained. Optimization for injection of water, gas, steam, polymer, and foam have all been studied.
The adjoint method has been applied in recent years to waterflooding optimization. Kraaijevanger et al. [111] use an adjoint method in waterfloods to determine sensitivities of the life cycle NPV with regards to well control variables in one simulation run. These sensitivities can then be used in an optimization loop to improve the well production. Jansen [23] proposes the use of optimal control theory with a gradient algorithm for optimizing NPV during production. Recently, a gradient based and multi-objective method is proposed for waterflooding optimization where a bi-objective function is optimized over a Pareto front [112].
GAs have found use in waterflooding rate optimization. Zangl and Hermann [113] argue that using only production data and simple geologic information, a GA can be employed to create a matrix that detects interference strength which can be transferred to a multi-tank material balance problem. This material balance can be utilized to detect irregular injection allocation and flow paths, allowing injection rates of individual water injection wells to be suitably altered. Li-xin and Jian-jun [114] assert that a hybrid GA minimizes injection energy consumption while maintaining a desired production in a high pressure waterflood. Mamghaderi and Pourafshary [40] use a GA with the CRM to allocate water volumes amongst injectors and maximize oil production. Safarzadeh et al. [115] use a multi-objective GA with a streamline simulation. They maintain that this combination allows for higher oil production, lower water cut, and less water lost to aquifers than traditional methods.
SA is being pursued to some extent in waterflooding optimization. Yang et al. [116] argue that both SA and a GA can be employed to optimize and control the nonlinear production-injection operation system for water and gas flooding. This technique is shown to slow down the flooding front in a stable manner. Further, Khan et al. [117] show that short term oil rates and long term recovery can be maximized in waterfloods by using constrained SA with a full field reservoir simulator. Constraints in this method are placed on the voidage replacement ratio, reservoir pressure, sweep efficiencies, and production and injection rates.
PSO is also finding some use in waterflooding optimization, but has not been studied extensively. Wang et al. [118] investigate the use of the ant colony particle swarm and find that the algorithm is effectively able to optimize waterflooding injection rates.
Well control optimization may also be performed using reduced order proxy models. As mentioned in Section 2.1, reduced order proxy models present a method for determining the relationship between injection and production wells. With these relationships, injection optimization can be performed using gradient or stochastic methods. These methods are particularly useful for large fields where high fidelity modeling would be computationally expensive. Various reduced order proxy models have been applied to fields under waterflooding or EOR. Weber [38] used the capacitance resistance model to optimize NPV at various oil prices using a gradient based solver. Other models such as finite impulse response and auto regressive models [42] that have been used for history matching injector producer relationships could be optimized with gradient based solvers or stochastic methods. Hourfar et al. [42] apply system identification techniques from the process control field and treat the reservoir as a linear multiple input multiple output (MIMO) process. Their results show simultaneous handling of reservoir nonlinearities and time-varying reservoir conditions with linear models that continuously adapt based on recent data. These simple models can easily be optimized, however their simplicity reduces the confidence in extrapolating these models into the future. Often these models are only valid for shorter time scales and must be refit with new data, making longer scale optimization more difficult with these models.
During well control optimization, determining the size of each control step is normally not performed a priori. This practice can lead to problems with too many or too few degrees of freedom. With too many control steps, optimization algorithms may find various equivalent solutions while computation times are higher. With too few time steps, the optimal solution may not be possible or misleading. Oliveira et al. [119] developed a method to determine the optimal number and size of control steps for well control optimization. The results show improvements in NPV while also decreasing computation time.
In addition to optimal injection flowrates to increase production pressure, artificial lift is often installed to supplement when there is low production pressure. The pump liquid level is detected throughout cyclic load and position trends referred to as downhole cards [120,121]. A liquid level is detected if the load shifts part way through the down cycle of a rod pump and adjustments can be made to maximize pump fillage [122]. By actively monitoring the liquid level, injector rates nearby can be increased or decreased to maintain a certain target level in the production well annulus. A future area of research is to coordinate injector action with pump-off action using variable stroke length and speed of rod pumping [123] to increase the reservoir NPV [124].
3.3. Coupled Well Placement and Well Control Optimization
One of the difficulties of coupled well placement and well control optimization is the differences in the problem type. The well placement problem generally has a non-smooth (not continuously differentiable) objective function while the well control problem has a smooth (continuously differentiable) objective function. This has led to the use of stochastic methods in the well placement problem, while well control optimization is often solved with local methods, such as the adjoint method.
Coupled well placement and well control optimization can improve economic recovery from reservoirs at the cost of increased computation. Coupled well placement optimization and well control is of growing interest in the literature. As has been mentioned previously, well placement and well control can be optimized separately. However, this generally leads to a lower NPV than coupled optimization. While coupled optimization can improve economic recovery from reservoirs, this method significantly increases the size of the optimization problem. This makes coupled optimization difficult to implement, particularly on larger fields and models. Humphries et al. [125] compared sequential and simultaneous solutions to the coupled well placement and well control problem. This study found that solving the coupled problem separately often led to better solutions than the simultaneous solution, potentially because the smaller solution space of the decoupled problem makes finding good solutions easier. Similar results have also been found for nonconventional wells [126,127]. Drouven and Grossmann [128] have applied Generalized Disjunctive Programming (GDP) coupled with a tailored solution method utilizing gradient based optimizers to well location optimization of shale gas wells combined with surface gathering system design and operational considerations. They found that profitability of investments could be significantly improved by combining well location and surface gathering considerations. In recent work Drouven et al. [129] optimize shell gas well placement and refracturing scheduling together. Tavallali et al. [130] also combine well placement and control. The results of both Drouven et al. [129] and Tavallali et al. [130] highlight valuable insight into the well placement and control interrelationship obtained by combining well placement and control optimization. Adjoint optimization is finding increased use in coupled well placement and injection optimization. Bellout et al. [87] focus on optimizing waterflooding rates and well placement through an adjoint method, selecting optimal well location as well as injector and producer optimal rates or bottom hole pressure. Zhang et al. [92] constrain the number and location of production wells before using the adjoint method. They vary the water injection rate of existing injection wells while keeping a fixed total injection rate, to maximize NPV over the production lifetime. Locations to drill new injection wells and individual well injection rates are the output of their method. Initially an injection well is placed in every grid block that does not already have one. During the adjoint optimization, all non-ideal injection well locations are removed from their respective grid blocks until an optimal number and location of wells is reached. Optimization criteria include maximization of NPV and minimization of drilling costs. As the program is run and well locations are eliminated, NPV is enhanced by redistributing the injection rates differently among injection wells [92]. Brouwer and Jansen [131] and Sarma et al. [132] provide a detailed analysis of the use of the adjoint method with well controls to maximize NPV. A gradient projection method is employed when optimizing individual well injection rates. Forouzanfar et al. [133] further investigate the use of the adjoint method with Bound Optimization by Quadratic Approximation algorithm, a derivative free algorithm, to determine the number of wells, well locations, and their controls. Sefat et al. [134] propose using a GA with a surrogate model to optimize injection and well location. The 3 different methods of applying GAs to injection optimization are:
- A GA can be applied with a high fidelity reservoir simulator, although this may require excessive computational time.
- GAs can be applied to a surrogate model to reduce computational time. In this instance a surrogate model, such as an adaptive ANN, is used with an intelligent sample selection algorithm derived from a simulator. The GA is used to optimize the surrogate model.
- A surrogate model is updated after each generation of the GA based on optimal solutions from the Pareto front.
Particle swarm has also shown some effectiveness in coupled placement and rate optimization. Isebor and Durlofsky [135], Isebor et al. [136] propose that a hybrid particle swarm-mesh adaptive direct search method is adequately able to optimize well location, well controls, and number of wells. This method filters for nonlinear constraint handling, along with a bi-objective optimization that seeks to minimize the objective function along with constraint violation, and is shown to outperform the sequential optimization of well location and injection rate.
Stochastic and gradient methods have been used extensively to solve both well placement and injection optimization problems. Table 2 provides an overview of the advantages and disadvantages of the optimization methods reviewed.

Table 2.
Comparison of methods for production optimization. A (+) indicates a benefit or positive feature and a (−) indicates a drawback or limitation of each method.
3.4. Optimization of Chemical Flooding
Chemical flooding involves the injection of one or more chemical in order to reduce the interfacial tension between the aqueous and oil phases or increase the viscosity of the aqueous phase, thereby increasing the mobility ratio and sweep efficiency. In microbial [154], polymer, surfactant, alkali-polymer, and foam processes concentrations, slug time, switching rates, and injection rates must all be optimized to maximize NPV. The adjoint method is shown to optimize chemical flooding effectively. Zhang et al. [92] are able to optimize polymer concentrations using the adjoint method found in [23]. Additionally Lei et al. [137] and Van Doren et al. [138] state that in polymer flooding the adjoint method is able to effectively compute the NPV gradient which can then be used to estimate optimal control variables such as injection and production rates, polymer concentrations, and polymer grading. Van Doren et al. [138] also propose the adjoint method can also be used effectively for alkali-surfactant polymer flooding and foam flooding. Namdar Zanganeh et al. [139] test the theory of [138] in applying the adjoint method to foam flooding and find that the adjoint method is effective when using a linear foam model. However, use of a nonlinear foam model presents problems as small time steps are required in the forward integration in order to converge to a solution for the semi-discrete problem while a high tolerance is needed in the backwards integration in order to obtain the adjoint [139].
Yong et al. [147] propose a GA with a surrogate model based on quadratic response surface to optimize injection parameters in a polymer flood for offshore reservoirs. Shurong et al. [141] propose a hybrid genetic-particle swarm algorithm to maximize NPV by holding slug concentrations constant and using control vector parameterization with constant parameters obtained through nonlinear programming. This hybrid algorithm, it is argued, is able to more quickly converge to a solution than a GA done independently through using the PSO position displacement strategy as a mutation operator [141]. Horowitz et al. [155] present a method of maximizing NPV by using a two stage method that utilizes an efficient global optimization algorithm [156] to find the optimal value for concentration of polymer in water, as well as duration of slugs and time at which to begin injections for individual injectors. This optimization is accomplished by first using a Latin hypercube technique to obtain an initial sample of designs, after which simulation runs are used to construct a metamodel. Thereafter, infill sampling criterion are used, in which the metamodel is used to lead the search for promising designs to be added to the sample to update the metamodel until desired criteria are met. Hui et al. [142] propose that a particle swarm algorithm to minimize water cut while maximizing production to find optimal polymer concentrations. Lei et al. [148] propose a hybrid GA that uses the position displacement method of particle swarm to solve a mixed integer optimization problem, which seeks to find optimal slug size and polymer concentration. Ekkawong [149] implements a multi-objective GA to optimize oil production and polymer utility function.
Various authors have examined optimizing production of steam-over-solvent processes for heavy oil reservoirs, looking specifically at injection rate and solvent concentrations as adjustable parameters to optimize NPV. Gates and Chakrabarty [145] utilize both GA and SA to optimize NPV for Steam Assisted Gravity Drainage (SAGD). Solvent additive for SAGD is optimized. Al-Gosayir et al. [150] examine the use of a hybrid GA in heterogeneous reservoirs. They investigate optimizing steam-over-solvent processes for fractured carbonate reservoirs by using a GA with a near-orthogonal array to better seed initial populations and a proxy model run to find the optimal injection rates and concentrations for cyclic injection. Zhao et al. [146] show that simulated annealing finds optimum pressure and temperature of injected hot water for recovery of thin heavy oil in various stages of reservoir depletion.
CO EOR is increasingly an important area of interest as a potential final use for carbon capture and sequestration initiatives [157,158]. Emera and Sarma [151] propose a GA to solve the minimum miscibility CO pressure needed for desired oil recovery. The proposed method uses a roulette wheel selection technique. Furthermore, Dehghani et al. [152] propose that a hybrid neural GA is useful at predicting minimum miscibility pressure needed for EOR. Ali Ahmadi et al. [143] argue that a hybrid artificial neural network and particle swarm algorithm are able determine the minimum miscible pressure. This method is better able to predict production in various thermodynamic environments [144]. Chen et al. [153] optimized a water-alternating-gas process using a hybrid GA. Little research has been devoted to adjoint methods in gas flooding optimization. Mehos and Ramirez [140] show that an adjoint method is effective at finding the minimum miscible CO pressure needed for optimal oil production.
4. Benchmark Models
Benchmark models have been developed to facilitate the comparison of different optimization methods. A benchmark model gives multiple researchers the exact same data and starting point. Thus the data produced by these groups can be compared more accurately. This section describes different benchmark models that have been provided by several organizations to facilitate such comparison, giving a brief review of three benchmarks, their properties, and the uses of each.
4.1. The Brugge Benchmark
In the months preceding the SPE Applied Technology Workshop in June 2008 SPE released the Brugge benchmark to participating researchers to compete to see who could design a history matching and optimization strategy that could achieve the highest NPV. The Brugge field is a synthetic oil field that is about 10 km by 3 km. The geologic model consists of 20 million cells, each cell containing all required reservoir properties. Historical data for the study was created using an upscaled version of the model containing 450,000 cells, and many participants used a model further upscaled to 60,000 cells to perform history matching and optimization. The reservoir is under-saturated with 20 producing wells and 10 injectors. Additional properties can be found in the paper by Peters et al. [62]. The Benchmark provides enough data to run and compare various history matching and optimization methods.
From the competition/workshop the groups involved used history matching and optimization techniques to optimize production with respect to NPV. These results were compared to the known solution. The truth case realized a NPV of USD. The highest realized NPV from the OU/Chevron group, and was USD, while the lowest was USD. The OU/Chevron group maximized the NPV with liquid rates as control variables using EnOpt and also used EnRML for their history matching strategy [159]. A detailed summary of the results is given by Peters et al. [62].
4.2. SPE-Comparative Solution Projects
The Society of Petroleum Engineers (SPE) has done 10 comparative studies, all on different topics. An in depth comparison of the 10 studies was written by Islam and Sepehrnoori [21]. Table 3 gives a summary of the focus of each benchmark project. Some of the SPE comparative studies have been applied to history matching and production optimization [30,42].

Table 3.
Summary of SPE benchmark problems for reservoir simulation, history matching, and optimization.
4.3. The Norne Benchmark
The Norne benchmark is one of the first data sets based on real field data. The field was discovered in 1991 and is located in the Norwegian Sea about 80 km North of the Heidrun field. Oil production began in November of 1997 with an estimated 160.6 MSm of oil in place and 90 MSm of it being recoverable. By the end of 2007 they have produced 77 MSm. The field is operated by Statoil USA, Eni Norge AS, and Petoro [160]. The benchmark was first released in 2009 and continues to exert itself as an industry standard for comparison. One of the benefits of the Norne Field is the availability of time lapse seismic data along with well data. A field case study in [161] evaluates various history matching and optimization methods applied to the Norne Field. PSO, EnKF, Quasi Newton method, and manual methods are all applied to the history matching problem and sequential quadratic programming, derivative free, and manual methods were used for the rate optimization.
The Norne field continues to be used to validate history matching techniques and recovery optimization. Chen and Dean used an iterative ensemble smoother that improved the history match solution over a manual algorithm [162]. Suman et al. [163] used PSO to history match the Norne benchmark using production and time lapse seismic data. Rwechungura et al. [44] compared various history matching techniques, including gradient and non-gradient techniques, using the Norne benchmark as a case study.
5. Conclusions and Future Work
This paper reviews optimization techniques used in history matching and production optimization. It combines the review of history matching optimization algorithms with a review of field development optimization, highlighting the connectivity of these processes. It reviews the state of the art in production optimization algorithms and finds that there is no one optimization method in use for history matching or production optimization that is clearly superior to others. Combined well placement and well control optimization techniques are also reviewed. Current benchmark models that have been applied to history matching and production optimization using waterflood and EOR are also discussed. With cyclical and competitive market drivers for energy production, maximizing the economic potential of a reservoir becomes increasingly relevant. Future research opportunities exist to improve history matching and optimization techniques such as uncertainty quantification, stochastic optimization, design of experiments to maximize model quality, detection of model over-parameterization and extrapolation error, hybrid modeling approaches that combine empirical and physics based methods, and large scale optimization methods [164] to better address the complexity of typical reservoirs.
There exists a large degree of uncertainty with many of the current models used for fast reservoir simulation. A select few have been used in both synthetic reservoir and benchmark simulations, and improvements are possible as field experiments are used to validate these methods. Accurate understanding of subsurface properties is not necessary for incremental recovery improvements but can be critical to maximize reservoir potential. Critical waterflooding elements are injector-producer relationships that can be regressed from production data or from high fidelity simulations. Improvements in reduced order proxy models are beneficial for legacy fields and fields where there is a great degree of uncertainty in the geologic parameters. Other examples of future work include fine tuning existing models on smaller drainage areas. Optimization techniques are often applied on an entire-field scale. Strategies for applying history matching and optimization on a smaller scale are not well developed. Such methods provides a more localized optimization approach that accounts for local reservoir heterogeneity. This is advantageous to improve injection and production strategies on a single or double well basis [165].
Most current research regarding history matching seeks to make computation faster and more accurate. Future work may focus on finding combinations of methods that outperform others. Specifically, hybrid research is being done to combine global and local methods to have the computation efficiency of local methods with the ability of global methods to find several equally accurate matches. Adjusting the EnKF to allow accurate matches for highly nonlinear reservoir models may also be a main area for future research. An emerging area of research is history matching reduced order, simplified physics based, and data driven models as opposed to full fidelity models.
The future research in optimization lies largely in the field of coupled well placement and controls optimization. Increased use of smart wells in industry can lead to greater optimization by providing more dynamic data which can provide better parameters values for injection and production rates [23]. The use of derivative free optimization methods provides the ability to solve noisy, nonlinear and discrete optimization problems but generally requires extensive computational time. In contrast, gradient based optimization is computational efficient yet may result in suboptimal local maximum solutions and has difficulty with noisy, nonlinear, and discrete problems. Combinations of stochastic and gradient methods that quickly find global maximums will be of interest and have the potential to eliminate many of the pitfalls of both individual methods.
Finally, combining history matching and optimization algorithms into a closed loop system is an area of future research. While this is an area of active research [24,65], validation of closed loop reservoir management on real field data is an area of particular interest.
Acknowledgments
This work was performed with support from the International Reservoir Simulation Research Institute (IRSRI) at Brigham Young University (BYU). The authors would like to acknowledge the helpful guidance from Hugh Hales, founder of IRSRI, and several others who have contributed to the review.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Enhanced Oil Recovery. Available online: http://energy.gov/fe/science-innovation/oil-gas-research/enhanced-oil-recovery (accessed on 16 May 2017).
- Mashayekhizadeh, V.; Kord, S.; Dejam, M. EOR potential within Iran. Spec. Top. Rev. Porous Media Int. J. 2014, 5, 325–354. [Google Scholar] [CrossRef]
- Mollaei, A.; Maini, B. Steam flooding of naturally fractured reservoirs: Basic concepts and recovery mechanisms. J. Can. Pet. Technol. 2010, 49, 65–70. [Google Scholar] [CrossRef]
- Baker, P. An experimental study of heat flow in steam flooding. Soc. Pet. Eng. J. 1969, 9, 89–99. [Google Scholar] [CrossRef]
- Akstinat, M. Gas evolution and change of oil composition during steam flooding of oil reservoirs. J. Pet. Geol. 1983, 5, 363–388. [Google Scholar] [CrossRef]
- Yitang, Z.; Xiuluan, L.; Xia, Z. Four fundamental principles for design and follow-up of steam flooding in heavy oil reservoirs. Pet. Explor. Dev. 2008, 35, 715–719. [Google Scholar]
- Saboorian-Jooybari, H.; Dejam, M.; Chen, Z. Heavy oil polymer flooding from laboratory core floods to pilot tests and field applications: Half-century studies. J. Pet. Sci. Eng. 2016, 142, 85–100. [Google Scholar] [CrossRef]
- Saboorian-Jooybari, H.; Dejam, M.; Chen, Z. Half-Century of Heavy Oil Polymer Flooding from Laboratory Core Floods to Pilot Tests and Field Applications. In Proceedings of the SPE Canada Heavy Oil Technical Conference, Calgary, AB, Canada, 9–11 June 2015; Society of Petroleum Engineers: Calgary, AB, Canada, 2015. [Google Scholar]
- Guo, Y.; Liang, Y.; Cao, M.; Feng, R.; Zhang, X.; Li, H.; Hu, J. Flow Behavior and Viscous-Oil-Microdisplacement Characteristics of Hydrophobically Modified Partially Hydrolyzed Polyacrylamide in a Repeatable Quantitative Visualization Micromodel. SPE J. 2017. [Google Scholar] [CrossRef]
- Seright, R.S. How Much Polymer Should Be Injected During a Polymer Flood? Review of Previous and Current Practices. SPE J. 2016. [Google Scholar] [CrossRef]
- Seright, R. How Much Polymer Should Be Injected During a Polymer Flood? In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 11–13 April 2016; Society of Petroleum Engineers: Tulsa, OK, USA, 2016. [Google Scholar]
- Liu, S.; Zhang, D.; Yan, W.; Puerto, M.; Hirasaki, G.J.; Miller, C.A. Favorable attributes of alkaline–surfactant–polymer flooding. SPE J. 2008, 13, 5–16. [Google Scholar] [CrossRef]
- Zerpa, L.E.; Queipo, N.V.; Pintos, S.; Salager, J.L. An optimization methodology of alkaline–surfactant– polymer flooding processes using field scale numerical simulation and multiple surrogates. J. Pet. Sci. Eng. 2005, 47, 197–208. [Google Scholar] [CrossRef]
- Samimi, S.E.; Masihi, M.; Gerami, S.; Ghazvini, M.G. An Improvement on Modeling of Forced Gravity Drainage in Dual Porosity Simulations Using a New Matrix-Fracture Transfer Function. Transp. Porous Media 2012, 94, 207–223. [Google Scholar] [CrossRef]
- Lin, L.; Yang, Z.; Liu, X.; Sun, J.; He, Y.; Guo, H. Experiments on the permeability limits of tight oil reservoirs for gas flood recovery. Spec. Top. Rev. Porous Media Int. J. 2016, 7, 385–390. [Google Scholar] [CrossRef]
- Jansen, J. Model-based control of subsurface flow. J. Process Control 2008, 18, 846–855. [Google Scholar] [CrossRef]
- Jansen, J.D.; Durlofsky, L.J. Use of reduced-order models in well control optimization. Optim. Eng. 2016, 18, 105–132. [Google Scholar] [CrossRef]
- Aanonsen, S.I.; Nævdal, G.; Oliver, D.S.; Reynolds, A.C.; Vallès, B. The ensemble Kalman filter in reservoir engineering—A review. SPE J. 2009, 14, 393–412. [Google Scholar] [CrossRef]
- Alvarado, V.; Manrique, E. Enhanced oil recovery: An update review. Energies 2010, 3, 1529–1575. [Google Scholar] [CrossRef]
- Franco, A.; Vaccaro, M. Numerical simulation of geothermal reservoirs for the sustainable design of energy plants: A review. Renew. Sustain. Energy Rev. 2014, 30, 987–1002. [Google Scholar] [CrossRef]
- Islam, A.W.; Sepehrnoori, K. A Review on SPE’s Comparative Solution Projects (CSPs). J. Pet. Sci. Res. 2013, 2. [Google Scholar] [CrossRef]
- Oliver, D.S.; Chen, Y. Recent progress on reservoir history matching: A review. Comput. Geosci. 2011, 15, 185–221. [Google Scholar] [CrossRef]
- Jansen, J. Adjoint-based optimization of multi-phase flow through porous media—A review. Comput. Fluids 2011, 46, 40–51. [Google Scholar] [CrossRef]
- Hou, J.; Zhou, K.; Zhang, X.S.; Kang, X.D.; Xie, H. A review of closed-loop reservoir management. Pet. Sci. 2015, 12, 114–128. [Google Scholar] [CrossRef]
- Beal, L.D.; Park, J.; Petersen, D.; Warnick, S.; Hedengren, J.D. Combined model predictive control and scheduling with dominant time constant compensation. Comput. Chem. Eng. 2017, 104, 271–282. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Hedengren, J.D.; Baxter, L.L. Plant-level dynamic optimization of cryogenic carbon capture with conventional and renewable power sources. Appl. Energy 2015, 149, 354–366. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Hedengren, J.D.; Baxter, L.L. Dynamic optimization of a hybrid system of energy-storing cryogenic carbon capture and a baseline power generation unit. Appl. Energy 2016, 172, 66–79. [Google Scholar] [CrossRef]
- Powell, K.M.; Eaton, A.N.; Hedengren, J.D.; Edgar, T.F. A continuous formulation for logical decisions in differential algebraic systems using mathematical programs with complementarity constraints. Processes 2016, 4, 7. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Hedengren, J.D.; Lewis, N.R.; Haseltine, E.L. Initialization strategies for optimization of dynamic systems. Comput. Chem. Eng. 2015, 78, 39–50. [Google Scholar] [CrossRef]
- Udy, J.; Blackburn, L.; Hedengren, J.; Darby, M. Reduced Order Modeling for Reservoir Injection Optimization and Forecasting. In Proceedings of the FOCAPO/CPC Conference, Tuscon, AZ, USA, 8–12 January 2017; Foundations of Computer Aided Process Operations/Chemical Process Control: Tuscon, AZ, USA, 2017. [Google Scholar]
- Todd, M.; Longstaff, W. The development, testing, and application of a numerical simulator for predicting miscible flood performance. J. Pet. Technol. 1972, 24, 874–882. [Google Scholar] [CrossRef]
- Wang, P.; Yotov, I.; Wheeler, M.; Arbogast, T.; Dawson, C.; Parashar, M.; Sepehrnoori, K. A New Generation EOS Compositional Reservoir Simulator: Part I-Formulation and Discretization. In Proceedings of the SPE Reservoir Simulation Symposium, Dallas, TX, USA, 8–11 June 1997; Society of Petroleum Engineers: Dallas, TX, USA, 1997. [Google Scholar]
- Kazemi, H.; Vestal, C.; Shank, D.G. An efficient multicomponent numerical simulator. Soc. Pet. Eng. J. 1978, 18, 355–368. [Google Scholar] [CrossRef]
- Blunt, M.J.; Jackson, M.D.; Piri, M.; Valvatne, P.H. Detailed physics, predictive capabilities and macroscopic consequences for pore-network models of multiphase flow. Adv. Water Resour. 2002, 25, 1069–1089. [Google Scholar] [CrossRef]
- Lee, K.; Ortega, A.; Jafroodi, N.; Ershaghi, I. A multivariate autoregressive model for characterizing producer producer relationships in waterfloods from injection/production rate fluctuations. SPE West. Reg. Meet. 2010, 13, 1–11. [Google Scholar]
- Liu, F.; Mendel, J.M.; Nejad, A.M. Forecasting injector/producer relationships from production and injection rates using an extended Kalman filter. SPE J. 2009, 14, 653–664. [Google Scholar] [CrossRef]
- Zhai, D.Y.; Mendel., J.M. An inequality-constrained extended Kalman filter for continual forecasting of interwell connectivities in waterfloods. SPE West. Reg. Meet. 2010. [Google Scholar] [CrossRef]
- Weber, D. The use of Capacitance-Resistance Models to Optimize Injection Allocation and Well Location in Water Floods. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2009. [Google Scholar]
- Sayarpour, M.; Zuluaga, E.; Kabir, C.S.; Lake, L.W. The use of capacitance–resistance models for rapid estimation of waterflood performance and optimization. J. Pet. Sci. Eng. 2009, 69, 227–238. [Google Scholar] [CrossRef]
- Mamghaderi, A.; Pourafshary, P. Water flooding performance prediction in layered reservoirs using improved capacitance-resistive model. J. Pet. Sci. Eng. 2013, 108, 107–117. [Google Scholar] [CrossRef]
- Jafroodi, N.; Zhang, D. New method for reservoir characterization and optimization using CRM–EnOpt approach. J. Pet. Sci. Eng. 2011, 77, 155–171. [Google Scholar] [CrossRef]
- Hourfar, F.; Moshiri, B.; Salahshoor, K.; Zaare-Mehrjerdi, M.; Pourafshary, P. Adaptive modeling of waterflooding process in oil reservoirs. J. Pet. Sci. Eng. 2016, 146, 702–713. [Google Scholar] [CrossRef]
- Verga, F.; Cancelliere, M.; Viberti, D. Improved application of assisted history matching techniques. J. Pet. Sci. Eng. 2013, 109, 327–347. [Google Scholar] [CrossRef]
- Rwechungura, R.W.; Dadashpour, M.; Kleppe, J. Advanced History Matching Techniques Reviewed. Proceeding of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 25–28 September 2011; Society of Petroleum Engineers: Manama, Bahrain, 2011. [Google Scholar]
- Stordal, A.S.; Szklarz, S.P.; Leeuwenburgh, O. A theoretical look at ensemble-based optimization in reservoir management. Math. Geosci. 2016, 48, 399–417. [Google Scholar] [CrossRef]
- Anifowose, F.A.; Labadin, J.; Abdulraheem, A. Ensemble machine learning: An untapped modeling paradigm for petroleum reservoir characterization. J. Pet. Sci. Eng. 2017, 151, 480–487. [Google Scholar] [CrossRef]
- Rahmati, H.; Nouri, A.; Pishvaie, M.R.; Bozorgmehri, R. A modified differential evolution optimization algorithm with random localization for generation of best-guess properties in history matching. Energy Sources Part A Recovery Util. Environ. Effects 2011, 33, 845–858. [Google Scholar] [CrossRef]
- Park, H.Y.; Datta-Gupta, A.; King, M.J. Handling conflicting multiple objectives using Pareto-based evolutionary algorithm during history matching of reservoir performance. J. Pet. Sci. Eng. 2014, 125, 48–66. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hajizadeh, Y.; Christie, M.; Demyanov, V. Ant colony optimization for history matching and uncertainty quantification of reservoir models. J. Pet. Sci. Eng. 2011, 77, 78–92. [Google Scholar] [CrossRef]
- Hajizadeh, Y.; Demyanov, V.; Mohamed, L.; Christie, M. Comparison of evolutionary and swarm intelligence methods for history matching and uncertainty quantification in petroleum reservoir models. In Intelligent Computational Optimization in Engineering; Springer: Berlin/Heidelberg, Germany, 2010; pp. 209–240. [Google Scholar]
- Jin, L.; van den Hoek, P.J.; Alpak, F.O.; Pirmez, C.; Fehintola, T.; Tendo, F.; Olaniyan, E.E. A comparison of stochastic data-integration algorithms for the joint history matching of production and Time-Lapse-Seismic data. SPE Reserv. Eval. Eng. 2012, 15, 498–512. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- He, J.; Sarma, P.; Durlofsky, L.J. Reduced-order flow modeling and geological parameterization for ensemble-based data assimilation. Comput. Geosci. 2013, 55, 54–69. [Google Scholar] [CrossRef]
- Heidari, L.; Gervais, V.; Ravalec, M.L.; Wackernagel, H. History matching of petroleum reservoir models by the ensemble Kalman Filter and parameterization methods. Comput. Geosci. 2012, 55, 84–95. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Wheeler, M.F.; Hoteit, I. An iterative stochastic ensemble method for parameter estimation of subsurface flow models. J. Comput. Phys. 2013, 242, 696–714. [Google Scholar] [CrossRef]
- Agbalaka, C.C.; Stern, D.; Oliver, D.S. Two-stage ensemble-based history matching with multiple modes in the objective function. Comput. Geosci. 2013, 55, 28–43. [Google Scholar] [CrossRef]
- Emerick, A.A.; Reynolds, A.C. Investigation of the sampling performance of ensemble-based methods with a simple reservoir model. Comput. Geosci. 2013, 17, 325–350. [Google Scholar] [CrossRef]
- Ding, D.Y. Development of a data partition technique for gradient-based optimization methods in history matching. SPE J. 2011, 16, 582–593. [Google Scholar] [CrossRef]
- Kaleta, M.P.; Hanea, R.G.; Heemink, A.W.; Jansen, J.D. Model-reduced gradient-based history matching. Comput. Geosci. 2010, 15, 135–153. [Google Scholar] [CrossRef]
- Bhark, E.; Jafarpour, B.; Datta-Gupta, A. An adaptively scaled frequency-domain parameterization for history matching. J. Pet. Sci. Eng. 2011, 75, 289–303. [Google Scholar] [CrossRef]
- Peters, L.; Arts, R.; Brouwer, G.; Geel, C.; Cullick, S.; Lorentzen, R.; Chen, Y.; Dunlop, N.; Vossepoel, F.; Xu, R.; et al. Results of the Brugge benchmark study for flooding optimization and history matching. SPE Reserv. Eval. Eng. 2010, 13, 391–405. [Google Scholar] [CrossRef]
- Naevdal, G.; Johnsen, L.M.; Aanonsen, S.I.; Vefring, E.H. Reservoir monitoring and continuous model updating using ensemble Kalman filter. SPE J. 2005, 10, 66–74. [Google Scholar] [CrossRef]
- Bianco, A.; Cominelli, A.; Dovera, L.; Nævdal, G.; Valles, B. History matching and production forecast uncertainty by means of the ensemble Kalman filter: A real field application. Procedings of the EUROPEC/EAGE Conference and Exhibition, London, UK, 11–14 June 2007; Society of Petroleum Engineers: London, UK, 2007. [Google Scholar]
- Jansen, J.D.; Brouwer, R.; Douma, S.G. Closed Loop Reservoir Management. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 2–4 February 2009; Society of Petroleum Engineers: The Woodlands, TX, USA, 2009. [Google Scholar]
- Skjervheim, J.; Evensen, G.; Aanonsen, S.; Rudd, B.; Johansen, T. Incorporating 4D Seismic Data in Reservoir Simulation Models Using Ensemble Kalman Filter. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005; pp. 1–11. [Google Scholar]
- Gu, Y.; Oliver, D. An iterative ensemble Kalman filter for multiphase fluid flow data assimilation. SPE J. 2007, 12, 438–446. [Google Scholar] [CrossRef]
- Cullick, A.S.; Johnson, W.D.; Shi, G. Improved and More Rapid History Matching with a Nonlinear Proxy and Global Optimization. In Proceedings of the SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers: San Antonio, TX, USA, 2006. [Google Scholar]
- Webb, S.J.; Bayless, J.S.; Dunlop, K.N.B. Enabling the ’Big Loop’-Ensuring Consistency of Geological and Reservoir Simulation Models. In Proceedings of the AAPG Annual Convention and Exhibition, Long Beach, CA, USA, 1–4 April 2007; pp. 1–4. [Google Scholar]
- Sarma, P.; Durlofsky, L.J.; Aziz, K.; Chen, W.H. Efficient real-time reservoir management using adjoint-based optimal control and model updating. Comput. Geosci. 2006, 10, 3–36. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. Direct search solution of numerical and statistical problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Echeverría Ciaurri, D.; Isebor, O.; Durlofsky, L. Application of derivative-free methodologies to generally constrained oil production optimization problems. Proced. Comput. Sci. 2010, 1, 1301–1310. [Google Scholar] [CrossRef]
- He, Z.; Yoon, S.; Datta-Gupta, A. Streamline-based production data integration with gravity and changing field conditions. SPE J. 2002, 7, 423–436. [Google Scholar] [CrossRef]
- Krymskaya, M.V.; Hanea, R.G.; Verlaan, M. An iterative ensemble Kalman filter for reservoir engineering applications. Comput. Geosci. 2009, 13, 235–244. [Google Scholar] [CrossRef]
- Chen, Y.; Oliver, D.S. Levenberg-Marquardt forms of the iterative ensemble smoother for efficient history matching and uncertainty quantification. Comput. Geosci. 2013, 17, 689–703. [Google Scholar] [CrossRef]
- Raniolo, S.; Dovera, L.; Cominelli, A.; Callegaro, C.; Masserano, F. History Match and Polymer Injection Optimization in a Mature Field Using the Ensemble Kalman Filter. In Proceedings of the IOR 2013—17th European Symposium on Improved Oil Recovery, St. Petersburg, Russia, 16–18 April 2013. [Google Scholar]
- Douma, S.G.; Abu-Shiekah, I.M.; Kindi, Z.Y. Full Field History Matching for Chemical Flooding with the Adjoint Method. In Proceedings of the SPE Kuwait Oil and Gas Show and Conference, Kuwait City, Kuwait, 8–10 October 2013; Society of Petroleum Engineers: Kuwait City, Kuwait, 2013. [Google Scholar]
- Xu, S.; Zhang, M.; Zeng, F.; Chan, C. Application of Genetic Algorithm (GA) in history matching of the Vapour Extraction (VAPEX) heavy oil recovery process. Nat. Resour. Res. 2014. [Google Scholar] [CrossRef]
- Lee, K.H.; Ortega, A.; Nejad, A.M.; Ershaghi, I. A Method for Characterization of Flow Units Between Injection-Production Wells Using Performance Data. In Proceedings of the 2008 SPE Western Regional and Pacific Section AAPG Joint Meeting, Bakersfield, CA, USA, 31 March–2 April 2008; pp. 419–446. [Google Scholar]
- Zhai, D.Y.; Jerry, M.; Mendel, F.L. A New Method for Continual Forecasting of Interwell Connectivitiy in Waterfloods Using an Extended Kalman Filter. SPE West. Reg. Meet. 2009. [Google Scholar] [CrossRef]
- Williams, M.; Keating, J.F.; Barghouty, M. The stratigraphic method: A structured approach to history matching complex simulation models. SPE Reserv. Eval. Eng. 1998, 1, 169–176. [Google Scholar] [CrossRef]
- Williams, G.; Mansfield, M.; MacDonald, D.; Bush, M. Top-down Reservoir Modelling. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004; Society of Petroleum Engineers: Houston, TX, USA, 2004. [Google Scholar]
- Yin, J.; Park, H.Y.; Datta-Gupta, A.; King, M.J.; Choudhary, M.K. A hierarchical streamline-assisted history matching approach with global and local parameter updates. J. Pet. Sci. Eng. 2011, 80, 116–130. [Google Scholar] [CrossRef]
- Cheng, H.; Dehghani, K.; Billiter, T.C. A Structured Approach for Probabilistic-Assisted History Matching Using Evolutionary Algorithms: Tengiz Field Applications. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 1–24 September 2008; Society of Petroleum Engineers: Denver, CO, USA, 2008. [Google Scholar]
- Ariadji, T.; Sukarno, P.; Sidarto, K.A.; Soewono, E.; Riza, L.S.; David, K. Optimization of Vertical Well Placement for Oil Field Development Based on Basic Reservoir Rock Properties using a Genetic Algorithm. ITB J. Eng. Sci. 2012, 44, 106–127. [Google Scholar] [CrossRef]
- Fahim Forouzanfar, A.; Gaoming Li, S. A Two-Stage Well Placement Optimization Method Based on Adjoint Gradient. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 20–22 September 2010. [Google Scholar]
- Bellout, M.C.; Echeverría Ciaurri, D.; Durlofsky, L.J.; Foss, B.; Kleppe, J. Joint optimization of oil well placement and controls. Comput. Geosci. 2012, 16, 1061–1079. [Google Scholar] [CrossRef]
- Zandvliet, M.; Handels, M.; Van Essen, G.; Brouwer, D.; Jansen, J.D. Adjoint-based well-placement optimization under production constraints. SPE J. 2008, 13, 392–399. [Google Scholar] [CrossRef]
- Handels, M.; Zandvliet, M.; Brouwer, R.; Jansen, J.D. Adjoint-Based Well-Placement Optimization under Production Constraints. In Proceedings of the SPE Reservoir Simulation Symposium; Society of Petroleum Engineers: Houston, TX, USA, 2007. [Google Scholar]
- Wang, C.; Li, G.; Reynolds, A.C. Optimal Well Placement for Production Optimization. In Proceedings of the Eastern Regional Meeting; Society of Petroleum Engineers: Lexington, KY, USA, 2007. [Google Scholar]
- Sarma, P.; Chen, W.H.; Durlofsky, L.J.; Aziz, K. Production optimization with adjoint models under nonlinear control-state path inequality constraints. SPE Reserv. Eval. Eng. 2008, 11, 326–339. [Google Scholar] [CrossRef]
- Zhang, K.; Li, G.; Reynolds, A.C.; Yao, J.; Zhang, L. Optimal well placement using an adjoint gradient. J. Pet. Sci. Eng. 2010, 73, 220–226. [Google Scholar] [CrossRef]
- Younis, R.M.; Aziz, K.; Tchelepi, H.; Alonso, J.J. Modern Advances in Software and Solution Algorithms for Reservoir Simulation; Stanford University: Stanford, CA, USA, 2011. [Google Scholar]
- Li, X.; Zhang, D. A backward automatic differentiation framework for reservoir simulation. Comput. Geosci. 2014, 18, 1009–1022. [Google Scholar] [CrossRef]
- Montes, G.; Bartolome, P.; Udias, A.L. The Use of Genetic Algorithms in Well Placement Optimization. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 25–28 March 2011; Society of Petroleum Engineers: Buenos Aires, Argentina, 2001. [Google Scholar]
- Farshi, M.M. Improving Genetic Algorithms for Optimum Well Placement. Master’s Thesis, Stanford University, Stanford, CA, USA, 2008. [Google Scholar]
- Bukhamsin, A.Y.; Farshi, M.M.; Aziz, K. Optimization of Multilateral Well Design and Location in a Real Field Using a Continuous Genetic Algorithm. In Proceedings of the SPE/DGS Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 4–7 April 2010; SPE: Al-Khobar, Saudi Arabia, 2010. [Google Scholar]
- Emerick, A.A.; Silva, E.; Messer, B.; Almeida, L.; Szwarcman, D.; Pacheco, M.; Vellasco, M. Well Placement Optimization Using a Genetic Algorithm With Nonlinear Constraints. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 2–4 February 2009; SPE: The Woodlands, TX, USA, 2009. [Google Scholar]
- Bouzarkouna, Z.; Ding, D.Y.; Auger, A. Partially Separated Meta-Models with Evolution Strategies for Well Placement Optimization. In Proceedings of the 73rd EAGE Conference & Exhibition Incorporating SPE EUROPEC, Vienna, Austria, 23–26 May 2011; pp. 1–9. [Google Scholar]
- Eberhart, R.C.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, New York, NY, USA, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Onwunalu, J.E.; Durlofsky, L.J. Application of a particle swarm optimization algorithm for determining optimum well location and type. Comput. Geosci. 2010, 14, 183–198. [Google Scholar] [CrossRef]
- Cheng, G.; An, Y.; Wang, Z.; Zhu, K. Oil Well Placement Optimization Using Niche Particle Swarm Optimization. In Proceedings of the 2012 Eighth International Conference on Computational Intelligence and Security, Guangzhou, China, 17–18 November 2012; pp. 61–64. [Google Scholar]
- Brits, R.; Engelbrecht, A.P.; Van den Bergh, F. A Niching Particle Swarm Optimizer. In Proceedings of the 4th Asia-Pacific Conference on Simulated Evolution and Learning, Singapore, 18–22 November 2002; pp. 692–696. [Google Scholar]
- Nwankwor, E.; Nagar, A.; Reid, D. Hybrid differential evolution and particle swarm optimization for optimal well placement. Comput. Geosci. 2013, 17, 249–268. [Google Scholar] [CrossRef]
- Ding, S.; Jiang, H.; Li, J.; Tang, G. Optimization of well placement by combination of a modified particle swarm optimization algorithm and quality map method. Comput. Geosci. 2014, 18, 747–762. [Google Scholar] [CrossRef]
- Min, B.; Park, C.; Kang, J.; Ahn, T.; Chung, S.; Kim, S. Optimal Injector Placement Coupled Multi-objective Genetic Algorithm with a Black-oil Simulator in Waterflooding Project. In Proceedings of the 73rd EAGE Conference & Exhibition, Vienna, Austria, 23–26 May 2011. [Google Scholar]
- Beckner, B.; Xong, X. Field Development Planning Using Simulated Annealing-Optimal Economic Well Scheduling and Placement; Technical Report; Society of Petroleum Engineers (SPE), Inc.: Dallas, TX, USA, 1995. [Google Scholar]
- Parashar, M.; Klie, H.; Catalyurek, U.; Kurc, T.; Bangerth, W.; Matossian, V.; Saltz, J.; Wheeler, M.F. Application of grid-enabled technologies for solving optimization problems in data-driven reservoir studies. Future Gener. Comput. Syst. 2005, 21, 19–26. [Google Scholar] [CrossRef]
- Bangerth, W.; Klie, H.; Wheeler, M.F.; Stoffa, P.L.; Sen, M.K. On optimization algorithms for the reservoir oil well placement problem. Comput. Geosci. 2006, 10, 303–319. [Google Scholar] [CrossRef]
- Afshari, S.; Aminshahidy, B.; Pishvaie, M.R. Application of an improved harmony search algorithm in well placement optimization using streamline simulation. J. Pet. Sci. Eng. 2011, 78, 664–678. [Google Scholar] [CrossRef]
- Kraaijevanger, J.; Egberts, P.J.P.; Valstar, J.R.; Buurman, H.W. Optimal Waterflood Design Using the Adjoint Method. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 26–28 February 2007; Society of Petroleum Engineers: Houston, TX, USA, 2007. [Google Scholar]
- Liu, X.; Reynolds, A. Gradient-based multi-objective optimization with applications to waterflooding optimization. Comput. Geosci. 2015, 20, 677–693. [Google Scholar] [CrossRef]
- Zangl, G.; Hermann, R. Waterflood Pattern Optimization Using Genetic Algorithms with Multi-tank Material Balance. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004; Society of Petroleum Engineers: Houston, TX, USA, 2004. [Google Scholar]
- Guan, X.J.; Wei, L.X.; Yang, J.J. Optimization of operation plan for water injection system in oilfield using hybrid genetic algorithm. Acta Pet. Sin. 2005, 3, 026. [Google Scholar]
- Safarzadeh, M.A.; Motealleh, M.; Moghadasi, J. A novel, streamline-based injection efficiency enhancement method using multi-objective genetic algorithm. J. Pet. Explor. Prod. Technol. 2015, 5, 73–80. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, Q.; Gu, Y. Integrated optimization and control of the production-injection operation systems for hydrocarbon reservoirs. J. Pet. Sci. Eng. 2003, 37, 69–81. [Google Scholar] [CrossRef]
- Khan, H.; Saputelli, L.A.; Ranjan, P.; Carvajal, G.A.; Knabe, S.P.; Wang, F. Multi-Objectives Constrained Waterflood Optimization in Tight Carbonates. In Proceedings of the SPE Reservoir Characterization and Simulation Conference and Exhibition, Abu Dhabi, UAE, 16–18 September 2013; Society of Petroleum Engineers: Abu Dhabi, UAE, 2013. [Google Scholar]
- Wang, Y.X.; Liu, C.L.; Wang, Y.F.; Zhou, S.H. Optimization in oilfield water injection system based on algorithm of ant colony-particle swarm method. J. Daqing Pet. Inst. 2010, 2, 014. [Google Scholar]
- Oliveira, D.F.; Reynolds, A. An adaptive hierarchical multiscale algorithm for estimation of optimal well controls. SPE J. 2014, 19, 909–930. [Google Scholar] [CrossRef]
- Everitt, T.A.; Jennings, J. An improved finite-difference calculation of downhole dynamometer cards for sucker-rod pumps. SPE Prod. Eng. 1992, 7, 121–127. [Google Scholar] [CrossRef]
- Gibbs, S. A review of methods for design and analysis of rod pumping installations. J. Pet. Technol. 1982, 34, 2–931. [Google Scholar] [CrossRef]
- Ehimeakhe, V.M. Calculating Pump Fillage for Well Control Using Transfer Point Location. In Proceedings of the SPE Eastern Regional Meeting, Morgantown, WV, USA, 13–15 October 2010; Society of Petroleum Engineers: Morgantown, WV, USA, 2010. [Google Scholar]
- Krug, D.; Nelsen, S.; Allison, J. Regenerative Hydraulic Lift System. U.S. Patent 8,562,308, 22 October 2013. [Google Scholar]
- Emerick, A.A.; Portella, R.C.M. Production Optimization With Intelligent Wells. In Proceedings of the Latin American & Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 15–18 April 2007; Society of Petroleum Engineers: Buenos Aires, Argentina, 2007. [Google Scholar]
- Humphries, T.D.; Haynes, R.D.; James, L.A. Simultaneous and sequential approaches to joint optimization of well placement and control. Comput. Geosci. 2014, 18, 433–448. [Google Scholar] [CrossRef]
- Humphries, T.D.; Haynes, R.D. Joint optimization of well placement and control for nonconventional well types. J. Pet. Sci. Eng. 2015, 126, 242–253. [Google Scholar] [CrossRef]
- Sun, Z.; Xin, Y.; Sun, Q.; Ma, R.; Zhang, J.; Lv, S.; Cai, M.; Wang, H. Numerical Simulation of the Depressurization Process of a Natural Gas Hydrate Reservoir: An Attempt at Optimization of Field Operational Factors with Multiple Wells in a Real 3D Geological Model. Energies 2016, 9, 714. [Google Scholar] [CrossRef]
- Drouven, M.G.; Grossmann, I.E. Multi-period planning, design and strategic models for long-term, quality-sensitive shale gas development. AIChE J. 2016. [Google Scholar] [CrossRef]
- Drouven, M.G.; Cafaro, D.C.; Grossmann, I.E. Stochastic Programming Models for Optimal Shale Well Development and Refracturing Planning under Uncertainty. AIChE J. 2016. [Google Scholar] [CrossRef]
- Tavallali, M.; Karimi, I.; Halim, A.; Baxendale, D.; Teo, K. Well placement, infrastructure design, facility allocation, and production planning in multireservoir oil fields with surface facility networks. Ind. Eng. Chem. Res. 2014, 53, 11033–11049. [Google Scholar] [CrossRef]
- Brouwer, D.; Jansen, J. Dynamic optimization of water flooding with smart wells using optimal control theory. SPE J. 2004, 9, 391–402. [Google Scholar] [CrossRef]
- Sarma, P.; Aziz, K.; Durlofsky, L.J. Implementation of Adjoint Solution for Optimal Control of Smart wells. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 31 January–2 Feburary 2005; Society of Petroleum Engineers: The Woodlands, TX, USA, 2005. [Google Scholar]
- Forouzanfar, F.; Reynolds, A.C.; Li, G. Optimization of the well locations and completions for vertical and horizontal wells using a derivative-free optimization algorithm. J. Pet. Sci. Eng. 2012, 86, 272–288. [Google Scholar] [CrossRef]
- Sefat, M.H.; Salahshoor, K.; Jamialahmadi, M.; Vahdani, H. The Development of Techniques for the Optimization of Water-flooding Processes in Petroleum Reservoirs Using a Genetic Algorithm and Surrogate Modeling Approach. Energy Sources Part A Recovery Util. Environ. Effects 2014, 36, 1175–1185. [Google Scholar] [CrossRef]
- Isebor, O.J.; Durlofsky, L.J. Biobjective optimization for general oil field development. J. Pet. Sci. Eng. 2014, 119, 123–138. [Google Scholar] [CrossRef]
- Isebor, O.J.; Durlofsky, L.J.; Ciaurri, D.E. A derivative-free methodology with local and global search for the constrained joint optimization of well locations and controls. Comput. Geosci. 2014, 18, 463–482. [Google Scholar] [CrossRef]
- Lei, Y.; Li, S.; Zhang, X.; Zhang, Q.; Guo, L. Optimal Control of Polymer Flooding Based on Maximum Principle. J. Appl. Math. 2012, 2012, 987975. [Google Scholar] [CrossRef]
- Van Doren, J.; Douma, S.G.; Wassing, L.B.M.; Kraaijevanger, J.; De Zwart, A.H. Adjoint-Based Optimization of Polymer Flooding. In Proceedings of the SPE Enhanced Oil Recovery Conference, Kuala Lumpur, Malaysia, 19–21 July 2011; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 2011. [Google Scholar]
- Namdar Zanganeh, M.; Kraaijevanger, J.; Buurman, H.; Jansen, J.; Rossen, W. Adjoint-Based Optimization of a Foam EOR Process. In Proceedings of the ECMOR 13th European Conference on the Mathematics of Oil Recovery, Biarritz, France, 10–13 September 2012. [Google Scholar]
- Mehos, G.J.; Ramirez, W.F. Use of Optimal Control Theory to Optimize Carbon Dioxide Miscible-Flooding Enhanced Oil Recovery. J. Pet. Sci. Eng. 1989, 2, 247–260. [Google Scholar] [CrossRef]
- Shurong, L.; Yang, L.; Xiaodong, Z.; Qiang, Z. Optimal Control Solving of Polymer Flooding Based on a Hybrid Genetic Algorithm. In Proceedings of the IEEE 2010 29th Chinese Control Conference (CCC), Beijing, China, 29–31 July 2010; pp. 5194–5198. [Google Scholar]
- Hui, Z.; Yang, L.; Lin, C. A quantitative mathematic model for polymer flooding water-cut variation. Pet. Explor. Dev. 2010, 37, 737–742. [Google Scholar]
- Ali Ahmadi, M.; Zendehboudi, S.; Lohi, A.; Elkamel, A.; Chatzis, I. Reservoir permeability prediction by neural networks combined with hybrid genetic algorithm and particle swarm optimization. Geophys. Prospect. 2013, 61, 582–598. [Google Scholar] [CrossRef]
- Sayyad, H.; Manshad, A.K.; Rostami, H. Application of hybrid neural particle swarm optimization algorithm for prediction of MMP. Fuel 2014, 116, 625–633. [Google Scholar] [CrossRef]
- Gates, I.; Chakrabarty, N. Optimization of steam assisted gravity drainage in McMurray reservoir. J. Can. Pet. Technol. 2006, 45, 54–62. [Google Scholar] [CrossRef]
- Zhao, D.W.; Wang, J.; Gates, I.D. Optimized solvent-aided steam-flooding strategy for recovery of thin heavy oil reservoirs. Fuel 2013, 112, 50–59. [Google Scholar] [CrossRef]
- Yong, L.J.; Liu, M.J.; Hanqiao, Z.W.J. Optimizing injection parameters of polymer flooding in offshore oilfields by combining surrogate model and genetic algorithm. China Offshore Oil Gas 2012, 4, 009. [Google Scholar]
- Lei, Y.; Li, S.; Zhang, X.; Zhang, Q.; Guo, L. Optimal control of polymer flooding based on mixed-integer iterative dynamic programming. Int. J. Control 2011, 84, 1903–1914. [Google Scholar] [CrossRef]
- Ekkawong, P. Multiobjective Design and Optimization of Polymer Flood Performance. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2013. [Google Scholar]
- Al-Gosayir, M.; Babadagli, T.; Leung, J.Y.W. Optimization of Solvent Additive SAGD Applications using Hybrid Optimization Techniques. In Proceedings of the SPE Enhanced Oil Recovery Conference, Kuala Lumpur, Malaysia, 19–21 July 2011; Society of Petroleum Engineers: Kuala Lumpur, Malaysia, 2011. [Google Scholar]
- Emera, M.K.; Sarma, H.K. Use of Genetic Algorithm to Predict Minimum Miscibility Pressure (MMP) Between Flue Gases and Oil in Design of Flue Gas Injection Project. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Kingdom of Bahrain, 12–15 March 2005; Kingdom of Bahrain Society of Petroleum Engineers: Kingdom of Bahrain, 2005. [Google Scholar]
- Dehghani, S.M.; Sefti, M.V.; Ameri, A.; Kaveh, N.S. Minimum miscibility pressure prediction based on a hybrid neural genetic algorithm. Chem. Eng. Res. Des. 2008, 86, 173–185. [Google Scholar] [CrossRef]
- Chen, S.; Li, H.; Yang, D.; Tontiwachwuthikul, P. Optimal parametric design for water-alternating-gas (WAG) process in a CO2-miscible flooding reservoir. J. Can. Pet. Technol. 2010, 49, 75–82. [Google Scholar] [CrossRef]
- Sen, R. Biotechnology in petroleum recovery: The microbial EOR. Prog. Energy Combust. Sci. 2008, 34, 714–724. [Google Scholar] [CrossRef]
- Horowitz, B.; Guimarães, L.J.D.N.; Dantas, V.; Afonso, S.M.B. A concurrent efficient global optimization algorithm applied to polymer injection strategies. J. Pet. Sci. Eng. 2010, 71, 195–204. [Google Scholar] [CrossRef]
- Jones, D.R. A taxonomy of global optimization methods based on response surfaces. J. Glob. Optim. 2001, 21, 345–383. [Google Scholar] [CrossRef]
- Dixon, T.; Yamaji, K.; van t Veld, K.; Mason, C.F.; Leach, A. The Economics of CO2 Sequestration through Enhanced Oil Recovery. Energy Proc. 2013, 37, 6909–6919. [Google Scholar]
- Jahangiri, H.R.; Zhang, D. Ensemble based co-optimization of carbon dioxide sequestration and enhanced oil recovery. Int. J. Greenh. Gas Control 2012, 8, 22–33. [Google Scholar] [CrossRef]
- Chen, Y.; Oliver, D.S. Ensemble-Based Closed-Loop Optimization Applied to Brugge Field. SPE Reserv. Eval. Eng. 2010, 2013, 56–71. [Google Scholar] [CrossRef]
- Rwechungura, R.W.; Suwartadi, E.; Dadashpour, M.; Kleppe, J.; Foss, B.A. The Norne Field Case—A Unique Comparative Case Study. SPE Intell. Energy Conf. Exhib. 2013. [Google Scholar] [CrossRef]
- Rwechungura, R.; Bhark, E.; Miljeteig, O.T.; Suman, A.; Kourounis, D.; Foss, B.; Hoierand, L.; Kleppe, J. Results of the First Norne Field Case on History Matching and Recovery Optimization Using Production and 4D Seismic Data. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012; Society of Petroleum Engineers: San Antonio, TX, USA, 2012. [Google Scholar]
- Chen, Y.; Oliver, D.S. History matching of the Norne full-field model with an iterative ensemble smoother. SPE Reserv. Eval. Eng. 2014, 17, 244–256. [Google Scholar] [CrossRef]
- Suman, A.; Fernández-Martínez, J.L.; Mukerji, T. Joint Inversion of Time-Lapse Seismic and Production Data for Norne Field. In Proceedings of the 2011 SEG Annual Meeting, San Antonio, TX, USA, 18–23 September 2011; Society of Exploration Geophysicists: San Antonio, TX, USA, 2011. [Google Scholar]
- Hedengren, J.D.; Shishavan, R.A.; Powell, K.M.; Edgar, T.F. Nonlinear modeling, estimation and predictive control in APMonitor. Comput. Chem. Eng. 2014, 70, 133–148. [Google Scholar] [CrossRef]
- Cao, F. Development of a Two-Phase Flow Coupled. Ph.D. Dissertation, University of Texas at Austin, Austin, TX, USA, 2014. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).