Sensitivity-Based Economic NMPC with a Path-Following Approach
Abstract
:1. Introduction
2. NMPC Problem Formulations
2.1. The NMPC Problem
| Algorithm 1: General NMPC algorithm. |
 |
2.2. Ideal NMPC and Advanced-Step NMPC Framework
- Solve the NMPC problem at time k with a predicted state value of time ,
- When the measurement becomes available at time , compute an approximation of the NLP solution using fast sensitivity methods,
- Update , and repeat from Step 1.
3. Sensitivity-Based Path-Following NMPC
3.1. Sensitivity Properties of NLP
- is an isolated minimizer, and the associated multipliers λ and μ are unique.
- for in a neighborhood of , the set of active constraints remains unchanged.
- for in a neighborhood of , there exists a k-times differentiable function , that corresponds to a locally unique minimum for (3).
3.2. Path-Following Based on Sensitivity Properties
| Algorithm 2: Path-following algorithm. |
 |
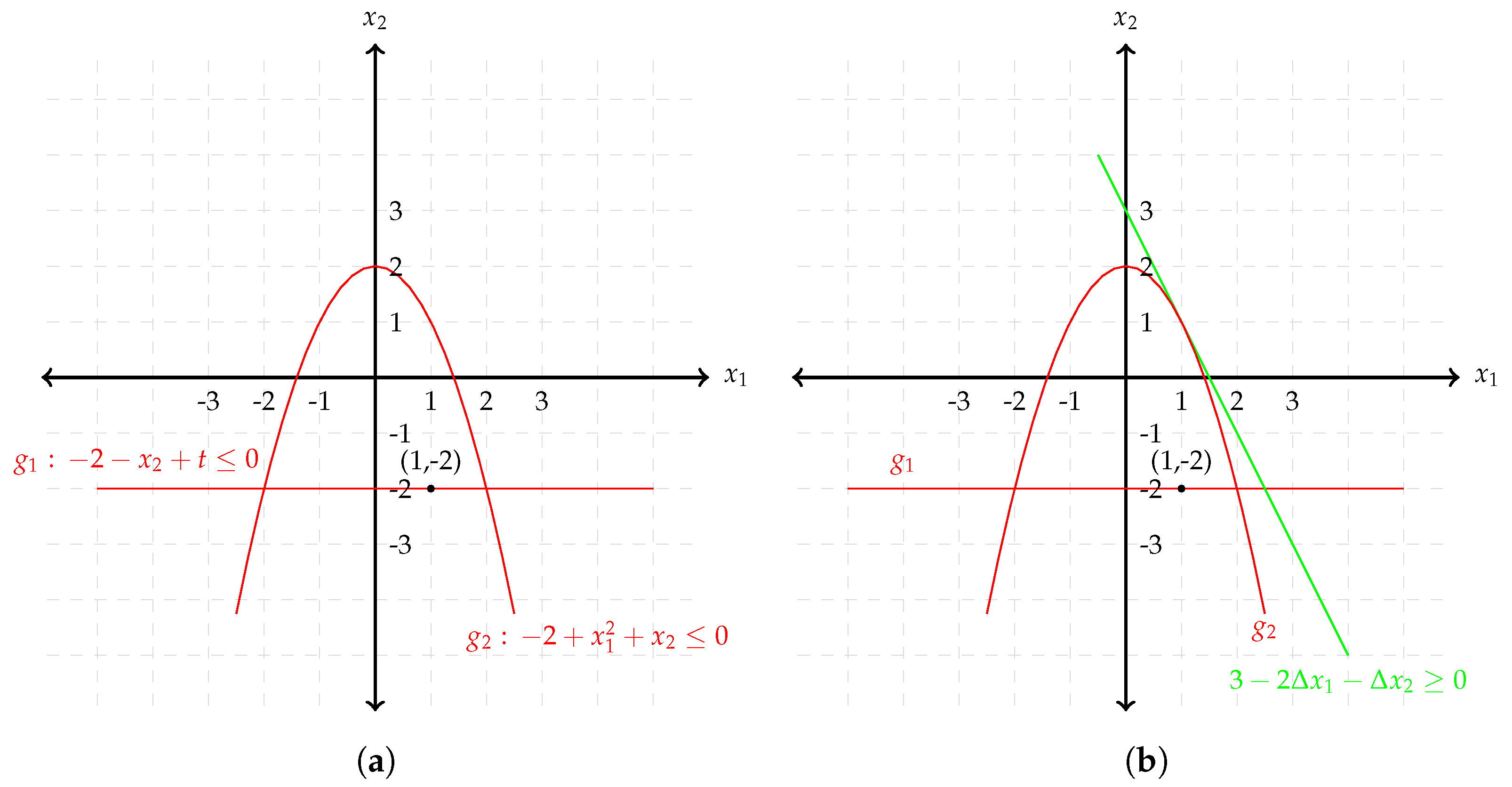
3.3. Discussion of the Path-Following asNMPC Approach
4. Numerical Case Study
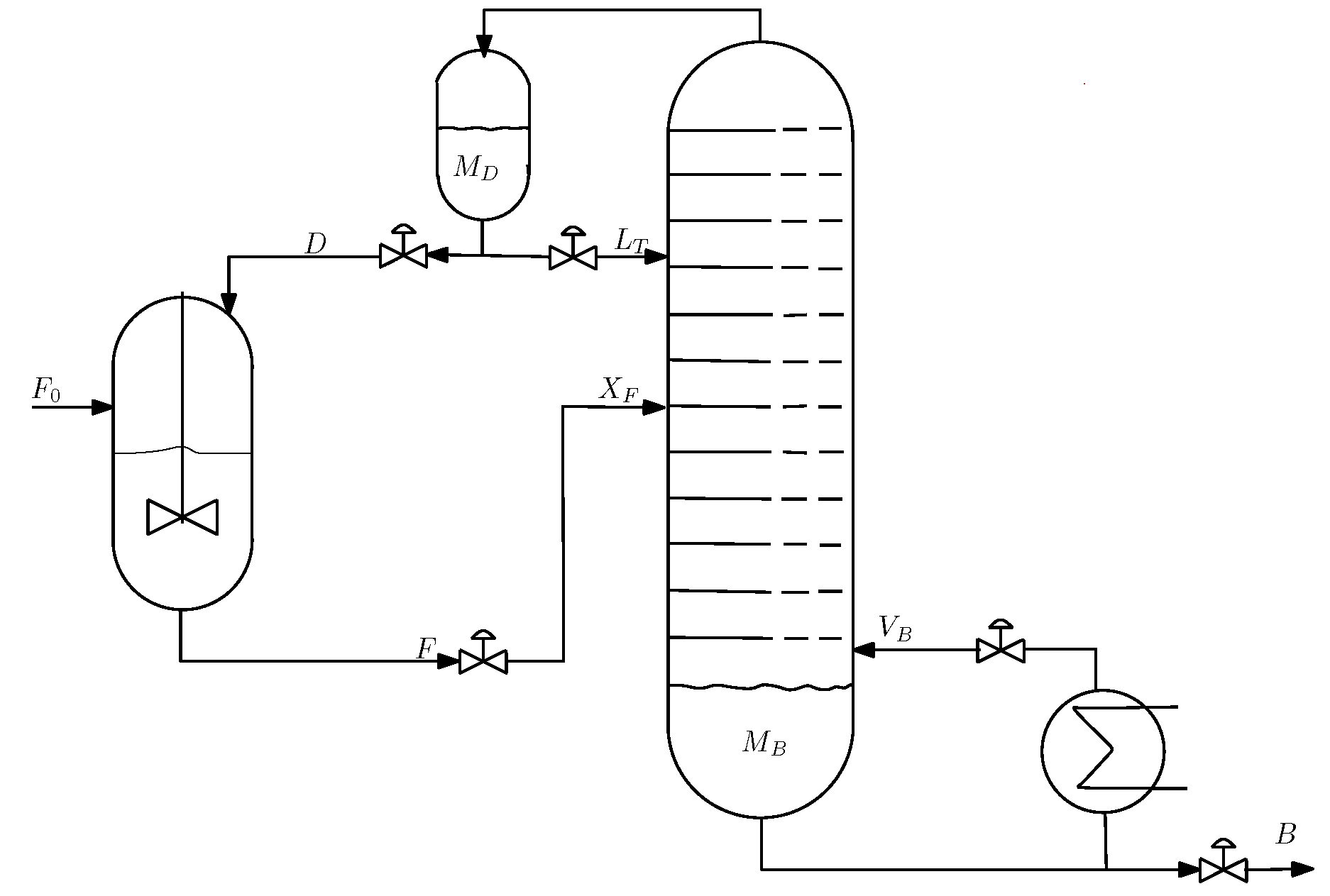
4.1. Process Description
4.2. Comparison of the Open-Loop Optimization Results
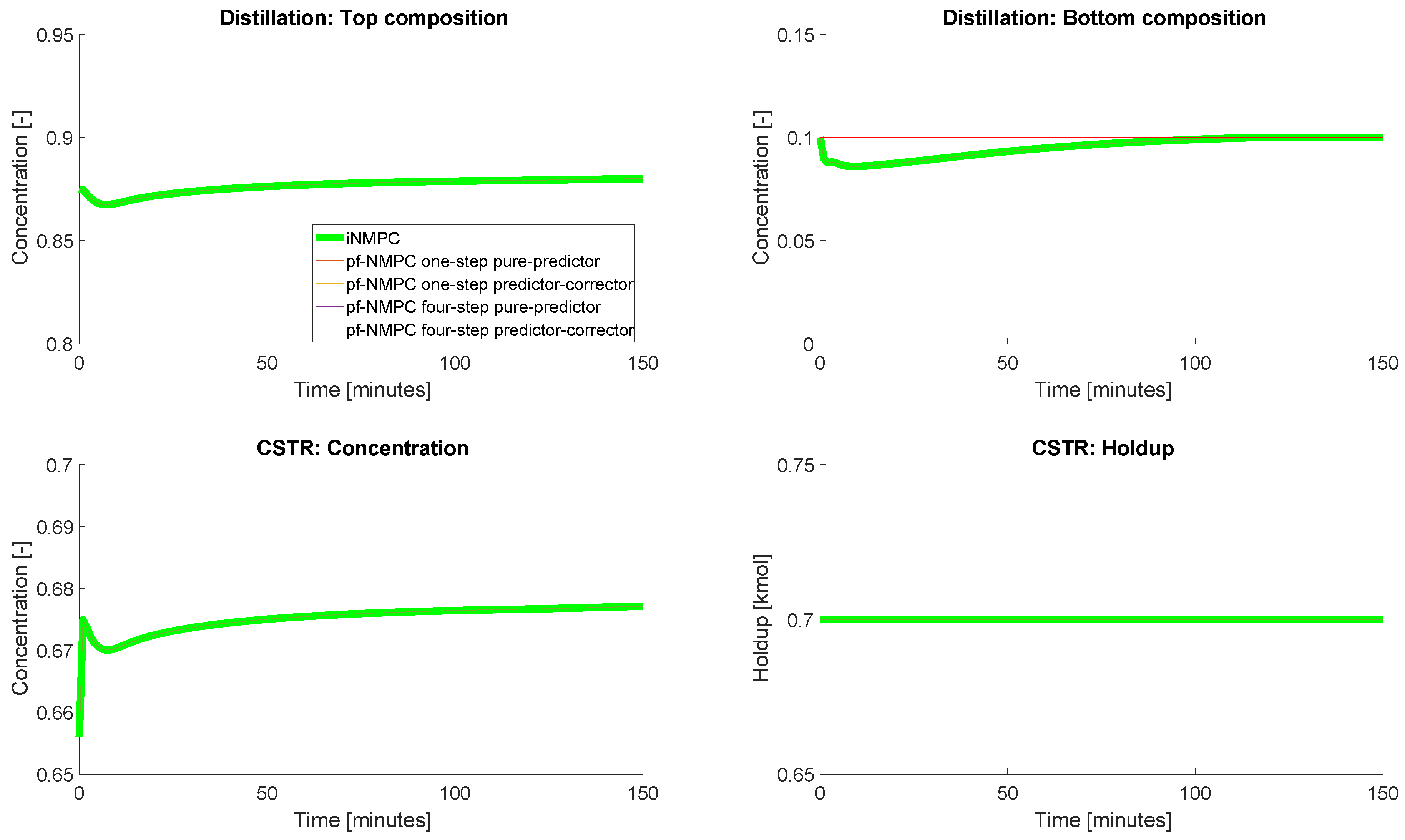
4.3. Closed-Loop Results: No Measurement Noise
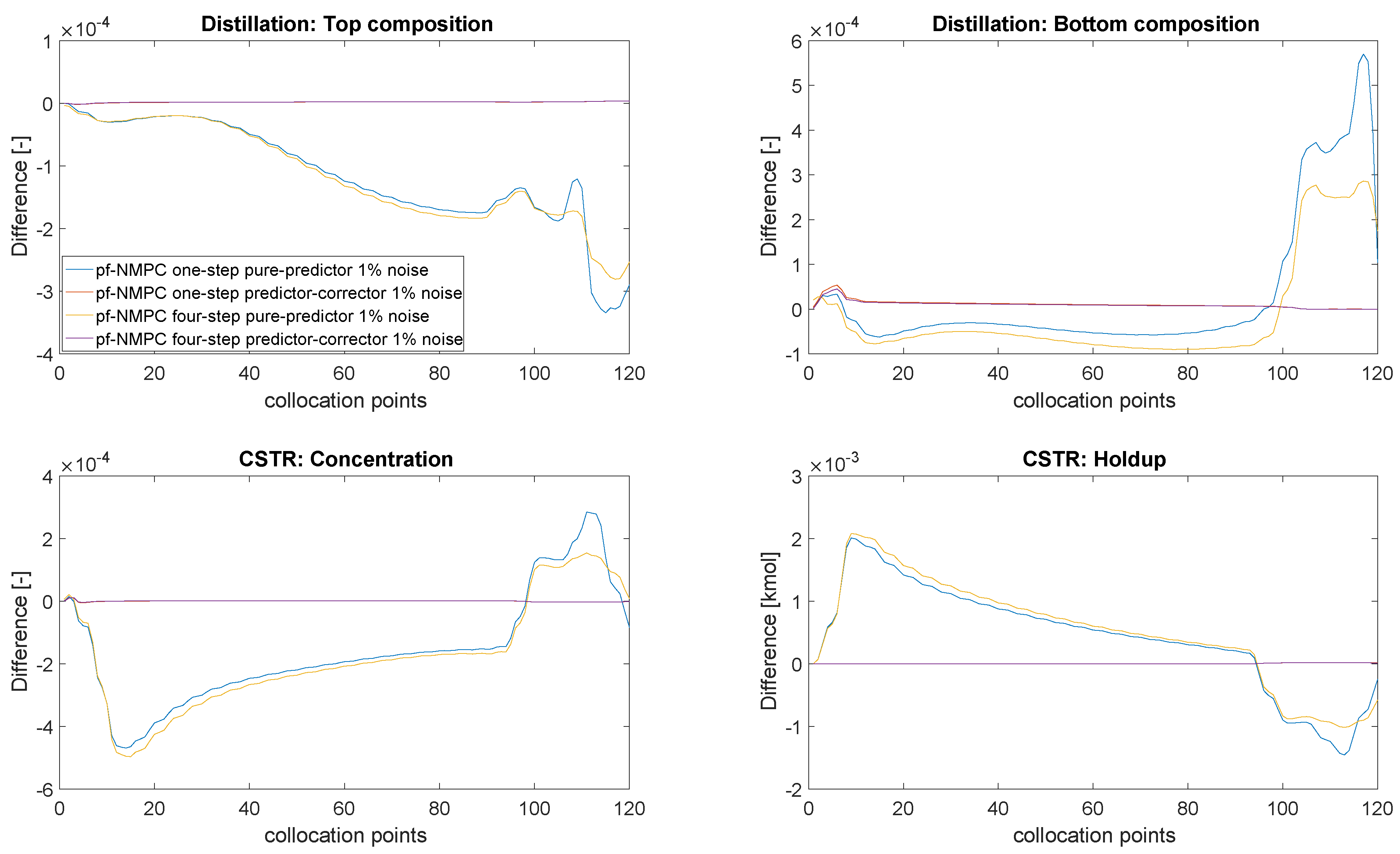
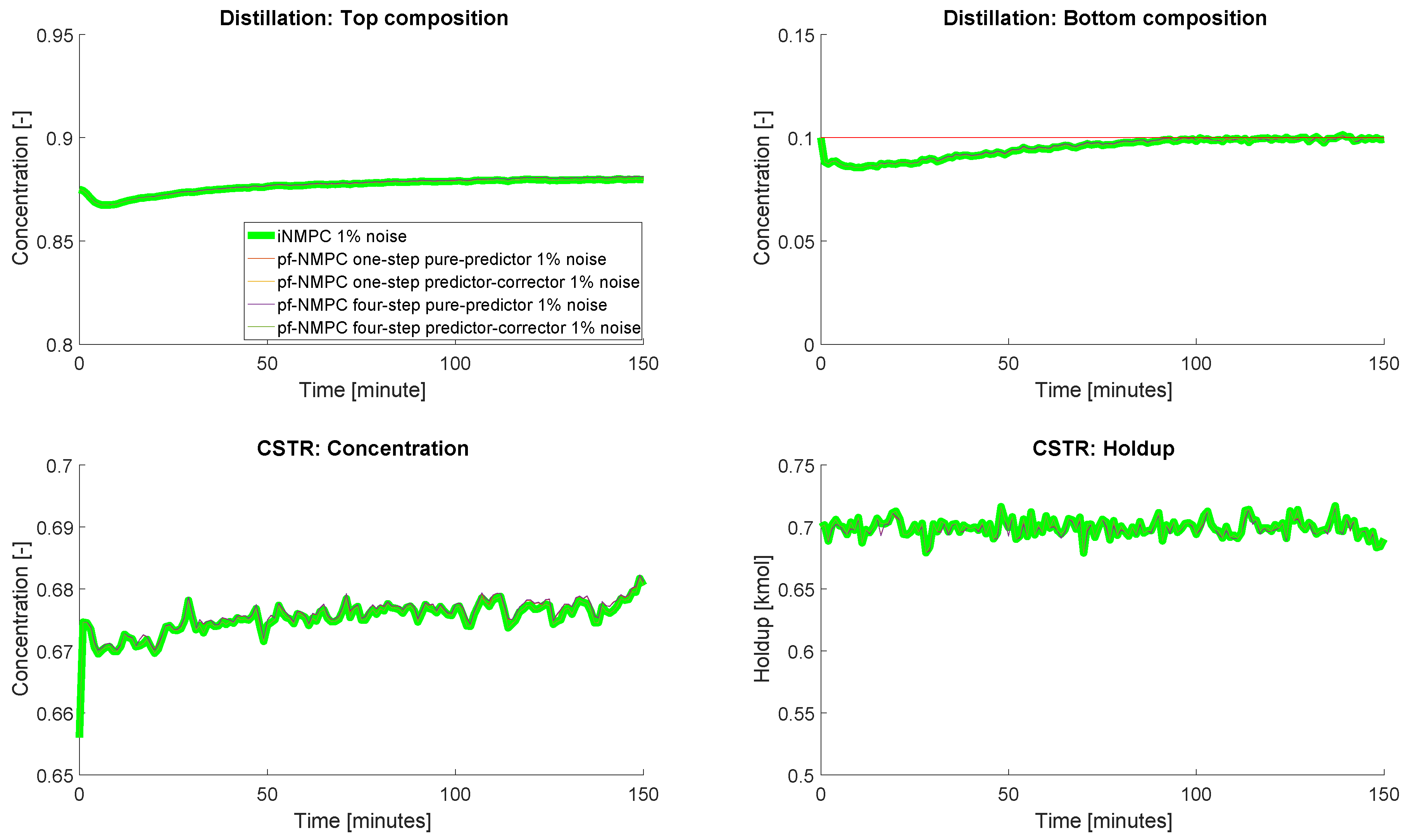
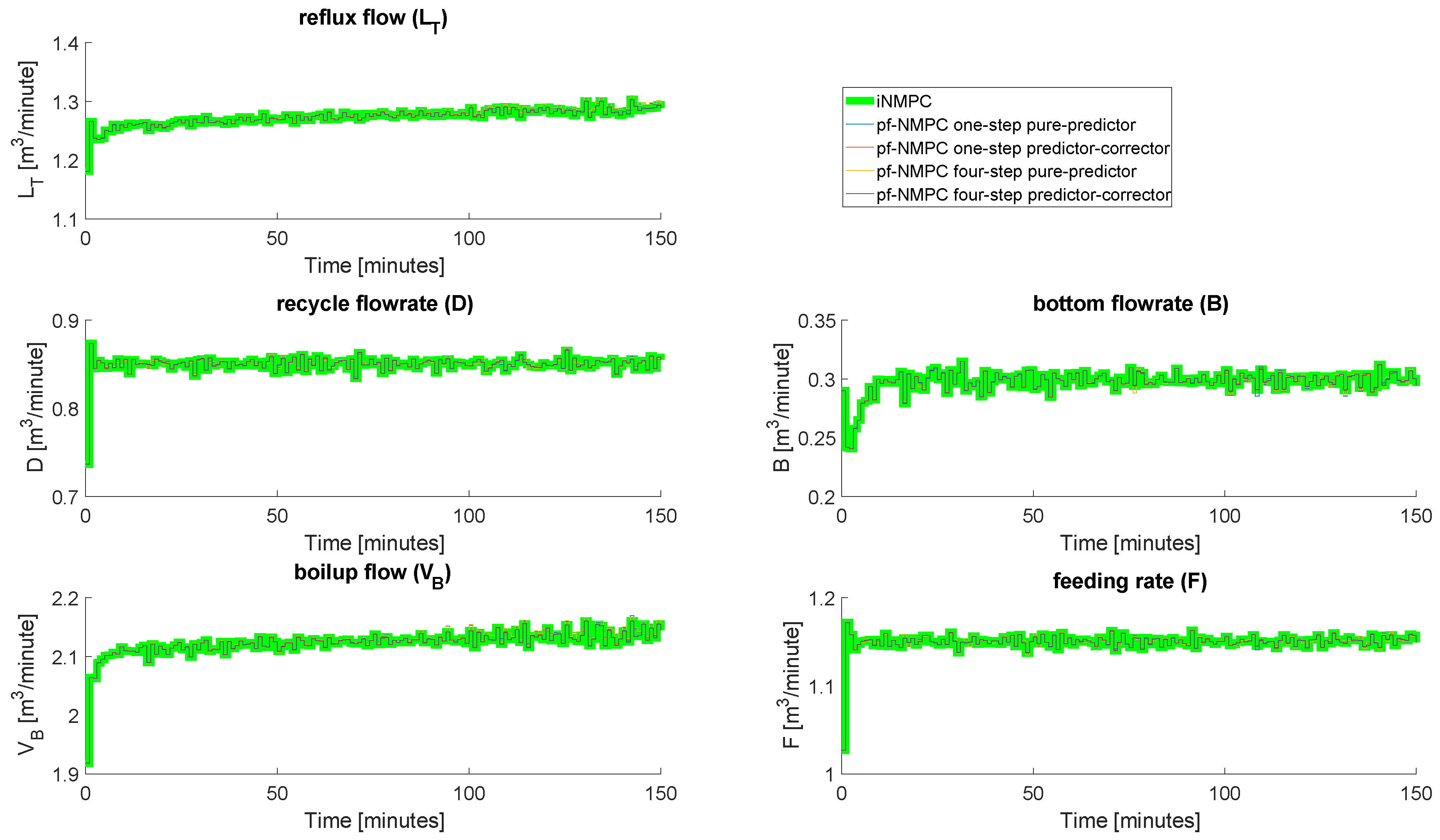
4.4. Closed-Loop Results: With Measurement Noise
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zanin, A.C.; Tvrzská de Gouvêa, M.; Odloak, D. Industrial implementation of a real-time optimization strategy for maximizing production of LPG in a FCC unit. Comput. Chem. Eng. 2000, 24, 525–531. [Google Scholar] [CrossRef]
- Zanin, A.C.; Tvrzská de Gouvêa, M.; Odloak, D. Integrating real-time optimization into the model predictive controller of the FCC system. Control Eng. Pract. 2002, 10, 819–831. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Amrit, R. Optimizing process economic performance using model predictive control. In Nonlinear Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2009; Volume 384, pp. 119–138. [Google Scholar]
- Rawlings, J.B.; Angeli, D.; Bates, C.N. Fundamentals of economic model predictive control. In Proceedings of the 51st IEEE Conference on Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012.
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive methods. J. Process Control 2014, 24, 1156–1178. [Google Scholar] [CrossRef]
- Tran, T.; Ling, K.-V.; Maciejowski, J.M. Economic model predictive control—A review. In Proceedings of the 31st ISARC, Sydney, Australia, 9–11 July 2014.
- Angeli, D.; Amrit, R.; Rawlings, J.B. On average performance and stability of economic model predictive control. IEEE Trans. Autom. Control 2012, 57, 1615–1626. [Google Scholar] [CrossRef]
- Idris, E.A.N.; Engell, S. Economics-based NMPC strategies for the operation and control of a continuous catalytic distillation process. J. Process Control 2012, 22, 1832–1843. [Google Scholar] [CrossRef]
- Findeisen, R.; Allgöwer, F. Computational delay in nonlinear model predictive control. In Proceedings of the International Symposium on Advanced Control of Chemical Proceses (ADCHEM’03), Hongkong, China, 11–14 January 2004.
- Zavala, V.M.; Biegler, L.T. The advanced-step NMPC controller: Optimality, stability, and robustness. Automatica 2009, 45, 86–93. [Google Scholar] [CrossRef]
- Diehl, M.; Bock, H.G.; Schlöder, J.P. A real-time iteration scheme for nonlinear optimization in optimal feedback control. SIAM J. Control Optim. 2005, 43, 1714–1736. [Google Scholar] [CrossRef]
- Würth, L.; Hannemann, R.; Marquardt, W. Neighboring-extremal updates for nonlinear model-predictive control and dynamic real-time optimization. J. Process Control 2009, 19, 1277–1288. [Google Scholar] [CrossRef]
- Biegler, L.T.; Yang, X.; Fischer, G.A.G. Advances in sensitivity-based nonlinear model predictive control and dynamic real-time optimization. J. Process Control 2015, 30, 104–116. [Google Scholar] [CrossRef]
- Wolf, I.J.; Marquadt, W. Fast NMPC schemes for regulatory and economic NMPC—A review. J. Process Control 2016, 44, 162–183. [Google Scholar] [CrossRef]
- Diehl, M.; Bock, H.G.; Schlöder, J.P.; Findeisen, R.; Nagy, Z.; Allgöwer, F. Real-time optimization and nonlinear model predictive control of processes governed by differential-algebraic equations. J. Process Control 2002, 12, 577–585. [Google Scholar] [CrossRef]
- Gros, S.; Quirynen, R.; Diehl, M. An improved real-time economic NMPC scheme for Wind Turbine control using spline-interpolated aerodynamic coefficients. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 935–940.
- Gros, S.; Vukov, M.; Diehl, M. A real-time MHE and NMPC scheme for wind turbine control. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 1007–1012.
- Ohtsuka, T. A continuation/GMRES method for fast computation of nonlinear receding horizon control. Automatica 2004, 40, 563–574. [Google Scholar] [CrossRef]
- Li, W.C.; Biegler, L.T. Multistep, Newton-type control strategies for constrained nonlinear processes. Chem. Eng. Res. Des. 1989, 67, 562–577. [Google Scholar]
- Pirnay, H.; López-Negrete, R.; Biegler, L.T. Optimal sensitivity based on IPOPT. Math. Program. Comput. 2002, 4, 307–331. [Google Scholar] [CrossRef]
- Yang, X.; Biegler, L.T. Advanced-multi-step nonlinear model predictive control. J. Process Control 2013, 23, 1116–1128. [Google Scholar] [CrossRef]
- Kadam, J.; Marquardt, W. Sensitivity-based solution updates in closed-loop dynamic optimization. In Proceedings of the DYCOPS 7 Conference, Cambridge, MA, USA, 5–7 July 2004.
- Würth, L.; Hannemann, R.; Marquardt, W. A two-layer architecture for economically optimal process control and operation. J. Process Control 2011, 21, 311–321. [Google Scholar] [CrossRef]
- Jäschke, J.; Yang, X.; Biegler, L.T. Fast economic model predictive control based on NLP-sensitivities. J. Process Control 2014, 24, 1260–1272. [Google Scholar] [CrossRef]
- Fiacco, A.V. Introduction to Sensitivity and Stability Analysis in Nonlinear Programming; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Bonnans, J.F.; Shapiro, A. Optimization problems with perturbations: A guided tour. SIAM Rev. 1998, 40, 228–264. [Google Scholar] [CrossRef]
- Levy, A.B. Solution sensitivity from general principles. SIAM J. Control Optim. 2001, 40, 1–38. [Google Scholar] [CrossRef]
- Kungurtsev, V.; Diehl, M. Sequential quadratic programming methods for parametric nonlinear optimization. Comput. Optim. Appl. 2014, 59, 475–509. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariate Feedback Control: Analysis and Design; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Andersson, J. A General Purpose Software Framework for Dynamic Optimization. Ph.D. Thesis, Arenberg Doctoral School, KU Leuven, Leuven, Belgium, October 2013. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Murtagh, B.A.; Saunders, M.A. A projected lagrangian algorithm and its implementation for sparse nonlinear constraints. Math. Program. Study 1982, 16, 84–117. [Google Scholar]

| Reaction | Reaction Rate Constant (min−1) | Activation Energy (in J/mol) |
|---|---|---|
| Parameter | Value |
|---|---|
| 1.5 | |
| number of stages | 41 |
| feed stage location | 21 |
| Average Approximation Error between ideal NMPC and Path-Following (PF) asNMPC | |
|---|---|
| PF with predictor QP, 1 step PF with predictor QP, 4 steps PF with predictor-corrector QP, 1 step PF with predictor-corrector QP, 4 steps | 4.516 4.517 1.333 × 10−2 1.282 × 10−2 |
| Economic NMPC Controller | Accumulated Stage Cost | |
|---|---|---|
| iNMPC | −296.42 | |
| pure-predictor QP: | ||
| pf-NMPC one step | −296.42 | |
| pf-NMPC four steps | −296.42 | |
| predictor-corrector QP: | ||
| pf-NMPC one step | −296.42 | |
| pf-NMPC four steps | −296.42 |
| Economic NMPC Controller | Accumulated Stage Cost | |
|---|---|---|
| iNMPC | −296.82 | |
| pure-predictor QP: | ||
| pf-NMPC one step | −297.54 | |
| pf-NMPC four steps | −297.62 | |
| predictor-corrector QP: | ||
| pf-NMPC one step | −296.82 | |
| pf-NMPC four steps | −296.82 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suwartadi, E.; Kungurtsev, V.; Jäschke, J. Sensitivity-Based Economic NMPC with a Path-Following Approach. Processes 2017, 5, 8. https://doi.org/10.3390/pr5010008
Suwartadi E, Kungurtsev V, Jäschke J. Sensitivity-Based Economic NMPC with a Path-Following Approach. Processes. 2017; 5(1):8. https://doi.org/10.3390/pr5010008
Chicago/Turabian StyleSuwartadi, Eka, Vyacheslav Kungurtsev, and Johannes Jäschke. 2017. "Sensitivity-Based Economic NMPC with a Path-Following Approach" Processes 5, no. 1: 8. https://doi.org/10.3390/pr5010008
APA StyleSuwartadi, E., Kungurtsev, V., & Jäschke, J. (2017). Sensitivity-Based Economic NMPC with a Path-Following Approach. Processes, 5(1), 8. https://doi.org/10.3390/pr5010008







