Embedded Control in Wearable Medical Devices: Application to the Artificial Pancreas
Abstract
:1. Introduction
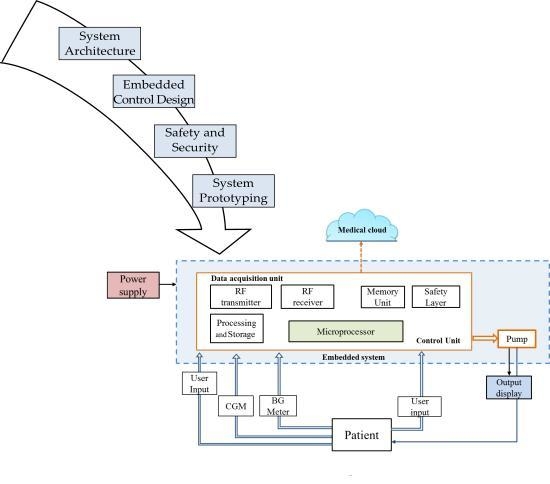
2. AP System Architecture
2.1. Components of the AP System
2.2. Hardware Configurations of the AP System
2.2.1. Configuration A
2.2.2. Configuration B
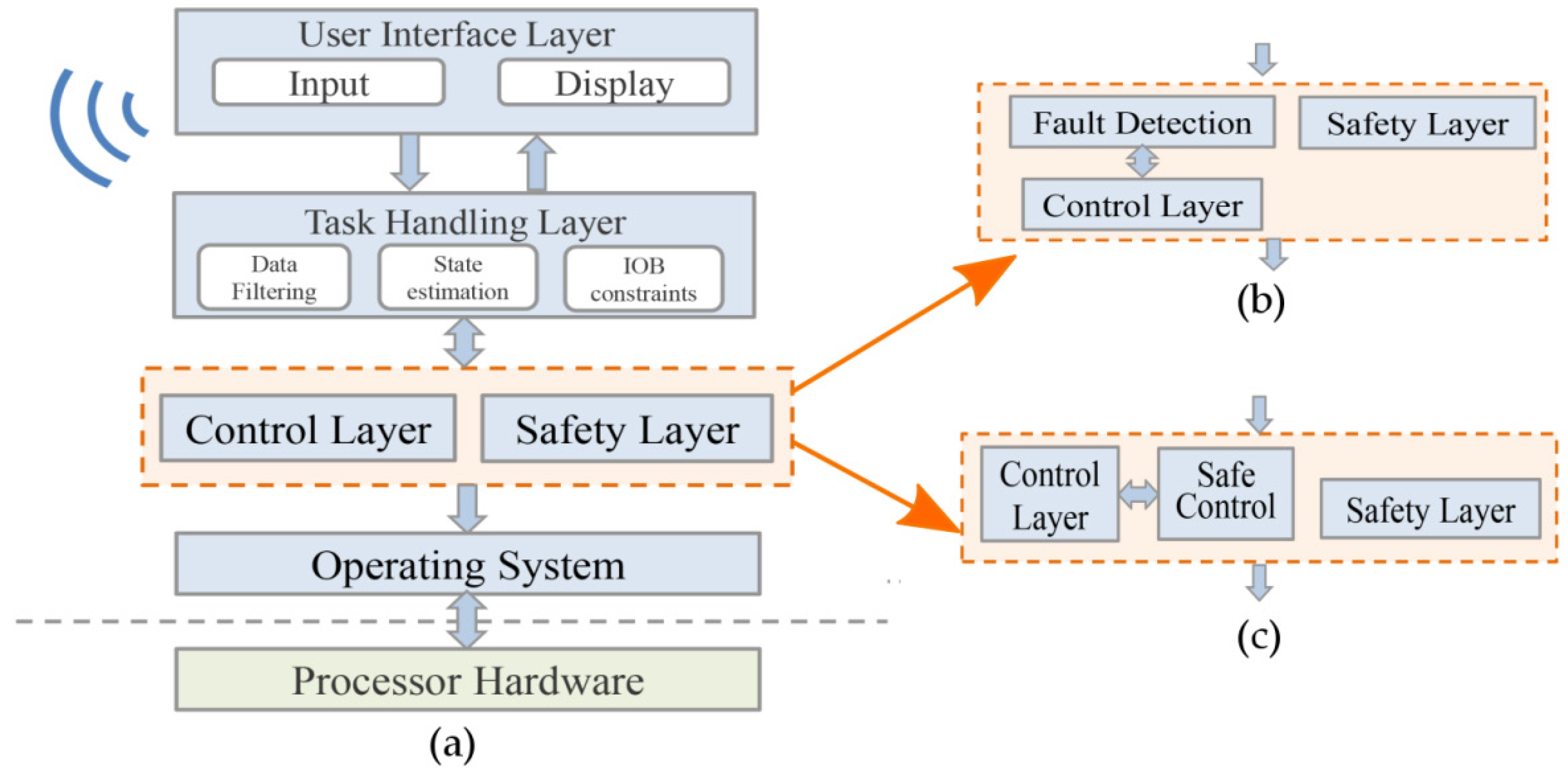
2.3. Software Architecture
2.3.1. User Interface Layer
2.3.2. Task Handling Layer
2.3.3. Control and Safety Layer
2.3.4. Operating System and Hardware Layers
3. Control Algorithms for the Artificial Pancreas
3.1. Proportional Integral Derivative Control
3.2. Fuzzy Logic Control
3.3. Model Predictive Control
3.3.1. Explicit/Multi-Parametric MPC
3.3.2. Modified On-Line MPC for Embedded Control Systems
3.3.3. Optimization Algorithms and Solvers
3.3.3.1. Active-Set Method
3.3.3.2. Interior Point Method
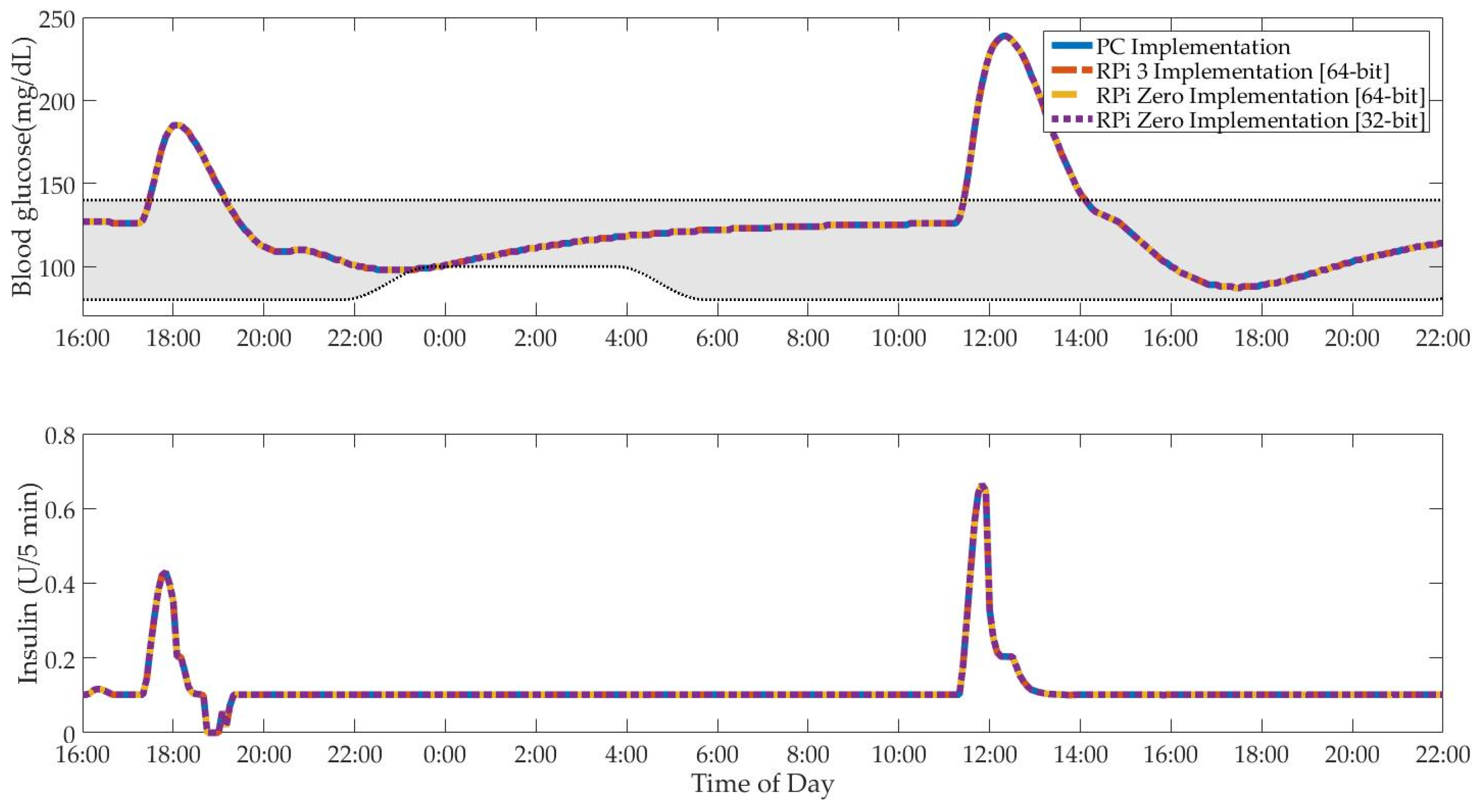
3.3.4. Performance Comparison
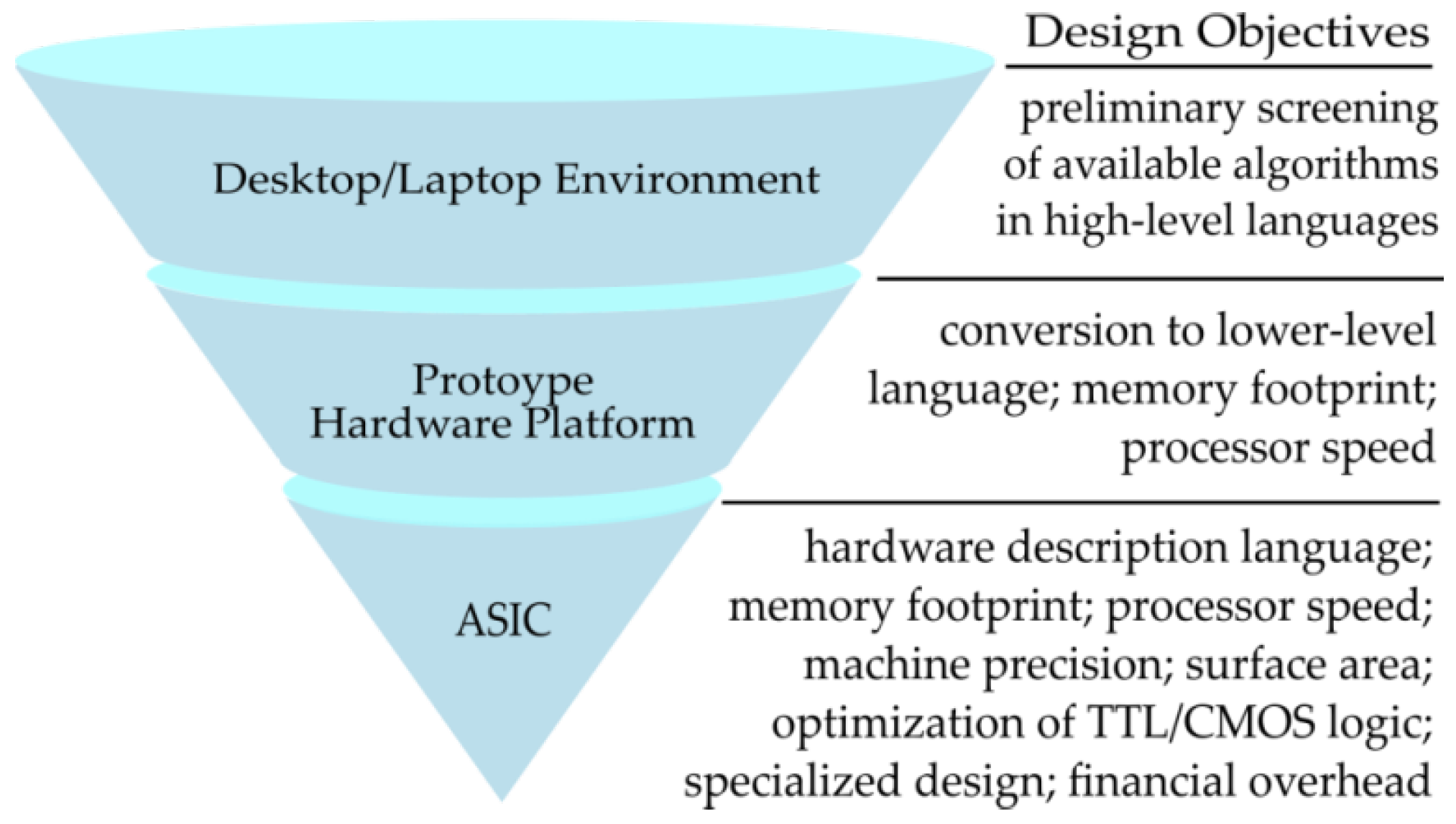
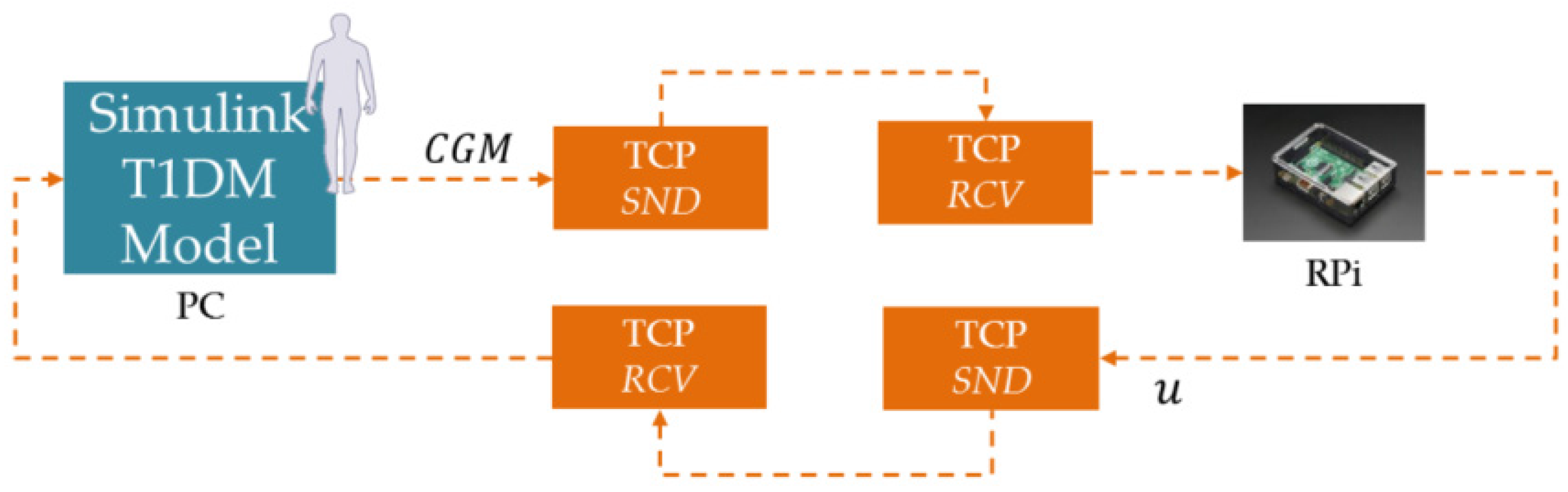
4. Brief Overview on Design Approaches
5. Key Challenges of Embedded Artificial Pancreas Systems
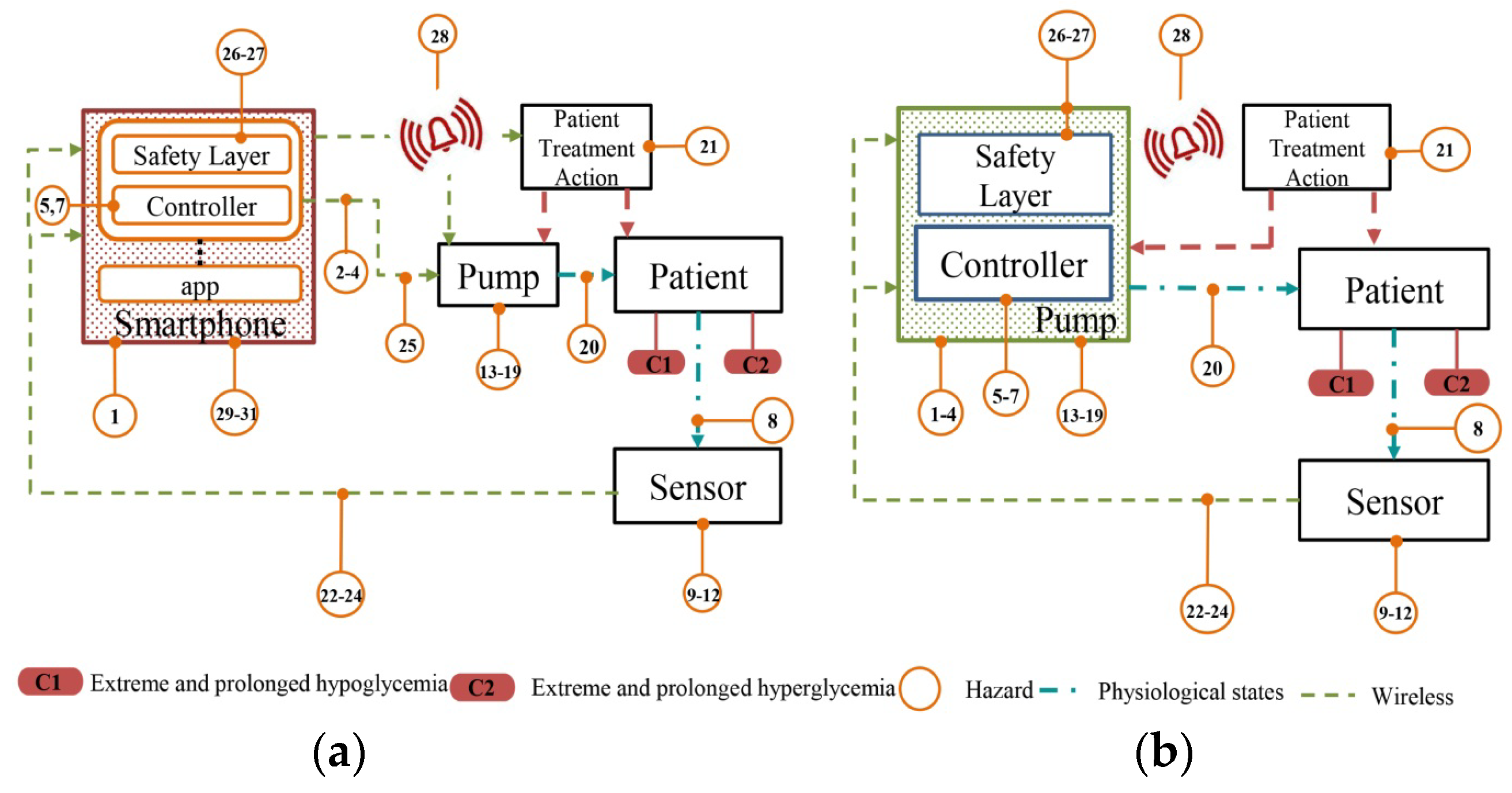
5.1. Known and Foreseeable Hazards Associated with the Operation of the AP System
5.2. Communication: Security and Confidentiality
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- National Center for Chronic Disease Prevention and Health Promotion. National Diabetes Statistics Report. 2014. Available online: https://www.cdc.gov/diabetes/pubs/statsreport14/national-diabetes-report-web.pdf (accessed on 5 May 2016). [Google Scholar]
- Doyle, F.J., III; Huyett, L.M.; Lee, J.B.; Zisser, H.C.; Dassau, E. Closed-loop artificial pancreas systems: Engineering the algorithms. Diabetes Care 2014, 37, 1191–1197. [Google Scholar] [CrossRef] [PubMed]
- Nimri, R.; Phillip, M. Artificial pancreas: Fuzzy logic and control of glycemia. Curr. Opin. Endocrinol. Diabetes Obes. 2014, 21, 251–256. [Google Scholar] [CrossRef] [PubMed]
- Mauseth, R.; Lord, S.M.; Hirsch, I.B.; Kircher, R.C.; Matheson, D.P.; Greenbaum, C.J. Stress testing of an artificial pancreas system with pizza and exercise leads to improvements in the system’s fuzzy logic controller. J. Diabetes Sci. Technol. 2015, 9, 1253–1259. [Google Scholar] [CrossRef] [PubMed]
- Ly, T.T.; Roy, A.; Grosman, B.; Shin, J.; Campbell, A.; Monirabbasi, S.; Liang, B.; Von Eyben, R.; Shanmugham, S.; Clinton, P.; et al. Day and night closed-loop control using the integrated medtronic hybrid closed-loop system in type 1 diabetes at diabetes camp. Diabetes Care 2015, 38, 1205–1211. [Google Scholar] [CrossRef] [PubMed]
- Pinsker, J.E.; Lee, J.B.; Dassau, E.; Seborg, D.E.; Bradley, P.K.; Gondhalekar, R.; Bevier, W.C.; Huyett, L.; Zisser, H.C.; Doyle, F.J., III. Randomized crossover comparison of personalized MPC and PID control algorithms for the artificial pancreas. Diabetes Care 2016, 39, 1135–1142. [Google Scholar] [CrossRef] [PubMed]
- Harvey, R.A.; Dassau, E.; Bevier, W.C.; Seborg, D.E.; Jovanovič, L.; Doyle, F.J., III; Zisser, H.C. Clinical evaluation of an automated artificial pancreas using zone-model predictive control and health monitoring system. Diabetes Technol. Ther. 2014, 16, 348–357. [Google Scholar] [CrossRef] [PubMed]
- Dassau, E.; Brown, S.A.; Basu, A.; Pinsker, J.E.; Kudva, Y.C.; Gondhalekar, R.; Patek, S.; Lv, D.; Schiavon, M.; Lee, J.B.; et al. Adjustment of open-loop settings to improve closed-loop results in type 1 diabetes: A multicenter randomized trial. J. Clin. Endocrinol. Metab. 2015, 100, 3878–3886. [Google Scholar] [CrossRef] [PubMed]
- Stewart, Z.A.; Wilinska, M.E.; Hartnell, S.; Temple, R.C.; Rayman, G.; Stanley, K.P.; Simmons, D.; Law, G.R.; Scott, E.M.; Hovorka, R.; et al. Closed-Loop Insulin Delivery during Pregnancy in Women with Type 1 Diabetes. N. Engl. J. Med. 2016, 375, 644–654. [Google Scholar] [CrossRef] [PubMed]
- Del Favero, S.; Place, J.; Kropff, J.; Messori, M.; Keith-Hynes, P.; Visentin, R.; Monaro, M.; Galasso, S.; Boscari, F.; Toffanin, C.; et al. Multicenter outpatient dinner/overnight reduction of hypoglycemia and increased time of glucose in target with a wearable artificial pancreas using modular model predictive control in adults with type 1 diabetes. Diabetes Obes. Metab. 2015, 17, 468–476. [Google Scholar] [CrossRef] [PubMed]
- Nimri, R.; Phillip, M. Toward Automation of Insulin Delivery—Management Solutions for Type 1 Diabetes. Endocr. Dev. 2016, 30, 1–13. [Google Scholar] [PubMed]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Joosten, D.A.; Van Den Boom, T.J.J.; Lombaerts, T.J.J. Fault-tolerant control using dynamic inversion and model-predictive control applied to an aerospace benchmark. In Proceedings of the 17th IFAC World Congress, Seoul, Korea, 6–11 July 2008; pp. 12030–12035.
- Hrovat, D.; Di Cairano, S.; Tseng, H.E.; Kolmanovsky, I.V. The development of Model Predictive Control in automotive industry: A survey. In Proceedings of the 2012 IEEE International Conference on Control Applications, Dubrovnik, Croatia, 3–5 October 2012; pp. 295–302.
- Valencia-Palomo, G.; Rossiter, J.A. Efficient suboptimal parametric solutions to predictive control for PLC applications. Control Eng. Pract. 2011, 19, 732–743. [Google Scholar] [CrossRef]
- Dassau, E.; Zisser, H.; Harvey, R.A.; Percival, M.W.; Grosman, B.; Bevier, W.; Atlas, E.; Miller, S.; Nimri, R.; Jovanovič, L.; et al. Clinical evaluation of a personalized artificial pancreas. Diabetes Care 2013, 36, 801–809. [Google Scholar] [CrossRef] [PubMed]
- Hovorka, R.; Elleri, D.; Thabit, H.; Allen, J.M.; Leelarathna, L.; El-Khairi, R.; Kumareswaran, K.; Caldwell, K.; Calhoun, P.; Kollman, C.; et al. Overnight closed-loop insulin delivery in young people with type 1 diabetes: A free-living, randomized clinical trial. Diabetes Care 2014, 37, 1204–1211. [Google Scholar] [CrossRef] [PubMed]
- El-Khatib, F.H.; Russell, S.J.; Magyar, K.L.; Sinha, M.; McKeon, K.; Nathan, D.M.; Damiano, E.R. Autonomous and continuous adaptation of a bihormonal bionic pancreas in adults and adolescents with type 1 diabetes. J. Clin. Endocrinol. Metab. 2014, 99, 1701–1711. [Google Scholar] [CrossRef] [PubMed]
- Gondhalekar, R.; Dassau, E.; Doyle, F.J., III. Periodic zone-MPC with asymmetric costs for outpatient-ready safety of an artificial pancreas to treat type 1 diabetes. Automatica 2016, 71, 237–246. [Google Scholar] [CrossRef]
- Jacobs, P.G.; El Youssef, J.; Castle, J.; Bakhtiani, P.; Branigan, D.; Breen, M.; Bauer, D.; Preiser, N.; Leonard, G.; Stonex, T.; et al. Automated control of an adaptive bihormonal, dual-sensor artificial pancreas and evaluation during inpatient studies. IEEE Trans. Biomed. Eng. 2014, 61, 2569–2581. [Google Scholar] [CrossRef] [PubMed]
- Kovatchev, B.P.; Renard, E.; Cobelli, C.; Zisser, H.C.; Keith-Hynes, P.; Anderson, S.M.; Brown, S.A.; Chernavvsky, D.R.; Breton, M.D.; Mize, L.B.; et al. Safety of outpatient closed-loop control: First randomized crossover trials of a wearable artificial pancreas. Diabetes Care 2014, 37, 1789–1796. [Google Scholar] [CrossRef] [PubMed]
- Keith-Hynes, P.; Mize, L.B.; Robert, A.; Place, J. The diabetes assistant: A smartphone-based system for real-time control of blood glucose. Electronics 2014, 3, 609–623. [Google Scholar] [CrossRef]
- Kovatchev, B.P.; Renard, E.; Cobelli, C.; Zisser, H.C.; Keith-Hynes, P.; Anderson, S.M.; Brown, S.A.; Chernavvsky, D.R.; Breton, M.D.; Farret, A.; et al. Feasibility of outpatient fully integrated closed-loop control. Diabetes Care 2013, 36, 1851–1858. [Google Scholar] [CrossRef] [PubMed]
- Anderson, S.M.; Raghinaru, D.; Pinsker, J.E.; Boscari, F.; Renard, E.; Buckingham, B.A.; Nimri, R.; Doyle, F.J., III; Brown, S.A.; Keith-Hynes, P.; et al. Multinational home use of closed-loop control is safe and effective. Diabetes Care 2016, 39, 1143–1150. [Google Scholar] [CrossRef] [PubMed]
- Renard, E.; Farret, A.; Kropff, J.; Bruttomesso, D.; Messori, M.; Place, J.; Visentin, R.; Calore, R.; Toffanin, C.; Di Palma, F.; et al. Day and Night Closed-Loop Glucose Control in Patients with Type 1 Diabetes under Free-Living Conditions: Results of a Single-Arm 1-Month Experience Compared with a Previously Reported Feasibility Study of Evening and Night at Home. Diabetes Care 2016, 39, 1151–1160. [Google Scholar] [CrossRef] [PubMed]
- Huyett, L.M.; Ly, T.T.; Reuschel-DiVirgilio, S.; Clay, S.M.; Bevier, W.C.; Gondhalekar, R.; Dassau, E.; Forlenza, G.P.; Doyle, F.J., III; Pinsker, J.E.; et al. Outpatient closed-loop control with unannounced moderate exercise in adolescents using zone model predictive control. Diabetes Technol. Ther. 2016, 18, A24. [Google Scholar]
- Kropff, J.; Del Favero, S.; Place, J.; Toffanin, C.; Visentin, R.; Monaro, M.; Messori, M.; Di Palma, F.; Lanzola, G.; Farret, A.; et al. 2 Month evening and night closed-loop glucose control in patients with type 1 diabetes under free-living conditions: A randomised crossover trial. Lancet Diabetes Endocrinol. 2015, 3, 10–15. [Google Scholar] [CrossRef]
- Russell, S.J.; Hillard, M.A.; Balliro, C.; Magyar, K.L.; Selagamsetty, R.; Sinha, M.; Grennan, K.; Mondesir, D.; Ehklaspour, L.; Zheng, H.; et al. Day and night glycaemic control with a bionic pancreas versus conventional insulin pump therapy in preadolescent children with type 1 diabetes: A randomised crossover trial. Lancet Diabetes Endocrinol. 2016, 4, 233–243. [Google Scholar] [CrossRef]
- Elleri, D.; Allen, J.M.; Biagioni, M.; Kumareswaran, K.; Leelarathna, L.; Caldwell, K.; Nodale, M.; Wilinska, M.E.; Acerini, C.L.; Dunger, D.B.; et al. Evaluation of a portable ambulatory prototype for automated overnight closed-loop insulin delivery in young people with type 1 diabetes. Pediatr. Diabetes 2012, 13, 449–453. [Google Scholar] [CrossRef] [PubMed]
- Thabit, H.; Tauschmann, M.; Allen, J.M.; Leelarathna, L.; Hartnell, S.; Wilinska, M.E.; Acerini, C.L.; Dellweg, S.; Benesch, C.; Heinemann, L.; et al. Home use of an artificial beta cell in type 1 diabetes. N. Engl. J. Med. 2015, 373, 2129–2140. [Google Scholar] [CrossRef] [PubMed]
- Thabit, H.; Lubina-Solomon, A.; Stadler, M.; Leelarathna, L.; Walkinshaw, E.; Pernet, A.; Allen, J.M.; Iqbal, A.; Choudhary, P.; Kumareswaran, K.; et al. Home use of closed-loop insulin delivery for overnight glucose control in adults with type 1 diabetes: A 4-week, multicentre, randomised crossover study. Lancet Diabetes Endocrinol. 2014, 2, 701–709. [Google Scholar] [CrossRef]
- Tauschmann, M.; Allen, J.M.; Wilinska, M.E.; Thabit, H.; Stewart, Z.; Cheng, P.; Kollman, C.; Acerini, C.L.; Dunger, D.B.; Hovorka, R. Day-and-night hybrid closed-loop insulin delivery in adolescents with type 1 diabetes: A free-living, randomized clinical trial. Diabetes Care 2016, 39. [Google Scholar] [CrossRef] [PubMed]
- Grosman, B.; Ilany, J.; Roy, A.; Kurtz, N.; Wu, D.; Parikh, N.; Voskanyan, G.; Konvalina, N.; Mylonas, C.; Gottlieb, R.; et al. Hybrid closed-loop insulin delivery in type 1 diabetes during supervised outpatient conditions. J. Diabetes Sci. Technol. 2016, 10, 708–713. [Google Scholar] [CrossRef] [PubMed]
- Blauw, H.; Van Bon, A.; Koops, R.; DeVries, J. Performance and safety of an integrated bihormonal artificial pancreas for fully automated glucose control at home. Diabetes Obes. Metab. 2016, 18, 671–677. [Google Scholar] [CrossRef] [PubMed]
- Reddy, M.; Herrero, P.; Sharkawy, M.; Pesl, P.; Jugnee, N.; Pavitt, D.; Godsland, I.; Alberti, G.; Toumazou, C.; Johnston, D.; et al. Metabolic control with the bio-inspired artificial pancreas in adults with type 1 diabetes: A 24-hour randomized controlled crossover study. J. Diabetes Sci. Technol. 2015, 17, 405–413. [Google Scholar] [CrossRef] [PubMed]
- Capozzi, D.; Lanzola, G. A generic telemedicine infrastructure for monitoring an artificial pancreas trial. Comput. Methods Programs Biomed. 2013, 110, 343–353. [Google Scholar] [CrossRef] [PubMed]
- Place, J.; Robert, A.; Ben Brahim, N.; Keith-Hynes, P.; Farret, A.; Pelletier, M.-J.; Buckingham, B.; Breton, M.; Kovatchev, B.; Renard, E. DiAs web monitoring: A real-time remote monitoring system designed for artificial pancreas outpatient trials. J. Diabetes Sci. Technol. 2013, 7, 1427–1435. [Google Scholar] [CrossRef] [PubMed]
- Altia Insulin Pump Starts GUI Revolution. Available online: http://www.altia.com/downloads/case_studies/tandem_case_study.pdf (accessed on 6 February 2016).
- Mossman, J. Insulin pumps: Design basics and tradeoffs. Available online: http://www.eetimes.com/document.asp?doc_id=1278073 (accessed on 2 January 2016).
- NXP and Insulet Corporation to Help Improve Diabetes Care. Available online: http://www.nxp.com/about/our-customers/nxp-and-insulet-corporation-to-help-improve-diabetes-care:CASE_STUDY_INSULET (accessed on 6 February 2016).
- Avizienis, A.; Laprie, J.; Randell, B. Fundamental Concepts of Dependability. In Proceedings of the 3rd IEEE Information Survivability Workshop (ISW-2000), Boston, MA, USA, 24–26 October 2000; pp. 7–12.
- Bequette, B.W. Challenges and recent progress in the development of a closed-loop artificial pancreas. Annu. Rev. Control 2012, 36, 255–266. [Google Scholar] [CrossRef] [PubMed]
- Patek, S.D.; Magni, L.; Dassau, E.; Toffanin, C.; De Nicolao, G.; Del Favero, S.; Breton, M.; Dalla Man, C.; Renard, E.; Zisser, H.; et al. Modular closed-loop control of diabetes. IEEE Trans. Biomed. Eng. 2012, 59, 2986–2999. [Google Scholar] [CrossRef] [PubMed]
- Harvey, R.A.; Dassau, E.; Zisser, H.; Seborg, D.E.; Jovanovič, L.; Doyle, F.J., III. Design of the health monitoring system for the artificial pancreas: Low glucose prediction module. J. Diabetes Sci. Technol. 2012, 6, 1345–1354. [Google Scholar] [CrossRef] [PubMed]
- Dassau, E.; Bequette, B.W.; Buckingham, B.A.; Doyle, F.J., III. Detection of a meal using continuous glucose monitoring. Diabetes Care 2008, 31, 295–300. [Google Scholar] [CrossRef] [PubMed]
- Turksoy, K.; Samadi, S.; Feng, J.; Littlejohn, E.; Quinn, L.; Cinar, A. Meal-detection in patients with type 1 diabetes: A new module for the multivariable adaptive artificial pancreas control system. IEEE J. Biomed. Health Inform. 2016, 20, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Weimer, J.; Rickels, M.; Peleckis, A.; Lee, I. Towards a Model-based Meal Detector for Type I Diabetics. In Proceedings of the 6th Medical Cyber-Physical Systems Workshop, Seattle, WA, USA, 13–16 April 2015.
- Bergenstal, R.M.; Klonoff, D.C.; Garg, S.K.; Bode, B.W.; Meredith, M.; Slover, R.H.; Ahmann, A.J.; Welsh, J.B.; Lee, S.W.; Kaufman, F.R. Threshold-based insulin-pump interruption for reduction of hypoglycemia. N. Engl. J. Med. 2013, 369, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Johansen, T.A. Toward dependable embedded model predictive control. IEEE Syst. J. 2014, PP, 1–12. [Google Scholar] [CrossRef]
- Colnaric, M. Design of embedded control systems. IEEE Int. Conf. Ind. Technol. 2003, 1, 22–30. [Google Scholar]
- Barroso, J. Modeling and Intelligent Control of a Distillation Column. Ph.D. Thesis, Technical University of Lisbon, Lisbon, Portugal, October 2009. [Google Scholar]
- Ng, K.C.; Wang, L.; Peake, I.D. Safety-Critical Multi-Core Software Architecture for Model Predictive Control. In Proceedings of the Australian Control Conference, Melbourne, Australia, 10–11 November 2011; pp. 434–439.
- Hildreth, C. A quadratic programming procedure. Nav. Res. Logist. Q. 1957, 4, 79–85. [Google Scholar] [CrossRef]
- Steil, G.M.; Grodsky, G.M. The artificial pancreas: Is it important to understand how the β cell controls blood glucose? J. Diabetes Sci. Technol. 2013, 7, 1359–1369. [Google Scholar] [CrossRef] [PubMed]
- Steil, G.M. Algorithms for a Closed-Loop Artificial Pancreas: The case for proportional-integral-derivative control. J. Diabetes Sci. Technol. 2013, 7, 1621–1631. [Google Scholar] [CrossRef] [PubMed]
- Steil, G.M.; Palerm, C.C.; Kurtz, N.; Voskanyan, G.; Roy, A.; Paz, S.; Kandeel, F.R. The effect of insulin feedback on closed loop glucose control. J. Clin. Endocrinol. Metab. 2011, 96, 1402–1408. [Google Scholar] [CrossRef] [PubMed]
- Weinzimer, S.A.; Steil, G.M.; Swan, K.L.; Dziura, J.; Kurtz, N.; Tamborlane, W.V. Fully automated closed-loop insulin delivery vs semi-automated hybrid control in pediatric patients with type 1 diabetes using an artificial pancreas. Diabetes Care 2008, 31, 934–939. [Google Scholar] [CrossRef] [PubMed]
- Atlas, E.; Nimri, R.; Miller, S.; Grunberg, E.A.; Phillip, M. MD-Logic Artificial Pancreas System: A pilot study in adults with type 1 diabetes. Diabetes Care 2010, 33, 1072–1076. [Google Scholar] [CrossRef] [PubMed]
- Magni, L.; Raimondo, D.M.; Bossi, L.; Dalla Man, C.; De Nicolao, G.; Kovatchev, B.; Cobelli, C. Model predictive control of type 1 diabetes: An in silico trial. J. Diabetes Sci. Technol. 2007, 1, 804–812. [Google Scholar] [CrossRef] [PubMed]
- Soru, P.; De Nicolao, G.; Toffanin, C.; Dalla Man, C.; Cobelli, C.; Magni, L. MPC based Artificial Pancreas: Strategies for individualization and meal compensation. Annu. Rev. Control 2012, 36, 118–128. [Google Scholar] [CrossRef]
- Grosman, B.; Dassau, E.; Zisser, H.C.; Jovanovič, L.; Doyle, F.J., III. Zone model predictive control: A strategy to minimize hyper- and hypoglycemic events. J. Diabetes Sci. Technol. 2010, 4, 961–975. [Google Scholar] [CrossRef] [PubMed]
- Gondhalekar, R.; Dassau, E.; Zisser, H.C.; Doyle, F.J., III. Periodic-Zone Model Predictive Control for Diurnal Closed-Loop Operation of an Artificial Pancreas. J. Diabetes Sci. Technol. 2013, 7, 1446–1460. [Google Scholar] [CrossRef] [PubMed]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A.; Doyle, F.J., III. Process Dynamics and Control; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Krasňanský, R.; Dvorščák, B.; Kozák, Š. Hardware Realization of Embedded Control Algorithm on FPGA. In Proceedings of the 5th International Conference on Computational Logics, Algebras, Programming, Tools, and Benchmarking, Venice, Italy, 25–29 May 2014; pp. 13–18.
- Astrom, K.J.; Wittenmark, B. Computer-Controlled Systems Theory and Design, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Chan, Y.F.; Moallem, M.; Wang, W. Efficient implementation of PID control algorithm using FPGA technology. In Proceedings of the 43rd IEEE Conference on Decision and Control (CDC), Atlantis, Paradise Island, Bahamas, 14–17 December 2004; Volume 5, pp. 4885–4890.
- Feng, G. A survey on analysis and design of model-based fuzzy control systems. IEEE Trans. Fuzzy Syst. 2006, 14, 676–697. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Teixeira, M.C.M.; Zak, S.H. Stabilizing controller design for uncertain nonlinear systems using fuzzy models. IEEE Trans. Fuzzy Syst. 1999, 7, 133–142. [Google Scholar] [CrossRef]
- Sánchez-Solano, S.; Cabrera, A.J.; Baturone, I.; Moreno-Velo, F.J.; Brox, M. FPGA implementation of embedded fuzzy controllers for robotic applications. IEEE Trans. Ind. Electron. 2007, 54, 1937–1945. [Google Scholar] [CrossRef]
- Taeed, F.; Salam, Z.; Ayob, S. FPGA implementation of a single-input fuzzy logic controller for boost converterwith the absence of an external analog-to-digital converter. IEEE Trans. Ind. Electron. 2012, 59, 1208–1217. [Google Scholar] [CrossRef]
- Gondhalekar, R.; Dassau, E.; Doyle, F.J., III. MPC Design for Rapid Pump-Attenuation and Expedited Hyperglycemia Response to Treat T1DM with an Artificial Pancreas. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 4224–4230.
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Georgiadis, M.; Dua, V. Multi-Parametric Model-Based Control Theory and Applications; Wiley: Weinhaim, Germany, 2007. [Google Scholar]
- Dua, P.; Kouramas, K.; Dua, V.; Pistikopoulos, E.N. MPC on a chip—Recent advances on the application of multi-parametric model-based control. Comput. Chem. Eng. 2008, 32, 754–765. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N. From multi-parametric programming theory to MPC-on-a-chip multi-scale systems applications. Comput. Chem. Eng. 2012, 47, 57–66. [Google Scholar] [CrossRef]
- Dua, P.; Doyle, F.J., III; Pistikopoulos, E.N. Model-based blood glucose control for Type 1 diabetes via parametric programming. IEEE Trans. Biomed. Eng. 2006, 53, 1478–1491. [Google Scholar] [CrossRef] [PubMed]
- Percival, M.W.; Wang, Y.; Grosman, B.; Dassau, E.; Zisser, H.; Jovanovič, L.; Doyle, F.J., III. Development of a multi-parametric model predictive control algorithm for insulin delivery in type 1 diabetes mellitus using clinical parameters. J. Process Control 2011, 21, 391–404. [Google Scholar] [CrossRef] [PubMed]
- Huyck, B.; Callebaut, L.; Logist, F.; Ferreau, H.J.; Diehl, M.; De Brabanter, J.; Van Impe, J.; De Moor, B. Implementation and Experimental Validation of Classic MPC on Programmable Logic Controllers. In Proceedings of the 20th Mediterranean Conference on Control & Automation (MED), Barcelona, Spain, 3–6 July 2012; pp. 679–684.
- Wang, Y.; Boyd, S. Fast model predictive control using online optimization. IEEE Trans. Control Syst. Technol. 2010, 18, 267–278. [Google Scholar] [CrossRef]
- Pannocchia, G.; Rawlings, J.B.; Wright, S.J. Fast, large-scale model predictive control by partial enumeration. Automatica 2007, 43, 852–860. [Google Scholar] [CrossRef]
- Cagienard, R.; Grieder, P.; Kerrigan, E.C.; Morari, M. Move blocking strategies in receding horizon control. J. Process Control 2007, 17, 563–570. [Google Scholar] [CrossRef]
- Kufoalor, D.K.M.; Aaker, V.; Johansen, T.A.; Imsland, L.; Eikrem, G.O. Automatically generated embedded model predictive control: Moving an industrial PC-based MPC to an embedded platform. Optim. Control Appl. Methods 2015, 36, 705–727. [Google Scholar] [CrossRef]
- Takács, B.; Kvasnica, M.; Di Cairano, S. Nearly-Optimal Simple Explicit MPC Regulators with Recursive Feasibility Guarantees. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 7089–7094.
- Kvasnica, M.; Fikar, M. Clipping-Based Complexity Reduction in Explicit MPC. IEEE Trans. Autom. Control 2012, 57, 1878–1883. [Google Scholar] [CrossRef]
- Johansen, T.A.; Grancharova, A. Approximate explicit model predictive control implemented via orthogonal search tree partitioning. IEEE Trans. Autom. Control 2003, 48, 810–815. [Google Scholar] [CrossRef]
- Bemporad, A.; Filippi, C. Suboptimal explicit receding horizon control via approximate multiparametric quadratic programming. J. Optim. Theory Appl. 2003, 117, 9–38. [Google Scholar] [CrossRef]
- Bemporad, A.; Filippi, C. An Algorithm for approximate multiparametric convex programming. Comput. Optim. Appl. 2006, 35, 87–108. [Google Scholar] [CrossRef]
- Jones, C.N.; Morari, M. Polytopic Approximation of explicit model predictive controllers. IEEE Trans. Autom. Control 2010, 55, 2542–2553. [Google Scholar] [CrossRef]
- Parisini, T.; Zoppoli, R. A Receding-horizon regulator for nonlinear-systems and a neural approximation. Automatica 1995, 31, 1443–1451. [Google Scholar] [CrossRef]
- Parisini, T.; Sanguineti, M.; Zoppoli, R. Nonlinear stabilization by receding-horizon neural regulators. Int. J. Control 1998, 70, 341–362. [Google Scholar] [CrossRef]
- Pin, G.; Filippo, M.; Pellegrino, F.A.; Parisini, T. Approximate Off-Line Receding Horizon Control of Constrained Nonlinear Discrete-Time Systems. In Proceedings of the European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 2420–2425.
- Pin, G.; Filippo, M.; Pellegrino, F.A.; Fenu, G.; Parisini, T. Approximate model predictive control laws for constrained nonlinear discrete-time systems: Analysis and offline design. Int. J. Control 2013, 86, 804–820. [Google Scholar] [CrossRef]
- Bleris, L.G.; Kothare, M.V. Real-time implementation of model predictive control. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 8–10 June 2005; pp. 4166–4171.
- Bleris, L.G.; Kothare, M.V.; Garcia, J.; Arnold, M.G. Embedded Model Predictive Control for System-on-a-chip Applications. In Proceedings of the 7th IFAC Symposium on Dynamics and Control of Process Systems (DYCOPS-7), Boston, MA, USA, 5–7 July 2004; Volume 1.
- Swartzlander, E.E.; Alexopoulos, A.G. The sign/logarithm number system. IEEE Trans. Comput. 1975, 24, 1238–1242. [Google Scholar] [CrossRef]
- Rossiter, J.A.; Kouvaritakis, B.; Bacic, M. Interpolation based computationally efficient predictive control. Int. J. Control 2004, 77, 290–301. [Google Scholar] [CrossRef]
- Ding, Y.; Rossiter, J.A. Comparisons and combinations of interpolation methods with conventional predictive control. In Proceedings of the Mediterranean Conference on Control and Automation (MED), Athens, Greece, 27–29 June 2007.
- Rossiter, J.A.; Pluymers, B.; De Moor, B. The potential of interpolation for simplifying predictive control and application to LPV systems. In Assessment and Future Directions of Nonlinear Model Predictive Control; Springer: Berlin, Germany, 2007; Volume 358, pp. 63–76. [Google Scholar]
- Valencia-Palomo, G. Efficient Implementations of Predictive Control. Ph.D. Thesis, University of Sheffield, Sheffield, UK, October 2010. [Google Scholar]
- Henriksson, D.; Cervin, A.; Akesson, J.; Arzen, K.E. Feedback scheduling of model predictive controllers. In Proceedings of the 8th IEEE Real-Time and Embedded Technology and Applications Symposium, San Jose, CA, USA, 25–27 September 2002; pp. 207–216.
- Marti, P.; Lin, C.; Brandt, S.A. Optimal State Feedback Based Resource Allocation for Resource-Constrained Control Tasks. In Proceedings of the 25th IEEE Real-Time Systems Symposium, Lisbon, Portugal, 5–8 December 2004.
- Cannon, M.; Kouvaritakis, B. Efficient Constrained Model Predictive Control with Asymptotic Optimality. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; pp. 2744–2749.
- Kouvaritakis, B.; Rossiter, J.A.; Schuurmans, J. Efficient robust predictive control. IEEE Trans. Autom. Control 2000, 45, 1545–1549. [Google Scholar] [CrossRef]
- Huyck, B.; Ferreau, H.J.; Diehl, M.; De Brabanter, J.; Van Impe, J.F.M.; De Moor, B.; Logist, F. Towards online model predictive control on a programmable logic controller: Practical considerations. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Friedlander, M.P.; Orban, D. A primal-dual regularized interior-point method for convex quadratic programs. Math. Program. Comput. 2012, 4, 71–107. [Google Scholar] [CrossRef]
- Rao, C.V.; Wright, S.J.; Rawlings, J.B. Application of interior-point methods to model predictive control. J. Optim. Theory Appl. 1998, 99, 723–758. [Google Scholar] [CrossRef]
- Lau, M.S.K.; Yue, S.P.; Ling, K.V.; Maciejowski, J.M. A comparison of interior point and active set methods for FPGA implementation of model predictive control. In Proceedings of the European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 156–161.
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Ferreau, H.J.; Bock, H.G.; Diehl, M. An online active set strategy to overcome the limitations of explicit MPC. Int. J. Robust Nonlinear Control 2008, 18, 816–830. [Google Scholar] [CrossRef]
- Mattingley, J.; Boyd, S. CVXGEN: A code generator for embedded convex optimization. Optim. Eng. 2012, 13, 1–27. [Google Scholar] [CrossRef]
- Domahidi, A.; Chu, E.; Boyd, S. ECOS: An SOCP solver for embedded systems. In Proceedings of the European Control Conference (ECC), Zürich, Switzerland, 17–19 July 2013; pp. 3071–3076.
- Wills, A.; Ninness, B. QPC—Quadratic Programming in C. Available online: http://sigpromu.org/quadprog/ (accessed on 10 March 2016).
- Domahidi, A. FORCES: Fast Optimization for Real-Time Control on Embedded Systems. Available online: http://forces.ethz.ch/doku.php?id=start (accessed on 15 March 2016).
- Andersen, M.S.; Dahl, J.; Vandenberghe, L. CVXOPT Documentation, Release 1.1.8. Available online: http://cvxopt.org (accessed on 12 March 2016).
- Diamond, S.; Boyd, S. CVXPY: A python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 2016, 17, 1–5. [Google Scholar]
- O’Donoghue, B.; Chu, E.; Parikh, N.; Boyd, S. Conic optimization via operator splitting and homogeneous self-dual embedding. J. Optim. Theory Appl. 2016, 169, 1–27. [Google Scholar] [CrossRef]
- Kovatchev, B.P.; Breton, M.; Dalla Man, C.; Cobelli, C. In silico preclinical trials: A proof of concept in closed-loop control of type 1 diabetes. J. Diabetes Sci. Technol. 2009, 3, 44–55. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M. Computers as Components: Principles of Embedded Computing System Design, 2nd ed.; Elsevier: Waltham, MA, USA, 2012. [Google Scholar]
- Kornecki, A.J.; Zalewski, J. Hardware certification for real-time safety-critical systems: State of the art. Annu. Rev. Control 2010, 34, 163–174. [Google Scholar] [CrossRef]
- Kornecki, A.; Zalewski, J. Certification of software for real-time safety-critical systems: State of the art. Innov. Syst. Softw. Eng. 2009, 5, 149–161. [Google Scholar] [CrossRef]
- Fries, R.C. Reliable Design of Medical Devices, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Vogel, D.A. Medical Device Software Verification, Validation and Compliance; Artech House: Norwood, MA, USA, 2011. [Google Scholar]
- Wiklund, M.E.; Kendler, J.; Strochlic, A.Y. Usability Testing of Medical Devices; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Ling, K.V.; Yue, S.P.; Maciejowski, J.M. A FPGA Implementation of Model Predictive Control. In Proceedings of the American Control Conference (ACC), Minneapolis, MN, USA, 14–16 June 2006; pp. 1930–1935.
- Fathy, H.K.; Filipi, Z.S.; Hagena, J.; Stein, J.L. Review of Hardware-in-the-Loop Simulation and Its Prospects in the Automotive Area. In Proceedings of the SPIE International Society for Optical Engineering, Kissimmee, FL, USA, 18–21 April 2006; Volume 6228, pp. 1–20.
- Suardi, A.; Kerrigan, E.C.; Constantinides, G.A. Fast FPGA prototyping toolbox for embedded optimization. In Proceedings of the European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2589–2594.
- Hartley, E.N.; Jerez, J.L.; Suardi, A.; Maciejowski, J.M.; Kerrigan, E.C.; Constantinides, G.A. Predictive control using an FPGA with application to aircraft control. IEEE Trans. Control Syst. Technol. 2014, 22, 1006–1017. [Google Scholar] [CrossRef]
- Jerez, J.L.; Constantinides, G.A.; Kerrigan, E.C. FPGA Implementation of an Interior Point Solver for Linear Model Predictive Control. In Proceedings of the International Conference on Field-Programmable Technology, Beijing, China, 8–10 December 2010; pp. 316–319.
- Wills, A.; Mills, A.; Ninness, B. FPGA Implementation of an Interior-Point Solution for Linear Model Predictive Control. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 14527–14532.
- Vouzis, P.D.; Bleris, L.G.; Arnold, M.G.; Kothare, M.V. A system-on-a-chip implementation for embedded real-time model predictive control. IEEE Trans. Control Syst. Technol. 2009, 17, 1006–1017. [Google Scholar] [CrossRef]
- Ingole, D.; Holaza, J.; Takács, B.; Kvasnica, M. FPGA-Based Explicit Model Predictive Control for Closed-Loop Control of Intravenous Anesthesia. In Proceedings of the International Conference on Process Control, Štrbské Pleso, Slovakia, 9–12 June 2015; pp. 42–47.
- Ingole, D.; Kvasnica, M. FPGA Implementation of Explicit Model Predictive Control for Closed Loop Control of Depth of Anesthesia. In Proceedings of the 5th IFAC Conference on Nonlinear Model Predictive Control, Seville, Spain, 17–20 September 2015; pp. 484–489.
- Zometa, P.; Kögel, M.; Faulwasser, T.; Findeisen, R. Implementation Aspects of Model Predictive Control for Embedded Systems. In Proceedings of the American Control Conference (ACC), Montréal, QC, Canada, 27–29 June 2012; pp. 1205–1210.
- Kalúz, M.; Klaušo, M.; Kvasnica, M. Real-Time Implementation of a Reference Governor on the Arduino Microcontroller. In Proceedings of the International Conference on Process Control (PC), Štrbské Pleso, Slovakia, 9–12 June 2015; pp. 350–356.
- Frison, G.; Jørgensen, J.B. MPC Related Computational Capabilities of ARMv7A Processors. In Proceedings of the European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 3419–3426.
- Blauw, H.; Keith-Hynes, P.; Koops, R.; DeVries, J.H. A review of safety and design requirements of the artificial pancreas. Ann. Biomed. Eng. 2016. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Jones, P.L.; Jetley, R. A hazard analysis for a generic insulin infusion pump. J. Diabetes Sci. Technol. 2010, 4, 263–283. [Google Scholar] [CrossRef] [PubMed]
- Cope, J.U.; Samuels-Reid, J.H.; Morrison, A.E. Pediatric Use of Insulin Pump Technology: A retrospective study of adverse events in children ages 1–12 years. J. Diabetes Sci. Technol. 2012, 6, 1053–1059. [Google Scholar] [CrossRef] [PubMed]
- Martins, L.E.G.; De Oliveira, T. A case study using a protocol to derive safety functional requirements from fault tree analysis. In Proceedings of the 22nd IEEE International Requirements Engineering Conference, Karlskrona, Sweden, 25–29 August 2014; pp. 412–419.
- Jerez, J.L.; Goulart, P.J.; Richter, S.; Constantinides, G.A.; Kerrigan, E.C.; Morari, M. Embedded online optimization for model predictive control at megahertz rates. IEEE Trans. Autom. Control 2014, 59, 3238–3251. [Google Scholar] [CrossRef]
- Picasso, B.; Pancanti, S.; Bemporad, A.; Bicchi, A. Receding–horizon control of LTI systems with quantized inputs. In Proceedings of the IFAC Conference on Analysis and Design of Hybrid Systems, St. Malo, France, 16–18 June 2003; pp. 295–300.
- Quevedo, D.E.; Goodwin, G.C.; De Doná, J.A. Finite constraint set receding horizon quadratic control. Int. J. Robust Nonlinear Control 2004, 14, 355–377. [Google Scholar] [CrossRef]
- Liberzon, D. Quantization, time delays, and nonlinear stabilization. IEEE Trans. Autom. Control 2006, 51, 1190–1195. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Seron, M.M.; Raković, S.V. Robust model predictive control of constrained linear systems with bounded disturbances. Automatica 2005, 41, 219–224. [Google Scholar] [CrossRef]
- Limon, D.; Alamo, T.; Salas, F.; Camacho, E.F. Input to state stability of min-max MPC controllers for nonlinear systems with bounded uncertainties. Automatica 2006, 42, 797–803. [Google Scholar] [CrossRef]
- Aguilera, R.P.; Quevedo, D.E. On the stability of MPC with a finite input alphabet. In Proceedings of the 18th IFAC World Congress, Milano, Italy, 28 August–2 September 2011; pp. 7975–7980.
- Aguilera, R.P.; Quevedo, D.E. Stability analysis of quadratic MPC with a discrete input alphabet. IEEE Trans. Autom. Control 2013, 58, 3190–3196. [Google Scholar] [CrossRef]
- Paul, N.; Kohno, T.; Klonoff, D.C. A review of the security of insulin pump infusion systems. J. Diabetes Sci. Technol. 2011, 5, 1557–1562. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Raghunathan, A.; Jha, N.K. Hijacking an Insulin Pump: Security Attacks and Defenses for a Diabetes Therapy System. In Proceedings of the 13th International Conference on e-Health Networking, Applications and Services, (Healthcom), Columbia, MO, USA, 13–15 June 2011; pp. 150–156.
- Hei, X.; Du, X.; Lin, S.; Lee, I.; Sokolsky, O. Patient infusion pattern based access control schemes for wireless insulin pump system. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 3108–3121. [Google Scholar] [CrossRef]
- Williams, P.A.; Woodward, A.J. Cybersecurity vulnerabilities in medical devices: A complex environment and multifaceted problem. Med. Devices Evid. Res. 2015, 8, 305–316. [Google Scholar] [CrossRef] [PubMed]
- Burleson, W.; Clark, S.S.; Ransford, B.; Fu, K. Design challenges for secure implantable medical devices. In Proceedings of the 49th Design Automation Conference (DAC), San Francisco, CA, USA, 3–7 June 2012; pp. 12–17.
- Lee, I.; Pappas, G.J.; Cleaveland, R.; Hatclif, J.; Krogh, B.H.; Lee, P.; Rubin, H.; Sha, L. High-confidence medical device software and systems. IEEE Comput. 2006, 39, 33–38. [Google Scholar] [CrossRef]
- Ankaralı, Z.E.; Abbasi, Q.H.; Demir, A.F.; Serpedin, E.; Qaraqe, K.; Arslan, H. A Comparative Review on the Security Research for Wireless Implantable Medical Devices. In Proceedings of the 4th International Conference on Wireless Mobile Communication and Healthcare (Mobihealth), Athens, Greece, 3–5 November 2014; pp. 246–249.
- Fan, J.; Reparaz, O.; Rožić, V.; Verbauwhede, I. Low-energy encryption for medical devices: Security adds an extra design dimension. In Proceedings of the IEEE/ACM Design Automation Conference (DAC), Austin, TX, USA, 2–6 June 2013; pp. 1–6.
- Johansen, T.A.; Jackson, W.; Schreiber, R.; Tøndel, P. Hardware synthesis of explicit model predictive controllers. IEEE Trans. Control Syst. Technol. 2007, 15, 191–197. [Google Scholar] [CrossRef]

| Hardware Specifications | ||||
|---|---|---|---|---|
| Configuration | (A) Smartphone | (B) Insulin Pump | ||
| Processor Core | ARM Cortex-A15 | ARM Cortex-M3 | MAXQ2010 | 8-bit S08 |
| Memory | 2 GB RAM | 96 KB on-chip RAM | 64 KB Flash | 2–128 KB Flash |
| 2 KB RAM | 0.128–12 KB RAM | |||
| CPU Clock Frequency | 1.5–1.7 GHz | 72 MHz | 10 MHz | 16–50 MHz |
| Integer ALU | 32-bit | 32-bit | 16-bit | 8-bit |
| FPU | Optional | ✘ | ✘ | ✘ |
| Solver | Quadprog | Quadprog | Quadprog | qpOASES | qpOASES | CVXGEN | QPC (qpas) | QPC (qpip) | ECOS |
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | IPM | ASM | ASM | ASM | ASM | IPM | ASM | IPM | IPM |
| Warm-start? | N | N | Y | N | Y | N | N | N | N |
| Case 1: Np = 20, Nc = 10 | |||||||||
| taver (±SD) (ms) | 8.6 (±3.3) | 12.9 (±20.6) | 9.9 (±14.5) | 13.7 (±6.9) | 12.7 (±6.1) | N/A | 0.4 (±0.3) | 4.3 (±1.9) | 7.2 (±2.5) |
| tmax (ms) | 34 | 114 | 93 | 49 | 48 | N/A | 2 | 15 | 30 |
| Case 2: Np = 12, Nc = 5 | |||||||||
| taver (±SD) (ms) | 7.9 (±2.8) | 6.6 (±7.6) | 5.8 (±6.0) | 2.5 (±1.4) | 2.5 (±1.3) | 3.0 (±0.7) | 0.2 (±0.15) | 1.6 (±0.7) | 6.6 (±2.3) |
| tmax (ms) | 33 | 46 | 53 | 22 | 10 | 8 | 2 | 5 | 39 |
| Solver | qpOASES | CVXGEN | ECOS | qpas | qpip |
|---|---|---|---|---|---|
| Code size (KB) | 835 | 1800 | 7 | 25 | 43 |
| Prototype Platform | Raspberry Pi Zero | Raspberry Pi 3 | ||
|---|---|---|---|---|
| Solver | CVXOPT | CVXPY | CVXOPT | CVXPY |
| Case 1: Np = 20, Nc= 10 | ||||
| taver ± SD (ms) | 128.8 ± 14.1 | 189.7 ± 16.3 | 50.0 ± 10.2 | 73.7 ± 11.7 |
| tmax (ms) | 196.8 | 268 | 104.8 | 143.2 |
| Energy Consumed (mAh) | 39.9 ± 0.2 | 59.9 ± 0.4 | 16.5 ± 0.0 | 25.1 ± 0.1 |
| Case 2: Np = 12, Nc = 5 | ||||
| taver ± SD (ms) | 56.9 ± 9.2 | 104.9 ± 11.3 | 22.4 ± 7.8 | 41.2 ± 9.6 |
| tmax (ms) | 110.3 | 269 | 40.2 | 98.2 |
| Energy Consumed (mAh) | 16.5 ± 0.2 | 32.4 ± 2.0 | 6.7 ± 0.4 | 13.2 ± 0.1 |
| Cause | Hazard |
|---|---|
| Control Unit | (1) Battery failure |
| (2) No value displayed | |
| (3) Over/under delivery of insulin | |
| (4) Over delivery of insulin | |
| Control Algorithm | (5) Numerical inaccuracies |
| (6) Resource limitation-suboptimal control action | |
| (7) Software aging | |
| CGM (continuous glucose monitoring) | (8) No signal |
| (9) Under/over reading | |
| (10) No glucose display | |
| (11) No communication | |
| (12) Receiver displays failure | |
| Insulin Pump | (13) Failure in reservoir |
| (14) Failure in delivery line | |
| (15) Battery failure | |
| (16) Mechanical/electrical failure | |
| (17) Request for new delivery while delivering previous bolus | |
| (18) Insulin delivered at maximum infusion rate (60 U/h) | |
| (19) Over/under/no delivery of insulin | |
| User | (20) Infusion set disconnected |
| (21) Over/under delivery of insulin | |
| Communication | (22) No communication between CGM and transmitter |
| (23) No communication between CGM and control unit | |
| (24) Loss of communication between CGM and insulin pump | |
| (25) No communication between control unit and insulin pump | |
| Safety Layer | (26) Algorithmic fault |
| (27) No detection made | |
| (28) Failure to trigger an alarm | |
| Handheld Device | (29) Operating system upgrade |
| (30) Interference with other applications | |
| (31) Cybersecurity vulnerabilities |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavitsanou, S.; Chakrabarty, A.; Dassau, E.; Doyle, F.J. Embedded Control in Wearable Medical Devices: Application to the Artificial Pancreas. Processes 2016, 4, 35. https://doi.org/10.3390/pr4040035
Zavitsanou S, Chakrabarty A, Dassau E, Doyle FJ. Embedded Control in Wearable Medical Devices: Application to the Artificial Pancreas. Processes. 2016; 4(4):35. https://doi.org/10.3390/pr4040035
Chicago/Turabian StyleZavitsanou, Stamatina, Ankush Chakrabarty, Eyal Dassau, and Francis J. Doyle. 2016. "Embedded Control in Wearable Medical Devices: Application to the Artificial Pancreas" Processes 4, no. 4: 35. https://doi.org/10.3390/pr4040035
APA StyleZavitsanou, S., Chakrabarty, A., Dassau, E., & Doyle, F. J. (2016). Embedded Control in Wearable Medical Devices: Application to the Artificial Pancreas. Processes, 4(4), 35. https://doi.org/10.3390/pr4040035