An Experimental Investigation to Facilitate an Improvement in the Design of an Electromagnetic Continuous Casting Mould
Abstract
:1. Introduction
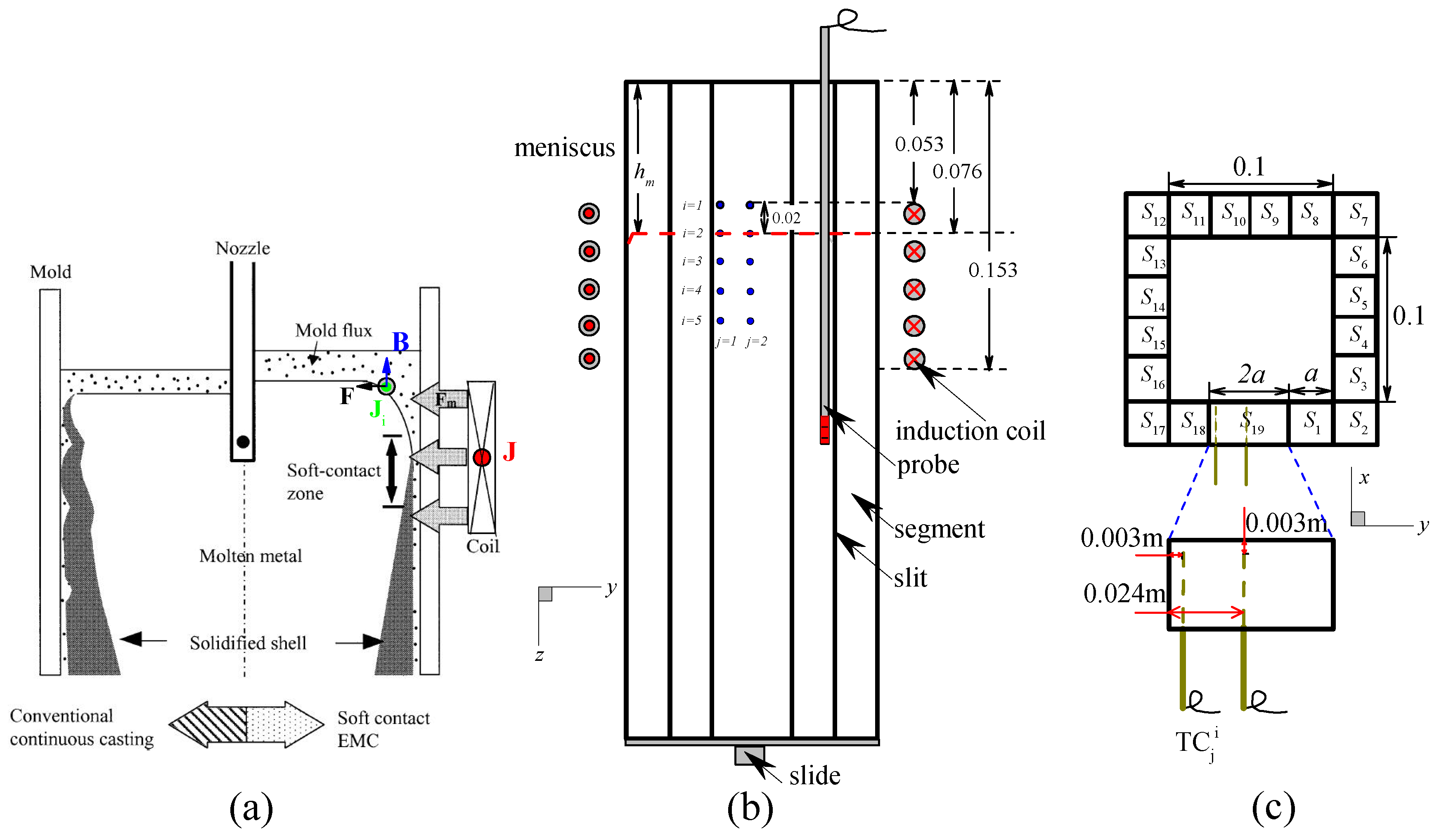
2. Basic Principles and the Experimental Facilities
2.1. Basic Principles
2.2. The Experimental Facilities
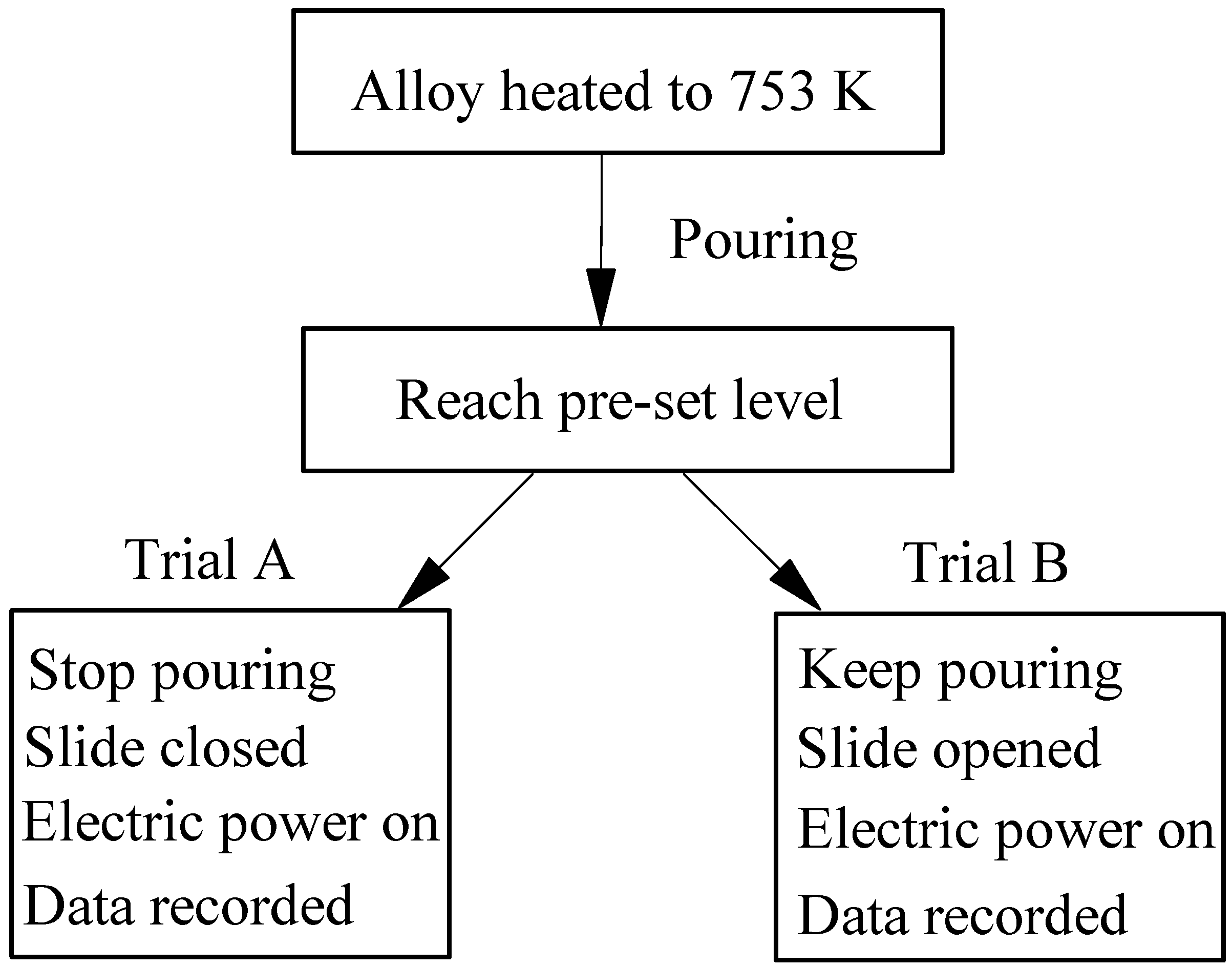
2.3. The Experimental Procedures
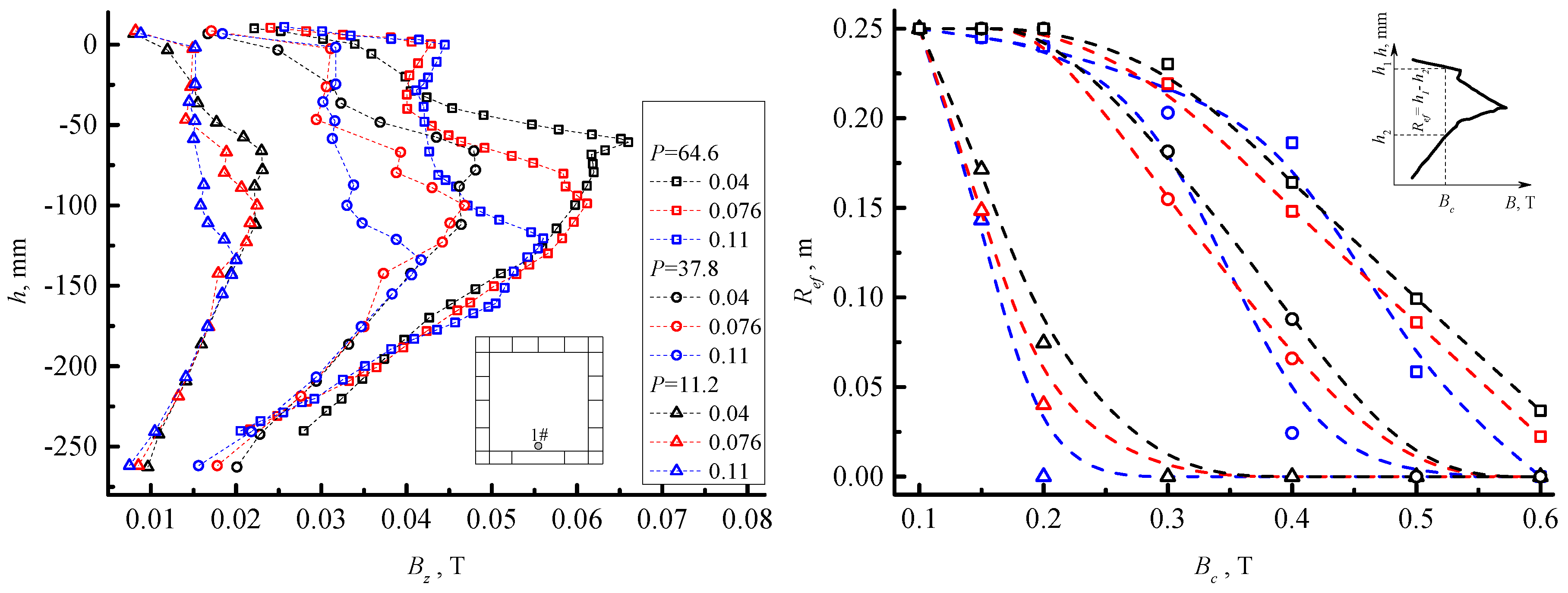
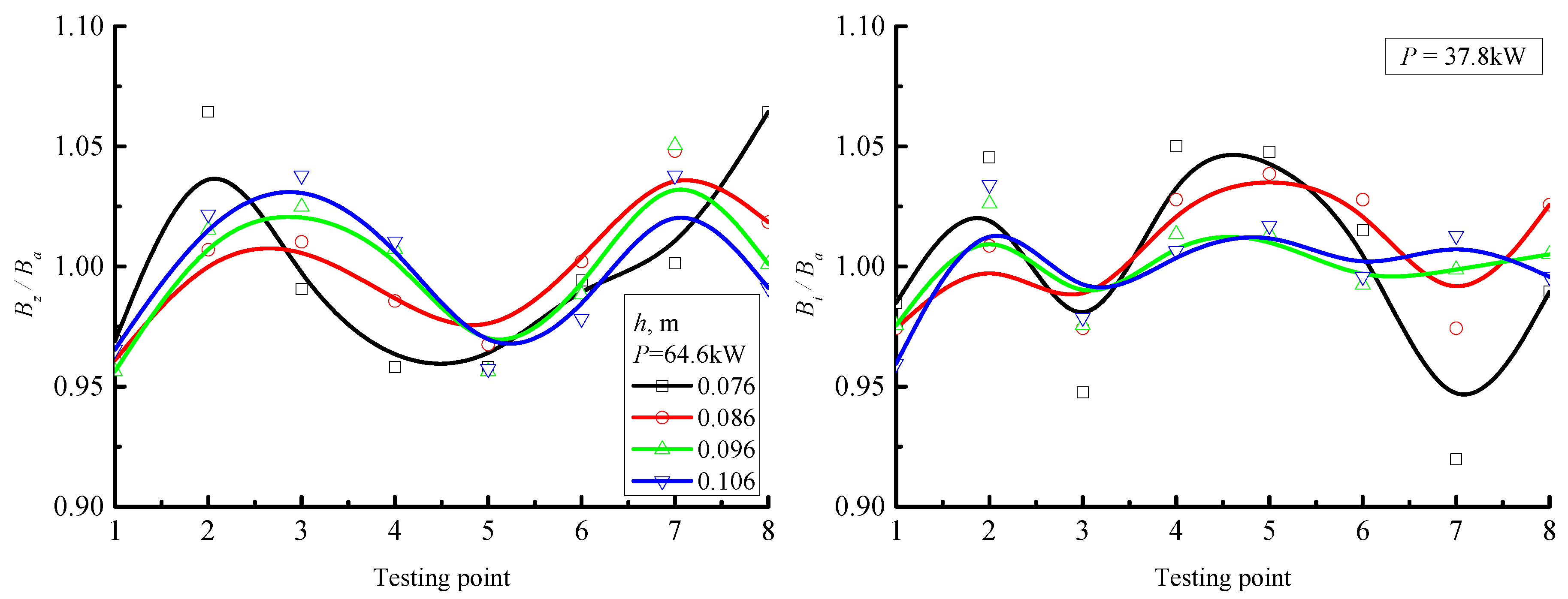
3. Magnetic Performance
3.1. Selection of hm
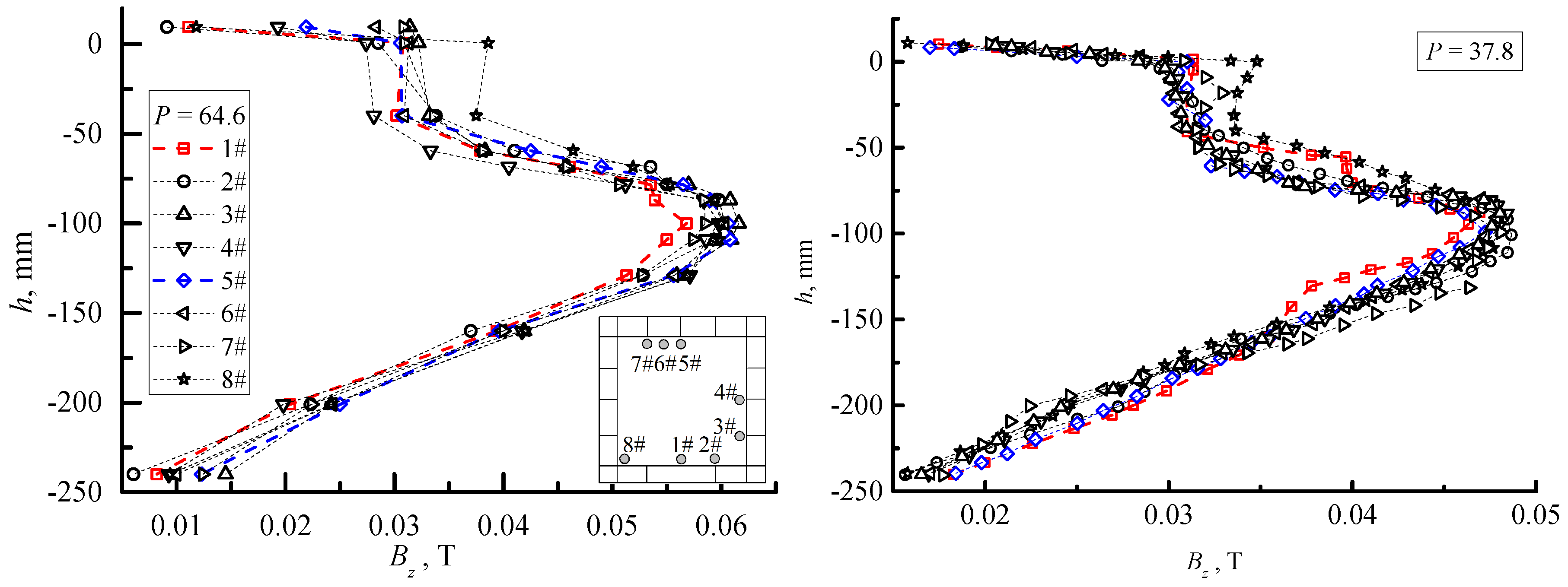
3.2. Overview of the Magnetic Field
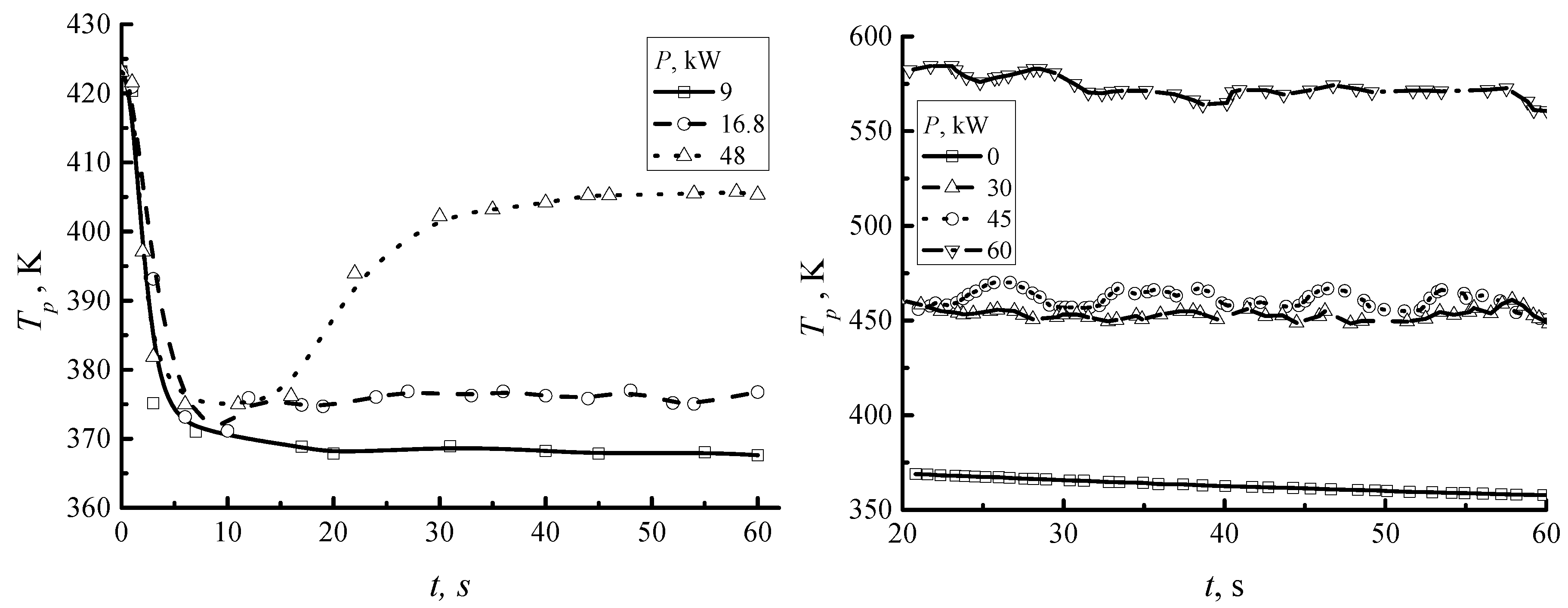
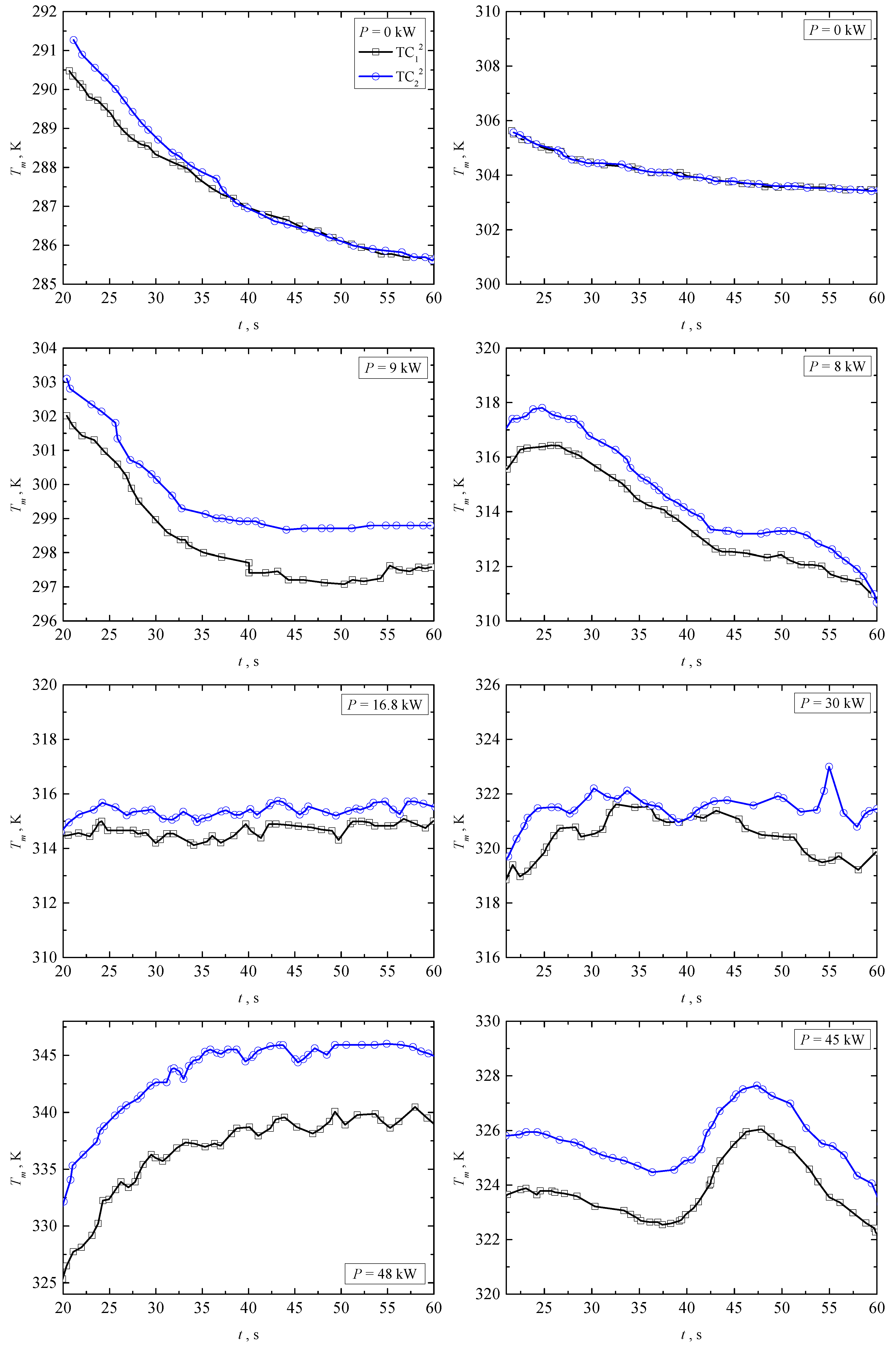
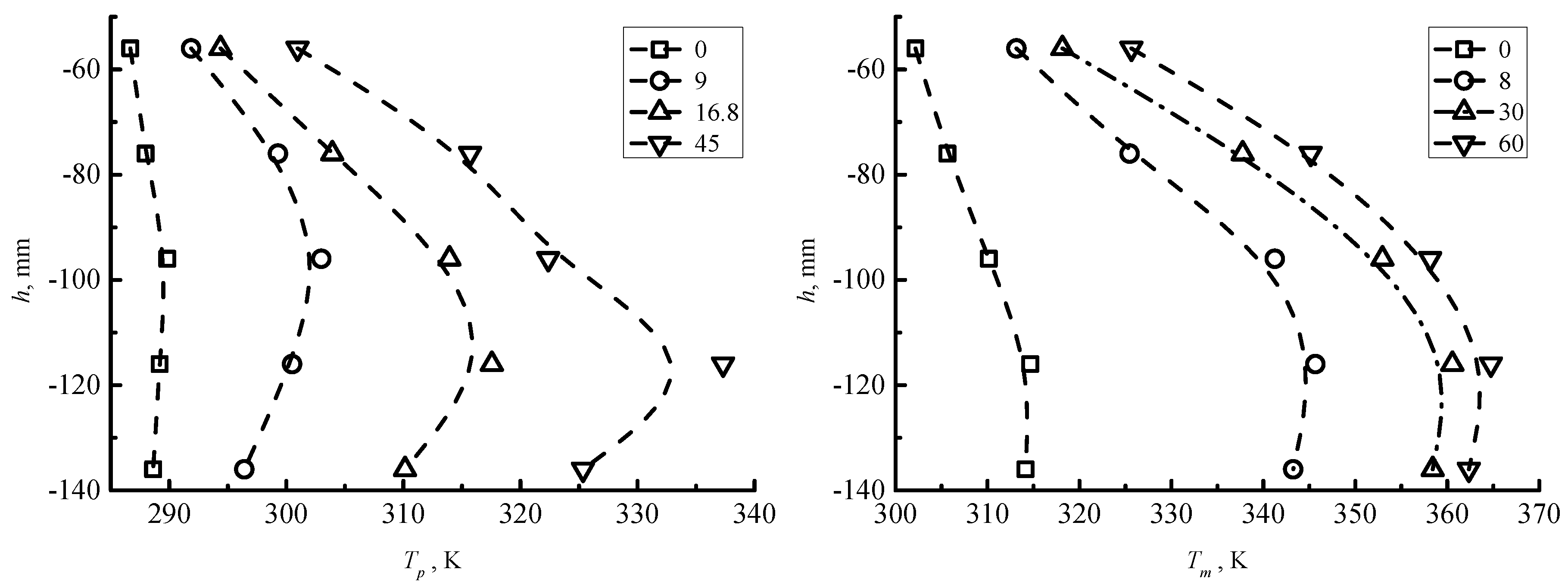
4. Thermal Performance
4.1. Alloy Pool Temperature Variation with P
4.2. Mould Wall Temperature with P
5. Conclusions
- the effective acting region Ref for the critical (expected) magnetic field Bc was defined. Ref highly depends on the external magnetic field and the relative location between the induction coil and the meniscus. Ref influence will be dominant whilst the liquid region in the mould is large.
- Uniformity of the magnetic field was achieved along the casting direction and in the circumferential direction, in the vicinity of the meniscus.
- The temperatures of the molten alloy pool and mould wall increase with increasing electric power input P. The temperature in the vicinity of the segment centre presents a higher value than that near the edge, especially at a high value of P.
- Along the casting direction, the location where the maximum temperature value appears moves towards the outlet of the mould as P is increased.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vives, C. Electromagnetic refining of aluminum alloys by the CREM process: Part I. working principle and metallurgical results. Metall. Mater. Trans. B 1989, 20, 623–629. [Google Scholar] [CrossRef]
- Vives, C.; Ricou, R. Experimental study of continuous electromagnetic casting of aluminum alloys. Metall. Mater. Trans. B 1985, 16, 377–384. [Google Scholar] [CrossRef]
- Toh, T.; Takeuchi, E.; Hojo, M.; Kawai, H.; Matsumura, S. Electromagnetic control of initial solidification in continuous casting of steel by low frequency alternating magnetic field. ISIJ Int. 1997, 37, 1112–1119. [Google Scholar] [CrossRef]
- Garnier, G.; Moreau, R. Effect of finite conductivity on the inviscid stability of an interface submitted to a high-frequency magnetic field. J. Fluid Mech. 1983, 127, 365–377. [Google Scholar] [CrossRef]
- Echeale, E.J.; Melcher, J.R. Instability of a planar liquid layer in an alternating magnetic field. J. Fluid Mech. 1982, 127, 27–40. [Google Scholar]
- Sheikholeslami, M.; Ellahi, R.; Hassan, M.; Soleimani, S. A study of natural convection heat transfer in a nanofluid filled enclosure with elliptic inner cylinder. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1906–1927. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhattu, M.M.; Vafai, K. Effect of heat and mass transfer on peristaltic flow in a non-uniform rectangular duct. Int. J. Heat Mass Transf. 2014, 71, 706–719. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Davood, D.G.; Javed, M.Y.; Ellahi, E. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means fo two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R.; Ashorynejad, H.R.; Domairry, G.; Hayat, T. Effect of heat transfer in flow of nanofluids over a permeable stretching wall in a porous medium. J. Comput. Theor. Nanosci. 2014, 11, 486–496. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, E. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with sinusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Nakata, H.; Inoue, T.; Mori, H.; Murakami, T.; Mominami, T. Improvement of billet surface quality by intra-high-frequency electromagnetic casting. ISIJ Int. 2002, 42, 264–272. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, E.; Deng, A.; He, J. Numerical simulation of influence of slit parameters of soft-contact mould on the distribution of magnetic field. Chin. J. Process Eng. 2006, 6, 713–717. [Google Scholar]
- Li, T.; Sassa, K.; Asai, S. Surface quality improvement of continuously cast metals by imposing intermittent high frequency magnetic field and synchronizing the field with mould oscillation. ISIJ Int. 1995, 36, 410–416. [Google Scholar] [CrossRef]
- Li, T.; Li, X.; Zhang, Z.; Jin, J. Effect of multielectromagnetic field on meniscus shape and quality of continuously cast metals. Ironmak. Steelmak. 2006, 31, 57–60. [Google Scholar] [CrossRef]
- Bermudez, A.; Muniz, M.C.; Sslgado, P. Asymptotic approximation and numerical simulation of electromagnetic casting. Metall. Mater. Trans. B 2003, 34, 83–91. [Google Scholar] [CrossRef]
- Evans, J.W. The Use of Electromagnetic Casting for Al Alloys and Other Metals. JOM 1995, 47, 38–41. [Google Scholar] [CrossRef]
- Evans, J.W. Mathematical modeling of meniscus profile and melt flow in electromagnetic casters. Metall. Mater. Trans. B 1988, 19, 397–408. [Google Scholar]
- Park, J.; Jeong, H.; Kim, H.; Kim, J. Laboratory scale continuous casting of steel billet with high frequency magnetic field. ISIJ Int. 2002, 42, 385–391. [Google Scholar] [CrossRef]
- Park, J.; Kim, H.; Jeong, H.; Kim, G.; Cho, M.; Chung, J.; Yoon, M.; Kim, K.; Cho, J. Continuous casting of steel billet with high frequency electromagnetic field. ISIJ Int. 2003, 43, 813–819. [Google Scholar] [CrossRef]
- Moreau, R. Magnetohydrodynamics; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Deng, A.; Xu, X.; Wang, E.; Zhang, L.; Zhang, X.; He, J. Experimental research on round steel billet electromagnetic soft contact continuous casting process. Iron Steel 2009, 44, 33–37. [Google Scholar]
- Fort, J.; Garnich, M.; Klymyshyn, N. Electromagnetic and thermal-flow modeling of a cold-wall crucible induction melter. Metall. Mater. Trans. B 2005, 36, 141–152. [Google Scholar] [CrossRef]
- Ren, Z.; Dong, H.; Deng, K.; Jiang, G. Influence of high frequency electromagnetic field on the initial solidification during electromagnetic continuous casting. ISIJ Int. 2001, 41, 981–985. [Google Scholar] [CrossRef] [Green Version]
- Na, X.; Xue, M.; Zhang, X.; Gan, Y. Numerical simulation of heat transfer and deformation of initial shell in soft contact continuous casting mould under high frequency electromagnetic field. J. Iron Steel Res. Int. 2007, 14, 14–21. [Google Scholar] [CrossRef]
- Na, X.; Zhang, X.; Gan, Y. Mathematical Analysis and Numerical Simulation of High Frequency Electromagnetic Field in Soft Contact Continuous Casting mould. ISIJ Int. 2002, 42, 974–981. [Google Scholar] [CrossRef]

| Melting Point | Density | Viscosity | Electric Conductivity | Magnetic Permeability |
|---|---|---|---|---|
| (K) | (kg/m3) | (S/m) | (m2/s) | (H/m) |
| 368.15 | 9500 | 1.1 × 106 | 3.4 × 10−7 | 4π × 10−7 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Deng, A.; Wang, E.; Sienz, J. An Experimental Investigation to Facilitate an Improvement in the Design of an Electromagnetic Continuous Casting Mould. Processes 2016, 4, 14. https://doi.org/10.3390/pr4020014
Zhang L, Deng A, Wang E, Sienz J. An Experimental Investigation to Facilitate an Improvement in the Design of an Electromagnetic Continuous Casting Mould. Processes. 2016; 4(2):14. https://doi.org/10.3390/pr4020014
Chicago/Turabian StyleZhang, Lintao, Anyuan Deng, Engang Wang, and Johann Sienz. 2016. "An Experimental Investigation to Facilitate an Improvement in the Design of an Electromagnetic Continuous Casting Mould" Processes 4, no. 2: 14. https://doi.org/10.3390/pr4020014
APA StyleZhang, L., Deng, A., Wang, E., & Sienz, J. (2016). An Experimental Investigation to Facilitate an Improvement in the Design of an Electromagnetic Continuous Casting Mould. Processes, 4(2), 14. https://doi.org/10.3390/pr4020014





