Surrogate Models for Online Monitoring and Process Troubleshooting of NBR Emulsion Copolymerization
Abstract
:1. Introduction
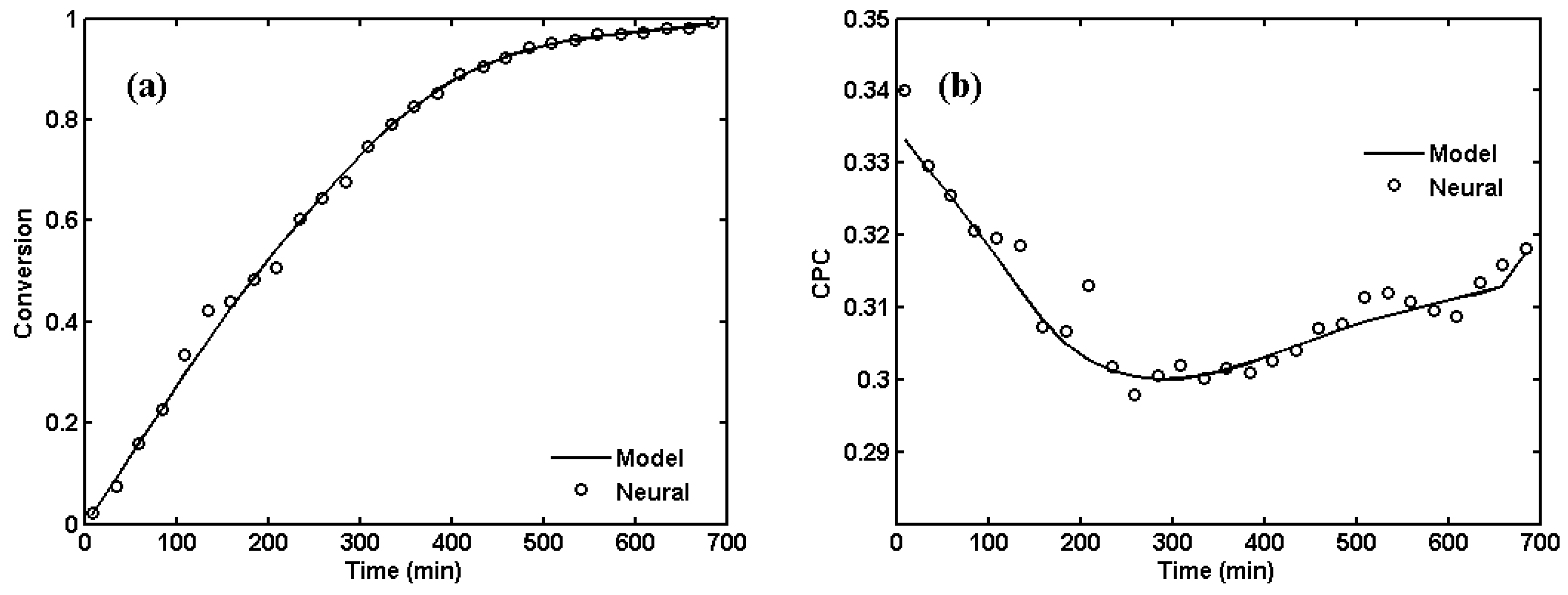
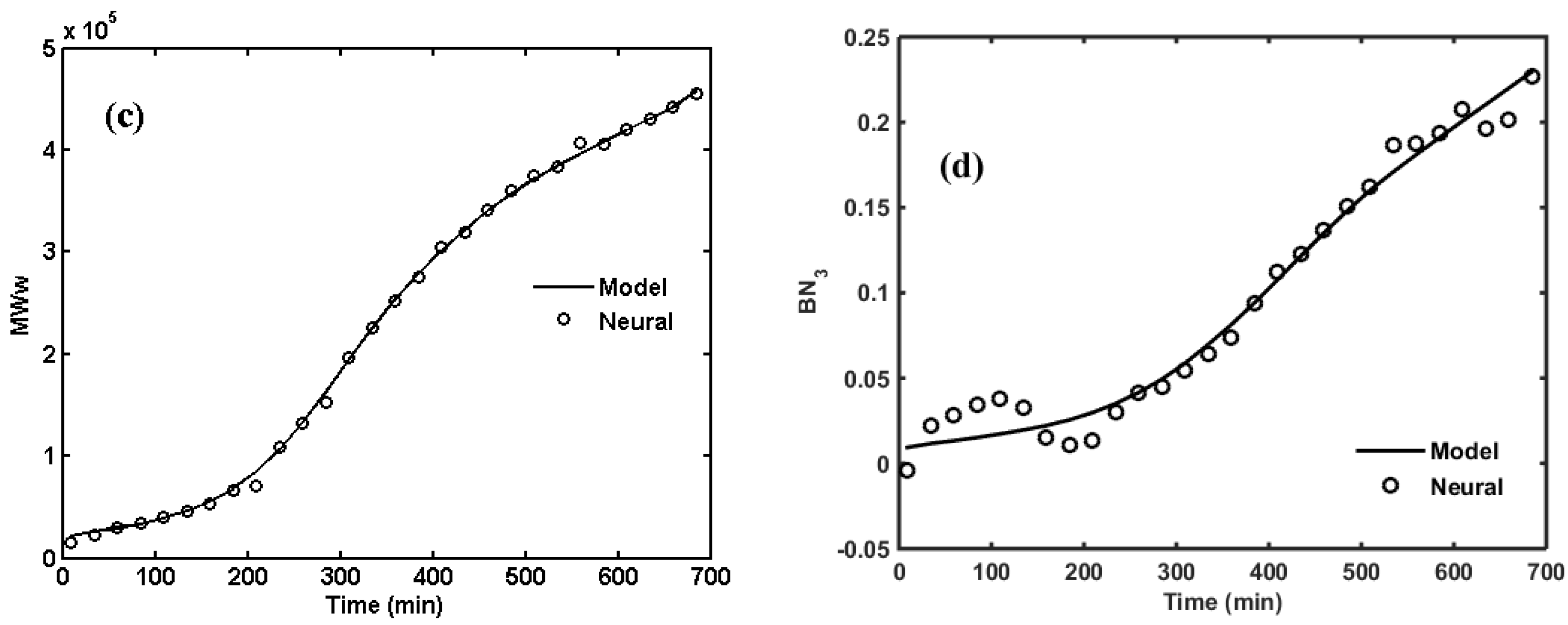
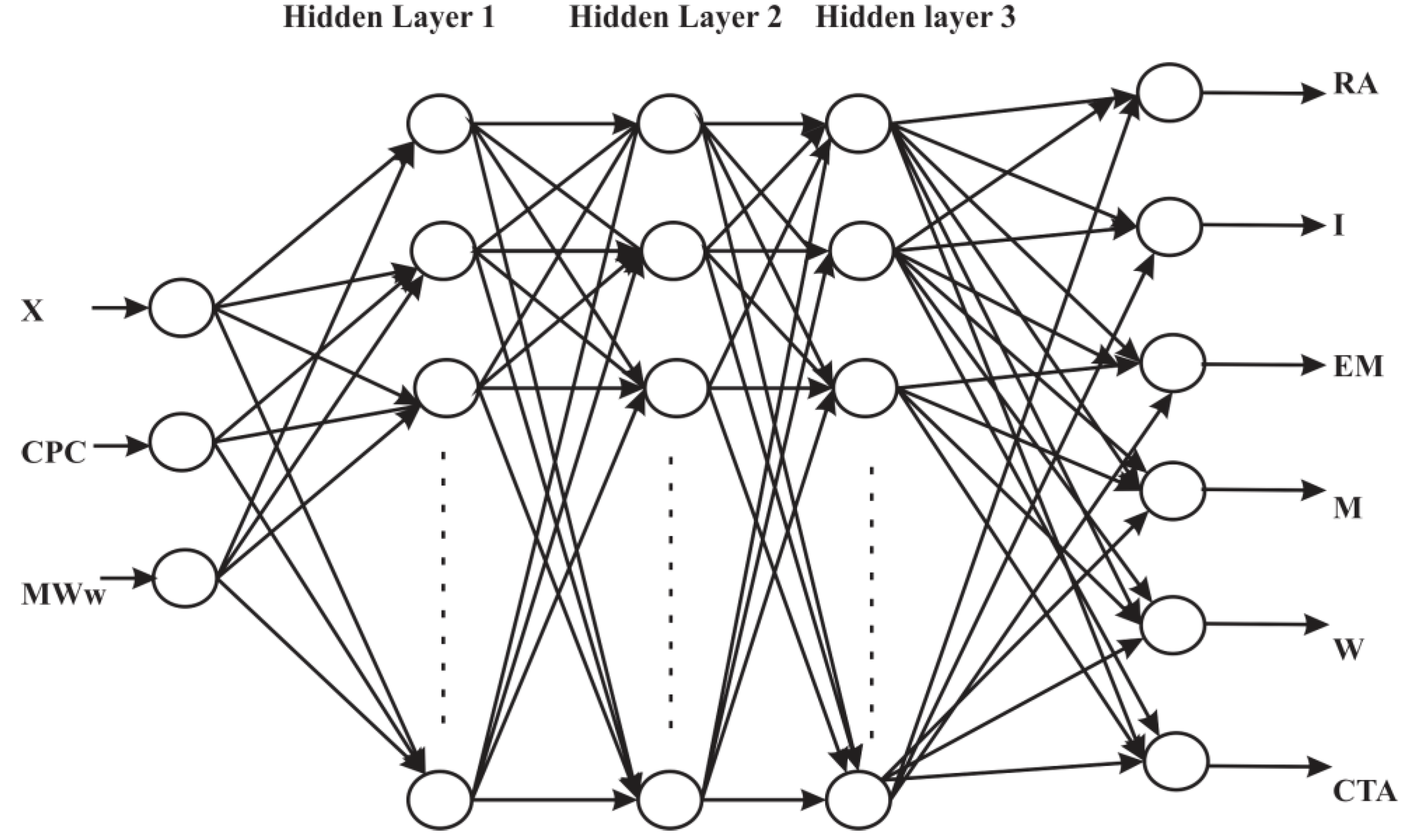
2. ANNs for NBR Emulsion Copolymerization in a Batch Reactor
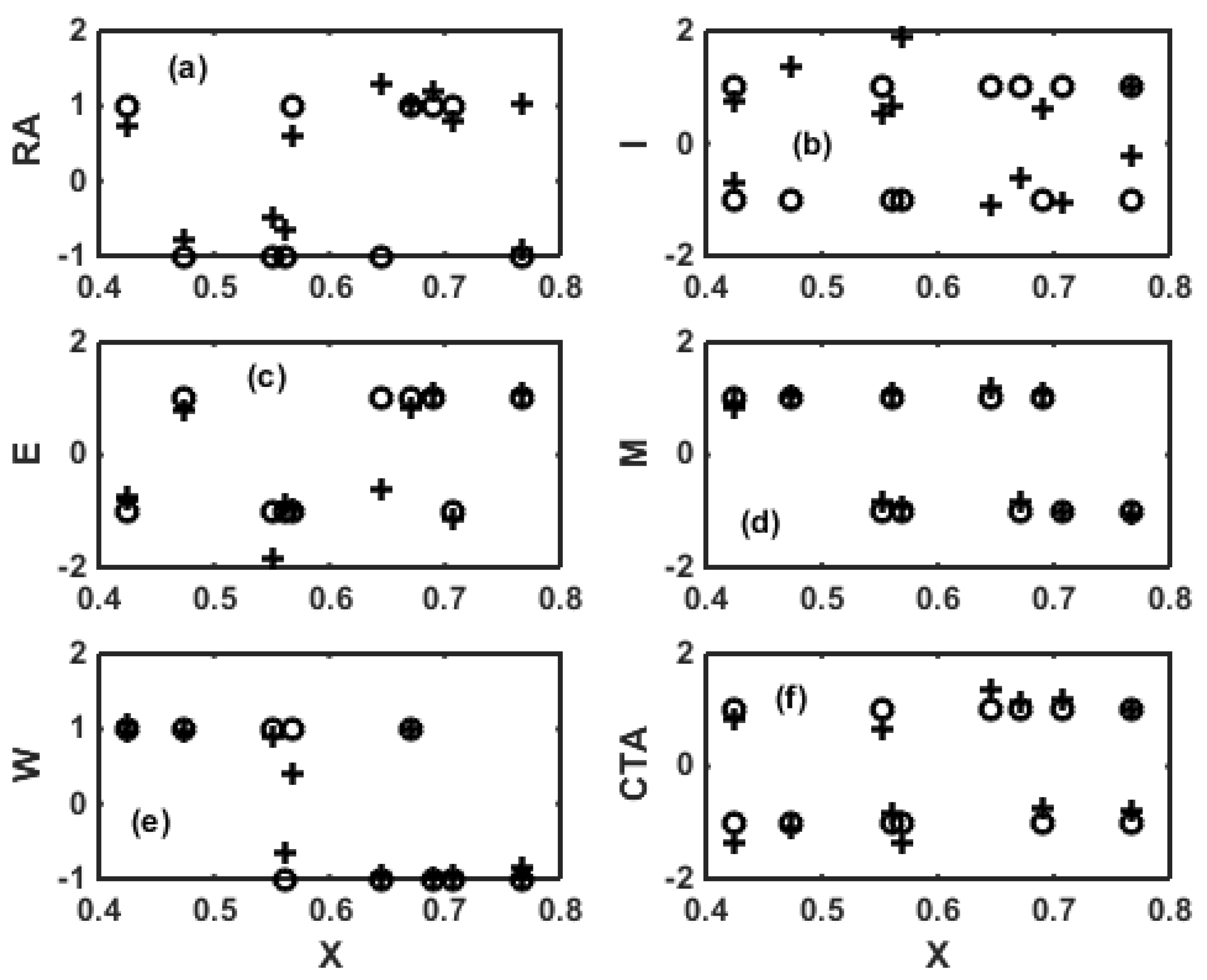
3. ANN for Inverse Modeling of NBR Emulsion Copolymerisation in a Train of CSTRs
4. Surrogate Modeling for NBR Emulsion Copolymerization
5. Transfer Function Models for the First CSTR in the Reactor Train
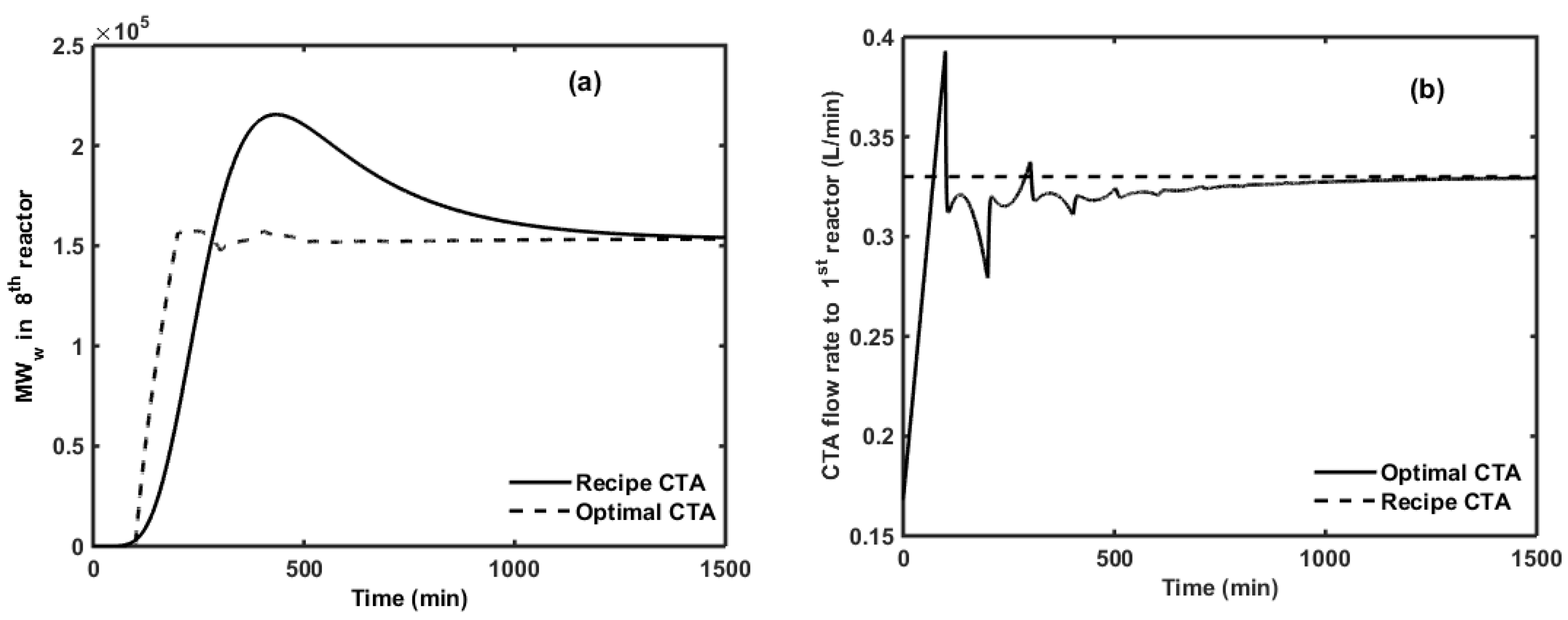
6. Optimal CTA Profile for Minimizing off-Spec Product
7. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| NBR | Nitrile Butadiene Rubber |
| AN | Acrylonitrile |
| Bd | Butadiene |
| CSTR | Continuous-Stirred Tank Reactor |
| ANN | Artificial Neural Network |
| MM | Mechanistic Model |
| EM | Empirical Model |
References
- Washington, I.D.; Duever, T.D.; Penlidis, A. Mathematical modeling of acrylonitrile-butadiene emulsion polymerization: Model development and validation. J. Macromol. Sci. A Pure Appl. Chem. 2010, 47, 747–769. [Google Scholar] [CrossRef]
- Dube’, M.A.; Penlidis, A.; Mutha, R.K.; Cluett, W.R. Mathematical modeling of emulsion copolymerization of acrylonitrile/butadiene. Ind. Eng. Chem. Res. 1996, 35, 4434–4448. [Google Scholar] [CrossRef]
- Scott, A.J.; Nabifar, A.; Madhuranthakam, C.R.; Penlidis, A. Bayesian design of experiments applied to a complex polymerization system: Nitrile butadiene rubber production in a train of CSTRs. Macromol. Theory Simul. 2015, 24, 13–27. [Google Scholar] [CrossRef]
- Madhuranthakam, C.R.; Penlidis, A. Modeling uses and analysis of production scenarios for acrylonitrile-butadiene (NBR) emulsions. Polym. Eng. Sci. 2011, 51, 1909–1918. [Google Scholar] [CrossRef]
- Madhuranthakam, C.R.; Penlidis, A. Improved operating scenarios for the production of acrylonitrile-butadiene emulsions. Polym. Eng. Sci. 2013, 53, 9–20. [Google Scholar] [CrossRef]
- Bhat, N.V.; McAvoy, T.J. Determining model structure for neural models by network stripping. Comput. Chem. Eng. 1992, 16, 271–281. [Google Scholar] [CrossRef]
- Nascimento, C.A.; Giudici, R.; Guardani, R. Neural network based approach for optimization of industrial chemical processes. Comput. Chem. Eng. 2000, 24, 2303–2314. [Google Scholar] [CrossRef]
- Ekpo, E.E.; Mujtaba, I.M. Evaluation of neural networks-based controllers in batch polymerisation of methyl methacrylate. Neurocomputing 2008, 71, 1401–1412. [Google Scholar] [CrossRef]
- Lightbody, G.; Irwin, G.W.; Taylor, A.; Kelly, K.; McCormick, J. Neural network modeling of a polymerization reactor. Proc. IEEE Int. Conf. Control. 1994, 1, 237–242. [Google Scholar]
- D’Anjou, A.; Torrealdea, F.J.; Leiza, J.R.; Asua, J.M.; Arzamendi, G. Model reduction in emulsion polymerization using hybrid first-principles/artificial neural network models. Macromol. Theory Simul. 2003, 12, 42–56. [Google Scholar] [CrossRef]
- Arzamendi, G.; d’Anjou, A.; Grana, M.; Leiza, J.R.; Asua, J.M. Model reduction in emulsion polymerization using hybrid first-principles/artificial neural network models 2a long chain branching kinetics. Macromol. Theory Simul. 2005, 14, 125–132. [Google Scholar] [CrossRef]
- Vijayabaskar, V.; Gupta, R.; Chakrabarti, P.P.; Bhowmick, A.K. Prediction of properties of rubber by using artificial neural networks. J. Appl. Polym. Sci. 2006, 100, 2227–2237. [Google Scholar] [CrossRef]
- Assenhaimer, C.; Machado, L.J.; Glasse, B.; Fritsching, U.; Guardani, R. Use of a spectroscopic sensor to monitor droplet size distribution in emulsions using neural networks. Can. J. Chem. Eng. 2014, 92, 318–323. [Google Scholar] [CrossRef]
- Delfa, G.M.; Boschetti, C.E. Optimization of the chain transfer agent incremental addition in SBR emulsion polymerization. J. Appl. Polym. Sci. 2012, 124, 3468–3477. [Google Scholar] [CrossRef]
- Hahn, J.; Edgar, T.F. An improved method for nonlinear model reduction using balancing of empirical gramians. Comput. Chem. Eng. 2002, 26, 1379–1397. [Google Scholar] [CrossRef]
- Fujisawa, T.; Penlidis, A. Copolymer composition control colicies: characteristics and applications. J. Macromol. Sci. A Pure Appl. Chem. 2008, 45, 115–132. [Google Scholar] [CrossRef]
- Minari, R.J.; Gugliotta, L.M.; Vega, J.R.; Meira, G.R. Continuous emulsion styrene-butadiene rubber (SBR) process: Computer simulation study for increasing production and for reducing transients between steady states. Ind. Eng. Chem. Res. 2006, 45, 245–257. [Google Scholar] [CrossRef]
- Minari, R.J.; Gugliotta, L.M.; Vega, J.R.; Meira, G.R. Continuous emulsion copolymerization of acrylonitrile and butadiene: Simulation study for reducing transients during changes of grade. Ind. Eng. Chem. Res. 2007, 46, 7677–7683. [Google Scholar] [CrossRef]
- Rivera-Toledo, M.; Flores-Tlacuahuac, A. A multiobjective dynamic optimization approach for a methyl-methacrylate plastic sheet reactor. Macromol. React. Eng. 2014, 8, 358–373. [Google Scholar] [CrossRef]
- Camargo, M.; Morel, L.; Fonteix, C.; Hoppe, S.; Hu, G.; Renaud, J. Development of new concepts for the control of polymerization processes: Multiobjective optimization and decision engineering. II. Application of a choquet integral to an emulsion copolymerization process. J. Appl. Polym. Sci. 2011, 120, 3421–3434. [Google Scholar] [CrossRef]
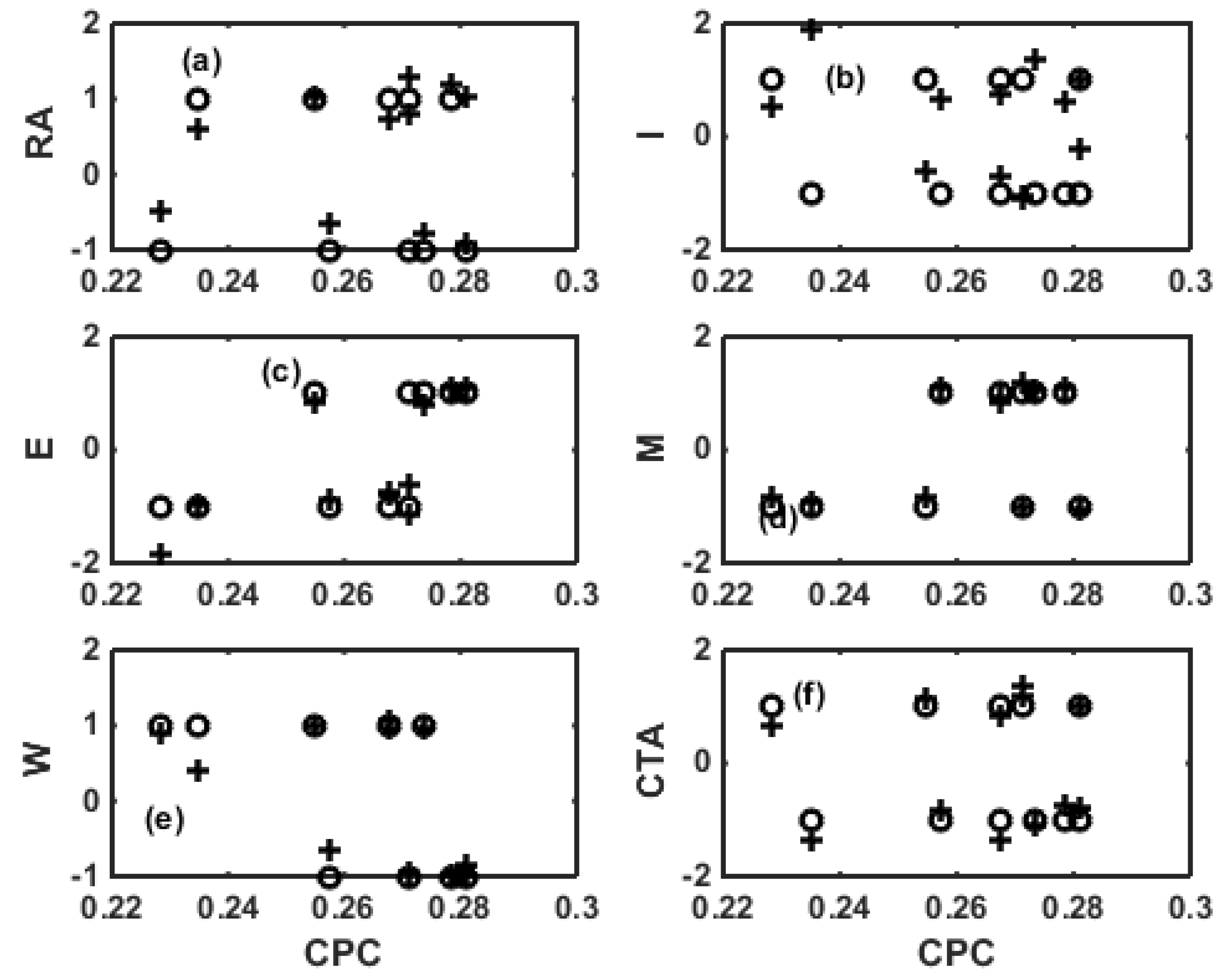
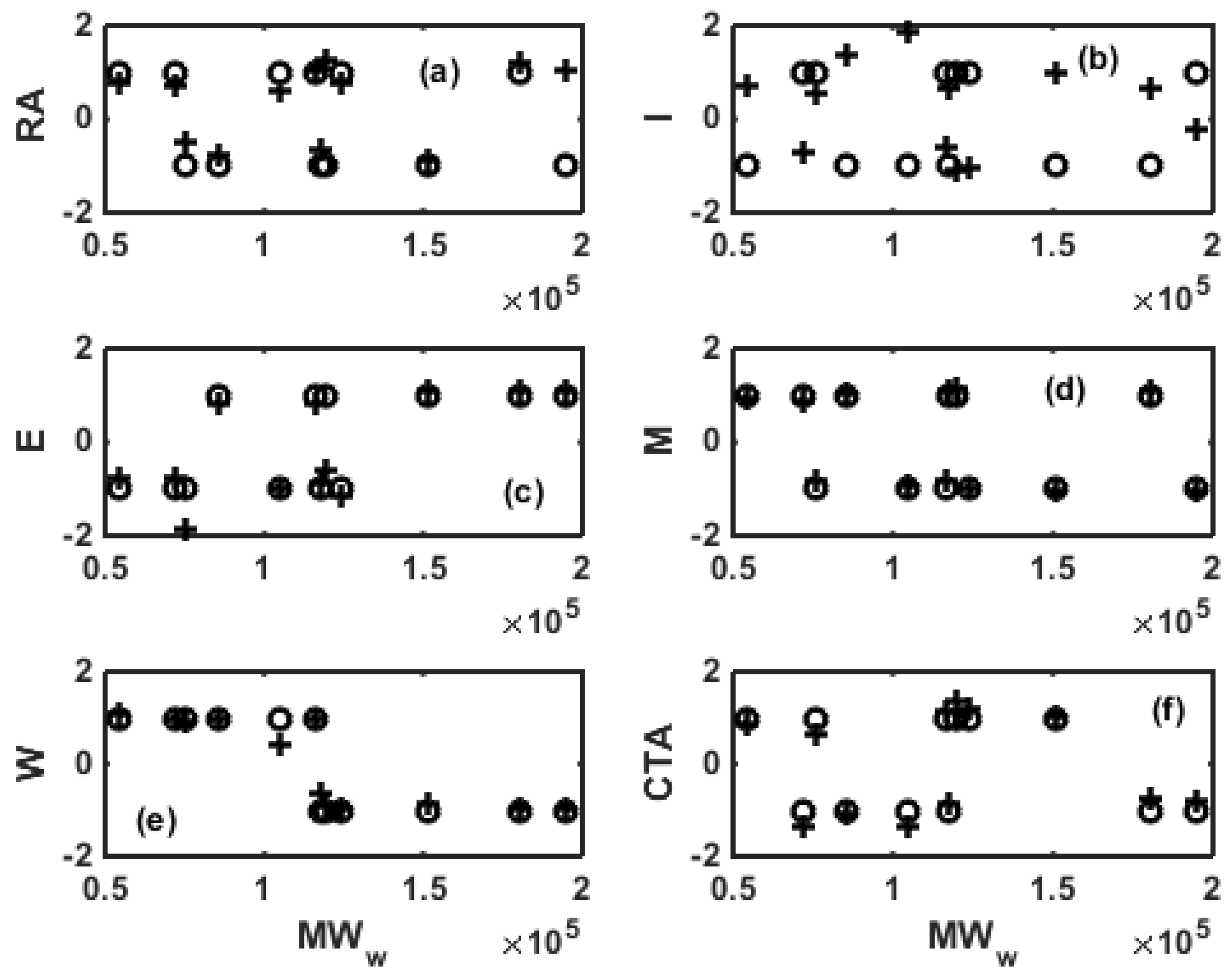
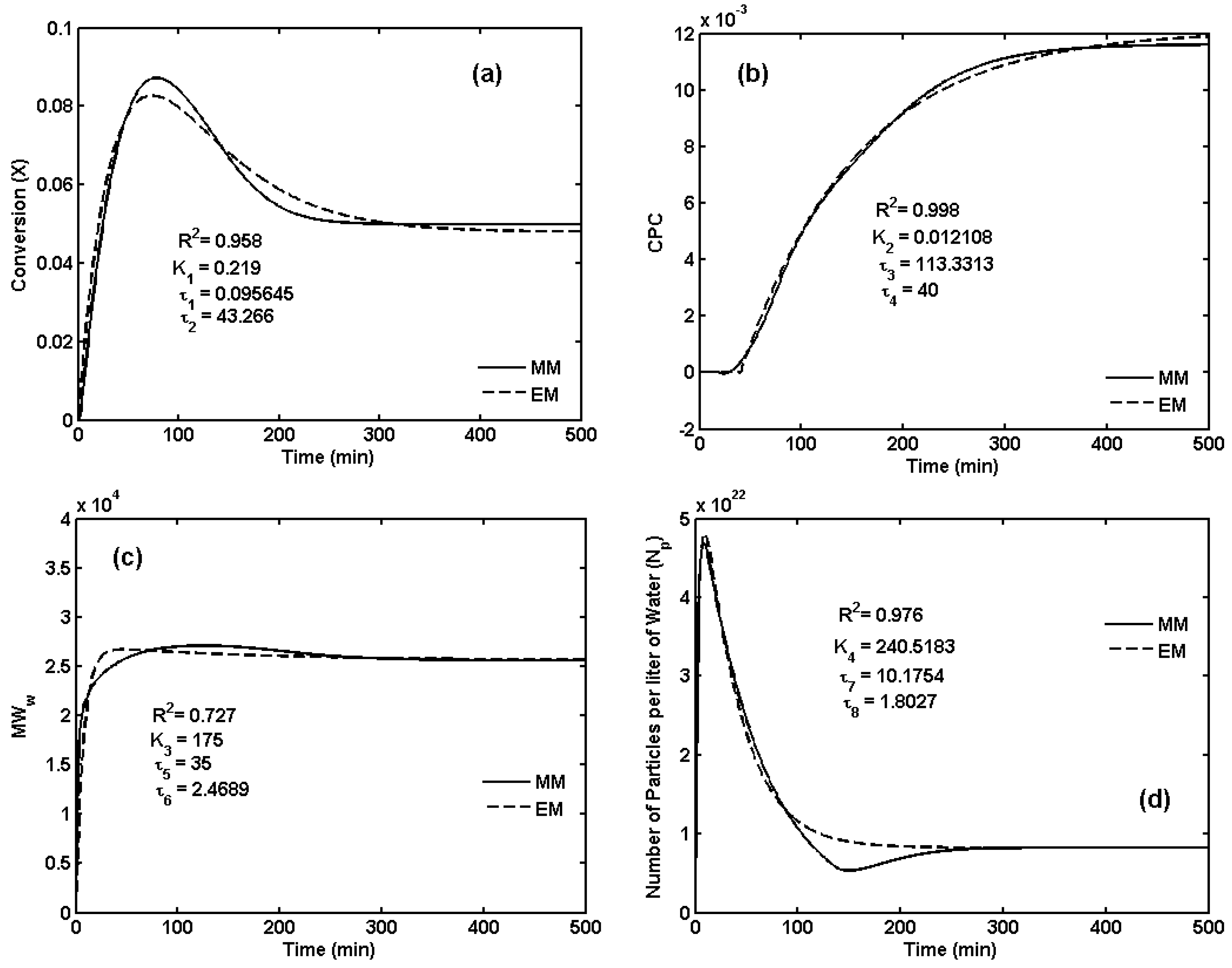
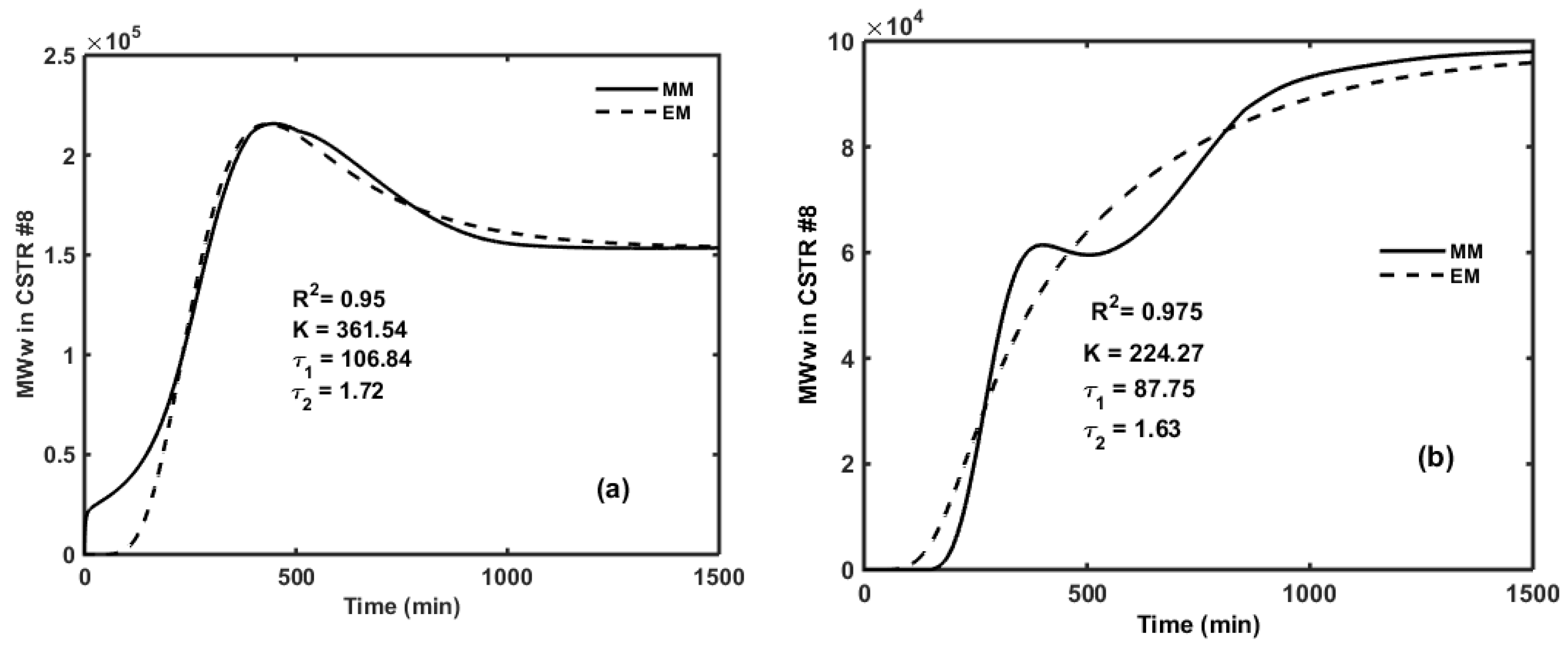
| Ingredient | Low Level (L/min) | High Level (L/min) |
|---|---|---|
| Sodium Formaldehyde Sulfoxylate (RA) | 0.165 | 0.22 |
| p-methane hydroperoxide (I) | 0.046 | 0.062 |
| Dresinate/Tamol (E) | 0.89/1.67 | 1.183/2.228 |
| Acrylonitrile/Butadiene (M) | 48.6/160.3 | 64.8/213.7 |
| Water (W) | 121.36 | 161.81 |
| tert-dodecyl Mercaptan (CTA) | 0.33 | 0.44 |
| Number of Neurons | Number of Hidden Layers | |||||
|---|---|---|---|---|---|---|
| Monomer | CTA | |||||
| 1 | 2 | 3 | 1 | 2 | 3 | |
| 5 | 0.1532 | 0.1593 | 0.0033 | 0.1370 | 0.0420 | 0.0405 |
| 10 | 0.0653 | 0.0289 | 0.0836 | 0.0677 | 0.0509 | 0.2600 |
| 15 | 0.0148 | 0.0659 | 0.0405 | 0.0143 | 0.2070 | 0.1355 |
| 20 | 0.0245 | 0.2412 | 0.0124 | 0.137 | 0.1175 | 0.0613 |
| # | X | CPC | MWw | Mean Squared Error (MSE) | |||||
|---|---|---|---|---|---|---|---|---|---|
| RA | I | E | M | W | CTA | ||||
| 1 | 0.5611 | 0.2573 | 1.17 × 105 | 0.1247 | 2.7766 | 0.0136 | 0.0105 | 0.1115 | 0.0255 |
| 2 | 0.7668 | 0.2811 | 1.51 × 105 | 0.0096 | 4.0446 | 0.0074 | 0.0042 | 0.0240 | 0.0001 |
| 3 | 0.4743 | 0.2735 | 8.54 × 104 | 0.0518 | 5.6491 | 0.0384 | 0.0014 | 0.0016 | 0.0068 |
| 4 | 0.5515 | 0.2285 | 7.56 × 104 | 0.2717 | 0.2051 | 0.7459 | 0.0300 | 0.0110 | 0.1170 |
| 5 | 0.7669 | 0.2811 | 1.95 × 105 | 4.1140 | 1.4764 | 0.0101 | 0.0015 | 0.0002 | 0.0396 |
| 6 | 0.6454 | 0.2711 | 1.19 × 105 | 5.2109 | 4.4500 | 2.6381 | 0.0287 | 0.0034 | 0.1231 |
| 7 | 0.5689 | 0.2349 | 1.05 × 105 | 0.1591 | 8.3361 | 0.0016 | 0.0076 | 0.3575 | 0.1394 |
| 8 | 0.4246 | 0.2676 | 5.45 × 104 | 0.0674 | 2.9982 | 0.0549 | 0.0037 | 0.0053 | 0.0211 |
| 9 | 0.6895 | 0.2784 | 1.80 × 105 | 0.0325 | 2.6604 | 0.0100 | 0.0094 | 0.0000 | 0.0626 |
| 10 | 0.7074 | 0.2713 | 1.24 × 105 | 0.0470 | 4.2123 | 0.0217 | 0.0001 | 0.0024 | 0.0424 |
| 11 | 0.4247 | 0.2676 | 7.22 × 104 | 0.0743 | 2.9586 | 0.0487 | 0.0206 | 0.0027 | 0.1336 |
| 12 | 0.6703 | 0.2547 | 1.16 × 105 | 0.0014 | 2.6040 | 0.0243 | 0.0321 | 0.0004 | 0.0246 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madhuranthakam, C.M.R.; Penlidis, A. Surrogate Models for Online Monitoring and Process Troubleshooting of NBR Emulsion Copolymerization. Processes 2016, 4, 6. https://doi.org/10.3390/pr4010006
Madhuranthakam CMR, Penlidis A. Surrogate Models for Online Monitoring and Process Troubleshooting of NBR Emulsion Copolymerization. Processes. 2016; 4(1):6. https://doi.org/10.3390/pr4010006
Chicago/Turabian StyleMadhuranthakam, Chandra Mouli R., and Alexander Penlidis. 2016. "Surrogate Models for Online Monitoring and Process Troubleshooting of NBR Emulsion Copolymerization" Processes 4, no. 1: 6. https://doi.org/10.3390/pr4010006
APA StyleMadhuranthakam, C. M. R., & Penlidis, A. (2016). Surrogate Models for Online Monitoring and Process Troubleshooting of NBR Emulsion Copolymerization. Processes, 4(1), 6. https://doi.org/10.3390/pr4010006







