Modeling of the Copolymerization Kinetics of n-Butyl Acrylate and d-Limonene Using PREDICI ®
Abstract
:1. Introduction
2. Experimental Section
| Monomer Feed (BA Molar Fraction) | BA (mol L−1) | Lim (mol L−1) | BPO (mol L−1) |
|---|---|---|---|
| fBA = 0.9 | 6.13 | 0.68 | 0.036 |
| fBA = 0.8 | 5.38 | 1.35 | 0.036 |
| fBA = 0.7 | 4.65 | 2.00 | 0.036 |
| fBA = 0.6 | 3.91 | 2.67 | 0.036 |
| fBA = 0.5 | 3.26 | 3.26 | 0.036 |
3. Model Development
| Description | Step in PREDICI ® | Variables | Initial Value (L mol−1 s−1 Unless Otherwise Stated) |
|---|---|---|---|
| Initiation | |||
| Initiator decomposition | I→2fR• | kd, f | kd = 2.52 × 10−5 s−1 [21], f = 0.6 |
| First propagation to Lim | R• + M1→Lim• | ki1 | 1.3 [10], adjusted value = 0.325 |
| First propagation to BA | R• + BA→BA• | ki2 | 4.97 × 104 [17,22] |
| Propagation | |||
| Self-propagation of Lim | PLim(s)• + Lim→PLim (s + 1)• | kp11 | 1.3 [10], adjusted value = 0.325 |
| Cross-propagation | PLim(s)• + BA→PBA (s + 1)• | kp12 | 19.9, adjusted value = 48.5 |
| Self-propagation of BA | PBA(s)• + BA→PBA (s + 1)• | kp22 | 4.97 × 104 [17,22], adjusted value = 2.49 × 105 |
| Cross-propagation | PBA(s)• + Lim→PLim (s + 1)• | kp21 | 8.2 × 103, adjusted value = 4.10 × 104 |
| Chain transfer | |||
| Chain transfer to BA | PLim(s)• + BA→P(s) + BA• | kfm12 | 1.44 × 10−2 |
| Chain transfer to BA | PBA(s)• + BA→P(s) + BA• | kfm22 | 3.68 × 10−1 [21] |
| Degradative chain transfer | PLim(s)• + Lim→P(s) + ALim• | kfm11 | 4.65 × 10−1 |
| Degradative chain transfer | PBA(s)• + Lim→P(s) + ALim• | kfm21 | 2.93 × 102 |
| Re-initiation of ALim• | ALim• + Lim→Lim• | kra1 | 1.67 × 10−10 [10] |
| Re-initiation of ALim• | ALim• + BA→BA• | kra2 | 1.67 × 10−8 [10] |
| Termination | |||
| By combination | PLim(s)• + PLim(r)•→P(s + r) | ktc11 | 1.79 × 108 |
| - | PLim(s)• + PBA(r)•→P(s + r) | ktc12 | 1.79 × 108 |
| - | PBA(s)• + PBA(r)•→P(s + r) | ktc22 | 1.79 × 108 [14,17] |
| - | ALim• + ALim•→AA | ktcaa | 9.95 × 107 |
| - | PLim(s)• + ALim•→P(s) | ktc1a | 1.79 × 108 |
| - | PBA(s)• + ALim•→P(s) | ktc2a | 1.79 × 108 |
| By disproportionation | PLim(s)• + PLim(r)•→P(s) + P(r) | ktd11 | 1.99 × 107 |
| - | PLim(s)• + PBA(r)•→P(s) + P(r) | ktd12 | 1.99 × 107 |
| - | PBA(s)• + PBA(r)•→P(s) + P(r) | ktd22 | 9.95 × 107 [14,17] |
| Intramolecular chain transfer of BA | |||
| Backbiting of BA | PBA(s)•→QBA(s)• | kbb | 5.76 × 103 [16,21] |
| Short-chain branching | QBA(s)•+Lim→PLim(s+1)• | kp21tert | 8.23 |
| Short-chain branching | QBA(s)•+BA→PBA(s+1)• | kp22tert | 49.9 [16,21] |
| Degradative chain transfer | QBA(s)•+Lim→P(s)+ALim• | kfm2atert | 1.83 |
| Termination of BA tertiary radicals | |||
| By combination (QBA•) | QBA(s)• + QBA(r)•→P(s + r) | ktc22tert−tert | 1.99 × 107 [14,17] |
| - | QBA(s)• + PBA(r)•→P(s + r) | ktc22tert−sec | 5.97 × 107 [14,17] |
| - | QBA(s)• + PLim(r)•→P(s + r) | ktc21tert−sec | 5.97 × 107 |
| - | QBA(s)• + ALim•→P(s) | ktc2atert−a | 9.95 × 107 |
| By disproportionation (QBA•) | QBA(s)• + QBA(r)•→P(s) + P(r) | ktd22tert−tert | 1.79 × 108 [14,17] |
| - | QBA(s)• + PBA(r)•→P(s) + P(r) | ktd22tert−sec | 1.39 × 108 [14,17] |
| - | QBA(s)• + PLim(r)•→P(s) + P(r) | ktd21tert−sec | 1.39 × 108 |
| - | QBA(s)• + ALim•→P(s) + A | ktd2atert−a | 9.95 × 107 |
3.1. Initiation
3.2. Propagation
3.3. Chain Transfer to BA and the Degradative Chain Transfer of Lim


3.4. Termination
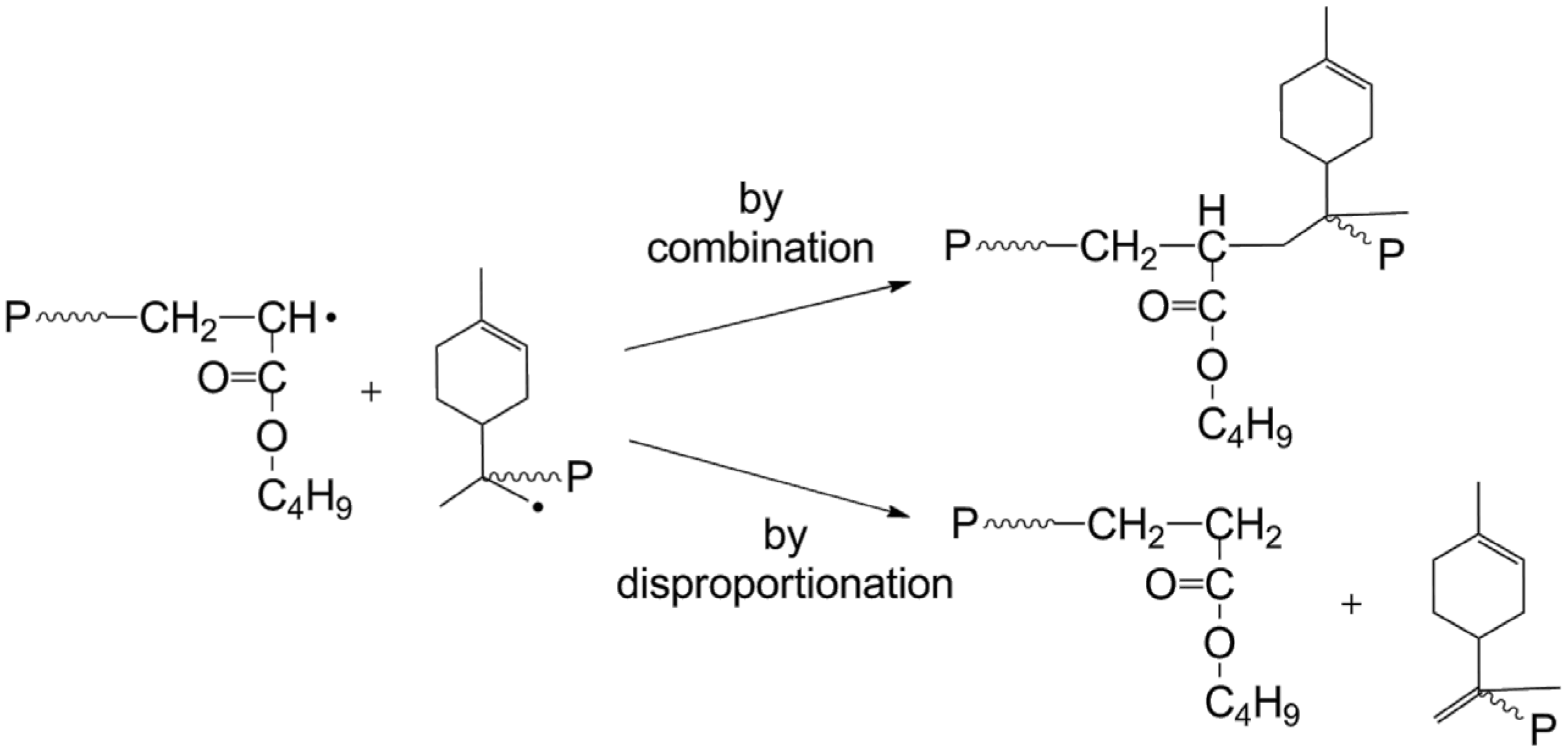
3.5. Backbiting of BA
4. Results And Discussion
4.1. Backbiting of BA
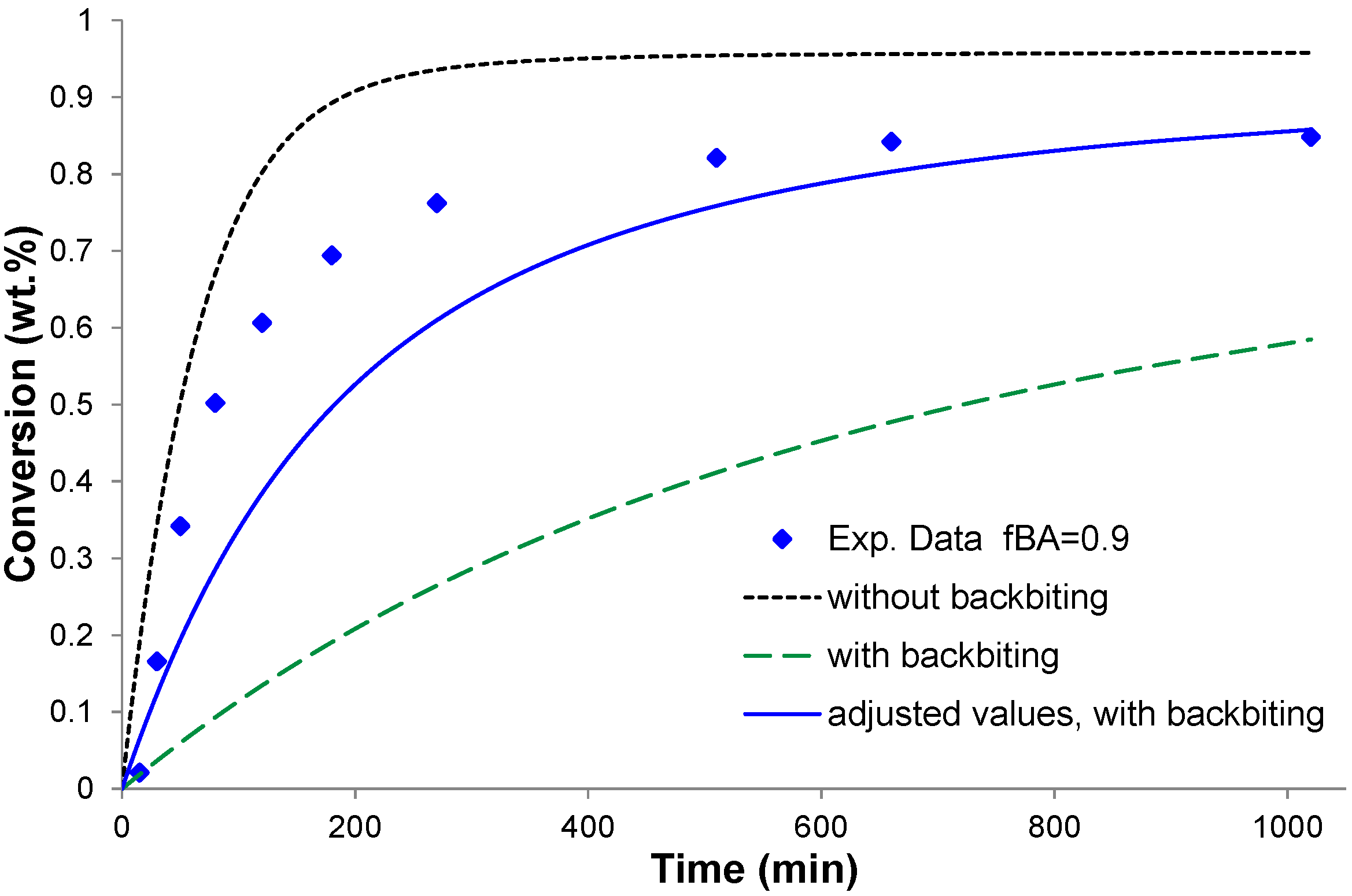
4.2. Conversion vs. Time Results
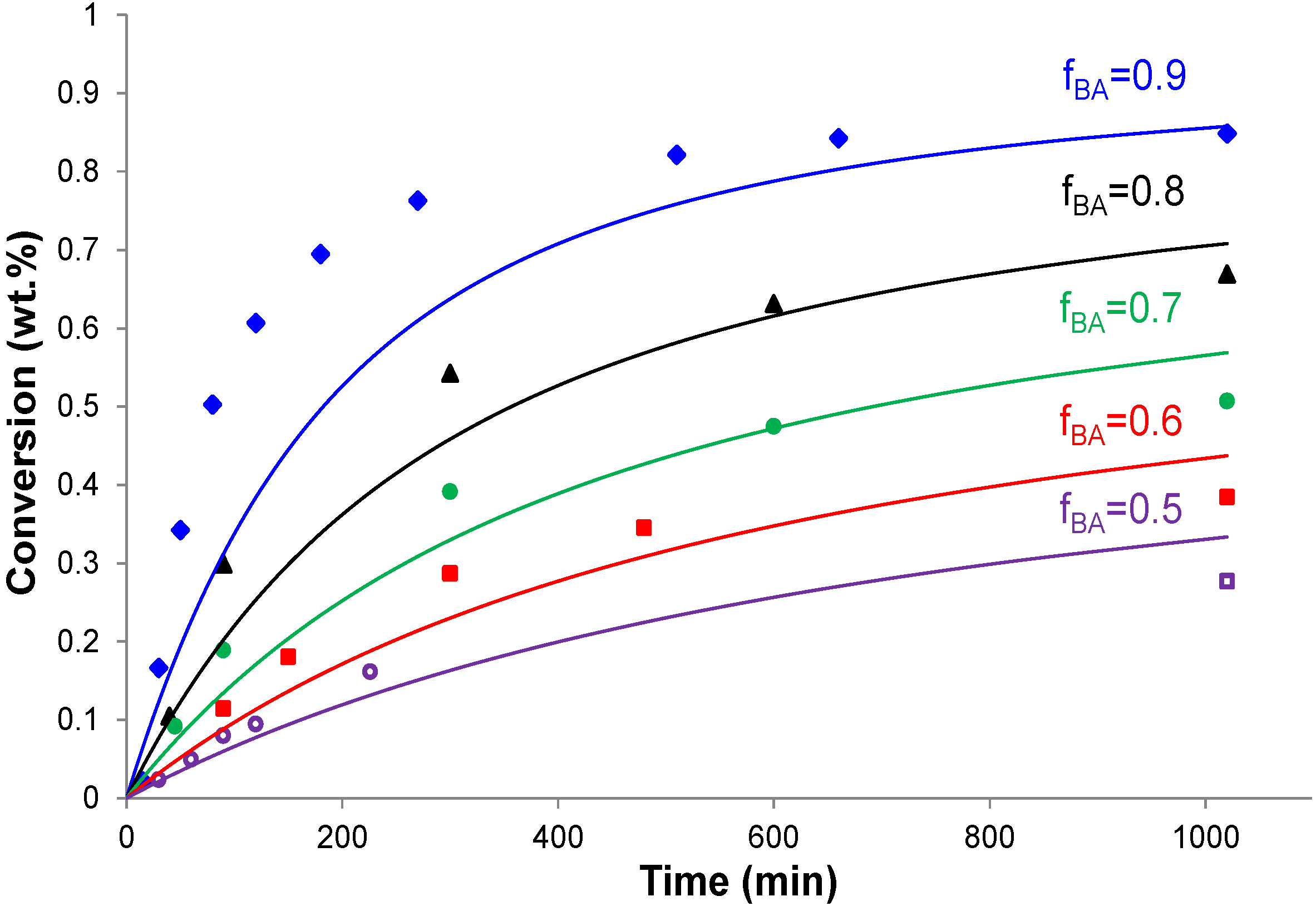
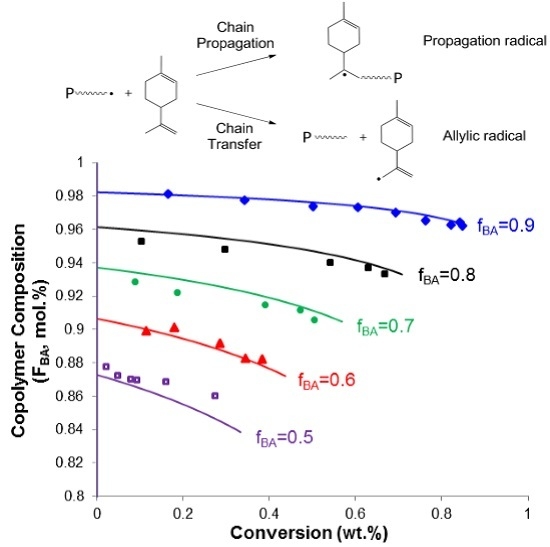
4.3. Copolymer Composition vs. Conversion
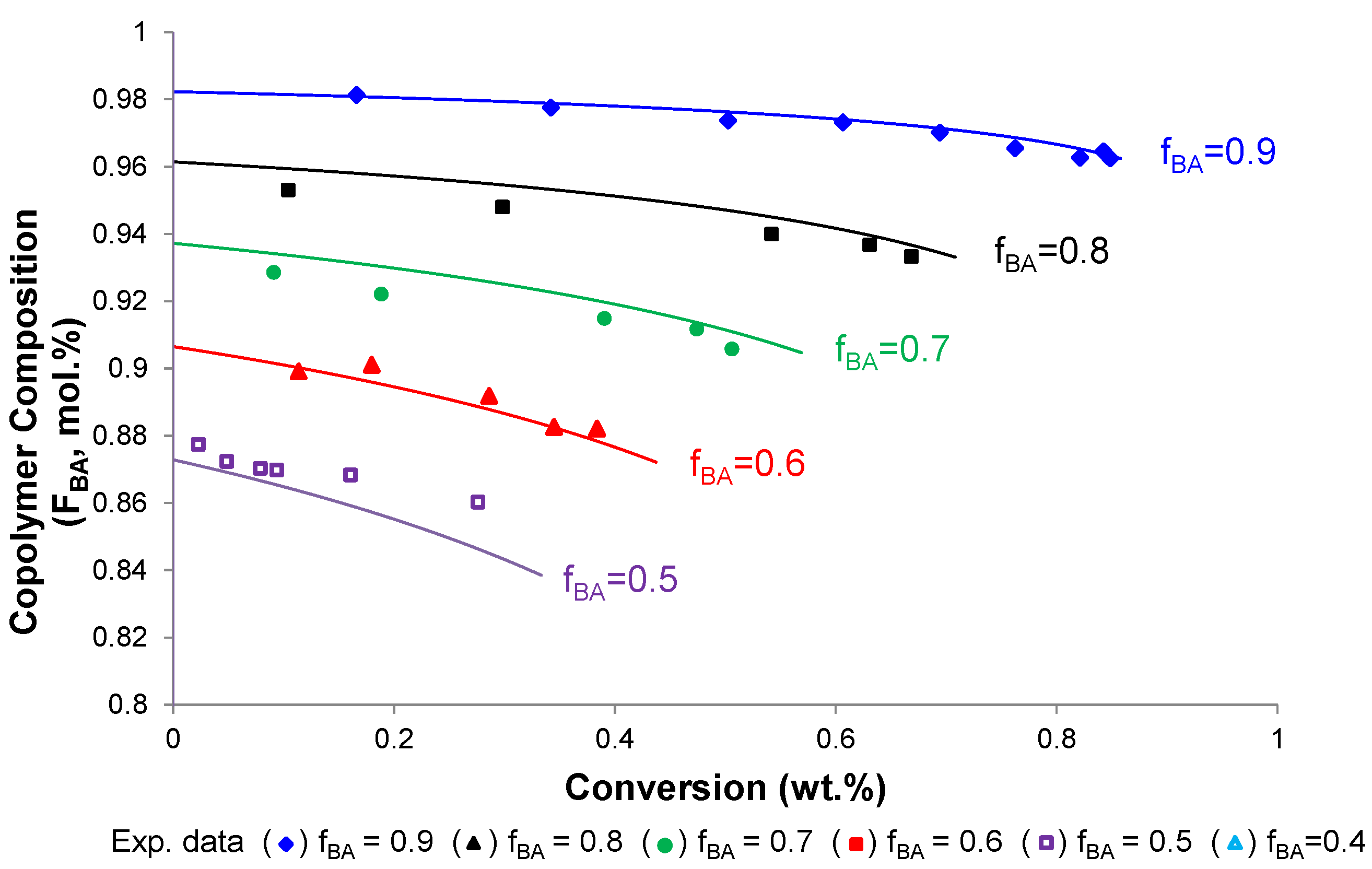
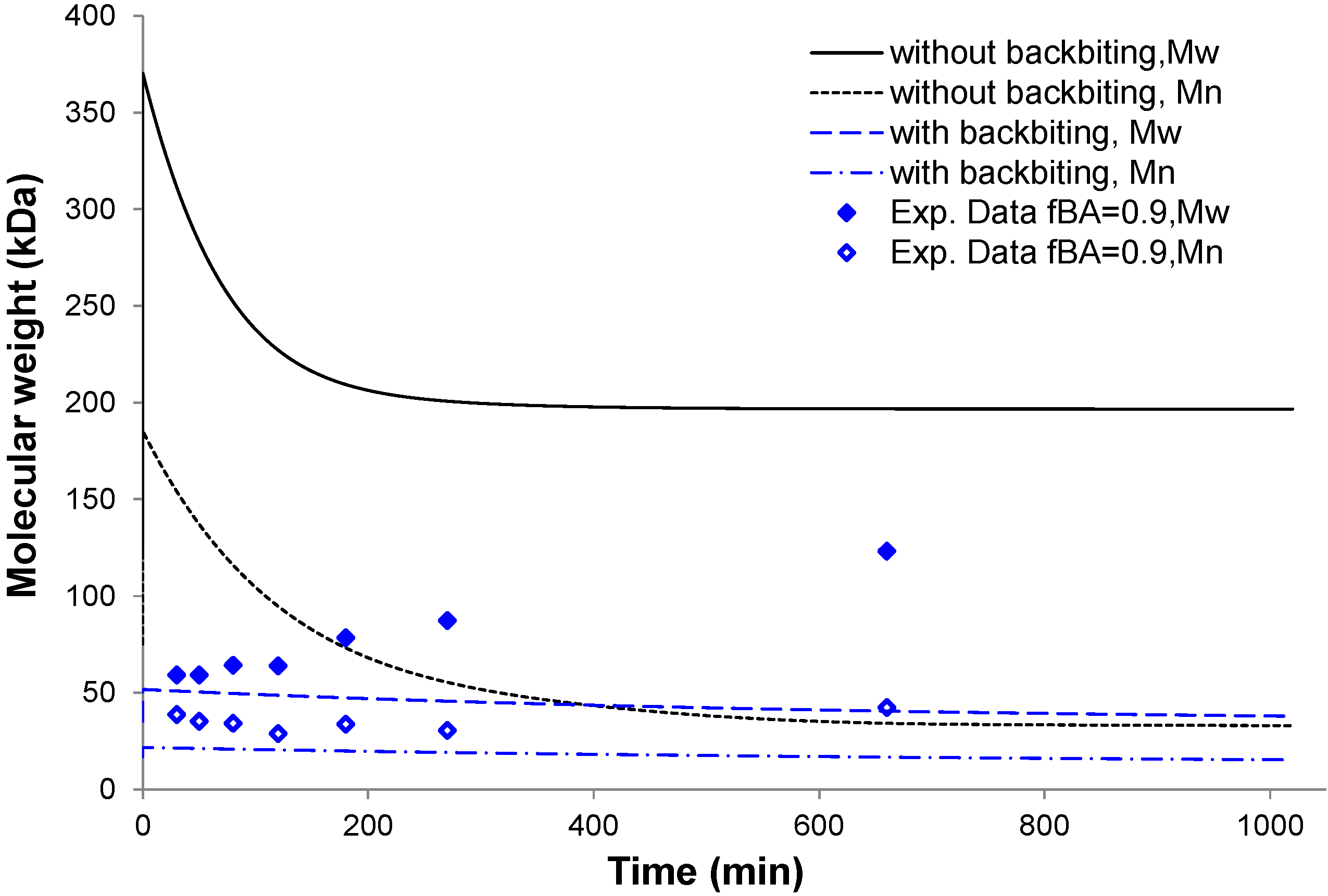
4.4. Molecular Weight of Soluble Copolymer
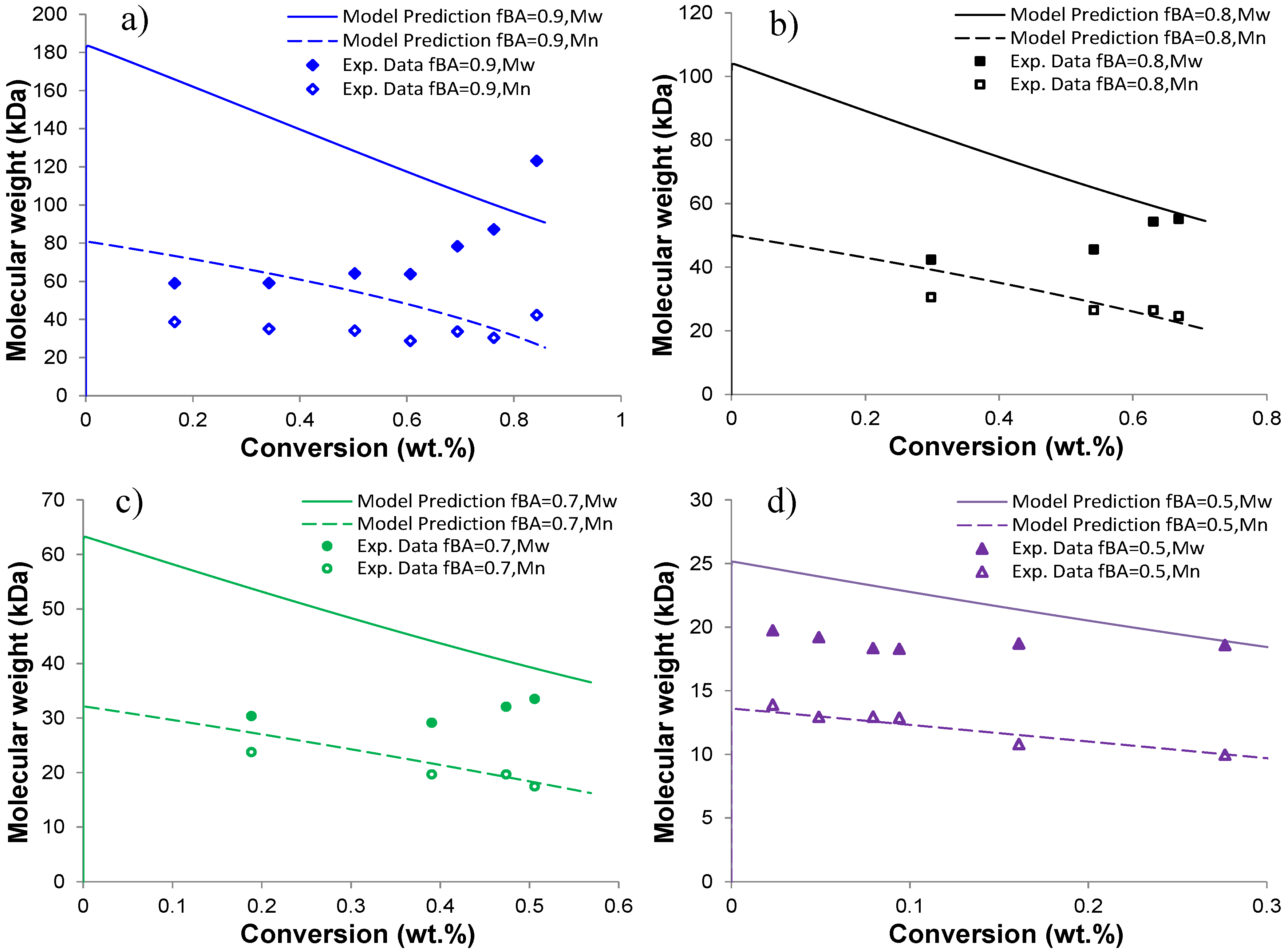
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Belgacem, M.N.; Alessandro, G. Monomers, Polymers and Composites from Renewable Resources; Elsevier: Amsterdam, The Netherlands, 2008; p. 543. [Google Scholar]
- Ahmed, J.; Tiwari, B.K.; Imam, S.H.; Rao, M.A. Starch-based Polymeric Materials and Nanocomposites: Chemistry, Processing, and Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Kim, Y.W.; Kim, M.J.; Chung, B.Y.; Bang, D.Y.; Lim, S.K.; Choi, S.M.; Lim, D.S.; Cho, M.C.; Yoon, K.; Kim, H.S.; et al. Safety evaluation and risk assessment of d-limonene. J. Toxicol. Environ. Health Pt B 2013, 16, 17–38. [Google Scholar] [CrossRef] [PubMed]
- Ciriminna, R.; Lomeli-Rodriguez, M.; Demma Cara, P.; Lopez-Sanchez, J.; Pagliaro, M. Limonene: A versatile chemical of the bioeconomy. Chem. Commun. 2014, 50, 15288–15296. [Google Scholar] [CrossRef] [PubMed]
- Wilbon, P.A.; Chu, F.; Tang, C. Progress in renewable polymers from natural terpenes, terpenoids, and rosin. Macromol. Rapid Commun. 2013, 34, 8–37. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.; Trevino, E.; Dubé, M.A. Copolymerization of limonene with n-butyl acrylate. Macromol. React. Eng. 2015, 9, 339–349. [Google Scholar] [CrossRef]
- Zhang, Y.; Dubé, M.A. Copolymerization of n-butyl methacrylate and d-limonene. Macromol. React. Eng. 2014, 8, 805–812. [Google Scholar] [CrossRef]
- Zhang, Y.; Dubé, M.A. Copolymerization of 2-Ethylhexyl acrylate and d-limonene. Polym. Plast Technol. Eng 2015, 54, 499–505. [Google Scholar] [CrossRef]
- Ren, S.; Zhang, L.; Dubé, M.A. Free-radical terpolymerization of n-butyl acrylate/butyl methacrylate/d-limonene. J. Appl. Polym. Sci. 2015, 132, 42821–42829. [Google Scholar] [CrossRef]
- Zhang, Y.; Dubé, M.A.; Vivaldo-Lima, E. Modeling degradative chain transfer in d-Limonene/n-butyl methacrylate free-radical copolymerization. J. Renew. Mat. 2015, 3, 318–326. [Google Scholar] [CrossRef]
- Li, D.; Grady, M.C.; Hutchinson, R.A. High-temperature semibatch free radical copolymerization of butyl methacrylate and butyl acrylate. Ind. Eng. Chem. Res. 2005, 44, 2506–2517. [Google Scholar] [CrossRef]
- Beuermann, S.; Paquet, D.A.; McMinn, J.H.; Hutchinson, R.A. Determination of free-radical propagation rate coefficients of butyl, 2-ethylhexyl, and dodecyl acrylates by pulsed-laser polymerization. Macromolecules 1996, 29, 4206–4215. [Google Scholar] [CrossRef]
- Lyons, R.A.; Hutovic, J.; Piton, M.C.; Christie, D.I.; Clay, P.A.; Manders, B.G.; Kable, S.H.; Gilbert, R.G. Pulsed-laser polymerization measurements of the propagation rate coefficient for butyl acrylate. Macromolecules 1996, 29, 1918–1927. [Google Scholar] [CrossRef]
- Peck, A.N.F.; Hutchinson, R.A. Secondary reactions in the high-temperature free radical polymerization of butyl acrylate. Macromolecules 2004, 37, 5944–5951. [Google Scholar] [CrossRef]
- Nikitin, A.N.; Hutchinson, R.A. Effect of intramolecular transfer to polymer on stationary free radical polymerization of alkyl acrylates, 2. Macromol. Theory Simul. 2006, 15, 128–136. [Google Scholar] [CrossRef]
- Rantow, F.S.; Soroush, M.; Grady, M.C.; Kalfas, G.A. Spontaneous polymerization and chain microstructure evolution in high-temperature solution polymerization of n-butyl acrylate. Polymer 2006, 47, 1423–1435. [Google Scholar] [CrossRef]
- Nikitin, A.N.; Hutchinson, R.A.; Buback, M.; Hesse, P. Determination of intramolecular chain transfer and midchain radical propagation rate coefficients for butyl acrylate by pulsed laser polymerization. Macromolecules 2007, 40, 8631–8641. [Google Scholar] [CrossRef]
- Gao, J.; Penlidis, A. A Comprehensive simulator/database package for reviewing free-radical homopolymerizations. J. Macromol. Sci. Part C 1996, 36, 199–404. [Google Scholar] [CrossRef]
- Gao, J.; Penlidis, A. A Comprehensive simulator/database package for reviewing free-radical copolymerizations. J. Macromol. Sci. Part C 1998, 38, 651–780. [Google Scholar] [CrossRef]
- Gao, J.; Penlidis, A. A Comprehensive simulator/database package for bulk/solution free-radical terpolymerizations. Macromol. Chem. Phys. 2000, 201, 1176–1184. [Google Scholar] [CrossRef]
- Dorschner, D. Multicomponent Free Radical Polymerization Model Refinements and Extensions with Depropagations. Master’s Thesis, University of Waterloo, Department of Chemical Engineering, Waterloo, ON, Canada, 2010. [Google Scholar]
- Asua, J.M.; Beuermann, S.; Buback, M.; Castignolles, P.; Charleux, B.; Gilbert, R.G.; Hutchinson, R.A.; Leiza, J.R.; Nikitin, A.N.; Vairon, J.; et al. Critically evaluated rate coefficients for free-radical polymerization, 5. Macromol. Chem. Phys. 2004, 205, 2151–2160. [Google Scholar] [CrossRef]
- Jun, W. Mathematical Modeling of Free-Radical Six Component Bulk and Solution Polymerization. Master’s Thesis, University of Waterloo, Department of Chemical Engineering, Waterloo, ON, Canada, 2008. [Google Scholar]
- Beuermann, S.; Buback, M. Rate coefficients of free-radical polymerization deduced from pulsed laser experiments. Prog. Polym. Sci. 2002, 27, 191–254. [Google Scholar] [CrossRef]
- Plessis, C.; Arzamendi, G.; Leiza, J.R.; Schoonbrood, H.A.S.; Charmot, D.; Asua, J.M. modeling of seeded semibatch emulsion polymerization of n-BA. Ind. Eng. Chem. Res. 2001, 40, 3883–3894. [Google Scholar] [CrossRef]
- Ahmad, N.M.; Heatley, F.; Lovell, P.A. Chain transfer to polymer in free-radical solution polymerization of n-butyl acrylate studied by NMR spectroscopy. Macromolecules 1998, 31, 2822–2827. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, S.; Vivaldo-Lima, E.; Dubé, M.A. Modeling of the Copolymerization Kinetics of n-Butyl Acrylate and d-Limonene Using PREDICI ®. Processes 2016, 4, 1. https://doi.org/10.3390/pr4010001
Ren S, Vivaldo-Lima E, Dubé MA. Modeling of the Copolymerization Kinetics of n-Butyl Acrylate and d-Limonene Using PREDICI ®. Processes. 2016; 4(1):1. https://doi.org/10.3390/pr4010001
Chicago/Turabian StyleRen, Shanshan, Eduardo Vivaldo-Lima, and Marc A. Dubé. 2016. "Modeling of the Copolymerization Kinetics of n-Butyl Acrylate and d-Limonene Using PREDICI ®" Processes 4, no. 1: 1. https://doi.org/10.3390/pr4010001
APA StyleRen, S., Vivaldo-Lima, E., & Dubé, M. A. (2016). Modeling of the Copolymerization Kinetics of n-Butyl Acrylate and d-Limonene Using PREDICI ®. Processes, 4(1), 1. https://doi.org/10.3390/pr4010001