A Computational Study of the Effects of Syk Activity on B Cell Receptor Signaling Dynamics
Abstract
:1. Introduction
2. Model Development
2.1. Biological Background
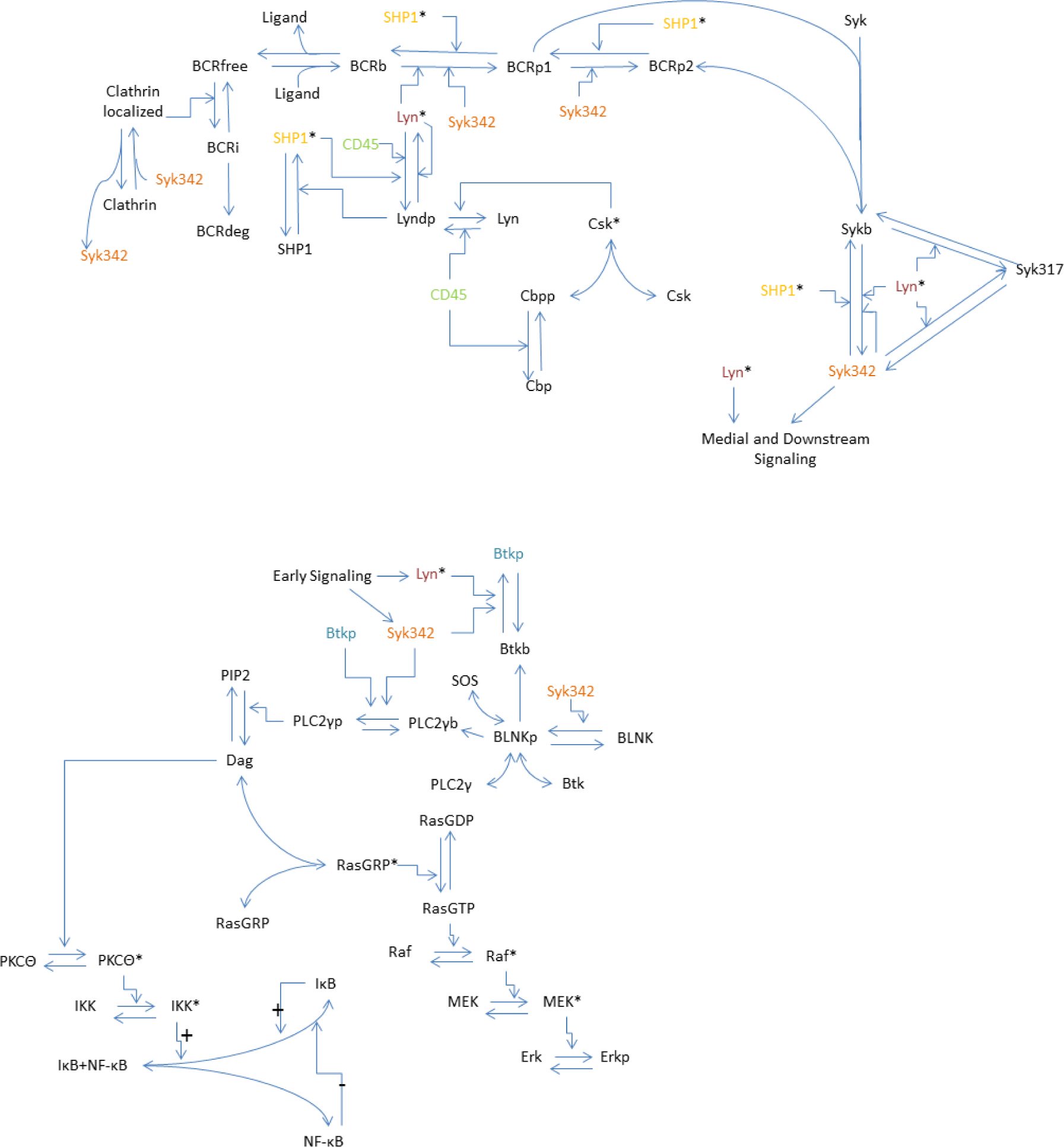
2.2. Model
2.3. Model Equations
3. Materials and Methods
3.1. Experimental Protocols
3.1.1. Cell Lines
3.1.2. Cellular Activation Assay
3.2. Sensitivity Analysis
3.3. Parameter Screening
3.4. Contour Analysis
4. Results
4.1. Sensitive Parameters
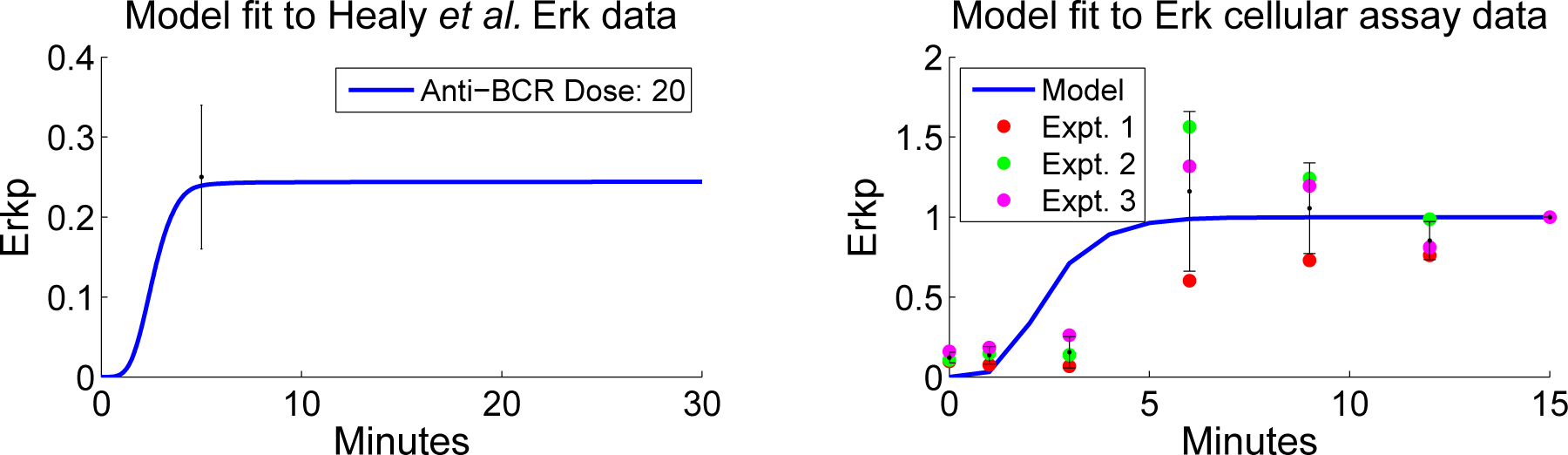
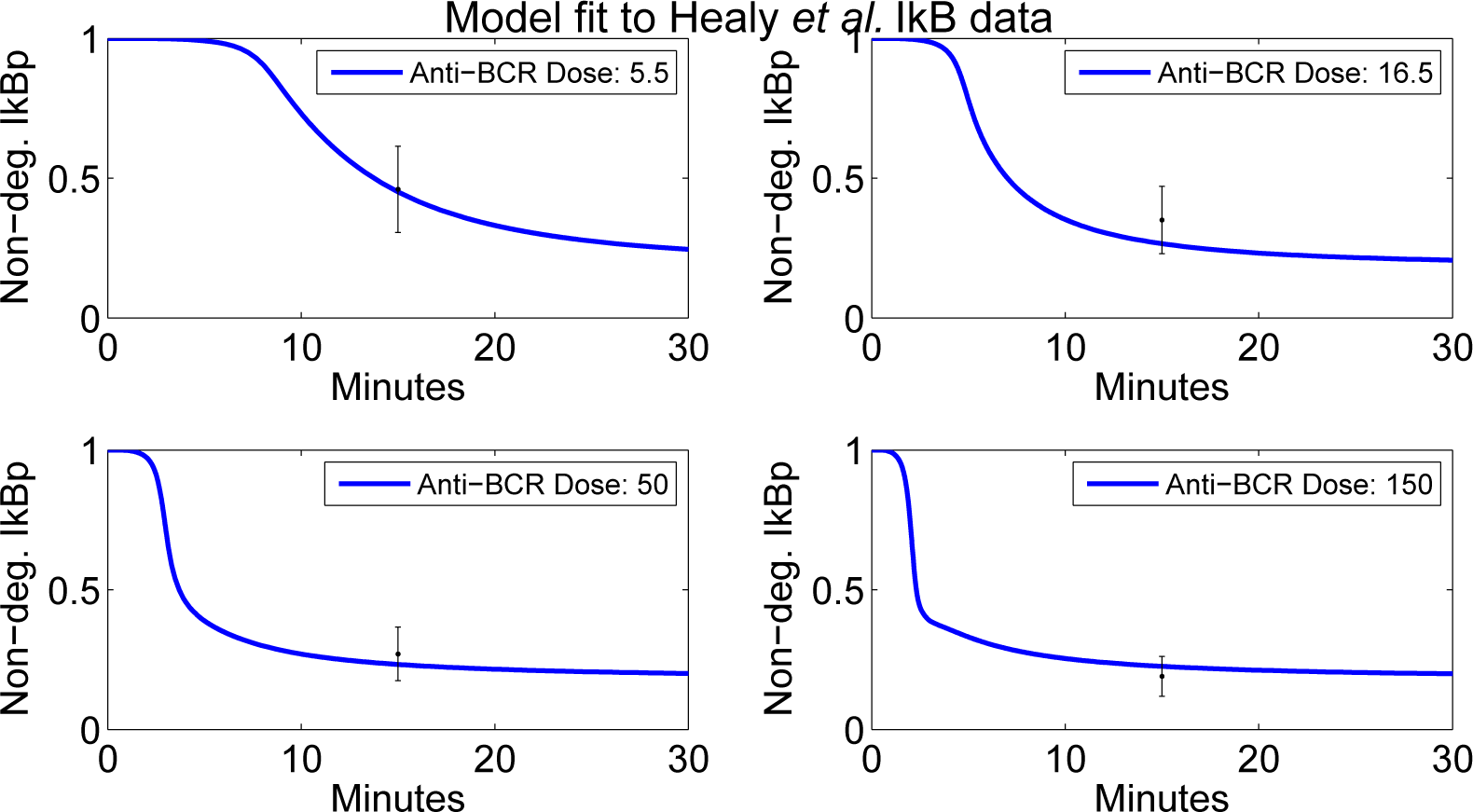
4.2. Parameter Screening and Fitting
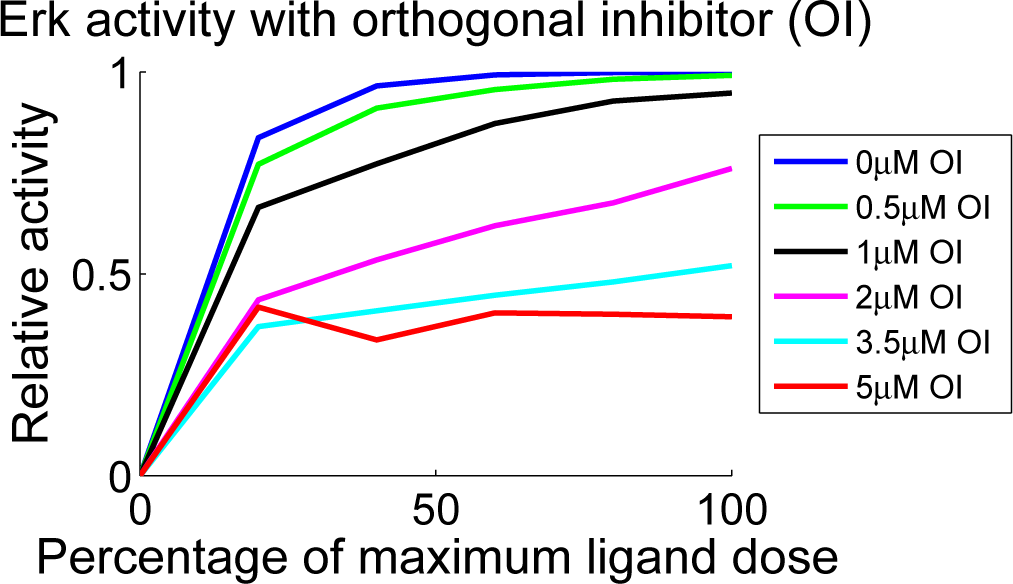
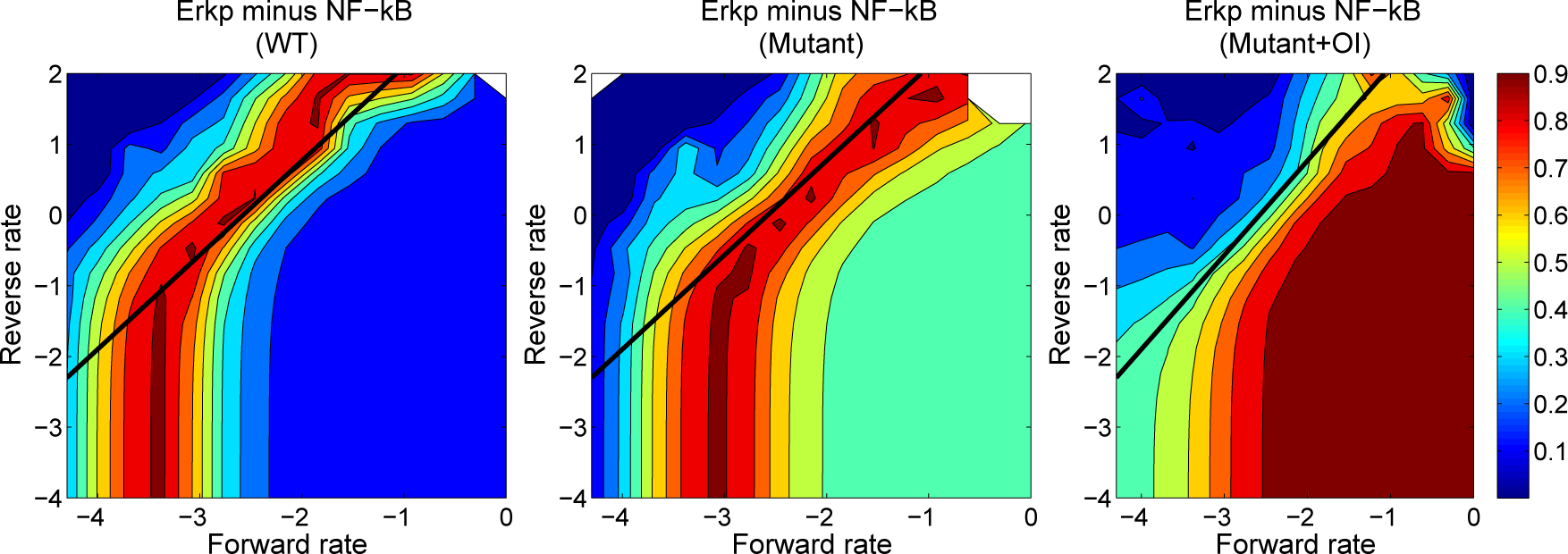
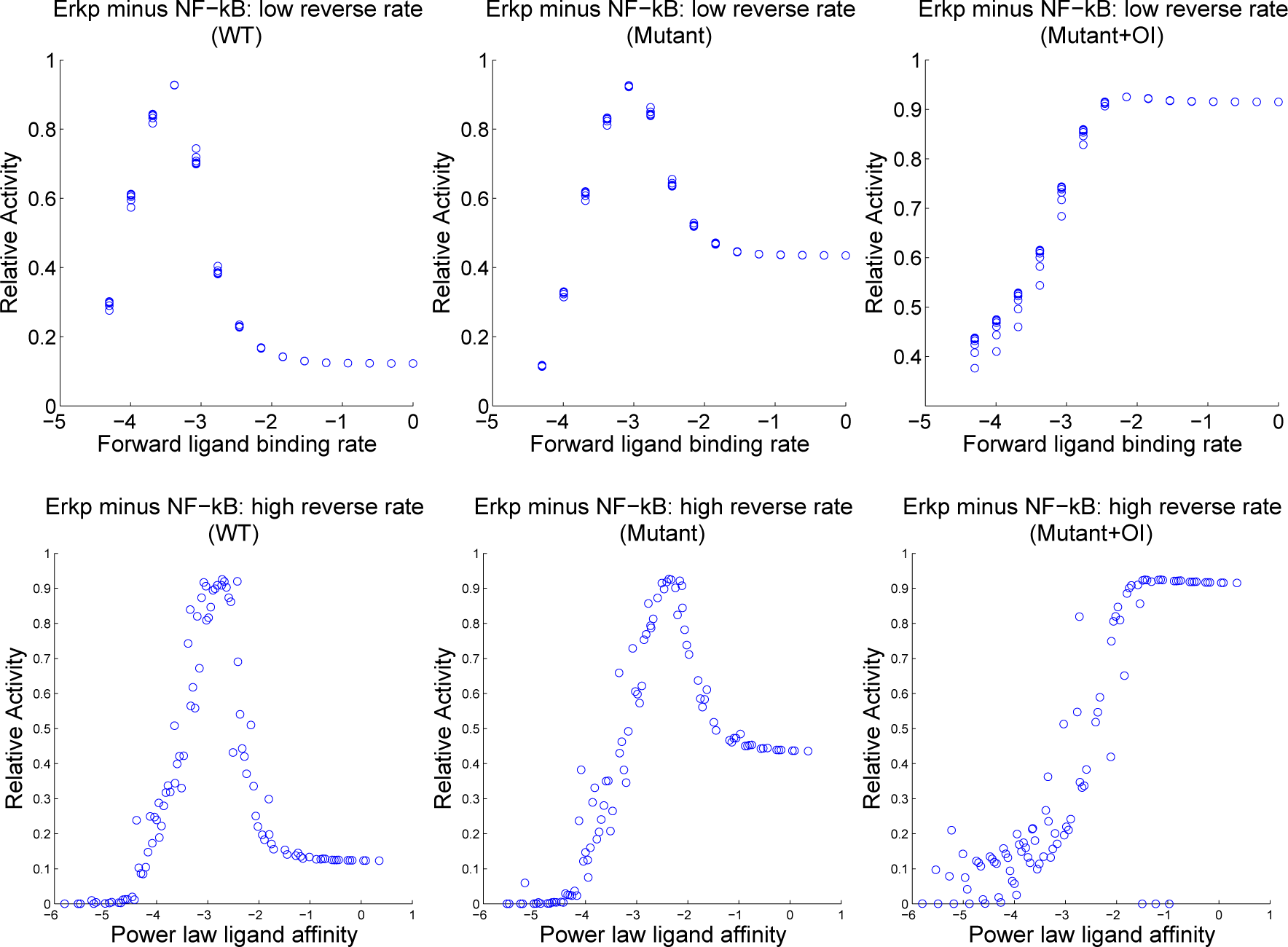
4.3. Contour Analysis
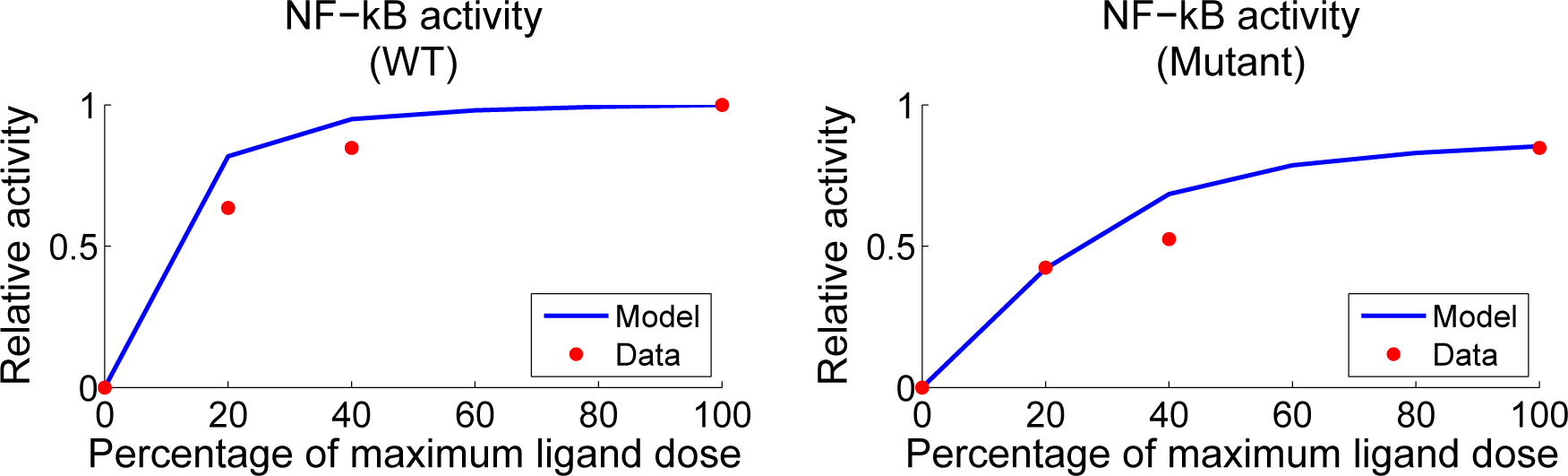
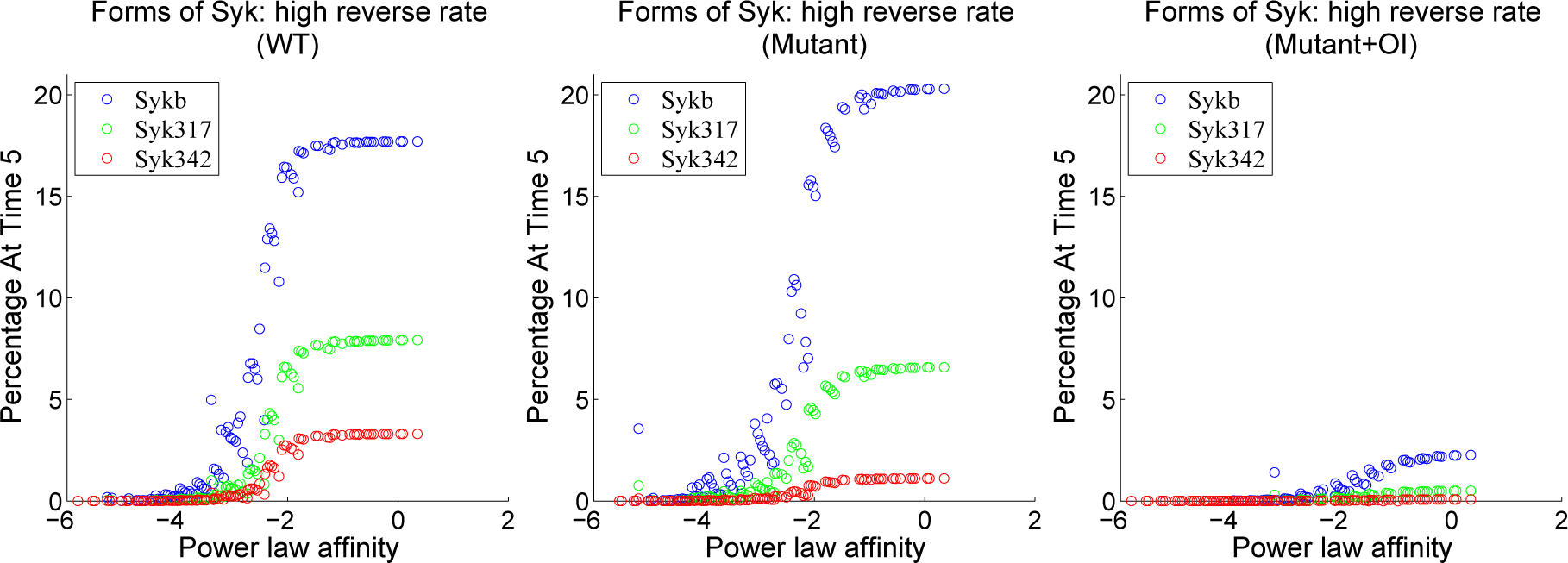
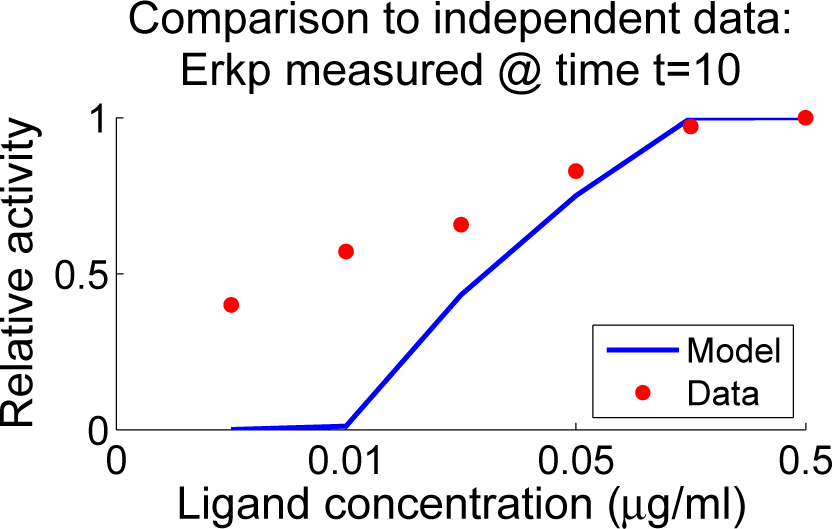
4.4. Independent Dataset Comparison
5. Conclusions and Future Directions
Supporting Information
processes-03-00075-s001.pdfAcknowledgments
Author Contributions
Conflicts of Interest
References
- Oh, H.; Ozkirimli, E.; Shah, K.; Harrison, M.L.; Geahlen, R.L. Generation of an Analog-sensitive Syk Tyrosine Kinase for the Study of Signaling Dynamics from the B Cell Antigen Receptor. J. Biol. Chem. 2007, 282, 33760–33768. [Google Scholar]
- Zheng, Y.; Rundell, A. Comparative study of parameter sensitivity analyses of the TCR-activated Erk-MAPK signalling pathway. IEE Proc. Syst. Biol. 2006, 153, 201–211. [Google Scholar]
- Perley, J.P.; Mikolajczak, J.; Harrison, M.L.; Buzzard, G.T.; Rundell, A.E. Multiple Model-Informed Open-Loop Control of Uncertain Intracellular Signaling Dynamics. PLoS Comput. Biol. 2014, 10, 1296–1310. [Google Scholar]
- Tsourkas, P.K.; Somkanya, C.D.; Yu-Yang, P.; Liu, W.; Pierce, S.K.; Raychaudhuri, S. Formation of BCR oligomers provides a mechanism for B cell affinity discrimination. J. Theor. Biol. 2012, 307, 174–182. [Google Scholar]
- Mukherjee, S.; Zhu, J.; Zikherman, J.; Parameswaran, R.; Kadlecek, T.A.; Wang, Q.; Au-Yeung, B.; Ploegh, H.; Kuriyan, J.; Das, J.; et al. Monovalent and Multivalent Ligation of the B Cell Receptor Exhibit Differential Dependence upon Syk and Src Family Kinases. Sci. Signal. 2013, 6, ra1. [Google Scholar]
- Chaudhri, V.K.; Kumar, D.; Misra, M.; Dua, R.; Rao, K.V.S. Integration of a Phosphatase Cascade with the Mitogen-activated Protein Kinase Pathway Provides for a Novel Signal Processing Function. J. Biol. Chem. 2010, 285, 1296–1310. [Google Scholar]
- Barua, D.; Hlavacek, W.S.; Lipniacki, T. A. Computational Model for Early Events in B Cell Antigen Receptor Signaling: Analysis of the Roles of Lyn and Fyn. J. Immunol. 2012, 189, 646–658. [Google Scholar]
- Healy, J.I.; Dolmetsch, R.E.; Timmerman, L.A.; Cyster, J.G.; Thomas, M.L.; Crabtree, G.R.; Lewis, R.S.; Goodnow, C.C. Different Nuclear Signals Are Activated by the B Cell Receptor during Positive Versus Negative Signaling. Immunity 1997, 6, 419–428. [Google Scholar]
- Skaggs, B.J.; Clark, M.R. Proximal B cell receptor signaling pathways. Signal Transduct. 2004, 4, 173–194. [Google Scholar]
- Kurosaki, T.; Hikida, M. Tyrosine kinases and their substrates in B lymphocytes. Immunol. Rev. 2009, 228, 132–148. [Google Scholar]
- Geahlen, R.L. Syk and pTyr’d: Signaling through the B cell antigen receptor. Biochim. Biophys. Acta 2009, 1793, 1115–1127. [Google Scholar]
- Ma, H.; Yankee, T.M.; Hu, J.; Asai, D.J.; Harrison, M.L.; Geahlen, R.L. Visualization of Syk-antigen receptor interactions using green fluorescent protein: Differential roles for Syk and Lyn in the regulation of receptor capping and internalization. J. Immunol. 2001, 166, 1507–1516. [Google Scholar]
- Veillette, A.; Latour, S.; Davidson, D. Negative regulation of immunoreceptor signaling. Ann. Rev. Immunol. 2002, 20, 669–707. [Google Scholar]
- Reth, M.; Brummer, T. Feedback regulation of lymphocyte signalling. Nat. Rev. Immunol. 2004, 4, 269–278. [Google Scholar]
- Andrews, S.F.; Wilson, P.C. The anergic B cell. Blood 2010, 115, 4976–4978. [Google Scholar]
- Perley, J.P.; Mikolajczak, J.; Buzzard, G.T.; Harrison, M.L.; Rundell, A.E. Resolving Early Signaling Events in T-Cell Activation Leading to IL-2 and FOXP3 Transcription. Processes 2014, 2, 867–900. [Google Scholar]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis. WileySeries in Probability and Statistics; Wiley: Chichester, UK, 2000. [Google Scholar]
- Buzzard, G. Global sensitivity analysis using sparse grid interpolation and polynomial chaos. Reliab. Eng. Syst. Saf. 2012, 107, 82–89. [Google Scholar]

| Reactions | Parameters | |
|---|---|---|
| Group 1 | BCR dynamics | rw0kf |
| Group 2 | Syk activation | rw7kr, rw9kf |
| Group 3 | Regulatory enzyme dynamics | N/A |
| Group 4 | Medial signaling | rw15kf, rw16kf, rw16kr |
| Group 5 | Medial signaling | r12skf, r13kf, r13kr |
| Group 6 | Erk pathway dynamics | r18kf, r19kf |
| Group 7 | NF-κB pathway dynamics | r38kf |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McGee, R.L.; Krisenko, M.O.; Geahlen, R.L.; Rundell, A.E.; Buzzard, G.T. A Computational Study of the Effects of Syk Activity on B Cell Receptor Signaling Dynamics. Processes 2015, 3, 75-97. https://doi.org/10.3390/pr3010075
McGee RL, Krisenko MO, Geahlen RL, Rundell AE, Buzzard GT. A Computational Study of the Effects of Syk Activity on B Cell Receptor Signaling Dynamics. Processes. 2015; 3(1):75-97. https://doi.org/10.3390/pr3010075
Chicago/Turabian StyleMcGee, Reginald L., Mariya O. Krisenko, Robert L. Geahlen, Ann E. Rundell, and Gregery T. Buzzard. 2015. "A Computational Study of the Effects of Syk Activity on B Cell Receptor Signaling Dynamics" Processes 3, no. 1: 75-97. https://doi.org/10.3390/pr3010075
APA StyleMcGee, R. L., Krisenko, M. O., Geahlen, R. L., Rundell, A. E., & Buzzard, G. T. (2015). A Computational Study of the Effects of Syk Activity on B Cell Receptor Signaling Dynamics. Processes, 3(1), 75-97. https://doi.org/10.3390/pr3010075





