Modeling the Dynamics of Acute Phase Protein Expression in Human Hepatoma Cells Stimulated by IL-6
Abstract
:1. Introduction
2. Model Development for the Kinetics of Acute Phase Proteins in IL-6 Stimulated Hepatocytes
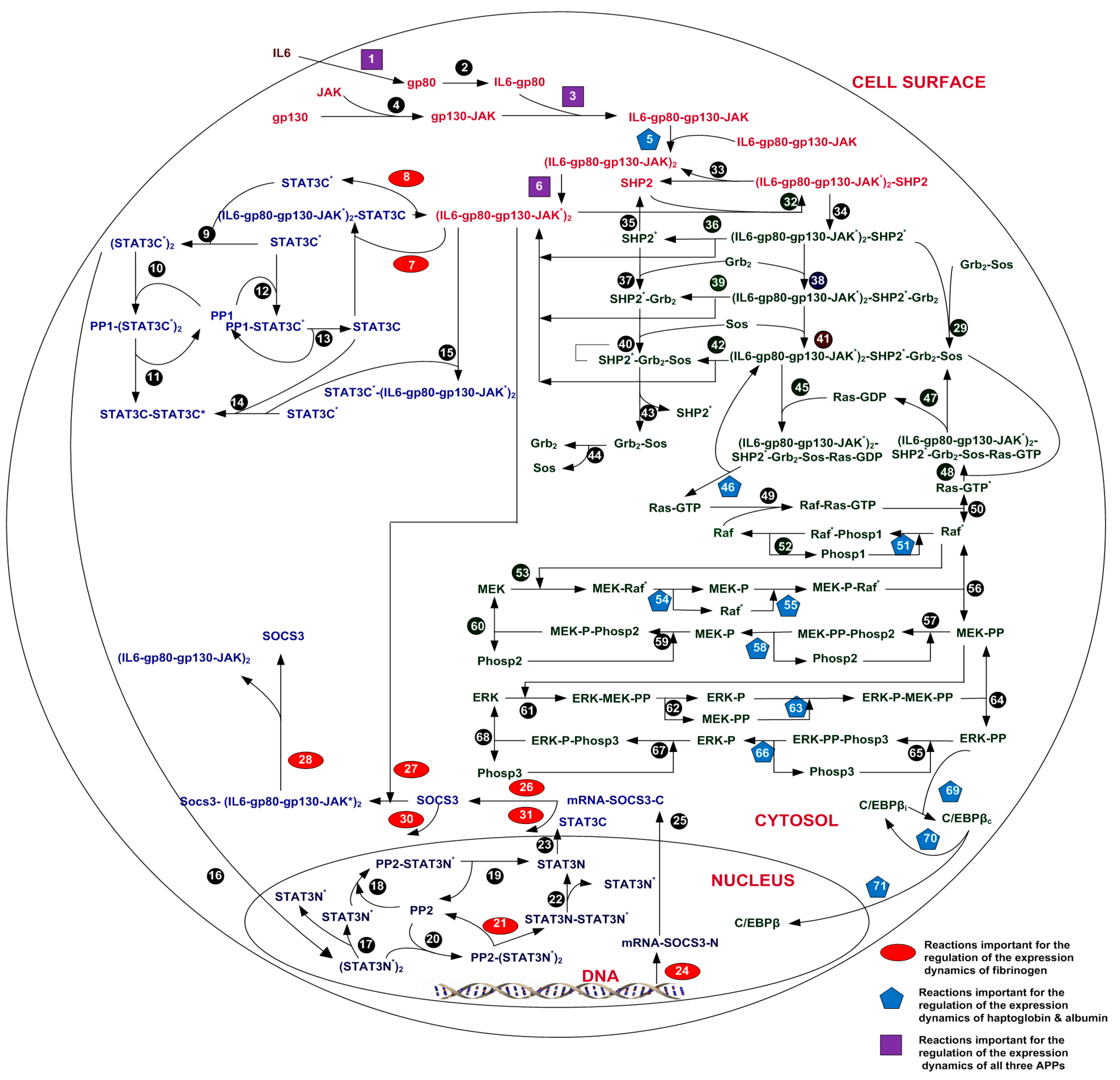
2.1. IL-6 Signal Transduction Model
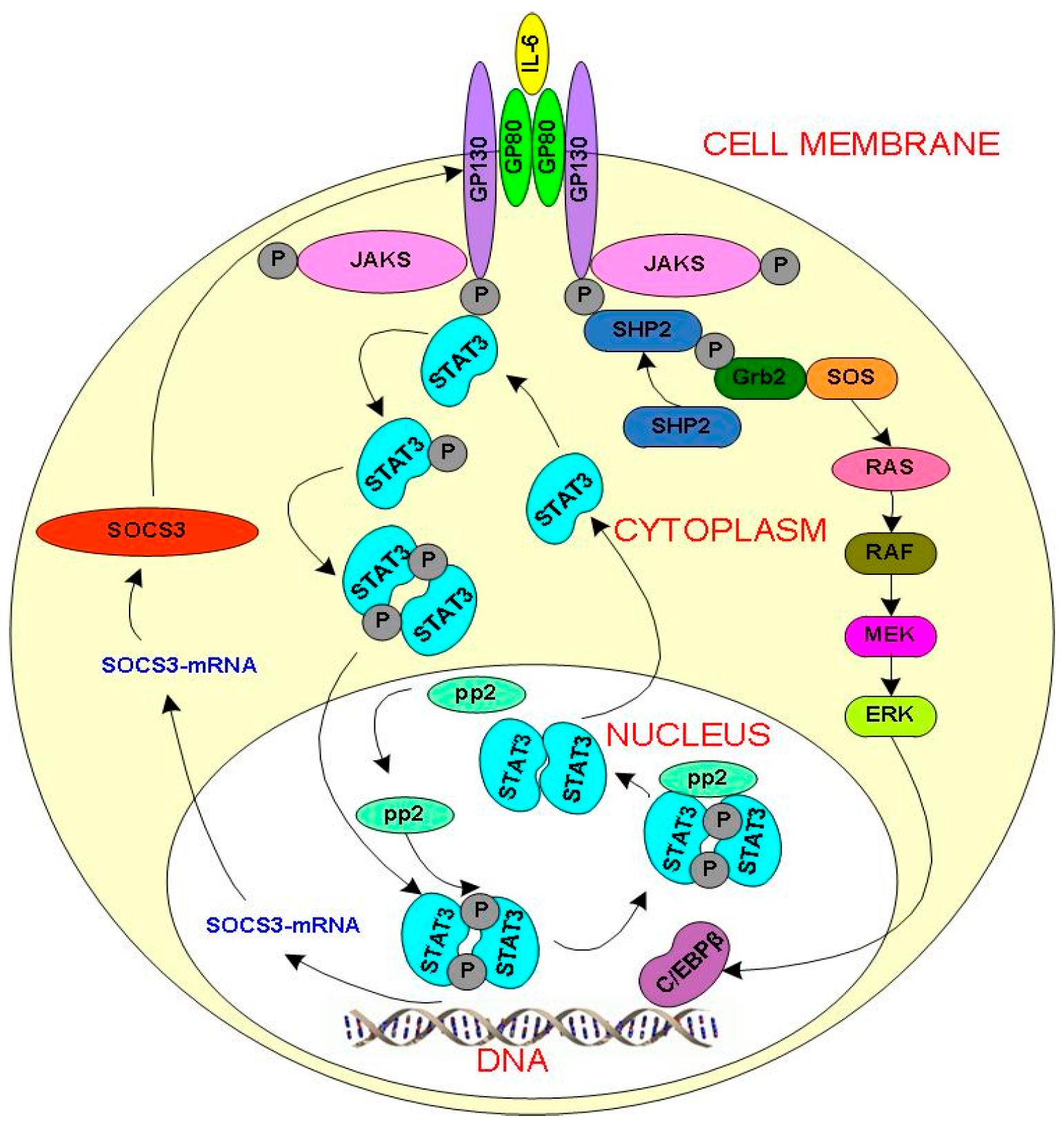
2.2. Extended Model of Acute Phase Protein Expression Dynamics
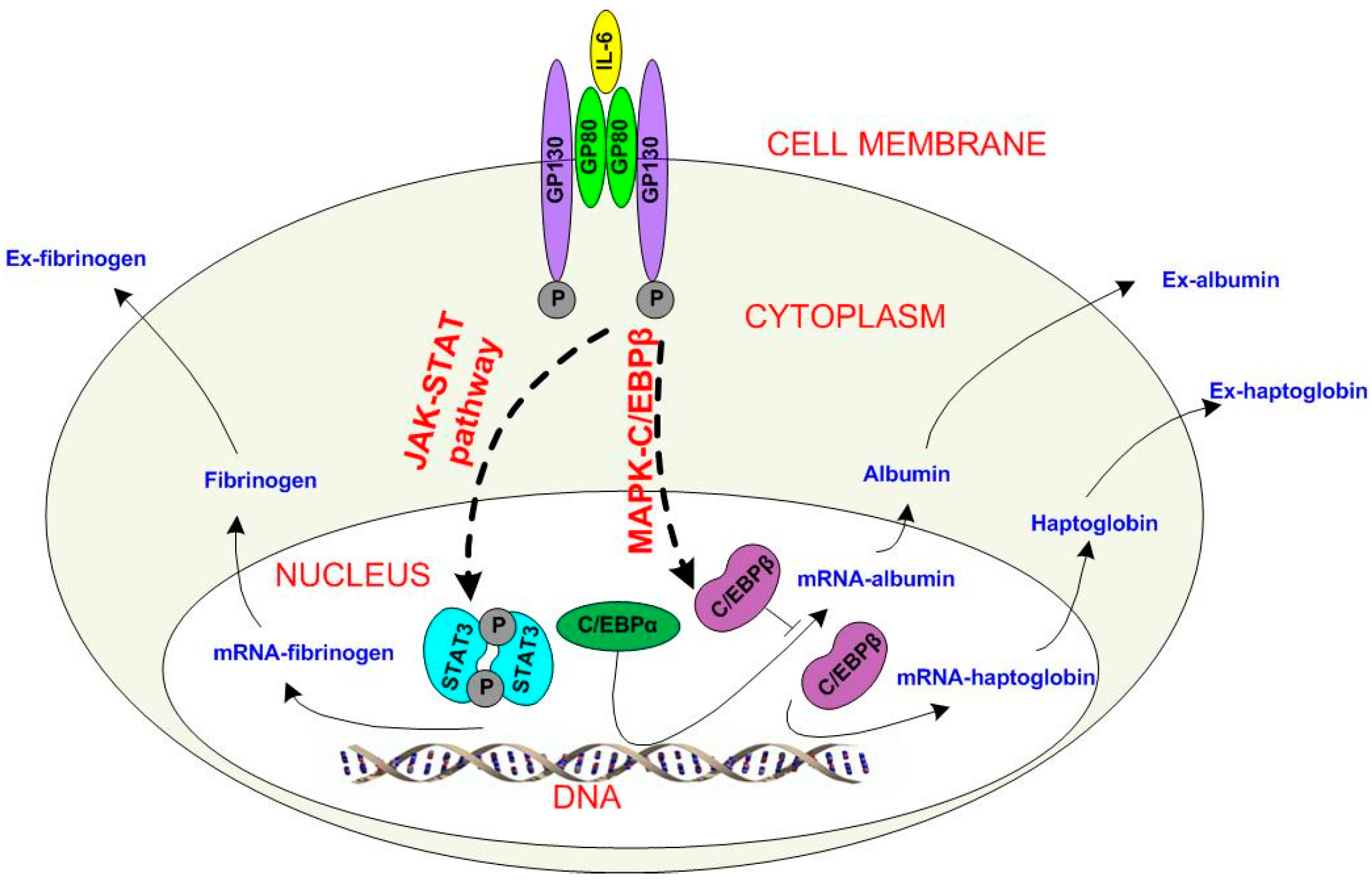
2.3. Estimation of Unknown Parameters in the Extended Model
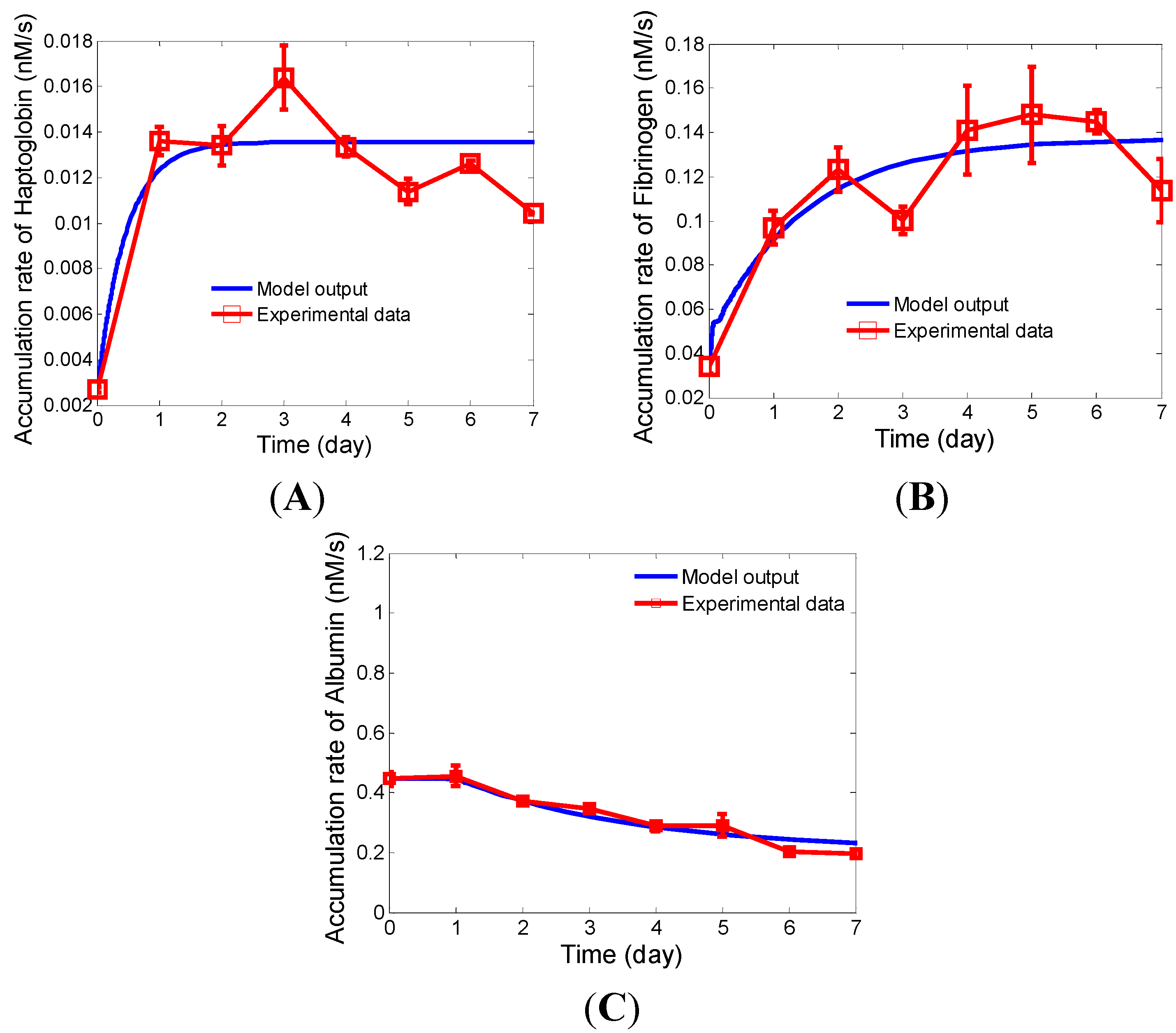
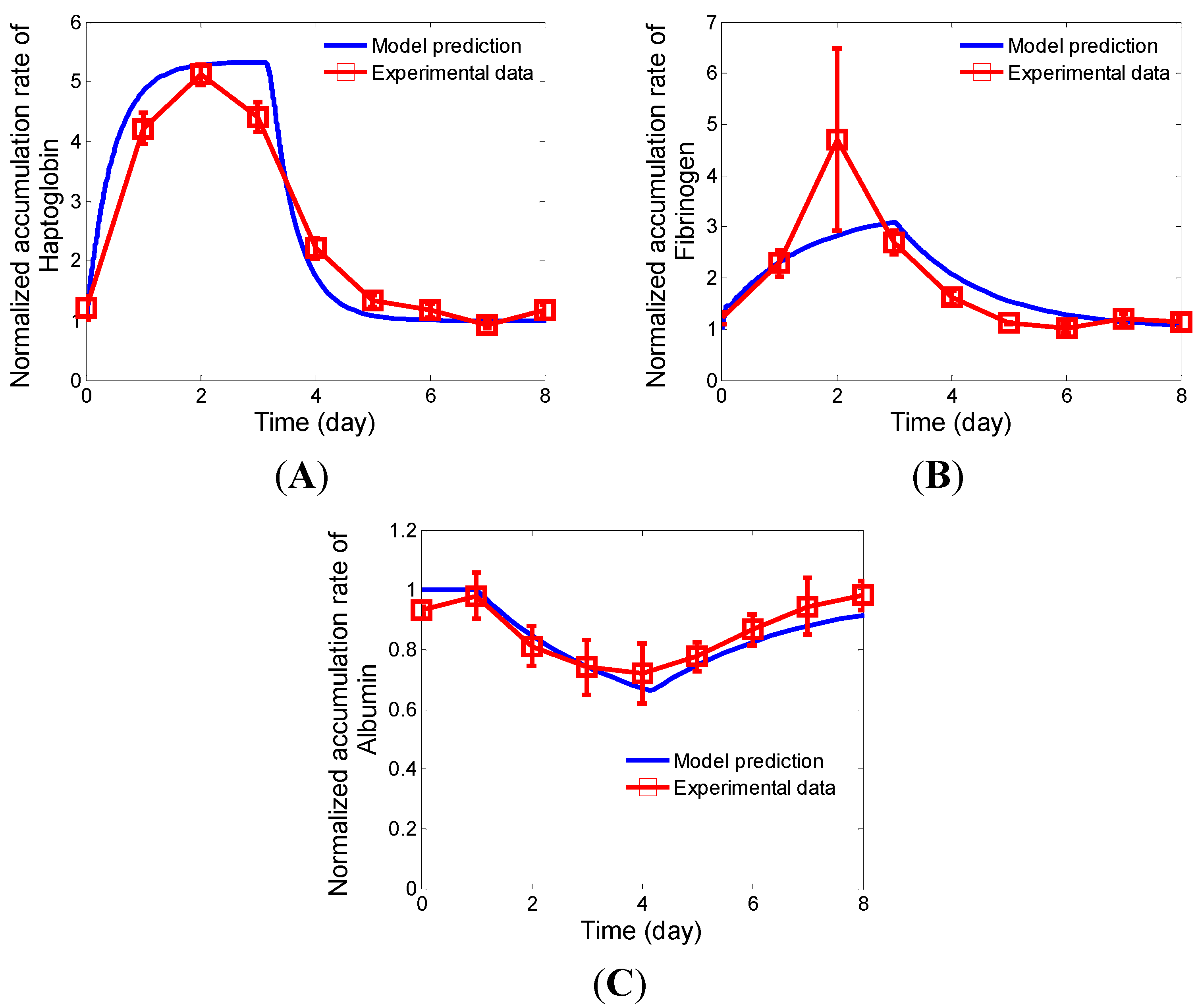
2.4. Validation of the Developed Model
2.4.1. Relaxation Kinetics of Albumin, Fibrinogen, and Haptoglobin in HepG2 Cultures under a Pulse-Chase Stimulation of IL-6
2.4.2. Steady State Values of Dose-Dependent Secretion Rates of Fibrinogen and Albumin in IL-6 Stimulated HepG2 Cultures
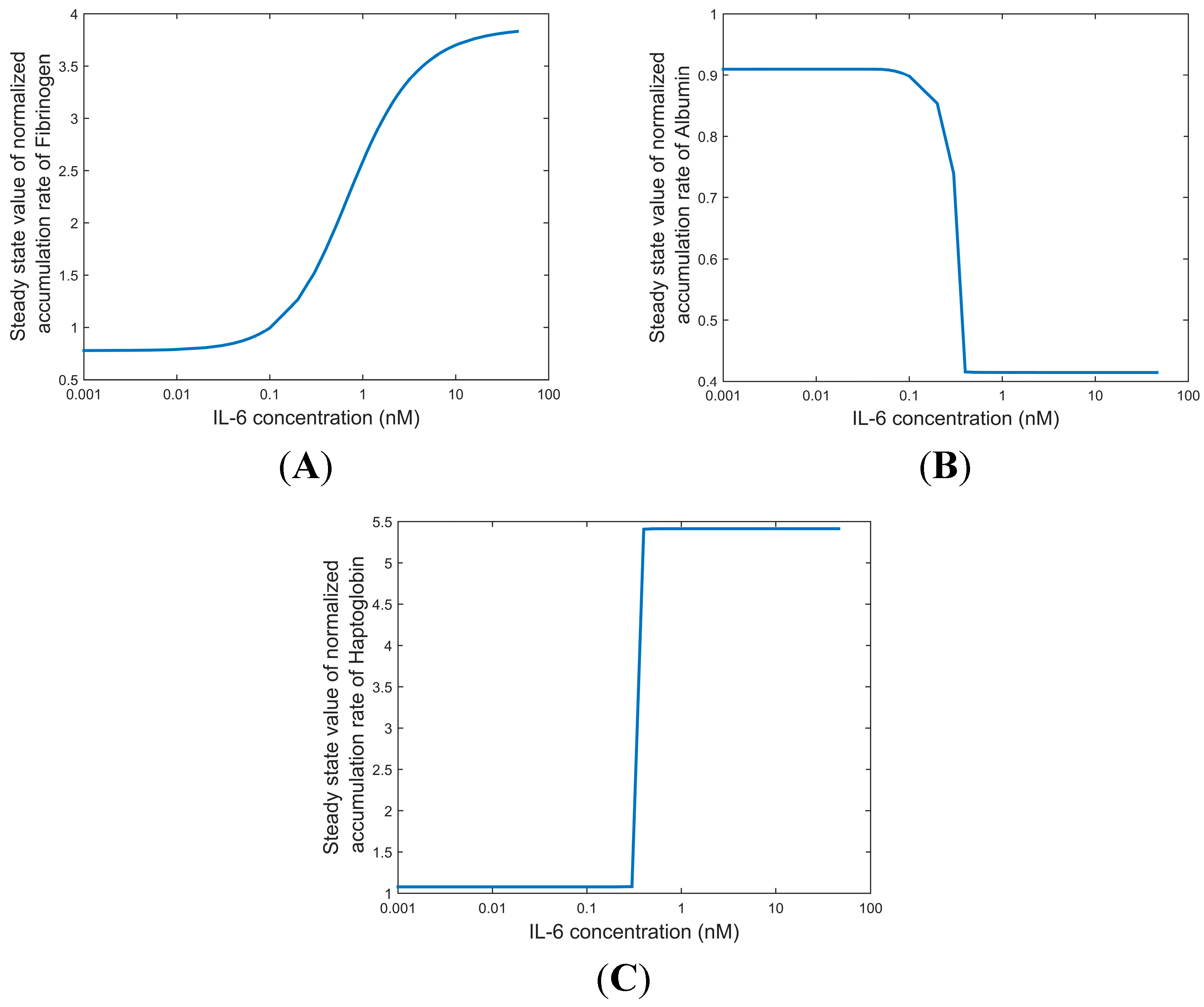
3. Investigation of Influence from the Reactions in IL-6 Signaling on the Expression Dynamics of Haptoglobin, Fibrinogen, and Albumin
| Rank, i | Impact on the Secretion Rate of Haptoglobin (j = 1) | Impact on the Secretion Rate of Fibrinogen (j = 2) | Impact on the Secretion Rate of Albumin (j = 3) | |||
|---|---|---|---|---|---|---|
| Parameter, pi | Sensitivity, |si,j| | Parameter, pi | Sensitivity, |si,j| | Parameter, pi | Sensitivity, |si,j| | |
| 1 | Vm_h | 7.8168 | Vm_f | 7.0475 | Vm_a | 3.7746 |
| 2 | kt-h | 4.0417 | Km-f | 3.7901 | ki_a | 1.0222 |
| 3 | Km_h | 3.0482 | kf7 | 2.0167 | Km_a | 1.0222 |
| 4 | kf51 | 0.5061 | Vm_24 | 1.8237 | kd_a | 1.0221 |
| 5 | kf55 | 0.3774 | k26 | 1.8237 | kt_a | 0.5915 |
| 6 | k58 | 0.3091 | kd31 | 1.8100 | kf51 | 0.1788 |
| 7 | kf71 | 0.0075 | kf27 | 1.8055 | kf55 | 0.1070 |
| 8 | kr71 | 0.0075 | kd30 | 1.8046 | k58 | 0.0764 |
| 9 | Km69 | 0.0045 | Km_24 | 1.7836 | kr71 | 0.0114 |
| 10 | Vm69 | 0.0044 | kt-f | 1.7688 | kf71 | 0.0114 |
| 11 | k70 | 0.0043 | kr27 | 1.7573 | Km69 | 0.0068 |
| 12 | kf1 | 0.0019 | k8 | 0.9580 | Vm69 | 0.0068 |
| 13 | k54 | 0.0011 | kr7 | 0.9403 | k70 | 0.0066 |
| 14 | kf46 | 0.0011 | k6 | 0.8621 | kf1 | 0.0015 |
| 15 | k6 | 0.0010 | kf28 | 0.7990 | k54 | 0.0011 |
| 16 | kf3 | 0.0008 | kf1 | 0.7675 | kf66 | 0.0010 |
| 17 | kr1 | 0.0008 | kf3 | 0.7628 | kf46 | 0.0009 |
| 18 | kr3 | 0.0007 | kr1 | 0.7621 | kr1 | 0.0009 |
| 19 | kr5 | 0.0006 | kr3 | 0.7619 | kr3 | 0.0009 |
| 20 | kf5 | 0.0006 | k21 | 0.7480 | kf63 | 0.0008 |
4. Virtual Screening of Drug Targets and Drugs for Acute Phase Response
4.1. A Model-Based Platform to Study the Influence from the Drug (Imidazo-Pyrrolopyridine) on Acute Phase Protein Secretion
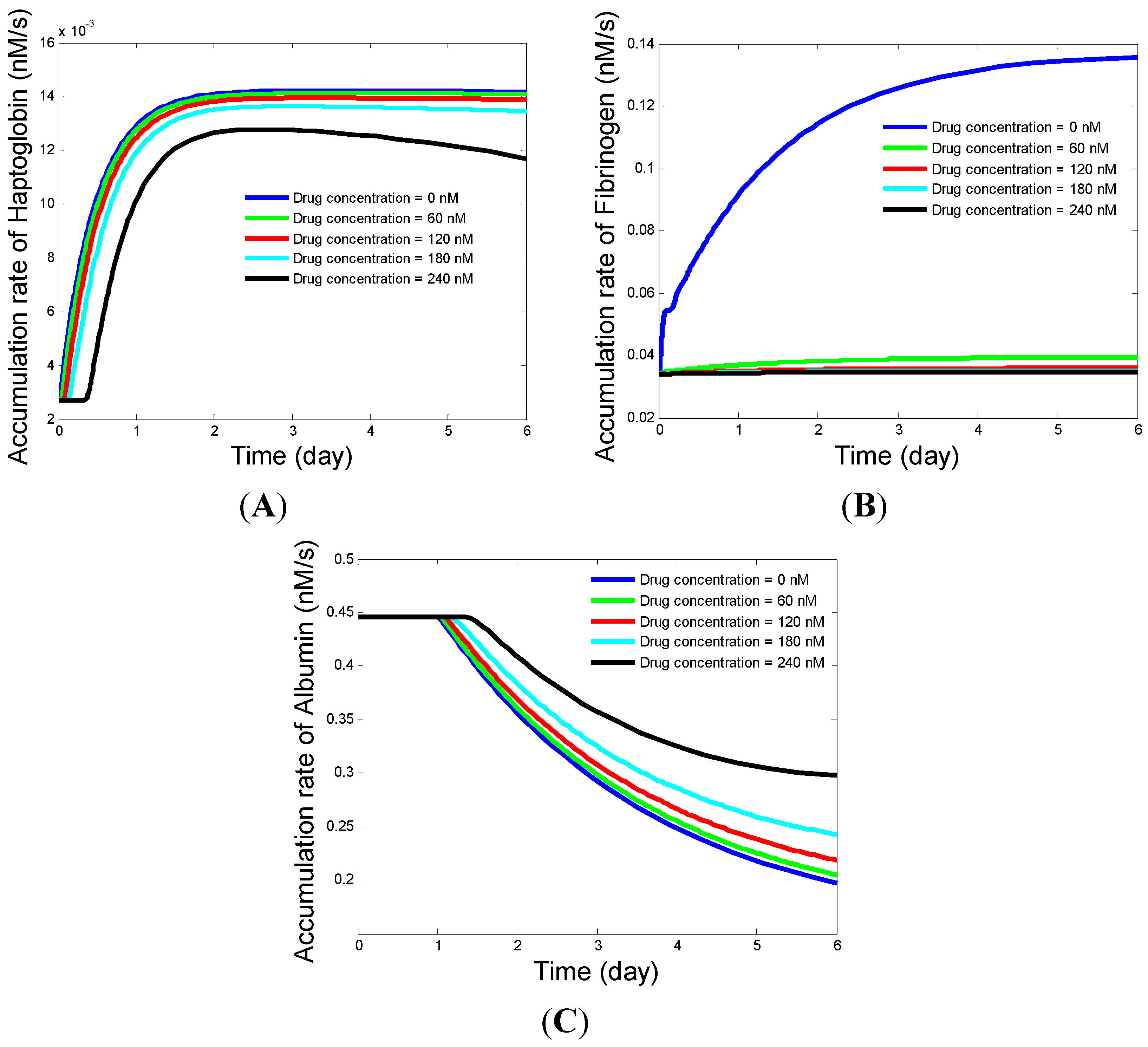
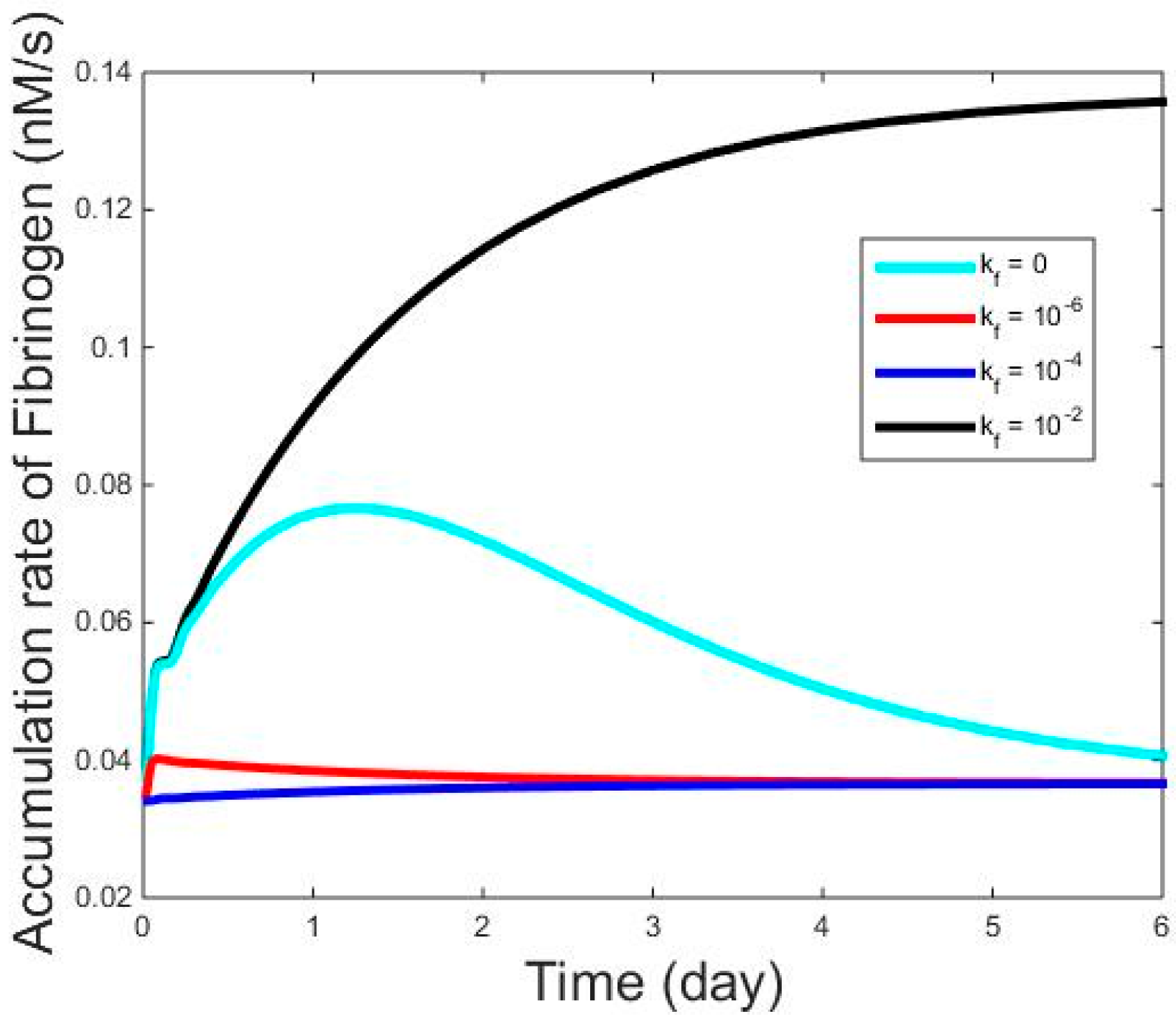
4.2. Ranking Drug Targets Based upon the Influence from Their Interaction with the Drug on the Dynamics of Acute Phase Proteins
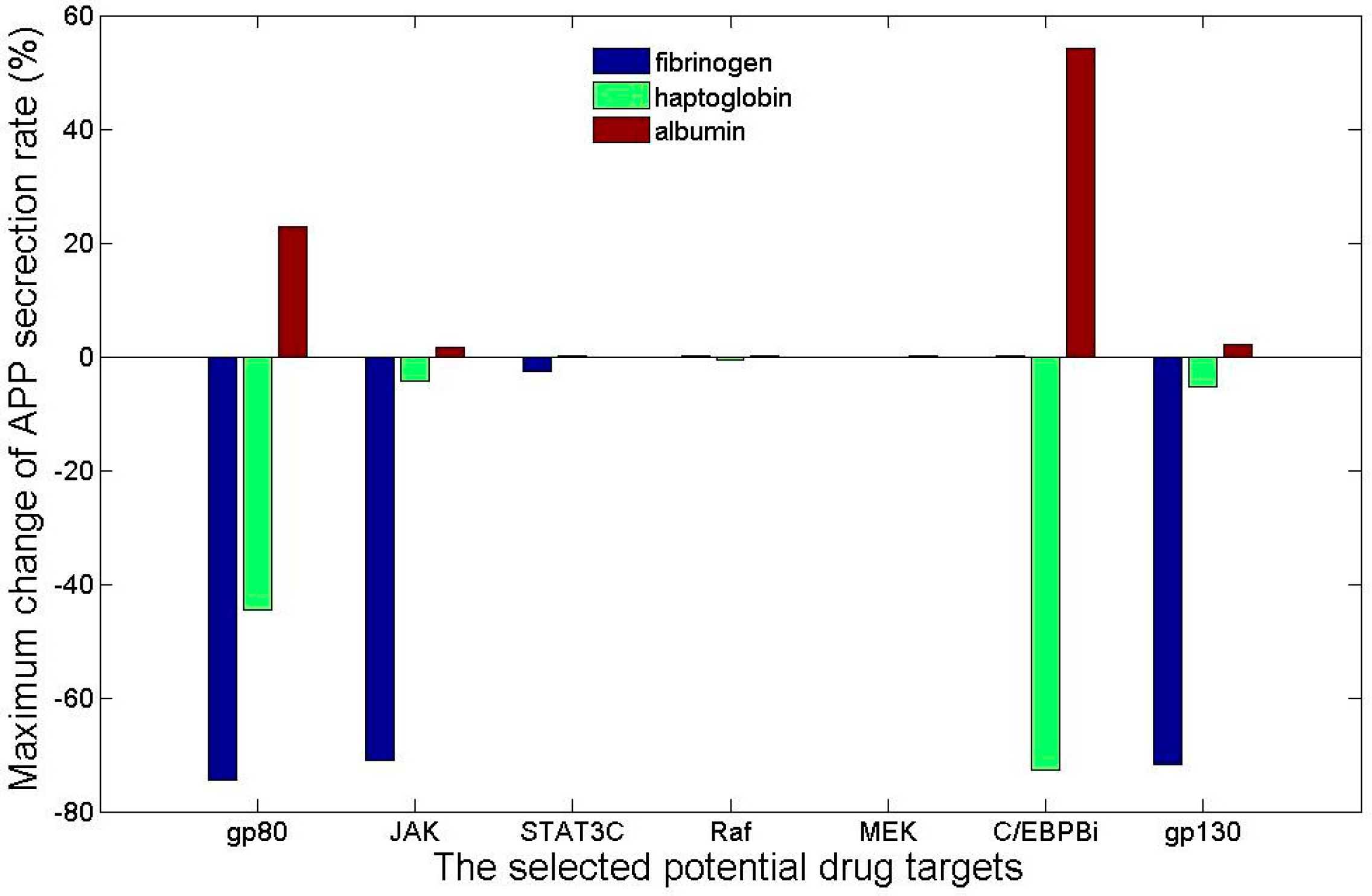
4.3. Influence of Multiple Drug Treatment on Acute Phase Protein Secretion
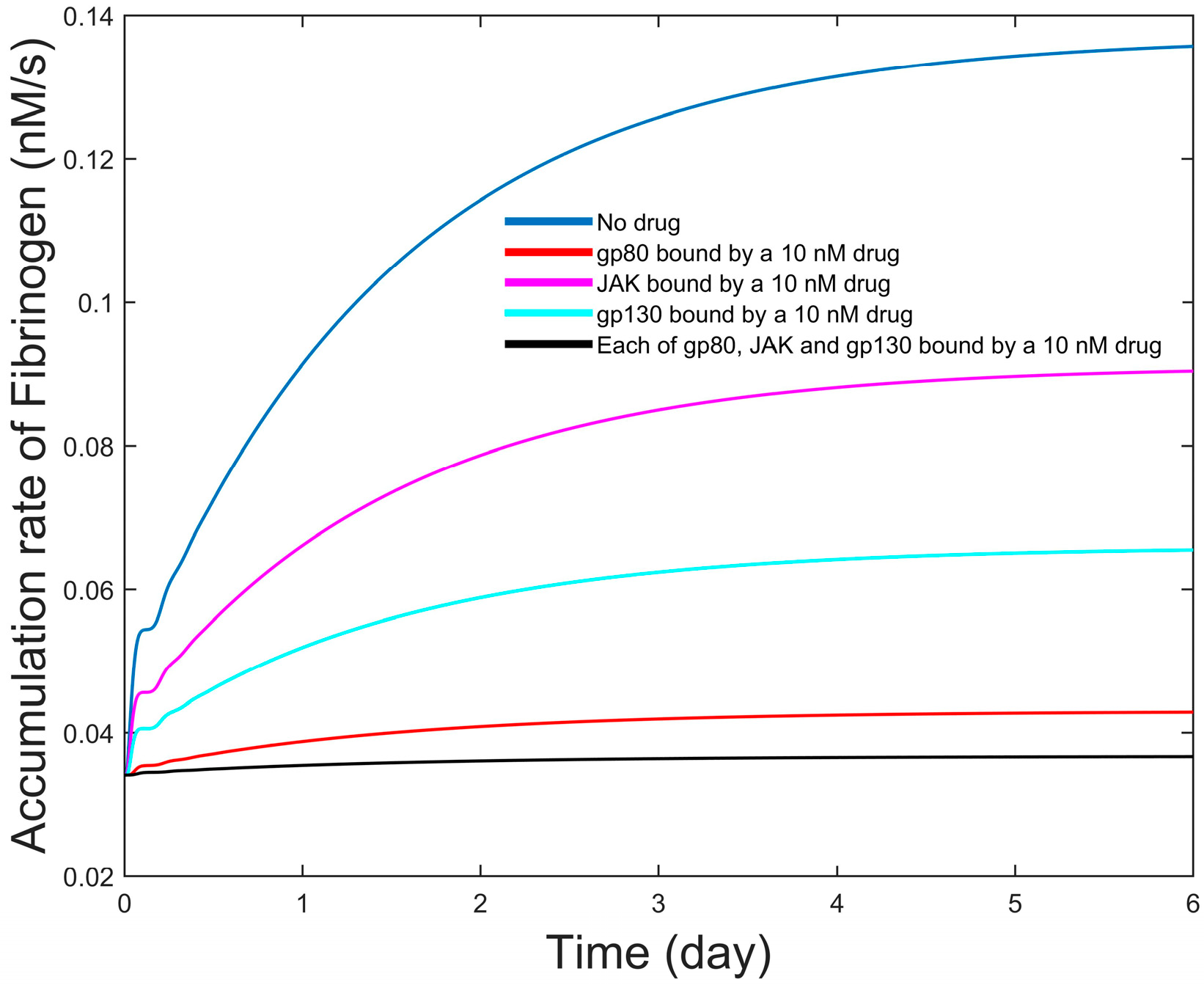
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Appendix
| Name | Value | Unit |
|---|---|---|
| Vm_h | 0.06457 | nM/s |
| Km_h | 99.7421 | nM |
| kt_h | 2.5389 × 10−5 | 1/s |
| Vm_f | 1.1841 | nM/s |
| Km_f | 58.1310 | nM |
| kt_f | 7.8158 × 10−6 | 1/s |
| ki_a | 1.0861 × 10−3 | 1/s |
| kd_a | 0.06866 | 1/s |
| Vm_a | 0.1470 | nM/s |
| Km_a | 0.5118 | nM |
| kt_a | 4.2195 × 10−6 | 1/s |
Conflicts of Interest
References
- Heinrich, P.C.; Castell, J.V.; Andus, T. Interleukin-6 and the acute phase response. Biochem. J. 1990, 2653, 621–636. [Google Scholar]
- Heinrich, P.C.; Behrmann, I.; Haan, S.; Hermanns, H.M.; Müller-Newen, G.; Schaper, F. Principles of interleukin (IL)-6-type cytokine signalling and its regulation. Biochem. J. 2003, 374, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Akira, S. IL-6-regulated transcription factors. Int. J. Biochem. Cell Biol. 1997, 29, 1401–1418. [Google Scholar] [CrossRef] [PubMed]
- Schindler, C.; Darnell, J.E., Jr. Transcriptional responses to polypeptide ligands: The JAK-STAT pathway. Annu. Rev. Biochem. 1995, 64, 621–651. [Google Scholar] [CrossRef] [PubMed]
- Yamada, S.; Shiono, S.; Joo, A.; Yoshimura, A. Control mechanism of JAK/STAT signal transduction pathway. FEBS Lett. 2003, 534, 190–196. [Google Scholar] [CrossRef] [PubMed]
- Kholodenko, B.N.; Demin, O.V.; Moehren, G.; Hoek, J.B. Quantification of short term signaling by the epidermal growth factor receptor. J. Biol. Chem. 1999, 274, 30169–30181. [Google Scholar] [CrossRef] [PubMed]
- Brightman, F.A.; Fell, D.A. Differential feedback regulation of the MAPK cascade underlies the quantitative differences in EGF and NGF signalling in PC12 cells. FEBS Lett. 2000, 482, 169–174. [Google Scholar] [CrossRef] [PubMed]
- Schoeberl, B.; Eichler-Jonsson, C.; Gilles, E.D.; Müller, G. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat. Biotechnol. 2002, 20, 370–375. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Jayaraman, A.; Hahn, J. Modeling regulatory mechanisms in IL-6 signal transduction in hepatocytes. Biotechnol. Bioeng. 2006, 95, 850–862. [Google Scholar] [CrossRef] [PubMed]
- Moya, C.; Huang, Z.; Cheng, P.; Jayaraman, A.; Hahn, J. Investigation of IL-6 and IL-10 signalling via mathematical modelling. IET Syst. Biol. 2011, 5, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Ryll, A.; Samaga, R.; Schaper, F.; Alexopoulos, L.G.; Klamt, S. Large-scale network models of IL-1 and IL-6 signalling and their hepatocellular specification. Mol. Biosyst. 2011, 7, 3253–3270. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, J.O.M.; Yarmush, M.L.; Toner, M. Interaction between heat shock and interleukin 6 stimulation in the acute-phase response of human hepatoma (HepG2) cells. Hepatology 1998, 28, 994–1004. [Google Scholar] [CrossRef] [PubMed]
- Araujo, R.P.; Petricoin, E.F.; Liotta, L.A. A mathematical model of combination therapy using the EGFR signaling network. Biosystems 2005, 80, 57–69. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Bai, H.; Ouyang, Q.; Lai, L.; Tang, C. Finding multiple target optimal intervention in disease-related molecular network. Mol. Syst. Biol. 2008, 4, 228. [Google Scholar] [CrossRef] [PubMed]
- Stump, K.L.; Lu, L.D.; Dobrzanski, P.; Serdikoff, C.; Gingrich, D.E.; Dugan, B.J.; Angeles, T.S.; Albom, M.S.; Ator, M.A.; Dorsey, B.D.; et al. A highly selective, orally active inhibitor of Janus kinase 2, CEP-33779, ablates disease in two mouse models of rheumatoid arthritis. Arthritis Res. Ther. 2011, 13, R68. [Google Scholar] [CrossRef] [PubMed]
- Quintás-Cardama, A.; Kantarjian, H.; Cortes, J.; Verstovsek, S. Janus kinase inhibitors for the treatment of myeloproliferative neoplasias and beyond. Nat. Rev. Drug Discov. 2011, 10, 318. [Google Scholar] [CrossRef]
- Kremer, J.M.; Bloom, B.J.; Breedveld, F.C.; Coombs, J.H.; Fletcher, M.P.; Gruben, D.; Krishnaswami, S.; Burgos-Vargas, R.; Wilkinson, B.; Zerbini, C.A.; et al. The Safety and Efficacy of a JAK Inhibitor in Patients With Active Rheumatoid Arthritis Results of a Double-Blind, Placebo-Controlled Phase IIa Trial of Three Dosage Levels of CP-690,550 Versus Placebo. Arthritis Rheum. 2009, 60, 1895–1905. [Google Scholar] [CrossRef] [PubMed]
- Hurley, C.A.; Blair, W.S.; Bull, R.J.; Chang, C.; Crackett, P.H.; Deshmukh, G.; Dyke, H.J.; Fong, R.; Ghilardi, N.; Gibbons, P.; et al. Novel triazolo-pyrrolopyridines as inhibitors of Janus kinase 1. Bioorg. Med. Chem. Lett. 2013, 23, 3592–3598. [Google Scholar] [CrossRef] [PubMed]
- Alam, T.; An, M.R.; Papaconstantinou, J. Differential expression of three C/EBP isoforms in multiple tissues during the acute phase response. J. Biol. Chem. 1992, 267, 5021–5024. [Google Scholar] [PubMed]
- Zhang, Z.; Fuller, G.M. Interleukin 1beta inhibits interleukin 6-mediated rat gamma fibrinogen gene expression. Blood 2000, 96, 3466–3472. [Google Scholar] [PubMed]
- Ruminy, P.; Gangneux, C.; Claeyssens, S.; Scotte, M.; Daveau, M.; Salier, J.P. Gene transcription in hepatocytes during the acute phase of a systemic inflammation: From transcription factors to target genes. Inflamm. Res. 2001, 50, 383–390. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.Y.; Chu, Y.F.; Hahn, J. Model simplification procedure for signal transduction pathway models: An application to IL-6 signaling. Chem. Eng. Sci. 2010, 65, 1964–1975. [Google Scholar] [CrossRef]
- Marianayagam, N.J.; Sunde, M.; Matthews, J.M. The power of two: Protein dimerization in biology. Trends Biochem. Sci. 2004, 29, 618–625. [Google Scholar] [CrossRef] [PubMed]
- Swanson, J.M.; Henchman, R.H.; McCammon, J.A. Revisiting free energy calculations: A theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophys. J. 2004, 86, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Moshage, H. Cytokines and the hepatic acute phase response. J. Pathol. 1997, 181, 257–266. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Karlsson, J.O.M.; Huang, Z. Modeling the Dynamics of Acute Phase Protein Expression in Human Hepatoma Cells Stimulated by IL-6. Processes 2015, 3, 50-70. https://doi.org/10.3390/pr3010050
Xu Z, Karlsson JOM, Huang Z. Modeling the Dynamics of Acute Phase Protein Expression in Human Hepatoma Cells Stimulated by IL-6. Processes. 2015; 3(1):50-70. https://doi.org/10.3390/pr3010050
Chicago/Turabian StyleXu, Zhaobin, Jens O. M. Karlsson, and Zuyi Huang. 2015. "Modeling the Dynamics of Acute Phase Protein Expression in Human Hepatoma Cells Stimulated by IL-6" Processes 3, no. 1: 50-70. https://doi.org/10.3390/pr3010050
APA StyleXu, Z., Karlsson, J. O. M., & Huang, Z. (2015). Modeling the Dynamics of Acute Phase Protein Expression in Human Hepatoma Cells Stimulated by IL-6. Processes, 3(1), 50-70. https://doi.org/10.3390/pr3010050






