Research on the Prediction of Pressure, Temperature, and Hydrate Inhibitor Addition Amount After Surface Mining Throttling

Abstract

During the trial mining process, ground horizontal pipes are prone to generating hydrates due to pressure and temperature changes, leading to ice blockage. Hydrate inhibitors are usually added on-site to prevent freezing blockage. However, existing addition methods have limitations, including poor real-time performance, insufficient accuracy in the addition amount, and dependence on manual adjustment. In view of this, this paper aims to develop models to predict the throttling pressure and temperature for horizontal ground pipes, and to indicate the amount of ethylene glycol needed to prevent freezing blockage, thereby laying the foundation for accurate, real-time prediction of fluid pressure and temperature and for controlling the addition amount. By integrating data-driven technologies and mechanism models, this study developed intelligent prediction systems for ground horizontal pipe throttling pressure and temperature, and for suppression of freeze-blocking ethylene glycol addition. First, a three-phase throttling mechanism model for oil, gas, and water is established using the energy conservation equation to accurately predict the pressure and temperature at the throttling points along the process. At the same time, HYSYS software is used to simulate various operating conditions and to fit the ethylene glycol addition amount prediction model. Finally, edge computing equipment is integrated to enable real-time data collection, prediction, and dynamic adjustment and optimization. The field measurement data of Well A showed that the model’s prediction error of pressure and temperature before and after throttling is less than 6%, and the prediction error of the ethylene glycol addition amount is less than 5%, which provides key technical support for safe and efficient operation of the trial mining process as well as for cost reduction and efficiency improvement.

1. Introduction

Test production serves as a critical link in gas field evaluation and production capacity construction, bearing significant implications for reservoir characterization, development scheme optimization, and subsequent efficient production. However, the production process is characterized by prominent fluctuations in key parameters such as gas production rate and liquid–gas ratio, coupled with complex and variable operating conditions. The surface horizontal pipe throttling system, as the core equipment for regulating pressure and flow, is prone to the Joule-Thomson effect during operation. This effect leads to a rapid temperature drop, which significantly increases the risk of natural gas hydrate formation and subsequent ice blockages. Such blockages not only disrupt the continuity of trial mining operations but also pose severe threats to operational safety. Particularly in gas reservoirs with high water-to-gas ratios, the presence of large quantities of liquid water further exacerbates the risk of hydrate plugging, making the problem more intractable.

Traditional downhole throttling models, such as the Thornhill-Craver method, are established based on steady-state assumptions. These models fail to fully account for the dynamic impacts of water-to-gas ratio changes on the throttling process in surface horizontal pipes. Consequently, they suffer from insufficient prediction accuracy and weak adaptability, which render them unable to meet the requirements of real-time optimization and control in the dynamic trial production process. In practical applications, this inadequacy often leads to inaccurate predictions of pressure and temperature, increasing the likelihood of hydrate formation and operational risks.

In the field of throttling modeling, extensive research has been conducted by scholars worldwide. Early work by Duns and Rose [1,2] laid the foundation by deriving throttling formulas based on the principle of energy conservation. Subsequent contributions, such as those by Poettman et al. [3] and Gilbert [4], were gradually refined by researchers including Ros, Secen [5], Baxendeil [6], Achong [7], Pilehvari [8], Osman [9], and Dokla [10]. Omana et al. [11] employed dimensional analysis to derive a dimensionless relationship for multiphase flow through chokes, while Fortunati [12] and Sachdeva [13] developed two-phase throttling models applicable to subcritical flow. Valvatne [14] integrated frictional and throttling pressure drops to establish a numerical model for downhole throttling, later comparing it with surface throttling behavior. Jiang et al. [15] further advanced the field by developing a coupled multi-stage throttling model through nodal-system analysis. Domestic research on throttling modeling began relatively later. Liu Jianyi et al. [16] proposed a two-phase gas–liquid throttling model for high gas–liquid-ratio gas wells. Zhou Xingfu et al. [17] developed a temperature-drop model for downhole throttling, and Li Nanxing et al. [18] created a new nozzle flow model using dimensional analysis and regression. Tang Shenglai et al. [19] investigated wellbore temperature and pressure distributions along with nozzle temperature-drop prediction. Xiao Yuyang [20] conducted laboratory simulation experiments to optimize a throttling model for high-water-cut gas wells and validated it using field data, providing valuable guidance for downhole throttling parameter optimization. Despite these advances, most existing models focus primarily on downhole throttling or specific steady-state conditions. There remains a notable lack of research on throttling pressure-temperature prediction for surface horizontal pipeline sections during trial production, particularly with regard to multiphase flow, thermal coupling, and sequential dynamic characteristics.

To inhibit freezing plugging, ethylene glycol is a commonly used hydrate inhibitor, and accurate prediction of its dosage is crucial. Traditional calculation methods primarily rely on the Hammerschmidt formula and process simulation software (such as HYSYS). Hu Yiwu et al. [21] developed a framework for systematically calculating the amount of ethylene glycol to be injected. Jiang Hong et al. [22] used HYSYS to optimize the injection amount model and established a linear correlation. Guo Zhou et al. [23] proposed an automatic iterative calculation method based on HYSYS. Liu Gang [24] addressed the issue of hydrate formation in gathering and transportation pipelines by using PIPEPHASE software 9.5 to simulate the hydrate formation temperature and location. Combined with the calculation and optimization of methanol inhibitor injection rate, precise control of inhibitor dosage was achieved, significantly reducing operational costs. In addition to relying on traditional thermodynamic formulas and process simulation software, the development of intelligent prediction models in recent years has provided a new approach to improving the accuracy of basic prediction data. Li En et al. [25] optimized the BP neural network by improving the sine-cosine algorithm, constructing a high-precision natural gas hydrate formation temperature prediction model. Its prediction results provide a more reliable phase equilibrium basis for the calculation of inhibitor dosage. Although these studies have improved the scientific rigor of calculations, they lack research on coupling and collaboration with throttling temperature and pressure prediction, and there are still common problems, such as poor real-time performance, reliance on manual adjustments, and difficulty in adapting to rapid switching of multiple operating conditions in the test production process.

To sum up, in response to the dual challenges of accurately predicting the throttling pressure and temperature of surface horizontal pipes and realizing the intelligent injection of ethylene glycol for hydrate inhibition during the test production process, existing research still exhibits obvious shortcomings in terms of model real-time performance, dynamic adaptability, and multi-technical integration. In view of this, this study intends to carry out the following research work: Based on the energy conservation equation, an oil-gas-water three-phase throttling mechanism model suitable for surface horizontal pipes will be established to characterize the pressure and temperature before and after throttling accurately; Ethylene glycol demand data under different operating conditions will be obtained through HYSYS software V12 simulation, and an injection amount prediction model will be fitted. Relying on the edge computing architecture, real-time dynamic adjustment and optimization of ethylene glycol injection amount will be achieved. Finally, an integrated intelligent decision-making system for surface horizontal pipe throttling and hydrate plugging prevention and control suitable for the test production process will be developed, providing solid technical support for ensuring the safe and efficient test production of gas fields.

2. Horizontal Pipe Throttling Pressure and Temperature Prediction Model

Although there are many calculation models about throttling, there are not many models that have been verified by field tests and are relatively common. The model selected in this article is completely derived based on theory, and the throttling calculation model established in this article is a model that has been verified by underground throttling calculations [26]. A more detailed derivation process can be found in the literature [27]. This article introduces it into the horizontal throttling calculation, as follows.

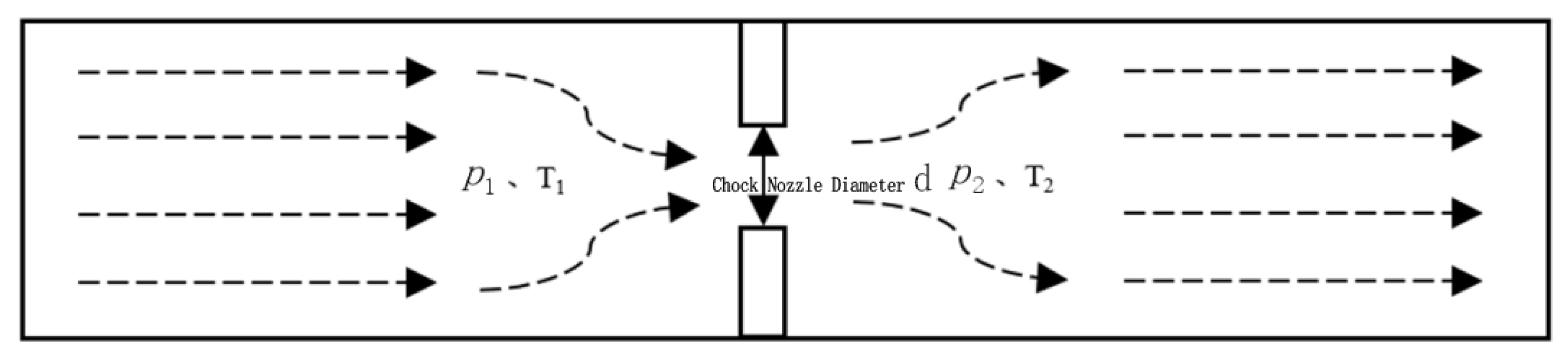
2.1. Oil-Gas-Water Three-Phase Throttling Model

Assuming that the height difference between the upstream of the throttle valve and the throttle valve orifice can be neglected, the work performed externally is zero, and the heat exchanged with the system can be ignored [27], the schematic diagram of the throttling is shown in Figure 1. According to the energy conservation equation, the following can be obtained:

$$144{\mathrm{p}}_1{\mathsf{\nu }}_1+{\displaystyle \frac{{\mathrm{V}}_1^2}{2{\mathrm{g}}_{\mathrm{c}}}}+{\mathrm{C}}_{\mathsf{\nu }}({\mathrm{T}}_1-{\mathrm{T}}_2)=144{\mathrm{p}}_2{\mathsf{\nu }}_2+{\displaystyle \frac{{\mathrm{V}}_2^2}{2{\mathrm{g}}_{\mathrm{c}}}}$$

(1)

In the formula: ${\mathrm{p}}_1$ is the pressure before throttling, MPa; ${\mathrm{v}}_1$ is the specific volume before throttling, m³/kg; ${\mathrm{V}}_1$ is the flow velocity before throttling, m/s; ${\mathrm{g}}_{\mathrm{c}}$ is the gravitational acceleration constant, m/s²; ${\mathrm{C}}_{\mathrm{v}}$ is the specific heat at constant volume, kJ/(kg·°C); ${\mathrm{T}}_1$ is the temperature before throttling, °C; ${\mathrm{T}}_2$ is the temperature after throttling, °C; ${\mathrm{p}}_2$ is the pressure after throttling, MPa; ${\mathrm{v}}_2$ is the specific volume after throttling, m³/kg; ${\mathrm{V}}_2$ is the flow velocity after throttling, m/s.

For any point in the throttling flow system, the following assumptions are made: ① all phases are at the same temperature; ② all components move at the same velocity; ③ the gas compression factor is constant; ④ the compressibility of liquids is negligible compared to gases; ⑤ the flow process is adiabatic and frictionless.

Based on one lbm of flowing fluid, by summing the energy contributions of each phase of gas, oil, and water, and considering the gas components, we obtain the following:

$$144\mathsf{\lambda }({\mathrm{p}}_1{\mathsf{\nu }}_1-{\mathrm{p}}_2{\mathsf{\nu }}_2)+144({\displaystyle \frac{{\mathrm{f}}_{\mathrm{o}}}{{\mathsf{\rho }}_{\mathrm{o}}}}+{\displaystyle \frac{{\mathrm{f}}_{\mathrm{w}}}{{\mathsf{\rho }}_{\mathrm{w}}}})({\mathrm{p}}_1-{\mathrm{p}}_2)+({\displaystyle \frac{{\mathrm{V}}_1^2-{\mathrm{V}}_2^2}{2{\mathrm{g}}_{\mathrm{c}}}})=0$$

(2)

In the formula: λ is the gas–liquid mixture correction factor, 1; ${\mathrm{f}}_{\mathrm{o}}$ is the volume fraction of the oil phase; ${\mathrm{f}}_{\mathrm{w}}$ is the volume fraction of the water phase; ${\mathsf{\rho }}_{\mathrm{o}}$ is the density of the oil phase, kg/m³; ${\mathsf{\rho }}_{\mathrm{w}}$ is the density of the water phase, kg/m³.

If all phases are at the same temperature, and the flow process is frictionless and adiabatic, then the following follows:

$$\begin{array}{ll}& \left[{\mathrm{f}}_{\mathrm{g}}\left({\mathrm{C}}_{\mathsf{\nu }\mathrm{g}}+{\displaystyle \frac{\mathrm{z}\mathrm{R}}{\mathrm{M}}}\right)+{\mathrm{f}}_{\mathrm{o}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{o}}+{\mathrm{f}}_{\mathrm{w}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{w}}\right]\mathrm{p}\mathrm{d}\mathsf{\nu }\\ & +({\mathrm{f}}_{\mathrm{g}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{g}}+{\mathrm{f}}_{\mathrm{o}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{o}}+{\mathrm{f}}_{\mathrm{w}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{w}})\mathsf{\nu }\mathrm{d}\mathrm{p}=0\end{array}$$

(3)

In the formula: ${\mathrm{f}}_{\mathrm{g}}$ is the gas volume fraction; ${\mathrm{C}}_{\mathrm{v}\mathrm{g}}$ is the constant-volume specific heat capacity of the gas phase, kJ/(kg·°C); z is the gas compressibility factor; R is the universal gas constant; M is the gas molar mass; ${\mathrm{C}}_{\mathrm{v}\mathrm{o}}$ is the constant-volume specific heat capacity of the oil phase, kJ/(kg·°C); ${\mathrm{C}}_{\mathrm{v}\mathrm{w}}$ is the constant-volume specific heat capacity of the water phase.

Now considering only the gas composition. If the gas is heated at a constant volume,

$$\mathrm{Q}={\mathrm{E}}_2-{\mathrm{E}}_1={\mathrm{C}}_{\mathsf{\nu }}({\mathrm{T}}_2-{\mathrm{T}}_1)$$

(4)

In the formula: Q is the heat change, kJ; E₁ is the initial internal energy, kJ; E₂ is the final internal energy, kJ.

$$\begin{array}{ll}& \mathrm{Q}={\mathrm{C}}_{\mathrm{p}}({\mathrm{T}}_2-{\mathrm{T}}_1)={\mathrm{C}}_{\mathsf{\nu }}({\mathrm{T}}_2-{\mathrm{T}}_1)+144\mathrm{p}({\mathsf{\nu }}_2-{\mathsf{\nu }}_1)\\ & ={\mathrm{C}}_{\mathsf{\nu }}({\mathrm{T}}_2-{\mathrm{T}}_1)+{\displaystyle \frac{\mathrm{z}\mathrm{R}}{\mathrm{M}}}({\mathrm{T}}_2-{\mathrm{T}}_1)\end{array}$$

(5)

Combining Equations (3)–(5), and letting,

$$\mathrm{n}=\left({\displaystyle \frac{{\mathrm{f}}_{\mathrm{g}}\mathrm{F}{\mathrm{C}}_{\mathsf{\nu }\mathrm{g}}+{\mathrm{f}}_{\mathrm{o}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{o}}+{\mathrm{f}}_{\mathrm{w}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{w}}}{{\mathrm{f}}_{\mathrm{g}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{g}}+{\mathrm{f}}_{\mathrm{o}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{o}}+{\mathrm{f}}_{\mathrm{w}}{\mathrm{C}}_{\mathsf{\nu }\mathrm{w}}}}\right)$$

(6)

Integrating yields the following:

$${\mathrm{p}}_1{\mathsf{\nu }}_1^{\mathrm{n}}={\mathrm{p}}_2{\mathsf{\nu }}_2^{\mathrm{n}}$$

(7)

In the formula: ${\mathrm{C}}_{\mathrm{p}}$ is the specific heat capacity at constant pressure, kJ/(kg·K); F is the gas–liquid interaction coefficient.

Let

$${\mathrm{p}}_{\mathrm{r}}={\mathrm{p}}_2/{\mathrm{p}}_1$$

(8)

Combining Equations (2), (7) and (8) yields the following:

$$\begin{array}{ll}& 144\mathsf{\lambda }{\mathrm{p}}_1{\mathsf{\nu }}_1[1-{\mathrm{p}}_{\mathrm{r}}^{(\mathrm{x}-1)/\mathrm{x}}]+144({\displaystyle \frac{{\mathrm{f}}_{\mathrm{o}}}{{\mathsf{\rho }}_{\mathrm{o}}}}+{\displaystyle \frac{{\mathrm{f}}_{\mathrm{w}}}{{\mathsf{\rho }}_{\mathrm{w}}}}){\mathrm{p}}_1(1-{\mathrm{p}}_{\mathrm{r}})\\ & +{\displaystyle \frac{{\mathrm{V}}_2^2}{2{\mathrm{g}}_{\mathrm{c}}}}[({\displaystyle \frac{{\mathrm{V}}_1}{{\mathrm{V}}_2}}{)}^2-1]=0\end{array}$$

(9)

From the mass conservation equation:

$${\displaystyle \frac{{\mathrm{A}}_1{\mathrm{V}}_1}{{\mathrm{f}}_{\mathrm{g}}{\mathsf{\nu }}_1+({\mathrm{f}}_{\mathrm{o}}/{\mathsf{\rho }}_{\mathrm{o}})+({\mathrm{f}}_{\mathrm{w}}/{\mathsf{\rho }}_{\mathrm{w}})}}={\displaystyle \frac{{\mathrm{A}}_2{\mathrm{V}}_2}{{\mathrm{f}}_{\mathrm{g}}{\mathsf{\nu }}_2+({\mathrm{f}}_{\mathrm{o}}/{\mathsf{\rho }}_{\mathrm{o}})+({\mathrm{f}}_{\mathrm{w}}/{\mathsf{\rho }}_{\mathrm{w}})}}$$

(10)

Combining Equations (9) and (10) yields the following:

$$\begin{array}{rrr}& {\mathrm{V}}_2=& \sqrt{{\displaystyle \frac{288{\mathrm{g}}_{\mathrm{c}}(\mathsf{\lambda }{\mathrm{p}}_1{\mathsf{\nu }}_1[1-{\mathrm{p}}_{\mathrm{r}}^{(\mathrm{x}-1)/\mathrm{n}}]+[({\mathrm{f}}_{\mathrm{o}}/{\mathsf{\rho }}_{\mathrm{o}})+({\mathrm{f}}_{\mathrm{w}}/{\mathsf{\rho }}_{\mathrm{w}})]{\mathrm{p}}_1(1-{\mathrm{p}}_{\mathrm{r}}))}{1-({\mathrm{A}}_2/{\mathrm{A}}_1{)}^2[({\mathrm{f}}_{\mathrm{g}}+{\mathsf{\alpha }}_1)/({\mathrm{f}}_{\mathrm{g}}{\mathrm{p}}_{\mathrm{r}}^{-1/\mathrm{n}}+{\mathsf{\alpha }}_1){]}^2}}}\end{array}$$

(11)

Consequently, the calculation model for the throttling section can be derived as follows:

$$\begin{array}{c}{\mathrm{w}}_{\mathrm{i}}={\mathrm{A}}_2\sqrt{(288{\mathrm{g}}_{\mathrm{c}}{\mathrm{p}}_1/{\mathsf{\nu }}_1)}\\ \sqrt{{\displaystyle \frac{\mathsf{\lambda }[1-{\mathrm{p}}_{\mathrm{r}}^{(\mathrm{n}-1)/\mathrm{n}}]+{\mathsf{\alpha }}_1(1-{\mathrm{p}}_{\mathrm{r}})}{\left[1-{\left(\frac{{\mathrm{A}}_2}{{\mathrm{A}}_1}\right)}^2{\left(\frac{{\mathrm{f}}_{\mathrm{g}}+{\mathsf{\alpha }}_1}{{\mathrm{f}}_{\mathrm{g}}{\mathrm{p}}_{\mathrm{r}}^{-1/\mathrm{n}}+{\mathsf{\alpha }}_1}\right)}^2\right]{\left({\mathrm{f}}_{\mathrm{g}}{\mathrm{p}}_{\mathrm{r}}^{-1/\mathrm{n}}+{\mathsf{\alpha }}_1\right)}^2}}}\end{array}$$

(12)

The maximum possible flow is determined by finding the value of pr for which dwi/dpr = 0.

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}{\mathrm{p}}_{\mathrm{r}}}}{\left({\displaystyle \frac{{\mathrm{w}}_{\mathrm{i}}}{{\mathrm{A}}_2\sqrt{288{\mathrm{g}}_{\mathrm{c}}{\mathrm{p}}_1/{\mathsf{\nu }}_1}}}\right)}^2=0$$

(13)

$$\begin{array}{c}\{2\lambda [1-{\mathrm{p}}_{\mathrm{r}}^{(\mathrm{n}-1)/\mathrm{n}}]+2{\mathsf{\alpha }}_1(1-{\mathrm{p}}_{\mathrm{r}})\}[1-{(\frac{{\mathrm{A}}_2}{{\mathrm{A}}_1})}^{\frac{{\mathrm{f}}_{\mathrm{g}}+{\mathsf{\alpha }}_1}{{\mathrm{f}}_{\mathrm{g}}{\mathrm{p}}_{\mathrm{r}}^{-1/\mathrm{n}}+{\mathsf{\alpha }}_1}}]\\ \left[{\displaystyle \frac{{\mathrm{f}}_{\mathrm{g}}}{\mathrm{n}}}{\mathrm{p}}_{\mathrm{r}}^{-(1+\mathrm{n})/\mathrm{n}}\right]+{\left({\displaystyle \frac{{\mathrm{A}}_2}{{\mathrm{A}}_1}}\right)}^2{\displaystyle \frac{{\mathrm{f}}_{\mathrm{g}}}{\mathrm{n}}}{\displaystyle \frac{{\left({\mathrm{f}}_{\mathrm{g}}+{\mathsf{\alpha }}_1\right)}^2{\mathrm{p}}_{\mathrm{r}}^{-(1+\mathrm{n})/\mathrm{n}}}{{\left({\mathrm{f}}_{\mathrm{g}}{\mathrm{p}}_{\mathrm{r}}^{-1/\mathrm{n}}+{\mathsf{\alpha }}_1\right)}^2}}\}\\ =[1-{(\frac{{\mathrm{A}}_2}{{\mathrm{A}}_1})}^{{\displaystyle \frac{{\mathrm{f}}_{\mathrm{g}}+{\mathsf{\alpha }}_1}{{\mathrm{f}}_{\mathrm{g}}{\mathrm{p}}_{\mathrm{r}}^{-1/\mathrm{n}}+{\mathsf{\alpha }}_1}}}]({\mathrm{f}}_{\mathrm{g}}{\mathrm{p}}_{\mathrm{r}}^{-1/\mathrm{n}}+{\mathsf{\alpha }}_1)\\ \times [\lambda ({\displaystyle \frac{\mathrm{n}-1}{\mathrm{n}}}){\mathrm{p}}_{\mathrm{r}}^{-1/\mathrm{n}}+{\mathsf{\alpha }}_1]\end{array}$$

(14)

In the formula: ${\mathsf{\alpha }}_1$ is the sum of the ratio of liquid phase volume fraction to density, divided by the combination parameter of the specific volume before throttling, ${\mathsf{\alpha }}_1={\displaystyle \frac{1}{{\mathrm{V}}_1}}({\displaystyle \frac{{\mathrm{f}}_{\mathrm{o}}}{{\mathsf{\rho }}_{\mathrm{o}}}}+{\displaystyle \frac{{\mathrm{f}}_{\mathrm{w}}}{{\mathsf{\rho }}_{\mathrm{w}}}})$, dimensionless; ${\mathrm{A}}_1$ is the flow area upstream of the throttle, m²; ${\mathrm{A}}_2$ is the flow area of the throttle throat, m²; ${\mathrm{w}}_{\mathrm{i}}$ is the isentropic mass flow rate, kg/s.

2.2. Throttling Pressure Drop Calculation

When natural gas flows through a downhole throttling device, due to the sudden reduction in the flow cross-section and the Bernoulli equation, its flow velocity increases rapidly, and the pressure drops significantly, as shown in Figure 2.

Since p_throttle is the pressure at the throat section, it is difficult to measure experimentally or in field applications. Therefore, Perkins (1993) [27] proposed defining the pressure in the downstream section of the nozzle as p₃, and Perry proposed the following formula to calculate p₃:

$${\mathrm{p}}_3={\mathrm{p}}_1-{\displaystyle \frac{\left({\mathrm{p}}_1−{\mathrm{p}}_2\right)}{[1{\left({\mathrm{d}}_{\mathrm{c}}/{\mathrm{d}}_{\mathrm{d}}\right)}^{1.85}]}}$$

(15)

With the known flow rate and pressure ${\mathrm{p}}_1$ of natural gas, as well as specific other parameters, the pressure after throttling, ${\mathrm{p}}_2$, can be determined through iterative calculation using Formula (5) under critical flow conditions, and the pressure drop $∆\mathrm{p}={\mathrm{p}}_1-{\mathrm{p}}_2$.

2.3. Throttle Temperature Drop Calculation

Since volume expansion results in energy loss after passing through the nozzle, the temperature after adiabatic decompression is designated as ${\mathrm{T}}_3$.

$${\mathrm{T}}_3=\mathsf{\alpha }{\left[{\displaystyle \frac{{\mathrm{p}}_3}{{\mathrm{p}}_1}}\right]}^{{\displaystyle \frac{\mathrm{k}-1}{\mathrm{k}}}}{\mathrm{T}}_1$$

(16)

The relationship between the temperature difference and pressure difference after throttling is as follows:

$$\mathsf{\Delta }\mathrm{T}={\mathrm{T}}_1-{\mathrm{T}}_3={\mathrm{T}}_1[1-\mathsf{\alpha }{\left({\displaystyle \frac{{\mathrm{p}}_3}{{\mathrm{p}}_1}}\right)}^{{\displaystyle \frac{\mathrm{k}-1}{\mathrm{k}}}}]$$

(17)

In the formula: ${\mathrm{T}}_1$, ${\mathrm{T}}_3$ are the temperatures before and after decompression, K; $\mathsf{\alpha }$ is the correction factor; ${\mathrm{p}}_1$, ${\mathrm{p}}_3$ are the absolute pressures before and after decompression, MPa; $\mathrm{k}$ is the isentropic index of natural gas.

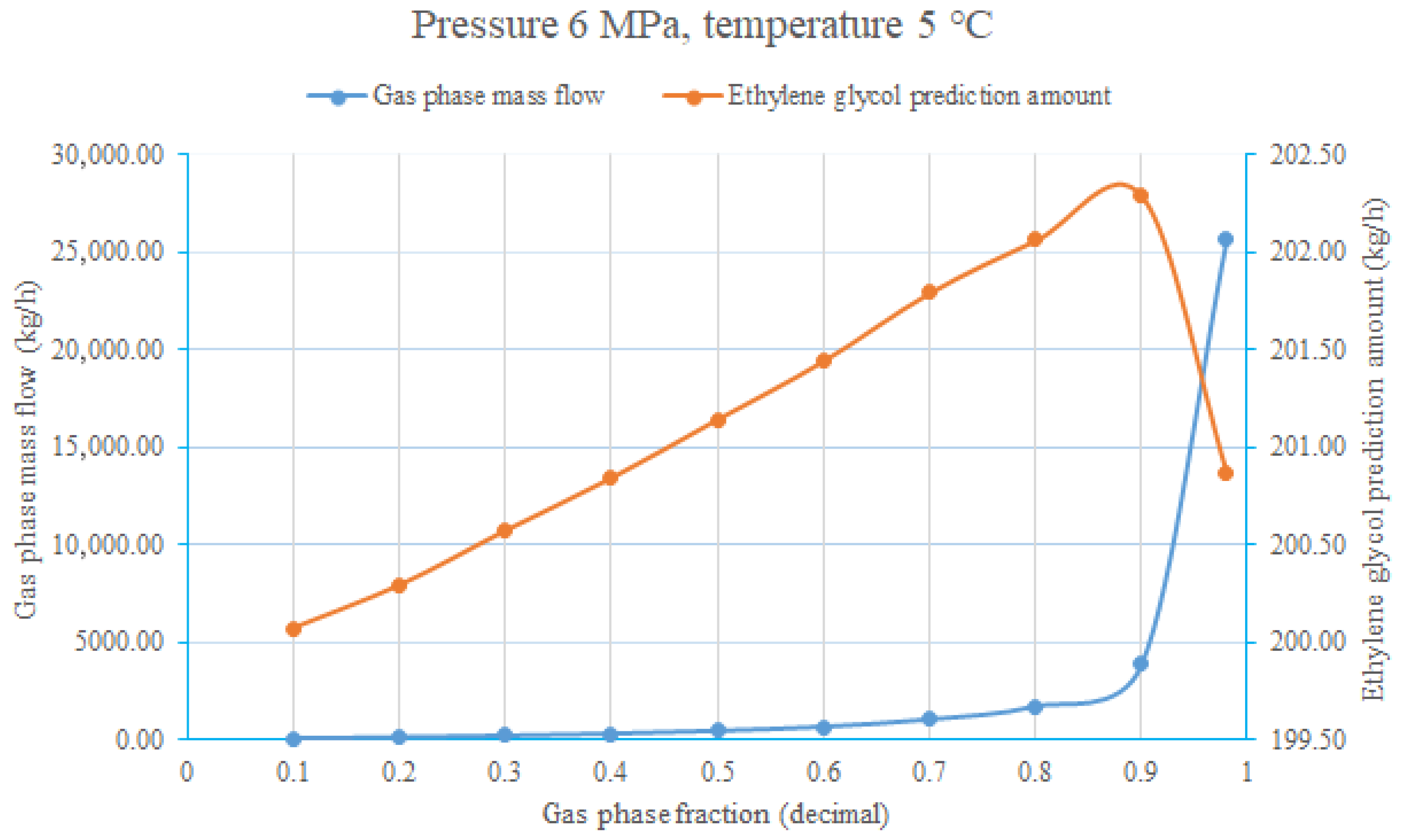
3. Predictive Model for Glycol Injection to Inhibit Freezing Blockage

The amount of glycol injection should be evaluated comprehensively in light of hydrate-inhibition requirements, actual production conditions, and economic factors. By combining the hydrate formation mechanism with the principle of glycol action, the core parameters that affect the glycol injection amount are identified, including liquid holdup along the line, gas composition, and other factors. The model is constructed using these key process parameters, which are monitored in real time, to determine an accurate calculation method for predicting the required injection amount.

First, hydrate formation conditions were systematically simulated in HYSYS using actual fluid compositions and thermodynamic models to determine the corresponding ethylene glycol (EG) injection requirements under various operating conditions. For example, the prediction results of the amount of ethylene glycol inhibitor added under the conditions of a liquid production volume of 416 kg/h, different pressures, temperatures, and gas production rates are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28. As can be seen from the figure, under the same conditions, as the gas production rate increases (the gas phase rate fraction becomes larger), the amount of ethylene glycol inhibitor that needs to be added also needs to increase. However, in most cases, when the gas production increases to a certain extent, such as when the gas phase volume fraction is greater than or equal to 0.9, as the gas production increases, the amount of ethylene glycol inhibition decreases. The analysis reason may be that due to the large amount of gas production, the liquid carried in the gas production fluid is diluted to a smaller concentration. At this time, it is difficult to form hydrates, so the amount of ethylene glycol inhibitor that needs to be added becomes smaller.

Second, based on data for glycol addition under different operating conditions (e.g., pressure and temperature) and the relationships between glycol addition and parameters such as the total mass flow rate, liquid mass flow rate, cross-section air holdup, temperature and pressure, an empirical glycol prediction model was fitted, as shown in Figure 29 and Figure 30.

The fitted equation is as follows:

$$\mathrm{y}={\displaystyle \frac{5561.792434\times {\left(145.03\mathrm{P}\right)}^{0.225243}}{{\left(1.8\mathrm{T}+32\right)}^{0.798647}}}\times {\displaystyle \frac{{\left(1−{\mathrm{H}}_{\mathrm{g}}\right)}^{0.0416295}}{{{\mathrm{W}}_{\mathrm{Liq}}}^{0.162831}}}\times ({{\mathrm{W}}_{\mathrm{total}}}^{0.038962})-444.544445$$

(18)

In the formula: P is pressure, MPa;

$\mathrm{T}$ is temperature, °C;

${\mathrm{H}}_{\mathrm{g}}$ is gas holdup (gas volume fraction);

${\mathrm{W}}_{\mathrm{Liq}}$ is liquid phase mass flow rate, kg/h;

${\mathrm{W}}_{\mathrm{total}}$ is the total mass flow rate of gas and liquid phases, kg/h.

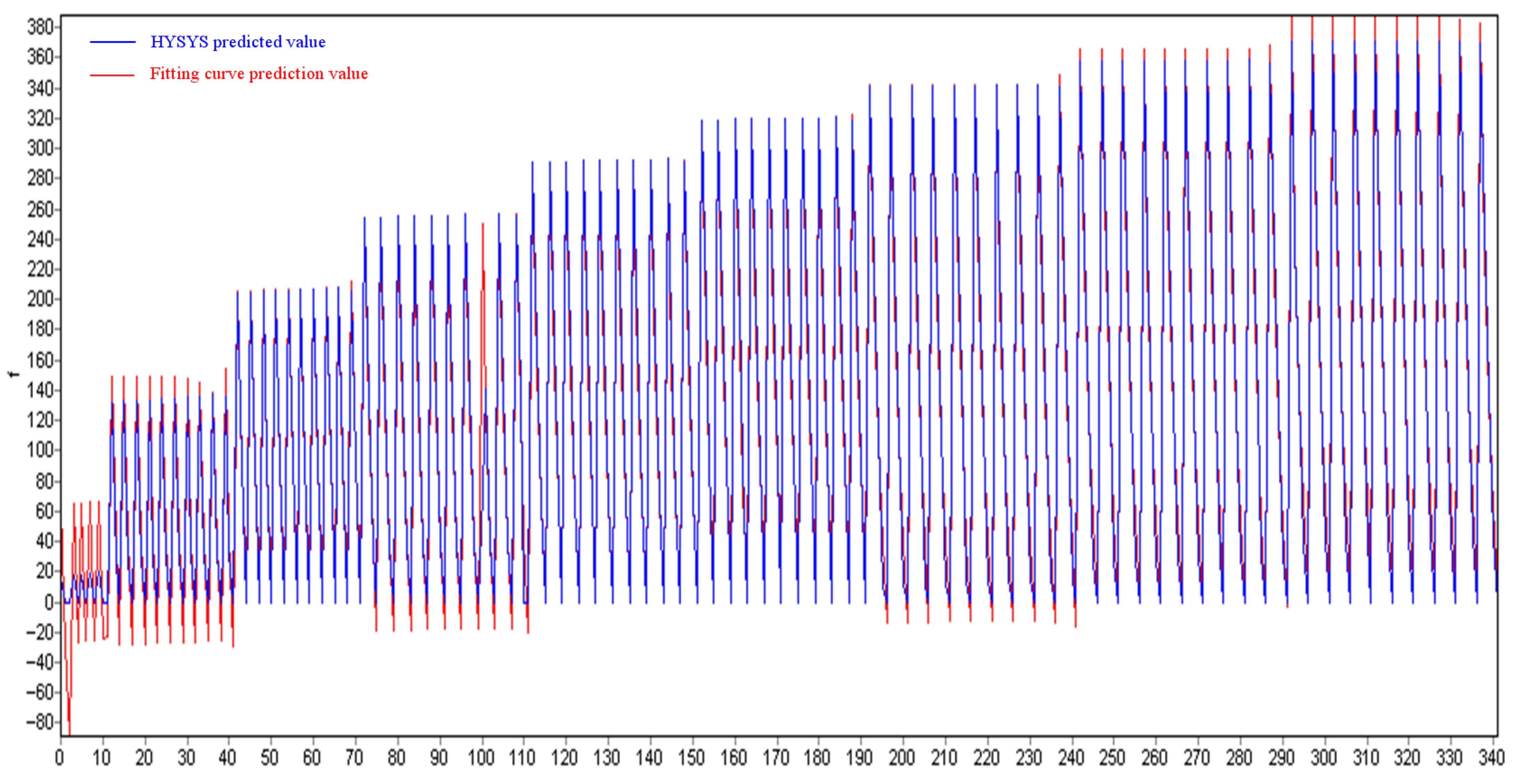
4. Real-Time Dynamic Adjustment and Optimization of the Calculation Process

Based on the model established above, real-time dynamic adjustment and optimization of the ethylene glycol dosage can be achieved through the following process, as shown in Figure 31.

5. Case Study Validation

Based on the research model, an algorithm was built as shown in Figure 32. Real-time production data from Well A were collected as shown in Figure 33 and processed to form a single-well experimental database. A demonstration was conducted to validate the ice blockage model step by step (prediction of pressure and temperature before and after throttling, and prediction of ethylene glycol dosage). The details are as follows, from Figure 34, Figure 35, Figure 36, Figure 37, Figure 38 and Figure 39 Figure 34 shows the field equipment flow chart, in which the sequence of the processes is marked. Figure 35 shows the interface for setting corresponding parameters according to the order of the process. Figure 36, Figure 37, Figure 38 and Figure 39, respectively, show the calculation results corresponding to simulation predictions.

5.1. Gas Well Production Environment Setup

Set parameters to simulate the natural flow production of a gas well, as shown in

Table 1. Production Conditions.

Wellhead Pressure (MPa)	Liquid Production (m3/d)	Gas Production (m3/d)
12.5	44.4	164,000

.

Calibrate to ensure that the wellhead oil pressure, temperature, gas output, and liquid production match those of the actual site, as shown in Figure 36. It can be seen from the figure that the liquid production rate at the node analysis intersection point (corresponding to the abscissa below) and the gas production rate at the same time (corresponding to the abscissa above).

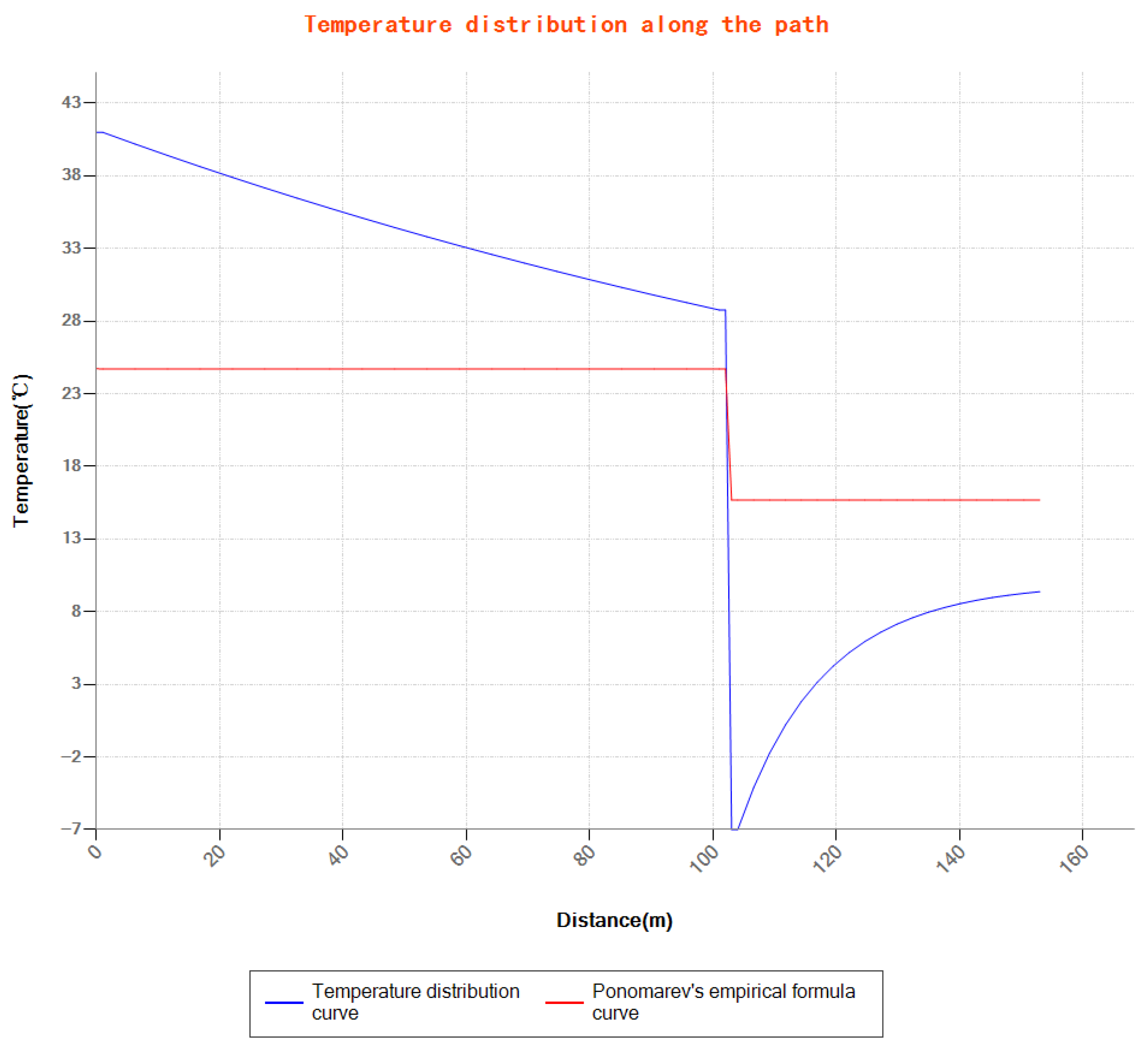
5.2. Prediction of Ground Pressure and Temperature Distribution Along the Path

The predicted ground pressure and temperature along the path are shown in Figure 37 and Figure 38, respectively. It can be seen from Figure 37 and Figure 38 that due to the small distance along the horizontal pipeline, the pressure drop along the way is small. Since the ambient temperature is lower than the temperature of gas and liquid production, the fluid transfers heat radially outward, and the heat is transferred from the fluid to the environment, and the temperature gradually decreases along the path. When the fluid passes through the choke, both the pressure and temperature undergo sudden changes. The pressure is significantly reduced after throttling, while the temperature is significantly reduced and then, due to the radial inward heat transfer from the environment to the fluid, the fluid temperature gradually recovers, but the recovered temperature will not exceed the ambient temperature. As shown in the figures, both pressure and temperature undergo abrupt changes at the throttling point. Figure 38 shows that after throttling, the temperature has fallen below the hydrate formation temperature, indicating the need to add a hydrate inhibitor.

It can be seen from the Figure 40, Figure 41, Figure 42 and Figure 43 comparison that the pressure and temperature changes after different chokes are different. The smaller the choke, the lower the pressure and temperature after throttling. Therefore, when there is a need for throttling and pressure reduction, it is necessary to select a larger choke size as much as possible while meeting the pressure requirements after throttling. Try to keep the temperature after throttling not too low to avoid easy formation of hydrates, and at the same time, reduce the amount of ethylene glycol inhibitor added.

5.3. Comparison with Measured Data

According to the hydrate inhibitor prediction model, the required glycol amount is 370.93 kg/h, as shown in Figure 39. Compared with actual field measurements, the model’s prediction errors for pressure and temperature before and after throttling are both less than 6%, and the prediction error for glycol dosage is 1.87%, which is less than 5%. The specific data are shown in

Table 2. Comparison of pressure and temperature before and after throttling.

	Pressure Before Throttling (MPa)	Temperature Before Throttling (°C)	Pressure After Throttling (MPa)	Temperature After Throttling (°C)
Actual	12.50	28.31	4.19	−7.41
Simulation Calculation	12.37	28.79	4.02	−6.97
Absolute Relative Error (%)			−4.11	−5.98

and

Table 3. Ethylene glycol prediction comparison.

	Ethylene Glycol Addition (kg/d)
Actual	378
Simulation Calculation	370.93
Absolute Relative Error (%)	1.87

below:

6. Conclusions

By carrying out simulation calculation research on the entire process of gas well gas testing and production, the following conclusions and understandings were obtained.

• Based on the law of energy conservation, the oil, gas, and water three-phase throttling model is derived, and the calculation method of multi-phase throttling pressure drop and temperature drop is proposed. The established three-phase throttling pressure and temperature prediction model theoretically reveals the dynamic changes in pressure and temperature during natural gas throttling with a certain liquid-to-gas ratio, providing a reliable basis for accurately predicting pressure and temperature parameters after throttling.
• Verified by field data from Well A, the model’s pressure and temperature prediction errors before and after throttling are both less than 6%, and the prediction error of the ethylene glycol injection amount required to suppress hydrates is less than 5%, indicating that the established model is highly reliable.
• The model can be deployed on edge computing devices to achieve real-time collection of production data, parameter prediction, and dynamic adjustment of ethylene glycol injection rate. In engineering applications, the ethylene glycol injection amount can be dynamically optimized based on the fluctuations of production parameters, such as gas production rate and liquid–gas ratio, during the trial production process. This not only avoids the risk of hydrate clogging caused by insufficient injection but also reduces the waste of resources caused by excessive injection. At the same time, providing data support for throttling device parameter optimization and pipeline safe operation has important practical significance for improving the safety, efficiency, and economy of natural gas trial production projects.