Investigation on Stress Propagation and Fatigue Damage Characteristics of Drill String Under Multiple Oscillation Actions
Abstract
1. Introduction
2. Review on Oscillation Mechanisms and Drill String Fatigue Damage
2.1. Vibration-Induced Drag Reduction Mechanism of Drill String
2.2. Drill String Fatigue Damage Mechanism
3. Drill String Vibration and Fatigue Damage Theoretical Model
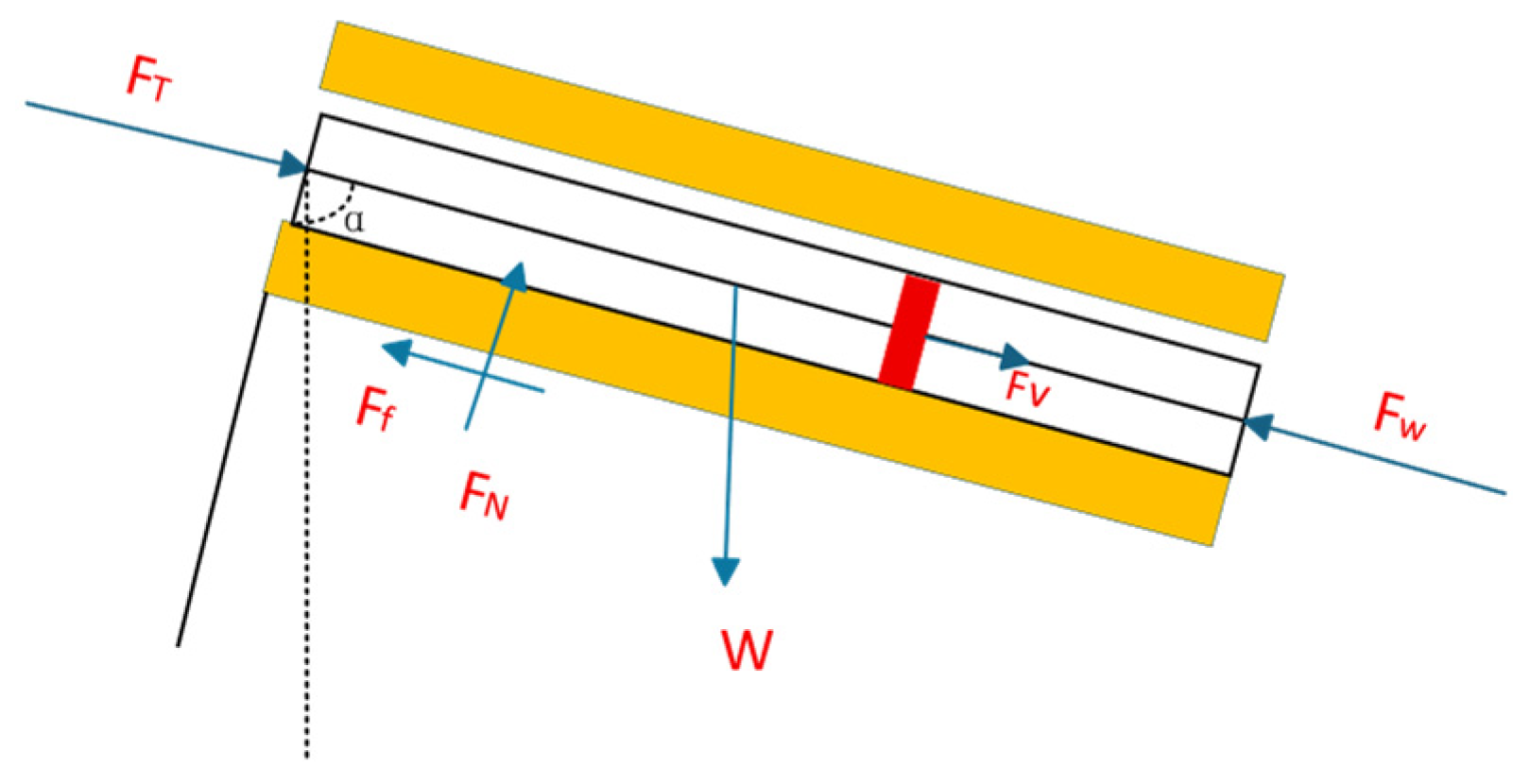
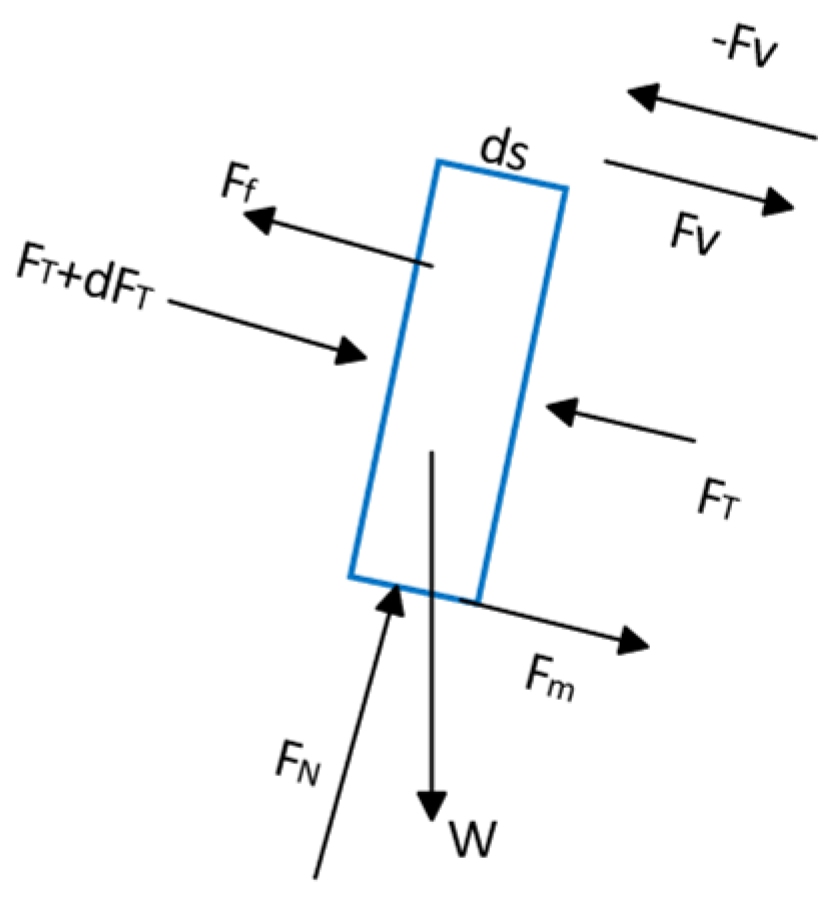
3.1. Drill String Dynamic Model Considering the Effect of Oscillators
- (1)
- The loading and deformation of the drill string remain within the elastic range;
- (2)
- The deformation of the borehole wall rock is neglected;
- (3)
- The drill string is assumed to stay in continuous contact with the borehole wall, and therefore its curvature is identical to the wellbore curvature;
- (4)
- Only the axial vibration of the drill string is considered;
- (5)
- The excitation force is transmitted axially toward both ends of the drill string;
- (6)
- During the instantaneous analysis, the rate of penetration (ROP) is taken as zero, and the displacement boundary condition at the bit remains unchanged.
3.2. Finite Element Model of the Drill String Considering the Influence of the Oscillator
3.3. Friction Model Between the Drill String and the Wellbore
3.4. Solution of the Vibration Equation Under the Combined Action of Two Oscillators
- (1)
- Initialization
- (2)
- For each time step
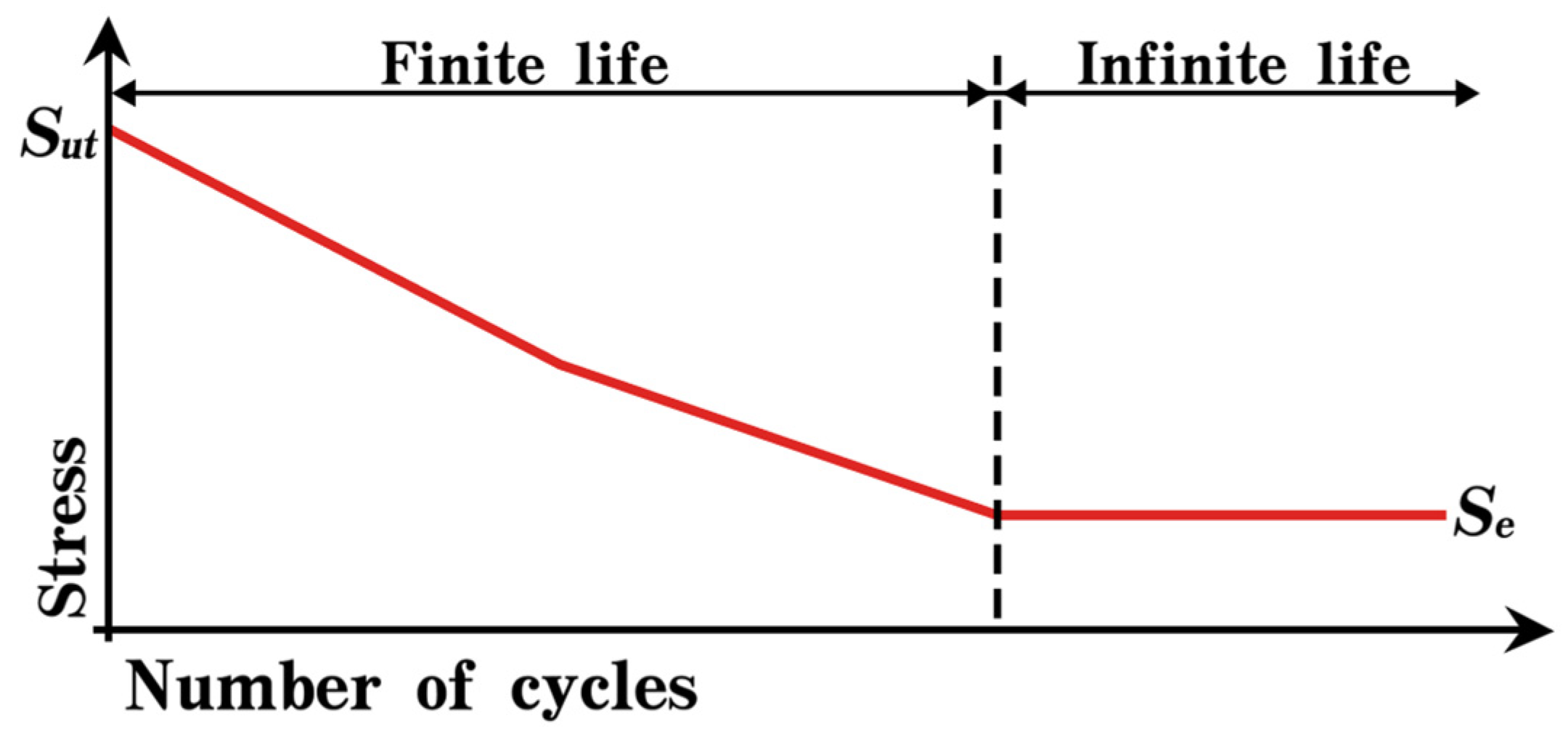
3.5. Cumulative Fatigue Damage of the Drill String Without Considering Initial Cracks
3.6. Crack Propagation Model of Drill Strings with Initial Micro-Cracks
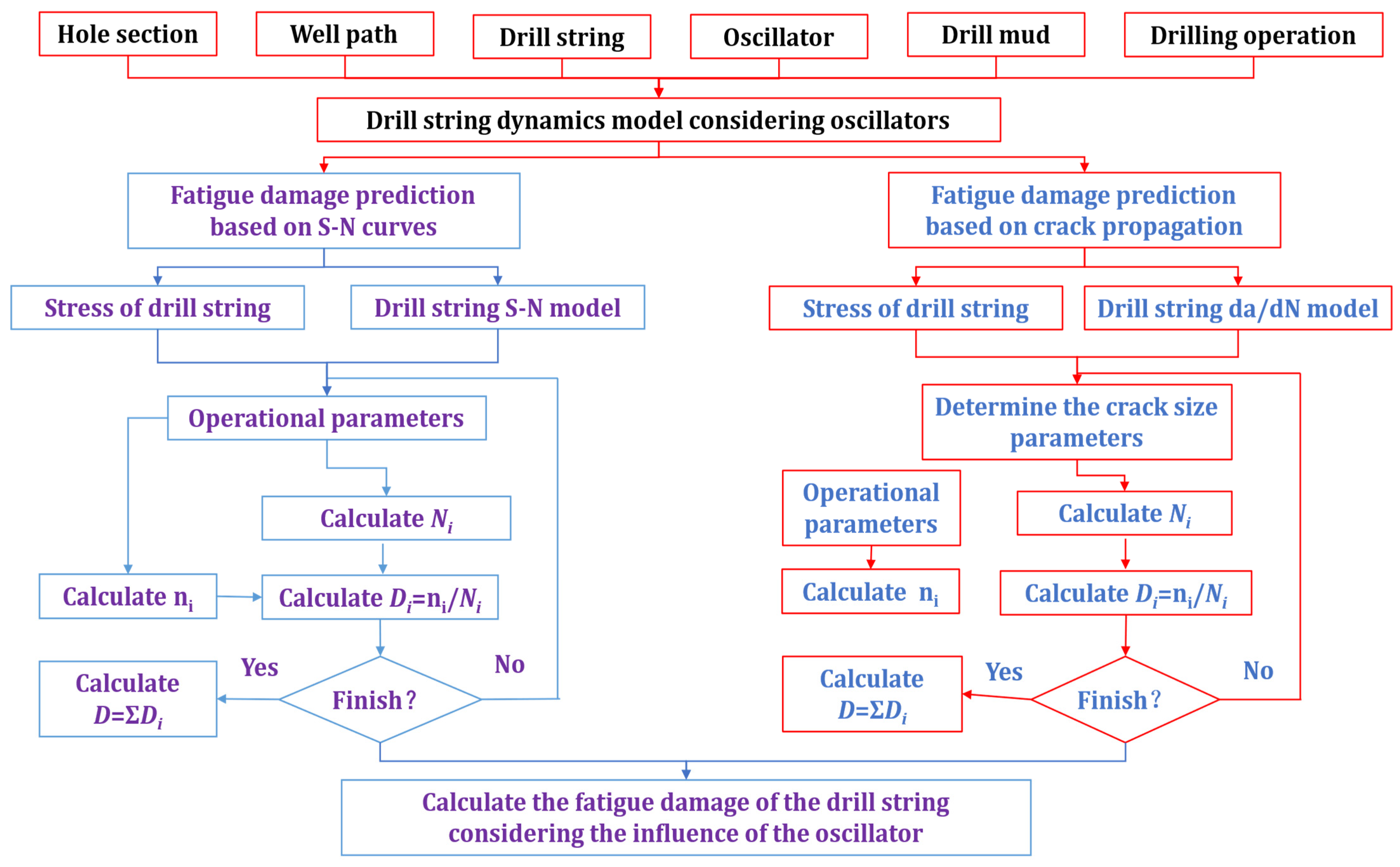
3.7. Computational Procedure for Drill String Fatigue Damage
4. Analysis of Vibration Propagation in Drill String and Its Impact on Fatigue Damage
4.1. Model Basic Parameters
- -
- Oscillator #1: excitation amplitude of 50 kN, excitation frequency of 10 Hz, installed 300 m away from the bit.
- -
- Oscillator #2: excitation amplitude of 50 kN, excitation frequency of 10 Hz, installed 800 m away from the bit.
4.2. Case with Only One Oscillator in Operation
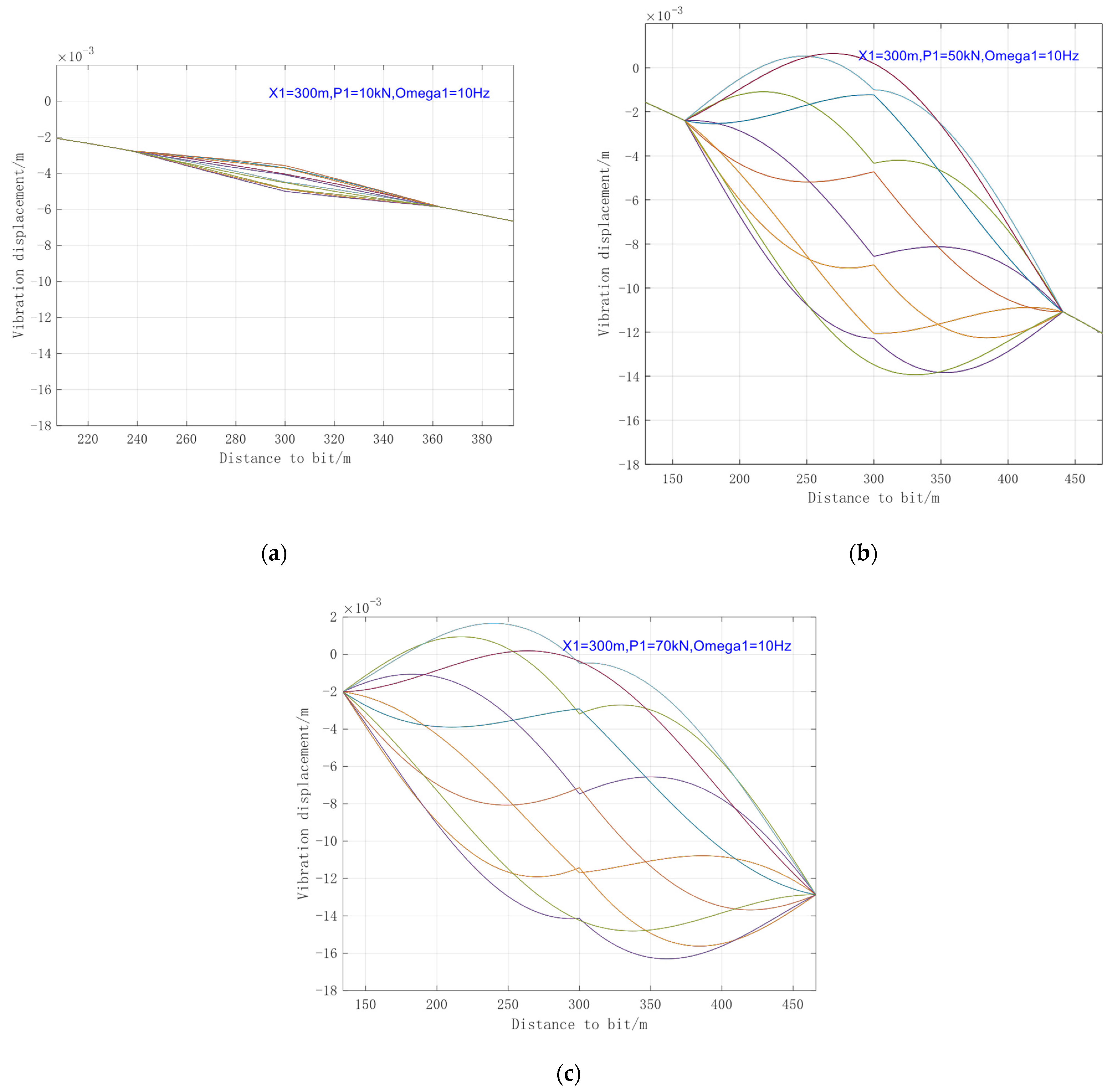
4.2.1. Influence of Excitation Amplitude
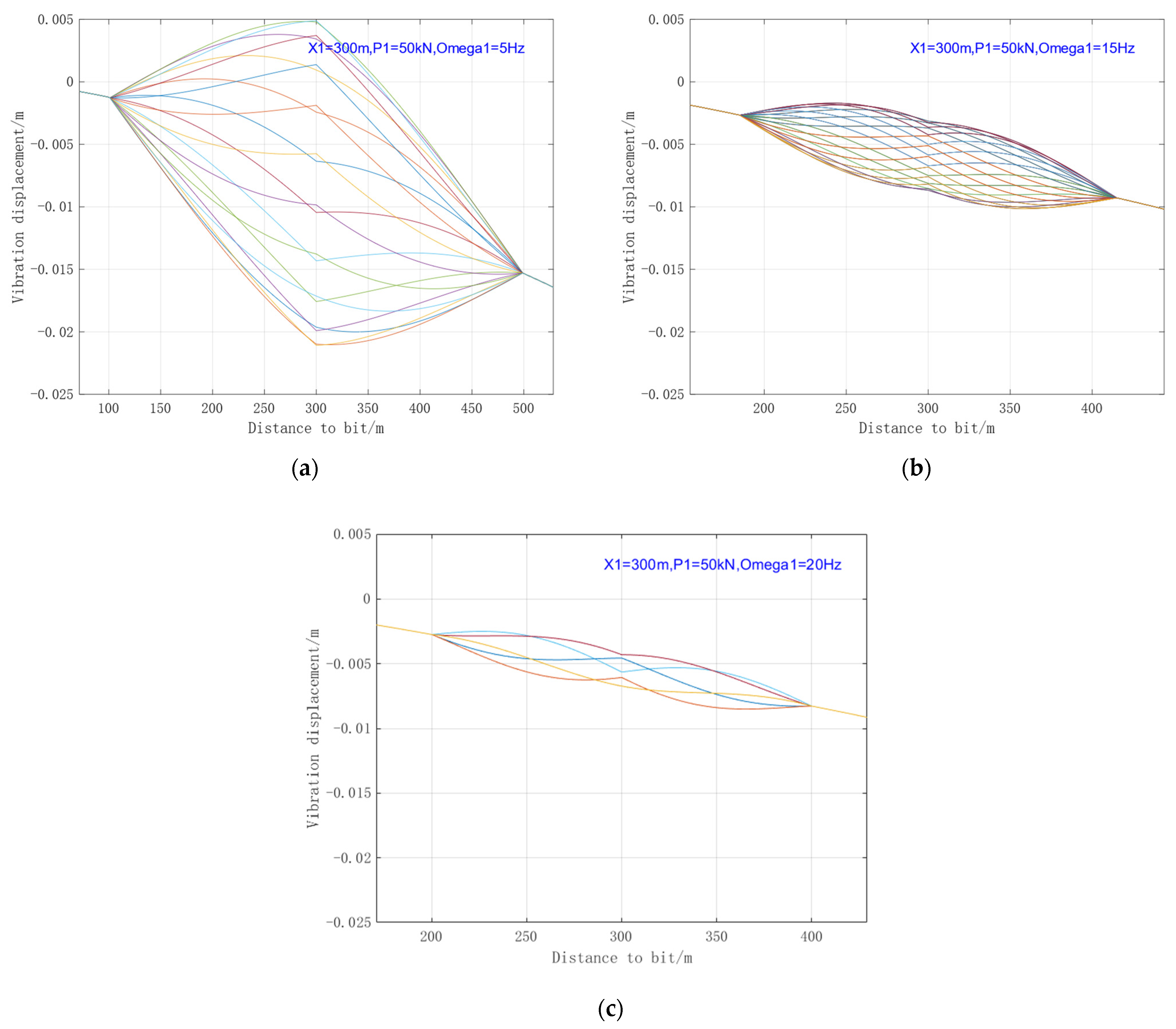
4.2.2. Influence of Excitation Frequency
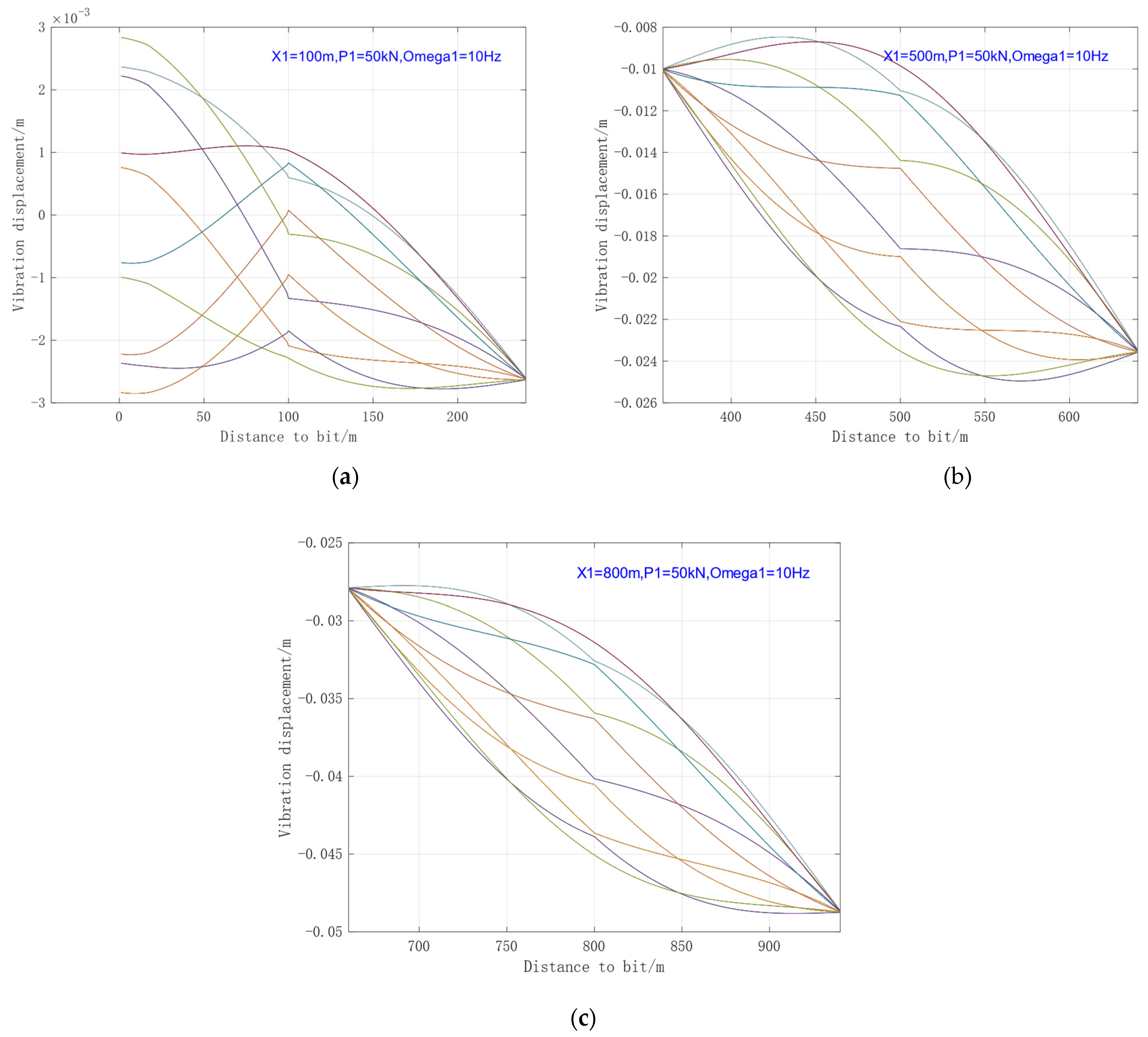
4.2.3. Influence of Installation Position
4.3. Operation with Both Oscillator #1 and #2 Active
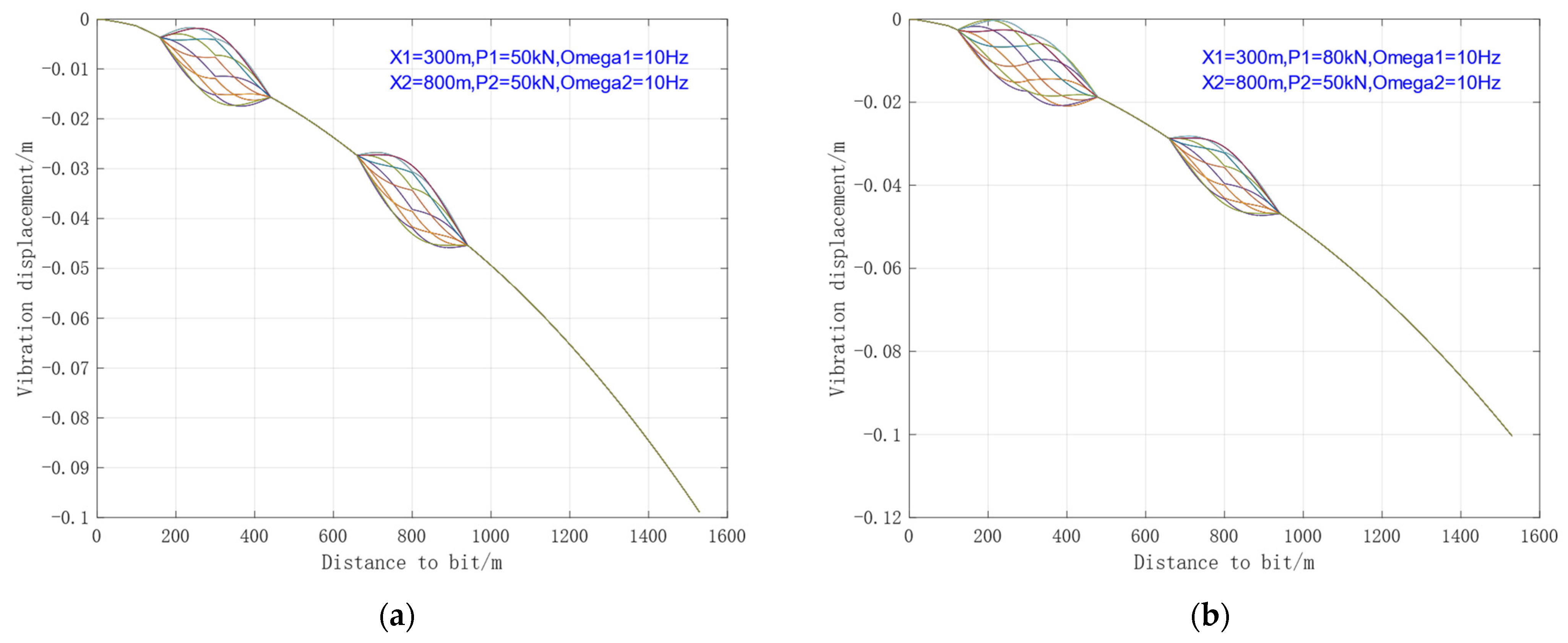
4.3.1. Scenario Without Mutual Interference Between Oscillators
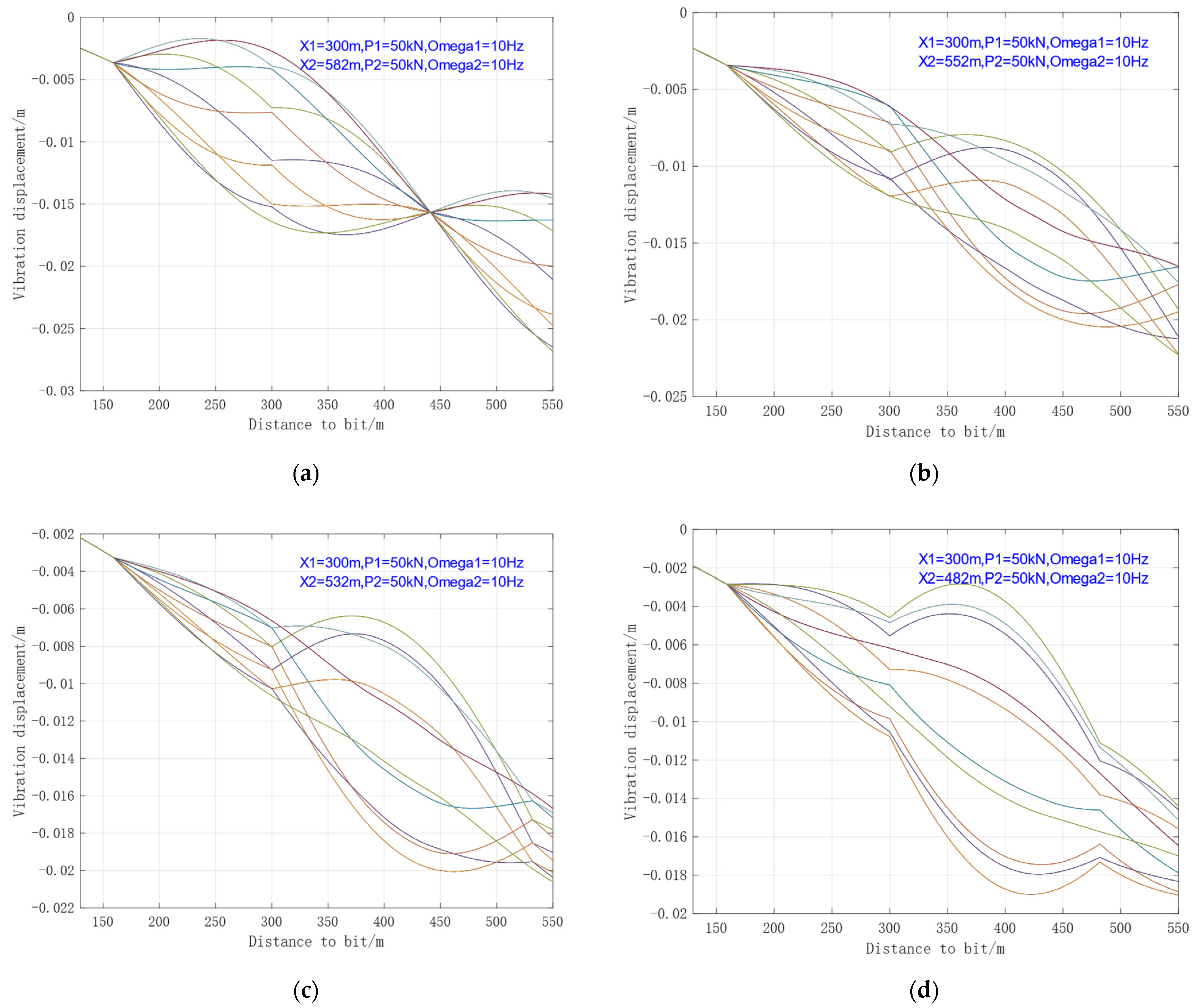
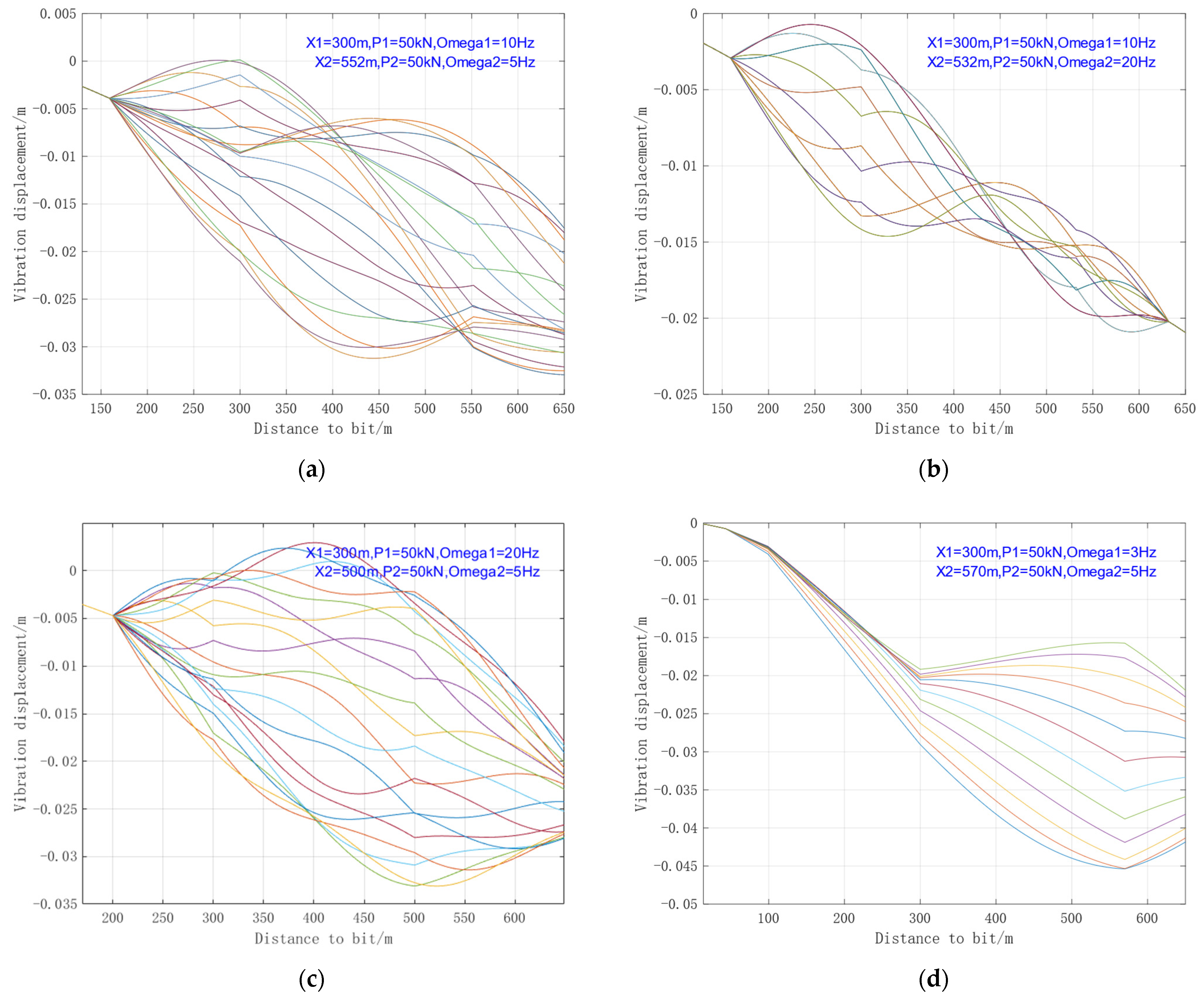
4.3.2. Scenario with Overlapping Vibration Ranges Between Oscillators
- (1)
- Same Excitation Frequencies of the Two Oscillators
- (2)
- Different Excitation Frequencies of the Two Oscillators
4.4. Influence of Oscillator Action on the Fatigue Damage of Drill Strings
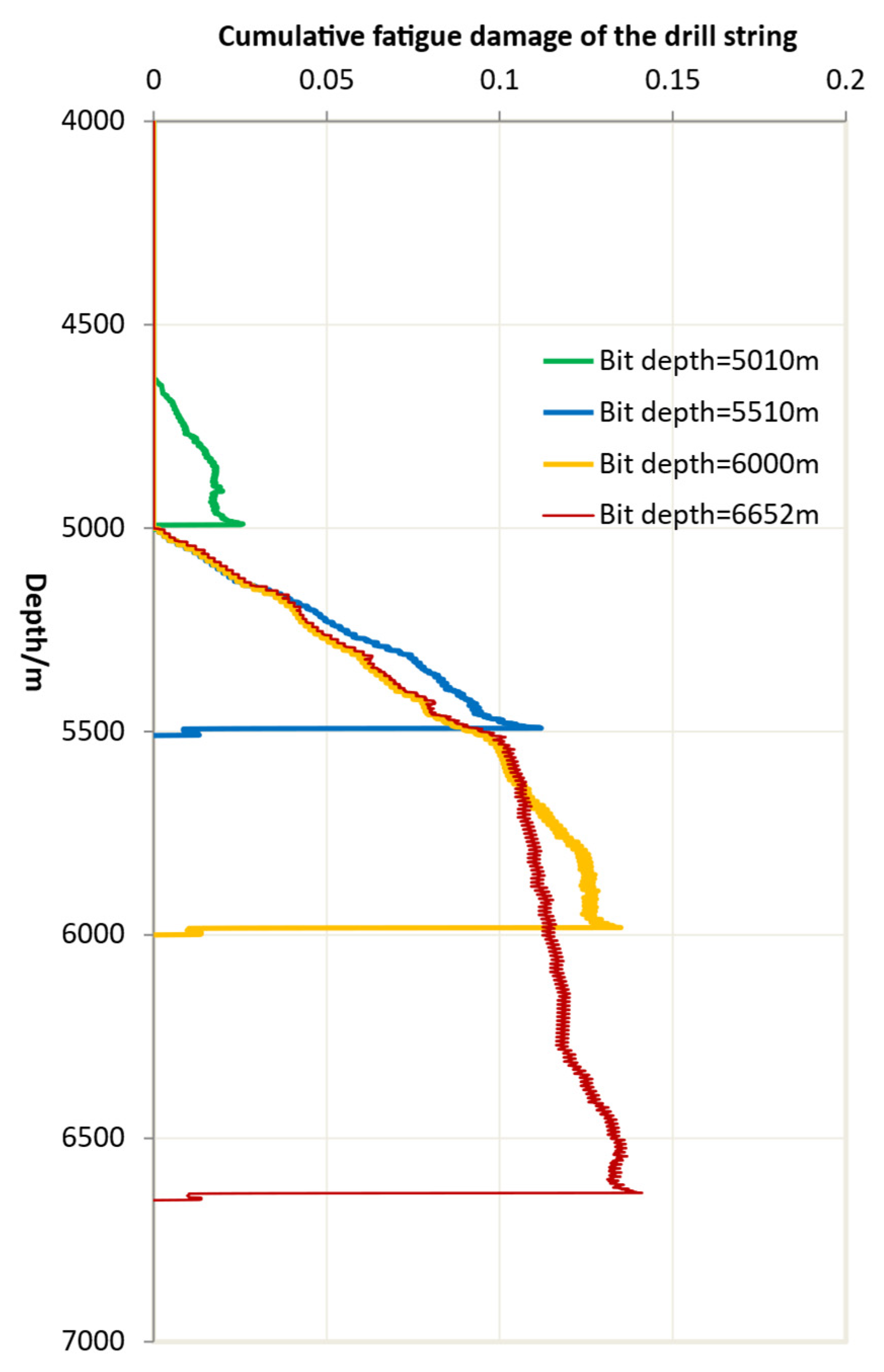
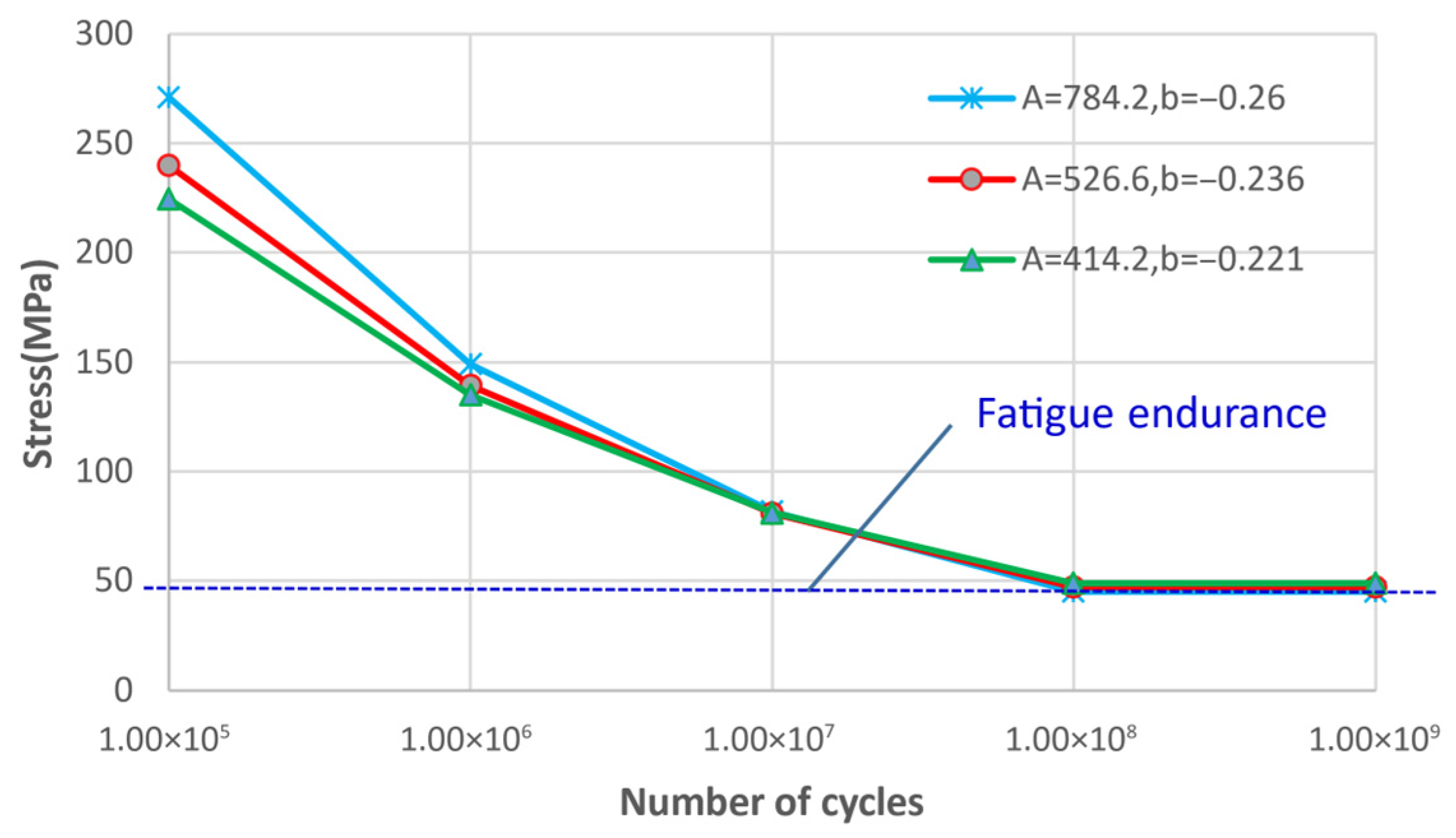
4.4.1. Fatigue Damage Analysis in No Initial Crack in the Drill String
4.4.2. When the Drill String Has an Initial Crack
5. Conclusions
- (1)
- The proposed dynamic model provides a novel methodology for investigating the transmission of vibrational stress waves and the characteristics of fatigue damage in horizontal well drilling under multi-source excitation.
- (2)
- Analysis of stress wave transmission in the drill string reveals that a larger excitation amplitude results in a greater range of vibration influence, while an increase in excitation frequency causes the vibration transmission range to exhibit a decaying trend. Even with optimized installation positioning, the effective range of a single oscillator in long horizontal sections remains limited.
- (3)
- When multiple oscillators operate simultaneously without overlapping vibration ranges, the overall effect of multiple oscillators is reflected as the independent operational contribution of each oscillator along the drill string. Through theoretical optimization of the arrangement, maximum coverage of the horizontal section can be achieved.
- (4)
- When multiple oscillators operate with overlapping vibration ranges, under the condition of the same excitation frequency, the vibration in the overlapping segment exerts adverse effects. If the oscillators work at different frequencies, the displacement envelope of the drill string tends to be irregular.
- (5)
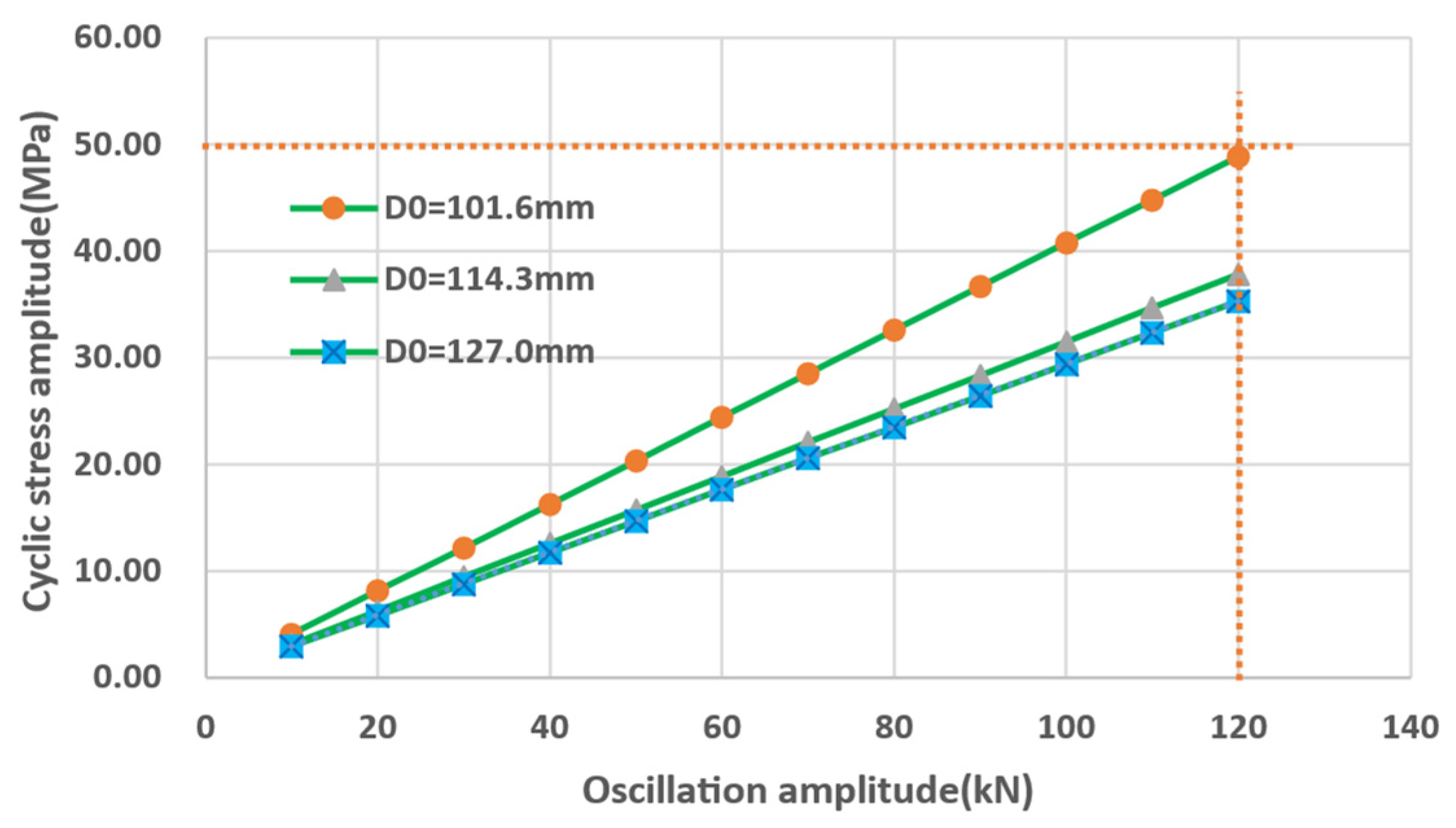
- Analysis of the influence of oscillators on the fatigue damage of drill strings without initial cracks shows that, within normal amplitude ranges (<100 kN) of oscillators generally do not contribute to fatigue damage in adjacent drill string sections. However, if the steel grade of the drill string is down-graded, and the oscillator’s amplitude is too large, it may still lead to fatigue damage to the drill string.
- (6)
- When micro-initial cracks exist in the drill string near a hydraulic oscillator, an increase in vibration amplitude leads to an exponential acceleration in crack propagation rate, significantly hastening the process of fatigue failure.
- (7)
- For drilling long horizontal sections, it is essential to optimize the installation positions, oscillation amplitudes, and frequencies of multiple oscillators based on specific field conditions. Simultaneously, timely inspection of the drill string within the oscillators’ influence range must be conducted to mitigate the risk of fatigue failure.
- (8)
- However, since drill string vibration is influenced by multiple factors—such as wellbore trajectory, hole size, BHA, oscillator type, WOB, torque, flow rate, and wellbore frictions—it is challenging to establish a universally applicable quantitative result. The results are for axial vibrations in a particular lateral section and may not directly capture coupled bending/torsion effects. In future research, the model will be applied to a broader range of field wells to statistically derive generally applicable operational guidelines, while scaled laboratory experiments on drill string vibration propagation will also be conducted for further investigation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Fw | the weight-on-bit reaction force (N) |
| the axial load (N) | |
| the normal contact force exerted by the borehole wall (N) | |
| the pipe friction force (N) | |
| the viscous fluid force generated by the drilling fluid (N) | |
| the oscillator excitation force (N) | |
| W | the weight of drill string (N) |
| the mass of the drill string (kg) | |
| the buoyancy factor (dimensionless) | |
| the maximum excitation-force amplitude (N) | |
| the excitation-force amplitude (N) | |
| the circular excitation frequency (rad/s) | |
| the structural damping coefficient | |
| the stiffness coefficient | |
| the axial displacement of the drill string (m) | |
| M | The mass matrix |
| K | the stiffness matrix |
| C | the damping matrix |
| Q | the load vector |
| Cs | the structural damping matrix |
| Cm | the drilling fluid damping matrix |
| Cf | the dry-friction damping matrix |
| v | the structural nodal displacement vector |
| the inclination of well path (rad) | |
| the dynamic friction coefficient (dimensionless) | |
| the circular frequency (rad/s) | |
| U | the vibration amplitude (m) |
| x | the position of axial vibration (m) |
| the equivalent viscous damping coefficient | |
| φ | the corresponding vibration phase (rad) |
| the ROP (m/h) | |
| μ | the friction coefficient |
| E | the elastic modulus (Pa) |
| the density of drill string (kg/m3) | |
| f(t) | The distributed forces acting on the drill string (N) |
| L | the influence length of the oscillator along the drill string (m) |
| Umax | the maximum axial vibration amplitude (m) |
| C0 | the propagation velocity of the excitation wave in the drill string (m/s) |
| Umax1 | the axial vibration amplitudes at the installation positions of the oscillator one (m) |
| Umax2 | the axial vibration amplitudes at the installation positions of the oscillator two (m) |
| U1 | the vibration amplitudes induced by the t the oscillator one (m) |
| U2 | the vibration amplitudes induced by the t the oscillator two (m) |
| ω1 | the excitation frequencies of the oscillator one (rad) |
| ω2 | the excitation frequencies of the oscillator two (rad) |
| X1 | the distances from the oscillator one to bit (m) |
| X2 | the distances from the oscillator two to bit (m) |
| L1 | the influence ranges of the oscillator one (m) |
| L2 | the influence ranges of the oscillator two (m) |
| β | the Newmark integration parameter one |
| γ | the Newmark integration parameter two |
| Δt | the time step |
| S | the cyclic stress amplitude |
| N | the corresponding number of cycles to failure |
| A | the material-dependent constant one |
| b | the material-dependent constant two |
| a | the crack depth (m) |
| the material constant one obtained from fatigue tests | |
| m | the material constant two obtained from fatigue tests |
| the stress-intensity-factor range ) | |
| the crack geometry factor | |
| the stress range between the maximum and minimum cyclic stresses (MPa) | |
| the crack semi-length (m) | |
| the initial crack (m) | |
| the critical crack (m) | |
| D0 | the average drill string diameter (m) |
References
- Jiang, Z.; Sun, G.; Chen, S.; Li, B.; Dong, H. Key drilling technologies for horizontal wells with ultra-long horizontal sections in Nanchuan shale gas field. Pet. Drill. Tech. 2022, 50, 20–26. [Google Scholar] [CrossRef]
- Fu, J.; Li, G.; Shi, H.; Tian, S.; Wang, D.; Zhang, Y. Research progress of the downhole vibration antifriction technology. China Pet. Mach. 2012, 40, 6–10+45. [Google Scholar]
- Chang, W.; Yi, X.; Wan, J.; Wei, S.; Jiang, S. Application of mechanical vibration drag reduction technology in slide drilling. Mech. Eng. 2015, 3, 146–148. [Google Scholar]
- NOV. Agitator Systems Handbook; NOV Wellbore Technologies: Houston, TX, USA, 2016. [Google Scholar]
- Altamimi, I.M.; Mokrani, S.; Zulkaf, A.H. Axial oscillation tool significantly mitigates the vibration level and enhances drilling performance in conjunction with standard RSS systems. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 1–10 November 2015. [Google Scholar] [CrossRef]
- Pohlman, R.; Lehfeldt, E. Influence of ultrasonic vibration on metallic friction. Ultrasonics 1966, 4, 178–185. [Google Scholar] [CrossRef]
- Newman, K.R.; Burnett, T.G.; Pursell, J.C.; Gouasmia, O. Modeling the affect of a downhole vibrator. In Proceedings of the SPE/ICoTA Coiled Tubing and Well Intervention Conference and Exhibition, The Woodlands, TX, USA, 31 March–1 April 2009. [Google Scholar] [CrossRef]
- Wicks, N.; Pabon, J.A.; Auzerais, F.M.; Kats, R.; Zheng, A.S. Modeling of axial vibrations to allow intervention in extended reach well. In Proceedings of the SPE Deepwater Drilling and Completions Conference, Galveston, TX, USA, 20–21 June 2012. [Google Scholar] [CrossRef]
- Wicks, N.; Pabon, J.A.; Zheng, A.S. Modeling and field trials of the effective tractoring force of axial. In Proceedings of the SPE Deepwater Drilling and Completions Conference, Galveston, TX, USA, 10–11 September 2014. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, P.; Wang, X.; Ma, T. Modeling friction-reducing performance of an axial oscillation tool using dynamic friction model. J. Nat. Gas Sci. Eng. 2016, 33, 397–404. [Google Scholar] [CrossRef]
- Zhang, S.; Li, N.; Xu, M.; Li, L.; Feng, Q.; Cheng, L. Selection and test of the placement position about hydraulic oscillator. Drill. Prod. Technol. 2020, 43, 20–23+6. [Google Scholar] [CrossRef]
- Shi, X.; Huang, W.; Gao, D. Influences of exeitation force forms of the hydraulie oscillator on drag reduction efficiency. China Pet. Mach. 2023, 51, 11–19. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Z.; Jiang, Z.; Xu, H.; Zhang, H.; Han, X. Development and field testing of the bionic peristaltic drilling tool. Pet. Drill. Tech. 2025, 53, 55–59. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative fatigue damage. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar] [CrossRef]
- Manson, S.S. Interfaces between fatigue creep and fracture. Int. J. Fract. 1966, 2, 327–363. [Google Scholar] [CrossRef]
- Paris, P.C.; Erdogan, F.A. Critical analysis of crack propagation laws. Trans. ASME J. Basic Eng. 1963, 85, 528–534. [Google Scholar] [CrossRef]
- Forman, R.G.; Kearney, V.E.; Engle, R.M. Numerical analysis of crack propagation in cyclic-loaded structures. J. Basic Eng. 1967, 89, 459–464. [Google Scholar] [CrossRef]
- Walker, K. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum. Eff. Environ. Complex Load Hist. Fatigue Life 1970, 1–14. [Google Scholar] [CrossRef]
- Howard, J.A.; Halbert, M.E.; Lubinski, A. Systematic Tracking of fatigue and crack growth to optimize drill string reliability. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 22–25 February 1993. [Google Scholar] [CrossRef]
- Wu, J. Drill-pipe bending and fatigue in rotary drilling of Horizontal wells. In Proceedings of the SPE Eastern Regional Meeting, Columbus, OH, USA, 23–25 October 1996. [Google Scholar] [CrossRef]
- Gao, B.; Gao, D. Analysis on Uncertainty of Drill String Lifespan. Pet. Drill. Tech. 2003, 31, 63–66. [Google Scholar]
- Lin, Y.; Luo, H.; Zou, B.; Shi, T.; Weng, X.; Li, R. Research on the failure mechanism and fatigue cycle life prediction of drillpipe. Oil Drill. Prod. Technol. 2004, 26, 19–22. [Google Scholar] [CrossRef]
- Chi, A.; Zhang, J.; Ge, W.; Guo, B. Prediction of Drillstring fatigue life under axial-torsional-combined vibration. In Proceedings of the SPE Unconventional Resources Conference/Gas Technology Symposium, Calgary, AB, Canada, 15–17 May 2006. [Google Scholar] [CrossRef]
- Ojanomare, C.; Cornetti, P.; Romagnoli, R.; Surace, C. Fatigue crack growth analysis of drill pipes during rotary drilling operations by the multiple reference state weight function approach. Eng. Fail. Anal. 2017, 74, 11–34. [Google Scholar] [CrossRef]
- Su, K.; Liu, D.; Jian, X.; Sun, Z.; Wan, L.; Zhuo, Y. Evaluation and influence factors analysis on corrosion fatigue life of the drill string. Drill. Eng. 2024, 51, 15–22. [Google Scholar] [CrossRef]
- Zhu, X.; Zeng, L.; Li, K. Drill string vibration analysis and pressurization scheme for medium shallow horizontal wells. J. Vib. Shock 2020, 39, 190–201. [Google Scholar]
- Johancsik, C.A.; Friesen, D.B.; Dawson, R. Torque and drag in directional well-prediction an measurement. J. Pet. Technol. 1984, 36, 987–992. [Google Scholar] [CrossRef]


| No | Parameters | Units | Values |
|---|---|---|---|
| 1 | Total measured depth | m | 6652 |
| 2 | Horizontal length | m | 1229 |
| 3 | Hole diameter | mm | 160 |
| 4 | Mud density | g/cm3 | 1.27 |
| 5 | Mud yield point | Pa | 5.8 |
| 6 | Mud plastic viscosity | mPa·s | 24 |
| 7 | Dynamic friction coefficient | / | 0.1 |
| 8 | Static friction coefficient | / | 0.25 |
| 9 | Element length | m | 1 |
| 10 | Time step | s | 0.01 |
| 11 | Stribeck velocity | m/s | 1.9 × 10−4 |
| 12 | Rayleigh damping coefficient αRL | / | 0.25 |
| 13 | Rayleigh damping coefficient βRL | / | 10−4 |
| 14 | Newmark-β method coefficient βNB | / | 0.25 |
| 15 | Newmark-β method coefficient γNB | / | 0.5 |
| Cases | Installation Position (to Bit) | Oscillator1 | Oscillator2 | Influence Ranges |
|---|---|---|---|---|
| 1 | 300 m, 800 m | 50 kN, 10 Hz | 50 kN, 10 Hz | 563.2 m (281.6, 281.6) |
| 2 | 300 m, 800 m | 80 kN, 10 Hz | 50 kN, 10 Hz | 633.9 m (352.3, 281.6) |
| Cases | Installation Positions (to Bit) | Amplitudes | Frequencies | Overlapping Range |
|---|---|---|---|---|
| 3 | 300 m, 582 m | 50 kN | 10 Hz | 0 m |
| 4 | 300 m, 552 m | 50 kN | 10 Hz | 30 m |
| 5 | 300 m, 532 m | 50 kN | 10 Hz | 50 m |
| 6 | 300 m, 482 m | 50 kN | 10 Hz | 100 m |
| Cases | Installation Positions (to Bit) | Amplitudes | Frequencies | Overlapping Range |
|---|---|---|---|---|
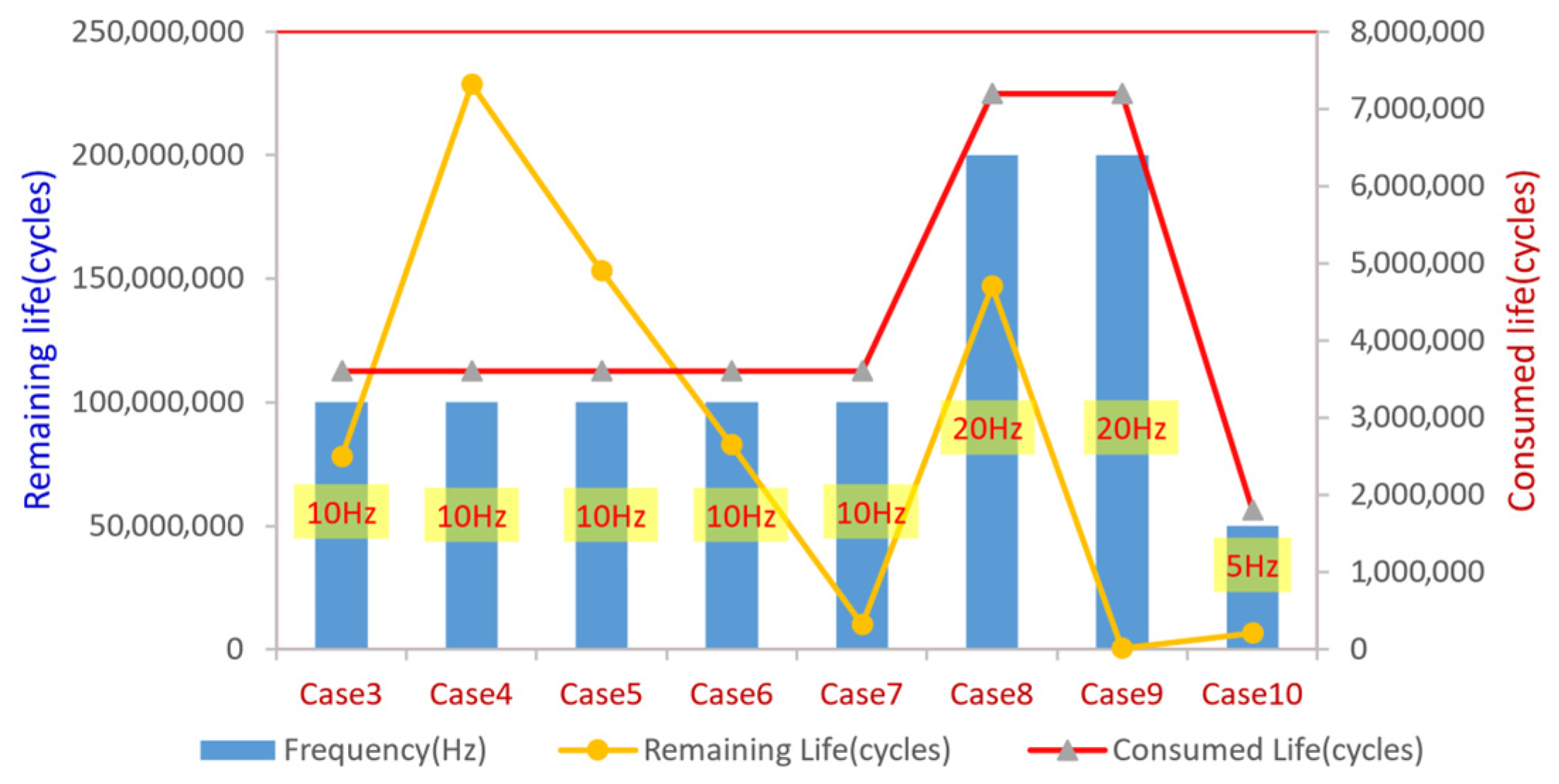
| 7 | 300 m, 552 m | 50 kN | 10 Hz, 5 Hz | 30 m |
| 8 | 300 m, 532 m | 50 kN | 10 Hz, 20 Hz | 50 m |
| 9 | 300 m, 500 m | 50 kN | 20 Hz, 5 Hz | 82 m |
| 10 | 300 m, 570 m | 50 kN | 3 Hz, 5 Hz | 12 m |
| Case3 | Case4 | Case5 | Case6 | Case7 | Case8 | Case9 | Case10 | |
|---|---|---|---|---|---|---|---|---|
| Oscillator Max Frequency (Hz) | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 | 20.00 | 20.00 | 5.00 |
| Drilling Segment Length (m) | 500.00 | 500.00 | 500.00 | 500.00 | 500.00 | 500.00 | 500.00 | 500.00 |
| ROP (m/h) | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 |
| Consumed life (cycle) | 3,600,000 | 3,600,000 | 3,600,000 | 3,600,000 | 3,600,000 | 7,200,000 | 7,200,000 | 1,800,000 |
| Remaining life (cycle) | 77,872,428 | 228,514,625 | 153,173,561 | 82,942,412 | 9,953,980 | 147,115,781 | 254,596 | 6,620,143 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Yang, Z.; Ding, J.; Liao, Y.; Xu, K.; Guan, Z.; Wang, H.; Wang, J.; Li, M.; Su, K. Investigation on Stress Propagation and Fatigue Damage Characteristics of Drill String Under Multiple Oscillation Actions. Processes 2026, 14, 43. https://doi.org/10.3390/pr14010043
Yang Z, Ding J, Liao Y, Xu K, Guan Z, Wang H, Wang J, Li M, Su K. Investigation on Stress Propagation and Fatigue Damage Characteristics of Drill String Under Multiple Oscillation Actions. Processes. 2026; 14(1):43. https://doi.org/10.3390/pr14010043
Chicago/Turabian StyleYang, Zhiguo, Jianxin Ding, Yuankai Liao, Kai Xu, Zhen Guan, Haitao Wang, Jianhua Wang, Meng Li, and Kanhua Su. 2026. "Investigation on Stress Propagation and Fatigue Damage Characteristics of Drill String Under Multiple Oscillation Actions" Processes 14, no. 1: 43. https://doi.org/10.3390/pr14010043
APA StyleYang, Z., Ding, J., Liao, Y., Xu, K., Guan, Z., Wang, H., Wang, J., Li, M., & Su, K. (2026). Investigation on Stress Propagation and Fatigue Damage Characteristics of Drill String Under Multiple Oscillation Actions. Processes, 14(1), 43. https://doi.org/10.3390/pr14010043





