Production Dynamics of Hydraulic Fractured Horizontal Wells in Shale Gas Reservoirs Based on Fractal Fracture Networks and the EDFM

Abstract

The development of shale gas reservoirs relies on complex fracture networks created via multistage hydraulic fracturing, yet most existing models still use oversimplified fracture geometries and therefore cannot fully capture the coupled effects of multiscale fracture topology on flow and production. To address this gap, in this study, we combine fractal geometry with the Embedded Discrete Fracture Model (EDFM) to analyze the production dynamics of hydraulically fractured horizontal wells in shale gas reservoirs. A tree-like fractal fracture network is first generated using a stochastic fractal growth algorithm, where the iteration number, branching number, scale factor, and deviation angle control the self-similar hierarchical structure and spatial distribution of fractures. The resulting fracture network is then embedded into an EDFM-based, fully implicit finite-volume simulator with Non-Neighboring Connections (NNCs) to represent multiscale fracture–matrix flow. A synthetic shale gas reservoir model, constructed using representative geological and engineering parameters and calibrated against field production data, is used for all numerical experiments. The results show that increasing the initial water saturation from 0.20 to 0.35 leads to a 26.4% reduction in cumulative gas production due to enhanced water trapping. Optimizing hydraulic fracture spacing to 200 m increases cumulative production by 3.71% compared with a 100 m spacing, while longer fracture half-lengths significantly improve both early-time and stabilized gas rates. Increasing the fractal iteration number from 1 to 3 yields a 36.4% increase in cumulative production and markedly enlarges the pressure disturbance region. The proposed fractal–EDFM framework provides a synthetic yet field-calibrated tool for quantifying the impact of fracture complexity and design parameters on shale gas well productivity and for guiding fracture network optimization.

1. Introduction

The rapid expansion of natural gas consumption, driven by China’s low-carbon energy transition, has intensified the need for stable and sustainable gas supplies [1]. However, conventional oil and gas reservoirs are increasingly constrained by production decline and insufficient reserve replacement, making unconventional resources—particularly shale gas—an indispensable component for ensuring energy security and long-term supply stability [2,3]. Multistage hydraulic fracturing of horizontal wells has become the core technique enabling commercial shale gas development. During this process, injected fracturing fluid creates main hydraulic fractures that interact with pre-existing natural fractures, ultimately forming irregular, multiscale fracture networks that govern the effectiveness of reservoir stimulation [4]. Accurately describing the morphology of such complex networks and predicting the resulting flow behavior remain major challenges in reservoir engineering [5].

The results of numerous studies have demonstrated that shale gas production is highly sensitive to the geometry, connectivity, and multiscale characteristics of fracture networks. Traditional bi-wing or symmetric fracture models cannot capture the branching, hierarchical growth patterns, or spatial heterogeneity observed in real hydraulic fractures, which limits their ability to represent flow pathways realistically [6]. To address these limitations, scholars have introduced fractal geometry into fracture modeling. Watanabe and Takahashi [7] first revealed the fractal nature of hydraulically induced fractures. Xu Peng [8] formulated dendritic self-similar networks to explain transport behavior in complex branching media. The results of subsequent studies by Guo Tiankui et al. [9] and Li Xianwen et al. [10] confirmed that stochastic fractal models can quantitatively characterize fracture spatial distribution and evolution, whereas Zhou et al. [11] successfully applied L-system-based fractal rules to reproduce multiscale self-similarity and bifurcation behavior. These studies collectively demonstrate that fractal theory provides a robust mathematical foundation for describing realistic fracture networks, yet its integration with advanced flow simulators remains insufficiently explored [12].

Regarding flow simulation, the Embedded Discrete Fracture Model (EDFM) has emerged as a powerful tool for representing complex fractures without requiring explicit grid refinement. Early EDFM developments established efficient treatments of fracture–matrix transmissibility relationships [13,14], followed by implementation in commercial simulators with improved accuracy and computational performance [15]. Subsequent enhancements have incorporated dual-porosity systems, multicomponent flow, and multiphysics coupling to more realistically represent fractured reservoirs [16,17,18,19]. The framework has been further strengthened through XFEM–EDFM hybridization [20], advanced intersection algorithms for corner-point grids [21,22], and extensions to stress-sensitive, non-Darcy, geothermal, and multiscale fracture systems [23,24,25,26,27,28,29]. More recently, the development of LEDFM [30] and DPEDFM [31], in addition to thermo-hydraulic coupled EDFM formulations [32], has significantly advanced the model’s applicability [33]. Nevertheless, despite these advancements, current EDFM applications rarely incorporate realistic fracture morphology derived from fractal geometry, leading to limitations in modeling the synergistic effects of complex fracture topology on flow and production dynamics [34,35].

In light of these gaps, there is a clear need for a modeling framework that integrates fractal-based fracture characterization with EDFM to simultaneously capture geometric complexity and multiscale flow behavior. Motivated by the above, we develop a fully implicit EDFM simulator in which fractal geometry is employed to construct realistic hierarchical fracture networks. The originality of this study lies in integrating a stochastic fractal fracture-network generator with a three-domain EDFM framework, enabling hierarchical fracture geometry and multiscale NNC interactions to be represented within a fully implicit simulator. This fractal–EDFM coupling, to our knowledge, has not been previously reported and provides new insight into the role of fracture complexity in controlling flow and production dynamics in shale gas reservoirs. By combining stochastic fractal structures with a finite-volume EDFM formulation, we systematically investigate the dynamic production response of fractured horizontal wells and quantitatively evaluate the influence of fracture complexity, hydraulic-fracturing parameters, and reservoir conditions on shale gas recovery.

2. Materials and Methods

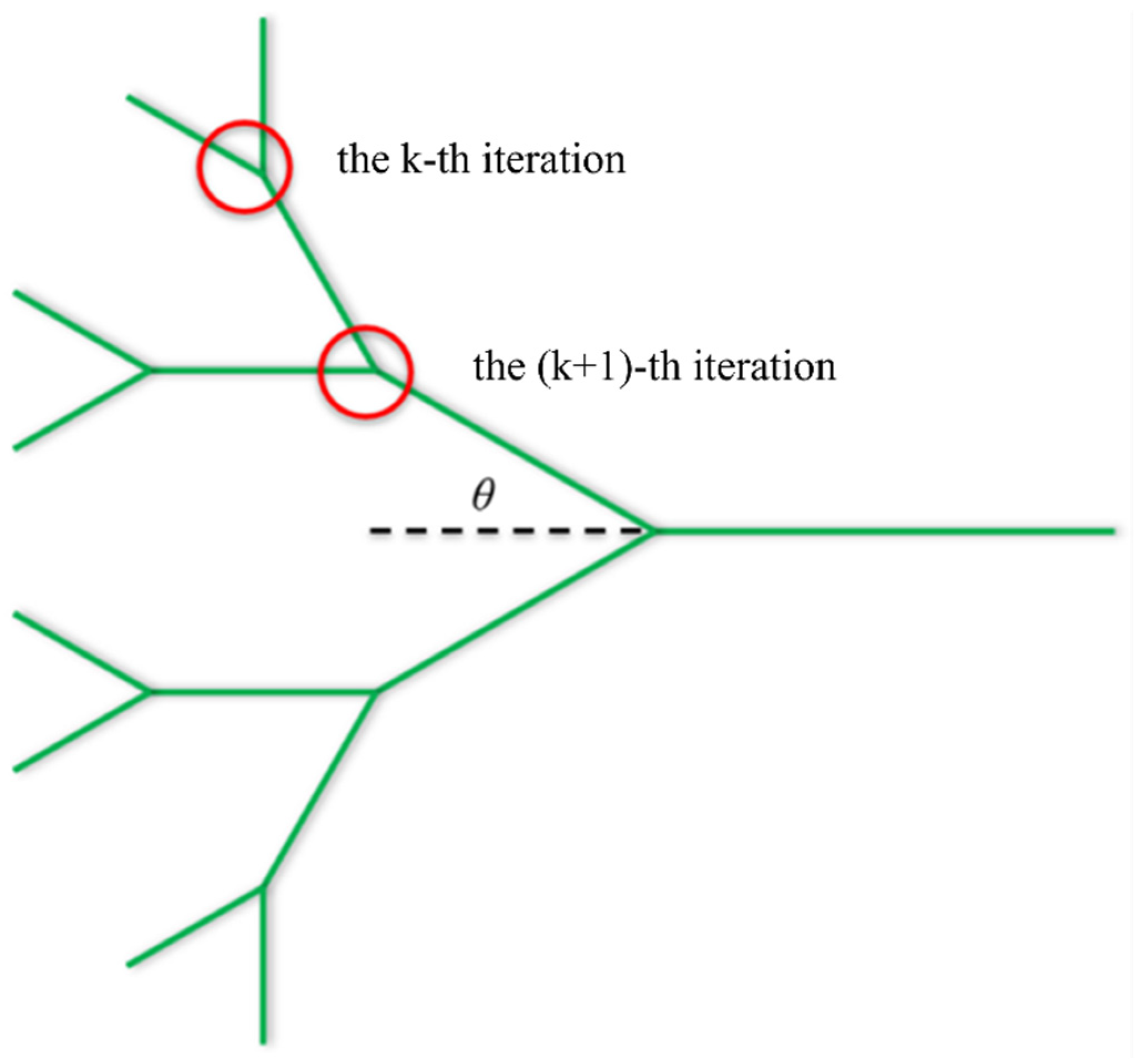
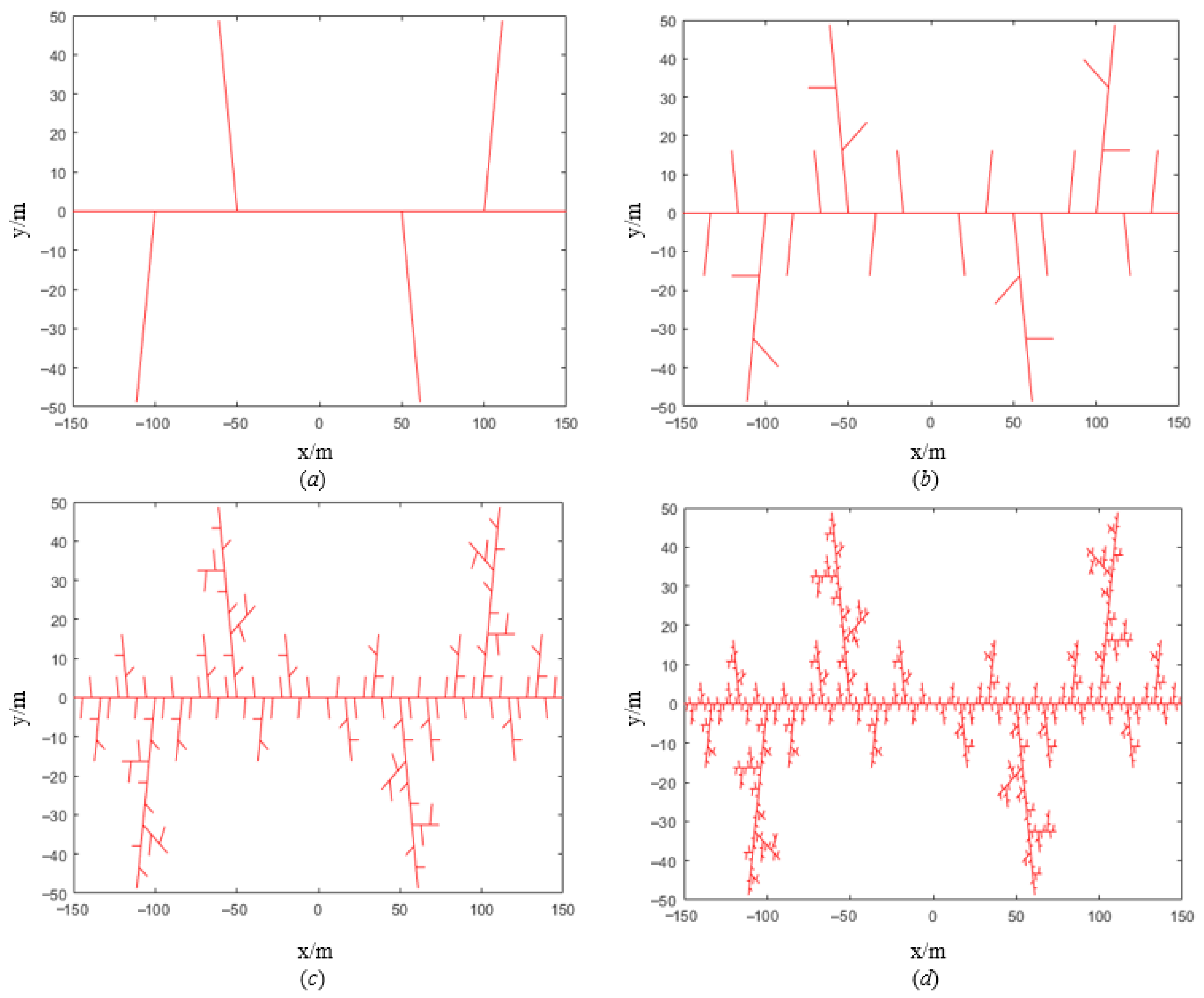
2.1. Fractal Fracture Model

In the development of unconventional hydrocarbon reservoirs, the geometry and spatial distribution of fracture systems exert a profound influence on flow behavior. Under the combined effects of tectonic stress, hydraulic fracturing operations, and lithological heterogeneity, reservoirs often exhibit fracture networks that are structurally complex and vary widely in scale. Conventional Euclidean geometry approaches have inherent limitations in characterizing such systems, as they fail to capture their irregularity and multiscale nature with sufficient accuracy. Consequently, fractal geometry theory has been introduced into the domains of rock mechanics and flow simulation. By employing a stochastic fractal growth system, dendritic fracture networks can be constructed to equivalently represent the complex fracture structures generated within individual fracturing stages [10]. As illustrated in Figure 1, the dendritic fractal network originates from an initial segment and branches progressively according to predefined angular and scaling rules, forming a self-similar fractal structure through recursive iterations [12,36].

The fractal fracture model, grounded in the principles of self-similarity and self-affinity in fractal geometry, statistically characterizes the spatial distribution of fracture systems. The model begins with an initial primary fracture and defines key parameters, including the iteration number (N), branching number (c), scaling factor (γ), and deviation angle (θ). The iteration number N represents the hierarchical depth of the fracture network; the branching number c controls the number of branches generated at each level; the scaling factor γ denotes the ratio of fracture lengths between successive levels; and the deviation angle θ determines the directional distribution of fracture propagation. Through the coordinated adjustment of these parameters, the fractal model can reproduce both the multilevel architecture and the directional complexity of fracture systems. The selected values of N, c, γ, and θ fall within the statistically reported parameter ranges for natural and hydraulic fractures in shale formations, ensuring that the generated networks are representative of documented fracture geometries.

Based on fractal geometry theory, the coordinates of the fracture endpoints, (x₁, y₁) and (x₂, y₂), are defined, together with the fracture length l and the parameters N, c, γ, and θ. A basic geometric unit comprises a primary fracture and four secondary branches, from which a dendritic fracture network is recursively generated using a branching algorithm. As illustrated in Figure 2, increasing the iteration number significantly enhances the structural complexity of the fracture network, leading to more pronounced hierarchical organization and self-similar characteristics.

2.2. Embedded Discrete Fracture Model

In shale gas reservoirs, fracture systems exhibit multiscale and irregular geometric characteristics. Conventional grid-refinement techniques incur excessive computational costs when handling such complex fracture structures, making them impractical for large-scale engineering simulations. The Embedded Discrete Fracture Model (EDFM) efficiently represents fracture geometry and flow behavior by “embedding” fractures into a structured matrix grid through a dimensional-reduction approach. Without requiring explicit meshing or grid refinement along fracture planes, EDFM enables effective coupling between fracture and matrix systems, thereby providing a powerful and computationally efficient framework for modeling unconventional reservoirs.

2.2.1. Model Construction and Basic Assumptions

To characterize the multiscale features of the fracture system, a dual-porosity model is established to separately describe the matrix and natural fracture systems, upon which discrete hydraulic fractures are superimposed. Following the commonly adopted simplifications in dual-porosity flow theory and EDFM-based multiphase simulations [13,14,15,16,17,18], the fundamental assumptions of the model are as follows:

• The reservoir temperature is constant, and the flow process is isothermal.
• The effects of CO₂ dissolution, residual trapping, and geochemical reactions within the reservoir are neglected.
• Supercritical CO₂ is treated as a gaseous component with high density and low viscosity.
• Discrete fractures possess heterogeneous properties such as aperture, length, azimuth, and effective height, exhibiting irregular spatial distribution.

Based on the dual-porosity theory, the mass transfer mechanism between the matrix and fracture systems is defined by introducing parameters such as volume fraction, porosity, and permeability to construct the component mass conservation equations. To avoid the computational overhead associated with grid refinement, discrete fractures are treated using an in-plane dimensional-reduction technique and embedded within a structured grid system. Each fracture surface is discretized into a set of grid elements, whose volumes are equivalently converted into pore volumes as follows:

$$V_{\mathrm{F}}=S_{\mathrm{seg}}{w}_{\mathrm{F}}$$

(1)

where S_seg denotes the normal surface area of the fracture grid element (m²), and w_F represents the fracture aperture (m).

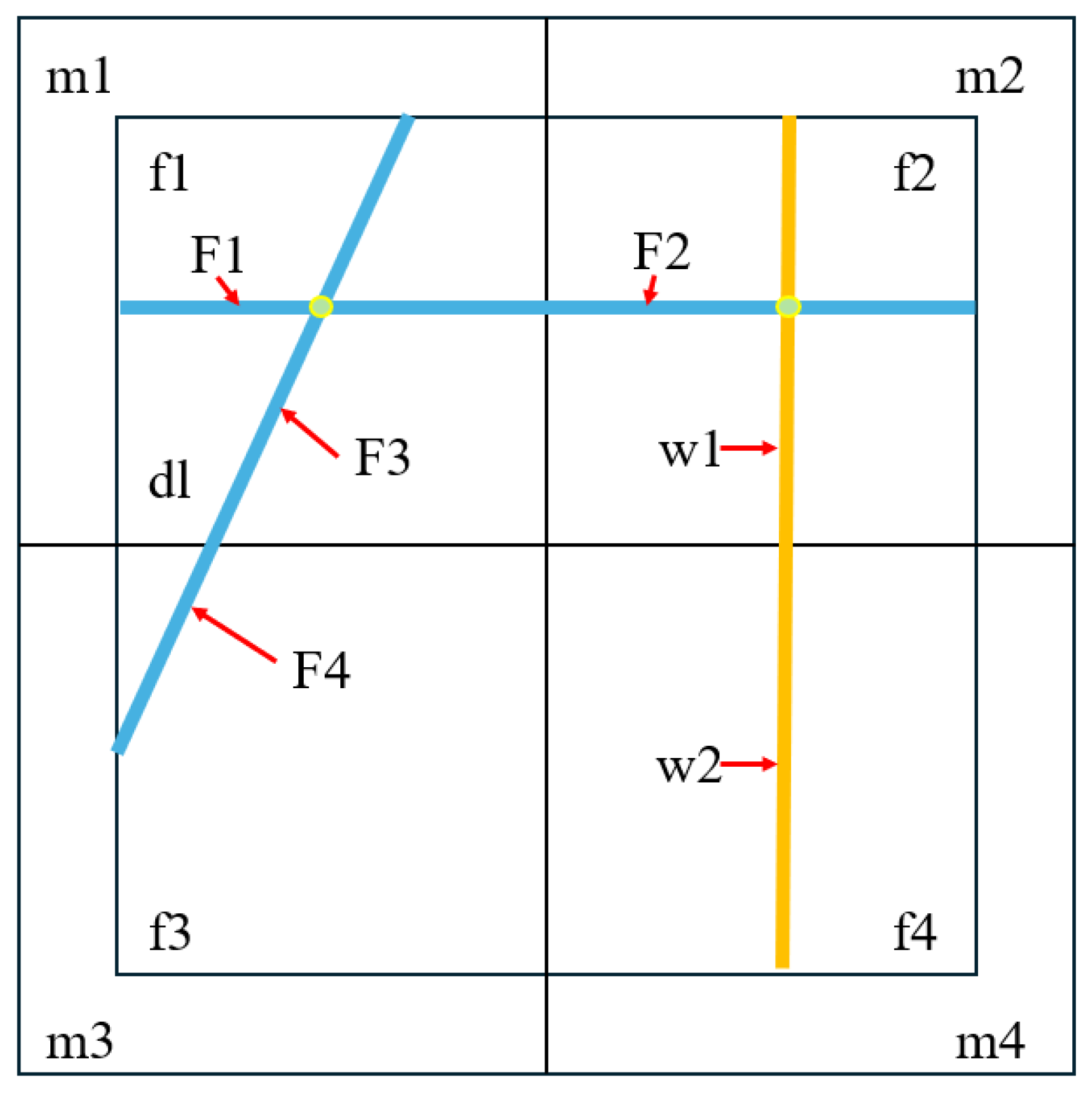
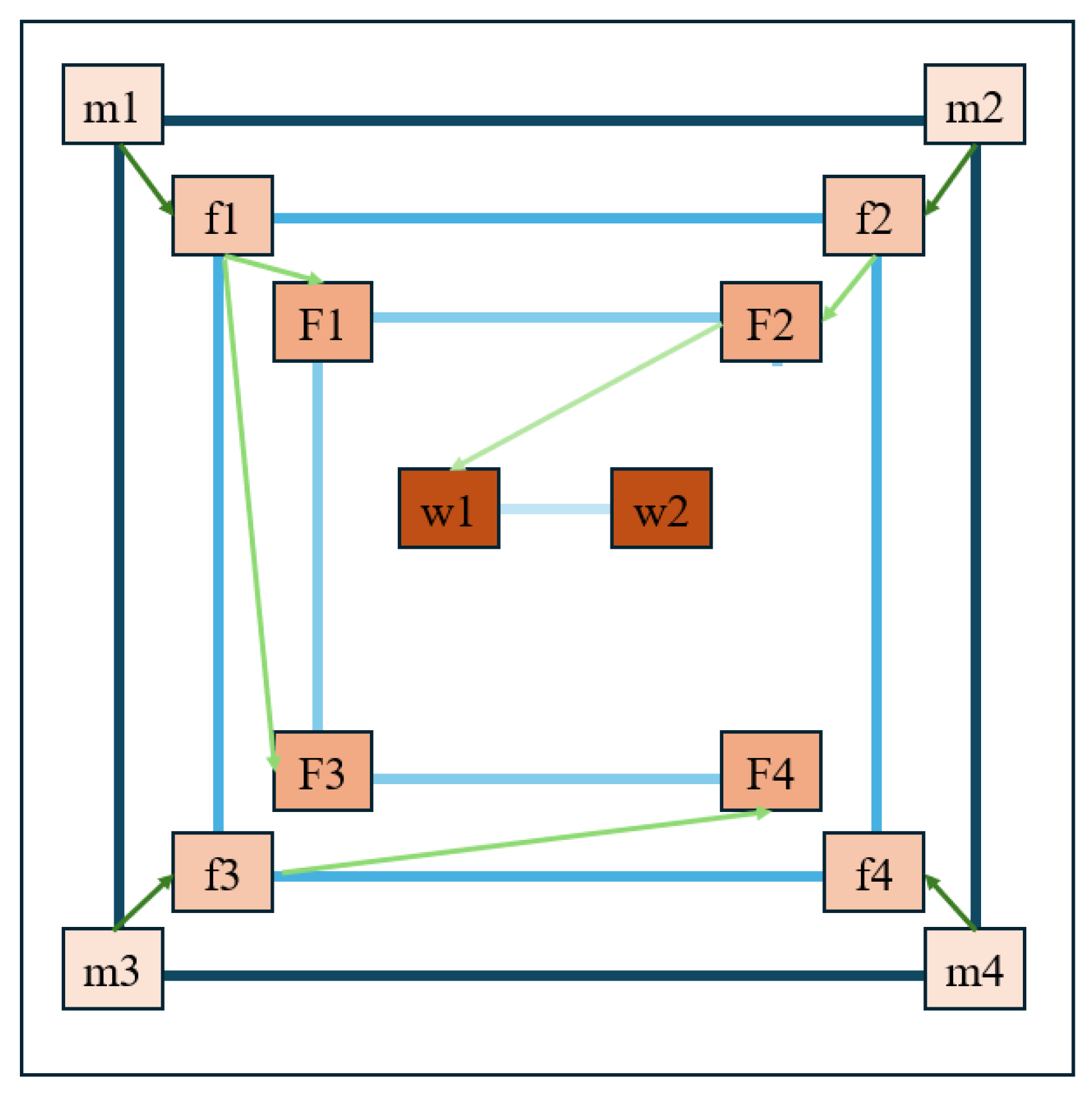
2.2.2. Treatment of Non-Neighboring Connections (NNCs)

To enable fluid transfer between fractures, between fractures and microfractures, and between fractures and wellbores, the EDFM introduces the Non-Neighboring Connection (NNC) mechanism. According to the type of connectivity, NNCs can be classified into four categories, as illustrated in Figure 3:

• Type I NNC: connections between fracture grids and intersected microfracture grids, such as those between f1 and F1, and between f3 and F4;
• Type II NNC: connections between non-adjacent fracture grids belonging to the same discrete fracture after subdivision by the structured grid, such as between F1 and F2, and between F3 and F4;
• Type III NNC: connections between intersecting discrete fractures, such as between F1 and F3;
• Type IV NNC: connections between fractures and the wellbore, such as between F2 and w1.

As illustrated in Figure 4, the coupling relationships among various types of NNCs are characterized by introducing transmissibility coefficients, which are computed in a preprocessing stage. Using these coefficients, the volumetric flow rate between any two grid cells connected by an NNC in phase l can be expressed by the following general equation:

$$q_{NNC}=T_{NNC}\Delta \Phi =G_{NNC}{f}_{\mathrm{p}}{f}_{\mathrm{s}}\Delta \Phi$$

(2)

where q_NNC denotes the fluid exchange rate between the NNC pair; T_NNC represents the transmissibility of the NNC pair; ΔΦ is the potential difference; f_p is the weakly nonlinear correction term related to pressure; and f_s is the strongly nonlinear correction term associated with saturation.

2.2.3. Fully Implicit Numerical Model

A fully implicit finite-volume scheme is adopted in this study, because it provides superior numerical stability and enables the use of larger time steps in strongly coupled gas–water flow, particularly within multiscale fracture networks wherein IMPES formulations often suffer from saturation instabilities and restrictive time-step requirements. The mathematical formulation of fluid flow used in this study is based on the standard mass conservation equation coupled with Darcy-type flux relations [37]:

$${\displaystyle \frac{\partial (\varphi {\rho }_l)}{\partial t}}+\nabla \cdot ({\rho }_l{v}_l)=q_l$$

(3)

where $\varphi$ is the porosity; l denotes the fluid phase; ${\rho }_l$ is the density of phase $l$ (kg/m³); t is the time (s); and $q_l$ is the source/sink term of phase l (kg·m⁻³·s⁻¹). Based on this formulation, the left-hand side of each grid equation represents the sum of inflow from adjacent grids, whereas the right-hand side corresponds to the accumulation of fluid mass within the grid cell. Positive flux denotes flow into the central grid cell, whereas negative flux represents outflow. Accordingly, based on the mass conservation equation and Darcy-type flux formulation discretized using the fully implicit finite-volume method [16,17], the governing flow equations for the different subsystems can be expressed as follows:

Matrix system (pores and microscale vugs):

$${\displaystyle \sum q_{\mathrm{mm},\mathrm{g}}}+{\displaystyle \sum q_{\mathrm{mf},\mathrm{g}}}={\displaystyle \frac{V_{\mathrm{b}}}{{\alpha }_{\mathrm{c}}\Delta t}}{\Delta }_t\left[{\displaystyle \frac{{\varphi }_{\mathrm{m}}}{B_{\mathrm{mg}}}}\right]$$

(4)

Microfracture system:

$${\displaystyle \sum q_{\mathrm{ff},\mathrm{g}}}+{\displaystyle \sum q_{\mathrm{fm},\mathrm{g}}}+{\displaystyle \sum q_{\mathrm{fF},\mathrm{g}}}=={\displaystyle \frac{V_{\mathrm{b}}}{{\alpha }_{\mathrm{c}}\Delta t}}{\Delta }_t\left[{\displaystyle \frac{{\varphi }_{\mathrm{f}}\left(1-s_{\mathrm{fw}}\right)}{B_{\mathrm{fg}}}}\right]$$

(5)

Discrete fracture system:

$${\displaystyle \sum q_{\mathrm{F},\mathrm{g}}}+{\displaystyle \sum q_{\mathrm{Ff},\mathrm{g}}}+{\displaystyle \sum q_{\mathrm{FF},\mathrm{g}}}+{\displaystyle \sum q_{\mathrm{Fw},\mathrm{g}}}={\displaystyle \frac{V_{\mathrm{b}}}{{\alpha }_{\mathrm{c}}\Delta t}}{\Delta }_t\left[{\displaystyle \frac{{\varphi }_{\mathrm{F}}\left(1-s_{\mathrm{Fw}}\right)}{B_{\mathrm{Fg}}}}\right]$$

(6)

where V_b is the grid volume (m³); α_c is the volumetric conversion factor, taken as 1 under the metric system; Δt is the time step (days); Σq_mm is the volumetric flow exchange between a matrix grid cell and its adjacent matrix cells during Δt (m³/d); Σq_mf is the volumetric flow exchange between a matrix grid cell and adjacent microfracture grids during Δt (m³/d); Σq_ff is the flow exchange between adjacent microfracture grids during Δt (m³/d); Σq_fF is the flow exchange between microfracture grids and adjacent discrete fracture grids during Δt (m³/d); Σq_fm is the flow exchange between microfracture grids and adjacent matrix grids during Δt (m³/d); Σq_F is the flow exchange between adjacent grids within the same discrete fracture during Δt (m³/d); Σq_Ff is the flow exchange between discrete fracture grids and adjacent microfracture grids during Δt (m³/d); Σq_FF is the flow exchange between grids of intersecting discrete fractures during Δt (m³/d); and Σq_Fw is the flow exchange between discrete fracture grids and adjacent well grids during Δt (m³/d), where negative values indicate production wells. The fully implicit finite-volume equations were solved using a Newton–Raphson iteration scheme with adaptive time-stepping. A backward Euler time discretization was applied, and the linearized systems were solved using a GMRES iterative solver with ILU preconditioning. Convergence was achieved when both residual and variable updates were below 10⁻⁵. All simulations were performed using an in-house EDFM compositional simulator developed in C++ under a 64-bit Windows environment [38].

3. Results and Discussion

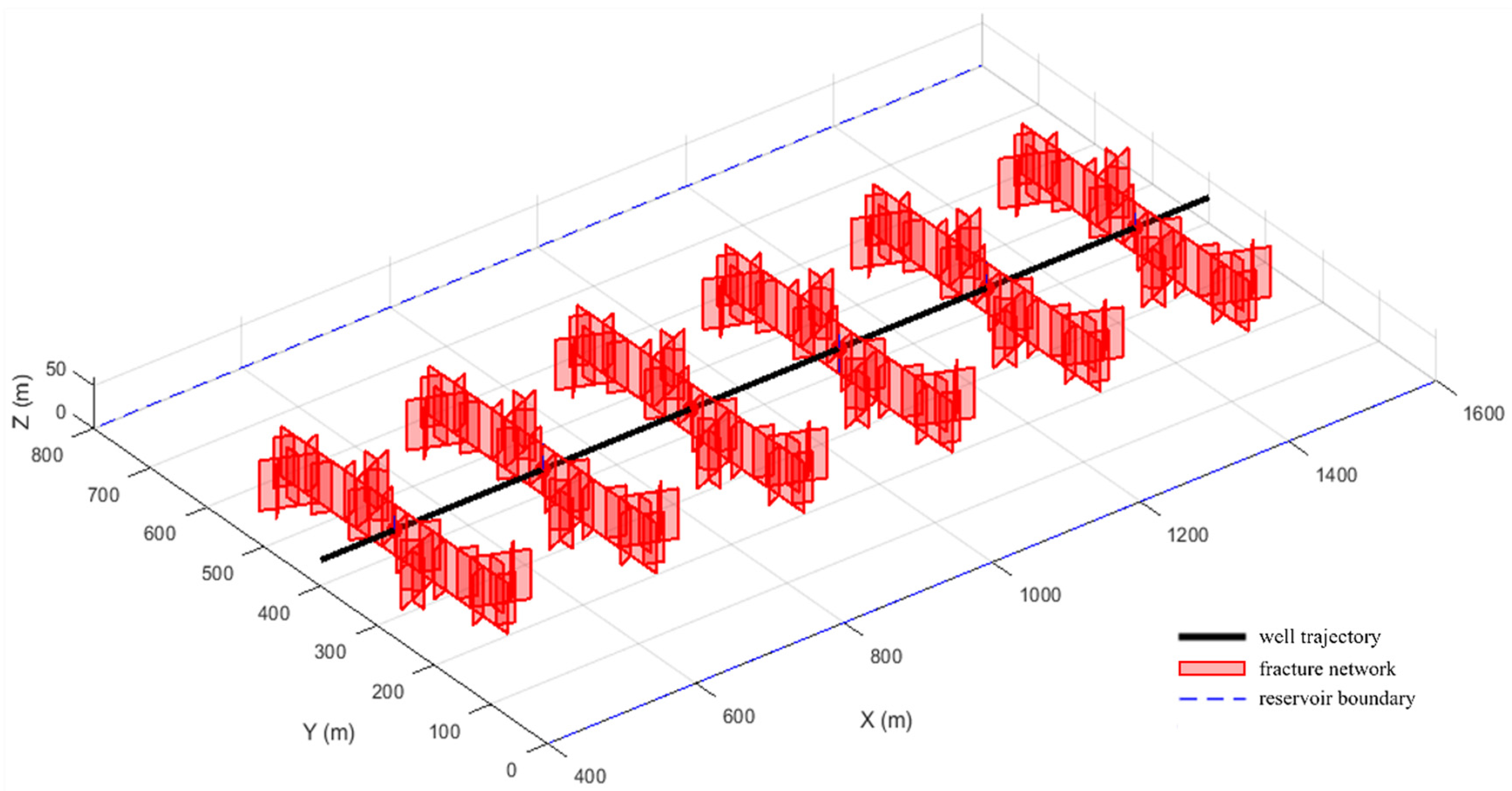
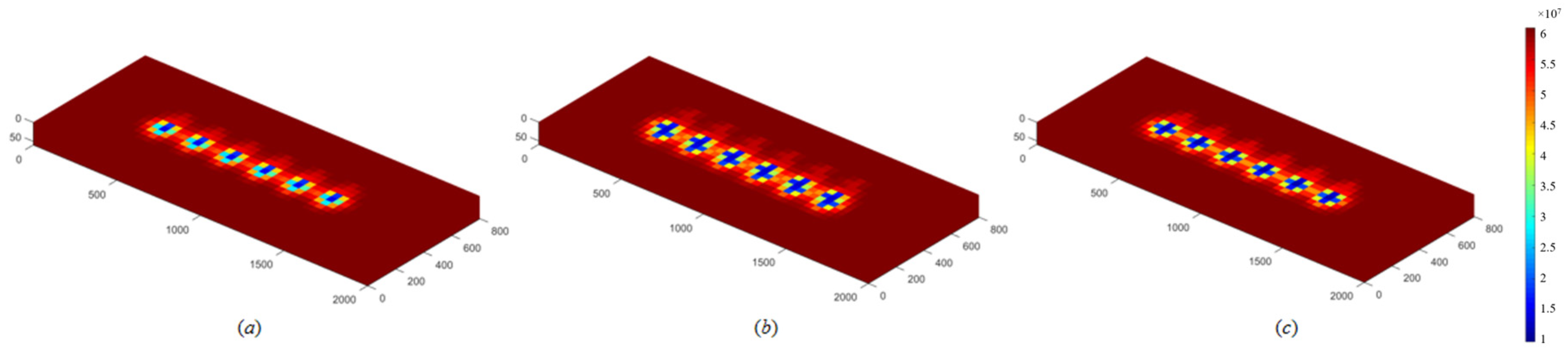
3.1. Fractured Horizontal Well Model with a Fractal Fracture Network

To simulate the production dynamics of the target shale reservoir, a numerical model incorporating multistage hydraulic fracturing effects was established. The numerical model is established by embedding the fractal fracture network introduced in Section 2.1 into the EDFM-based fully implicit simulator described in Section 2.2, followed by defining the reservoir geometry, fracture stages, grid discretization, and fluid and rock properties. The reservoir domain is defined with dimensions of 2000 m × 1000 m × 60 m, and the horizontal well section extends 1800 m in length. Six fracturing stages are evenly spaced along the wellbore, with the geometry and parameter configuration of each fracture stage illustrated in Figure 5. The key model parameters, which are obtained from geological and engineering data of the target shale reservoir together with representative values reported in previous shale gas studies [1,2,3,4,5], are summarized in

Table 1. Physical and computational parameters of the fractured horizontal well model with a fractal fracture network.

Parameter	Value	Parameter	Value
Initial reservoir pressure, pi, MPa	60	Formation temperature, T, K	353.15
Reservoir thickness, h, m	90	Grid step size, x × y × z, m	40 × 40 × 3
Matrix permeability, kom, mD	1.6 × 10−4	Initial water saturation, Sf0	0.35
Matrix porosity, ϕom	0.07	Wellbore radius, rw, m	0.1
Iteration number, N	3	Fractal branch number, c	3
Scale factor, γ	0.6	Deviation angle, θ	30
Hydraulic fracture permeability, kF, mD	200	Hydraulic fracture aperture, wF, m	0.002
Microfracture permeability, kf, mD	0.001	Well constraint, BHP, MPa	35

. The component properties adopted in the gas compositional model are listed in

Table 2. Gas composition of the shale reservoir.

Component	Content
Methane (CH4)	84.4%
Nitrogen (N2)	2%
Carbon dioxide (CO2)	10%
Light hydrocarbons (C2–C5)	3%
Intermediate hydrocarbons (C6–C10)	0.5%
Heavy hydrocarbons (C11+)	0.1%

. It should be noted that the numerical model constructed in this study is synthetic, with all reservoir and fracture parameters chosen from representative ranges reported in previous shale gas studies rather than from a specific field well. This synthetic setup ensures full control of fracture geometry for fractal–EDFM coupling and allows the results to be interpreted as methodological insights rather than field-specific predictions.

The numerical results were verified through two mechanisms. First, we determined whether the simulated pressure and production trends match the expected behavior of fractured horizontal wells. Second, we confirmed that the model responses are consistent with published EDFM benchmark cases [13,14,15,16,17,18].

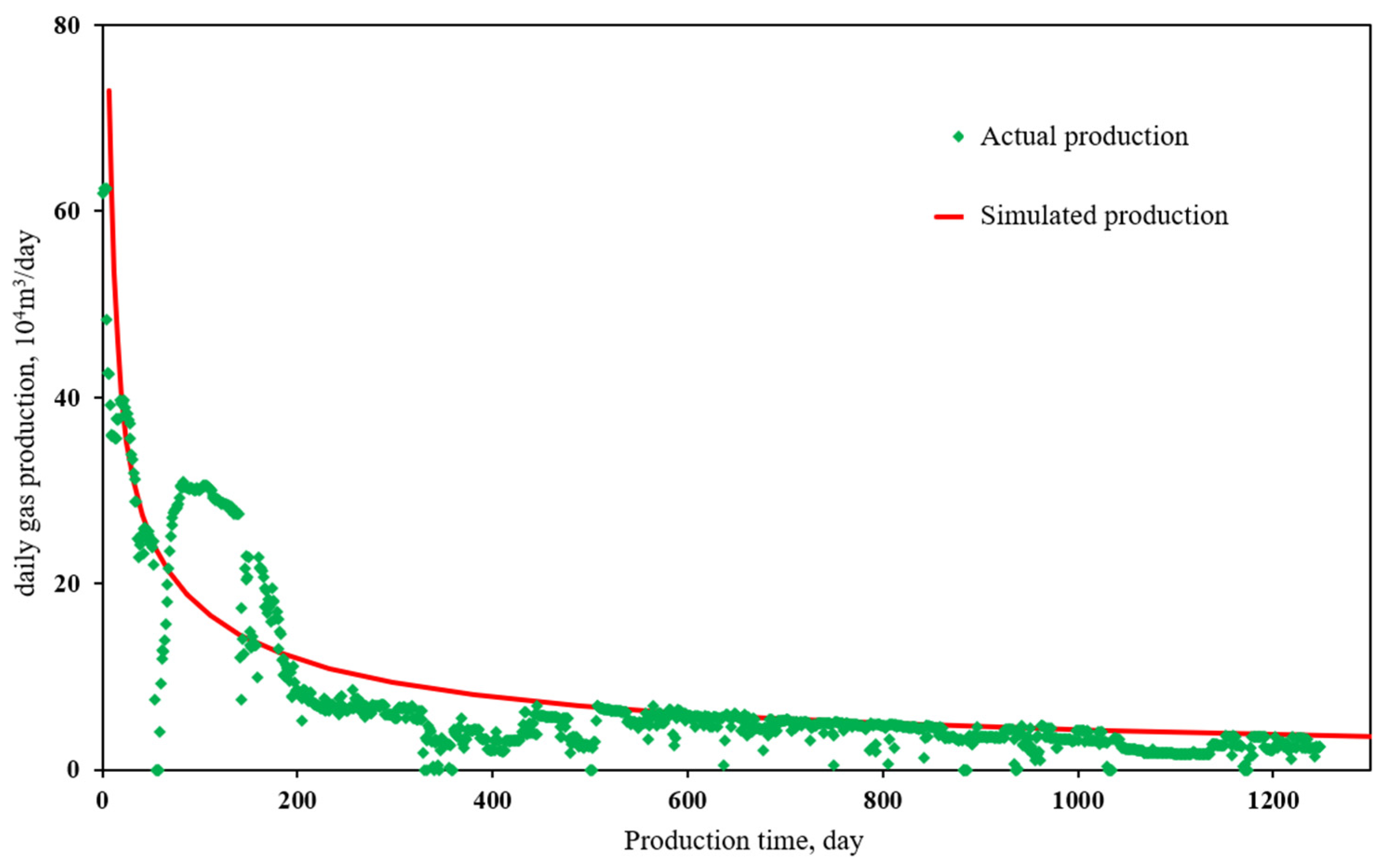
3.2. Model Verification

To evaluate the reliability and applicability of the proposed fractal–EDFM, a production history-matching study was conducted using field data from a shale gas horizontal well. Based on the reservoir and fracturing parameters listed in Table 1, the numerical model was calibrated within the single-well control region to reproduce the long-term production behavior. A comparison between the simulated daily gas rate and the actual production history is presented in Figure 6. The fractal–EDFM successfully captures the key characteristics of shale gas well performance, including the sharp early-time decline caused by near-fracture pressure depletion, the mid-term transition to a stabilized decline trend, and the low-rate production behavior observed at late times.

The good agreement between model results and field data demonstrates that the proposed fractal–EDFM can accurately describe gas–water two-phase flow in complex multiscale fracture networks. This verification confirms the model’s capability for analyzing production dynamics and supports its application in subsequent sensitivity analyses and optimization studies.

3.3. Production Dynamics Analysis of Fractured Horizontal Wells

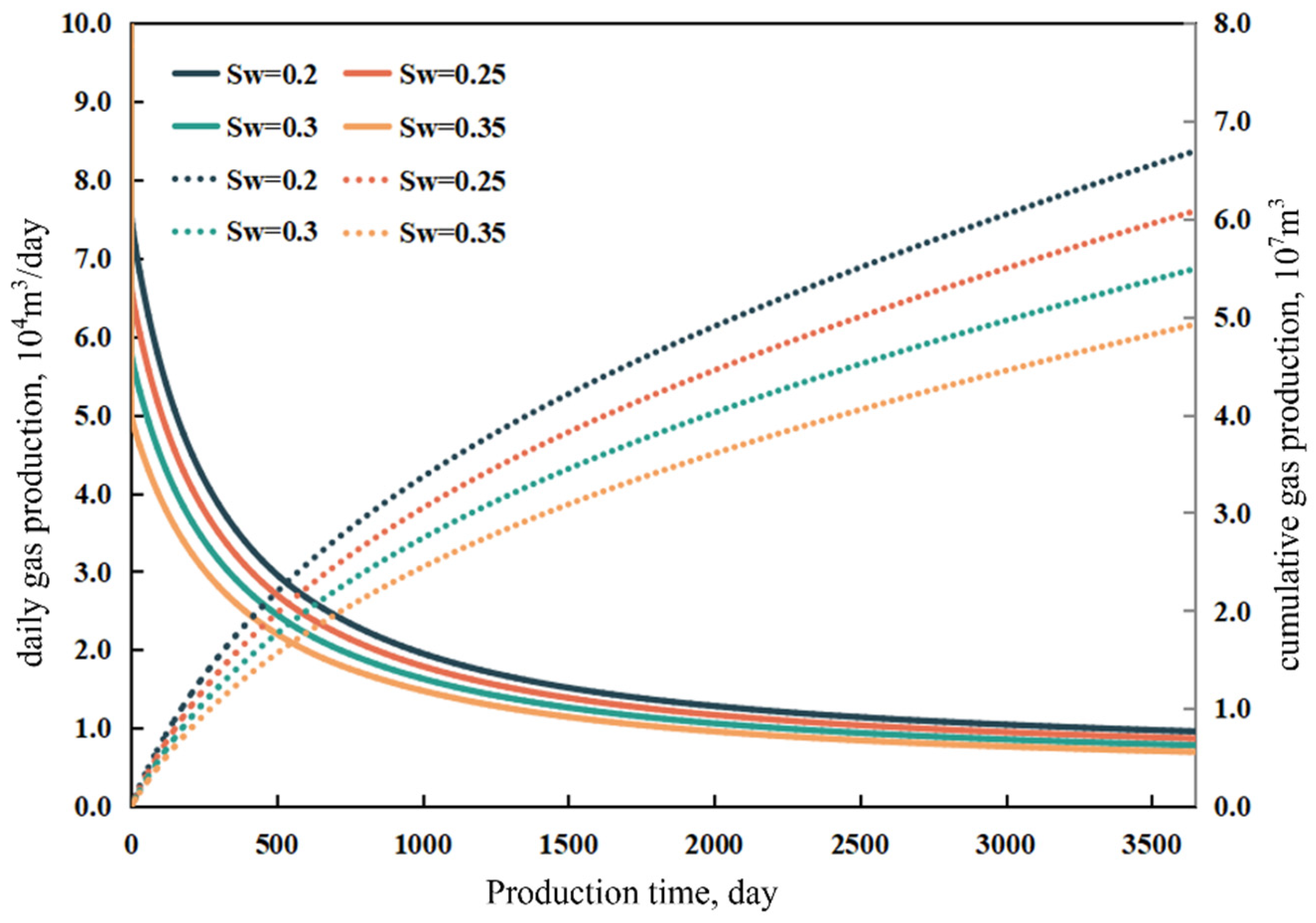
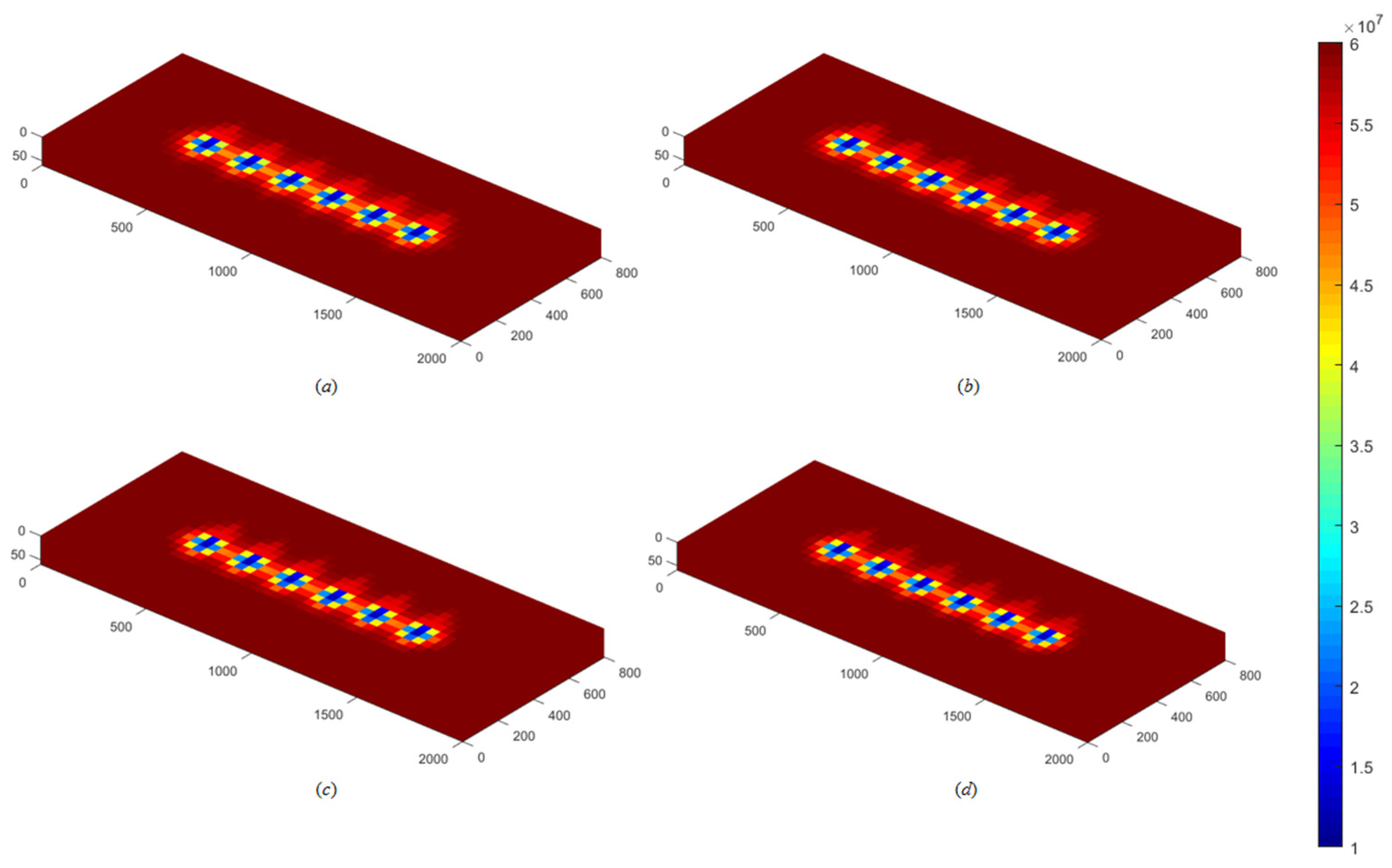
3.3.1. Influence of Initial Water Saturation

The initial water saturation (Sw) of the reservoir exerts significant control on the productivity of fractured horizontal wells. The selected range of Sw (0.20–0.35) reflects typical irreducible and clay-bound water saturations reported for overmature marine shale formations, where capillary-bound water may locally increase values up to 0.35. Under the specified initial conditions (with Sw increasing from 0.20 to 0.35), the water-phase trapping effect during the two-phase gas–water flow becomes progressively more pronounced. As Sw increases from 0.20 to 0.35, the capillary resistance to gas flow is enhanced, resulting in systematic reductions in daily gas production rate, cumulative gas production, and the yields of all gas components (CH₄, N₂, CO₂, C₂–C₅, C₆–C₁₀, C₁₁⁺) (Figure 7,

Table 3. Production dynamics of the horizontal well under different initial water saturations.

Initial Water Saturation	Cumulative Gas Production (107 m3)	CH4 (107 m3)	N2 (106 m3)	CO2 (107 m3)	C2–C5 (106 m3)	C6–C10 (106 m3)	C11+ (105 m3)
0.2	6.693	3.835	1.587	1.247	4.420	1.458	6.227
0.25	6.080	3.484	1.442	1.132	4.016	1.324	5.713
0.3	5.491	3.146	1.302	1.023	3.626	1.196	5.209
0.35	4.923	2.821	1.167	0.917	3.251	1.072	4.715

). Meanwhile, the elevated water saturation decreases the effective gas-phase permeability of the reservoir, thereby impeding gas migration toward the fracture system. The variations in pressure-field distribution shown in Figure 8 clearly illustrate the intensified flow resistance near the wellbore region. These results indicate that an increase in initial water saturation suppresses gas well productivity through the water-locking effect.

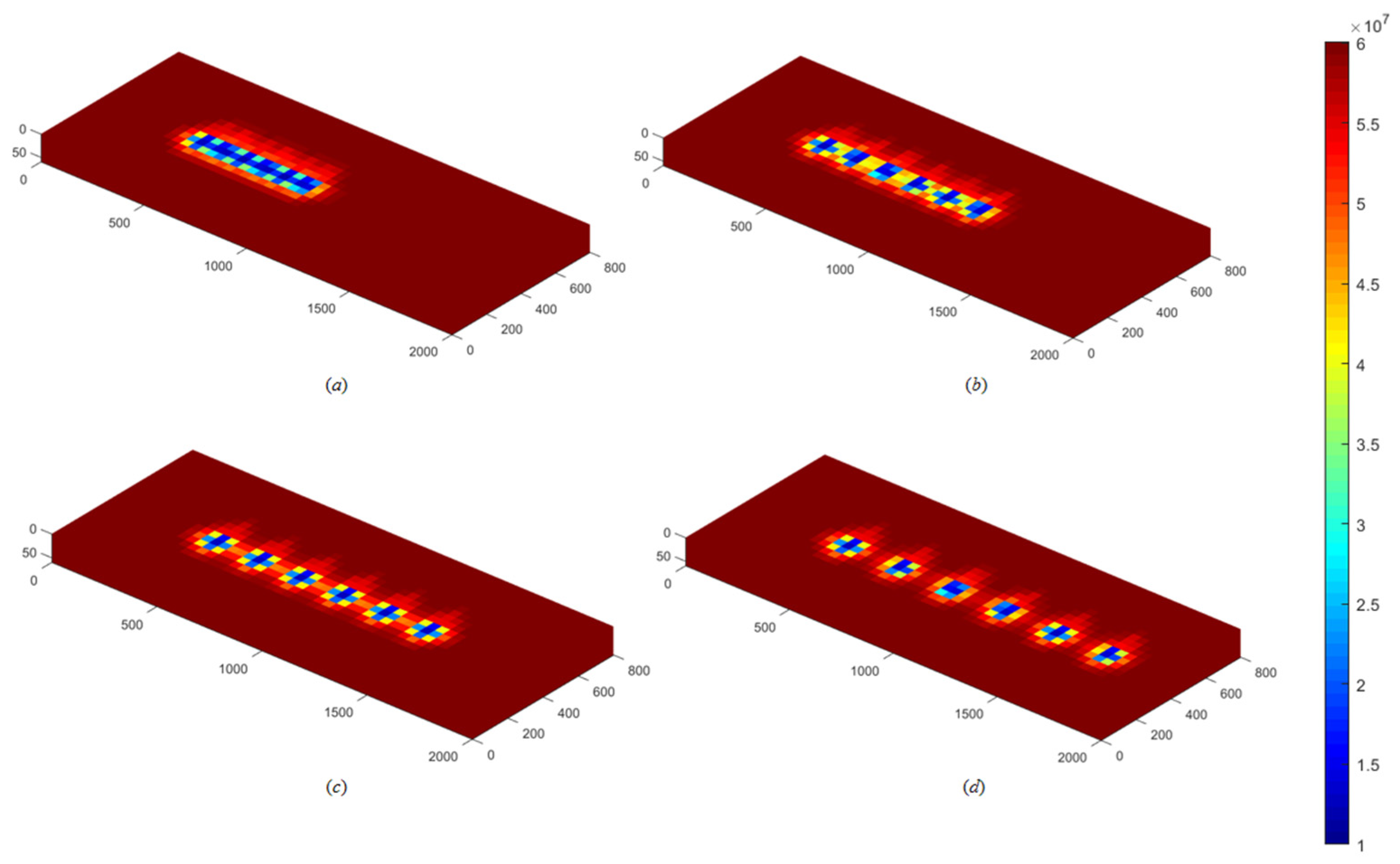
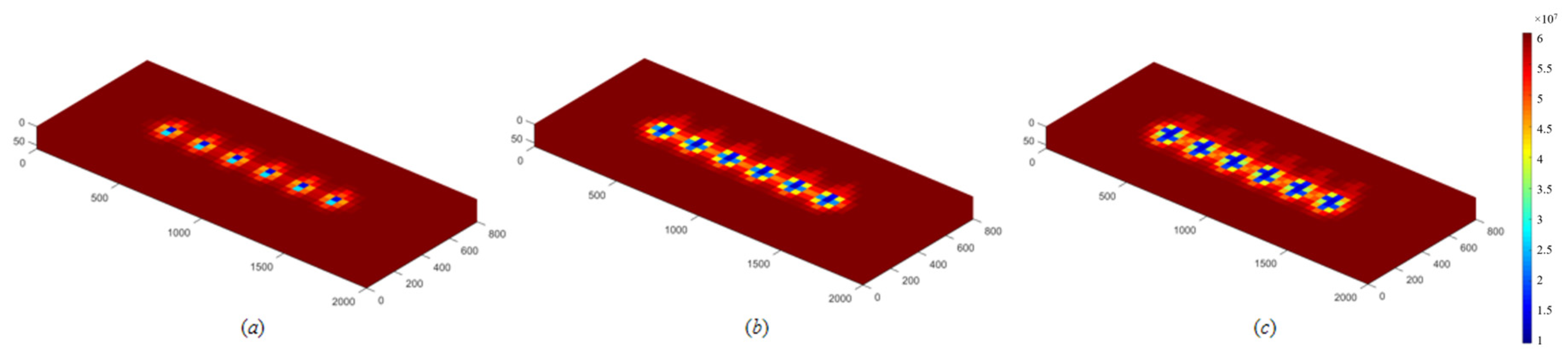
3.3.2. Influence of Hydraulic Fracture Spacing

To elucidate the impact of hydraulic fracture spacing on the productivity of fractured horizontal wells, four spacing scenarios (100 m, 150 m, 200 m, and 250 m) were simulated, yielding cumulative gas productions of 5.294 × 10⁷ m³, 5.415 × 10⁷ m³, 5.491 × 10⁷ m³, and 5.376 × 10⁷ m³, respectively. As illustrated in Figure 9, the cumulative gas production initially increases and then decreases with increasing fracture spacing, reaching a maximum of 5.491 × 10⁷ m³ at a spacing of 200 m. Under the condition of a constant number of fractures, narrower spacing (e.g., 100 m) intensifies fracture interference and drives non-uniform fluid redistribution within the reservoir, as indicated by the highly concentrated pressure contours around adjacent fractures in Figure 10. Moreover, the 100 m spacing causes the pressure depletion to become highly localized near the fractures, resulting in a noticeably reduced pressure-propagation range compared with wider spacing scenarios, which in turn lowers the overall reservoir drainage efficiency and suppressing cumulative gas recovery. Therefore, in practical hydraulic fracturing design, the fracture spacing should be optimized by balancing the trade-off between fracture conductivity and reservoir stimulation efficiency to achieve synergistic enhancement of production performance and fracturing effectiveness.

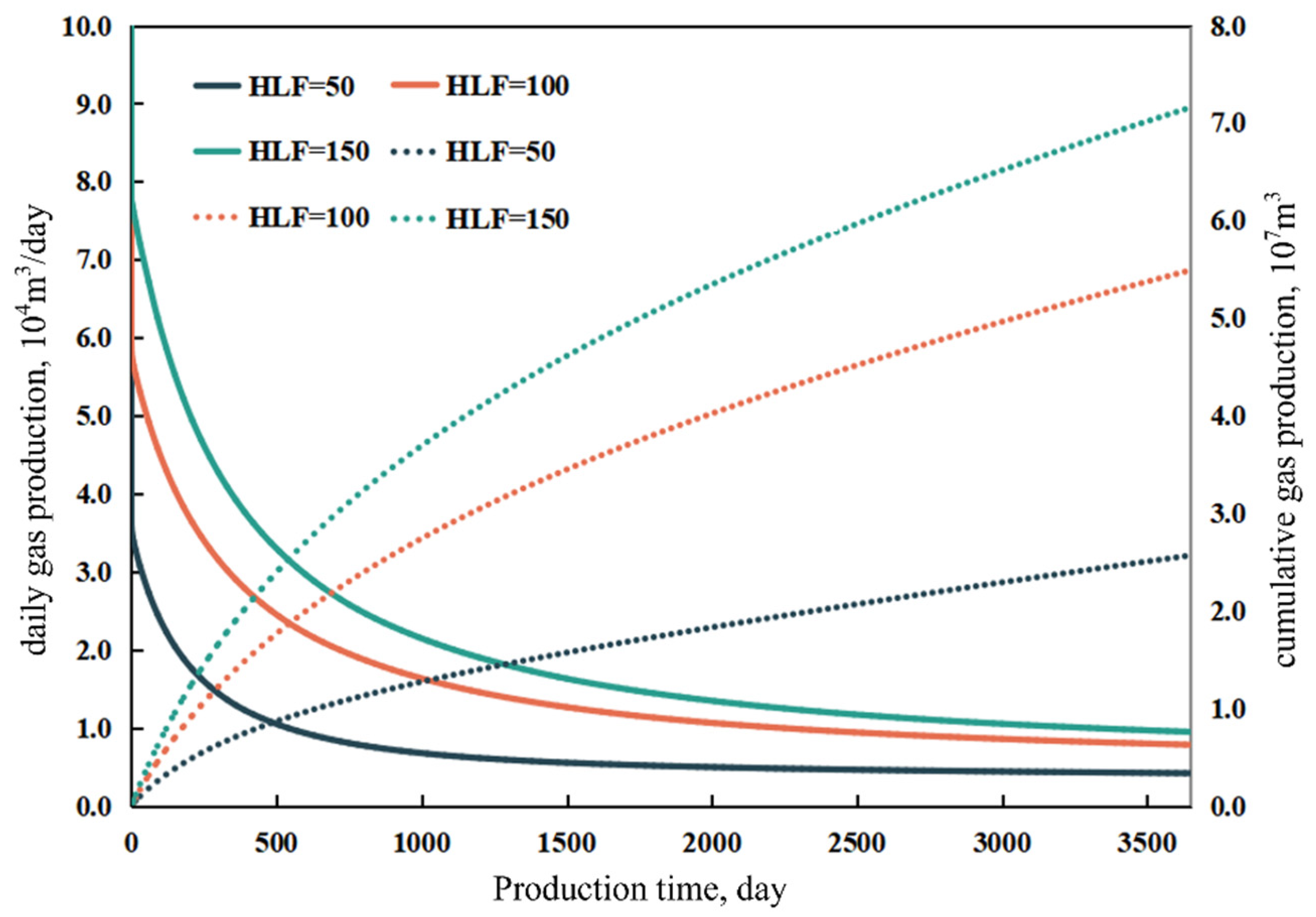
3.3.3. Influence of Hydraulic Fracture Half-Length

Under the condition of a constant number of fractures, increasing the hydraulic fracture half-length (HLF) significantly enlarges the effective flow-conducting area and enhances the connectivity between the reservoir and the wellbore, thereby improving shale gas recovery. As illustrated in Figure 11, a larger fracture half-length effectively increases both the daily and cumulative gas production of a single well, although the incremental productivity gain exhibits a diminishing return trend. These findings indicate that, in practical fracturing design, the trade-off between operational cost and production benefit should be carefully balanced to achieve the optimal match between stimulation effectiveness and economic performance. The pressure distribution under different fracture half-lengths (Figure 12) further elucidates the underlying mechanism: as the hydraulic fracture half-length increases, the pressure propagation range expands correspondingly, leading to higher cumulative gas recovery. The production performance curves presented in Figure 11 demonstrate that a longer fracture half-length results in higher initial production rates, while maintaining elevated production levels during the stabilized production stage.

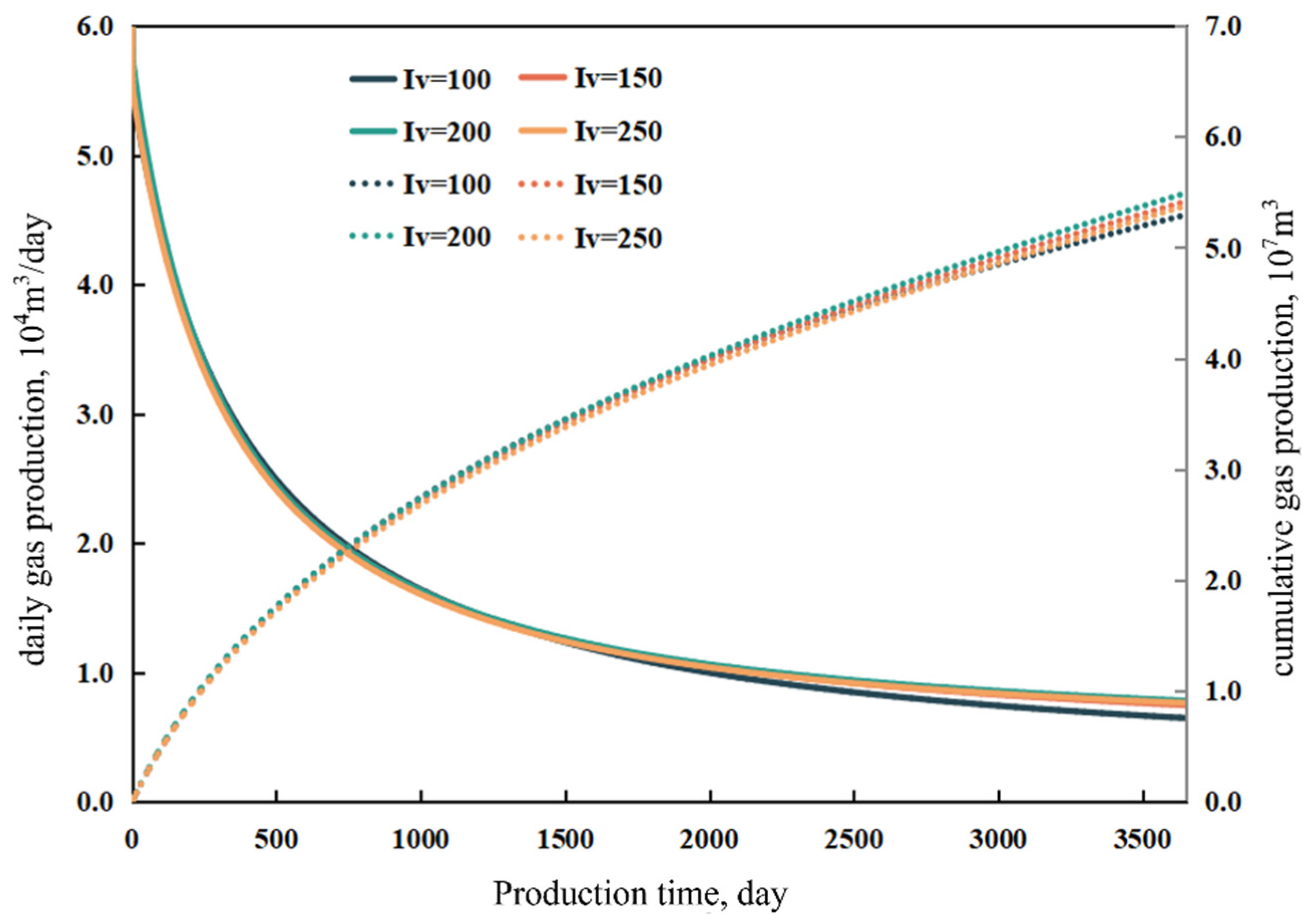
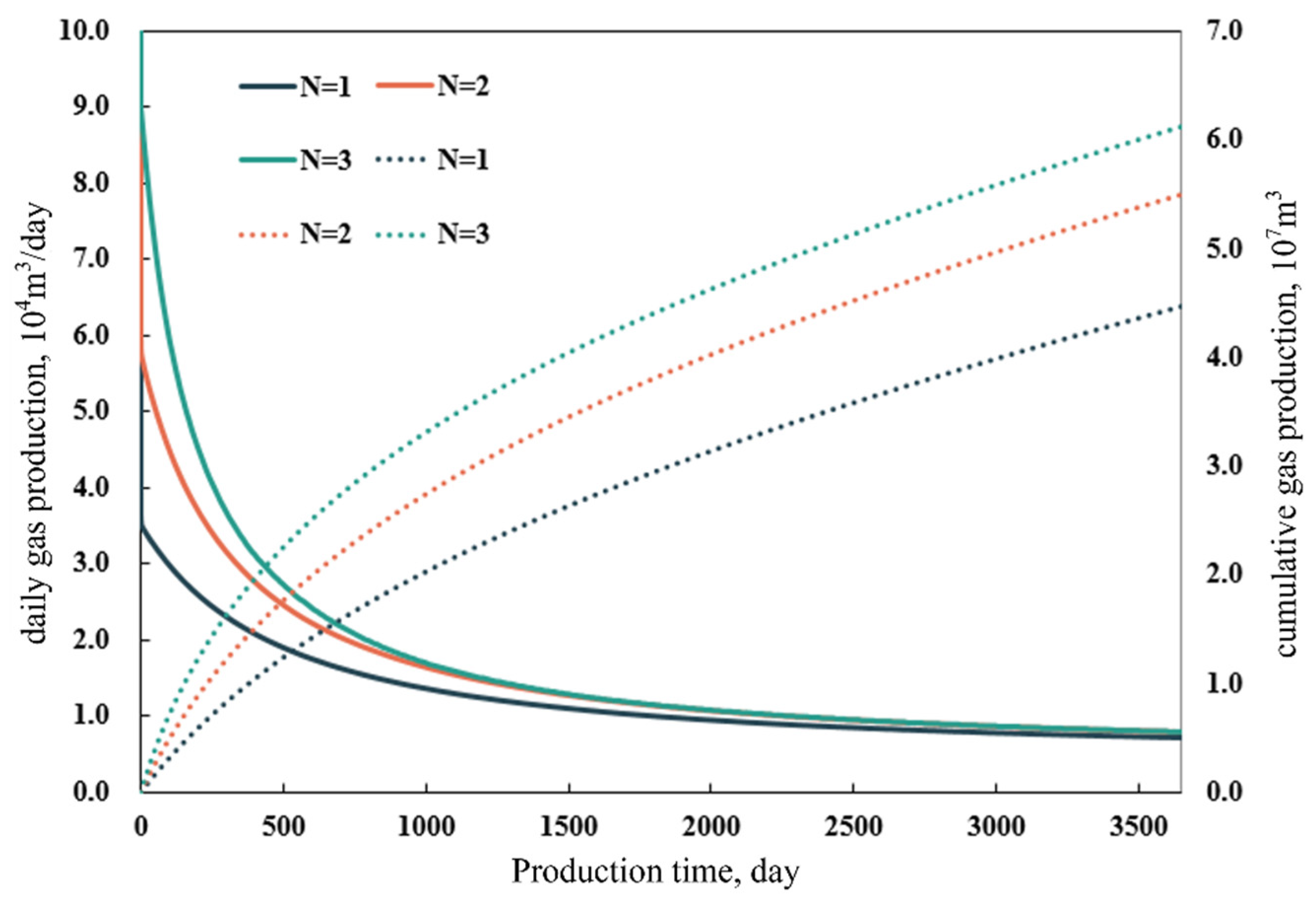
3.3.4. Influence of Fracture Iteration Number

The fracture iteration number (N) characterizes the geometric complexity of hydraulic fracture propagation. Among all fractal parameters, N governs the hierarchical depth and overall structural complexity of the fracture network, exerting first-order control on flow connectivity and production behavior. Therefore, it is selected as the primary parameter for sensitivity analysis in this study. As shown in Figure 13 and Figure 14, numerical simulation results reveal that N exerts a pronounced influence on the production dynamics of shale gas wells: when N increases from 1 to 3, the cumulative gas production rises by 36.4%. A higher iteration number (N = 3) significantly alters the flow field characteristics, manifested as higher initial gas production rates, larger near-wellbore pressure drops, and a markedly expanded pressure disturbance range. These results indicate that increasing fracture complexity enhances productivity through two synergistic mechanisms: (1) strengthening the flow conductivity of branched fractures and improving early-time gas supply, and (2) intensifying fracture network interactions, thereby enlarging the pressure disturbance region. Moreover, the productivity gain exhibits a nonlinear diminishing trend with increasing N, suggesting that once fracture complexity exceeds a critical threshold, the incremental benefit becomes marginal. It should also be noted that the computational cost rises quickly with increasing N, and simulations with N ≥ 4 become substantially more expensive due to the rapid growth of fracture segments and NNCs. Therefore, parameter optimization should be performed according to geological conditions: for reservoirs with well-developed natural fractures, N ≥ 3 is recommended to accurately capture complex fracture propagation behavior, whereas for relatively homogeneous formations, N = 2 provides a balanced trade-off between simulation accuracy and computational efficiency.

3.4. Model Limitations

Although the proposed fractal–EDFM effectively characterizes multiscale fracture networks and reproduces production performance, several simplifying assumptions should be acknowledged.

• The model does not account for stress-dependent fracture closure or aperture reduction. In reality, fracture conductivity may decrease over time due to increasing effective stress, which could modify long-term production behavior.
• Fracture permeability, aperture, and connectivity are assumed to remain constant throughout the simulation. Potential dynamic evolution of fracture properties—such as proppant embedment, deformation, or shear dilation—is not included. This simplification is commonly adopted in field-scale EDFM simulations because long-term production is governed primarily by reservoir drainage behavior rather than small late-time variations in fracture deformation. While the present fractal algorithm describes static fracture geometry, it could, in principle, be coupled with geomechanical models to simulate dynamic fracture propagation under evolving stress fields.
• The simulations assume constant reservoir temperature. Thermal effects, such as temperature-dependent gas properties or thermoelastic responses, are neglected.
• The fine-scale fractal–EDFM is constructed at high resolution only within the near-well drainage region to capture detailed fracture interactions. For multiwell, field-scale simulations—where such resolution is computationally infeasible—the detailed fractal geometry can be retained locally, whereas the far-field reservoir is represented using a coarse dual-porosity/dual-permeability model with effective properties calibrated from the fine-scale results. This hybrid strategy preserves the key drainage behavior while maintaining computational tractability.

These limitations should be considered when interpreting the results, and the authors of future studies could incorporate coupled geomechanical modeling, thermal effects, and dynamic fracture-property evolution to further enhance predictive capability.

4. Conclusions

Based on fractal geometry and the Embedded Discrete Fracture Model (EDFM), a numerical simulator was developed to investigate the production dynamics of hydraulically fractured horizontal wells in shale gas reservoirs. The proposed model systematically elucidates the controlling mechanisms of complex fracture network structures on production evolution. The main conclusions are as follows:

• The fractal fracture model accurately characterizes the heterogeneity of fracture networks. By adjusting key parameters such as the iteration number (N), branching number (c), scale factor (γ), and deviation angle (θ), the model captures the self-similar features of fracture geometry and spatial statistics, providing a robust theoretical framework for modeling complex hydraulic fracture networks.
• The EDFM exhibits significant advantages in simulating multiscale fracture–matrix interactions. By employing the Non-Neighboring Connection (NNC) mechanism to describe inter-domain fluid exchange, the EDFM effectively represents irregular fracture geometries without local grid refinement, thereby enhancing computational efficiency, numerical stability, and accuracy.
• Reservoir and fracturing parameters exert strong influences on production dynamics. When the initial water saturation increases to 0.35, the capillary retention effect causes a 26.4% decline in cumulative gas production compared with the base case (Sw = 0.20). An optimal fracture spacing of 200 m effectively mitigates inter-well interference, improving cumulative gas production by 3.71% relative to the 100 m case. Increasing the hydraulic fracture half-length markedly enhances gas well productivity, yielding higher initial rates and sustained production plateaus. Moreover, increasing the iteration number (N) significantly alters the flow field characteristics—manifested as higher early-time production, greater near-wellbore pressure drops, and an expanded pressure disturbance range.
• The proposed fractal–EDFM coupled approach demonstrates strong engineering applicability. It provides a theoretical and technical basis for optimizing fracture network parameters and designing field development strategies, offering reliable support for the efficient exploitation of shale gas reservoirs.