Fermentation Kinetics Beyond Viability: A Fitness-Based Framework for Microbial Modeling
Abstract
1. Introduction
2. Materials and Methods
- -
- The availability of well-characterized kinetic profiles for biomass and product, which enabled a critical and exhaustive evaluation of the model proposed in the present work.
- -
- The type of substrate and microorganisms used, prioritizing systems employing complex substrates and mixed microbial cultures.
- -
- The application of traditional mathematical models that do not account for cellular fitness.
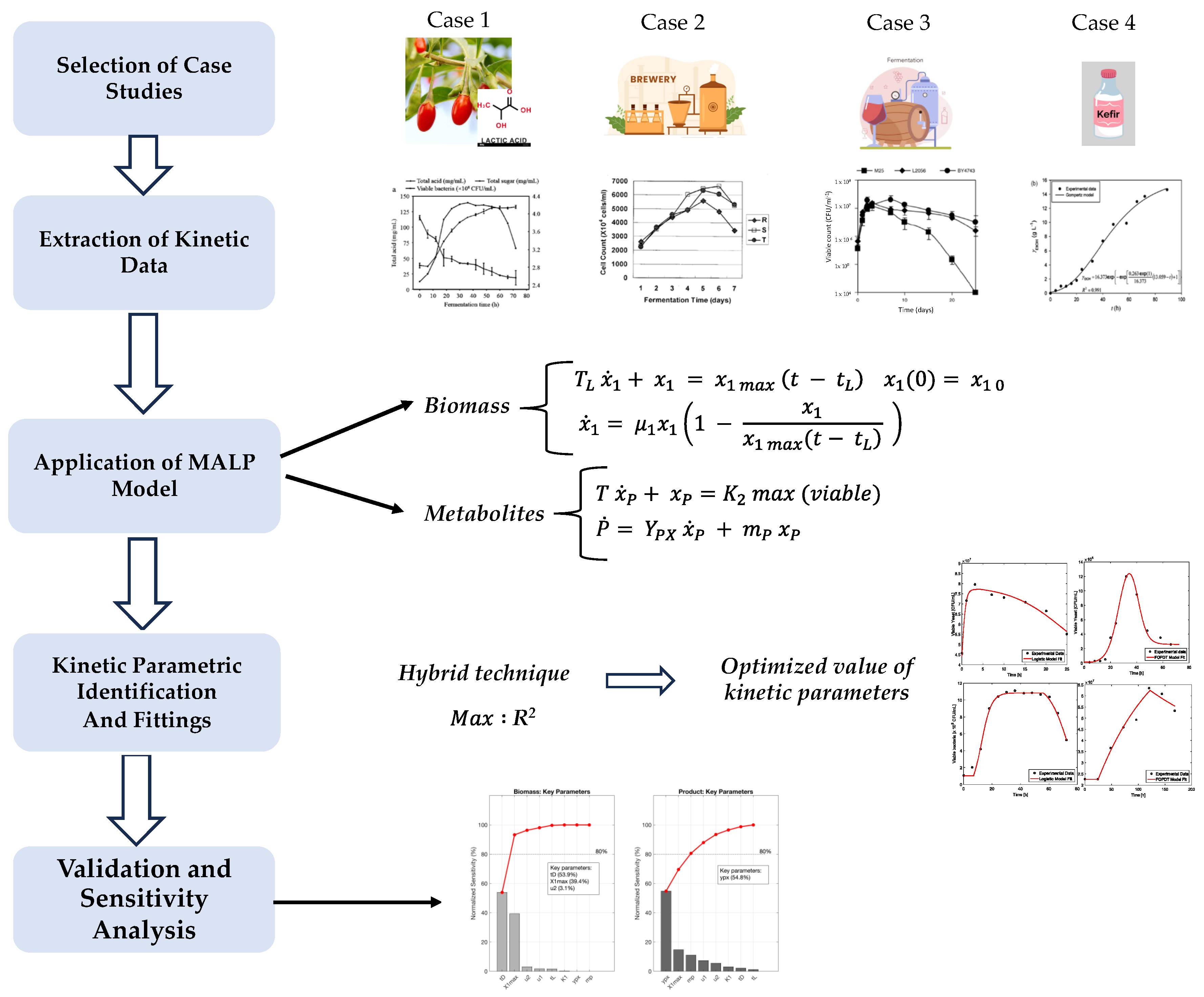
2.1. Mathematical Modeling
2.1.1. Microbial Growth
Model 1: First Order Plus Dead Time
- Equation for DeadCells
- Viable Cells
Model 2: Logistic Growth Model
- Equation for Total Cells
- Equation for Dead Cells
- Viable Cells
2.1.2. Metabolite Synthesis
- (1)
- Only physiologically competent cells contribute to metabolite production, i.e., the productive cells (7);
- (2)
- In turn, physiological activity varies over time, meaning that not all productive cells participate equally or simultaneously in metabolite synthesis.
- is the product formation rate [g/mL.h];
- is the productive cell rate [CFU/mL.h];
- is the growth-associated product yield coefficient [gproduct/CFU];
- is the maintenance-associated product formation coefficient [gproduct/CFU.h];
- is the maximum viable cell population [CFU/mL];
- is a constant bounded within a biologically meaningful range;
- T is the system time constant cells xp [h].
2.2. Sensitivity Analysis
2.3. Data Analysis
3. Results and Discussion
3.1. Model Performance and Fitting Accuracy
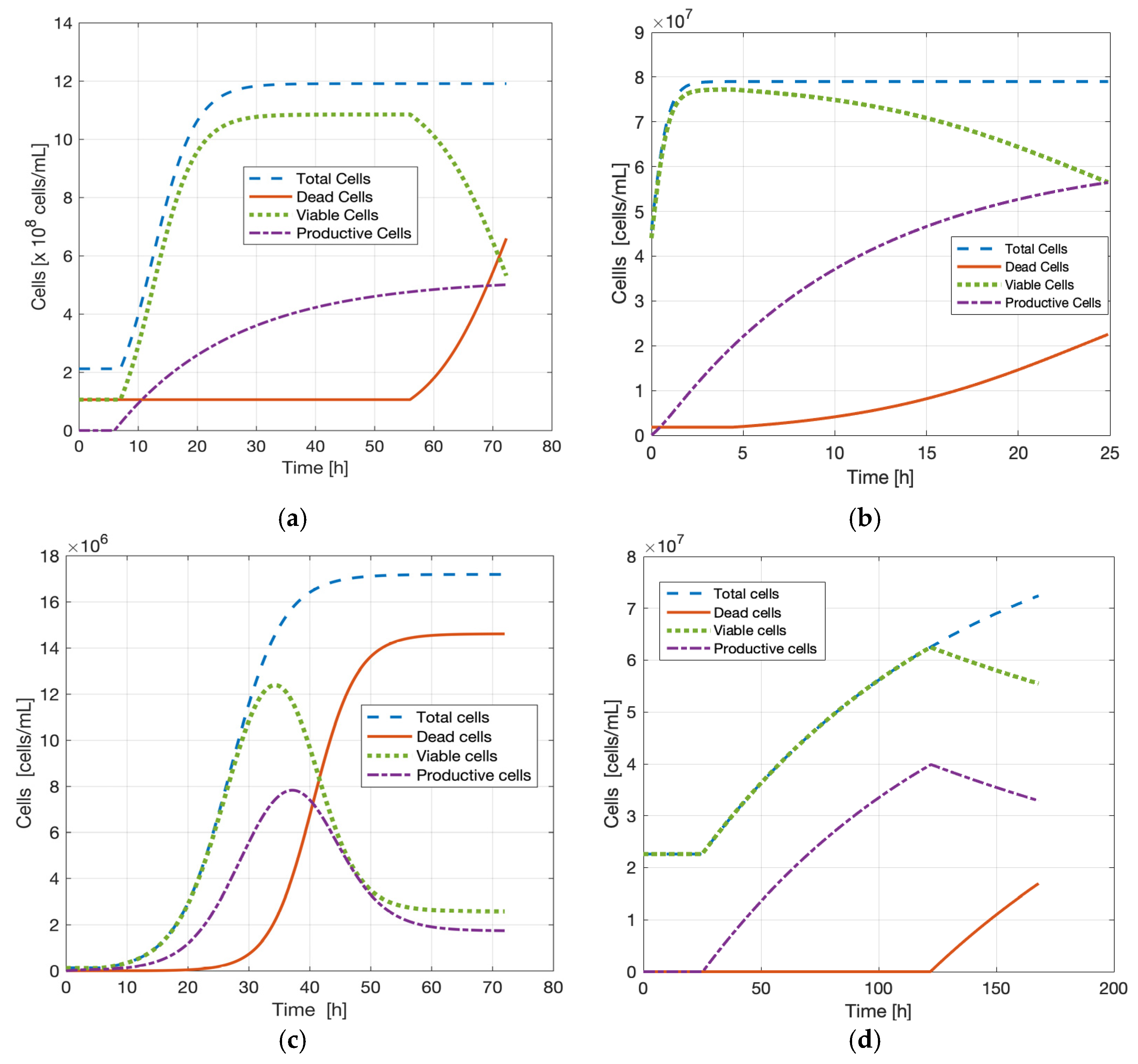
3.2. Interpretation of the Productive Cell Dynamics
3.3. Impact of Model Structure on Predictive Insight
3.4. Analysis of Models Adjustments
3.4.1. Kinetic Modeling of Biomass Growth
3.4.2. Kinetic Modeling of Metabolite Production
- Simultaneously capture growth-associated and non-growth-associated production phases.
- Accurately represent system-specific behaviors (e.g., microbial consortia dynamics, strain variability).
- Improve prediction accuracy by accounting for functional heterogeneity in viable cell populations.
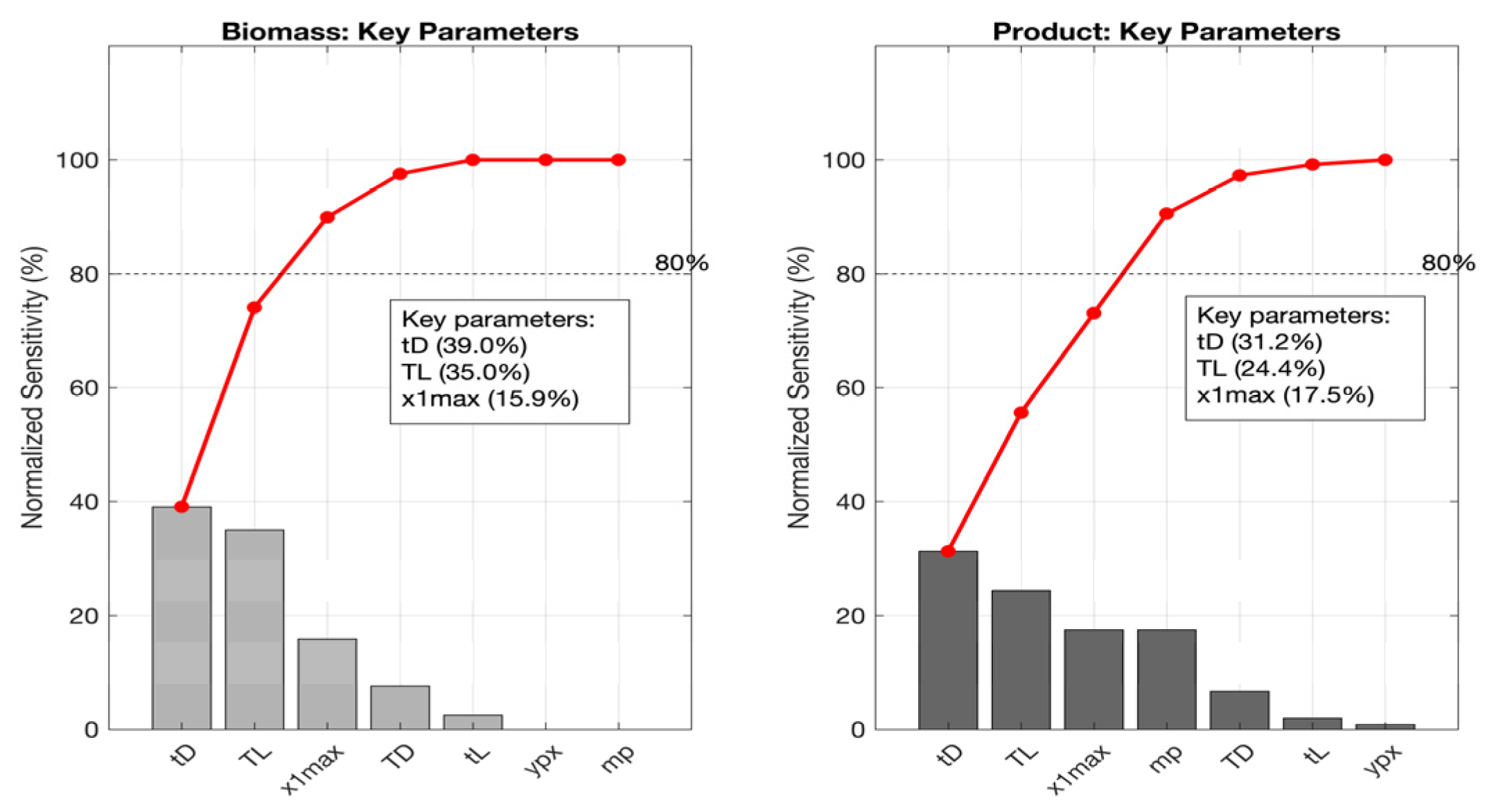
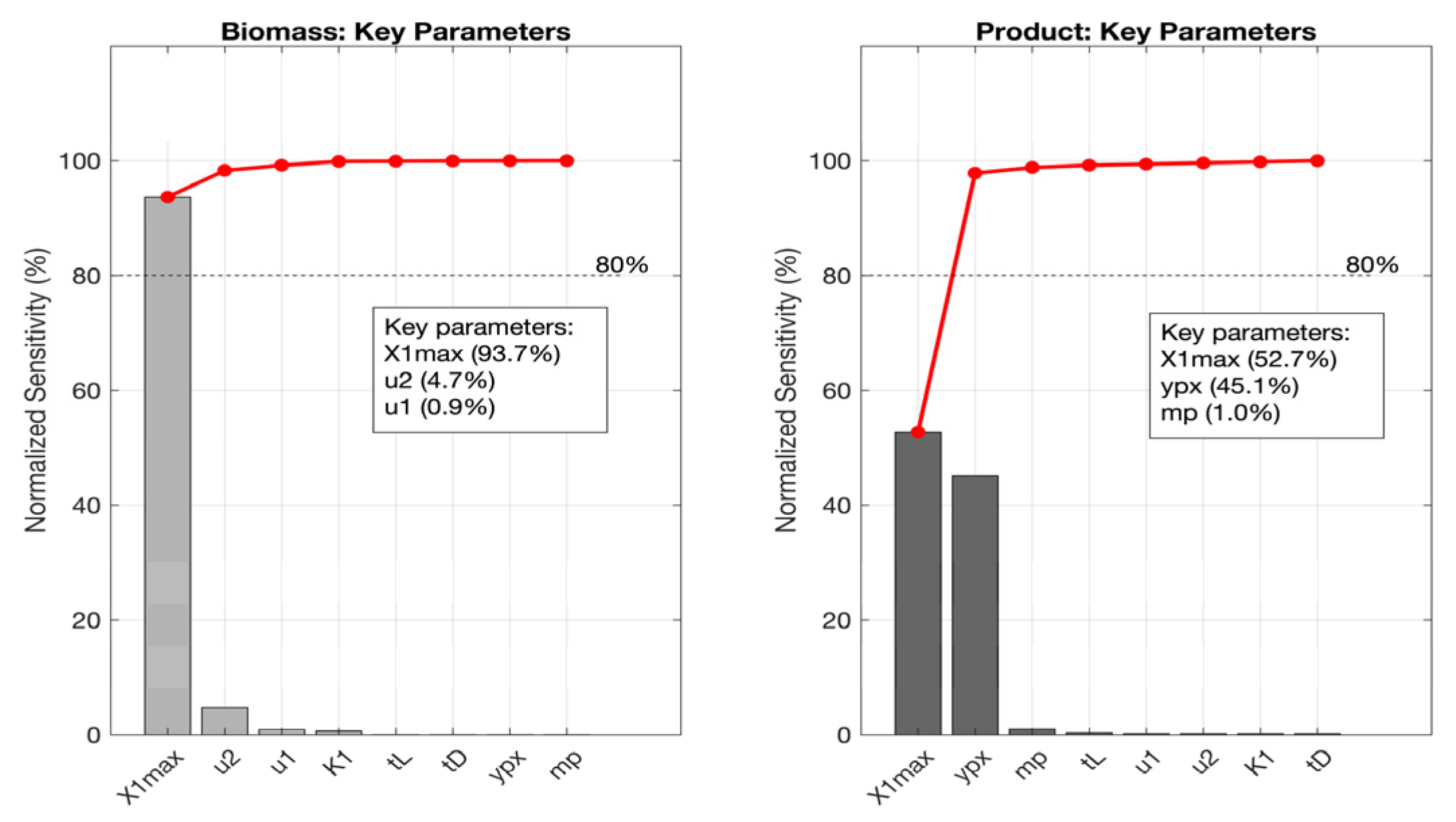
3.5. Local Sensitivity Analysis
3.5.1. Lactic Acid Fermentation
3.5.2. Kefir Fermentation
3.5.3. Wine Fermentation
3.5.4. Beer Fermentation
3.6. Simulations of Cellular Subpopulations Using the MALP Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nigam, P.S. An Overview of Microorganisms’ Contribution and Performance in Alcohol Fermentation Processing a Variety of Substrates. Curr. Biotechnol. 2017, 6, 9–16. [Google Scholar] [CrossRef]
- Dimopoulou, M.; Dols-Lafargue, M. Exopolysaccharides Producing Lactic Acid Bacteria in Wine and Other Fermented Beverages: For Better or for Worse? Foods 2021, 10, 2204. [Google Scholar] [CrossRef]
- Delvigne, F.; Goffin, P. Microbial Heterogeneity Affects Bioprocess Robustness: Dynamic Single-Cell Analysis Contributes to Understanding of Microbial Populations. Biotechnol. J. 2014, 9, 61–72. [Google Scholar] [CrossRef]
- Moimenta, A.R.; Troitiño-jordedo, D.; Henriques, D.; Contreras-ruíz, A.; Minebois, R.; Morard, M. An Integrated Multiphase Dynamic Genome-Scale Model Explains Batch Fermentations Led by Species of the Saccharomyces Genus. mSystems 2025, 10, e01615-24. [Google Scholar] [CrossRef]
- Mu, X.; Zhang, F. Diverse Mechanisms of Bioproduction Heterogeneity in Fermentation and Their Control Strategies. J. Ind. Microbiol. Biotechnol. 2023, 50, kuad033. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, F.S.; Udugama, I.A.; Seibold, G.M.; Sugiyama, H.; Gernaey, K.V. Digital Models in Biotechnology: Towards Multi-Scale Integration and Implementation. Biotechnol. Adv. 2022, 60, 108015. [Google Scholar] [CrossRef]
- My, R.; Gupte, A.P.; Bizzotto, E.; Frizzarin, M.; Antoniali, P.; Campanaro, S.; Favaro, L. Unveiling the Fitness of Saccharomyces Cerevisiae Strains for Lignocellulosic Bioethanol: A Genomic Exploration through Fermentation Stress Tests. New Biotechnol. 2025, 85, 63–74. [Google Scholar] [CrossRef] [PubMed]
- Vicente, J.; Benito, S.; Marquina, D.; Santos, A. Subpopulation-Specific Gene Expression in Lachancea Thermotolerans Uncovers Distinct Metabolic Adaptations to Wine Fermentation. Curr. Res. Food Sci. 2025, 10, 100954. [Google Scholar] [CrossRef] [PubMed]
- González-Figueredo, C.; Flores-Estrella, R.A.; Rojas-Rejón, O.A. Fermentation: Metabolism, Kinetic Models, and Bioprocessing; IntechOpen: Rijeka, Croatia, 2018; Volume 1. [Google Scholar]
- Nithya, A.; Misra, S.; Panigrahi, C.; Dalbhagat, C.G.; Mishra, H.N. Probiotic Potential of Fermented Foods and Their Role in Non-Communicable Diseases Management: An Understanding through Recent Clinical Evidences. Food Chem. Adv. 2023, 3, 100381. [Google Scholar] [CrossRef]
- Bai, F.; Cai, P.; Yao, L.; Shen, Y.; Li, Y.; Zhou, Y.J. Inducible Regulating Homologous Recombination Enables Precise Genome Editing in Pichia Pastoris without Perturbing Cellular Fitness. Trends Biotechnol. 2025, 43, 1385–1402. [Google Scholar] [CrossRef]
- Santos, M.F.; de Paula, S.C.S.E.; da Silva, L.M.; Filho, A.M.M.; Saraiva, S.H.; Teixeira, L.J.Q. Multi-Optimization of Operational Parameters for Malt Extract Production by Centrifugal Block Freeze Concentration. Innov. Food Sci. Emerg. Technol. 2023, 89, 103488. [Google Scholar] [CrossRef]
- Liu, H.; Li, N.; Wang, Y.; Cheng, T.; Yang, H.; Peng, Q. Study on Fermentation Kinetics, Antioxidant Activity and Flavor Characteristics of Lactobacillus plantarum CCFM1050 Fermented Wolfberry Pulp. Food Innov. Adv. 2024, 3, 126–134. [Google Scholar] [CrossRef]
- Mavrommati, M.; Economou, C.N.; Kallithraka, S.; Papanikolaou, S.; Aggelis, G. Simultaneous Improvement of Fructophilicity and Ethanol Tolerance of Saccharomyces cerevisiae Strains through a Single Adaptive Laboratory Evolution Strategy. Carbon Resour. Convers. 2024, 8, 100270. [Google Scholar] [CrossRef]
- Cao, K.-F.; Chen, Z.; Sun, Y.-G.; Huang, B.-H.; Shi, Q.; Mao, Y.; Wu, Y.-H.; Lu, Y.; Hu, H.-Y. Modeling and Optimization of Synergistic Ozone-Ultraviolet-Chlorine Process for Reclaimed Water Disinfection: From Laboratory Tests to Software Simulation. Water Res. 2023, 243, 120373. [Google Scholar] [CrossRef]
- Avery, S.V. Phenotypic Diversity and Fungal Fitness. Mycologist 2005, 19, 74–80. [Google Scholar] [CrossRef]
- Zacchetti, B.; Wösten, H.A.; Claessen, D. Multiscale Heterogeneity in Filamentous Microbes. Biotechnol. Adv. 2018, 36, 2138–2149. [Google Scholar] [CrossRef] [PubMed]
- Byrne, A.S.; Bissonnette, N.; Tahlan, K. Mechanisms and Implications of Phenotypic Switching in Bacterial Pathogens. Can. J. Microbiol. 2024, 71, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Povolotsky, T.L.; Barazany, H.L.; Shacham, Y.; Kolodkin-Gal, I. Bacterial Epigenetics and Its Implication for Agriculture, Probiotics Development, and Biotechnology Design. Biotechnol. Adv. 2024, 75, 108414. [Google Scholar] [CrossRef]
- Müller, S.; Harms, H.; Bley, T. Origin and Analysis of Microbial Population Heterogeneity in Bioprocesses. Curr. Opin. Biotechnol. 2010, 21, 100–113. [Google Scholar] [CrossRef]
- Ruarte, P.J.; Leiva Alaniz, M.J.; Vergara, S.C.; Groff, M.C.; Pantano, M.N.; Mestre, M.V.; Scaglia, G.J.E.; Maturano, Y.P. Mathematical Modeling for Fermentation Systems: A Case Study in Probiotic Beer Production. Fermentation 2025, 11, 184. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Xiong, Z.; Geng, Y.; Cui, D.; Pavlostathis, S.G.; Chen, H.; Luo, Q.; Qiu, G.; Dong, Q.; et al. Synergistic Optimization of Baffles and Aeration to Improve the Light/Dark Cycle of Microalgae Photobioreactor for Enhanced Nitrogen Removal Performance: Computational Fluid Dynamics and Experimental Verification. Bioresour. Technol. 2024, 410, 131293. [Google Scholar] [CrossRef]
- Mannazzu, I.; Angelozzi, D.; Belviso, S.; Budroni, M.; Farris, G.A.; Goffrini, P.; Lodi, T.; Marzona, M.; Bardi, L. Behaviour of Saccharomyces cerevisiae Wine Strains during Adaptation to Unfavourable Conditions of Fermentation on Synthetic Medium: Cell Lipid Composition, Membrane Integrity, Viability and Fermentative Activity. Int. J. Food Microbiol. 2008, 121, 84–91. [Google Scholar] [CrossRef]
- Shimizu, C.; Araki, S.; Kuroda, H.; Takashio, M.; Shinotsuka, K. Yeast Cellular Size and Metabolism in Relation to the Flavor and Flavor Stability of Beer. J. Am. Soc. Brew. Chem. 2001, 59, 122–129. [Google Scholar] [CrossRef]
- Zajšek, K.; Goršek, A. Modelling of Batch Kefir Fermentation Kinetics for Ethanol Production by Mixed Natural Microflora. Food Bioprod. Process. 2010, 88, 55–60. [Google Scholar] [CrossRef]
- Wu, Z.; Sheintuch, M.; Xu, P. Population Dynamics of Engineered Microbes under Metabolic Stress and Reward in Batch and Continuous Reactors. Chem. Eng. J. 2024, 502, 158049. [Google Scholar] [CrossRef]
- González-Hernández, Y.; Perré, P. Building Blocks Needed for Mechanistic Modeling of Bioprocesses: A Critical Review Based on Protein Production by CHO Cells. Metab. Eng. Commun. 2024, 18, e00232. [Google Scholar] [CrossRef] [PubMed]
- Groff, M.C.; Scaglia, G.; Ortiz, O.A.; Noriega, S.E. Modification of the Luedeking and Piret Model with a Delay Time Parameter for Biotechnological Lactic Acid Production. Biotechnol. Lett. 2022, 44, 415–427. [Google Scholar] [CrossRef]
- Turon, V.; Baroukh, C.; Trably, E.; Latrille, E.; Fouilland, E.; Steyer, J.P. Use of Fermentative Metabolites for Heterotrophic Microalgae Growth: Yields and Kinetics. Bioresour. Technol. 2015, 175, 342–349. [Google Scholar] [CrossRef]
- Qiu, M.; Cao, P.; Cao, L.; Tan, Z.; Hou, C.; Wang, L.; Wang, J. Parameter Determination of the 2S2P1D Model and Havriliak–Negami Model Based on the Genetic Algorithm and Levenberg–Marquardt Optimization Algorithm. Polymers 2023, 15, 2540. [Google Scholar] [CrossRef]
- Fernández, C.; Pantano, N.; Godoy, S.; Serrano, E.; Scaglia, G. Optimización de Parámetros Utilizando Los Métodos de Monte Carlo y Algoritmos Evolutivos. Aplicación a Un Controlador de Seguimiento de Trayectoria En Sistemas No Lineales. Rev. Iberoam. Autom. Inform. Ind. 2018, 16, 89. [Google Scholar] [CrossRef]
- Scaglia, G.; Serrano, M.E.; Albertos, P. Linear Algebra Based Controllers; Springer International Publisher: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]






| Fermentation System | ||||
|---|---|---|---|---|
| Parameters | Lactic Acid [13] | Lactic Wine [23] | Ethanol Kefir [25] | Ethanol Beer [24] |
| L. plantarum | S. cerevisiae Wine Strain/Grape Must | Kefir Microbial Consortium/SUCROSE | S. cerevisiae Brewing Strain/Wort | |
| Logistic | Logistic | FOPDT | FOPDT | |
| tL | 7 h | 0 h | 11.9 h | 115 h |
| TL | - | - | 14.9 h | 25 h |
| tD | 56 h | 4.4 h | 33.1 h | 122 h |
| TD | - | - | 21.2 h | 140 h |
| μ1 | 0.28 | 1.94 | - | - |
| μ2 | 0.146 | 0.161 | - | - |
| X1,max | 1.19 × 108 | 7.9 × 107 | 3.05 × 107 | 7 × 107 |
| K1 | 0.95 | 0.52 | - | - |
| LOF | 1.18 | 0.01 | 0.1 | 0.08 |
| MSE | 0.09 | 0.001 | 0.0082 | 0.01 |
| F-statistic | 1.36 | 1.351 | 1.200 | 1.37 |
| p-value | 0.3101 | 0.362 | 0.3893 | 0.355 |
| R2 | 99.13% | 97.50% | 98.39% | 97.53% |
| Fermentation System | ||||
|---|---|---|---|---|
| Parameters | Lactic Acid [13] | Ethanol Wine [23] | Ethanol Kefir [25] | Ethanol Beer [24] |
| L. plantarum | S. cerevisiae Wine Strain/Grape Must | Kefir Microbial Consortium/Sucrose | S. cerevisiae Brewing Strain/Wort | |
| Logistic | Logistic | FOPDT | FOPDT | |
| yp/x | 15.33 | 1.25 × 10−6 | 6.0 × 10−8 | 2.8 × 10−7 |
| mp | 0.00178 | 1.10 × 10−8 | 3.93 × 10−8 | 4.98 × 10−9 |
| LOF | 126.7 | 50.65 | 10.41 | 12.08 |
| MSE | 9.75 | 8.441 | 0.7435 | 1.51 |
| F-statistic | 1.2 | 1.534 | 1.426 | 4.63 |
| p-value | 0.3851 | 0.3444 | 0.274 | 0.0422 |
| R2 | 99.16% | 99.13% | 97.12% | 99.65% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruarte, P.J.; Groff, M.C.; Pantano, M.N.; Vergara, S.C.; Leiva Alaniz, M.J.; Mestre, M.V.; Maturano, Y.P.; Scaglia, G.J.E. Fermentation Kinetics Beyond Viability: A Fitness-Based Framework for Microbial Modeling. Processes 2025, 13, 3018. https://doi.org/10.3390/pr13093018
Ruarte PJ, Groff MC, Pantano MN, Vergara SC, Leiva Alaniz MJ, Mestre MV, Maturano YP, Scaglia GJE. Fermentation Kinetics Beyond Viability: A Fitness-Based Framework for Microbial Modeling. Processes. 2025; 13(9):3018. https://doi.org/10.3390/pr13093018
Chicago/Turabian StyleRuarte, Pablo Javier, María Carla Groff, María Nadia Pantano, Silvia Cristina Vergara, María José Leiva Alaniz, María Victoria Mestre, Yolanda Paola Maturano, and Gustavo Juan Eduardo Scaglia. 2025. "Fermentation Kinetics Beyond Viability: A Fitness-Based Framework for Microbial Modeling" Processes 13, no. 9: 3018. https://doi.org/10.3390/pr13093018
APA StyleRuarte, P. J., Groff, M. C., Pantano, M. N., Vergara, S. C., Leiva Alaniz, M. J., Mestre, M. V., Maturano, Y. P., & Scaglia, G. J. E. (2025). Fermentation Kinetics Beyond Viability: A Fitness-Based Framework for Microbial Modeling. Processes, 13(9), 3018. https://doi.org/10.3390/pr13093018







