Multi-Objective Path Planning for Warehouse Inspection of Mobile Robots Considering Power Limitations and Multiple Charging Points
Abstract
1. Introduction
2. Backgrounds and Methods
2.1. Warehouse Simulation Model Construction
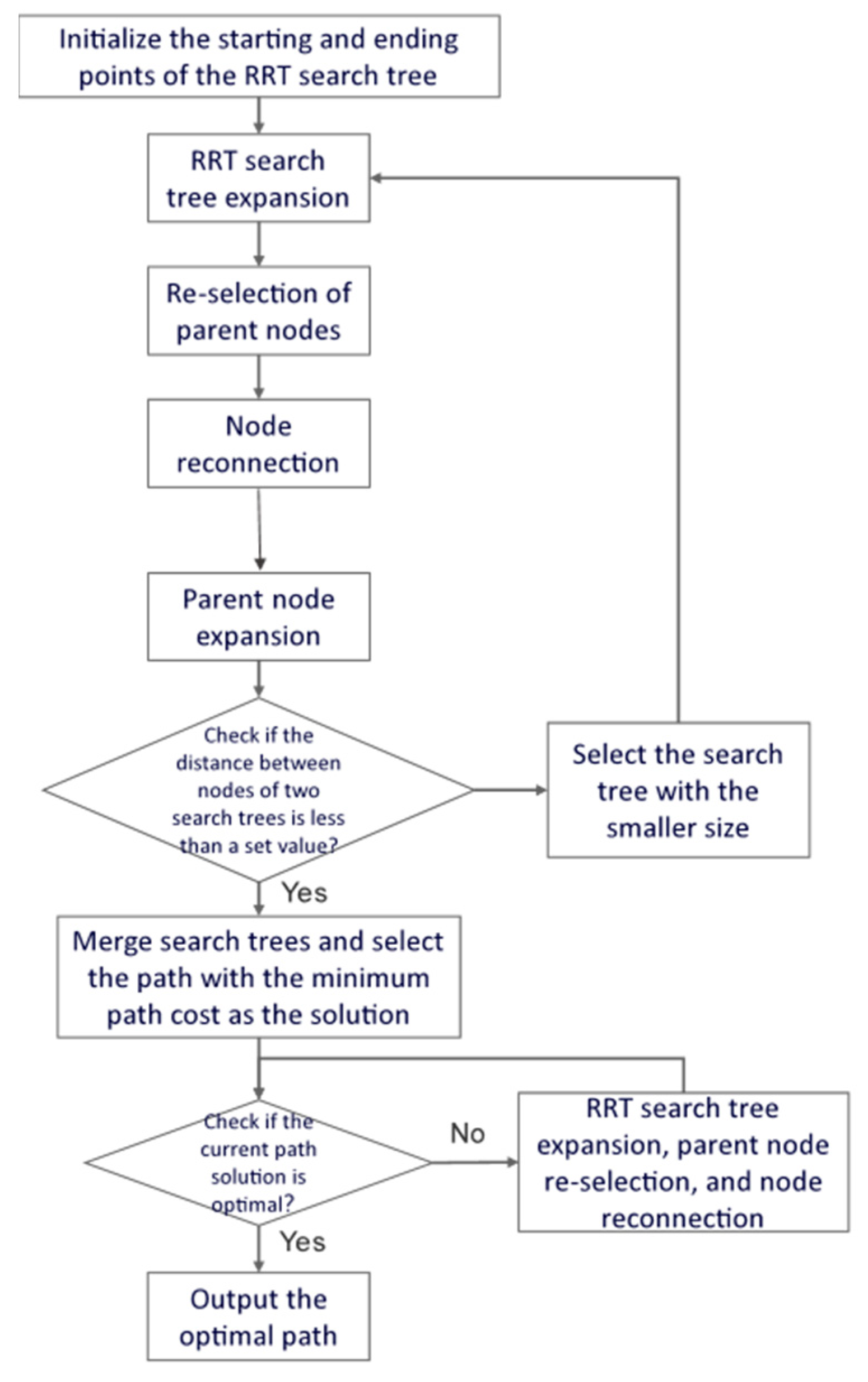
2.2. Local Path Planning Based on B-RRT* Algorithm
2.2.1. Problem Definition
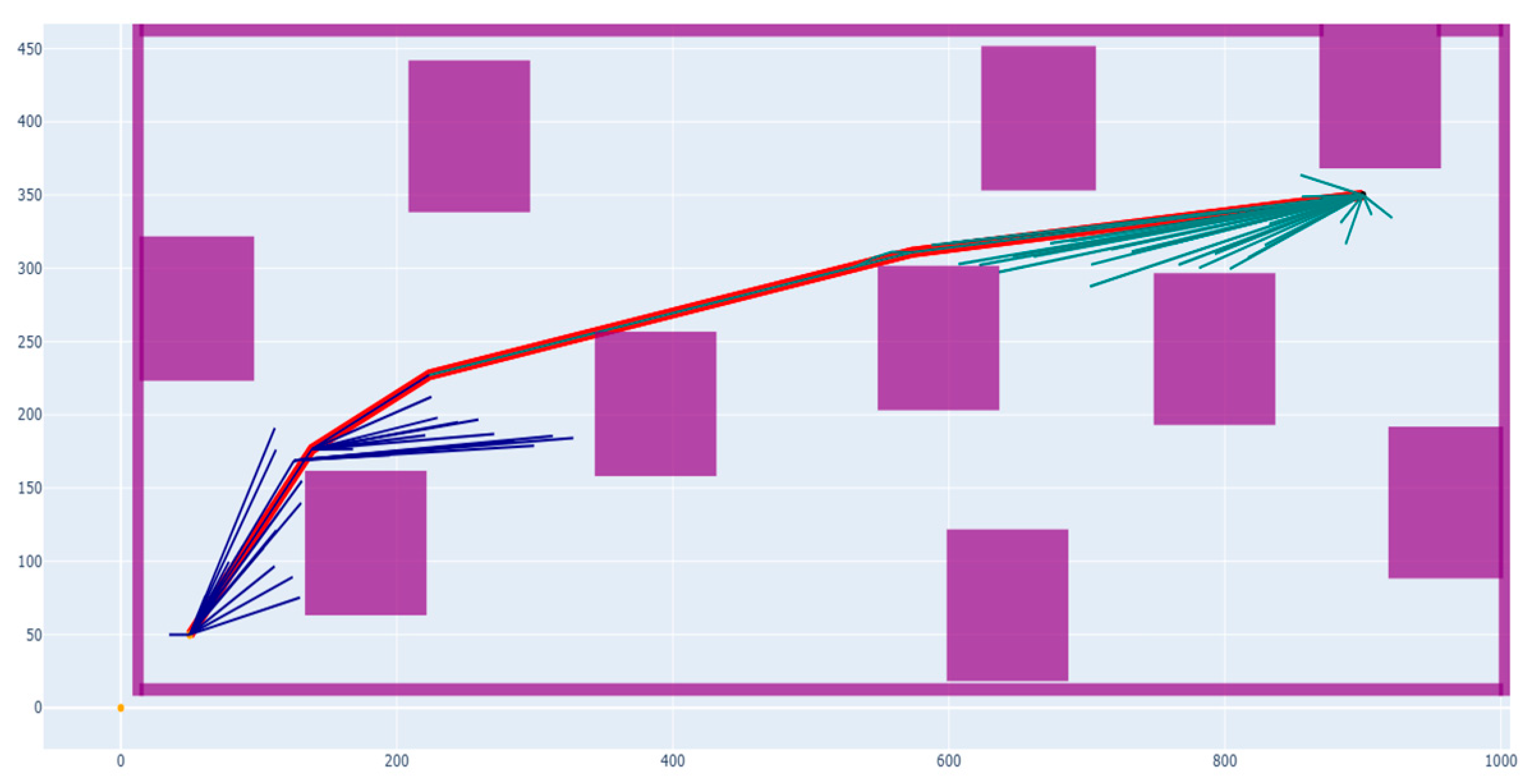
2.2.2. Adaptive Gaussian Distribution Sampling
- The external enhancement function increases the density of sampling points that are close to the obstacle and in the empty area outside the obstacle.
- The internal suppression function reduces the density of sampling points that are close to and inside the obstacle.
- Determine the mean and covariance Σ of the Gaussian distribution, and the regularization parameter , and obtain the initial point c in the Gaussian distribution .
- The Euclidean distance between the sampling point and the nearest obstacle is calculated. According to the position function and of the sampling point c, the weight value of the sampling function is determined according to the position function. The expression of the position function is shown in Equation (7):
- Determine whether the value of the weighting function exceeds the threshold, and if so, consider the sample point to be used.
2.2.3. Dynamic Target Bias
2.2.4. Improved B-RRT* Algorithm
| Algorithm 1 Improved B-RRT* |
| 1: Input Start point , goal point , map space , obstacle space , step size , maximun iterations , bias weight 2: Output Optimized path 3: Initialize two trees: and 4: Add to and to 5: Set bias threshold 6: 7: for to do 8: Adaptive Sampling 9: Generate 10: if then 11: 12: else 13: Compute Gaussian mean based on current node and target 14: Define obstacle weight functions: 15: Generate using weighted Gaussian distribution 16: end if 17: Nearest Neighbor Search: 18: Find closest to 19: Steer and Collision Check: 20: Generate by moving from toward with step size 21: if then 22: Add to tree 23: end if 24: Parent Selection and Rewiring: 25: Choose parent of minimizing path cost 26: Rewire nearby nodes if cost is reduced 27: Dynamic Target Bias Adjustment: 28: Update : /2, , 29: Tree Connection: 30: if exists such that then 31: Merge and 32: Compute path cost 33: end if 34: if valid path found then 35: Extract minimum cost path 36: break 37: end if 38: end for 39: Return: |
2.3. Charging Scheduling Strategy and Model Construction Under Multiple Charging Points
2.3.1. Description of the Charging Scheduling Problem for Multiple Charging Points
2.3.2. Charging Scheduling Planning for Multiple Charging Points
- Study which inspection task the robot will complete before going to the charging point.
- When the robot is ready to charge, we should study which charging point the robot chooses to supplement its power.
2.3.3. Model Building
- The mobile robot with full power has 100 units of power, and the power consumption of each inspection task and the power consumption from one inspection task to the next inspection task are based on unit power.
- The moving speed of the robot is constant, and it takes the same time to consume each unit of electricity during the moving process.
- The charging rate of each charging point is the same, and the time to replenish each unit of power consumption is the same.
- For the convenience of management, the robot starts the inspection task from a fixed charging point and returns to the charging point after the inspection task is finished.
- When the robot reaches the charging point, it will not leave until the battery is full.
- When the charging point is set reasonably, it is considered that there is no repeat access to the charging point, and there is no movement from one charging point to the charging point.
3. Results
3.1. Experimental Environment
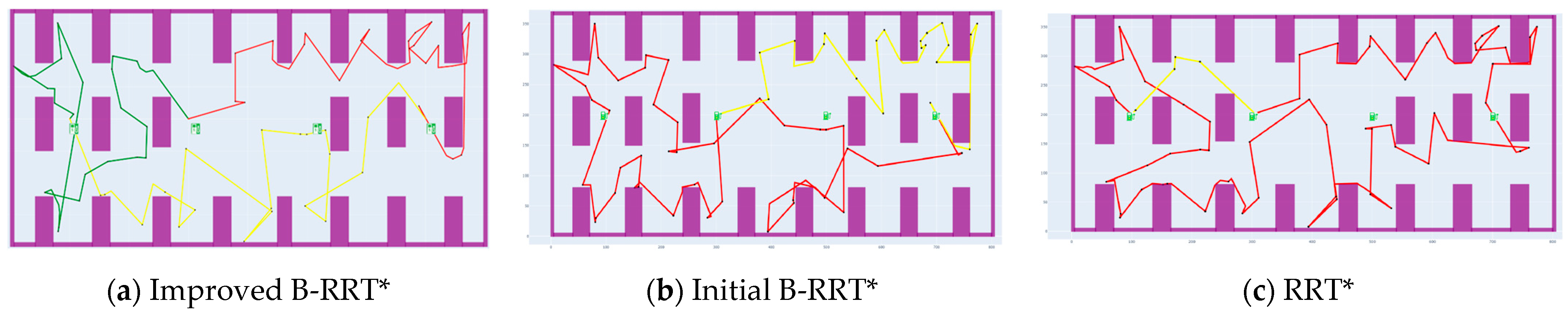
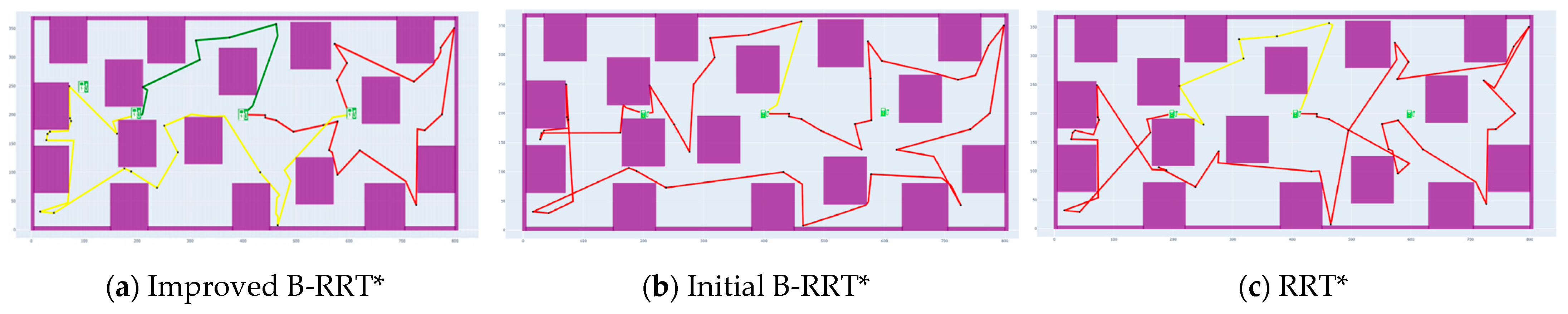
3.2. Simulation Verification
- -
- Case 1:
- -
- Case 2:
- -
- Case 3:
- -
- Case 4:
4. Discussions
- The optimization model considers the power supply problem in the face of multi-task points, and sets up charging points in the appropriate locations to make the model closer to the actual operation situation. Before the robot dog plans its path according to the tasks to be inspected, it will give priority to the current battery power reserve, the consumption cost during the execution of the task, and the consumption cost during the execution of the task. After the execution of a task, when its own power cannot be used to reach the next task, it will give priority to the nearest charging point, and then re-plan the path until all the tasks to be carried out can be covered. The optimal path-planning scheme with the minimum total cost and satisfying charging demands was formed. It should be noted that in this study, the charging stations were distributed uniformly according to the warehouse layout, which occasionally led to redundant stations. Optimizing the number and placement of charging stations is beyond the scope of this paper but represents an important direction for future research, which could be addressed using facility location models or heuristic optimization methods.
- In different scale test scenarios, from a small number of inspection points to a large number of complex distributed inspection points, the model shows good solution speed. To ensure that the performance gains are not the result of random variations inherent in sampling-based algorithms, we conducted paired t-tests across 10 independent runs for each scenario. The results show that the differences between the improved B-RRT* and the baseline algorithms are statistically significant in terms of all three performance metrics (p < 0.05). This confirms that the observed improvements are robust and reliable, rather than coincidental. For the scene containing 20 task points to be inspected, the longest solution time is 29.59 s, and the average solution time is about 20.93 s according to the complexity of the map. As the scale of the scene increases to a medium scale (40 or 60 task points to be inspected), the solving time increases, but it can still be controlled in a reasonable range, and the average time of 40 task points is about 88.09 s. For 60 task points, due to the number of task points being too high and some maps being more complex, the solution time is 233.95 s. With the increase in map complexity, the solution time also increases slightly, but it is also far lower than the solution time of traditional path-planning algorithms in similar scenarios. Additional experiments showed that the improved B-RRT* is robust to parameter variations: while step size, number of samples, and bias weight influence the trade-off between efficiency and path quality, the algorithm consistently outperforms the baselines across a wide range of settings.
- The path-planning model and solution results have strong adaptability in the actual robot dog inspection scene. By modifying the battery capacity, power consumption during task execution and path cost, the number and location of inspection points and the location of charging points can be set, the factory inspection environment can be simulated, and the order of inspection points can be reasonably arranged to meet the requirements of inspection tasks under different circumstances. From the cost–benefit point of view, this path-planning scheme has significant application value. By optimizing the path planning, the invalid walking distance of the robot dog is reduced and the energy consumption is reduced. This not only prolongs the working time of the robot dog after a single charge and reduces the number of charges, but also reduces the equipment loss and maintenance cost caused by frequent charging, and efficient path planning improves the inspection efficiency, meaning inspection tasks can be completed in a shorter time, indirectly bringing the improvement of economic benefits.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pei, Z.; Wan, M.; Du, R.; Li, Y.; Chen, Y. Charging scheduling considering the release time of carrying machinery under multiple charging piles. Comput. Integr. Manuf. Syst. 2021, 4, 1089–1098. (In Chinese) [Google Scholar]
- Ravankar, A.; Ravankar, A.A.; Watanabe, M.; Hoshino, Y.; Rawankar, A. Multi-robot path planning for smart access of distributed charging points in map. Artif. Life Robot. 2021, 26, 52–60. [Google Scholar] [CrossRef]
- Hao, B.; Du, H.; Dai, X.; Liang, H. Automatic recharging path planning for cleaning robots. Mob. Inf. Syst. 2021, 2021, 5558096. [Google Scholar] [CrossRef]
- Li, Z. Research on Path Planning Problem of Electric Logistics Vehicle Considering Different Power Supply Modes. Ph.D. Thesis, Shenyang University of Technology, Shenyang, China, 2021. (In Chinese). [Google Scholar]
- Yuan, J. Research on Electric Bus Driving Plan Considering Charging Continuity and Demand Response. Ph.D. Thesis, Shenyang University of Technology, Shenyang, China, 2023. (In Chinese). [Google Scholar]
- Alizadeh, M.; Wai, H.T.; Scaglione, A.; Goldsmith, A.; Fan, Y.Y.; Javidi, T. Optimized path planning for electric vehicle routing and charging. In Proceedings of the 2014 52nd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 30 September–3 October 2014; IEEE: New York, NY, USA, 2014; pp. 25–32. [Google Scholar]
- Duchoň, F.; Babinec, A.; Kajan, M.; Beňo, P.; Florek, M.; Fico, T.; Jurišica, L. Path planning with modified a star algorithm for a mobile robot. Procedia Eng. 2014, 96, 59–69. [Google Scholar] [CrossRef]
- Noreen, I.; Khan, A.; Habib, Z. Optimal path planning using RRT* based approaches: A survey and future directions. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 97–107. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Yuan, Q. Application of Dijkstra algorithm in robot path-planning. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Inner Mongolia, China, 15–17 July 2011; IEEE: New York, NY, USA, 2011; pp. 1067–1069. [Google Scholar]
- Zhang, T.; Li, Q. Mobile robot path planning based on B-RRT * FND algorithm. Control. Decis. 2023, 11, 3121–3127. (In Chinese) [Google Scholar]
- Meng, W.L.; Pu, Y.B.; Gong, Y. Fusion of local–global strategy for AUV path planning in unknown environment. J. Syst. Simul. Online First. 29 October 2024. [Google Scholar]
- Fu, Y.; Wang, W.; Liu, M.; Chang, L.; Lu, J. Path planning of unmanned vessel based on improved P-RRT* algorithm. Control. Eng. 2024, 1–8. [Google Scholar] [CrossRef]
- Zhao, P.; Chang, Y.; Wu, W.; Luo, H.; Zhou, Z.; Qiao, Y.; Li, Y.; Zhao, C.; Huang, Z.; Liu, B.; et al. Dynamic RRT: Fast Feasible Path Planning in Randomly Distributed Obstacle Environments. J. Intell. Robot. Syst. 2023, 107, 48. [Google Scholar] [CrossRef]
- Ganesan, S.; Ramalingam, B.; Mohan, R.E. A hybrid sampling-based RRT* path planning algorithm for autonomous mobile robot navigation. Expert Syst. Appl. 2024, 258, 125206. [Google Scholar] [CrossRef]
- Wu, Z.; Meng, Z.; Zhao, W.; Wu, Z. Fast-RRT: A RRT-based optimal path finding method. Appl. Sci. 2021, 11, 11777. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z. Ant colony optimization for traveling salesman problem based on parameters optimization. Appl. Soft Comput. 2021, 107, 107439. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Abdollahzadeh, B. An efficient harris hawk optimization algorithm for solving the travelling salesman problem. Clust. Comput. 2022, 25, 1981–2005. [Google Scholar] [CrossRef]
- Bo, H.; Jun, L.I.U.; Hang, L.I.; Xuan, L.I.; Rongcheng, H.E. Research on Path Planning Methods for Multi-axis Sorting Robotic Arms under Complex Working Conditions. Manuf. Technol. Mach. Tool 2025, 7, 24–33. [Google Scholar]
- Song, J.-H.; Liu, Y.-T.; Guo, S.-J. Robot Path planning based on AIP-RRT* and GGF-APF in dynamic environment. J. Instrum. Meters 2025, 46, 51–64. [Google Scholar] [CrossRef]
- Noreen, I.; Khan, A.; Habib, Z. A comparison of RRT, RRT* and RRT*-smart path planning algorithms. Int. J. Comput. Sci. Netw. Secur. 2016, 16, 20. [Google Scholar]
- Shen, J.; Fu, X.; Wang, H.; Shen, S. Fast path planning for underwater robots by combining goal-biased Gaussian sampling with focused optimal search. Comput. Electr. Eng. 2021, 95, 107412. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, S.; Yu, Y.; Wu, Z. Path planning for material scheduling in Industrial Internet scenarios based on an improved RRT* algorithm. J. Frankl. Inst. 2025, 362, 107716. [Google Scholar] [CrossRef]
- Liu, C.; Xiao, F.; Ma, Y.; Chen, H.; Wu, Y.; Li, Z.; Guo, L. An enhanced RRT* algorithm with biased sampling and dynamic stepsize strategy for ship route planning in the high-risk areas. Ocean Eng. 2025, 332, 121466. [Google Scholar] [CrossRef]
- Liu, A.; Yuan, J. Robot path planning based on goal biased bidirectional RRT* algorithm. Comput. Eng. Appl. 2022, 58, 234–240. [Google Scholar]
- Adibeli, J.O.; Liu, Y.-K.; Chao, N.; Awodi, N.J. Modified bidirectional rapidly exploring random tree star (Bi-RRT*) algorithm with variable node parameter for optimized path planning in nuclear decommissioning environment. Nucl. Eng. Des. 2025, 433, 113876. [Google Scholar] [CrossRef]
- Xiong, Z.; Hou, W.; Wang, C.; Chen, H. Classified-RRT*: Node classification RRT*-based algorithm with improved solution performance and convergence rate. Expert Syst. Appl. 2025, 296, 129118. [Google Scholar] [CrossRef]






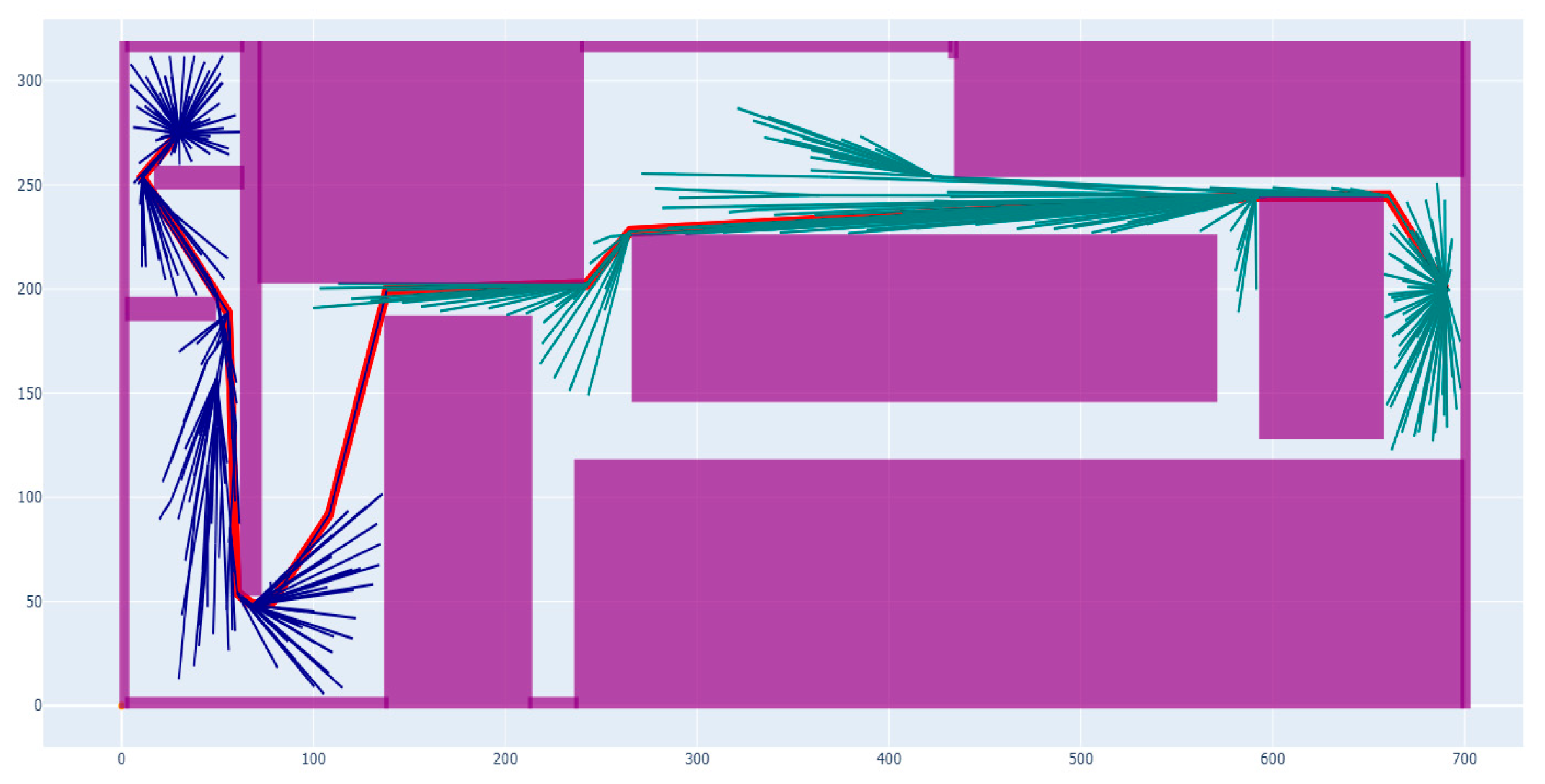

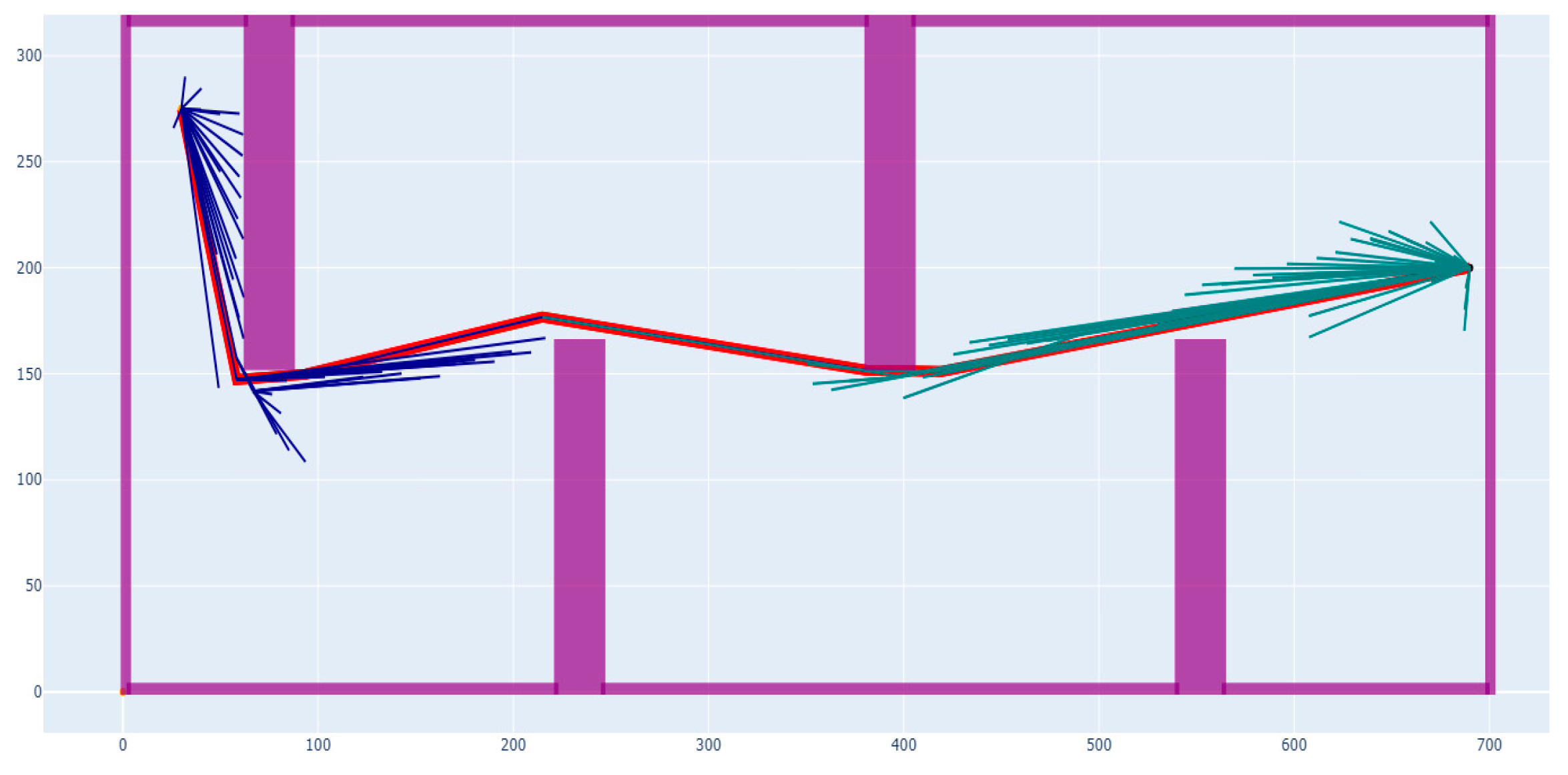
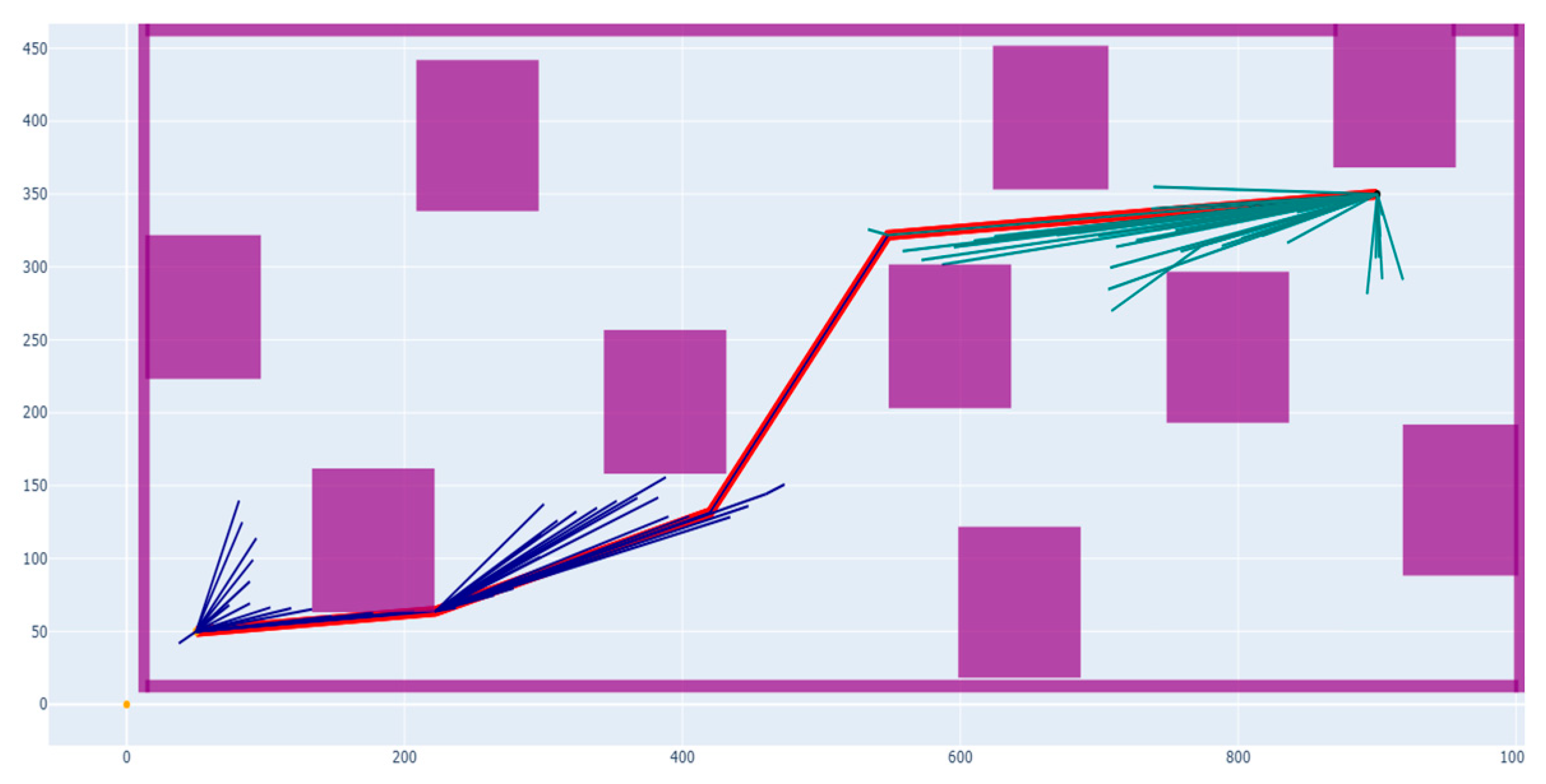











| Environment | Algorithm | Operation Time/s | The Path Length/m | Number of Sampling Points | Operation Success Rate |
|---|---|---|---|---|---|
| Complex | B-RRT* | 3.76 | 57.76 | 861 | 93% |
| Improving B-RRT* | 2.75 | 50.49 | 537 | 95% | |
| Easy | B-RRT* | 1.03 | 42.02 | 299 | 100% |
| Improving B-RRT* | 0.81 | 38.27 | 207 | 100% | |
| Irregularity | B-RRT* | 0.62 | 49.62 | 156 | 100% |
| Improving B-RRT* | 0.48 | 47.33 | 186 | 100% |
| Symbol | Symbol Description |
|---|---|
| The total power consumption of the path in the inspection process | |
| Patrol the power consumed by task i | |
| Power consumption from patrol task i to patrol task j, where i ≠ j | |
| Power consumption from charging point i to patrol task j | |
| Power consumption from charging point i to charging point j | |
| Equal to 1 when the robot moves from patrol task i to patrol task j, and 0 otherwise, where i ≠ j | |
| It is equal to 1 when the robot moves from charging point i to inspection task j, and 0 otherwise | |
| It is equal to 1 when the robot moves from patrol task j to charging point i, and 0 otherwise | |
| It is equal to 1 when the robot moves from charge point i to charge point j, and 0 otherwise | |
| Collection of inspection points | |
| Set of charging points, where charging point 0 is the start and end point of the inspection | |
| The remaining power at inspection task point i | |
| The remaining power to complete inspection task i | |
| The remaining amount of power to reach charging point i |
| Types of Local Algorithms | Number of Mission Points | Average Local Solution Time /s * | Average Number of Sampling Points | Average Global Solution Time /s ** | Average Total Path Cost |
|---|---|---|---|---|---|
| RRT* | 20 | 24.239 | 389 | 1.016 | 114.369 |
| Initial B-RRT* | 8.730 | 179 | 1.038 | 113.334 | |
| Improved B-RRT* | 7.591 | 146 | 0.989 | 103.977 | |
| RRT* | 40 | 126.519 | 715 | 38.955 | 178.494 |
| Initial B-RRT* | 48.901 | 300 | 39.887 | 171.289 | |
| Improved B-RRT* | 42.522 | 235 | 37.988 | 156.001 | |
| RRT* | 60 | 405.682 | 849 | 101.659 | 248.489 |
| Initial B-RRT* | 149.658 | 302 | 104.586 | 242.460 | |
| Improved B-RRT* | 133.624 | 256 | 99.586 | 219.819 |
| Types of Local Algorithms | Number of Mission Points | Average Local Solution Time /s * | Average Number of Sampling Points | Average Global Solution Time /s ** | Average Total Path Cost |
|---|---|---|---|---|---|
| RRT* | 20 | 56.369 | 389 | 1.106 | 168.569 |
| Initial B-RRT* | 24.512 | 197 | 1.031 | 162.350 | |
| Improved B-RRT* | 20.017 | 164 | 0.983 | 154.619 | |
| RRT* | 40 | 186.652 | 468 | 24.205 | 189.657 |
| Initial B-RRT* | 85.623 | 252 | 23.062 | 184.487 | |
| Improved B-RRT* | 69.849 | 224 | 21.964 | 175.702 | |
| RRT* | 60 | 462.145 | 715 | 85.694 | 206.215 |
| Initial B-RRT* | 188.497 | 292 | 83.977 | 197.393 | |
| Improved B-RRT* | 171.361 | 243 | 79.978 | 187.993 |
| Types of Local Algorithms | Number of Mission Points | Average Local Solution Time /s * | Average Number of Sampling Points | Average Global Solution Time /s ** | Average Total Path Cost |
|---|---|---|---|---|---|
| RRT* | 20 | 83.654 | 596 | 3.235 | 135.594 |
| Initial B-RRT* | 31.642 | 424 | 3.121 | 132.547 | |
| Improved B-RRT* | 26.368 | 319 | 2.972 | 123.932 | |
| RRT* | 40 | 189.652 | 769 | 31.236 | 191.641 |
| Initial B-RRT* | 90.414 | 471 | 31.479 | 188.005 | |
| Improved B-RRT* | 75.345 | 356 | 29.980 | 176.949 | |
| RRT* | 60 | 568.954 | 804 | 186.669 | 206.364 |
| Initial B-RRT* | 219.574 | 497 | 184.885 | 203.839 | |
| Improved B-RRT* | 182.978 | 374 | 176.081 | 192.395 |
| Types of Local Algorithms | Number of Mission Points | Average Local Solution Time /s * | Average Number of Sampling Points | Average Global Solution Time /s ** | Average Total Path Cost |
|---|---|---|---|---|---|
| RRT* | 20 | 61.173 | 295 | 2.234 | 149.155 |
| Initial B-RRT* | 21.783 | 181 | 2.122 | 135.947 | |
| Improved B-RRT* | 18.942 | 157 | 2.021 | 129.473 | |
| RRT* | 40 | 193.087 | 389 | 22.658 | 170.927 |
| Initial B-RRT* | 60.154 | 240 | 23.107 | 173.948 | |
| Improved B-RRT* | 52.308 | 209 | 22.007 | 164.712 | |
| RRT* | 60 | 228.727 | 759 | 59.236 | 209.592 |
| Initial B-RRT* | 106.925 | 389 | 59.880 | 211.589 | |
| Improved B-RRT* | 92.978 | 338 | 57.028 | 201.513 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Jin, S.; Li, W.; Li, S.; Guo, J.; Gao, X. Multi-Objective Path Planning for Warehouse Inspection of Mobile Robots Considering Power Limitations and Multiple Charging Points. Processes 2025, 13, 3011. https://doi.org/10.3390/pr13093011
Zhang J, Jin S, Li W, Li S, Guo J, Gao X. Multi-Objective Path Planning for Warehouse Inspection of Mobile Robots Considering Power Limitations and Multiple Charging Points. Processes. 2025; 13(9):3011. https://doi.org/10.3390/pr13093011
Chicago/Turabian StyleZhang, Jinming, Shuli Jin, Wenshuo Li, Shanghe Li, Jiaming Guo, and Xiaoyong Gao. 2025. "Multi-Objective Path Planning for Warehouse Inspection of Mobile Robots Considering Power Limitations and Multiple Charging Points" Processes 13, no. 9: 3011. https://doi.org/10.3390/pr13093011
APA StyleZhang, J., Jin, S., Li, W., Li, S., Guo, J., & Gao, X. (2025). Multi-Objective Path Planning for Warehouse Inspection of Mobile Robots Considering Power Limitations and Multiple Charging Points. Processes, 13(9), 3011. https://doi.org/10.3390/pr13093011







