The Potential of CFD in Sustainable Microbial Fermenter Design: A Review
Abstract
1. Introduction
| Application | Description | Reference |
|---|---|---|
| Resolution of contrary process requirements | Bioreactor processes involve multiple functions:
necessitating a design compromise. Computational models help in process design through the following:
| [25,47] |
| Transition from a batch mode of operation to continuous | Sensor, inlet, outlet, and baffle placement in a continuous stirred bioreactor (CSBR) can be modelled before transitioning from a batch process. This modelling strategy offers the following:
| [47,48] |
| Scale-down and scale-up analysis | Flow analysis is crucial when scaling processes up/down. Mean flow and turbulence scale differently with reactor size and speed. Traditional scaling uses empirical rules and experience. CFD simulations help with the following:
| [30,49] |
| Investigation of new reactor concepts | CFD simulations predict flow, heat transfer, and reactions in reactors. CFD simulations beforehand can be more economical and faster than physical testing. Key contributions include the following:
| [50] |
| Tool for additional process understanding | CFD with digital twins reduces time, costs, and resources. Virtual labs help as bioreactors are expensive and require training. Combining CFD and digital twins improves process understanding and efficiency. | [20] |
| Optimization of operating conditions | CFD optimizes impeller design and operating parameters (speed, temperature, aeration, tank size, liquid height, pH). Enhances mixing efficiency and mass transfer rates. Leads to optimal conditions for cell cultures and improved productivity. | [21,26] |
| Prediction potential | CFD, combined with kinetic models (e.g., Higbie’s penetration model), predicts key process parameters. Helps estimate mass transfer and mixing times. | [31,51,52] |
2. Green Metrics for Sustainability—Link to CFD-Parametrized Design of Aerated STBRs
| CFD Output | Green Metric(s) | Impact on Process Sustainability |
|---|---|---|
| Power draw | WARIEN Energy intensity | Translates directly into electricity consumption; higher power demand increases water-related CO2 emissions and operational energy footprint. |
| Volumetric mass transfer coefficient Gas hold-up | PMI WARIEN | Determines oxygen transfer efficiency; influences aeration energy demand and compressor load, affecting both resource use and carbon footprint. |
| Bubble size distribution | PMI Energy intensity | Controls interfacial area and gas–liquid mass transfer; links sparger and impeller design to oxygen transfer efficiency and energy demand. |
| Mixing time Residence time distribution | PMI Resource intensity | Affects solvent and buffer consumption for cleaning and process consistency; improved mixing reduces dead zones and associated waste streams. |
| Shear stress | E-factor Yield-related metrics | High local shear can damage cells, lower yield and increase by-product formation; directly linked to waste generation and overall process efficiency. |
2.1. Energy Utilization in Fermenters and Its Quantification
- Quantifying the electricity usage for each component individually requires detailed experimental setups and precise measurement techniques. Many studies do not focus on the quantification of specific energy inputs of each STBR design parameter that is associated with energy consumption.
- The specific design, operational parameters, and biochemical reaction mechanisms and the microorganisms in STBRs can vary widely, affecting the energy consumption of each of the components involved in energy consumption. This variation makes it challenging to create generic models applicable even across different STBR systems.
- Research in bioprocessing often prioritizes parameters like oxygen transfer rates, cell growth, and product yield within the context of the optimization of the hydrodynamic conditions for improved product yields and cell growth and conditions. This focus results in fewer studies dedicated to energy usage quantification and modelling.
2.2. Green Metrics and CFD
3. Important Parameters for STBR Characterization
| Parameter | Definition | Equation | References |
|---|---|---|---|
| Power number P0 (also known as the Newton number) | Directly related to the stirrer torque Often utilized to compare different impellers If critical level of turbulence is exceeded P0 becomes constant for many impellers | [81,92] | |
| Reynolds number Re | Dimensionless number used to characterize flow regime based on the ratio of inertial to viscous forces | [93,94] | |
| Mixing time tm | Ability of a bioreactor to efficiently mix the contents are defined by the mixing time A measure of how much time is required to achieve a desired degree of homogeneity (usually 95%) Convection and turbulence are driving forces for mixing and mass transfer | [30,88,95,96] | |
| O2 mass transfer coefficient | As O2 as a low solubility in water-like media, continuous aeration of the system is required O2 can become the limiting factor in high cell density cultivations | [88] | |
| Shear stress τ | Velocity gradients act on the cells as shear and normal stresses Depends on the effective viscosity of the broth and the shear rate, which depends on the impeller geometry and stirring speed | [93] | |
| Volumetric mass transfer coefficient kLa | Used to describe the mass transfer capacity in a bioreactor Different approaches towards calculating kLa Values of kL and a depend on the eddy dissipation rate () Describes how efficiently the gas is distributed in the medium by the impeller | [88,97] |
Dimensionless Numbers
| Dimensionless Number | Definition | Equation |
|---|---|---|
| Power number P0 (also known as the Newton number) | Directly related to the stirrer torque Often utilized to compare different impellers If critical level of turbulence is exceeded, P0 becomes constant for many impellers | |
| Reynolds number Re | Used to characterize flow regime based on the ratio of inertial to viscous forces | |
| Knudsen number Kn | Characterizes the boundary conditions of a fluid flow | |
| Prandtl number Pr | Correlates the fluid viscosity with its thermal conductivity | |
| Schmidt number Sc | Establishes a correlation between the fluid viscosity and its diffusion coefficient | |
| Froude number Fr | Represents the ratio between inertial and gravitational forces | |
| Galilei number Ga | Defined by the ratio of the gravity to viscous forces | |
| Peclet number Pe | Correlates convective and diffusive transport phenomena | |
| Weber number We | Defined as the ratio of inertia to surface tension forces | |
| Courant number C | Represents the distance travelled by the fluid compared to the cell size |
4. Basics of Fluid Mechanics and CFD
4.1. Fermentation and Fluid Mechanics
4.2. The Governing Equations and Conservation Laws
4.3. The CFD Simulation Process
4.4. CFD Simulation Methodologies
4.4.1. Mesh Influence on the Simulation
| Numerical Method | Bioprocess CFD Applications | Advantages/Notes | References |
|---|---|---|---|
| FVM (with Reynolds Averaged Navier–Stokes RANS, Large Eddy Simulations LES, Direct Numerical Simulation DNS) | Hydrodynamics, mixing, impeller effects, turbulence models, mixing time in stirred bioreactors | Common in industrial and research settings; supports turbulence modeling (RANS, LES, DNS) | [47,62,69,79,89,145,146,147,148,149] |
| Euler–Lagrange/Compartment (Parcel-Based) | Modeling environmental gradients, Lagrangian microbial phase, zone-wise behavior for scale-down applications | Enables tracking microbial exposure to gradients; high computational intensity | [6] |
| LBM with LES hybrid | Substrate gradients, hydrodynamics in large-scale stirred reactors, microbial perspective | Offers dynamic accuracy with reduced computational costs vs. FVM; promising method | [24,141,142,143,150] |
| Multiphase Modeling with Population Balances (Euler–Euler + Multiple Size Groups MUSIG) | Gas-liquid mixing, bubble size distribution, kLa and oxygen transfer in industrial-scale fermenters | Captures multiphase interactions and mass transfer; computationally intensive | [151,152,153,154,155,156,157] |
| FEM | Multi-physics modeling, enzymatic/kinetic network integration, broader bioprocess simulations | Accurate for complex coupled systems; less common in fluid flow-specific bioreactor studies | [158] |
| Compartmental/Hybrid Models (CFD-based) | Integration of kinetics and fluid dynamics without full CFD; mixing time prediction in fermenters | Balances accuracy and efficiency; useful for real-time or scale-up models | [84,159,160,161,162,163] |
4.4.2. Impeller Rotation Modelling Approaches
4.4.3. Turbulence Modelling
4.4.4. Multiphase Modelling
4.5. CFD Models in Bioreactor Modelling
4.6. CFD Models and Artificial Intelligence (AI) Methods
| Aim | Operational Set-Up | Operating Conditions | Validation | CFD Model | Results | Reference |
|---|---|---|---|---|---|---|
| Experimental validation comparison with simulation | Two cylindrical bioreactors STBR 1: baffled, Rushton turbine, air injected with a ring sparger at the bottom of the tank into water STBR 2: baffled, three impellers with the bottom impeller being a Rushton, and the middle and top are pitched-blade downflow turbines | Superficial velocity: 0.01 m/s Uniform bubble diameter 0.5 cm for STBR 2 For tri-phase the particle diameter is constant at 150 µm and density of 1190 kg/m3 Impeller speeds of 3.78 and 5.08 RPS for two-phase simulations | X-ray Computed Tomography (CT) Experiments for gas hold-up measurements | Solvers: Reacting two phase Euler foam for STBR 1, Reacting multiphase Euler foam with tri-phase for STBR 2: air, water and polymethyl methacrylate particles No-slip boundary condition at the tank wall and baffles Constant gas inlet velocity and atmospheric pressure at gas inlet and outlet respectively | Good agreement of gas hold-up in STBR 1 between simulations and experimental data Similarly also for STBR 2 with the exception of the calculated gassed power consumption smaller than experimental value Bottom Rushton turbine flooded with particles in tri-phase simulation, with a radial pumping flow at the upper turbines | [8] |
| MRF evaluation | Reactor: Height = Diameter = 30 cm Four baffles of 3 cm width arranged at 90° intervals along the tank Impeller: 45° pitched turbine blade “Pumping down” impeller with four blades Axial location 10 cm from reactor bottom and diameter of 10 cm | - | Laser-Doppler Anemometry (LDA) | MRF RANS k-ε turbulence model Solver: SIMPLE algorithm | Simulation results somewhat match the experimental velocity profiles Velocity vector plots and turbulence intensity contour plots Axial velocity depicted as a function of dimensionless radial coordinate Biggest discrepancy in the axial velocity profile near the impeller Size of MRF domain near the impeller can influence the solution Zone interfaces should not be close to the impeller or baffles | [215] |
| Mixing time and kLa with prediction potential | Torispherical-bottomed cylindrical and baffled STBR with one impeller in an up-pumping configuration Liquid level H = 0.7–1.65 T Loading volume range of 150–350 L | Agitation speeds of 150, 320 and 400 RPM | Tracer experiments with sodium chloride Power number | Standard RANS k-ε turbulence model Average Navier–Stokes Euler–Euler approach for steady state runs Transient rotor–stator interface approach for unsteady state runs | Mixing time for power inputs for water and xanthan gum ranging from 0.5 to 9.2 kWm−3 using the CFD model CFD model to predict kLa validated with independent data and as accurate as empirical correlations for kLa estimation Bubble size dependent on gas flowrate and power input for the investigated conditions | [31] |
| Validation of a Euler–Lagrange modelling approach coupling a CFD-based compartment model (Eulerian approach) and a stochastic model based on a Continuous-Time Markov Chain (Lagrangian approach) | Hemispheric bottom vessel H = T = 0.305 m Working volume of 20 L Axial impeller Di = 0.125 m Clearance from bottom Ci = T/3 Two baffles positioned 180° from each other | Water as single phase Rotational speed 100 RPM | PIV optical trajectography Tracer experiments with 4 mL NaCl solution | Standard RANS k-ε turbulence model SM | Good reproducibility of the concentration evolution after pulse injection by the CFD simulation Good representation of the turbulent flow by the CFD/compartment model However, no consideration of gas phase and thus only suitable for cultures with low oxygen demand | [211] |
| Evaluation of mixing in baffled and unbaffled vessels | Different reactor types | Distilled water at 25° Mixing speeds of 30, 90, 120 and 200 RPM | Tracer experimental tests with 1M NaCl solution and conductivity measurements Dissolution of sucrose | MRF RANS k-ε turbulence model Python script utilized to discretize the normal distribution of the sucrose crystals into 100 size classes | Good agreement between experimental and simulated tracer and sucrose dissolution tests 3D geometry of the stirred vessel and the impeller strongly affect the fluid flow, and it should be good practice to use CFD to examine this effect as assumptions (such as the improvement of axial flow with baffles) is not always to be observed | [29] |
| Prediction of bubble size distribution (BSD) and a more efficient approach towards optimized mixing | Cylindrical STBR with spherical bottom Three impellers: Rushton impeller, two three-blade propeller type impellers with each blade bent at a 24° angle Four baffles in STBR Pipe sparger | Impeller speed 200 RPM | kLa prediction | MRF k-ε turbulence model Euler–Euler multiphase Population balance model | Optimized mixing achieved by increasing shear in the system through an increase of impeller speed to create smaller bubbles Good agreement of CFD with experimental results | [212] |
| Modelling: Aerobic fermentation | STBR with impeller types of bent blade disc turbine, concaved blade disc turbine, and Rushton turbine of 4 baffles T = 175 mm Height of the tank = 240 mm H = 125 mm Bw = 12 mm; height of baffles = 220 mm; clearance of baffles and tank wall = 2 mm Di = 12 mm Height of impeller above tank bottom C = 47.5 mm Height of air sparger above tank bottom G = 10 mm Thirteen holes are evenly distributed along sparger | Impeller speeds: 400–700 RPM | Experimental fermentation | CFD-Taguchi approach Iteration: 1000 steps Two-phase RNG k-ε turbulence model Eulerian multiphase conditions: average bubble diameter 4 mm | Three key viscosity values and their corresponding consistency phases as control parameters were identified by examining the viscosity growth curve throughout the reaction Control parameters were subjected to quantitative assessment to gauge their impact on the fermentations | [213] |
| CFD-based kinetic in an industrial bioreactor | Stirred tank reactor with Rushton turbines Sparger in the rotating domain Baffles and coils in the stationary field | Glucose was inserted through the top at feed rates: 0.5 kg/s, 1.0 kg/s, 1.5 kg/s, and 2.0 kg/s Impeller speed 69 RPM | - | Single liquid phase Standard RANS k-ε turbulence model Steady state | Cells were found to flourish in aerobic conditions, but some sections also experienced anaerobic digestion As the mass flow rate increased, the area undergoing anaerobic digestion expanded Glucose content varied by 2–5% at all flow rates due to uncertainties in the kinetic factors that govern aerobic metabolism As the fed-batch process advanced, the glucose gradient level increased due to the larger capacity and longer mixing time At the beginning of the study, the model showed the most significant response to the basic model | [214] |
| Investigation of gas-liquid two-phase flow characteristics in stirred tank with two combined dual impellers | Cylindrical tank (T = 420 mm) with standard ellipsoidal at the bottom of the tank Four equally spaced baffles Clearance between baffle and tank wall 2 mm Heigh of liquid in tank 500 mm Ring sparger (diameter 210 mm) below the lower impeller with 20 downward-facing holes Three impellers used with diameter T/2 (2 impellers used in combination in each set-up): Six-bent-bladed turbine (6BT) as the lower impeller Six-inclined-blade down-pumping turbine (6ITD) Six-inclined-blade up-pumping turbine (6ITU) as the upper impeller | Tap water and air used Gas flowrate 0.76 m3/h For CFD simulations: Impeller speed 60–120 RPM For PIV measurements: Impeller speed 60 RPM | PIV CFD-PBM coupled model validated based on power consumption experiments and BSD | MRF Standard RANS k-ε turbulent model Euler-Euler multiphase model PBM to solve BSD with Luo break-up and Luo and Svendsen coalescence—MUSIG model | Effects of impeller speed and gas flowrate on flow fields, gas hold-up, BSD, gas-liquid interfacial area examined Presence of gas changes the flow field structure and can improve fluid mixing with 6BT + 6ITU 6BT + 6ITU can achieve more uniform bubble sizes with improved bubble dispersion performance compared to the other impeller configuration (6BT + 6ITD) Gas hold-up distribution and gas-liquid interfacial area with this configuration more well-distributed Gas hold-up vastly improved with increasing impeller speeds compared with increasing gas flowrates High impeller speeds more beneficial to the increase of gas hold-up in comparison to gas flowrates CFD simulations of power consumption close to experimental data with a maximum deviation of 6.3% | [152] |
| Investigation of utilization of LES approach to simulate and predict different aspects of mixing in a stirred tank | Baffled tank with diameter T = 270 mm Liquid height in tank H = T = 270 mm Rushton turbine with diameter 90 mm with a distance of 90 mm from the vessel bottom | Water at 25 °C used Impeller speed 250 RPM | Experimental data available in literature | MRF as a starting point and then switched to unsteady state (SM) Standard RANS k-ε turbulent model used as a starting point until steady state flow field; these results used as initial approximations for LES turbulent model Smagorinsky–Lilly model as a subgrid model | Flow field, power consumption, mixing time, turbulent kinetic energy and turbulent dissipation rate were predicted Good agreement between CFD simulations and experimental data—mean tangential and axial velocities, radial average velocities, power consumption and mixing time Mixing time depends on feed points due to a couple of reasons: 1. Inner rotating mesh was main promoter of tracer distribution 2. Lack of tangential exchange of tracer between flow loops which were in between the baffles Increasing the Re value creates a stronger radial out-flow which pushes the tracer into the recirculation loops and reduces mixing times Comparison of LES and RANS predictions of the tracer concentration profile with experimental data demonstrates improved predictions with LES that can result in more reliable design of the mixing process CFD model deviate from experimental data closer to the impeller tip as the simulated flow field shows this to be mostly symmetrical but experimental data are slightly skewed toward the upper side of the impeller | [145] |
| Investigation of the effect of modelling approach, discretization scheme and turbulence model on turbulent flow in stirred tanks | Dish-bottomed cylindrical tank T = H = 0.19 m Four equally spaced baffles with width T/10 Six-blade 45° pitched blade turbine with diameter Di = T/2 Hub diameter 0.2D Positioned at T/3 on a shaft that extended from the vessel base to the liquid surface | Water at 273 K Impeller rotational speed 300 RPM (Re = 45,000) Up- and down-pumping configuration | LDV | SM, frozen-rotor model and circumferential averaging model Standard RANS k-ε turbulent model and RNG k-ε turbulent model | Choice of impeller model only slightly affect the mean radial and axial flow patterns in the impeller discharge region and only slightly underpredict the dimensionless turbulent kinetic energy Discretization scheme had no effect on mean radial and axial velocities in the vessel and underpredicted the dimensionless turbulent kinetic energy, with first order schemes underpredicting it the most First order UW underpredicted a swirling region underneath the impeller Both turbulence models had no significant effect on the mean radial and axial velocities Dimensionless turbulent kinetic energy values also underpredicted by both turbulence models, especially in the discharge region of the impeller CFD simulations somewhat underpredicted dimensionless turbulent kinetic energy and power numbers and overpredicted the circulation numbers in both up- and down- pumping configurations LES predicted better the kinetic energy levels that match better with the experimental data Discrepancies in the prediction of turbulent parameters maybe come from Reynolds averaging | [146] |
| Identification of various flow regimes in dual Rushton turbines stirred bioreactor for various gas flowrates and impeller speeds | Baffled cylindrical acrylic vessel with T = 160 mm and height 250 mm Dual impellers mounted on the shaft First impeller 90 mm and the second 110 mm from the vessel bottom Rushton turbine with diameter 64 mm Liquid height of 240 mm Ring sparger | Different flowrates and impeller speeds used for various different tests Gas flowrates 0.3, 0.5 and 1.0 vvm Impeller rotation speeds range 200–600 RPM Tracer experiments: hydrochloric acid | Tracer experimental tests with 1 M hydrochloric acid solution and pH measurements Measurements of gas hold-up distribution | MRF Standard k-ε turbulence model Euler–Euler multiphase model MUSIG model with break-up and coalescence modelled using isotropic turbulence theory | Gas hold-up increases with an increase in impeller rotational speed Mixing time varied depending on the operating flow regimes Good agreement between experimental data and CFD simulations | [210] |
| Model development of gas-liquid mixing and bubble size distribution to predict the effect of using ring or pipe spargers and impeller diameter on kLa | 50 L two-chamber single-use bioreactor vessel T = 38 cm and height = 67 cm H = 42 cm Three-blade impeller pitched at 30° Di = 22.8 cm Air sparger was a pipe with length 3.1 cm and pore sizes of 10 μm | For CFD, different Di, pipe spargers with different lengths and ring sparger with different diameters examined. Impeller tip speeds of 0.6, 1.2 and 1.8 m/s Air sparging rate set at 0.02, 0.05 and 0.1 vvm | kLa measurements PIV | MRF k-ε dispersed turbulence model Euler–Euler model Population balance model with different sizes of bins | Population balance model accounted for bubble coalescence and break-up absolutely necessary for accurate prediction of multiphase flow Ring sparger showed better performance over the pipe sparger when comparing kLa and ga hold-up Optimum diameter shown to be 80% of the impeller diameter kLa prediction with constant bubble size simulation proved to be very different from experimental results Population balance with different bin sizes predicted more realistic kLa values kLa directly proportional to the impeller-to-vessel diameter ratio raised to the power of 2.8 | [208] |
| Analysis of the influence of impeller configuration and rotational speed on hydrodynamic behavior and mixing performance of the STBR with double impeller | 0.02 m3 fermenter; T = 0.263 m Two different impeller configurations utilized Clearance from tank bottom Ci = 0.088 m Four baffles Baffle width 0.025 m Total liquid volume 0.015 m3; H = 1.14T | Water at room temperature Three different impeller speeds: 50, 100 and 150 RPM | Power number comparison | Simulations performed with the High-Performance Computing Virtual Laboratory Canada MRF k-ε turbulence model | Good agreement of power values between simulations and experimentally measured values Higher interaction between impellers with an increase in rotational speed Increase in rotational speed leads to a rise in power values, average strain rate magnitude and average shear stress values, with a simultaneous decrease in mixing time Different impeller configurations exhibit different Flow numbers, power numbers and average shear stress values | [79] |
| Characterization of heterogenous cell population in an STBR with unideal mixing | E. coli 0.9 m3 stirred tank reactor | Only indirectly experimentally validated | Euler–Lagrange simulations with Lagrangian reaction coupling Structured cellular model applied for sugar uptake | CFD simulations and kinetic model validation with experimental data from literature Glucose concentration field data is qualitatively verified from experimental observations from the literature | [209] |
4.7. Limitations of CFD
5. Outlook and Future Applications
| Trend | Topic | Research Tasks | Sustainability/Credibility Impact | References |
|---|---|---|---|---|
| Hybrid CFD + AI/ML surrogates | Efficient investigation of process space design Reduced computational burden | Develop benchmark datasets Validate surrogate accuracy | Lower energy use for simulation Faster optimization, leading to reduced experimental trials | [6,159,223] |
| Digital twins and real-time control | Online monitoring and prediction Soft-sensors for gradients and kLa | Integrate CFD-reduced models with process analytical technology sensors Demonstrate predictive control in pilot STBRs | Enables continuous/ circular manufacturing Improved resource efficiency and robustness | [235,263,264,265] |
| Verification, validation, and uncertainty quantification | Higher credibility and reproducibility | Standardize reporting (mesh, turbulence models, CPU, runtimes) | Accurate predictions Improved regulatory acceptance Reproducible science | [64,266] |
| Advanced multiphase modeling (PBM-CFD, LBM) | Better bubble/droplet size prediction Interfacial dynamics | Benchmark breakup/coalescence kernels Compare Euler–Euler vs. Euler–Lagrange vs. mesh-free | More accurate O2 transfer and kLa leads to optimized aeration and lower power demand | [24,141,142,143,150,151,152,153,154,155,156,157] |
| Dynamic thermophysical property modeling | Capture time-dependent viscosity | Couple biomass/ rheology correlations with CFD | Better representation of real broth leads to improved scale-up reliability | [112,115] |
| CFD + biokinetic modeling via compartmental or integrated approaches | Link hydrodynamics to metabolic kinetics Simulate gradients of substrates, oxygen, and products Accelerate fermentation modeling | Develop hybrid CFD-kinetic models Validate compartment approaches | Enables realistic prediction of product yield, quality, and waste streams and supports efficient scale-up and process sustainability | [6,69,159,161,211,222,248] |
| CFD × Sustainability metrics | Link reactor physics to environmental footprint | Combine CFD outputs (power consumption, kLa, mixing) with lifecycle and technoeconomic assessment frameworks Case studies for E. coli STBRs | Enables energy- and carbon-aware design Supports sustainable bioprocessing | [23,267] |
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Definition |
| a | Specific Surface |
| AG | Gas Bubble Surface |
| cp | Specific Heat Capacity |
| C1 | Constant for Oxygen Diffusivity |
| dB | Gas Bubble Diameter |
| DL | Oxygen Diffusivity |
| D, Γ | Diffusion Coefficient |
| dO2 | Solved Oxygen Concentration |
| dO2* | Maximum Solved Oxygen Concentration |
| F ⃗ | Force Vector |
| ∆x | Differentially Small Change in Distance |
| ∆t | Differentially Small Time Step |
| k | Turbulent Kinetic Energy |
| kL | Oxygen Transfer Coefficient |
| Lchar | Characteristic Length |
| M | Torque |
| N | Rotational Speed |
| P | Power |
| Po | Power Number |
| qO2 | Specific Oxygen Requirement |
| Sφ | Source Term of Variable φ |
| T | Temperature |
| tm | Mixing Time |
| u ⃗ | Velocity Vector |
| ux | Velocity Component in x-Direction |
| u, v, w | Velocity Components in 3 Directions |
| V | Volume |
| x | 3D Cartesian Coordinate |
| X | Biomass Concentration |
| αG | Phase Fraction of Gaseous Bubbles |
| αk | Phase Fraction of Phase k |
| γave | Average Shear Rate |
| γ | Surface Tension Force |
| δ | Partial Derivative |
| ε | Turbulent Energy Dissipation Rate in Liquid Phase per Unit Mass |
| ϵ | Average Viscous Dissipation Rate of Turbulent Energy per Unit Mass |
| η | Molecular Viscosity (Spatial Scale) |
| λ | Mean Free Path Length |
| λh | Heat Conductivity |
| μ | Dynamic Viscosity |
| μeff | Effective Viscosity |
| μ | Liquid Viscosity |
| νL, ν | Kinematic Viscosity |
| π | Pi |
| ρ | Density of Liquid Phase |
| θ95 | Mixing Time at 95% Homogeneity |
| τ | Shear Stress |
| τave | Average Shear Stress |
| τη | Time Scale |
| φ | Any Generic Variable |
| ω | Specific Dissipation Rate |
| ∆ | Nabla Operator |
| Convective Mass Transfer | |
| Molecular Diffusion | |
| Net Rate of Production | |
| Sub- and Superscripts | |
| ave | Average |
| char | Characteristic |
| eff | Effective |
| i | Impeller |
| G | Gaseous Phase |
| h, k | For Two Different Phases |
| L | Liquid Phase |
| m | Mixing |
| 0 | Referred to Actual Value |
| 95 | 95% Homogeneity |
| Acronyms and Abbreviations | |
| AI | Artificial Intelligence |
| AMI | Arbitrary Mesh Interface |
| ANN | Artificial Neural Network |
| API | Active biopharmaceutical Ingredient |
| Bw | Wall Baffles |
| BSD | Bubble Size Distribution |
| C | Courant Number |
| CAD | Computer-Aided Design |
| CAGR | Compound Annual Growth Rate |
| CCD | Charge Coupled Device |
| CFD | Computational Fluid Dynamics |
| CFD-ANN-NSGA | Computational Fluid Dynamics–ArtificialNeural Network–Non-dominated SortingGenetic Algorithm |
| Ci | Impeller Clearance |
| CSBR | Continuously Stirred Bioreactor |
| CT | Computed Tomography |
| Di | Impeller Diameter |
| DES | Detached Eddy Simulation |
| DNA | Deoxyribonucleic Acid |
| DNS | Direct Numerical Simulation |
| DoE | Design of Experiments |
| E. coli | Escherichia coli |
| E-Factor | Environmental Factor |
| FEM | Finite Element Methods |
| Fr | Froude Number |
| FVM | Finite Volume Methods |
| Ga | Galilei Number |
| H | Liquid Height |
| HCl | Hydrochloric Acid |
| Kn | Knudsen Number |
| LB | Lattice Boltzmann |
| LBM | Lattice Boltzmann Methods |
| LCA | Life Cycle Assessment |
| LDA | Laser Doppler Anemometry |
| LDV | Laser Doppler Velocimetry |
| LES | Large Eddy Simulation |
| ML | Machine Learning |
| MMI | Mass Manufacturing Intensity |
| MRF | Multiple Reference Frames |
| MUSIG | Multiple Size Group |
| NaCl | Sodium Chloride |
| N-S | Navier-Stokes |
| Ne | Newton Number |
| OTR | Oxygen Take-up Rate |
| OUR | Oxygen Uptake |
| PBE | Population Balance Equation |
| PBM | Population Balance Model |
| PDEs | Partial Differential Equations |
| Pe | Peclet Number |
| PIV | Particle Image Velocimetry |
| PLIF | Planar Laser-Induced Fluorescence |
| PMI | Process Mass Intensity |
| Pr | Prandtl Number |
| QbD | Quality-by-Design |
| RANS | Reynolds-Averaged Navier–Stokes |
| rDNA | Recombinant Deoxyribonucleic Acid |
| Re | Reynolds Number |
| RNG | Re-Normalization Group |
| RPM | Revolutions Per Minute |
| RSM | Reynolds Stress Model |
| RTD | Residence Time Distribution |
| R&D | Research and Development |
| Sc | Schmidt Number |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
| SM | Sliding Mesh |
| SPH | Smoothed Particle Hydrodynamics |
| SST | Shear Stress Transport |
| STBR | Stirred Tank Bioreactor |
| SUS | Single-Use Systems |
| T | Tank Diameter |
| TEA | Techno-Economic Analysis |
| UDF | User-Defined Function |
| UW | Upwind |
| VOF | Volume of Fluid |
| W | Impeller Blade Length |
| WARIEN | Water Related Impact of Energy |
| We | Weber Number |
| 6BT | Six-Bent Blade Turbine |
| 6ITD | Six-Inclined Blade Down-pumping Turbine |
| 6ITU | Six-Inclined Blade Up-pumping Turbine |
References
- Buarque, F.S.; Lemes, A.C.; Coelho, M.A.Z. Advances in Industrial Biotechnology: Bioprocess and Bioseparation. Processes 2025, 13, 1101. [Google Scholar] [CrossRef]
- Show, P.L. Special Issue on “Biotechnology for Sustainability and Social Well Being”. Processes 2021, 9, 216. [Google Scholar] [CrossRef]
- Szkodny, A.C.; Lee, K.H. Biopharmaceutical Manufacturing: Historical Perspectives and Future Directions. Annu. Rev. Chem. Biomol. Eng. 2022, 13, 141–165. [Google Scholar] [CrossRef]
- Griffiths, E. Quality standards for biopharmaceuticals: The importance of good manufacturing practice. GaBI J. 2020, 9, 97–99. [Google Scholar] [CrossRef]
- Martin, D.K.; Vicente, O.; Beccari, T.; Kellermayer, M.; Koller, M.; Lal, R.; Marks, R.S.; Marova, I.; Mechler, A.; Tapaloaga, D.; et al. A brief overview of global biotechnology. Biotechnol. Biotechnol. Equip. 2021, 35, S5–S14. [Google Scholar] [CrossRef]
- Singh, V.K.; del Val, I.J.; Glassey, J.; Kavousi, F. Integration Approaches to Model Bioreactor Hydrodynamics and Cellular Kinetics for Advancing Bioprocess Optimisation. Bioengineering 2024, 11, 546. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, J.; Tillegreen, C.B.; Petranovic, D. Innovation trends in industrial biotechnology. Trends Biotechnol. 2022, 40, 1160–1172. [Google Scholar] [CrossRef]
- Hu, X.; Dogan Ilgun, A.; Passalacqua, A.; Fox, R.O.; Bertola, F.; Milosevic, M.; Visscher, F. CFD simulations of stirred-tank reactors for gas-liquid and gas-liquid-solid systems using OpenFOAM®. Int. J. Chem. React. Eng. 2021, 19, 193–207. [Google Scholar] [CrossRef]
- Gundinger, T.; Kittler, S.; Kubicek, S.; Kopp, J.; Spadiut, O. Recombinant Protein Production in E. coli Using the phoA Expression System. Fermentation 2022, 8, 181. [Google Scholar] [CrossRef]
- Schmideder, A.; Weuster-Botz, D. High-performance recombinant protein production with Escherichia coli in continuously operated cascades of stirred-tank reactors. Ind. Microbiol. Biotechnol. 2017, 44, 1021–1029. [Google Scholar] [CrossRef]
- Buffo, M.M.; Esperança, M.N.; Farinas, C.S.; Badino, A.C. Relation between pellet fragmentation kinetics and cellulolytic enzymes production by Aspergillus niger in conventional bioreactor with different impellers. Enzym. Microb. Technol. 2020, 139, 109587. [Google Scholar] [CrossRef] [PubMed]
- Spadiut, O.; Capone, S.; Krainer, F.; Glieder, A.; Herwig, C. Microbials for the production of monoclonal antibodies and antibody fragments. Trends Biotechnol. 2014, 32, 54–60. [Google Scholar] [CrossRef]
- Kopp, J.; Kittler, S.; Slouka, C.; Herwig, C.; Spadiut, O.; Wurm, D.J. Repetitive Fed-Batch: A Promising Process Mode for Biomanufacturing with E. coli. Front. Bioeng. Biotechnol. 2020, 8, 573607. [Google Scholar] [CrossRef]
- Gu, Q.; Yang, S.; Mohsin, A.; Yu, J.; Zhuang, Y.; Li, C. Optimization of oxygen transfer and power consumption in aerobic bioprocess by designing disc turbine impeller based on CFD-Taguchi method. Sci. Rep. 2025, 15, 8102. [Google Scholar] [CrossRef]
- Zhu, L.; Liao, Y.; Chang, X.; Su, M.; Ou, Y.; Wu, S.; Wu, Z.; Yang, H.; Li, J.; Huang, H. A Comparative Study of the Performance of Orbitally Shaken Bioreactors (OSRs) and Stirred Tank Bioreactors (STRs). Processes 2024, 12, 2849. [Google Scholar] [CrossRef]
- Sarkis, M.; Fyfe, A.T.; Kontoravdi, C.; Papathanasiou, M.M. Towards a Net Zero, socially sustainable and eco-efficient biopharma industry: How far are we? Curr. Opin. Chem. Eng. 2024, 44, 101027. [Google Scholar] [CrossRef]
- Sheldon, R.A. Metrics of Green Chemistry and Sustainability: Past, Present, and Future. ACS Sustain. Chem. Eng. 2018, 6, 32–48. [Google Scholar] [CrossRef]
- Benison, C.H.; Payne, P.R. Manufacturing mass intensity: 15 Years of Process Mass Intensity and development of the metric into plant cleaning and beyond. Curr. Res. Green Sustain. Chem. 2022, 5, 100229. [Google Scholar] [CrossRef]
- Jimenez-Gonzalez, C.; Lund, C. Green metrics in pharmaceutical development. Curr. Opin. Green Sustain. Chem. 2022, 33, 100564. [Google Scholar] [CrossRef]
- Seidel, S.; Eibl-Schindler, R.; Eibl, D. Laboratory-independent exploration of stirred bioreactors and their fluid dynamics. Educ. Chem. Eng. 2023, 42, 80–87. [Google Scholar] [CrossRef]
- Xu, C.; Liu, X.; Ding, C.; Zhou, X.; Xu, Y.; Gu, X. Power consumption and oxygen transfer optimization for C5 sugar acid production in a gas-liquid stirred tank bioreactor using CFD-Taguchi method. Renew. Energy 2023, 212, 430–442. [Google Scholar] [CrossRef]
- Seidel, S.; Mozaffari, F.; Maschke, R.W.; Kraume, M.; Eibl-Schindler, R.; Eibl, D. Automated Shape and Process Parameter Optimization for Scaling Up Geometrically Non-Similar Bioreactors. Processes 2023, 11, 2703. [Google Scholar] [CrossRef]
- Panunzi, A.; Moroni, M.; Mazzelli, A.; Bravi, M. Industrial Case-Study-Based Computational Fluid Dynamic (CFD) Modeling of Stirred and Aerated Bioreactors. ACS Omega 2022, 7, 25152–25163. [Google Scholar] [CrossRef]
- Kersebaum, J.; Flaischlen, S.; Hofinger, J.; Wehinger, G.D. Simulating Stirred Tank Reactor Characteristics with a Lattice Boltzmann CFD Code. Chem. Eng. Technol. 2024, 47, 586–595. [Google Scholar] [CrossRef]
- Sharma, C.; Malhotra, D.; Rathore, A.S. Review of Computational fluid dynamics applications in biotechnology processes. Biotechnol. Prog. 2011, 27, 1497–1510. [Google Scholar] [CrossRef] [PubMed]
- Hoseini, S.S.; Najafi, G.; Ghobadian, B.; Akbarzadeh, A.H. Impeller shape-optimization of stirred-tank reactor: CFD and fluid structure interaction analyses. Chem. Eng. J. 2021, 413, 127497. [Google Scholar] [CrossRef]
- Ramírez, L.A.; Pérez, E.L.; Díaz, C.G.; Luengas, D.A.C.; Ratkovich, N.; Reyes, L.H. CFD and Experimental Characterization of a Bioreactor: Analysis via Power Curve, Flow Patterns and k L a. Processes 2020, 8, 878. [Google Scholar] [CrossRef]
- Mishra, S.; Kumar, V.; Sarkar, J.; Rathore, A.S. CFD based mass transfer modeling of a single use bioreactor for production of monoclonal antibody biotherapeutics. Chem. Eng. J. 2021, 412, 128592. [Google Scholar] [CrossRef]
- Oblak, B.; Babnik, S.; Erklavec-Zajec, V.; Likozar, B.; Pohar, A. Digital Twinning Process for Stirred Tank Reactors/Separation Unit Operations through Tandem Experimental/Computational Fluid Dynamics (CFD) Simulations. Processes 2020, 8, 1511. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E.; Santos, V.E. Fluid dynamic conditions and oxygen availability effects on microbial cultures in STBR: An overview. Biochem. Eng. J. 2020, 164, 107803. [Google Scholar] [CrossRef]
- Bach, C.; Yang, J.; Larsson, H.; Stocks, S.M.; Gernaey, K.V.; Albaek, M.O.; Krühne, U. Evaluation of mixing and mass transfer in a stirred pilot scale bioreactor utilizing CFD. Chem. Eng. Sci. 2017, 171, 19–26. [Google Scholar] [CrossRef]
- Haddadi, B.; Jordan, C.; Harasek, M. Cost efficient CFD simulations: Proper selection of domain partitioning strategies. Comput. Phys. Commun. 2017, 219, 121–134. [Google Scholar] [CrossRef]
- Wu, B. CFD Analysis of Mechanical Mixing in Anaerobic Digesters. Trans. ASABE 2009, 52, 1371–1382. [Google Scholar] [CrossRef]
- Babi, D.K.; Griesbach, J.; Hunt, S.; Insaidoo, F.; Roush, D.; Todd, R.; Staby, A.; Welsh, J.; Wittkopp, F. Opportunities and challenges for model utilization in the biopharmaceutical industry: Current versus future state. Curr. Opin. Chem. Eng. 2022, 36, 100813. [Google Scholar] [CrossRef]
- Rogers, L.; Jensen, K.F. Continuous manufacturing—The Green Chemistry promise? Green Chem. 2019, 21, 3481–3498. [Google Scholar] [CrossRef]
- Baumann, M.; Moody, T.S.; Smyth, M.; Wharry, S. A Perspective on Continuous Flow Chemistry in the Pharmaceutical Industry. Org. Process. Res. Dev. 2020, 24, 1802–1813. [Google Scholar] [CrossRef]
- Dallinger, D.; Kappe, C.O. Why flow means green—Evaluating the merits of continuous processing in the context of sustainability. Curr. Opin. Green Sustain. Chem. 2017, 7, 6–12. [Google Scholar] [CrossRef]
- Lee, S.L.; O’Connor, T.F.; Yang, X.; Cruz, C.N.; Chatterjee, S.; Madurawe, R.D.; Moore, C.M.V.; Yu, L.X.; Woodcock, J. Modernizing Pharmaceutical Manufacturing: From Batch to Continuous Production. J. Pharm. Innov. 2015, 10, 191–199. [Google Scholar] [CrossRef]
- Burange, A.S.; Osman, S.M.; Luque, R. Understanding flow chemistry for the production of active pharmaceutical ingredients. iScience 2022, 25, 103892. [Google Scholar] [CrossRef]
- Partopour, B.; Pollard, D. Advancing biopharmaceutical manufacturing: Economic and sustainability assessment of end-to-end continuous production of monoclonal antibodies. Trends Biotechnol. 2025, 43, 462–475. [Google Scholar] [CrossRef]
- Kopp, J.; Spadiut, O. A Guideline to Set Up Cascaded Continuous Cultivation with E. coli Bl21 (DE3). In Bioreactors in Stem Cell Biology: Methods and Protocols; Turksen, K., Ed.; Springer: New York, NY, USA, 2022; pp. 223–240. [Google Scholar] [CrossRef]
- Domokos, A.; Nagy, B.; Szilágyi, B.; Marosi, G.; Nagy, Z.K. Integrated Continuous Pharmaceutical Technologies—A Review. Org. Process. Res. Dev. 2021, 25, 721–739. [Google Scholar] [CrossRef]
- Jiménez-González, C.; Poechlauer, P.; Broxterman, Q.B.; Yang, B.; am Ende, D.; Baird, J.; Bertsch, C.; Hannah, R.E.; Dell’Orco, P.; Noorman, H.; et al. Key Green Engineering Research Areas for Sustainable Manufacturing: A Perspective from Pharmaceutical and Fine Chemicals Manufacturers. Org. Process. Res. Dev. 2011, 15, 900–911. [Google Scholar] [CrossRef]
- Argoud, S.; Budzinski, K.; D’Aquila, D.; Madabhushi, S.R.; Smith, P. Green metrics for biologics. Curr. Opin. Green Sustain. Chem. 2022, 35, 100614. [Google Scholar] [CrossRef]
- Cataldo, A.L.; Sissolak, B.; Metzger, K.; Budzinski, K.; Shirokizawa, O.; Luchner, M.; Jungbauer, A.; Satzer, P. Water related impact of energy: Cost and carbon footprint analysis of water for biopharmaceuticals from tap to waste. Chem. Eng. Sci. X 2020, 8, 100083. [Google Scholar] [CrossRef]
- Yu, X.; Chen, K.; Zhou, C.; Wang, Q.; Chu, J.; Yao, Z.; Liu, Y.; Sun, Y. Bioreactor Design Optimization Using CFD for Cost-Effective ACPase Production in Bacillus subtilis. Fermentation 2025, 11, 386. [Google Scholar] [CrossRef]
- Joshi, J.B.; Nere, N.K.; Rane, C.V.; Murthy, B.N.; Mathpati, C.; Patwardhan, A.W.; Ranade, V.V. CFD simulation of stirred tanks: Comparison of turbulence models. Part I: Radial flow impellers. Can. J. Chem. Eng. 2011, 89, 23–82. [Google Scholar] [CrossRef]
- Ding, J.; Wang, X.; Zhou, X.-F.; Ren, N.-Q.; Guo, W.-Q. CFD optimization of continuous stirred-tank (CSTR) reactor for biohydrogen production. Bioresour. Technol. 2010, 101, 7005–7013. [Google Scholar] [CrossRef] [PubMed]
- Cappello, V.; Plais, C.; Vial, C.; Augier, F. Scale-up of aerated bioreactors: CFD validation and application to the enzyme production by Trichoderma reesei. Chem. Eng. Sci. 2021, 229, 116033. [Google Scholar] [CrossRef]
- Kamla, Y.; Ameur, H.; Karas, A.; Arab, M.I. Performance of new designed anchor impellers in stirred tanks. Chem. Pap. 2020, 74, 779–785. [Google Scholar] [CrossRef]
- Coroneo, M.; Montante, G.; Paglianti, A.; Magelli, F. CFD prediction of fluid flow and mixing in stirred tanks: Numerical issues about the RANS simulations. Comput. Chem. Eng. 2011, 35, 1959–1968. [Google Scholar] [CrossRef]
- Kálal, Z.; Jahoda, M.; Fořt, I. CFD Prediction of Gas-Liquid Flow in an Aerated Stirred Vessel Using the Population Balance Model. Chem. Process. Eng. 2014, 35, 55–73. [Google Scholar] [CrossRef]
- Chen, Z.; Lian, J.Z.; Zhu, H.; Zhang, J.; Zhang, Y.; Xiang, X.; Huang, D.; Tjokro, K.; Barbarossa, V.; Cucurachi, S.; et al. Application of Life Cycle Assessment in the pharmaceutical industry: A critical review. J. Clean. Prod. 2024, 459, 142550. [Google Scholar] [CrossRef]
- Fitzpatrick, J.J.; Gloanec, F.; Michel, E.; Blondy, J.; Lauzeral, A. Application of Mathematical Modelling to Reducing and Minimising Energy Requirement for Oxygen Transfer in Batch Stirred Tank Bioreactors. Chemengineering 2019, 3, 14. [Google Scholar] [CrossRef]
- Humbird, D.; Davis, R.; Tao, L.; Kinchin, C.; Hsu, D.; Aden, A.; Schoen, P.; Lukas, J.; Olthof, B.; Worley, M.; et al. Process Design and Economics for Biochemical Conversion of Lignocellulosic Biomass to Ethanol: Dilute-Acid Pretreatment and Enzymatic Hydrolysis of Corn Stover; NREL/TP-5100-47764; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2011; p. 1013269. [Google Scholar] [CrossRef]
- Ascanio, G.; Castro, B.; Galindo, E. Measurement of Power Consumption in Stirred Vessels—A Review. Chem. Eng. Res. Des. 2004, 82, 1282–1290. [Google Scholar] [CrossRef]
- Fitzpatrick, J.J. Insights from Mathematical Modelling into Energy Requirement and Process Design of Continuous and Batch Stirred Tank Aerobic Bioreactors. ChemEngineering 2019, 3, 65. [Google Scholar] [CrossRef]
- Lalor, F.; Fitzpatrick, J.; Sage, C.; Byrne, E. Sustainability in the biopharmaceutical industry: Seeking a holistic perspective. Biotechnol. Adv. 2019, 37, 698–707. [Google Scholar] [CrossRef]
- Alves, S.S.; Vasconcelos, J.M.T. Optimisation of agitation and aeration in fermenters. Bioprocess Biosyst. Eng. 1996, 14, 119–123. [Google Scholar] [CrossRef]
- Kaiser, S.C.; Werner, S.; Jossen, V.; Blaschczok, K.; Eibl, D. Power Input Measurements in Stirred Bioreactors at Laboratory Scale. J. Vis. Exp. 2018, 135, e56078. [Google Scholar] [CrossRef]
- Davis, R.; Tao, L.; Tan, E.C.D.; Biddy, M.J.; Beckham, G.T.; Scarlata, C.; Jacobson, J.; Cafferty, K.; Ross, J.; Lukas, J.; et al. Process Design and Economics for the Conversion of Lignocellulosic Biomass to Hydrocarbons: Dilute-Acid and Enzymatic Deconstruction of Biomass to Sugars and Biological Conversion of Sugars to Hydrocarbons; NREL/TP-5100-60223; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2013. [Google Scholar] [CrossRef]
- Jamshidian, R.; Scully, J.; Akker, H.E.V.D. A computational fluid dynamics study of mass transfer in a large-scale aerated stirred bioreactor. Chem. Eng. J. 2025, 509, 160723. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. Towards a robust CFD modelling approach for reliable hydrodynamics and mass transfer predictions in aerobic stirred fermenters. Biochem. Eng. J. 2022, 181, 108405. [Google Scholar] [CrossRef]
- Reid, A.; Rossi, R.; Cottini, C.; Benassi, A. CFD simulation of a Rushton turbine stirred-tank using open-source software with critical evaluation of MRF-based rotation modeling. Meccanica 2025, 60, 1613–1637. [Google Scholar] [CrossRef]
- Nogueira, A.L. Transient CFD Simulation of Vortex Formation in a Stirred Multiphase Flow. In Multiphase Flow Dynamics: A Perspective from the Brazilian Academy and Industry; Ferreira Martins, M., Ramos, R., Belich, H., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 211–219. [Google Scholar] [CrossRef]
- Becker, J.; Manske, C.; Randl, S. Green chemistry and sustainability metrics in the pharmaceutical manufacturing sector. Curr. Opin. Green Sustain. Chem. 2022, 33, 100562. [Google Scholar] [CrossRef]
- Sheldon, R.A.; Bode, M.L.; Akakios, S.G. Metrics of green chemistry: Waste minimization. Curr. Opin. Green Sustain. Chem. 2022, 33, 100569. [Google Scholar] [CrossRef]
- Nickel, N.; Fitschen, J.; Haase, I.; Kuschel, M.; Schulz, T.W.; Wucherpfennig, T.; Schlüter, M. Novel sparging strategies to enhance dissolved carbon dioxide stripping in industrial scale stirred tank reactors. Front. Chem. Eng. 2024, 6, 1470991. [Google Scholar] [CrossRef]
- Hanspal, N.; DeVincentis, B.; Thomas, J.A. Modeling multiphase fluid flow, mass transfer, and chemical reactions in bioreactors using large-eddy simulation. Eng. Life Sci. 2022, 23, e2200020. [Google Scholar] [CrossRef] [PubMed]
- Ottinger, M.; Wenk, I.; Pereira, J.C.; John, G.; Junne, S. Single-Use Technology in the Biopharmaceutical Industry and Sustainability: A Contradiction? Chem. Ing. Tech. 2022, 94, 1883–1891. [Google Scholar] [CrossRef]
- Whitford, W.G.; Petrich, M.A.; Flanagan, W.P. Environmental impacts of single-use systems. In Single-Use Technology in Biopharmaceutical Manufacture; Eibl, R., Eibl, D., Eds.; Wiley: Hoboken, NJ, USA, 2019; pp. 169–179. [Google Scholar] [CrossRef]
- Budzinski, K.; Constable, D.; D’aQuila, D.; Smith, P.; Madabhushi, S.R.; Whiting, A.; Costelloe, T.; Collins, M. Streamlined life cycle assessment of single use technologies in biopharmaceutical manufacture. New Biotechnol. 2022, 68, 28–36. [Google Scholar] [CrossRef]
- Kreitmayer, D.; Gopireddy, S.R.; Matsuura, T.; Aki, Y.; Katayama, Y.; Sawada, T.; Kakihara, H.; Nonaka, K.; Profitlich, T.; Urbanetz, N.A.; et al. Numerical and Experimental Investigation of the Hydrodynamics in the Single-Use Bioreactor Mobius® CellReady 3 L. Bioengineering 2022, 9, 206. [Google Scholar] [CrossRef]
- Scully, J.; Considine, L.B.; Smith, M.T.; McAlea, E.; Jones, N.; O’Connell, E.; Madsen, E.; Power, M.; Mellors, P.; Crowley, J.; et al. Beyond heuristics: CFD-based novel multiparameter scale-up for geometrically disparate bioreactors demonstrated at industrial 2kL–10kL scales. Biotechnol. Bioeng. 2020, 117, 1710–1723. [Google Scholar] [CrossRef]
- Jamshidzadeh, M.; Griesz, A.U.; Jensen, J.W.; Krühne, U.; Woodley, J.M.; Gernaey, K.V.; Nikel, P.I.; Junicke, H. Cfd-Guided Scaling of Pseudomonas putida Fermentation. Biochem. Eng. J. 2025, 213, 109549. [Google Scholar] [CrossRef]
- Yang, O.; Qadan, M.; Ierapetritou, M. Economic Analysis of Batch and Continuous Biopharmaceutical Antibody Production: A Review. J. Pharm. Innov. 2020, 15, 182–200. [Google Scholar] [CrossRef]
- Posadas-Navarro, D.; Palacios, C.; Blancas-Cabrera, A.; Trujillo-Roldán, M.A.; Salinas-Vázquez, M.; Ascanio, G. Flow Patterns of Multiple Axial-Radial Impellers for Potential Use in Aerated Stirred Tanks. Chem. Eng. Technol. 2022, 45, 860–867. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, G.; Duan, J.; Wang, W. Mixing characteristics in a vessel equipped with cylindrical stirrer. Results Phys. 2018, 10, 699–705. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Tamer, M.; Villegas, R.M.; Chiappetta, A.; Ein-Mozaffari, F. Application of CFD to Analyze the Hydrodynamic Behaviour of a Bioreactor with a Double Impeller. Processes 2019, 7, 694. [Google Scholar] [CrossRef]
- Heidari, A. CFD simulation of impeller shape effect on quality of mixing in two-phase gas–liquid agitated vessel. Chin. J. Chem. Eng. 2020, 28, 2733–2745. [Google Scholar] [CrossRef]
- Stanbury, P.F.; Whitaker, A.; Hall, S.J. Chapter 9—Aeration and agitation. In Principles of Fermentation Technology, 3rd ed.; Stanbury, P.F., Whitaker, A., Hall, S.J., Eds.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 537–618. [Google Scholar] [CrossRef]
- Karimi, A.; Golbabaei, F.; Mehrnia, M.; Mohammad, K.; Neghab, M.; Nikpey, A.; Pourmand, M. Investigation of Gas Hold up and Power Consumption in a Stirred Tank Bioreactor Using Single and Dual Impeller Configurations. J. Occup. Hyg. 2013, 5, 109–116. [Google Scholar]
- Kadic, E.; Heindel, T.J. Stirred-Tank Bioreactors. In An Introduction to Bioreactor Hydrodynamics and Gas-Liquid Mass Transfer; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; pp. 69–123. [Google Scholar] [CrossRef]
- Delafosse, A.; Collignon, M.; Calvo, S.; Delvigne, F.; Crine, M.; Thonart, P.; Toye, D. CFD-based compartment model for description of mixing in bioreactors. Chem. Eng. Sci. 2014, 106, 76–85. [Google Scholar] [CrossRef]
- Debab, A.; Chergui, N.; Bekrentchir, K.; Bertrand, J. An Investigation of Heat Transfer in a Mechanically Agitated Vessel. J. Appl. Fluid Mech. 2011, 4, 43–50. [Google Scholar] [CrossRef]
- Salho, A.K.; Hamzah, D.A. A Review of Stirred Tank Dynamics: Power Consumption, Mixing Time and Impeller Geometry. Int. J. Heat Technol. 2024, 42, 1081–1092. [Google Scholar] [CrossRef]
- Antognoli, M.; Galletti, C.; Bacci di Capaci, R.; Pannocchia, G.; Scali, C. Numerical Investigation of the Mixing of Highly Viscous Liquids with Cowles Impellers. Chem. Eng. Trans. 2019, 74, 973–978. [Google Scholar] [CrossRef]
- Werner, S.; Kaiser, S.; Kraume, M.; Eibl, D. Computational fluid dynamics as a modern tool for engineering characterization of bioreactors. Pharm. Bioprocess. 2014, 2, 85–99. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; McClur, D.D.; Kavanagh, J.M.; Cassells, B.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Computational fluid dynamics modelling of hydrodynamics, mixing and oxygen transfer in industrial bioreactors with Newtonian broths. Biochem. Eng. J. 2022, 177, 108265. [Google Scholar] [CrossRef]
- Kadic, E.; Heindel, T.J. Modeling Bioreactors. In An Introduction to Bioreactor Hydrodynamics and Gas-Liquid Mass Transfer; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; pp. 58–68. [Google Scholar] [CrossRef]
- Rathore, A.S.; Sharma, C.; Persad, A. Use of computational fluid dynamics as a tool for establishing process design space for mixing in a bioreactor. Biotechnol. Prog. 2012, 28, 382–391. [Google Scholar] [CrossRef]
- Rushton, J.H. Power characteristics of mixing impellers Part 1. Chem. Eng. Prog. 1950, 46, 395–404. [Google Scholar]
- Baehr, H.D.; Stephan, K. Heat and Mass Transfer; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Reynolds, O. XXIX. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Philos. Trans. R. Soc. Lond. 1997, 174, 935–982. [Google Scholar] [CrossRef]
- Nere, N.K.; Patwardhan, A.W.; Joshi, J.B. Liquid-Phase Mixing in Stirred Vessels: Turbulent Flow Regime. Ind. Eng. Chem. Res. 2003, 42, 2661–2698. [Google Scholar] [CrossRef]
- Nienow, A.W.; Edwards, M.F.; Harnby, N. Mixing in the Process Industries, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1997. [Google Scholar]
- Higbie, R. The Rate of Absorption of Pure Gas into a Still Liquid during Short Periods of Exposure. Trans. Am. Inst. Chem. Engrs. 1935, 31, 365–389. [Google Scholar]
- Doran, P.M. Fluid Flow. In Bioprocess Engineering Principles; Elsevier: Amsterdam, The Netherlands, 2013; pp. 201–254. [Google Scholar] [CrossRef]
- Knudsen, M. Molecular Effusion and Transpiration. Nature 1909, 80, 491–492. [Google Scholar] [CrossRef]
- Hobbs, B.; Ord, A. (Eds.) Chapter 12—Fluid Flow. In Structural Geology; Elsevier: Amsterdam, The Netherlands, 2015; pp. 365–421. [Google Scholar] [CrossRef]
- Schaepe, S.; Kuprijanov, A.; Sieblist, C.; Jenzsch, M.; Simutis, R.; Lübbert, A. kLa of stirred tank bioreactors revisited. J. Biotechnol. 2013, 168, 576–583. [Google Scholar] [CrossRef]
- Hager, W.H.; Castro-Orgaz, O. William Froude and the Froude Number. J. Hydraul. Eng. 2017, 143, 02516005. [Google Scholar] [CrossRef]
- Nienow, A.W. Stirring and Stirred-Tank Reactors. Chem. Ing. Tech. 2014, 86, 2063–2074. [Google Scholar] [CrossRef]
- Hixson, A.W.; Luedeke, V.D. Wall Friction in Liquid Agitation Systems. Ind. Eng. Chem. 1937, 29, 927–933. [Google Scholar] [CrossRef]
- Ruzicka, M. On dimensionless numbers. Chem. Eng. Res. Des. 2008, 86, 835–868. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM and Matlab; Springer International Publishing: Cham, Switzerland, 2016; Volume 113. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Lomax, H.; Pulliam, T.H.; Zingg, D.W. Fundamentals of Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Newton, J.M.; Schofield, D.; Vlahopoulou, J.; Zhou, Y. Detecting cell lysis using viscosity monitoring in E. coli fermentation to prevent product loss. Biotechnol. Prog. 2016, 32, 1069–1076. [Google Scholar] [CrossRef] [PubMed]
- Voulgaris, I.; Chatel, A.; Hoare, M.; Finka, G.; Uden, M. Evaluation of options for harvest of a recombinant E. coli fermentation producing a domain antibody using ultra scale-down techniques and pilot-scale verification. Biotechnol. Prog. 2016, 32, 382–392. [Google Scholar] [CrossRef]
- Buckland, B.C.; Gbewonyo, K.; Jain, D.; Glazomitsky, K.; Hunt, G.; Drew, S.W. Oxygen transfer efficiency of hydrofoil impellers in both 800 L and 19,000 L fermentors. In Proceedings of the 2nd International Conference on Fluid Dynamics, London, UK, 11–13 May 1988; p. 16. [Google Scholar]
- Sadino-Riquelme, M.C.; Rivas, J.; Jeison, D.; Donoso-Bravo, A.; Hayes, R.E. Investigating a Stirred Bioreactor: Impact of Evolving Fermentation Broth Pseudoplastic Rheology on Mixing Mechanisms. Fermentation 2022, 8, 102. [Google Scholar] [CrossRef]
- Goudar, C.T.; Strevett, K.A.; Shah, S.N. Influence of microbial concentration on the rheology of non-Newtonian fermentation broths. Appl. Microbiol. Biotechnol. 1999, 51, 310–315. [Google Scholar] [CrossRef]
- Nunez-Ramirez, D.M.; Medina-Torres, L.; Valencia-Lopez, J.J.; Calderas, F.; Lopez-Miranda, J.; Medrano-Roldan, H.; Solis-Soto, A. Study of the Rheological Properties of a Fermentation Broth of the Fungus Beauveria bassiana in a Bioreactor Under Different Hydrodynamic Conditions. J. Microbiol. Biotechnol. 2012, 22, 1494–1500. [Google Scholar] [CrossRef]
- Kontogiannis, A.; Hodgkinson, R.; Reynolds, S.; Manchester, E.L. Learning rheological parameters of non-Newtonian fluids from velocimetry data. J. Fluid Mech. 2025, 1011, R3. [Google Scholar] [CrossRef]
- Non-Newtonian Fluids in ANSYS Fluent. Available online: https://cfdland.com/non-newtonian-fluids-in-ansys-fluent/ (accessed on 5 September 2025).
- Westermaier, S.; Kowalczyk, W. Implementation of Non-Newtonian Fluid Properties for Compressible Multiphase Flows in OpenFOAM. Open J. Fluid Dyn. 2020, 10, 135–150. [Google Scholar] [CrossRef]
- Volger, R.; Puiman, L.; Haringa, C. Bubbles and Broth: A review on the impact of broth composition on bubble column bioreactor hydrodynamics. Biochem. Eng. J. 2024, 201, 109124. [Google Scholar] [CrossRef]
- Mast, Y.; Ghaderi, A.; Takors, R. Real Case Study of 600 m3 Bubble Column Fermentations: Spatially Resolved Simulations Unveil Optimization Potentials for l-Phenylalanine Production with Escherichia coli. Biotechnol. Bioeng. 2025, 122, 265–286. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Wang, G.; Deshmukh, A.T.; van Winden, W.A.; Chu, J.; van Gulik, W.M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Computational fluid dynamics simulation of an industrial P. chrysogenum fermentation with a coupled 9-pool metabolic model: Towards rational scale-down and design optimization. Chem. Eng. Sci. 2018, 175, 12–24. [Google Scholar] [CrossRef]
- Kaya, U.; Gopireddy, S.; Urbanetz, N.; Kreitmayer, D.; Gutheil, E.; Nopens, I.; Verwaeren, J. Quantifying the hydrodynamic stress for bioprocesses. Biotechnol. Prog. 2023, 39, e3367. [Google Scholar] [CrossRef]
- Sharifi, F.; Behzadfar, E.; Ein-Mozaffari, F. Analyzing Local Shear Rate Distribution in a Dual Coaxial Mixing Bioreactor Handling Herschel–Bulkley Biopolymer Solutions through Computational Fluid Dynamics. Processes 2023, 11, 3387. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.-H.; Liu, C. (Eds.) Chapter 3—Governing Equations for CFD—Fundamentals. In Computational Fluid Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2013; pp. 61–121. [Google Scholar] [CrossRef]
- Wechselberger, P.; Sagmeister, P.; Herwig, C. Real-time estimation of biomass and specific growth rate in physiologically variable recombinant fed-batch processes. Bioprocess Biosyst. Eng. 2012, 36, 1205–1218. [Google Scholar] [CrossRef]
- Mahnert, C.; Oyarzún, D.A.; Berrios, J. Multiscale modelling of bioprocess dynamics and cellular growth. Microb. Cell Factories 2024, 23, 315. [Google Scholar] [CrossRef]
- Hirsch, C. (Ed.) Chapter 1—The Basic Equations of Fluid Dynamics. In Numerical Computation of Internal and External Flows, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2007; pp. 27–64. [Google Scholar] [CrossRef]
- Systèmes, D. 3DEXPERIENCE CATIA: Branchenführende Software für Produktdesign und Konstruktion. Dassault Systèmes. Available online: https://discover.3ds.com/de/3dexperience-catia-industry-leading-product-design-and-engineering-software (accessed on 1 September 2025).
- FreeCAD: Your Own 3D Parametric Modeler. Available online: https://www.freecad.org/ (accessed on 1 September 2025).
- Solidworks. The Solution for 3D CAD, Design and Product Development. Available online: https://www.solidworks.com/ (accessed on 1 September 2025).
- OpenFOAM | Free CFD Software | The OpenFOAM Foundation. Available online: https://openfoam.org/ (accessed on 1 September 2025).
- Ansys Fluent. Fluid Simulation Software. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 1 September 2025).
- Jia, Z.; Xu, L.; Duan, X.; Mao, Z.-S.; Zhang, Q.; Yang, C. CFD simulation of flow and mixing characteristics in a stirred tank agitated by improved disc turbines. Chin. J. Chem. Eng. 2022, 50, 95–107. [Google Scholar] [CrossRef]
- Niño, L.; Gelves, R.; Ali, H.; Solsvik, J.; Jakobsen, H. Applicability of a modified breakage and coalescence model based on the complete turbulence spectrum concept for CFD simulation of gas-liquid mass transfer in a stirred tank reactor. Chem. Eng. Sci. 2020, 211, 115272. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, F. Gas–liquid mixing in the stirred tank equipped with semi-circular tube baffles. Int. J. Chem. React. Eng. 2023, 21, 299–312. [Google Scholar] [CrossRef]
- Brannock, M.; Leslie, G.; Wang, Y.; Buetehorn, S. Optimising mixing and nutrient removal in membrane bioreactors: CFD modelling and experimental validation. Desalination 2009, 250, 815–818. [Google Scholar] [CrossRef]
- Chen, S.; Ouyang, Y.; Vandewalle, L.A.; Heynderickx, G.J.; Van Geem, K.M. CFD analysis on hydrodynamics and residence time distribution in a gas-liquid vortex unit. Chem. Eng. J. 2022, 446, 136812. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.-H.; Liu, C. (Eds.) Chapter 2—CFD Solution Procedure—A Beginning. In Computational Fluid Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2013; pp. 31–60. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.-H.; Liu, C. (Eds.) Chapter 4—CFD Techniques—The Basics. In Computational Fluid Dynamics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2013; pp. 123–175. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics. Available online: https://www.worldscientific.com/worldscibooks/10.1142/5340 (accessed on 3 September 2025).
- Hafeez, M.B.; Krawczuk, M. A Review: Applications of the Spectral Finite Element Method. Arch. Comput. Methods Eng. 2023, 30, 3453–3465. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Haringa, C. An analysis of organism lifelines in an industrial bioreactor using Lattice-Boltzmann CFD. Eng. Life Sci. 2022, 23, e2100159. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann Method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Nikolić, D.D.; Frawley, P.J. Application of the Lagrangian meshfree approach to modelling of batch crystallisation: Part I—Modelling of stirred tank hydrodynamics. Chem. Eng. Sci. 2016, 145, 317–328. [Google Scholar] [CrossRef]
- Zadghaffari, R.; Moghaddas, J.; Revstedt, J. Large-eddy simulation of turbulent flow in a stirred tank driven by a Rushton turbine. Comput. Fluids 2010, 39, 1183–1190. [Google Scholar] [CrossRef]
- Aubin, J.; Fletcher, D.; Xuereb, C. Modeling turbulent flow in stirred tanks with CFD: The influence of the modeling approach, turbulence model and numerical scheme. Exp. Therm. Fluid Sci. 2004, 28, 431–445. [Google Scholar] [CrossRef]
- Rave, K.; Lehmenkühler, M.; Wirz, D.; Bart, H.-J.; Skoda, R. 3D flow simulation of a baffled stirred tank for an assessment of geometry simplifications and a scale-adaptive turbulence model. Chem. Eng. Sci. 2021, 231, 116262. [Google Scholar] [CrossRef]
- Murthy, B.; Joshi, J. Assessment of standard k−ε, RSM and LES turbulence models in a baffled stirred vessel agitated by various impeller designs. Chem. Eng. Sci. 2008, 63, 5468–5495. [Google Scholar] [CrossRef]
- Joshi, J.B.; Nere, N.K.; Rane, C.V.; Murthy, B.N.; Mathpati, C.; Patwardhan, A.W.; Ranade, V.V. CFD simulation of stirred tanks: Comparison of turbulence models (Part II: Axial flow impellers, multiple impellers and multiphase dispersions). Can. J. Chem. Eng. 2011, 89, 754–816. [Google Scholar] [CrossRef]
- Sharma, K.V.; Straka, R.; Tavares, F.W. Lattice Boltzmann Methods for Industrial Applications. Ind. Eng. Chem. Res. 2019, 58, 16205–16234. [Google Scholar] [CrossRef]
- Mast, Y.; Takors, R. Novel experimental data-driven bubble breakage model for universal application in Euler-Lagrange multiphase frameworks. Chem. Eng. Sci. 2024, 284, 119509. [Google Scholar] [CrossRef]
- Wang, S.; Bu, Q.; Luan, D.; Zhang, Y.; Li, L.; Wang, Z.; Shi, W. Study on gas–liquid flow characteristics in stirred tank with dual-impeller based on CFD-PBM coupled model. Chin. J. Chem. Eng. 2021, 38, 63–75. [Google Scholar] [CrossRef]
- Gu, D.; Wen, L.; Xu, H.; Ye, M. Study on hydrodynamics characteristics in a gas-liquid stirred tank with a self-similarity impeller based on CFD-PBM coupled model. J. Taiwan Inst. Chem. Eng. 2023, 143, 104688. [Google Scholar] [CrossRef]
- Li, S.; Yang, R.; Wang, C.; Han, H.; Shen, S.; Wang, H. CFD–PBM Simulation on Bubble Size Distribution in a Gas–Liquid–Solid Flow Three-Phase Flow Stirred Tank. ACS Omega 2022, 7, 1934–1942. [Google Scholar] [CrossRef] [PubMed]
- Krepper, E.; Lucas, D.; Frank, T.; Prasser, H.-M.; Zwart, P.J. The inhomogeneous MUSIG model for the simulation of polydispersed flows. Nucl. Eng. Des. 2008, 238, 1690–1702. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D.; Krepper, E.; Schmidtke, M. Development of a generalized coalescence and breakup closure for the inhomogeneous MUSIG model. Nucl. Eng. Des. 2011, 241, 1024–1033. [Google Scholar] [CrossRef]
- Luzi, G.; McHardy, C. Modeling and Simulation of Photobioreactors with Computational Fluid Dynamics—A Comprehensive Review. Energies 2022, 15, 3966. [Google Scholar] [CrossRef]
- Martins, R.C.; Fachada, N. Finite Element Procedures for Enzyme, Chemical Reaction and “In-Silico” Genome Scale Networks. arXiv 2015, arXiv:1508.02506. [Google Scholar] [CrossRef]
- Carfort, J.L.N.D.; Pinto, T.; Krühne, U. An Automatic Method for Generation of CFD-Based 3D Compartment Models: Towards Real-Time Mixing Simulations. Bioengineering 2024, 11, 169. [Google Scholar] [CrossRef]
- Bisgaard, J.; Zahn, A.J.; Tajsoleiman, T.; Rasmussen, T.; Huusom, J.K.; Gernaey, K.V. Data-based dynamic compartment model: Modeling of E. coli fed-batch fermentation in a 600 m3 bubble column. J. Ind. Microbiol. Biotechnol. 2022, 49, kuac021. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cassells, B.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Development of dynamic compartment models for industrial aerobic fed-batch fermentation processes. Chem. Eng. J. 2021, 420, 130402. [Google Scholar] [CrossRef]
- Nauha, E.K.; Kálal, Z.; Ali, J.M.; Alopaeus, V. Compartmental modeling of large stirred tank bioreactors with high gas volume fractions. Chem. Eng. J. 2018, 334, 2319–2334. [Google Scholar] [CrossRef]
- Tajsoleiman, T.; Spann, R.; Bach, C.; Gernaey, K.V.; Huusom, J.K.; Krühne, U. A CFD based automatic method for compartment model development. Comput. Chem. Eng. 2019, 123, 236–245. [Google Scholar] [CrossRef]
- Deng, L.; Yin, J.; He, Q.; Cao, X.; Zhang, C.; Cui, J.; Li, B. An efficient three-dimensional mesh quality optimization method based on gradient-enhanced probabilistic model. Comput. Phys. Commun. 2025, 312, 109602. [Google Scholar] [CrossRef]
- Zadghaffari, R.; Moghaddas, J.; Revstedt, J. A mixing study in a double-Rushton stirred tank. Comput. Chem. Eng. 2009, 33, 1240–1246. [Google Scholar] [CrossRef]
- Ramonet, F.; Kovacevic, M.; Haddadi, B.; Jordan, C.; Harasek, M. Bioreactor Mixing: A Comparison of Computational Fluid Dynamics and Experimental Approaches in the Pursuit of Sustainable Bioprocessing for the Bioeconomy. Chem. Eng. Trans. 2023, 105, 265–270. [Google Scholar] [CrossRef]
- Sadino-Riquelme, M.C.; Rivas, J.; Jeison, D.; Donoso-Bravo, A.; Hayes, R.E. Computational modelling of mixing tanks for bioprocesses: Developing a comprehensive workflow. Can. J. Chem. Eng. 2022, 100, 3210–3226. [Google Scholar] [CrossRef]
- Seidel, S.; Schirmer, C.; Maschke, R.W.; Rossi, L.; Eibl, R.; Eibl, D. Computational Fluid Dynamics for Advanced Characterisation of Bioreactors Used in the Biopharmaceutical Industry—Part I: Literature Review. In Computational Fluid Dynamics—Recent Advances, New Perspectives and Applications; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Huang, W.; Li, K. CFD Simulation of Flows in Stirred Tank Reactors Through Prediction of Momentum Source. In Nuclear Reactor Thermal Hydraulics and other Applications; IntechOpen: London, UK, 2013. [Google Scholar] [CrossRef]
- Dubey, H.; Das, S.K.; Panda, T. Numerical simulation of a fully baffled biological reactor: The differential circumferential averaging mixing plane approach. Biotechnol. Bioeng. 2006, 95, 754–766. [Google Scholar] [CrossRef]
- Foukrach, M.; Bouzit, M.; Ameur, H.; Kamla, Y. Effect of Agitator’s Types on the Hydrodynamic Flow in an Agitated Tank. Chin. J. Mech. Eng. 2020, 33, 37. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. Analysis of the power losses in geared transmissions—Measurements and CFD calculations based on open source codes. In International Gear Conference 2014, Lyon, France, 26–28 August 2014; Velex, P., Ed.; Chandos Publishing: Oxford, UK, 2014; pp. 1131–1140. [Google Scholar] [CrossRef]
- Yang, C.; Mao, Z.-S. (Eds.) Chapter 3—Multiphase stirred reactors. In Numerical Simulation of Multiphase Reactors with Continuous Liquid Phase; Academic Press: Oxford, UK, 2014; pp. 75–151. [Google Scholar] [CrossRef]
- De-La-Concha-Gómez, A.; Metropolitana, U.A.; Ramírez-Muñoz, J.; Márquez-Baños, V.; Haro, C.; Alonso-Gómez, A. Effect of The Rotating Reference Frame Size for Simulating A Mixing Straight-Blade Impeller in a Baffled Stirred Tank. Rev. Mex. Ing. Quimica 2019, 18, 1143–1160. [Google Scholar] [CrossRef]
- Kresta, S.M.; Etchels, A.W., III; Dickey, D.S.; Atiemo-Oteng, V.A. Advances in Industrial Mixing: A Companion to the Handbook of Industrial Mixing; John Wiley and Sons: Hoboken, NJ, USA, 2016; Available online: https://technology.matthey.com/content/journals/10.1595/205651317X696225 (accessed on 6 September 2025).
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Turbulence. In Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow. Cambridge Aspire Website. Available online: https://www.cambridge.org/highereducation/books/an-introduction-to-turbulent-flow/1544AA34040E22C492D357EDCB06810A/space-and-time-scales-of-turbulence/89523F1124CADBCA05F6E97D77CFAD18 (accessed on 2 September 2025).
- Chen, G.; Xiong, Q.; Morris, P.J.; Paterson, E.G.; Sergeev, A.; Wang, Y.-C. OpenFOAM for Computational Fluid Dynamics. Not. Am. Math. Soc. 2014, 61, 354. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Levin, V.; Hunt, J.C.R.; Phillips, O.M.; Williams, D. Dissipation of energy in the locally isotropic turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1997, 434, 15–17. [Google Scholar] [CrossRef]
- Coleman, G.N.; Sandberg, R.D. A Primer on Direct Numerical Simulation of Turbulence—Methods, Procedures and Guidelines; AFM-09/01a; University of Southampton: Southampton, UK, 2010. [Google Scholar]
- Wagner, C.; Shishkin, A.; Shishkina, O. The use of Direct Numerical Simulations for solving industrial flow problems. In Direct and Large-Eddy Simulation VIII; Kuerten, H., Geurts, B., Armenio, V., Fröhlich, J., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 397–404. [Google Scholar] [CrossRef]
- Yeoh, S.; Papadakis, G.; Yianneskis, M. Numerical Simulation of Turbulent Flow Characteristics in a Stirred Vessel Using the LES and RANS Approaches with the Sliding/Deforming Mesh Methodology. Chem. Eng. Res. Des. 2004, 82, 834–848. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Van den Akker, H.E. The Details of Turbulent Mixing Process and their Simulation. In Computational Fluid Dynamics; Marin, G.B., Ed.; Academic Press: Cambridge, MA, USA, 2006; Volume 31, pp. 151–229. [Google Scholar] [CrossRef]
- Revstedt, J.; Fuchs, L.; Trägȧrdh, C. Large eddy simulations of the turbulent flow in a stirred reactor. Chem. Eng. Sci. 1998, 53, 4041–4053. [Google Scholar] [CrossRef]
- Jia, Z.; Zhang, S.; Fang, K.; Kong, B.; Xie, M.; Zhang, Q.; Yang, C. Assessment of stress-blended eddy simulation on prediction of flow characteristics in a Rushton impeller stirred tank. Chem. Eng. Sci. 2024, 284, 119442. [Google Scholar] [CrossRef]
- Agarwal, A.; Singh, G.; Prakash, A. Numerical investigation of flow behavior in double-rushton turbine stirred tank bioreactor. Mater. Today Proc. 2021, 43, 51–57. [Google Scholar] [CrossRef]
- Elmisaoui, S.; Boukharfane, R.; Khamar, L.; Ghidaglia, J.-M. Assessment of subgrid-scale models for large-eddy simulation of a gas-liquid stirred reactor. In Computer Aided Chemical Engineering; Kokossis, A.C., Georgiadis, M.C., Pistikopoulos, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 52, pp. 175–181. [Google Scholar] [CrossRef]
- Tamburini, A.; Brucato, A.; Ciofalo, M.; Gagliano, G.; Micale, G.; Scargiali, F. CFD simulations of early- to fully-turbulent conditions in unbaffled and baffled vessels stirred by a Rushton turbine. Chem. Eng. Res. Des. 2021, 171, 36–47. [Google Scholar] [CrossRef]
- Pohar, A.; Babnik, S.; Erklavec-Zajec, V.; Oblak, B.; Likozar, B. A Review of Computational Fluid Dynamics (CFD) Simulations of Mixing in the Pharmaceutical Industry. Biomed. J. Sci. Tech. Res. 2020, 27, 20732–20736. [Google Scholar] [CrossRef]
- Jamshidian, R.; Scully, J.; Van den Akker, H.E. Two-fluid simulations of an aerated lab-scale bioreactor. Chem. Eng. Res. Des. 2023, 196, 254–275. [Google Scholar] [CrossRef]
- Gu, D.; Song, Y.; Xu, H.; Wen, L.; Ye, M. CFD simulation and experimental analysis of solid-liquid mixing characteristics in a stirred tank with a self-similarity impeller. J. Taiwan Inst. Chem. Eng. 2023, 146, 104878. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, Z.; Cai, Y.; Cao, H.; Cai, Z.; Bao, Y. Power consumption and mass transfer in a gas-liquid-solid stirred tank reactor with various triple-impeller combinations. Chem. Eng. Sci. 2017, 170, 464–475. [Google Scholar] [CrossRef]
- Zheng, C.; Guo, J.; Wang, C.; Chen, Y.; Zheng, H.; Yan, Z.; Chen, Q. Experimental study and simulation of a three-phase flow stirred bioreactor. Chin. J. Chem. Eng. 2019, 27, 649–659. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Katopodes, N.D. (Ed.) Chapter 12—Volume of Fluid Method. In Free-Surface Flow; Butterworth-Heinemann: Oxford, UK, 2019; pp. 766–802. [Google Scholar] [CrossRef]
- Seidel, S.; Eibl, D. Influence of Interfacial Force Models and Population Balance Models on the kLa Value in Stirred Bioreactors. Processes 2021, 9, 1185. [Google Scholar] [CrossRef]
- Drew, D.A.; Passman, S.L. Theory of Multicomponent Fluids; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ishii, M. Thermo-fluid dynamic theory of two-phase flow. NASA STI/Recon Tech. Rep. A 1975, 75, 29657. [Google Scholar]
- Krýsa, P.; Šoóš, M. Modelling of Bubble Breakage and Coalescence in Stirred and Sparged Bioreactor Using the Euler-Lagrange Approach. Int. J. Heat Mass Transf. 2022, 199, 123466. [Google Scholar] [CrossRef]
- Weber, A.; Bart, H.-J. Flow Simulation in a 2D Bubble Column with the Euler-Lagrange and Euler-Euler Method. Open Chem. Eng. J. 2017, 12, 1–13. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. Towards a CFD-PBE simulation of aerated stirred tanks at high gas hold ups and different flow regimes. Chem. Eng. Res. Des. 2022, 180, 425–436. [Google Scholar] [CrossRef]
- Montante, G.; Horn, D.; Paglianti, A. Gas–liquid flow and bubble size distribution in stirred tanks. Chem. Eng. Sci. 2008, 63, 2107–2118. [Google Scholar] [CrossRef]
- Chernyshev, A.; Schmidt, A.; Chernysheva, V. An Impact of the Discrete Representation of the Bubble Size Distribution Function on the Flow Structure in a Bubble Column Reactor. Water 2023, 15, 778. [Google Scholar] [CrossRef]
- Ranganathan, P.; Sivaraman, S. Investigations on hydrodynamics and mass transfer in gas–liquid stirred reactor using computational fluid dynamics. Chem. Eng. Sci. 2011, 66, 3108–3124. [Google Scholar] [CrossRef]
- Nienow, A.W. Reactor Engineering in Large Scale Animal Cell Culture. Cytotechnology 2006, 50, 9–33. [Google Scholar] [CrossRef]
- Amer, M.; Feng, Y.; Ramsey, J.D. Using CFD simulations and statistical analysis to correlate oxygen mass transfer coefficient to both geometrical parameters and operating conditions in a stirred-tank bioreactor. Biotechnol. Prog. 2019, 35, e2785. [Google Scholar] [CrossRef] [PubMed]
- Lapin, A.; Schmid, J.; Reuss, M. Modeling the dynamics of E. coli populations in the three-dimensional turbulent field of a stirred-tank bioreactor—A structured–segregated approach. Chem. Eng. Sci. 2006, 61, 4783–4797. [Google Scholar] [CrossRef]
- Ahmed, S.U.; Ranganathan, P.; Pandey, A.; Sivaraman, S. Computational fluid dynamics modeling of gas dispersion in multi impeller bioreactor. J. Biosci. Bioeng. 2010, 109, 588–597. [Google Scholar] [CrossRef]
- Delafosse, A.; Calvo, S.; Collignon, M.-L.; Delvigne, F.; Crine, M.; Toye, D. Euler–Lagrange approach to model heterogeneities in stirred tank bioreactors—Comparison to experimental flow characterization and particle tracking. Chem. Eng. Sci. 2015, 134, 457–466. [Google Scholar] [CrossRef]
- Sarkar, J.; Shekhawat, L.K.; Loomba, V.; Rathore, A.S. CFD of mixing of multi-phase flow in a bioreactor using population balance model. Biotechnol. Prog. 2016, 32, 613–628. [Google Scholar] [CrossRef] [PubMed]
- Shu, L.; Yang, M.; Zhao, H.; Li, T.; Yang, L.; Zou, X.; Li, Y. Process optimization in a stirred tank bioreactor based on CFD-Taguchi method: A case study. J. Clean. Prod. 2019, 230, 1074–1084. [Google Scholar] [CrossRef]
- Wright, M.R.; Bach, C.; Gernaey, K.V.; Krühne, U. Investigation of the effect of uncertain growth kinetics on a CFD based model for the growth of S. cerevisiae in an industrial bioreactor. Chem. Eng. Res. Des. 2018, 140, 12–22. [Google Scholar] [CrossRef]
- Mittal, G.; Kikugawa, R.I. Computational fluid dynamics simulation of a stirred tank reactor. Mater. Today Proc. 2021, 46, 11015–11019. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; Kavanagh, J.M.; Cassells, B.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V.; McClure, D.D. Modelling of industrial-scale bioreactors using the particle lifeline approach. Biochem. Eng. J. 2023, 198, 108989. [Google Scholar] [CrossRef]
- Mayer, F.; Cserjan-Pusch, M.; Haslinger, B.; Shpylovyi, A.; Sam, C.; Soos, M.; Hahn, R.; Striedner, G. Computational fluid dynamics simulation improves the design and characterization of a plug-flow-type scale-down reactor for microbial cultivation processes. Biotechnol. J. 2023, 18, e2200152. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, S.K.; Majumder, C.B.; Ray, A. The Effect of Impeller–Sparger Geometry on the Gas Holdup in an Oxygen–Water System Using an Agitated and Sparged Tank Contactor. Ind. Eng. Chem. Res. 2021, 60, 10445–10453. [Google Scholar] [CrossRef]
- Prado, E.; Dyrness, A. Using CFD Multiphase Modeling to Predict Bioreactor Performance | Pharmaceutical Engineering. Available online: https://ispe.org/pharmaceutical-engineering/september-october-2020/using-cfd-multiphase-modeling-predict-bioreactor (accessed on 6 September 2025).
- Maluta, F.; Alberini, F.; Paglianti, A.; Montante, G. Hydrodynamics, power consumption and bubble size distribution in gas-liquid stirred tanks. Chem. Eng. Res. Des. 2023, 194, 582–596. [Google Scholar] [CrossRef]
- Ali, H.; Zhu, S.; Solsvik, J. Effects of geometric parameters on volumetric mass transfer coefficient of non-Newtonian fluids in stirred tanks. Int. J. Chem. React. Eng. 2022, 20, 697–711. [Google Scholar] [CrossRef]
- Sadino-Riquelme, M.; Donoso-Bravo, A.; Zorrilla, F.; Valdebenito-Rolack, E.; Gómez, D.; Hansen, F. Computational fluid dynamics (CFD) modeling applied to biological wastewater treatment systems: An overview of strategies for the kinetics integration. Chem. Eng. J. 2023, 466, 143180. [Google Scholar] [CrossRef]
- Cantarero-Rivera, F.J.; Yang, R.; Li, H.; Qi, H.; Chen, J. An artificial neural network-based machine learning approach to correct coarse-mesh-induced error in computational fluid dynamics modeling of cell culture bioreactor. Food Bioprod. Process. 2024, 143, 128–142. [Google Scholar] [CrossRef]
- Chen, F.; Xiao, Z.; Luo, Z.; Jiang, P.; Chen, J.; Ji, Y.; Zhu, J.; Lu, X.; Mu, L. Prediction of mass transfer performance in gas-liquid stirred bioreactor using machine learning. Chin. J. Chem. Eng. 2025, 84, 211–226. [Google Scholar] [CrossRef]
- Chen, M.; Xia, J. Chapter 3—Optimization parameters for efficient scale-up of fermentation process. In Scale-Up and Chemical Process for Microbial Production of Plant-Derived Bioactive Compounds; Wei, Y., Ji, X.-J., Cao, M., Eds.; Academic Press: Cambridge, MA, USA, 2024; pp. 29–42. [Google Scholar] [CrossRef]
- Helleckes, L.M.; Hemmerich, J.; Wiechert, W.; von Lieres, E.; Grünberger, A. Machine learning in bioprocess development: From promise to practice. Trends Biotechnol. 2023, 41, 817–835. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, J.; Xie, S.; Li, X.; Liu, H.; Wang, L.; Hong, C.; Li, G.; Chen, K. Establishment of CFD-ANN-NSGA-II model for stirred reactor design. Chem. Eng. Sci. 2025, 311, 121614. [Google Scholar] [CrossRef]
- Zhao, X.; Fan, H.; Lin, G.; Fang, Z.; Yang, W.; Li, M.; Wang, J.; Lu, X.; Li, B.; Wu, K.; et al. Multi-objective optimization of radially stirred tank based on CFD and machine learning. AIChE J. 2024, 70, e18324. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Ranjbarrad, S.; Ein-Mozaffari, F.; Lohi, A. Application of Machine Learning Models in Coaxial Bioreactors: Classification and Torque Prediction. ChemEngineering 2024, 8, 42. [Google Scholar] [CrossRef]
- Alavijeh, M.K.; Lee, Y.Y.; Gras, S.L. A perspective-driven and technical evaluation of machine learning in bioreactor scale-up: A case-study for potential model developments. Eng. Life Sci. 2024, 24, e2400023. [Google Scholar] [CrossRef]
- Savage, T.; Basha, N.; McDonough, J.; Krassowski, J.; Matar, O.; del Rio Chanona, E.A. Machine learning-assisted discovery of flow reactor designs. Nat. Chem. Eng. 2024, 1, 522–531. [Google Scholar] [CrossRef]
- Fyfe, C.; Barrington, H.; Gordon, C.M.; Reid, M. A Computer Vision Approach toward Verifying CFD Models of Stirred Tank Reactors. Org. Process. Res. Dev. 2024, 28, 3661–3673. [Google Scholar] [CrossRef]
- McConkey, R.; Yee, E.; Lien, F.-S. A curated dataset for data-driven turbulence modelling. Sci. Data 2021, 8, 255. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y.; Zhang, Z. CFDBench: A Large-Scale Benchmark for Machine Learning Methods in Fluid Dynamics. arXiv 2023, arXiv:2310.05963. [Google Scholar]
- Isoko, K.; Cordiner, J.L.; Kis, Z.; Moghadam, P.Z. Bioprocessing 4.0: A pragmatic review and future perspectives. Digit. Discov. 2024, 3, 1662–1681. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Seidel, S.; Maschke, R.W.; Werner, S.; Jossen, V.; Eibl, D. Oxygen Mass Transfer in Biopharmaceutical Processes: Numerical and Experimental Approaches. Chem. Ing. Tech. 2021, 93, 42–61. [Google Scholar] [CrossRef]
- Shi, P.; Rzehak, R. Bubbly flow in stirred tanks: Euler-Euler/RANS modeling. Chem. Eng. Sci. 2018, 190, 419–435. [Google Scholar] [CrossRef]
- Luan, D.; Zhang, S.; Wei, X.; Chen, Y. Study on mathematical model to predict aerated power consumption in a gas-liquid stirred tank. Results Phys. 2017, 7, 4085–4088. [Google Scholar] [CrossRef]
- Karimi, A.; Golbabaei, F.; Mehrnia, M.; Neghab, M.; Nikpey, A.; Pourmand, M. Oxygen mass transfer in a stirred tank bioreactor using different impeller configurations for environmental purposes. J. Environ. Health Sci. Eng. 2013, 10, 6. [Google Scholar] [CrossRef]
- Miana, M.; Santamaría, A.M.; Carbajo, J.B.; Bengoechea, C.; García, G.; Izquierdo, S. A Practical Approach for Biochemical Modeling in the CFD Evaluation of Novel Anaerobic Digester Concepts for Biogas Production. Processes 2023, 11, 2851. [Google Scholar] [CrossRef]
- Hutmacher, D.W.; Singh, H. Computational fluid dynamics for improved bioreactor design and 3D culture. Trends Biotechnol. 2008, 26, 166–172. [Google Scholar] [CrossRef]
- Rotondi, M.; Grace, N.; Betts, J.; Bargh, N.; Costariol, E.; Zoro, B.; Hewitt, C.J.; Nienow, A.W.; Rafiq, Q.A. Design and development of a new ambr250® bioreactor vessel for improved cell and gene therapy applications. Biotechnol. Lett. 2021, 43, 1103–1116. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Wu, C.; Xiao, B.; Xia, W. Computational Fluid Dynamic Approach for Biological System Modeling. arXiv 2005, arXiv:q-bio/0508006. [Google Scholar] [CrossRef]
- Eibl, P.; Rustige, S.; Witz, C.; Khinast, J. Chapter Four—LBM for two-phase (bio-)reactors. In Advances in Chemical Engineering; Van den Akker, H.E.A., Ed.; Academic Press: Cambridge, MA, USA, 2020; Volume 55, pp. 219–285. [Google Scholar] [CrossRef]
- Delvigne, F.; Goffin, P. Microbial heterogeneity affects bioprocess robustness: Dynamic single-cell analysis contributes to understanding of microbial populations. Biotechnol. J. 2014, 9, 61–72. [Google Scholar] [CrossRef]
- Wang, G.; Haringa, C.; Tang, W.; Noorman, H.; Chu, J.; Zhuang, Y.; Zhang, S. Coupled metabolic-hydrodynamic modeling enabling rational scale-up of industrial bioprocesses. Biotechnol. Bioeng. 2020, 117, 844–867. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Understanding gradients in industrial bioreactors. Biotechnol. Adv. 2021, 46, 107660. [Google Scholar] [CrossRef]
- Sadrehaghighi, I. Mesh Sensitivity & Mesh Independence Study; CFD Open Series: Annapolis, MD, USA, 2021. [Google Scholar] [CrossRef]
- Ali, B.A.; Kumar, B.; Madana, V.S.T. Experimental and computational investigation of solid suspension and gas dispersion in a stirred vessel. Phys. Fluids 2022, 34, 113318. [Google Scholar] [CrossRef]
- Fan, Y.; Sun, J.; Jin, J.; Zhang, H.; Chen, W. The effect of baffle on flow structures and dynamics stirred by pitch blade turbine. Chem. Eng. Res. Des. 2021, 168, 227–238. [Google Scholar] [CrossRef]
- Mendoza, F.; Bañales, A.L.; Cid, E.; Xuereb, C.; Poux, M.; Fletcher, D.F.; Aubin, J. Hydrodynamics in a stirred tank in the transitional flow regime. Chem. Eng. Res. Des. 2018, 132, 865–880. [Google Scholar] [CrossRef]
- de Lamotte, A.; Delafosse, A.; Calvo, S.; Delvigne, F.; Toye, D. Investigating the effects of hydrodynamics and mixing on mass transfer through the free-surface in stirred tank bioreactors. Chem. Eng. Sci. 2017, 172, 125–142. [Google Scholar] [CrossRef]
- Taghavi, M.; Moghaddas, J. Using PLIF/PIV techniques to investigate the reactive mixing in stirred tank reactors with Rushton and pitched blade turbines. Chem. Eng. Res. Des. 2019, 151, 190–206. [Google Scholar] [CrossRef]
- Bisgaard, J.; Muldbak, M.; Tajsoleiman, T.; Rydal, T.; Rasmussen, T.; Huusom, J.K.; Gernaey, K.V. Characterization of mixing performance in bioreactors using flow-following sensor devices. Chem. Eng. Res. Des. 2021, 174, 471–485. [Google Scholar] [CrossRef]
- Ochieng, A.; Onyango, M. CFD simulation of the hydrodynamics and mixing time in a stirred tank. Chem. Ind. Chem. Eng. Q. 2010, 16, 379–386. [Google Scholar] [CrossRef]
- Mavros, P. Flow Visualization in Stirred Vessels: A Review of Experimental Techniques. Chem. Eng. Res. Des. 2001, 79, 113–127. [Google Scholar] [CrossRef]
- Luty, P.A.; Prończuk, M.R.; Bizon, K.D. Optical shadowgraphy analysis of gas bubble equivalent diameters: Factors influencing measurement accuracy in bubble flows. Green Sci. 2024, 26, 72–80. [Google Scholar] [CrossRef]
- Povolny, A.; Batsaikhan, M.; Ihara, T.; Takahashi, H.; Kikura, H. Bubble Size Measurement by the Ultrasonic Pulse Echo with Tracking Technique. J. Flow Control Meas. Vis. 2018, 7, 11–27. [Google Scholar] [CrossRef]
- Lucas, D. Qualification of CFD-models for multiphase flows. Kerntechnik 2016, 81, 167–169. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. Euler-Euler simulation of mass-transfer in bubbly flows. Chem. Eng. Sci. 2016, 155, 459–468. [Google Scholar] [CrossRef]
- Khan, I.; Wang, M.; Zhang, Y.; Tian, W.; Su, G.; Qiu, S. Two-phase bubbly flow simulation using CFD method: A review of models for interfacial forces. Prog. Nucl. Energy 2020, 125, 103360. [Google Scholar] [CrossRef]
- Moser, A.; Appl, C.; Pörtner, R.; Baganz, F.; Hass, V.C. A New Concept for the Rapid Development of Digital Twin Core Models for Bioprocesses in Various Reactor Designs. Fermentation 2024, 10, 463. [Google Scholar] [CrossRef]
- Xing, Z.; Duane, G.; Chelius, C.; Smith, L.; Borys, M.C.; Khetan, A. Validation of a CFD model for cell culture bioreactors at large scale and its application in scale-up. J. Biotechnol. 2024, 387, 79–88. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, C.L.; Pace, Z.; Thomas, J.A.; DeVincentis, B.; Sirasitthich, C.; Egan, S.; Lee, J. CFD-based bioreactor model with proportional-integral-derivative controller functionality for dissolved oxygen and pH. Biotechnol. Bioeng. 2024, 121, 655–669. [Google Scholar] [CrossRef]
- Chu, M. Uncertainty Quantification in Computational Fluid Dynamics: Physics and Machine Learning Based Approaches. arXiv 2024, arXiv:2312.14684v2. [Google Scholar]
- Jahanian, A.; Ramirez, J.; O’HAra, I. Advancing precision fermentation: Minimizing power demand of industrial scale bioreactors through mechanistic modelling. Comput. Chem. Eng. 2024, 188, 108755. [Google Scholar] [CrossRef]
- Piscaglia, F.; Ghioldi, F. GPU Acceleration of CFD Simulations in OpenFOAM. Aerospace 2023, 10, 792. [Google Scholar] [CrossRef]
- de León, H.M.; Straathof, A.; Haringa, C. Dynamic compartment models: Towards a rapid modeling approach for fed-batch fermentations. Chem. Eng. Sci. 2025, 308, 121396. [Google Scholar] [CrossRef]
- Madabhushi, S.R.; Gavin, J.; Xu, S.; Cutler, C.; Chmielowski, R.; Rayfield, W.; Tugcu, N.; Chzen, H. Quantitative assessment of environmental impact of biologics manufacturing using process mass intensity analysis. Biotechnol. Prog. 2018, 34, 1566–1573. [Google Scholar] [CrossRef]
- NEA. Best Practice Guidelines for the Use of CFD in Nuclear Reactor Safety Applications—2024 Update; OECD Publishing: Paris, France, 2025. [Google Scholar]
- Cudak, M.; Rakoczy, R. Hydrodynamics of gas-liquid and biophase-gas-liquid systems in stirred tanks of different scales. Korean J. Chem. Eng. 2022, 39, 2959–2971. [Google Scholar] [CrossRef]
- Li, X.; Scott, K.; Kelly, W.J.; Huang, Z. Development of a Computational Fluid Dynamics Model for Scaling-up Ambr Bioreactors. Biotechnol. Bioprocess Eng. 2018, 23, 710–725. [Google Scholar] [CrossRef]
- Pathak, M.; Devi, T.T. CFD Investigation of Impact of Vessel configuration and Different Impeller Types in Stirred Tank. IOP Conf. Ser. Mater. Sci. Eng. 2020, 1004, 012006. [Google Scholar] [CrossRef]

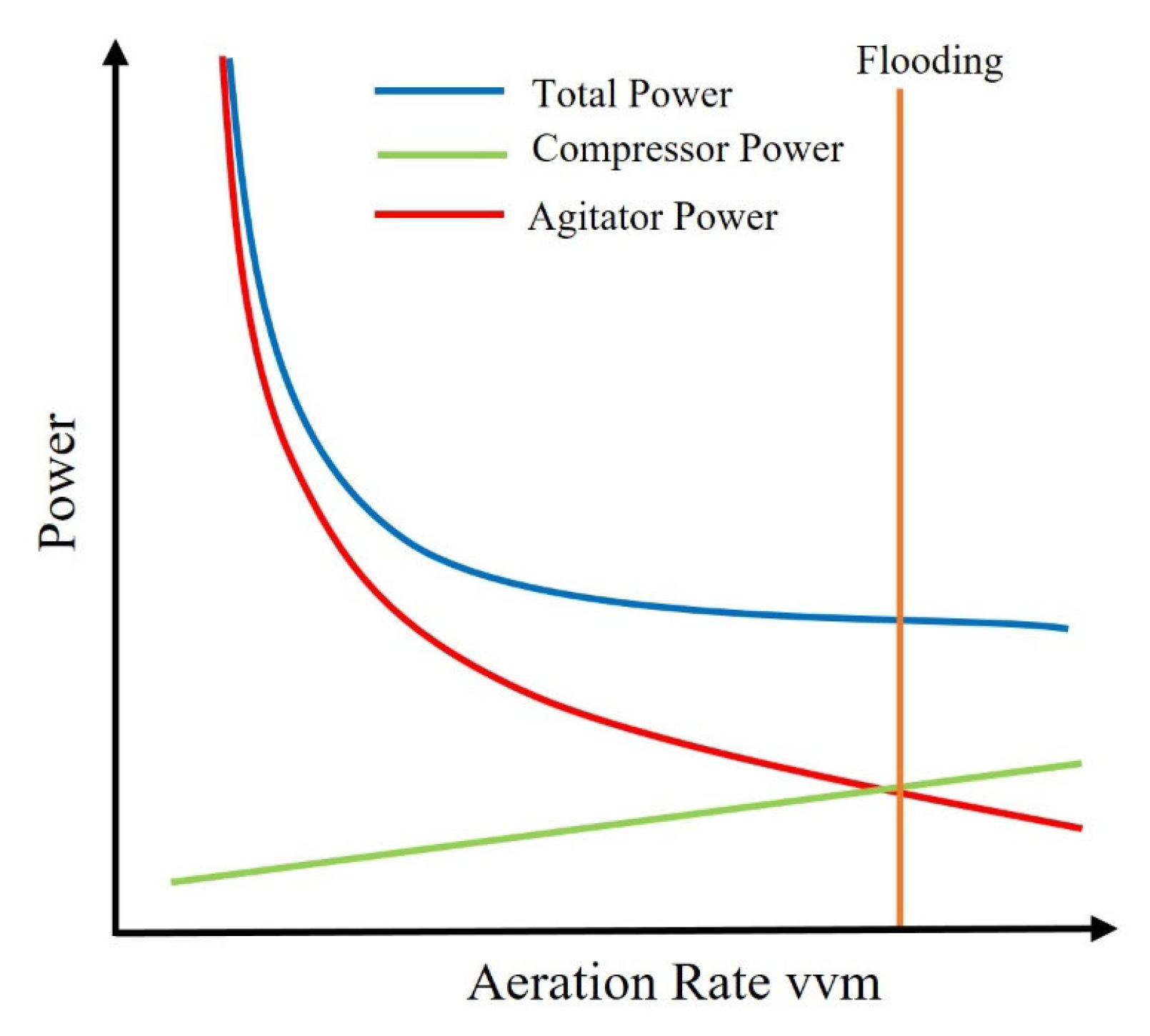
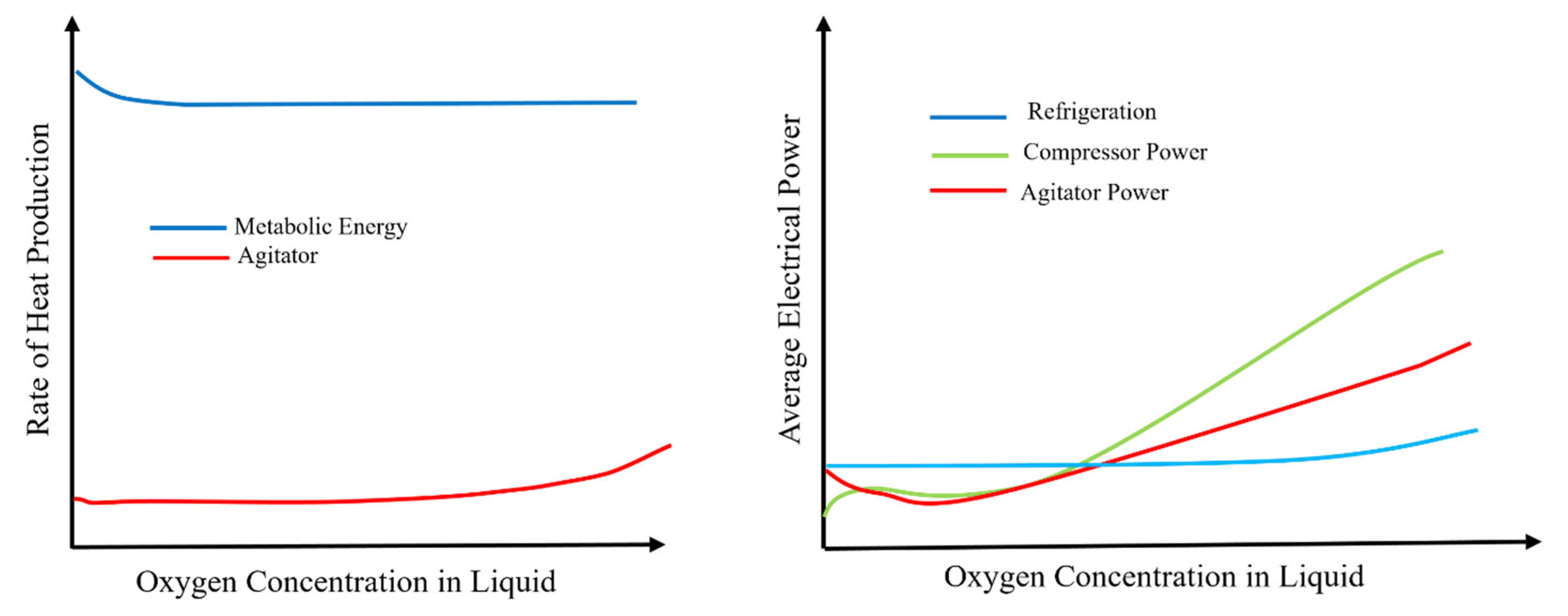
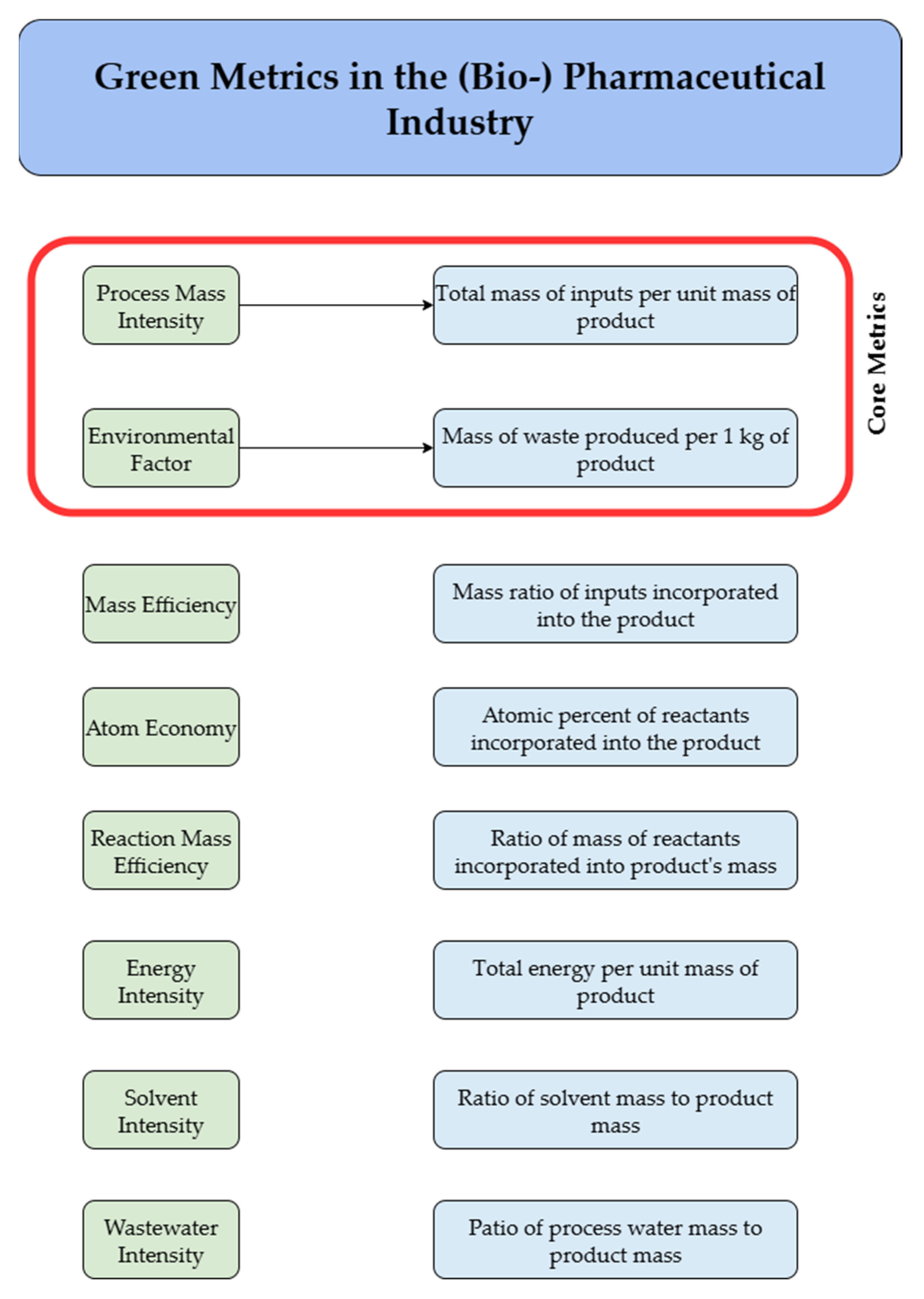
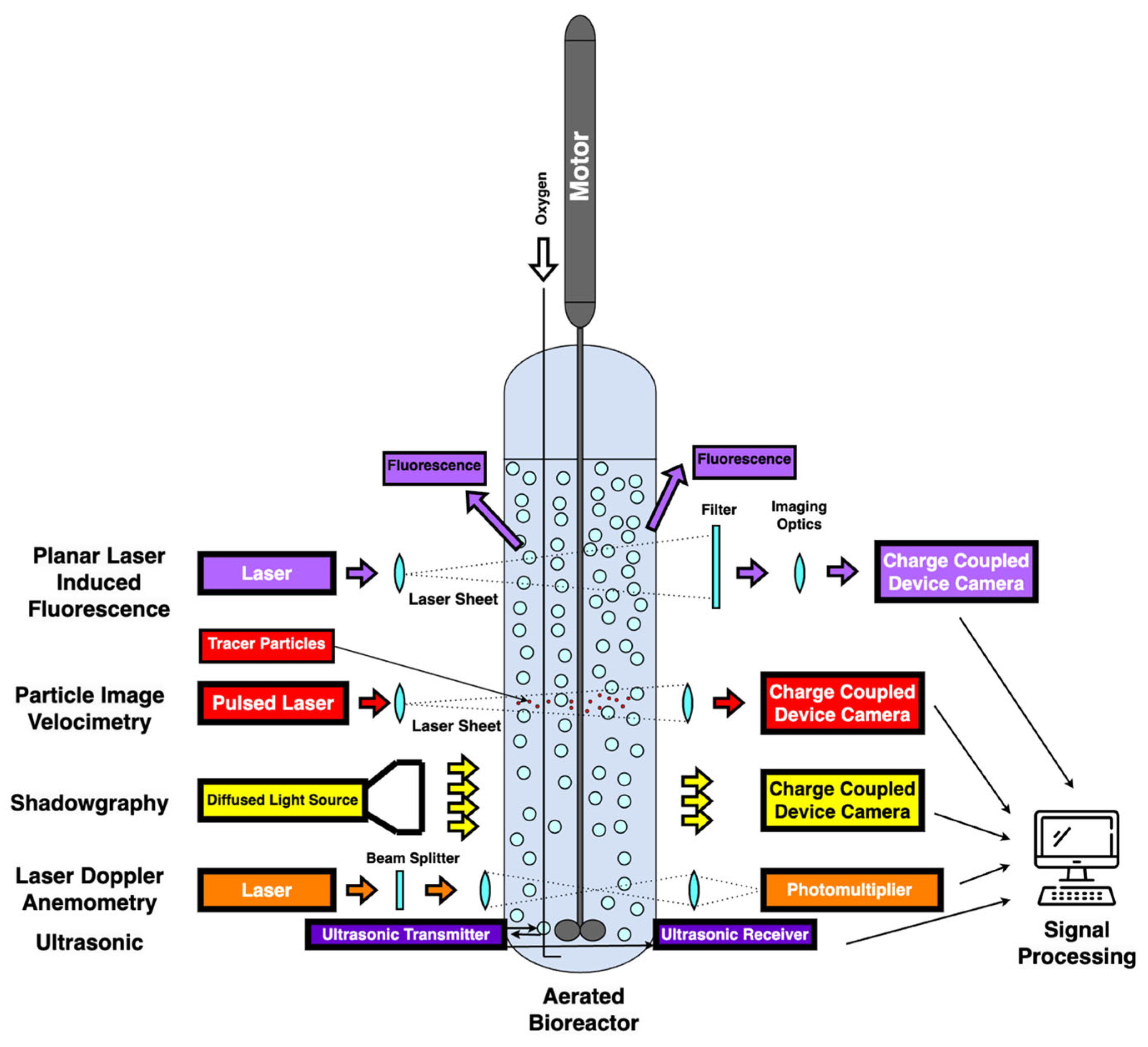
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imran, F.; Bösenhofer, M.; Jordan, C.; Harasek, M. The Potential of CFD in Sustainable Microbial Fermenter Design: A Review. Processes 2025, 13, 3005. https://doi.org/10.3390/pr13093005
Imran F, Bösenhofer M, Jordan C, Harasek M. The Potential of CFD in Sustainable Microbial Fermenter Design: A Review. Processes. 2025; 13(9):3005. https://doi.org/10.3390/pr13093005
Chicago/Turabian StyleImran, Fatima, Markus Bösenhofer, Christian Jordan, and Michael Harasek. 2025. "The Potential of CFD in Sustainable Microbial Fermenter Design: A Review" Processes 13, no. 9: 3005. https://doi.org/10.3390/pr13093005
APA StyleImran, F., Bösenhofer, M., Jordan, C., & Harasek, M. (2025). The Potential of CFD in Sustainable Microbial Fermenter Design: A Review. Processes, 13(9), 3005. https://doi.org/10.3390/pr13093005









