Abstract
Water scarcity is a problem affecting millions of people in the world, including northern Chile, with several cities declared under water scarcity by the Chilean government. This paper numerically evaluates an atmospheric water generator based on a single vapor compression refrigeration system using R410A. The monthly water harvesting rate and specific energy consumption are calculated for nine cities distributed throughout northern Chile. Every component is modeled in a modular way, using semi-empirical models, and integrated into an overall model. For the nine cities considered in this study, the monthly water harvesting varies between a maximum of 5518 L, obtained for Huasco during January, and a minimum of 0 L, in Combarbalá and Vicuña in some months during winter. In the case of the specific energy consumption, it varies between 0.355 and 1.146 kWh/L. By taking the period between December and April, the system can collect an average of 3868 L/month, with an average specific energy consumption of 0.533 kWh/L. The working domain of the system is strongly limited by the Chilean climate conditions, which is mainly influenced by the Humboldt Current. This restricts the operational efficiency of the AWGs, especially during the colder and drier months. Nonetheless, the modular modeling approach allows for flexible adaptation and optimization of the system across different geographic locations.
1. Introduction
Nowadays, most of the freshwater for human consumption comes from rivers, lakes, and groundwater reservoirs [1]. However, the availability of these sources has been affected both by indiscriminate human use and climate change [2]. According to [3], by the end of 2021, 8.25 million people suffered from freshwater rationing. On the other hand, inadequate sanitation is also a problem, exposing people to diseases such as cholera and typhoid fever. In this global scenario, Chile is one of the most affected countries by the upcoming water scarcity crisis [4], with several cities and regions located in central and northern Chile declared under water scarcity by the Chilean government.
Sea water desalination arises as the most promising alternative water source; nevertheless, brine production in the areas where these plants are installed is a threat to the surrounding biodiversity [5]. Isolated areas without piped distribution networks or water trucks will not be able to take advantage of this method either [6].
In this context, atmospheric water seems to be a good alternative, having a potential close to 12.9 × 1012 m3 [7]. This has led the scientific community to seek new methods for harvesting water from the atmosphere. The existing atmospheric water harvesting methods can be classified into the following four groups: passive methods, active refrigeration methods, sorption methods, and hybrid technologies [8]. Among these, active refrigeration systems are the most used by manufacturers [9,10,11,12,13,14,15], because they allow greater water harvesting rates () than passive methods, which can only operate in the presence of dew or fog [16]. Nevertheless, this type of system needs electrical energy to operate [17].
On the other hand, sorption methods employ adsorption material to collect water from the atmosphere [8,18], but these materials need thermal energy for the desorption cycle to recover the collected water. A more innovative and complex system corresponds to the hybrid/integrated system, combining two or more methods to increase the performance of one of them, such as desiccant wheels [19,20], membranes [21], or a combination of both [22].
Since it is a well-developed technology, with several experimental investigations and a generalized use by atmospheric water generator (AWG) manufacturers, this article will be focused on active refrigeration systems [9,10,11,12,13,14,15]. This technique uses either vapor compression refrigeration (VCR) or thermoelectric cooling systems [17] to condense atmospheric water by cooling the air below its dew point temperature [23]. The first one is mostly used by AWG manufacturers and will be analyzed in this study.
Concerning the performance of commercial AWGs, some manufacturers report the following specific energy consumptions (SECs) under the specified ambient temperature and relative humidity: 0.28 kWh/L at 30 °C and 80% (Model Thunder) [9], 0.24 kWh/L at 22.6 °C and 60% (Model GEN-M1) [10], 0.36 kWh/L at 28 °C and 80% (Model RoL50) [11], 0.4 kWh/L at 30 °C and 80% (Model EA60) [13], and 0.29 kWh/L at 30 °C and 80% (Model ASWEA-250 Elite) [14]. It is observed that most manufacturers specify their AWG at high ambient temperatures and high relative humidities, except Watergen [10], who specify their AWGs at 22.6 °C and 60%. For the same working conditions (30 °C and 80%), the SEC varies between 0.28 kWh/L and 0.4 kWh/L.
On the other hand, for the results reported in the scientific literature, Zolfagharkani et al. [24] developed a mathematical model of an AWG, which was simulated under the climate conditions of Iran, reaching a water production near 8.4 L/day with a SEC of 1.83 kWh/L at 20 °C and 30% of relative humidity, and 27.6 L/day and 0.3 kWh/L at 30 °C and 80% of relative humidity. These systems do not present a good performance under dry climate conditions [8,22,23,25], because their efficiency decreases considerably due to the higher sensible heat that the evaporator must remove to condense atmospheric water, reducing its thermal capacity to remove latent heat, which is directly proportional to the amount of collected water [26].
In the same way, under some climate conditions, the system is not able to operate at dew point temperatures lower than 4 °C, because of the risk of frost formation on the evaporator surface [17,26]. This problem was noted by Raveesh et al. [27], who carried out several simulations by considering the climate conditions of thirty Indian cities. In winter their system was limited by weather conditions, obtaining few operating hours, which reduced the amount of harvested water. On the other hand, under humid climate conditions, VCR systems present good performances; however, due to the high moisture content of the air in those conditions, the system will not be able to cool the air down to 6 °C and therefore might not be able to extract all the available water circulating through the evaporator. In a parametric analysis, the system proposed by these authors was not able to produce water at an ambient condition of 20 °C and 30% of relative humidity; however, at 30 °C and 80% of relative humidity it was able to produce 34.8 L/day with a SEC of 0.5 kWh/L.
Patel et al. [25] developed a prototype that was tested under different climate conditions. Under warm and dry conditions (40 °C and 27% of relative humidity), the system was able to produce 6.72 L/day with a SEC of 4.71 kWh/L, and under warm and humid conditions, (35 °C and 95% of relative humidity) the system was able to produce 42.7 L/day with a SEC of 0.75 kWh/L.
According to the literature review, VCR systems are widely used as AWGs. However, there is still a large gap for improvement in these systems, which can be addressed with a correct selection of the system components or with new types of technologies. Furthermore, operating limitations such as dew point temperatures below 4 °C and the worst performance under dry climate conditions remain a challenge. In this paper, an AWG based on a VCR system is mathematically modelled by using a variable speed compressor and a variable speed axial fan. This combination has not been analyzed in previous studies and allows us to generate more flexibility in the system operation, increasing the amount of collected water, as long as the climate conditions allow it. The scope of this article is to address and to contribute to the understanding of the AWG based on VCR systems, by evaluating the performance of one of these systems using two types of modulation: compressor speed and axial fan speed, under different Chilean climate conditions. The model allows changing the operating conditions of the compressor and fan to maximize the amount of harvested water and to guarantee that the system is working under safe operating conditions (in terms of refrigerant temperature and pressure, compressor speed, compressor input power, fan speed, and frost formation). The modular approach used in the modeling allows for flexible adaptation and optimization of the system in different geographic locations, by identifying certain working conditions that are limited by physical or technical constraints.
2. Materials and Methods
2.1. Climate Conditions
Nine cities of northern Chile are selected according to their water scarcity level (Köppen classification): Copiapó (BWk), Huasco (BWh), Vallenar (BWk), Vicuña (BSk), Ovalle (BSh), Combarbalá (BWh), Salamanca (BSh), Los Vilos (BSk), and Petorca (BSh). The climate conditions considered are the dry bulb temperature (T), the relative humidity (RH), and atmospheric pressure (P), which are extracted from the Meteonorm Software (version 7.0) using a time-step of 1 h [28] and considering a typical meteorological year. Figure 1 shows a map of the selected cities with the addition of the location of the Chilean capital (Santiago) for reference. The climatic variations between the selected cities are a result of the combination of latitude (transition from the world’s driest desert to steppe and Mediterranean climates), topography (the Andes Mountains and the Coastal Range), sea relative altitude, and the influence of the Humboldt Current.
Figure 1.
Map of northern Chile showing the position of the 9 cities and Santiago.
As information for the readers, in this article, the following guideline will be used to name the variables and the subscripts when multiple fluids are assessed: . For example, is used for the enthalpy of the refrigerant at the supply conditions of the superheated zone of the condenser . If one or more of the described subscripts is not necessary, it will be omitted.
The monthly moisture harvesting index (), proposed by Gido et al. [26], is used to assess the feasibility and the energy requirements of the atmospheric water harvesting system. It is calculated with Equation (1), with a reference air condition of 4 °C at the evaporator exhaust to avoid any problem of frosting formation. Figure 2 shows the monthly for the selected cities. The behavior of the indicator is similar for all cities, where summer and winter have the highest and lowest values, respectively. Some cities, such as Vicuña, Combarbalá, Salamanca, and Petorca, present an lower than 0.1 during winter. On the other hand, Huasco is expected to be the most suitable location for AWGs, since it presents the highest in almost all months.
where and are, respectively, the specific humidity and the specific enthalpy at the ambient conditions, and are the specific humidity and the specific enthalpy at the reference conditions, and is the specific enthalpy of condensation.
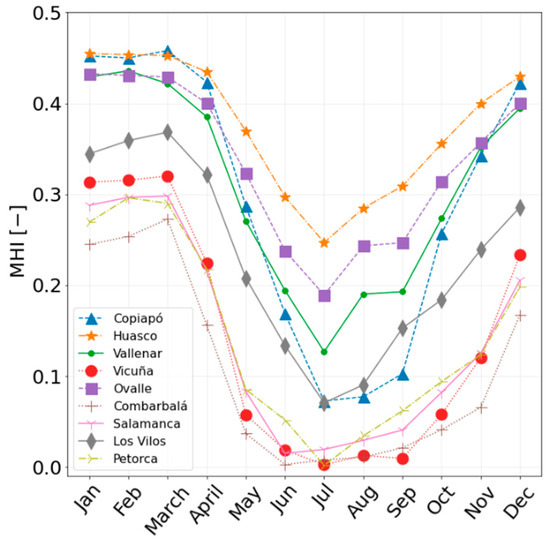
Figure 2.
Monthly MHI index distribution for the evaluated cities.
Figure 3 shows the hourly distribution of the most important properties of the atmospheric air in these cities: specific humidity, wet bulb temperature, relative humidity, and dry bulb temperature. In general, Chilean ambient temperatures are lower than the ones of other cities reported in the literature using this kind of system.
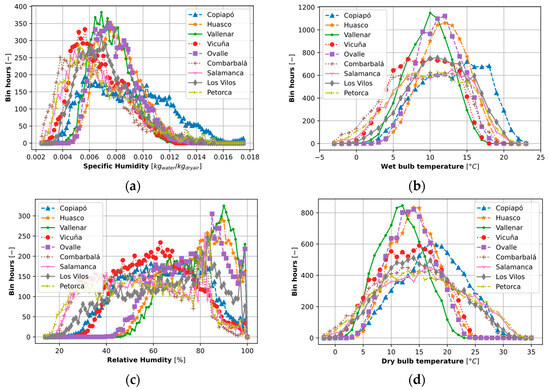
Figure 3.
Hourly distribution of (a) specific humidity, (b) wet bulb temperature, (c) relative humidity, and (d) dry bulb temperature, in the selected cities.
2.2. System Design
The system is designed based on a single VCR cycle that considers an evaporator, a compressor, a condenser, an expansion valve, and an axial fan. These components and the VCR system are presented in Figure 4. The evaporator is used to remove the sensible and latent load from the air, causing condensation of the atmospheric water on its surface. The air exhausting the evaporator is conducted to the condenser, where it is heated, and finally it is discharged to the ambient through an axial fan. The system is designed to collect around 150 L/day at the following ambient average conditions: dry bulb temperature of 20 °C, relative humidity of 60%, and atmospheric pressure of 1 atm. This condition was selected as a good compromise for the system size and because it is the average meteorological condition of the Chilean northern cities during the months when the system can operate more efficiently (higher water collection).
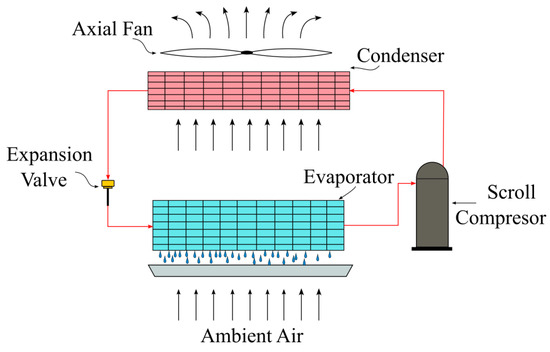
Figure 4.
Schematic of the evaluated AWG.
To maximize the harvested water and to avoid any risk of frost formation, the system is forced to operate at an air temperature of 6 °C at the evaporator exhaust. When there is no operating restriction, the system is forced to work at its highest capacity, with the compressor running at 120 Hz. When the compressor input power is higher than 3.6 kW (the maximum compressor input power), it is limited to this value, and the compressor speed is determined by the mathematical model. On the other hand, when the air mass flow rate exceeds 0.7 kg/s (the maximum air mass flow rate delivered by the axial fan), it is fixed at this value, and the compressor speed is determined by the mathematical model. At low air mass flow rates, it is fixed at 0.14 kg/s (the minimum air mass flow rate delivered by the axial fan), and the air temperature at the evaporator exhaust is, in this case, determined by the mathematical model. It guarantees that the AWG is working within its working domain (safe conditions).
2.3. Mathematical Models
The system model is decomposed into four modular models: scroll compressor, tube-and-fin air cooled condenser, tube-and-fin air heated evaporator, and axial fan, which are modelled by using a semi-empirical approach. The refrigerant considered in this study is R410A. Although it is a refrigerant that will be phased out, because of its high global warming potential (GWP of 2088), it is very common among commercial AWGs. Thus, its use allows us to create a good base for further studies using alternative refrigerants such as R290 and R1234yf, with lower GWPs, 3 and lower than 1, respectively.
2.3.1. Compressor Model
The scroll compressor is modelled with a mathematical model similar to the one proposed by Winandy et al. [29], but taking into account the internal leakage of the compressor and the pressure drop introduced by the compressor discharge check valve. It is assumed that the compressor imposes the refrigerant mass flow rate circulating through the system and the refrigerant temperature at the compressor exhaust. The compressor model also allows us to determine the compressor input power.
The compressor’s refrigerant mass flow rate is determined through Equations (2) and (3), and can be considered as the sum of the refrigerant mass flow rate coming from the evaporator , and the refrigerant mass flow rate of the compressor’s internal leakage . Finally, the refrigerant mass flow rate trapped by the compressor depends on the compressor swept volume, the compressor speed, and the corresponding specific volume.
where , , and are the mass flow rate trapped by the compressor, coming from the evaporator, and due to the internal leakages, respectively. is the compressor swept volume, is the compressor rotational speed, and is the refrigerant specific volume entering to the compression chamber.
The compressor input power is divided into the internal compression power and the compressor electromechanical loss , as indicated in Equation (4). The internal compression considers an isentropic compression from to and an isochoric compression from to , as indicated in Equation (5). Here, the electromechanical loss is assumed to follow the law indicated in Equation (6).
where , , and are the specific enthalpy, the specific volume, and the refrigerant pressure at the adapted conditions, respectively, is the specific enthalpy at the supplied conditions , is the refrigerant pressure at the exhaust conditions , and are parameters of the compressor losses model, and is the reference compressor rotational speed.
The parameters of the compressor model are identified from the catalogue data of the Copeland compressor XPV0182 by considering 120 values and then validated with 1448 values. The model can predict the refrigerant mass flow rate, the refrigerant exhaust temperature, and the compressor input power with a root mean square error of 3.2%, 8.5 °C, and 6.1%, respectively.
2.3.2. Condenser Model
The condenser was modelled by using a three-zones approach: superheated, two-phase, and subcooled, as proposed by Cuevas et al. [30]. Each zone is evaluated through two energy balances and one fluid-to-fluid heat transfer determined with the ε-NTU method, as indicated in Equations (7)–(9) for the superheated zone.
where is the superheated zone heat flow, is the refrigerant mass flow rate, and are the refrigerant specific enthalpies at the supply and exhaust conditions of the superheated zone, respectively. is the air mass flow rate, and are the air specific enthalpies at the exhaust and supply conditions of the superheated zone, respectively. is the heat exchanger effectiveness, is the minimum capacity rate, and are the refrigerant and air temperatures at the supply conditions of this zone, respectively.
The heat exchanger effectiveness is determined by considering a counterflow configuration. The two-phase and subcooled zones are analyzed similarly, but in the case of the two-phase zone, the effectiveness is determined with the equation proposed for phase change.
The air-side heat transfer coefficient is determined with a correlation identified by Kays and London [31]. For the refrigerant side, Baehr and Stephan’s [32] single-phase correlation was used for laminar regime, and Gnielinski’s correlation [33] for turbulent regime. Two-phase refrigerant heat transfer coefficient was determined using the correlation proposed by Thome et al. [34], as indicated in Equations (10)–(13). For the frictional pressure drop on the refrigerant side, the correlation suggested by Friedel [35] was implemented.
where is the Colburn factor, is the Reynolds number, is the Nusselt number, is the Graetz number, is the Prandtl number, and the friction factor.
Another variable determined by the model is the condenser air-side pressure drop, which is calculated with the method proposed in Kays and London [31], defined in Equation (14).
where is the air-side pressure drop, is the contraction pressure drop, is the frictional pressure drop, is the acceleration pressure variation, and is the expansion pressure drop.
The frictional pressure drop is determined by using the friction factor recommended by Kays and London [31], defined in Equation (15).
The contraction pressure drop , acceleration pressure variation , and expansion pressure drop are also determined as proposed by Kays and London [31]. Finally, the condenser geometry considered in this study is presented in Table 1.

Table 1.
Heat exchanger dimensions.
2.3.3. Evaporator Model
The evaporator is modelled similarly to the condenser. In this case it is divided into two zones: two-phase and superheated. The main difference in this heat exchanger is on the air side, because it is designed to condense the water from the atmospheric air. Here, the assumptions proposed by Braun [36] and the modelling approach proposed by Ding et al. [37] are used, assuming that the cooling coil heat flow is equal to the maximum between the heat flow determined by assuming a completely dry regime, and the heat flow determined by assuming a completely wet regime on the air-side.
The heat transfer in dry regime is determined as described for the condenser, but for the wet regime a fictitious moist air is defined, which is characterized through a fictitious heat capacity. In wet regime, the heat flow on the air-side is determined as indicated in Equations (16) and (17).
where is the heat flow in wet regime, is the air mass flow rate circulating through the coil, and are the moist air specific enthalpies at the coil supply and exhaust conditions, respectively, and are the moist air specific humidities at the coil supply and exhaust conditions, respectively, is the water specific enthalpy at the water condensing conditions, is the heat capacity ratio of the fictitious moist air, and are the wet bulb temperatures of the moist air at the coil supply and exhaust conditions, respectively.
The fluid-to-fluid heat transfer is also determined using the method and the assumptions mentioned previously to determine the heat exchanger effectiveness.
In wet regime, the exhaust conditions of the air are determined as indicated in ASHRAE HVAC systems and equipment [38], by considering a constant surface temperature and by assuming that the air in contact with the heat exchanger surface is saturated. Thus, the air conditions at the evaporator exhaust are determined with Equations (18)–(21).
where , , and are the moist air specific enthalpies at the coil supply, coil exhaust, and surface conditions, respectively, is the coil contact effectiveness, , , and are the moist air specific humidities at the coil supply, coil exhaust, and surface conditions, respectively, is the number of transfer units at the coil surface conditions, is the air -ide thermal resistance, and is the air heat capacity rate under dry regime.
The heat transfer coefficients on the refrigerant-side in single phase and on the air-side are determined with the same correlations presented for the condenser; however, for the two-phase zone, the correlation proposed by Shah [39] is used.
The mass flow rate of the condensed water is determined as indicated in Equation (22).
can also be related to the through Equation (23).
where is the water specific volume at the water condensing conditions.
Finally, the evaporator geometry considered in this study is the one presented in Table 1.
2.3.4. Fan Model
The fan is modelled through three dimensionless factors: flow factor, pressure factor, and power factor, which are defined in Equations (24)–(26).
where , , and are the flow, pressure, and power factors, is the volume flow rate supplied by the fan, is the area of the circle defined by the impeller diameter, is the fan peripheral velocity, is the fan total pressure head, is the air density, and is the fan isentropic effectiveness.
In this case, the pressure factor was set as the independent variable, whereas the flow and power factors were determined through polynomials laws based on the fan catalogue data.
where and are constants of the polynomial models.
The constants of the polynomial laws are identified using the catalogue data of the axial fan W3G-400 of the manufacturer ebm-papst.
2.3.5. Integrated System Model
The individual component models described previously are interconnected to define the overall system model. Figure 5 presents the interconnections between every model by showing the inputs and outputs of the overall model. For the system, it is assumed that the air temperature at the evaporator exhaust is maintained at a constant value of 6 °C, which defines the refrigerant mass flow rate that must be handled by the compressor, also imposing the compressor speed. The evaporator and condenser air-side pressure drops and the air mass flow rate define the axial fan speed.
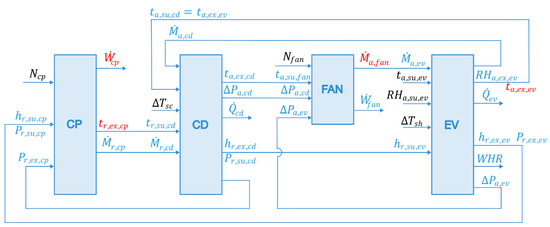
Figure 5.
Principle of the system modelling (variables colored in black are inputs of the model, colored in red are variables that must be checked to ensure safe working conditions, while the rest are determined by the mathematical model). CP represents the compressor model, CD the condenser model, FAN the axial fan model, and EV the evaporator model, respectively.
Two monthly indicators are determined with the results of the simulations: the monthly water harvesting () and the monthly specific energy consumption (), as defined in Equations (29) and (30).
where and are the initial and final time considered for the integration.
2.4. Simulation Conditions
The system is simulated throughout a typical meteorological year. The monthly data are classified by using the BIN method, with the wet bulb temperature as reference. Firstly, the system is simulated by considering a compressor speed of 120 Hz and an air temperature at the evaporator exhaust of 6 °C. The model determines the compressor speed, the compressor input power, and the axial fan speed. The constraints in the operation of the system are compressor speed between 15 Hz and 120 Hz, maximum compressor input power of 3.6 kW, and air mass flow rate between 0.14 kg/s and 0.7 kg/s. When the working conditions are outside of these limits, the system is forced to work within these safe conditions by modifying the compressor speed or the air temperature at the evaporator exhaust.
3. Results and Discussion, Limitations and Further Studies
3.1. Results and Discussion
As an example, Table 2 presents the results for Copiapó. Seasonal behavior in the system performance in the water production is observed, which decreases during winter due to a lower ambient temperature and to a lower number of operating hours. It decreases to 24% in July. The monthly water harvesting varies between 561 L in July and 4902 L in March, with higher water productions during summer (from December to March). For this city, the SEC varies between 0.448 and 0.678. Concerning the operating conditions, the average compressor speed varies between 90 and 116 Hz, and the average air mass flow rate between 0.349 kg/s and 0.674 kg/s. It is observed that during winter, when the ambient temperature decreases, the system modifies its working conditions by reducing the compressor speed and by increasing the air mass flow rate circulating through the evaporator.

Table 2.
Results obtained for Copiapó.
Regarding the operating costs, these can be determined using the SEC and the monthly energy consumption. The first one allows us to determine the operating costs to produce 1 L of freshwater and the second one the monthly costs. The Chilean cost of 1 kWh of electricity is of the order of 255 pesos/kWh, i.e., approximately 0.264 USD/kWh (in September 2025). Thus, the cost to produce 1 L of water varies between 0.118 USD/L and 0.170 USD/L, and the monthly costs vary between 90 USD and 727 USD. Firstly, compared with reverse osmosis technology, with SECs as low as 0.002 kWh/L [40], AWGs are not competitive. On the other hand, the monthly costs are too high for a family having problems with water scarcity, because these families are mainly located in the countryside. Thus, there is still a challenge to improve the performance of AWG systems to reduce its energy consumption and to combine them with renewables technologies such as photovoltaic panels.
For the other cities the results have a similar trend, with Huasco being the city with the highest water harvesting, as shown in Figure 6. This city is located in the coastal zone and in northern Chile. On the other hand, the city with a lower water harvesting is Combarbalá, which is located in the central Chilean valley and also in northern Chile. Combarbalá and Vicuña have meteorological conditions that do not allow us to harvest water during June and August, respectively. By considering the results of the nine cities, the water harvesting varies between a maximum of 5518 L, obtained in Huasco during the month of January, and a minimum 0 L, as indicated previously in Combarbalá and Vicuña. The average water harvesting for the nine cities between December and April is 3868 L/month, almost 129 L/day, with an average SEC of 0.533 kWh/L.
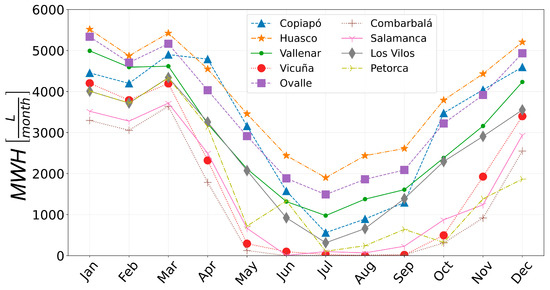
Figure 6.
Monthly water harvesting rate for the cities considered in this study.
Concerning the SEC, it varies between 0.355 and 1.146 kWh/L, with Vallenar, Ovalle, and Huasco presenting the lowest values, and thus the most favorable conditions for this technology. On the other hand, Combarbalá presents the highest SEC and, therefore, it is the most unfavorable city for this technology.
Comparing the results with the ones reported in the literature, the results obtained here follow the same trend, with higher water production under warm and humid conditions and lower SEC, and lower water production under cold and dry conditions, even with no water production under these conditions. Compared to the results of SECs reported by the AWG manufacturers, only the climate conditions used by Watergen [20] are similar to the Chilean climate conditions. This manufacturer reports a SEC of 0.24 kWh/L at 22.6 °C and 60%. In this study, the lowest SEC is of the order of 0.37 kWh/L, but for a monthly value, which takes into account different working conditions. The highest SEC obtained here is near 1.15 kWh/L for Combarbalá, but again using a monthly base.
In Huasco, the most favorable Chilean city for water harvesting of this study, the average monthly SEC varies between 0.37 kWh/L and 0.47 kWh/L, as shown in Figure 7. By considering the results of Ravesh et al. [27], who use refrigerant R134a, the most favorable cities present SECs varying between 0.51 kWh/L for Kolkata (Aw) and 0.95 kWh/L for Bengaluru (Aw). Both Indian cities have tropical wet and dry or savanna climate conditions (Aw), which are more favorable for AWGs than Chilean climate conditions. In spite of that, the system evaluated in Chilean cities presents better SECs, which indicates that using an AWG able to control the refrigerant mass flow rate, with a variable speed compressor, and the air mass flow rate, with a variable speed fan, allows to improve the performance of AWGs.
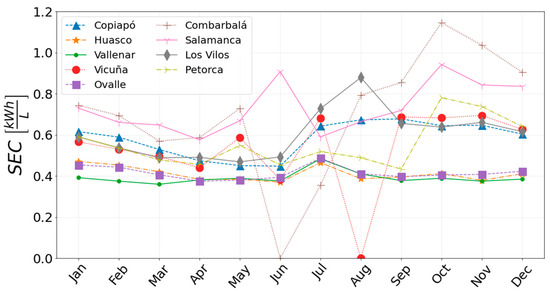
Figure 7.
Monthly average SEC.
In terms of the influence of the geographical location on the collected water, there is not a clear correlation. The cities where the AWG presents the higher water collection are Huasco (BWh) and Ovalle (BSh), the first one located in the coastal zone and the second one located in the central valley. Both cities present higher average relative humidities throughout the year compared to the other cities: between 76% and 83% for Huasco and between 72% and 82% for Ovalle, and average temperatures varying between 11 °C and 18 °C in Huasco and Ovalle. On the other hand, cities such as Combarbalá (BWh) and Salamanca (BSh), having the worst performance and the same Köppen classification as the previous cities, present average relative humidities varying between 44% and 67% in Combarbalá and 45% and 68% in Salamanca, and average temperatures varying between 7.0 °C and 22.5 °C in Combarbalá and 8.5 °C and 24 °C in Salamanca. In conclusion, relative humidity plays a more important role in the water collection than the ambient temperature. It is mainly due to the lower sensible load that the evaporator has to manage in climates with higher relative humidities.
Another analysis that is not covered in this study is the effect of the projections of the climate conditions due to climate change. There are several future scenarios to determine the projected climate conditions, which are classified as SSP1-2.6, SSP2-4.5, SSP4-6.0, and SSP5-8.5 [41]. In all these scenarios, precipitations and high mountain snowfall in northern Chile will decrease, further aggravating the problem of water scarcity in this zone. In terms of ambient temperatures and relative humidities, and considering the moderate scenario (SSP2-4.5), an increase in the average ambient temperatures and in the evapotranspiration is projected. Thus, it is expected that projected conditions will favor the use of AWGs based on VCR systems, decreasing the non-operating hours due to low temperatures and increasing the water potential in the atmospheric air.
3.2. Limitations of This Study and Further Studies
Among the limitations of this study, one of the most important is the way that the climate data are reduced. Ideally, an hourly simulation should have been developed, but to reduce the computation time and to avoid convergence problems, the climate data were reduced using the bin method. In a future study, the model will be developed in a more robust computation platform, such as python, to develop an hourly simulation accounting the 8760 h of a year. Another limitation is the control model, which is idealized. It could be improved using a dynamic modeling approach in a future study.
Another limitation corresponds to the validation of the overall model with experimental data. Although the model is based on conservation laws and constitutive equations, and some of the individual models have been validated with catalogue data, there are some physical phenomena that must be verified with experimental data, such as mass transfer, convective heat transfer coefficient, and pressure drops.
In terms of the limitations to implement the system evaluated in this study, the main limitation is its poor performance under dry climate conditions, which penalizes the water collection throughout the year. It could be improved in further studies combining AWGs based on VCR systems with other technologies that allow increasing the water content in the air stream, such as desiccant wheels, adsorption materials, and membranes.
Another limitation of AWGs based on VCR systems is their high energy consumption, thus the main efforts in future research must be focused to reduce it. Among the potential improvements, the integration of hybrid systems stands out, such as the one proposed by Cendoya et al. [22]. Other improvements include applying a hydrophobic coating on the evaporator surface and the implementation of an adaptive control strategy to set the AWG operating conditions according to the ambient conditions, thereby maximizing collected water. Although AWGs based on VCR systems are not competitive in terms of operating costs, this kind of technology can be installed even in the most remote locations, for example, rural communities that currently receive water from tanker trucks.
4. Conclusions
An atmospheric water generator based on a vapor compression refrigeration cycle was modeled to evaluate the potential of this kind of technology under the Chilean climate conditions. According to the results, this kind of system presents good potential in some northern cities, allowing to collect an average of 3868 L/month between December and April in the nine cities analyzed in this study, i.e., an average daily collection of almost 129 L/day. The SEC varies between 0.355 and 1.146 kWh/L, which is strongly influenced by the climate conditions. Concerning the operating conditions, during winter, when the ambient temperature decreases, the compressor speed and the air mass flow rate must be reduced to meet the constraints imposed on the system operation.
The Chilean climate conditions, mainly influenced by the Humboldt Current, limit the operation of this kind of system during winter, with some of the selected cities not being able to operate in some months. A possible improvement for future evaluations of atmospheric water harvesting systems is their combination with other technologies that allow increasing the water content in the air stream, such as desiccant wheels, adsorption materials, and membranes.
Author Contributions
Conceptualization, C.C., A.C., D.S. and M.P.; methodology, C.C., A.C., D.S. and M.P.; software, A.C., D.S. and M.P.; validation, C.C., A.C., D.S. and M.P.; investigation, C.C., A.C., D.S. and M.P.; resources, C.C.; writing—original draft preparation, C.C., A.C., D.S. and M.P.; writing—review and editing, C.C., A.C., D.S. and M.P.; supervision, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the ANID FONDEF ID22I10051.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- United Nations, Summary Progress Update 2021: SDG 6—Water and Sanitation for all. 2021. Available online: https://www.unwater.org/publications/summary-progress-update-2021-sdg-6-water-and-sanitation-all (accessed on 20 August 2025).
- World Meteorological Organization, WMO Statement on the State of the Global Climate in 2019. 2020. Available online: https://library.wmo.int/viewer/56228/download?file=1248_en.pdf&type=pdf&navigator=1 (accessed on 20 August 2025).
- Alvarado, R. Chile Lidera la Crisis Hídrica en América Latina. 2022. Available online: https://uchile.cl/noticias/184816/dia-mundial-del-agua-chile-lidera-la-crisis-hidrica-en-america-latina (accessed on 20 August 2025).
- Water Resource Institute, Aqueduct Water Risk Atlas. Available online: https://www.wri.org/applications/aqueduct/water-risk-atlas/ (accessed on 20 August 2025).
- Alvez, A.; Aitken, D.; Rivera, D.; Vergara, M.; McIntyre, N.; Concha, F. At the crossroads: Can desalination be a suitable public policy solution to address water scarcity in Chile’s mining zones? J. Environ. Manag. 2020, 258, 110039. [Google Scholar] [CrossRef]
- Zhou, Y.; Tol, R. Evaluating the costs of desalination and water transport. Water Resour. Res. 2005, 41, W03003. [Google Scholar] [CrossRef]
- Keyyam, I.; Al-Nimr, M.; Khashan, S.; Keewan, A. A new solar atmospheric water harvesting integrated system using CPV/T—Stirling engine—Absorption cooling cycle and vapor compression refrigeration cycle. Int. J. Energy Res. 2021, 45, 16400–16417. [Google Scholar] [CrossRef]
- Raveesh, G.; Goyal, R.; Tyagi, S. Advances in atmospheric water generation technologies. Energy Convers. Manag. 2021, 239, 114226. [Google Scholar] [CrossRef]
- Aeronero. Atmospheric Water Generator: Thunder. Available online: https://aeronero.life/product/thunder (accessed on 20 August 2025).
- Watergen. Atmospheric Water Generator: GEN-M1. Available online: https://www.watergen.com/commercial/gen-m1/ (accessed on 20 August 2025).
- RainofLife. Atmospheric Water Generator: RoL 50. Available online: https://rainoflife.com/en/rol50/ (accessed on 20 August 2025).
- Veragon. Atmospheric Water Generator. Available online: https://veragon.com/product/ (accessed on 20 August 2025).
- Hendrx. Atmospheric Water Generator: HR-90HK. Available online: https://www.hendrxwater.com/product/17.html (accessed on 20 August 2025).
- Atlantis Solar. Atmospheric Water Generator. Available online: https://www.atlantissolar.com/atlantis_h2o_elite.html (accessed on 20 August 2025).
- Tsunami Products. Atmospheric Water Generator. Available online: https://www.tsunamiproducts.com/products (accessed on 20 August 2025).
- Jarimi, H.; Powell, R.; Riffat, S. Review of sustainable methods for atmospheric water harvesting. Int. J. Low-Carbon Technol. 2020, 15, 253–276. [Google Scholar] [CrossRef]
- Nikkhah, H.; Azmi, W.; Nikkhah, A.; Najafi, A.; Babaei, M.; Fen, C.; Nouri, A.; Mohammad, A.; Lun, A.; Yong, N.; et al. A comprehensive review on atmospheric water harvesting technologies: From thermodynamic concepts to mechanism and process development. J. Water Process Eng. 2023, 53, 103728. [Google Scholar] [CrossRef]
- Ybyraiymkul, D.; Chen, Q.; Burhan, M.; Akhtar, F.; AlRowais, R.; Shahzad, M.; Kum Ja, M.; Choon Ng, K. Innovative solid desiccant dehumidification using distributed microwaves. Sci. Rep. 2023, 13, 7386. [Google Scholar] [CrossRef] [PubMed]
- Heidari, A.; Roshandel, R.; Vakiloroaya, V. An innovative solar assisted desiccant-based evaporative cooling system for co-production of water and cooling in hot and humid climates. Energy Convers. Manag. 2019, 185, 396–409. [Google Scholar] [CrossRef]
- Tu, R.; Hwang, Y. Performance analyses of a new system for water harvesting from moist air that combines multi-stage desiccant wheels and vapor compression cycles. Energy Convers. Manag. 2019, 198, 111811. [Google Scholar] [CrossRef]
- Wang, W.; Xie, S.; Pan, Q.; Dai, Y.; Wang, R.; Ge, T. Air-cooled adsorption-based device for harvesting water from island air. Renew. Sustain. Energy Rev. 2021, 141, 110802. [Google Scholar] [CrossRef]
- Cendoya, A.; Cuevas, C.; Wagemann, E. Numerical Evaluation of a Hybrid Atmospheric Water Harvesting System for Human Consumption. J. Water Process Eng. 2023, 56, 104464. [Google Scholar] [CrossRef]
- Cattani, L.; Cattani, P.; Magrini, A. Air to water generator integrated system real application: A study case in a worker village in United Arab Emirates. Appl. Sci. 2023, 13, 3094. [Google Scholar] [CrossRef]
- Zolfagharkhani, S.; Zamen, M.; Shahmardan, M. Thermodynamic analysis and evaluation of a gas compression refrigeration cycle for fresh water production from atmospheric air. Energy Convers. Manag. 2018, 170, 97–107. [Google Scholar] [CrossRef]
- Patel, J.; Patel, K.; Mudgal, A.; Panchal, H.; Sadasivuni, K. Experimental investigations of atmospheric water extraction device under different climatic conditions. Sustain. Energy Technol. Assess. 2020, 38, 100677. [Google Scholar] [CrossRef]
- Gido, B.; Friedler, E.; Broday, D. Assessment of atmospheric moisture harvesting by direct cooling. Atmos. Res. 2016, 182, 156–162. [Google Scholar] [CrossRef]
- Raveesh, G.; Goyal, R.; Tyagi, S. Parametric analysis of atmospheric water generation system and its viability in Indian cities. Therm. Sci. Eng. Prog. 2023, 39, 101682. [Google Scholar] [CrossRef]
- Meteonorm Version 7—Meteonorm (en). Available online: https://meteonorm.com/ (accessed on 20 August 2025).
- Winandy, E.; Saavedra, C.; Lebrun, J. Experimental analysis and simplified modelling of a hermetic scroll refrigeration compressor. Appl. Therm. Eng. 2002, 22, 107–120. [Google Scholar] [CrossRef]
- Cuevas, C.; Lebrun, J.; Lemort, V.; Ngendakumana, P. Development and validation of a condenser three zones model. Appl. Therm. Eng. 2009, 29, 3542–3551. [Google Scholar] [CrossRef]
- Kays, W.; London, A. Compact Heat Exchangers, 2nd ed.; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Incropera, F.; Bergman, T.; Lavine, A.; Dewitt, D. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gnielinski, V. Ein neues Berechnungsverfahren für die Wärmeübertragung im Übergangsbereich zwischen laminarer und turbulenter Rohrströmung. Eng. Res. 1995, 61, 240–248. [Google Scholar] [CrossRef]
- Thome, J.; El Hajal, J.; Cavallini, A. Condensation in horizontal tubes, part 2: New heat transfer model based on flow regimes. Int. J. Heat Mass Transfer. 2003, 46, 3365–3387. [Google Scholar] [CrossRef]
- Friedel, L. Improved friction pressure drop correlations for horizontal and vertical two-phase pipe flow. In Proceedings of the European Two-phase Group Meeting, Ispra, Italy, 5–8 June 1979; pp. 485–492. [Google Scholar]
- Braun, J.; Klein, S.; Mitchell, J. Effectiveness models for cooling towers and cooling coils. ASHRAE Trans. 1989, 95, 164–174. [Google Scholar]
- Ding, X.; Eppe, J.; Lebrun, J.; Wasacz, M. Cooling Coil Models to be used in Transient and/or Wet Regimes. Theoretical Analysis and Experimental Evaluation. In Proceedings of the Third International Conference on System Simulation in Buildings, Liege, Belgium, 3–5 December 1990. [Google Scholar]
- ASHRAE. coils. In ASHRAE Handbook-HVAC Systems and Equipment; American Society of Heating, Refrigerating, and Air-Conditioning Engineers: Atlanta, GA, USA, 2012; pp. 23.1–23.16. [Google Scholar]
- Shah, M. Chart correlation for saturated boiling heat transfer: Equations and further study. ASHRAE Trans. 1982, 88, 185–196. [Google Scholar]
- Feo-García, J.; Pulido-Alonso, A.; Florido-Betancor, A.; Florido-Suárez, N.R. Cost Studies of Reverse Osmosis Desalination Plants in the Range of 23,000–33,000 m3/day. Water 2024, 16, 910. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC) Climate Change 2021—The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. Available online: https://www.ipcc.ch/assessment-report/ar6/ (accessed on 10 September 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).