A Method for Load Forecasting of Distribution Transformers Based on Parameter-Efficient Fine-Tuning of Large Language Models in Power System

Abstract

Distribution grids are essential to power systems, as they ensure the safe and reliable operation of power systems. It is important to forecast the operational status of each distribution transformer. Consequently, there is an urgent need to develop load forecasting models that exhibit robust generalization and exceptional accuracy. However, distribution transformers are numerous, exhibit strong inherent features. Single-device load samples are scarce, with widespread few-shot issues. Traditional models rely on massive amounts of data and computational resources, making it challenging to balance computational costs, generalization ability, and accuracy. To address these issues, this paper analyzes the inherent features of distribution transformers and fine-tunes large language models using parameter-efficient fine-tuning methods to reduce training costs while preserving their generalization capabilities and accuracy. Experimental results demonstrate that this method achieves significantly higher accuracy than baseline models in few-shot scenarios.

1. Introduction

As a critical component of the power system, the distribution network covers a large area and is responsible for the important task of power transmission [1,2]. Among its components, distribution transformers serve as key hubs in the distribution network [3]. Their safe and stable operation directly impacts the reliability of the power supply. Accurately predicting the operational status of each distribution transformer and proactively identifying potential hazards is crucial for ensuring the safe and reliable operation of the distribution network [4,5].

Distribution transformers are numerous, widely distributed, and operate in complex environmental conditions [6,7,8,9]. When the power load exceeds the rated capacity of the distribution transformer, the internal temperature of the transformer rises rapidly, increasing its lifespan loss, reducing operational reliability, and posing a threat to the safe and reliable power supply of the distribution network [10,11,12]. Researchers have focused on power load forecasting to prevent overloading events and further optimize grid dispatch strategies. Traditional power load forecasting methods primarily include time series analysis [13], regression analysis [14], Kalman filtering [15], exponential smoothing [16], and gray forecasting methods [17]. Traditional power load forecasting methods are constructed based on the statistical patterns of historical load data, offering advantages such as low computational cost and high interpretability. They have been widely applied in regional-level and system-level power load forecasting. However, the power load of distribution transformers is highly influenced by user electricity consumption habits, and the nonlinear characteristics of distribution transformer power loads are significantly more pronounced than those at regional and system levels. This results in a significant reduction in the forecasting accuracy of traditional methods when forecasting the power load of distribution transformers [18,19].

With the continuous improvement of computer performance, artificial intelligence (AI) technology has gradually emerged in multiple fields [20]. In recent years, AI technology has become the primary research method in power load forecasting. AI technology primarily includes methods such as support vector machines, random forests, and deep learning. Among these, deep learning methods, with their unique model structure and excellent nonlinear feature extraction capabilities, have gradually become a research hotspot among scholars in recent years and achieved breakthrough progress in multiple fields [21]. In recent years, load forecasting methods for distribution transformers have primarily focused on improvements to Long Short-Term Memory (LSTM), Transformer, and Convolutional Neural Network (CNN) models, as well as their integration with other models. As an improved version of Recurrent Neural Networks (RNNs), LSTM effectively addresses the gradient vanishing and explosion issues of traditional RNNs through special gating mechanisms (such as forget gate, input gate, and output gate) [22]. Specifically, the forget gate filters out redundant temporal features to retain key information. The input gate updates the parameters of memory units. The output gate integrates the current input with the memory state to selectively generate prediction results, thereby avoiding training instability caused by parameter sharing. To fully exploit the temporal features in historical load data, the reference [23] further extended this framework by constructing a Bi-directional Long Short-Term Memory (Bi-LSTM) model, which includes two independent LSTM units: one processes data in chronological order, and the other processes data in reverse order, thereby comprehensively capturing the temporal patterns in load data. To reduce the computational cost of the model and improve its prediction efficiency, the reference [24] constructed a Gate Recurrent Unit (GRU) model, a simplified variant of LSTM, which contains only two components: a reset gate and an update gate. The update gate regulates the relationship between the current input and historical information, controlling the degree of information retention. The reset gate determines whether to ignore certain historical features and adjusts their influence on the current state. This design enables GRU to dynamically adjust its memory and update processes, thereby better adapting to different time series data. The above methods use a recursive structure and must be calculated sequentially. To solve this problem, the reference [25] constructs a Temporal Convolutional Network (TCN) model based on the CNN network structure. This model comprises convolutional layers and residual connections, which can flexibly control the size of the receptive field by adjusting the network depth to extract features of different scales from historical load data. To fully consider the impact of external factors such as weather on power load, the reference [26] employs a Transformer model to construct a load forecasting model. The Transformer model fundamentally redefines traditional sequence processing architectures by abandoning the inherent frameworks of CNN and LSTM, instead relying entirely on self-attention mechanisms to model global dependencies within temporal data. The core of this model lies in the self-attention mechanism, which dynamically assigns differentiated weights to each element in the input sequence. It also quantifies the dependencies between different positions. Building upon this, the model integrates multiple self-attention modules through a multi-head self-attention mechanism, enabling parallel analysis of raw data features across multiple subspaces. This not only enhances feature expression capabilities but also significantly improves prediction accuracy.

The above methods rely heavily on massive training data and feature engineering during training, and the load forecasting models are often limited to a single objective [27,28]. However, there are numerous distribution transformers, and their installation environments vary greatly, as do load sequences, which exhibit high heterogeneity. Missing data can lead to overfitting or underfitting of prediction models, and the above methods experience a sharp decline in prediction accuracy under few-shot conditions [29,30]. To address these issues, scholars have explored transfer learning algorithms to improve the accuracy of models in few-shot scenarios [31,32,33]. The reference [34] employs multiple kernel learning to extract the spatiotemporal correlation of power loads, thereby reducing the complexity of the prediction model and significantly alleviating the overfitting problem in few-shot scenarios. The reference [35] quantifies the spatiotemporal correlation of power load by sharing model parameters and fully leveraging prior knowledge, enabling the model to achieve effective transfer in few-shot scenarios. However, the aforementioned methods require a high degree of similarity between the source domain features and the target domain features [36,37]. When the data features of the source domain and target domain differ significantly, negative transfer issues may arise.

To address the aforementioned issues, this paper proposes a method for load forecasting of distribution transformers based on a parameter-efficient fine-tuning method of large language models. This paper leverages the superior generalization ability of large language models to quantify the spatiotemporal correlation and inherent features of distribution transformers, thereby enhancing the generalization ability of the load forecasting model in few-shot scenarios. A parameter-efficient fine-tuning method is proposed to reduce the computational cost of the load forecasting model effectively. In summary, the main contributions of this paper are as follows:

(1)

This paper proposes a method for load forecasting of distribution transformers based on parameter-efficient fine-tuning method of large language models, effectively improving the prediction accuracy and generalization ability in few-shot scenarios.

(2)

This paper thoroughly examines the spatiotemporal correlation and inherent features of power loads in distribution transformers. It employs the Linde–Buzo–Gray algorithm and the dynamic mode decomposition algorithm to separate and analyze the spatiotemporal correlation and inherent characteristics of power loads, thereby enhancing the generalization capability of the prediction model.

(3)

This paper presents a parameter-efficient fine-tuning method based on simultaneous perturbation stochastic approximation, which effectively reduces the computational cost of the model and enhances its efficiency.

2. Load Forecasting Method for Distribution Transformers Based on Large Language Models

Existing load forecasting methods for distribution transformers mainly rely on much historical load data. However, there are many distribution transformers in distribution networks, and each distribution transformer may not have sufficient training data, which can lead to overfitting or underfitting of the model. Relevant scholars have used transfer learning algorithms to solve few-shot issues and fully use existing a priori knowledge of distribution transformers to construct transfer learning models. However, this method requires a strong correlation between the target and source domains, but the inherent features of distribution transformers cannot meet this requirement. Therefore, this paper fully uses the generalization ability of a large language model (LLM) to propose a load forecasting model for distribution transformers based on LLM.

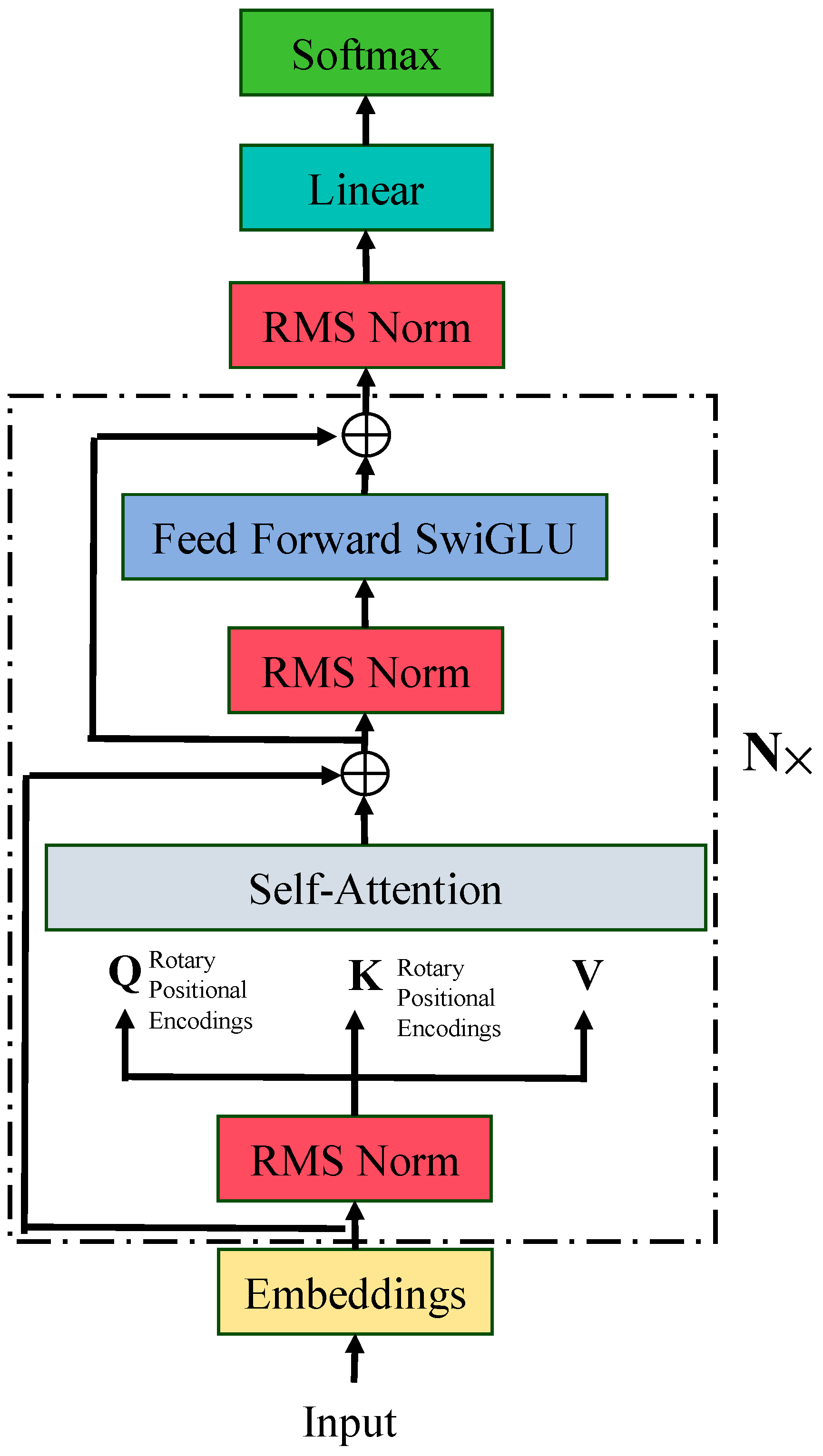
Owing to the rapid development of computer technology, AI technology has made significant strides. In 2020, OpenAI announced the release of the GPT-3 model, which is primarily based on the Transformer model and relies on massive amounts of training data and extensive computational resources to optimize model parameters. This model has fully demonstrated that large language models possess exceptional generalization capabilities. After pre-training, the parameters of LLMs contain a wealth of prior knowledge, enabling them to adapt quickly to new scenarios. In recent years, to further explore the application potential of LLMs in various scenarios, ultra-large-scale parameter AI models such as LLaMA and Flamingo have emerged. This paper selects the LLaMA model as the primary subject for analysis. The LLaMA model is an improvement over the Transformer model, constructed using only the Decoder model. It employs the Causal Mask method to enhance the model’s expressive capabilities while preventing information leakage. The partial structure of the LLaMA model is shown in Figure 1.

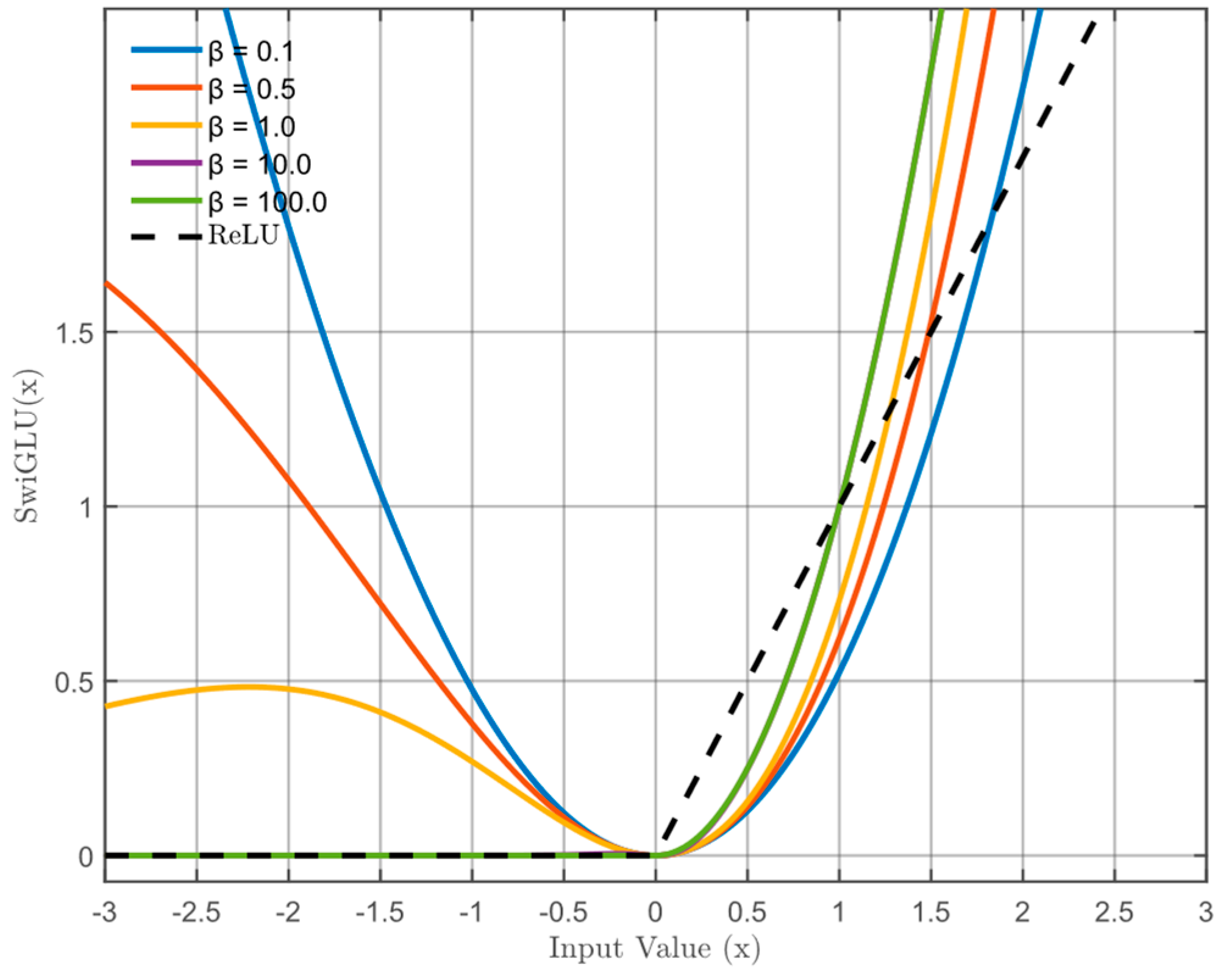
The LLaMA model uses RMSNorm instead of LayerNorm to scale input vectors, making them invariant to scaling. This accelerates model convergence and reduces computational complexity during training. The Rotary Position Embedding (RoPE) method is used to encode the position of input vectors. This encoding method cleverly combines absolute position encoding and relative position encoding, making the position encoding sensitive to the dimension of the input vectors. When the LLaMA model processes long-sequence data, as the dimension increases, the influence of RoPE rotation position encoding gradually weakens, thereby reducing the interference of redundant features. The LLaMA model replaces the ReLU activation function with the SwiGLU activation function, enabling the model to characterize complex data features. Additionally, the smooth and continuous characteristics of the SwiGLU activation function help mitigate the issue of gradient vanishing during training. The SwiGLU activation function is illustrated in Figure 2.

As can be seen from the figure above, the SwiGLU activation function is based on the Swish activation function and the GLU activation function, which gives the SwiGLU activation function better nonlinear feature capture capabilities and filters out secondary information through a gating mechanism, enabling the LLaMA model to quantify the long-range dependencies inherent in high-dimensional sequential data. The ReLU activation function lacks a gating mechanism. It has a gradient of zero in the negative interval, which prevents the model from effectively extracting key features and reduces its generalization ability.

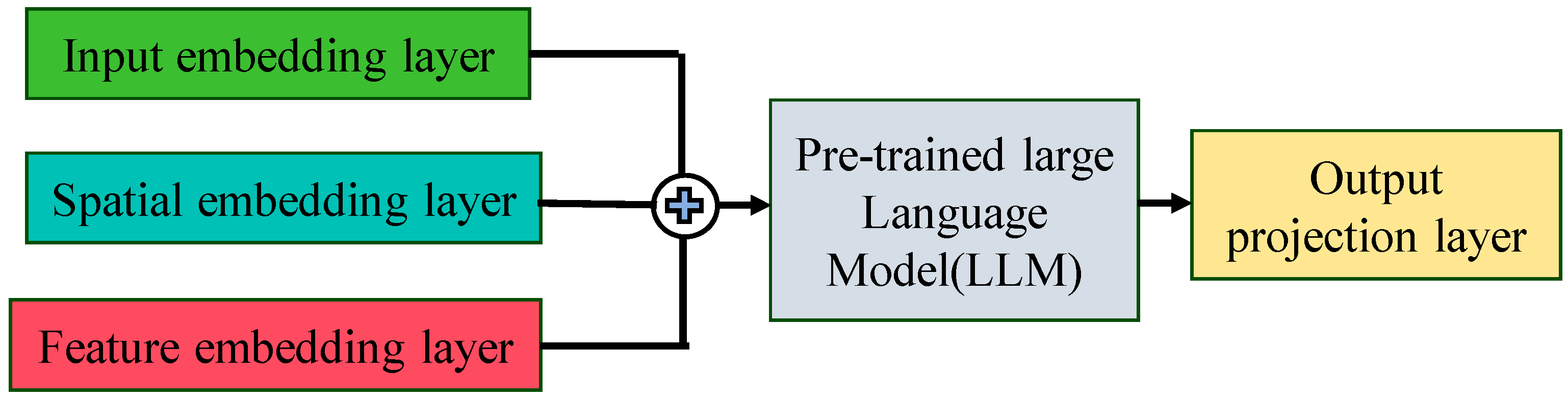
The LLaMA model, with its distinctive model structure, exhibits excellent generalization capabilities and can rapidly adapt to new scenarios, yielding remarkable results across multiple fields. However, the LLaMA model has a large number of parameters, and directly fine-tuning its parameters would incur high computational costs. To adapt to the characteristics of the distribution transformer load forecasting scenario, this paper leverages the superior generalization ability of the LLaMA model to deeply explore the spatiotemporal correlations and inherent features of the distribution transformer. The distribution transformer load data is encoded, and the spatiotemporal correlations and inherent features of the distribution transformer loads are integrated. The main model structure proposed in this paper is shown in Figure 3.

3. A Method for Feature Extraction of Distribution Transformers Based on the Linde–Buzo–Gray and Dynamic Mode Decomposition Algorithms

Distribution transformers have relatively low voltage ratings, and the load composition of each distribution transformer varies. Users’ electricity consumption habits easily influence power loads and exhibit distinct inherent features. Additionally, under similar environmental temperature conditions, users typically exhibit similar electricity consumption habits. For example, during high-temperature weather, users typically turn on their air conditioners to cool down. This causes the air conditioning load of each distribution transformer to rise rapidly. Therefore, under similar conditions, distribution transformers located near each other exhibit temporal and spatial correlations. To fully explore and quantify the temporal and spatial correlations and inherent features of distribution transformers, this paper employs the Linde–Buzo–Gray (LBG) algorithm and the dynamic mode decomposition (DMD) algorithm to investigate data features and enhance the accuracy of distribution transformer load forecasting model.

3.1. The Quantification Method of Spatiotemporal Correlation

The primary factors influencing the spatiotemporal correlation of distribution transformers include the load composition of transformers and the temperature of the power supply area [21]. Blindly assuming that transformers located nearby have spatiotemporal correlation can lead to feature redundancy, thereby reducing the predictive accuracy of the model. For example, during late-night hours when electricity prices are lower, many factories reduce production costs by conducting production activities during this time. Such industrial loads remain at relatively high levels during late-night hours, while most residential loads cease during this period, resulting in lower levels of residential loads. Therefore, this study employs the Linde–Buzo–Gray (LBG) algorithm to identify distribution transformers with spatiotemporal correlation [6].

This paper selects variance, mean, linearity, and other related features of distribution transformer load time sequence data as clustering features. The main features selected in this paper are shown in

Table 1. Partial features of time series power load data.

Features	Description
Mean	Mean
Var	Variance
Linearity	Strength of linearity
ACF1	First order of autocorrelation
Peak	Strength of peaks
Curvature	Strength of curvature
Entropy	Spectral entropy
Spikiness	Strength of spikiness

.

During the clustering process, the LBG algorithm categorizes the sequential load data of distribution transformers by measuring the similarity of different characteristics of the sequential load data of different distribution transformers [6]. Distribution transformer load curves with similar characteristics, such as load curve change patterns, peak times, and load composition, are grouped into the same category, fully considering the spatiotemporal correlation between distribution transformers, thereby laying a solid foundation for improving model accuracy.

3.2. The Quantification Method for Inherent Features of Distribution Transformers

To fully capture the inherent features of distribution transformers, this paper employs the dynamic mode decomposition (DMD) algorithm to analyze the sequential power load data. The DMD algorithm can extract the potential patterns contained in the sequential data and decompose the nonlinear complex features into multiple superimposed linear features. To capture the potential patterns in the sequential data, this paper converts the original sequential data. This paper uses the Hankel operator to construct a multi-dimensional augmented data matrix [33]. The primary process is as follows.

$$\begin{array}{cc}{O}_{it}& =\left[\begin{array}{cccc}{x}_{it}(1)& x_{it}(2)& \cdots & x_{it}(K+1-c)\\ x_{it}(2)& x_{it}(3)& \cdots & x_{it}(K+2-c)\\ ⋮& ⋮& \ddots & ⋮\\ x_{it}(c)& x_{it}(c+1)& \cdots & x_{it}(K)\end{array}\right]\hfill \\ & =\left[o_1,o_2,\cdots ,o_{K+1-c}\right],\hfill \end{array}$$

(1)

In the above equation, distribution transformers power load data $x_{it}\in {ℝ}^K$, $x_{it}$ represents ith distribution transformers historical load data. Within a short period, load data for distribution transformers exhibits local correlation, and current load data can be obtained by a linear combination of previous time points [33], as shown below.

$$\begin{array}{l}{x}_{it}(a)={\displaystyle \sum _{w=1}^q{\alpha }_w}{x}_{it}(a-w)+e_a\approx {\displaystyle \sum _{w=1}^q{\alpha }_w}{x}_{it}(a-w),\\ \end{array}$$

(2)

In the above equation, $e_a$ represents residual error. This paper refers to reference [33] and ignores residual error. Therefore, vectors at adjacent time steps satisfy a linear relationship. The elements in the multi-dimensional augmented data matrix are as follows:

$$\left\{\begin{array}{l}{O}_1=\left[o_1,\cdots ,o_{K-c}\right]\in {ℝ}^{c\times (K-c)}\hfill \\ O_2=\left[o_2,\cdots ,o_{K-c+1}\right]\in {ℝ}^{c\times (K-c)}.\hfill \end{array}\right.$$

(3)

After ignoring the residual error, the above equation can be converted to

$$O_2\approx \mathcal{A}{O}_1,$$

(4)

In the above equation, linear operator $\mathcal{A}\in {ℝ}^{c\times c}$. Linear operators contain the main characteristics of sequential load data for distribution transformers, such as oscillation mode, attenuation trend, or growth trend. Due to the high dimensionality of multi-dimensional augmented data matrices, in order to reduce computational complexity and avoid overfitting, this paper refers to reference [33] to perform singular value decomposition (SVD) on multi-dimensional augmented data matrices. The primary process is as follows.

$$O_1\approx U_r{\Sigma }_r{V}_r^{†}$$

(5)

In the above equation, left singular vectors $U_r\in {ℝ}^{c\times r}$ represents the typical features of power load fluctuations in distribution transformers. Right singular vectors $V_r\in {ℝ}^{(K-c)\times r}$ represents the evolution coefficient of each typical fluctuation pattern, such as periodic weighting. Diagonal matrix ${\Sigma }_r=\mathrm{diag}\left[{\sigma }_1,\cdots ,{\sigma }_r\right]\in {ℝ}^{r\times r}$ represents the importance of each pattern of change. $V_r^{†}$ denotes the conjugate transpose of $V_r$. In order to ignore noise and minor fluctuations, this paper refers to reference [33] to project high-dimensional operators onto low-dimensional subspaces. The primary process is as follows.

$$\tilde{\mathcal{A}}=U_r^{†}\mathcal{A}{U}_r\approx U_r^{†}{O}_2{V}_r{\Sigma }_r^{-1},$$

(6)

In the above equation, project matrix $O_2$ onto subspace $U_r$ to obtain the next state in the low-dimensional space. This avoids dependence on the original high-dimensional operator. Finally, through the above derivation, we can obtain the following equation.

$$\tilde{\mathcal{A}}=Q\Lambda Q^{†},$$

(7)

In the above equation, $Q\in {ℝ}^{r\times r},\Lambda =\mathrm{diag}\left({\lambda }_1,\cdots ,{\lambda }_r\right)\in {ℝ}^{r\times r}$. The above equation performs feature decomposition on the operator after dimension reduction, breaks down the typical fluctuation features and time-varying patterns of the sequential load data of distribution transformers, and enhances the generalization ability of the load forecasting model in few-shot scenarios. When $\left|{\lambda }_i\right|\approx 1$, it indicates that this type of fluctuation pattern hardly decays, such as industrial loads that are at high levels during working days and working hours. When $\left|{\lambda }_i\right|<1$, it indicates that this type of fluctuation pattern gradually decays over time, such as short-term peak loads.

4. A Parameter-Efficient Fine-Tuning Method Based on the Simultaneous Perturbation Stochastic Approximation Algorithm

LLMs have a large number of model parameters. During the training phase, LLM often requires millions of dollars in computational costs to mine and quantify general knowledge. Although LLMs can quickly adapt to different new scenarios, they have significant limitations in highly specialized distribution transformer load forecasting scenarios. This is because the training data for distribution transformer load forecasting scenarios is exceptionally scarce. The issue of data imbalance results in significant limitations for LLM in highly specialized scenarios. Therefore, this paper needs to fine-tune LLM while strictly limiting computational costs. Existing fine-tuning techniques for LLM primarily fall into two categories: full fine-tuning and partial fine-tuning (PEFT). Full fine-tuning requires updating all parameters of the LLM, resulting in high computational costs and limited scalability. Additionally, full fine-tuning may cause the complex structure of the LLM to over-adapt to the distribution transformer load forecasting scenario during fine-tuning, leading to catastrophic forgetting. Therefore, this paper selects PEFT technology for fine-tuning the LLM.

In the distribution transformer load forecasting model, this paper freezes the parameters of the LLM and adapts it to the characteristics of the distribution transformer load forecasting scenario by constructing an input embedding layer, a spatial embedding layer, a feature extraction layer, and an output projection layer. The parameters of the input embedding layer, spatial embedding layer, feature extraction layer, and output projection layer are fine-tuned using the error backpropagation algorithm. To improve computing efficiency and reduce training costs, this paper uses a linear layer as the basic structure of the input embedding layer, spatial embedding layer, feature extraction layer, and output projection layer [33]. In the input embedding layer, the sequential data of the distribution transformer load is cleaned and normalized. The equation for the input embedding layer is shown below.

$$E_{it}^1=x_{it}^{{\mathrm{n}}_{-}\mathrm{p}}{W}_1^{\top }+b_1,$$

(8)

In the above equation, $E_{it}^1$ is part of the input vector of the LLM, and $W_1$ and $b_1$ are learnable parameters. These parameters enable the LLM to quickly adapt to the specific characteristics of load forecasting scenarios for distribution transformers.

The load composition of distribution transformers varies significantly, and adjacent distribution transformers may exhibit different temporal fluctuation patterns. For example, the peak times and peak-to-valley differences in the load curves of distribution transformers with a high proportion of industrial loads may differ markedly from those of distribution transformers with a high proportion of residential loads, even if the two transformers are located in close proximity. There is no significant spatiotemporal correlation between the two distribution transformers. To solve the above problems, this paper uses the LBG algorithm to screen out distribution transformers with spatiotemporal correlation. In order to enable the load forecasting model to consider the spatiotemporal correlation between distribution transformers fully, this paper uses a weighted average method to aggregate the load data of similar distribution transformers. The specific equation is shown below.

$$x_{it}^{\mathrm{agg}}={\displaystyle \frac{x_{it}^{\mathrm{n}}+{\displaystyle \sum _{j\in {\mathcal{N}}^i}{x}_{jt}^{\mathrm{n}}}}{B+1}}$$

(9)

In the above equation, $x_{it}^{\mathrm{agg}}\in {ℝ}^K$ represents the aggregated load sample. This paper randomly selects $B$ distribution transformers from $N$ similar distribution transformers, and these samples constitute the set ${\mathcal{N}}^i$. $x_{jt}$ represents the transformer related to the i-th transformer $x_{it}$, and $x_{jt}^{\mathrm{n}}$ represents the normalized data. In the spatial embedding layer, this paper uses the aggregated features as part of the input vector for the LLM, enabling the LLM to consider the spatiotemporal correlation between distribution transformers sufficiently [33]. The specific equation is shown below.

$$E_{it}^2=x_{it}^{\mathrm{agg}}{W}_2^{\top }+b_2,$$

(10)

In the above equation, $W_2$ and $b_2$ are learnable parameters. These parameters enable LLM to capture the spatiotemporal correlations that exist between distribution transformers quickly. $E_{it}^2$ is part of the input vector of the LLM.

This paper uses the DMD algorithm to extract the inherent features of distribution transformers. In the feature extraction layer, the features extracted by the DMD algorithm are used as part of the input vector for LLM [33]. The specific equation is shown below.

$$E_{it}^3=v_{it}{W}_3^{\top }+b_3,$$

(11)

In the above equation, $v_{it}=\left({\lambda }_1;\cdots ,{\lambda }_r;{\sigma }_1;\cdots ;{\sigma }_r\right)$ represents the main fluctuation pattern of the load data, and $W_3$ and $b_3$ are learnable parameters.

To enable the LLM to sufficiently consider the spatiotemporal correlation and inherent features of distribution transformers, this paper concatenates the above feature vectors as input vectors for the LLM. The input vectors are shown in the following equation.

$$E_{it}=\left[\begin{array}{c}{E}_{it}^1\\ E_{it}^2\\ E_{it}^3\end{array}\right]$$

(12)

In the above equation, $E_{it}$ represents the input vectors for the LLM. In the output projection layer, this paper uses a linear layer to convert the abstract vector output by the LLM into distribution transformer load data [33]. The expression of the output projection layer is shown below.

$${\widehat{y}}_{it}=h_{it}{W}_4^{\top }+b_4,$$

(13)

In the above equation, $W_4$ and $b_4$ are learnable parameters, ${\widehat{y}}_{it}$ represents the load forecasting value of the distribution transformer, and $h_{it}$ represents the embedding of the last hidden layer of LLM. LLM structures are complex and have numerous model parameters. Traditional error backpropagation algorithms require the usage of all LLM parameters, greatly increasing computational costs.

In order to reduce the training cost of the load forecasting model for distribution transformers and improve inference efficiency, this paper selects the simultaneous perturbation stochastic approximation (SPSA) algorithm to enhance the traditional error backpropagation algorithm [33]. The SPSA algorithm is based on the Simultaneous Perturbation Gradient Approximation method and the Stochastic Newton method. It uses a Gain Sequence and Perturbation Distribution to ensure the convergence of the algorithm. The SPSA algorithm efficiently estimates gradients by simultaneously randomly perturbing all parameters. It only requires two function evaluations to achieve gradient estimation, significantly reducing computational costs. The SPSA algorithm is insensitive to model parameter dimensions and can solve high-dimensional optimization problems with constant computational costs. Based on the SPSA algorithm, LLM can quickly adapt to the characteristics of power distribution transformer load forecasting scenarios at a low price.

The improved optimization algorithm can efficiently optimize the learnable parameters in the input embedding layer, spatial embedding layer, feature extraction layer, and output projection layer. This paper calculates the first-order gradients of $W_4$ and $b_4$ [33]. The specific equation is shown below.

$$\left\{\begin{array}{l}\nabla W_4:={\displaystyle \frac{\partial L}{\partial W_4}}={\displaystyle \frac{\partial L}{\partial {\widehat{y}}_{it}}}{\displaystyle \frac{\partial {\widehat{y}}_{it}}{\partial W_4}}\hfill \\ \nabla b_4:={\displaystyle \frac{\partial L}{\partial b_4}}={\displaystyle \frac{\partial L}{\partial {\widehat{y}}_{it}}}{\displaystyle \frac{\partial {\widehat{y}}_{it}}{\partial b_4}}\hfill \end{array}\right.$$

(14)

In the above equation, $L$ represents the loss function. Next, this paper adopts the SPSA algorithm [33] to calculate the zero-order gradients for $\left\{W_j,b_j;j=1,2,3\right\}$. The specific equation is shown below.

$$\widehat{\nabla }{\Theta }^{\prime }={\displaystyle \frac{L\left({\Theta }^{\prime }+ϵZ\right)-L\left({\Theta }^{\prime }-ϵZ\right)}{2ϵ}}z$$

(15)

In the above equation, ${\Theta }^{\prime }=\left\{W_j,b_j;j=1,2,3\right\}$. $Z$ represents a vector chosen randomly from the standard Gaussian distribution, and $ϵ$ represents perturbation scale parameter. After obtaining the gradient, this paper uses the adaptive moment estimation (Adam) method to optimize the model parameters. In the t-th iteration, the main optimization process of the model parameters is as follows [33].

$$\left\{\begin{array}{l}{\mathcal{M}}_{(t)}={\beta }_1{\mathcal{M}}_{(t-1)}+\left(1-{\beta }_1\right)\nabla {\Theta }_{(t-1)}\hfill \\ {\mathcal{V}}_{(t)}={\beta }_2{\mathcal{V}}_{(t-1)}+\left(1-{\beta }_2\right){\left(\nabla {\Theta }_{(t-1)}\right)}^2\hfill \\ {\widehat{\mathcal{M}}}_{(t)}={\displaystyle \frac{{\mathcal{M}}_{(t)}}{1-{\beta }_1^{(t)}}}\hfill \\ {\widehat{\mathcal{V}}}_{(t)}={\displaystyle \frac{{\mathcal{V}}_{(t)}}{1-{\beta }_2^{(t)}}}\hfill \\ {\Theta }_{(t)}={\Theta }_{(t-1)}-\alpha {\widehat{\mathcal{M}}}_{(t)}/\left(\sqrt{{\widehat{\mathcal{V}}}_{(t)}}+\gamma \right),\hfill \end{array}\right.$$

(16)

In the above equation, ${\mathcal{M}}_{(t)}$ and ${\mathcal{V}}_{(t)}$ represent the biased first moment estimate and second raw moment estimate, respectively; ${\widehat{\mathcal{M}}}_{(t)}$ and ${\widehat{\mathcal{V}}}_{(t)}$ represent the biased-corrected first moment estimate and second raw moment estimate, respectively; ${\beta }_1$ and ${\beta }_2$ represent the hyperparameters that control the exponential decay rates; and $\alpha$ and $\gamma$ represent the learning rate and small constant for numerical stability, respectively.

5. Experiments and Results

To validate the effectiveness of the proposed method, this paper selects LSTM [10], N-BEATS [35], and Autoformer [38] as baseline models, and LLaMa-7B as the primary LLM. The baseline models are trained on the same aggregated dataset as the proposed model. The training data set and validation data set use the same ratio. The models are fine-tuned using the same target data. To fully characterize the error characteristics of the load forecasting model, this paper selects relative Mean Absolute Error (rMAE), Mean Absolute Percentage Error (MAPE) and Normalized Root Mean Square Error (NRMSE) as the primary error indicators. The original definition of MAPE is shown below.

$$\mathrm{MAPE}={\displaystyle \frac{100\%}{n}}{\displaystyle \sum _{i=1}^n\left|\frac{{\stackrel{⌢}{L}}_i-L_i}{L_i}\right|}$$

(17)

MAPE converts the prediction error into a relative percentage, reflecting the degree of deviation between the predicted results and the actual results. It is calculated by dividing the absolute error between the predicted value and the actual value of the distribution transformer load data by the actual value. Next, the average value of all samples is taken. In summary, MAPE emphasizes the relative error in prediction results. This metric standardizes prediction errors from 0% to 100%, facilitating comparisons between multiple prediction models and enabling power companies to select models with superior prediction performance more easily. The NRMSE indicator is an improvement on the RMSE indicator. First, the sum of the squares of all errors is calculated and then divided by the sum of the squares of the actual values. NRMSE is a dimensionless indicator that can be applied to distribution transformers with different load levels. The three indicators comprehensively reflect the error characteristics of the forecast results. This paper selects the power load dataset of a province in China as the main research object. The data set used in this paper has a time granularity of 1 h. Two distribution transformers were selected to verify the effectiveness of the model in a few-shot scenario. Since this research involves confidential data, the relevant data has been anonymized in this paper. For missing values and outliers in the data set, the interquartile range (IQR) method was used to identify outliers, and linear interpolation was used to supplement the missing values and outliers. The linear interpolation method is shown below.

$$L(t)=L_i+{\displaystyle \frac{L_{i+1}-L_i}{t_{i+1}-t_i}}\left(t-t_i\right)$$

(18)

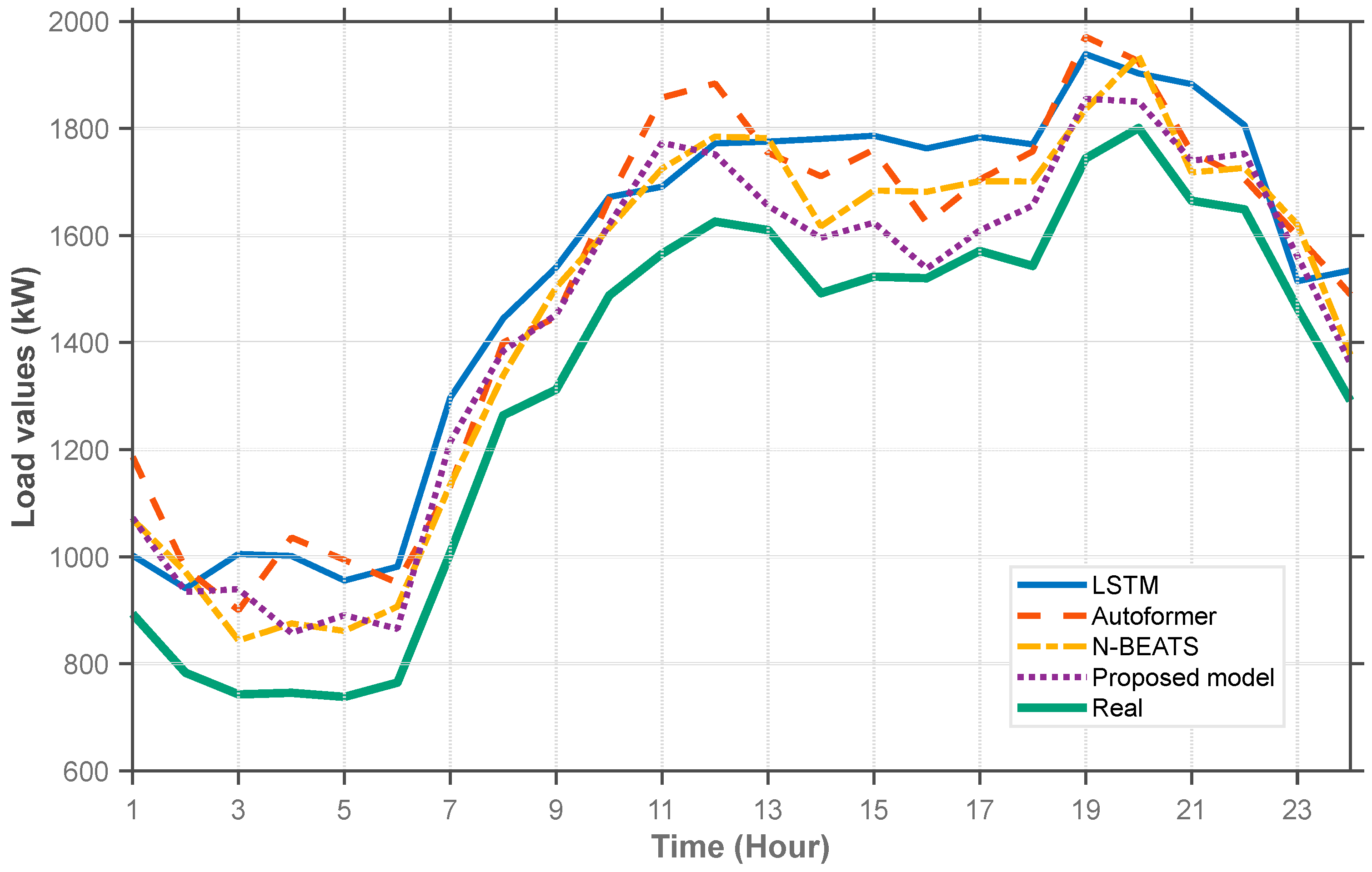
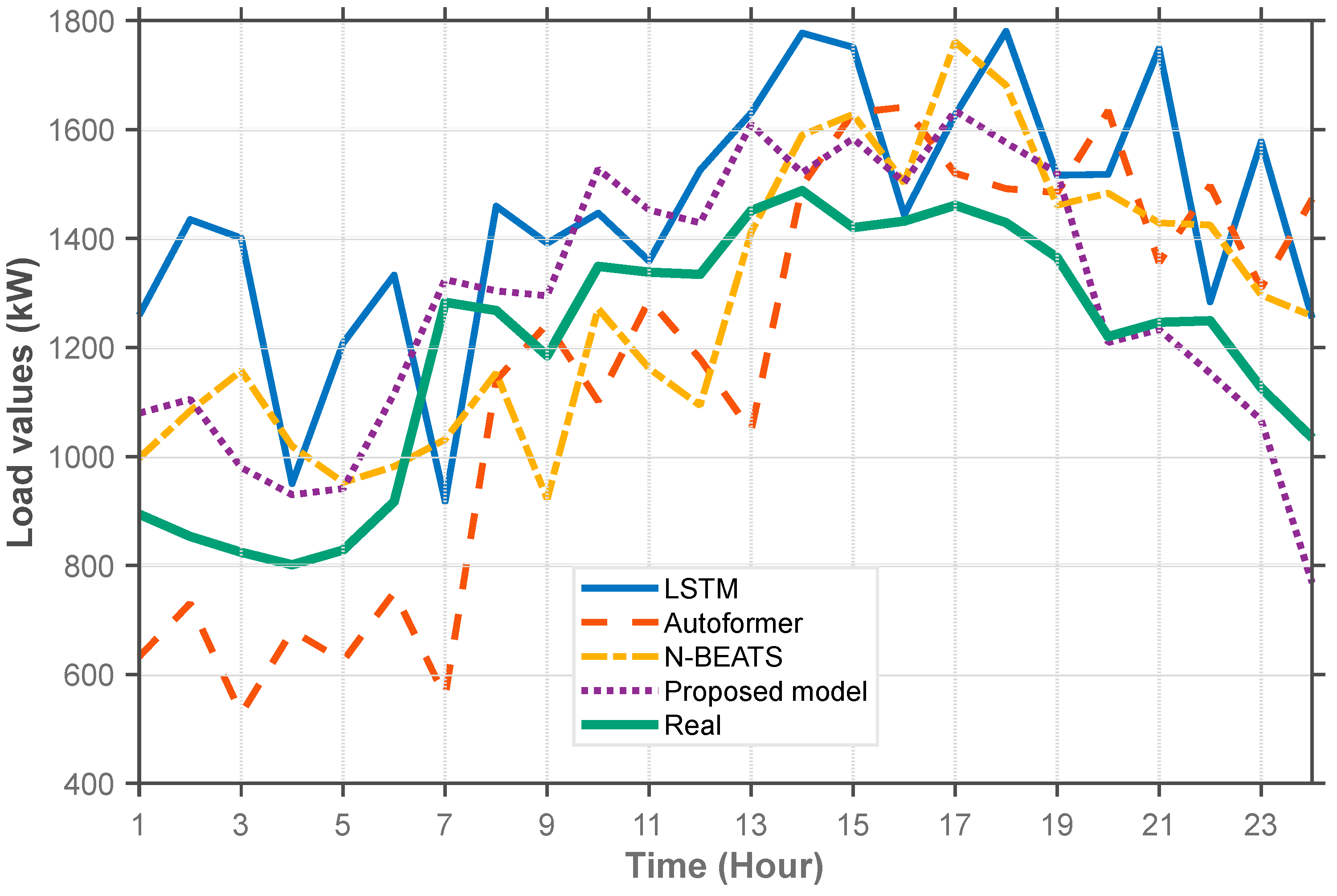
In the above equation, $t_i$ and $t_{i+1}$ represent two adjacent time points. $L(t)$ represents missing or abnormal power load data. The prediction results of each method are shown in Figure 4.

As seen from the above figure, the method in this paper effectively predicts changes in the load of distribution transformers and accurately reflects peak load times. Such prediction results can help power companies anticipate possible transformer overload events and arrange remedial measures. Autoformer uses an encoder–decoder architecture, with Series Decomposition Block and Auto-Correlation as its core. This model structure enables Autoformer to capture long-term dependencies in sequential load data effectively. However, there are few load samples for the first distribution transformer, making it impossible to effectively fine-tune the model parameters of Autoformer, which results in low prediction accuracy.

LSTM uses a chain structure to capture the fluctuation patterns in sequential power load data through a special gate mechanism. The forget gate in LSTM effectively avoids the problems of gradient disappearance and gradient explosion during training. However, LSTM cannot be effectively fine-tuned with the limited load data of the first distribution transformer, and its prediction accuracy is lower than that of the method proposed in this paper.

The model and the benchmark models in this paper were trained and verified using high-quality data sets, eliminating the impact of missing values and outliers on the model. Based on the power load forecasting curve of the model in this paper, the model accurately reflects the fluctuation characteristics of real data and has good ability to repeat the data dynamic features, which fully verifies the effectiveness of the model in this paper. The load forecasting results of the second distribution transformer are shown in Figure 5.

As can be seen from the figure above, the prediction accuracy of N-BEATS significantly decreases on the second distribution transformer. N-BEATS adopts a two-layer architecture consisting of Stack and Block, where each Block comprises multiple fully connected layers, and each Stack comprises multiple Blocks. The outputs of multiple Stacks are accumulated to form the final prediction result of the N-BEATS model. Reference [35] uses the Model-Agnostic Meta-Learning (MAML) optimization algorithm to optimize N-BEATS.

The MAML algorithm mainly includes inner-layer optimization and outer-layer optimization. In the inner-layer optimization stage, the model parameters are fine-tuned for a single prediction object. In the outer-layer optimization stage, the meta-model parameters are optimized using the features of multiple prediction objects. The inner-layer optimization and outer-layer optimization are repeated until the meta-model converges. At this point, N-BEATS can quickly adapt to new prediction objects. The new prediction objects must be highly correlated with the training data to ensure high prediction accuracy. If the correlation decreases, the prediction accuracy of N-BEATS will significantly decline. Therefore, N-BEATS achieves high prediction accuracy on the first transformer but shows a significant drop in prediction accuracy on the second transformer. The method proposed in this paper achieves high prediction accuracy on both the first and second distribution transformers. The prediction errors of various methods are shown in

Table 2. Prediction error of each model.

Model	The 1st Transformer				The 2nd Transformer
	MAPE	rMAE	R2	NRMSE	MAPE	rMAE	R2	NRMSE
LSTM	16.77	0.15	0.66	15.04	25.21	0.23	−0.9	25.89
Autoformer	15.77	0.14	0.70	14.15	18.29	0.17	−0.3	21.35
N-BEATS	11.18	0.10	0.84	10.09	15.73	0.15	0.26	16.01
Proposed model	10.19	0.08	0.88	9.12	11.18	0.10	0.61	11.54

, which fully validates the effectiveness of the proposed method.

The rMAE indicator is dimensionless, allowing power companies to select appropriate prediction models from different data sets. As can be seen from Table 2, the prediction errors of each model on the second distribution transformer increased to varying degrees. This is because the power load of the second distribution transformer is less regular, and the dependency between the time series data has undergone dynamic changes. The model proposed in this paper, leveraging the exceptional generalization capabilities of LLM, can quickly adapt to new data features, fully validating the advantages of the proposed model.

In order to fully verify the effectiveness of each component of the model in this paper, ablation experiments were conducted on two transformers to validate the effectiveness of each component of the model. The spatial embedding layer and feature extraction layer were selected as the main objects for analysis. The results of the ablation experiments are shown in

Table 3. Results of ablation experiment.

Variants	The 1st Transformer			The 2nd Transformer
	MAPE	rMAE	NRMSE	MAPE	rMAE	NRMSE
Feature extraction layer	10.92	0.08	9.36	11.93	0.13	12.77
Spatial embedding layer	11.02	0.09	9.84	12.51	0.15	13.18
Proposed model	10.19	0.08	9.12	11.18	0.10	11.54

.

As can be seen from the table above, after losing the spatial embedding layer or feature extraction layer, the prediction accuracy decreased to varying degrees, which fully verifies the effectiveness of the spatial embedding layer and feature extraction layer in improving the accuracy of distribution transformers.

To validate the training cost of the proposed method, this paper compares the memory and time used by different baseline models during the training stage of the first distribution transformer. The main results are shown in

Table 4. Memory and time used by each model during training stage.

Model	Mem (MiB)	Time (s)
LSTM	216	106.4
Autoformer	2950	542.7
N-BEATS	1128	1671.1
Proposed model	492	852.3

.

This paper accesses LLaMa-7B through cloud services. The memory and time used in the training stage are mainly used to optimize the parameters of the input embedding layer, spatial embedding layer, feature extraction layer, and output projection layer. As seen from the table above, this paper effectively reduces training costs. It enables LLaMa-7B to quickly adapt to the characteristics of power distribution transformer load forecasting scenarios with only a small amount of memory.

6. Conclusions

Facing the large number of distribution transformers, the load data of different distribution transformers show different inherent features, and the few-shot problem is common. This paper proposes a method for load forecasting distribution transformers based on parameter-efficient fine-tuning of large language models. This paper utilizes the superior generalization ability of large language model (LLM) to enhance the accuracy of load forecasting model in few-shot scenarios. Through the Linde–Buzo–Gray algorithm, the spatiotemporal correlation between distribution transformers is analyzed. Key features are extracted from the original load data based on the dynamic mode decomposition algorithm. The proposed model captures the inherent features of each distribution transformer, converting time series load data into low-dimensional dynamic features, combining singular value decomposition to extract the main fluctuation patterns, and finally generating an embedded representation suitable for LLMs through linear transformation, which significantly improves the generalization ability of the model in few-shot scenarios. Since the proposed model accesses LLaMa-7B through cloud services, the computing cost of the proposed model is significantly reduced, and the memory of the proposed model is only 492 MiB. This paper proposes a parameter-efficient fine-tuning method that freezes the LLM parameters and adapts the LLM to the characteristics of the distribution transformer load forecasting scenario by constructing an input embedding layer, a spatial embedding layer, a feature extraction layer, and an output projection layer. The simultaneous perturbation stochastic approximation algorithm is used to fine-tune the parameters of the input embedding layer, spatial embedding layer, feature extraction layer, and output projection layer.

The experimental results demonstrate that the proposed method achieves high prediction accuracy in few-shot scenarios. It can rapidly capture and infer the potential fluctuation patterns of different distribution transformers based on limited data. This method significantly enhances the grid company’s ability to identify potential risks in distribution grids and effectively prevents distribution transformer overload incidents. In future work, we will further explore the impact of enterprise working schedules, emergency events, typhoon disaster event, power grid expansion and other sudden events on the load of distribution transformers, continue to optimize the sensitivity of the prediction model to various types of events, and enhance the edge deployment performance of the prediction model.