Design and Crushing Characteristics of Double-Rotor Vertical-Shaft-Impact Sand-Making Machine
Abstract
1. Introduction
2. Double-Rotor Structural Design
3. Double-Rotor Optimal Speed Analysis
4. Crushing Characteristics Analysis
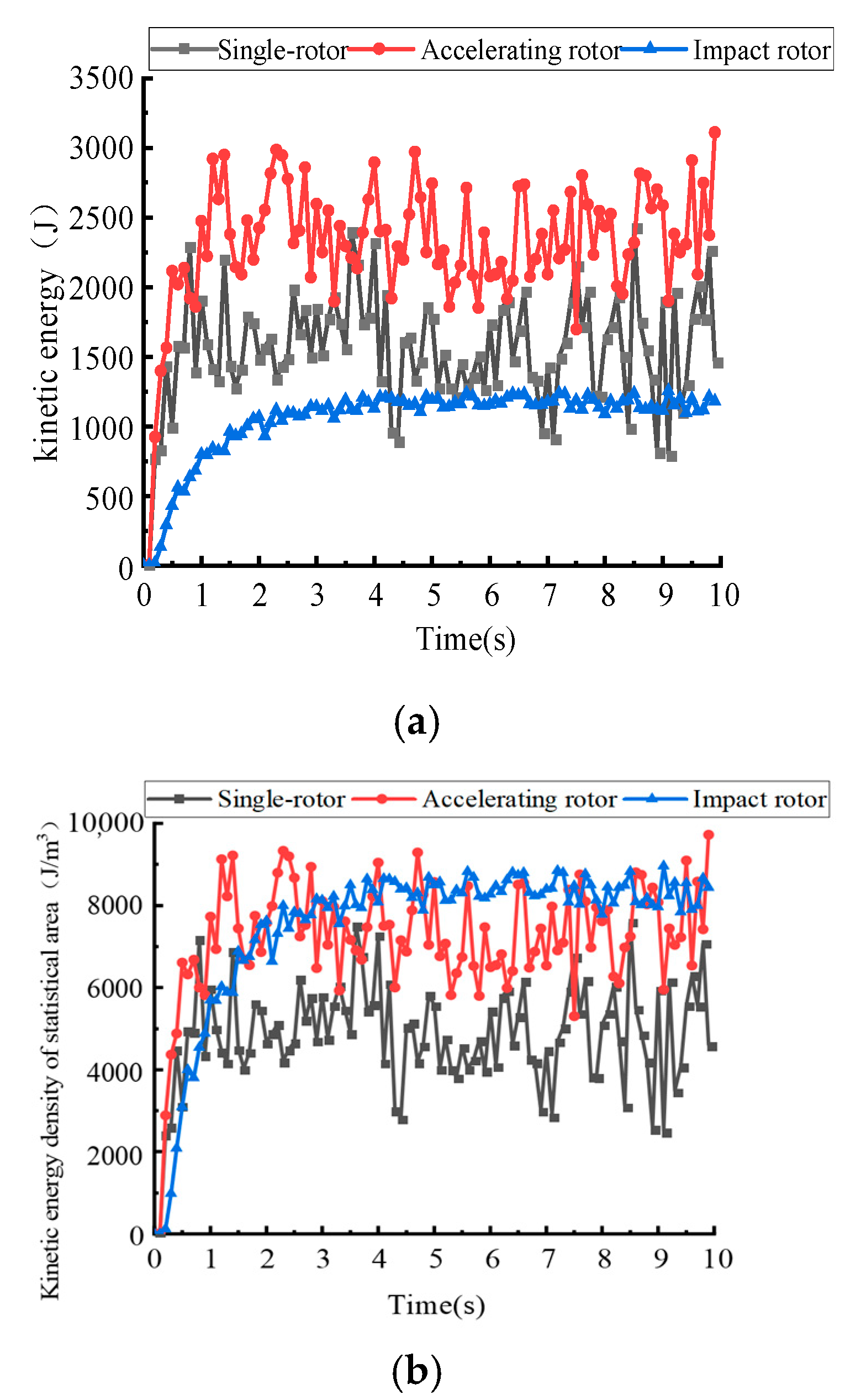
4.1. Kinetic Energy of Particles in Main Crushing Area
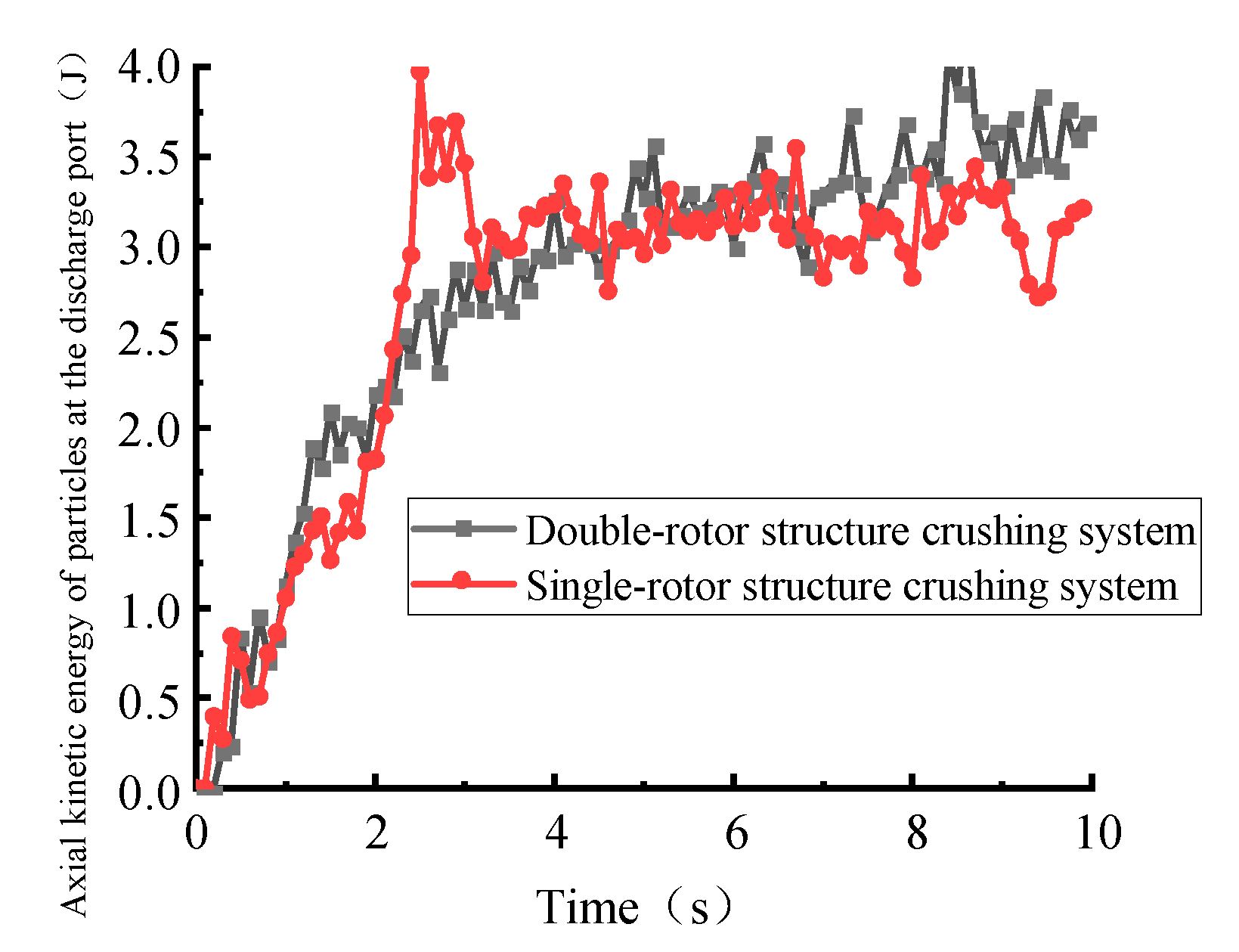
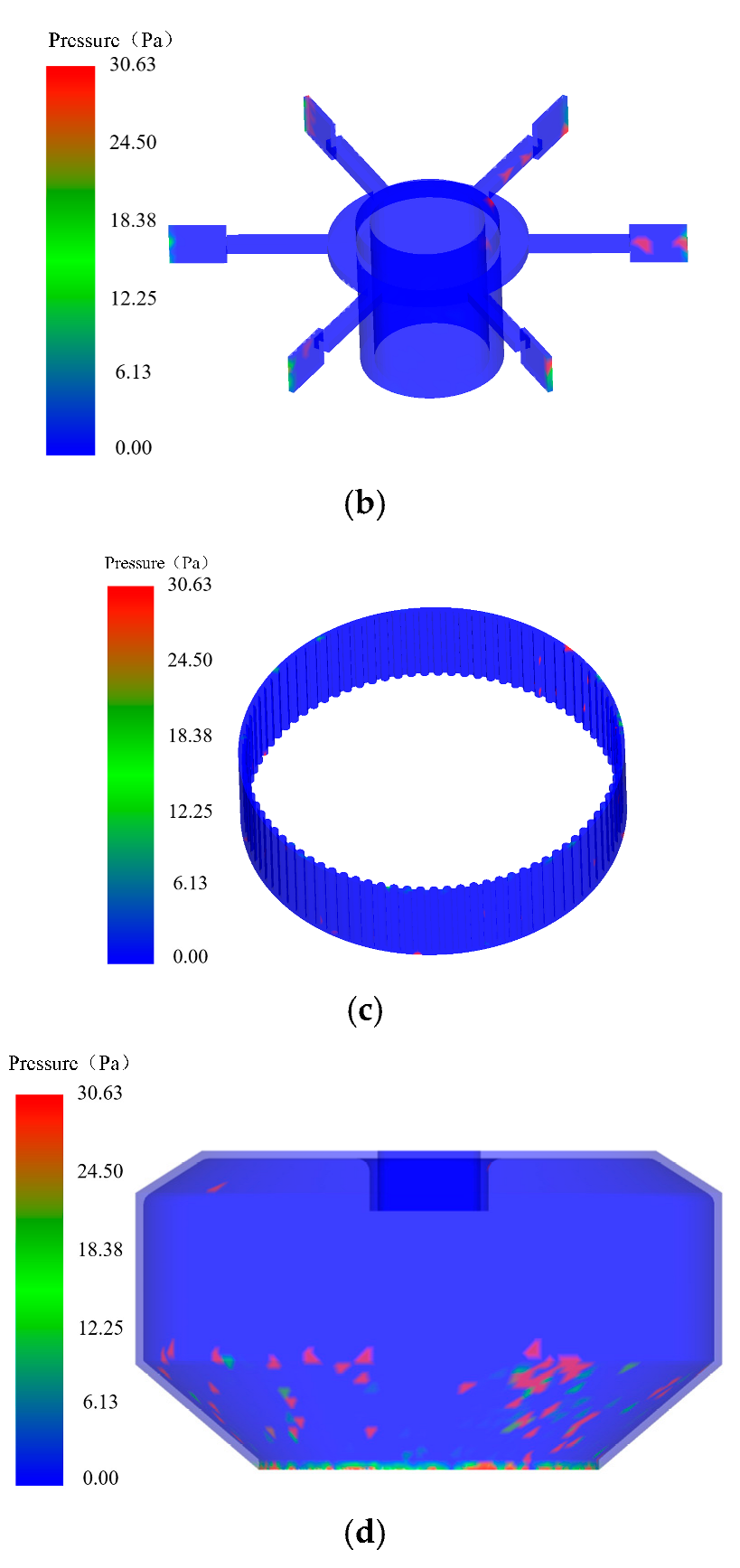
4.2. Discharge Port Wear Analysis
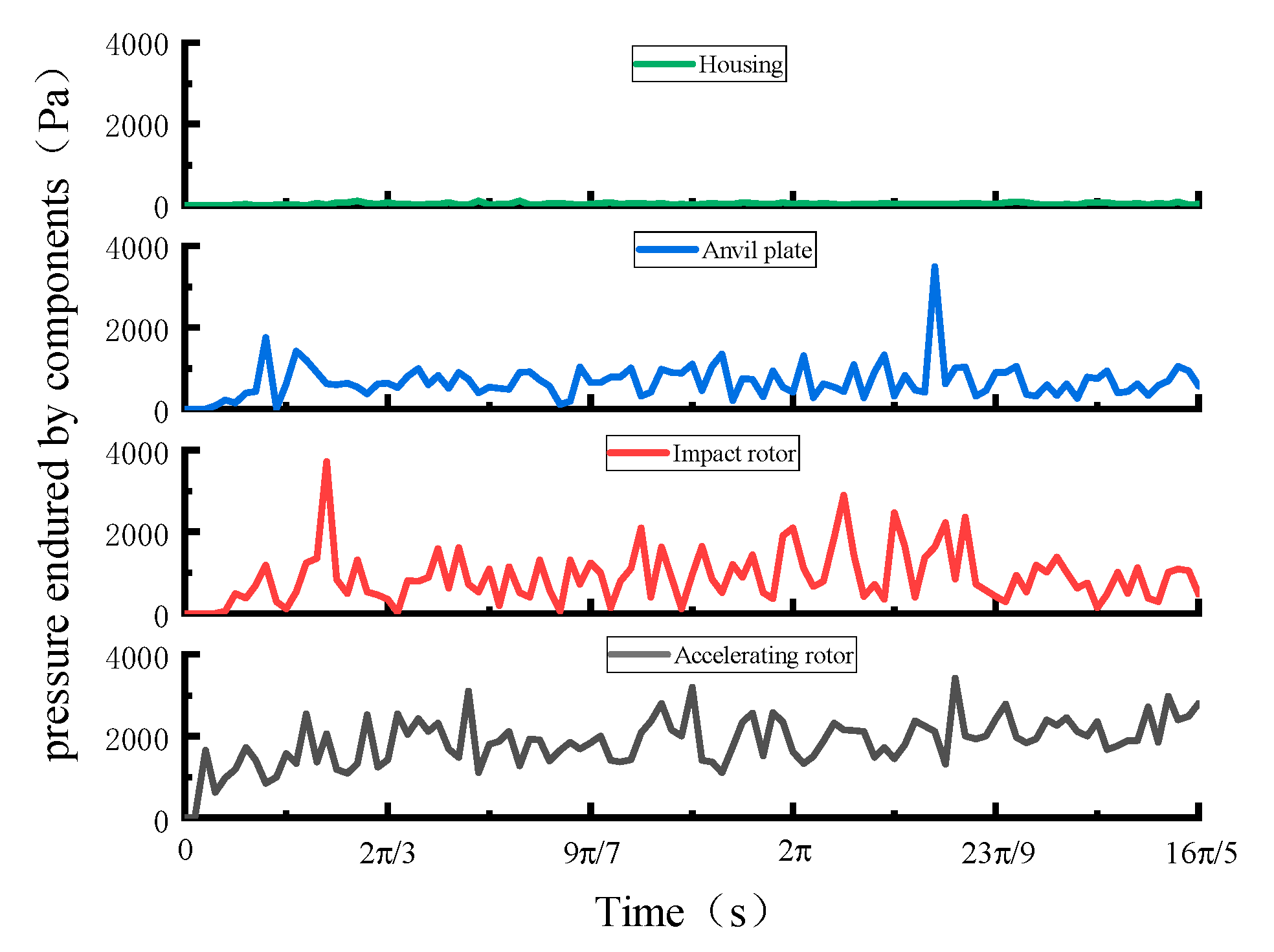
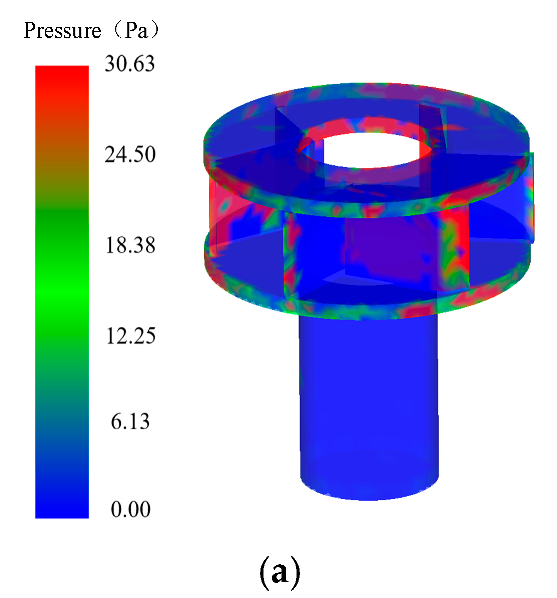
4.3. Component Wear Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Khasawneh, Y. Development and Testing of a Novel Mathematical-physical Model for the Design of Ring Armor for the Vertical Shaft Impact Crushers. Miner. Eng. 2021, 170, 106994. [Google Scholar] [CrossRef]
- Feifei, F.; Jinfa, S.; Jie, Y.; Junxu, M. Correlation between the Angle of the Guide Plate and Crushing Performance in Vertical Shaft Crushers. Shock Vib. 2022, 2022, 9991855. [Google Scholar]
- Boettcher, A.-C.; Beusen, D.; Lueddecke, A.; Overbeck, A.; Schilde, C.; Kwade, A. Single and Multiple Breakage Events in Fine Particle Breakage Testing with a Rigidly-mounted Roll Mill. Miner. Eng. 2022, 178, 107390. [Google Scholar] [CrossRef]
- Oliveira, A.L.R.; Rodriguez, V.A.; De Carvalho, R.M.; Powell, M.; Tavares, L. Mechanistic Modeling and Simulation of a Batch Vertical Stirred Mill. Miner. Eng. 2020, 156, 106487. [Google Scholar] [CrossRef]
- Zhenmin, L.; Weihao, C.; Wei, Z.; Zhang, X.; Wen, B. Theoretical, Numerical, and Experimental Study on the Synchronization in a Vibrator-pendulum Coupling System. Arch. Civ. Mech. Eng. 2022, 22, 157. [Google Scholar]
- Grunditz, S. Modeling of Vertical Shaft Impact Crushers. 2021. Available online: https://research.chalmers.se/publication/523453/file/523453_Fulltext.pdf (accessed on 1 April 2021).
- Luo, M.; Yang, H.J.; Fang, Y.H. An Investigation on Sand Production of Vertical Shaft Impact Crusher Using EDEM. Adv. Mater. Res. 2014, 3381, 1226–1230. [Google Scholar] [CrossRef]
- Duan, R.D.; Wang, S.; Zhao, F.; Su, D.N. Analysis of Particle Motion in Vertical Shaft Impact Crusher Rotor. Adv. Mater. Res. 2011, 1168, 54–57. [Google Scholar] [CrossRef]
- Bwalya, M.M.; Ngonidzashe, C. Numerical Simulation of a Single and Double-Rotor Impact Crusher Using Discrete Element Method. Minerals 2022, 12, 143. [Google Scholar] [CrossRef]
- Feng, F.; Shi, J.; Yang, J.; Ma, J. Study on Wear form of Split Cone of Vertical Shaft Impact Crusher. J. Sci. Res. Rep. 2020, 26, 13–20. [Google Scholar] [CrossRef]
- Simon, G.; Gauti, A.; Erik, H.; Evertsson, M. Fit-for-Purpose VSI Modelling Framework for Process Simulation. Minerals 2020, 11, 40. [Google Scholar]
- Dündar, H. Rotor Speed-Size Reduction Relationship In A Vertical Shaft Impact Crusher. Bilimsel Madencilik Derg. 2018, 3, 189–196. [Google Scholar] [CrossRef]
- Jie, Y.; Feifei, F.; Junxu, M.; Shi, J. Wear Law and Parameter Optimization Study on the Split Cone of a Vertical Shaft Impact Crusher. Math. Probl. Eng. 2021, 2021, 9976571. [Google Scholar] [CrossRef]
- Wu, C.; Zhao, L.; Cao, Z. Collision Energy Analysis within the Vertical Shaft Impact Crusher Based on the Computational Fluid Dynamics-Discrete Element Method. ACS Omega 2024, 9, 7967–7975. [Google Scholar] [CrossRef]
- Wu, C.; Zhao, L.; Cao, Z. The Crushing Distribution Morphology of a Single Particle Subjected to Rotary Impact. ACS Omega 2024, 9, 31464–31476. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Wang, G.; Sun, G.; Wang, S.; Guan, W.; Chen, Z. DEM simulation and optimization of crushing chamber shape of gyratory crusher based on Ab-t10 model. Miner. Eng. 2024, 209, 108606. [Google Scholar] [CrossRef]
- Kuang, D.M.; Long, Z.L.; Ogwu, I.; Chen, Z. A discrete element method (DEM)-based approach to simulating particle breakage. Acta Geotech. 2021, 17, 2751–2764. [Google Scholar] [CrossRef]
- Zeren, C.; Guoqiang, W.; Duomei, X.; Cui, D. Simulation and optimization of crushing chamber of gyratory crusher based on the DEM and GA. Powder Technol. 2021, 384, 36–50. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, G.; Xue, D.; Bi, Q. Simulation and optimization of gyratory crusher performance based on the discrete element method. Powder Technol. 2020, 376, 93–103. [Google Scholar] [CrossRef]
- Chonghui, W.; Hainian, W.; Markus, O.; Hasan, M.R.M. Investigation on the morphological and mineralogical properties of coarse aggregates under VSI crushing operation. Int. J. Pavement Eng. 2020, 22, 1611–1624. [Google Scholar] [CrossRef]
- Fang, H.; Yang, J.; Song, Y.; Huang, W.; Chen, J. Simulation and experimental study on the stone powder separator of a vertical shaft impact crusher. Adv. Powder Technol. 2020, 31, 1013–1022. [Google Scholar] [CrossRef]
- Segura-Salazar, J.; Barrios, P.G.; Rodriguez, V.; Tavares, L.M. Mathematical modeling of a vertical shaft impact crusher using the Whiten model. Miner. Eng. 2017, 111, 222–228. [Google Scholar] [CrossRef]
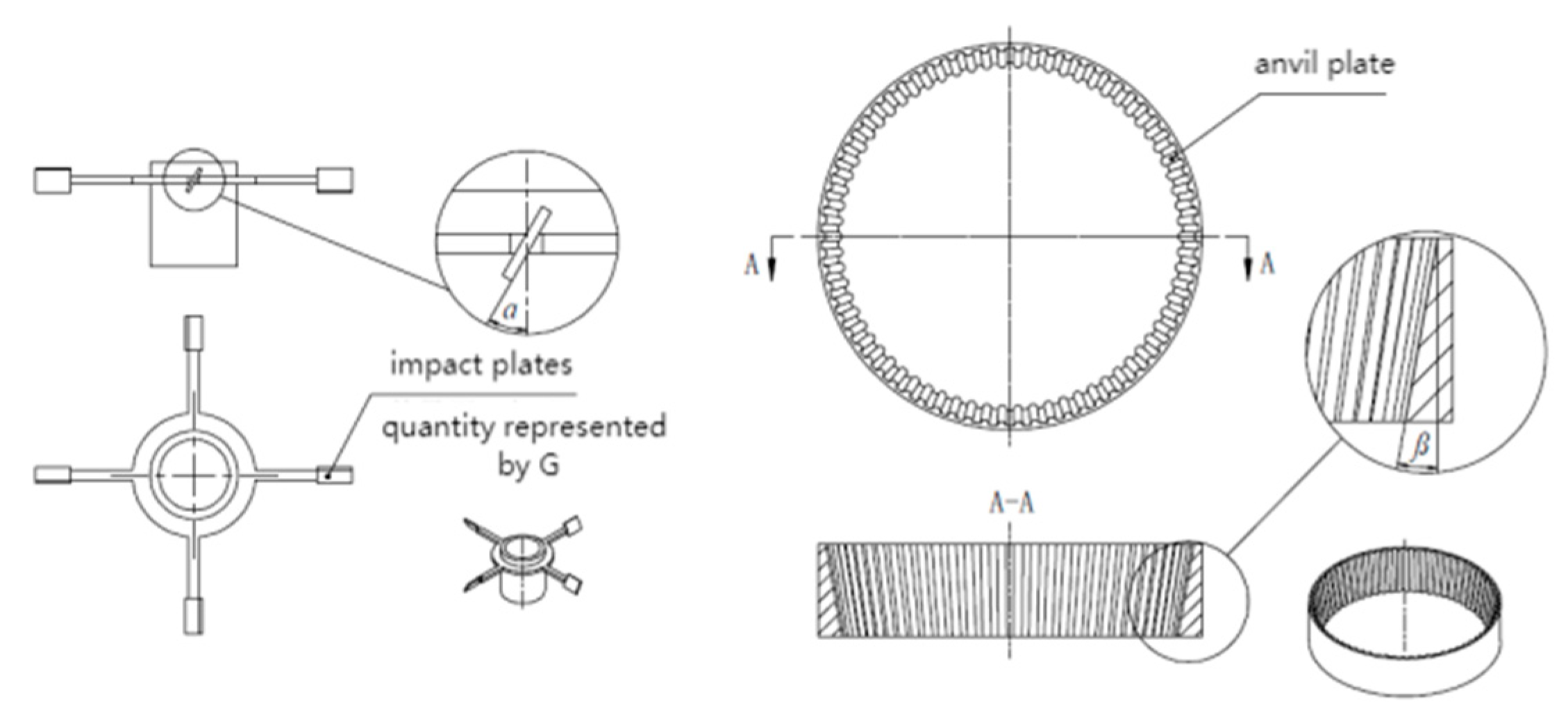
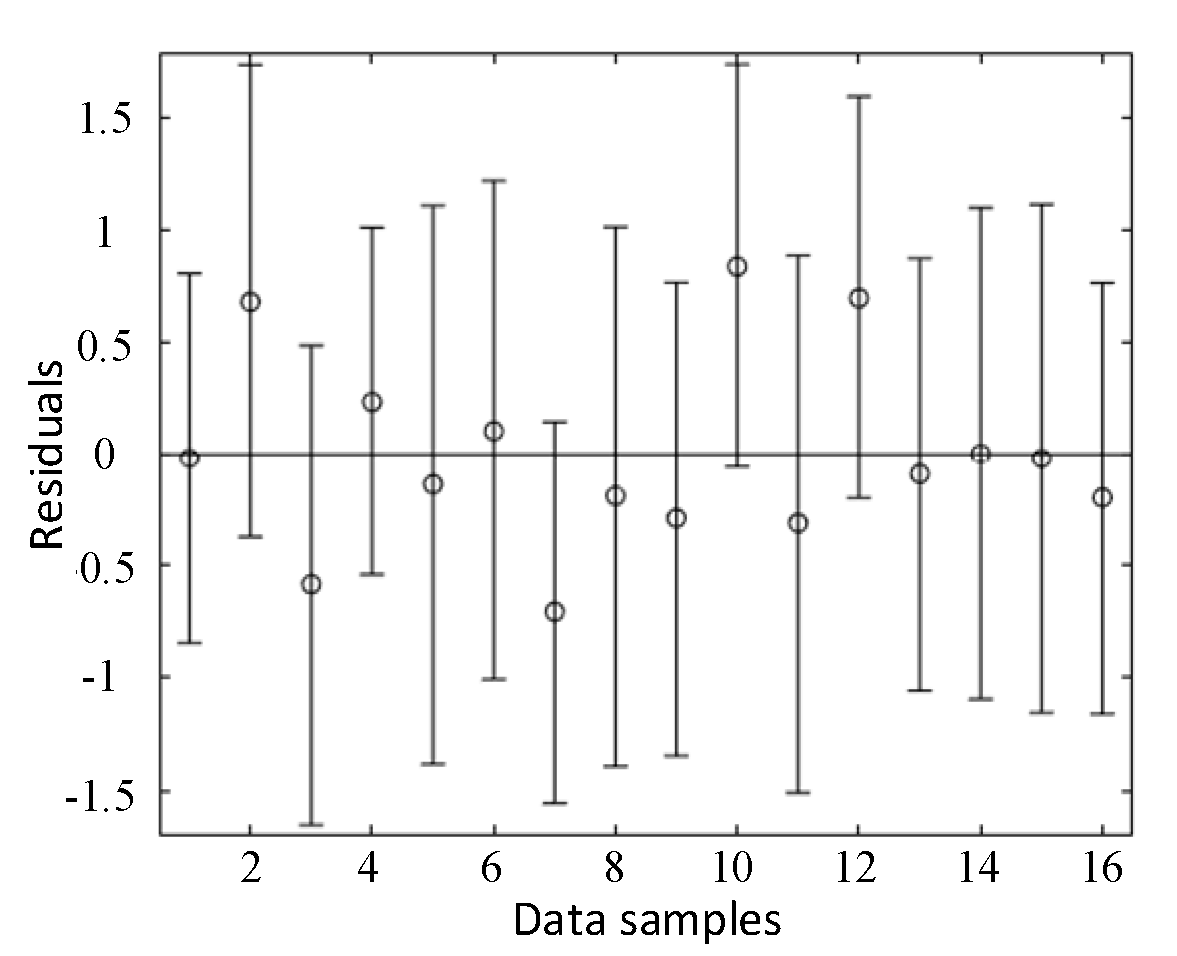
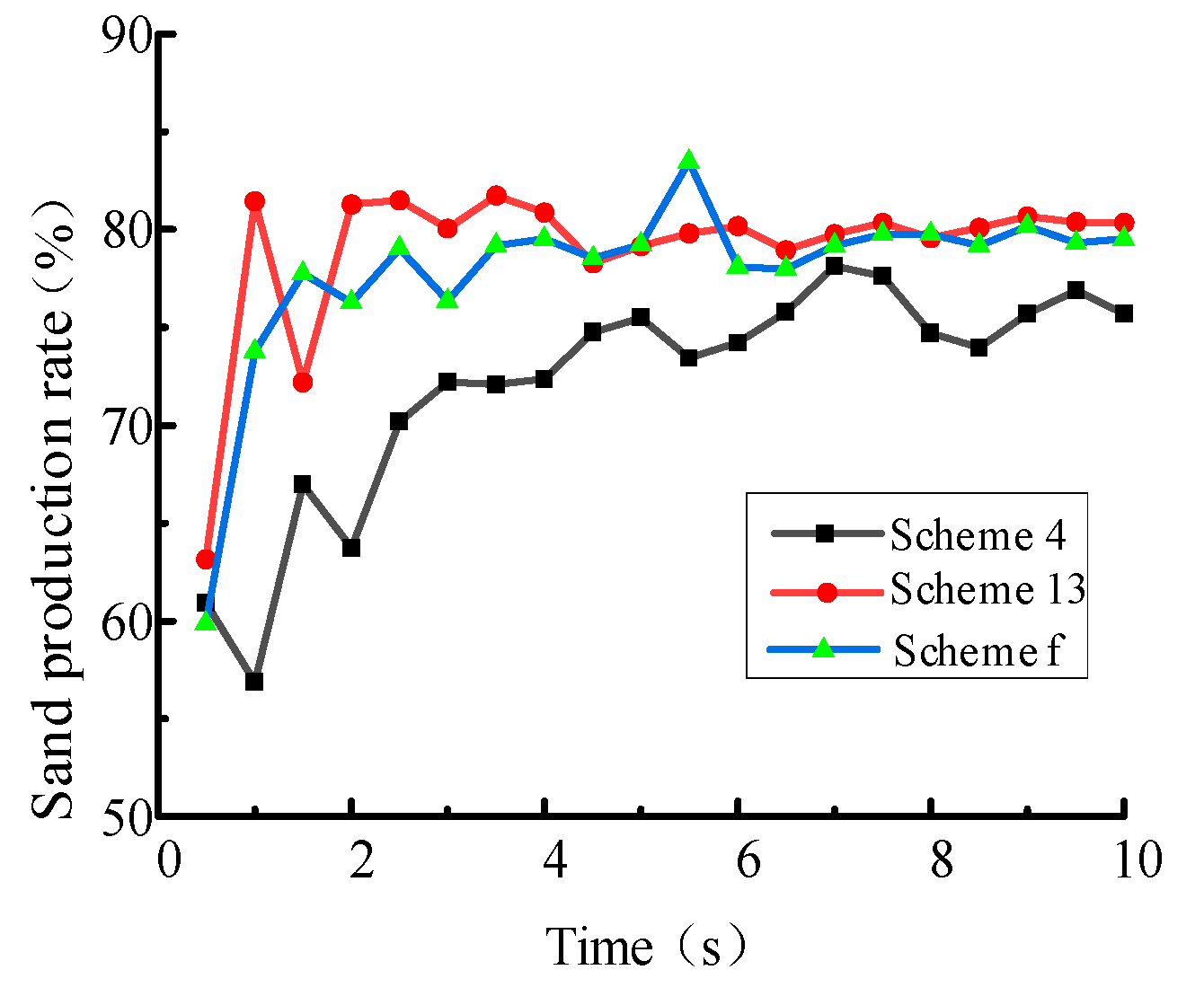
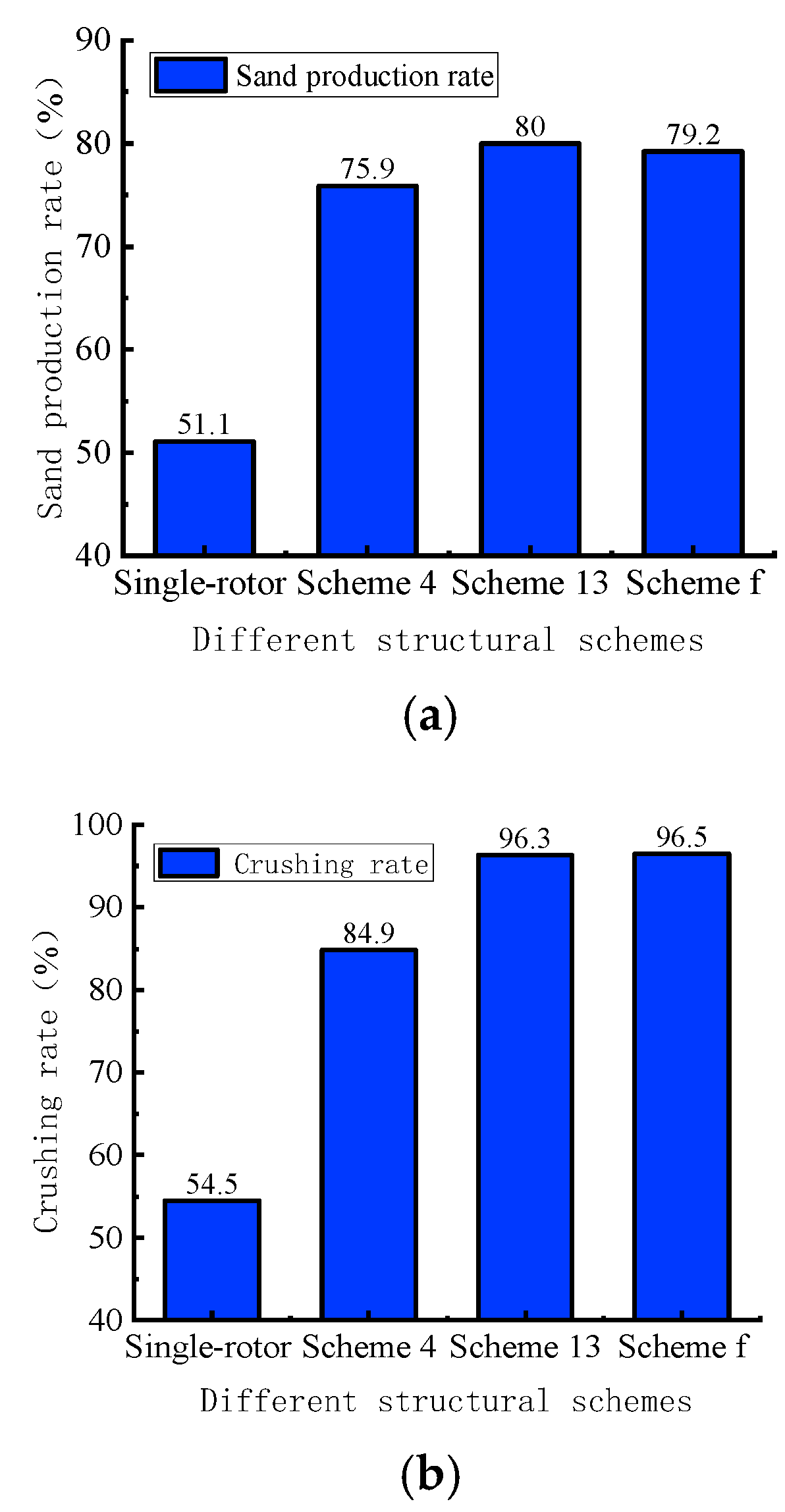
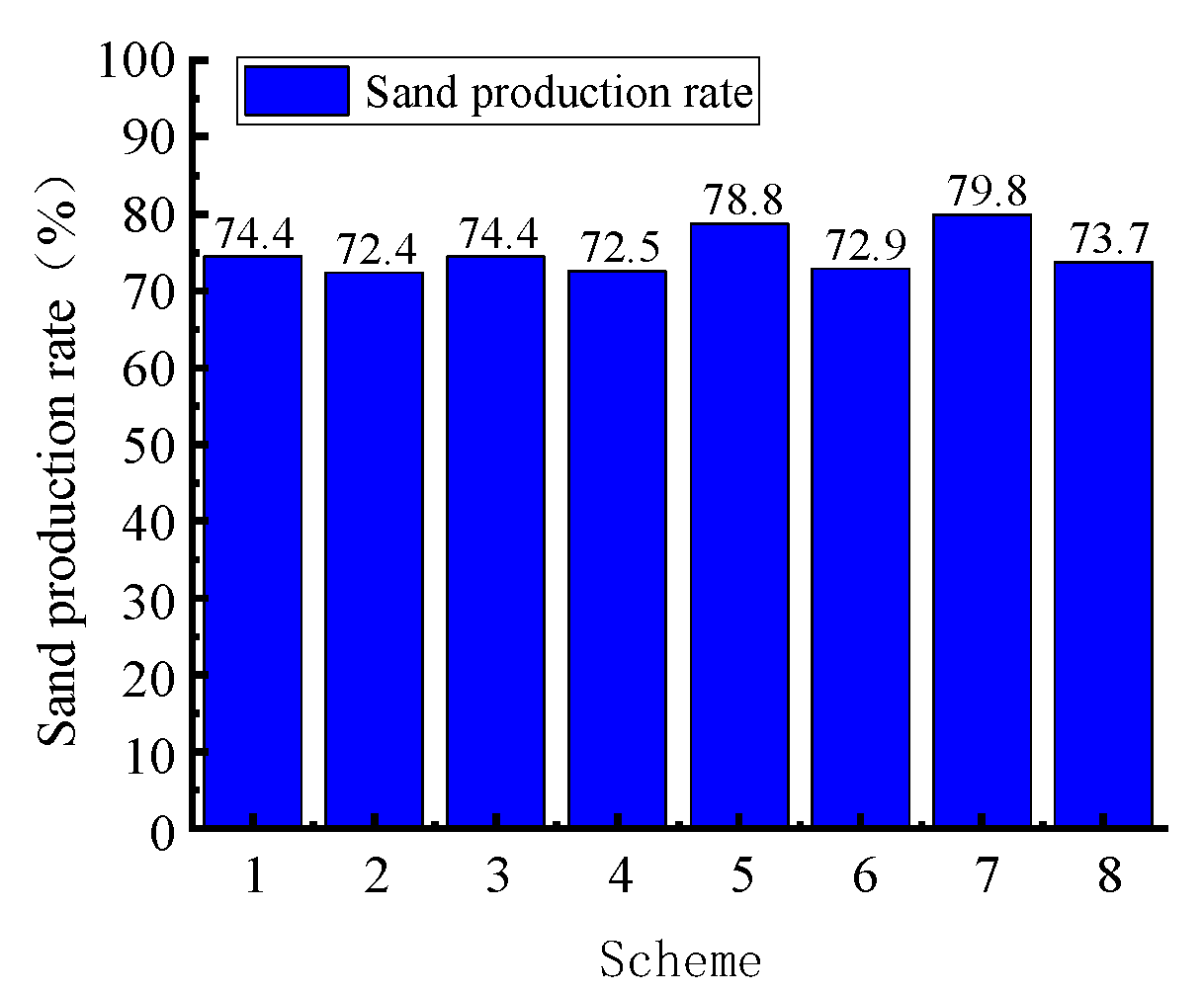
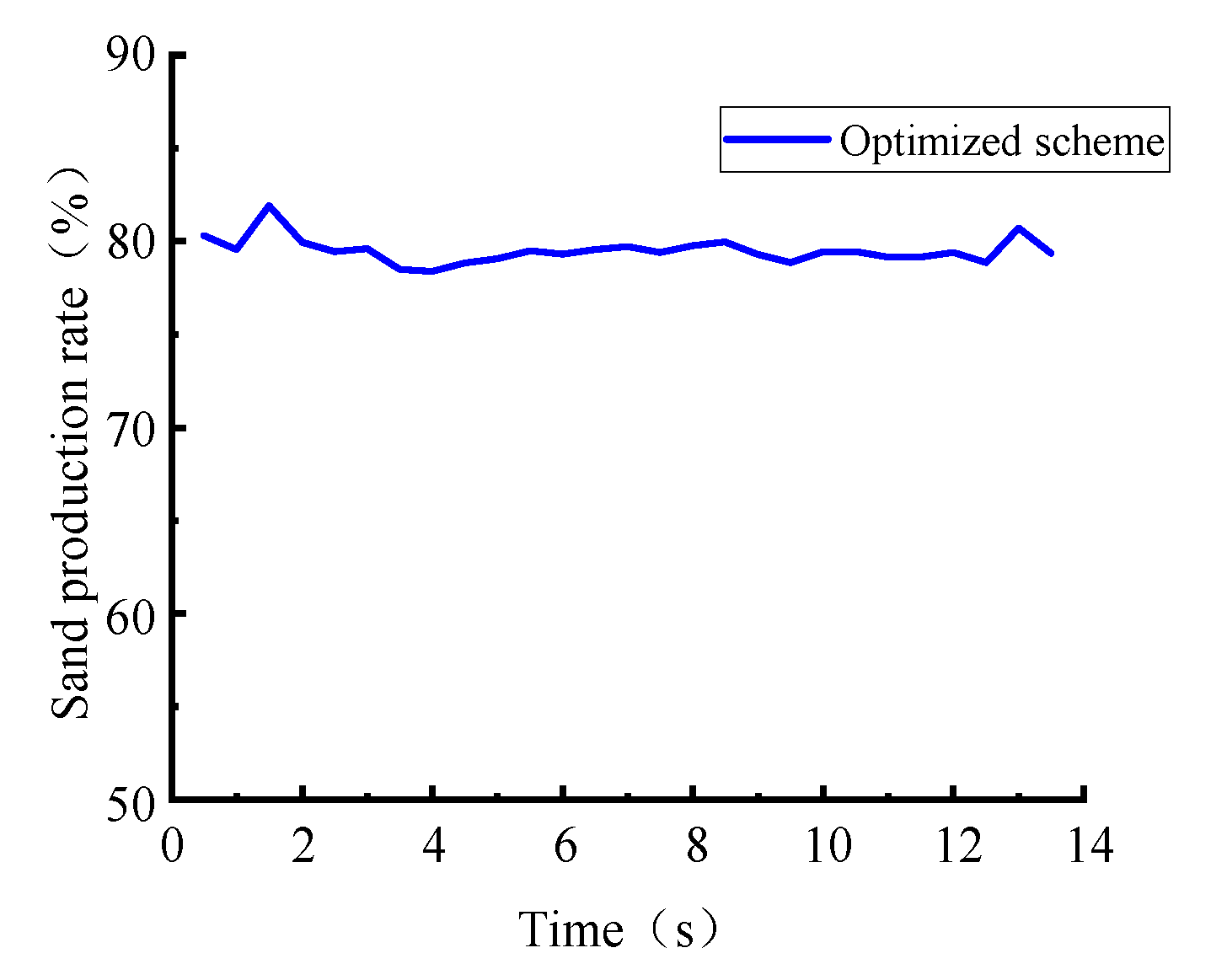
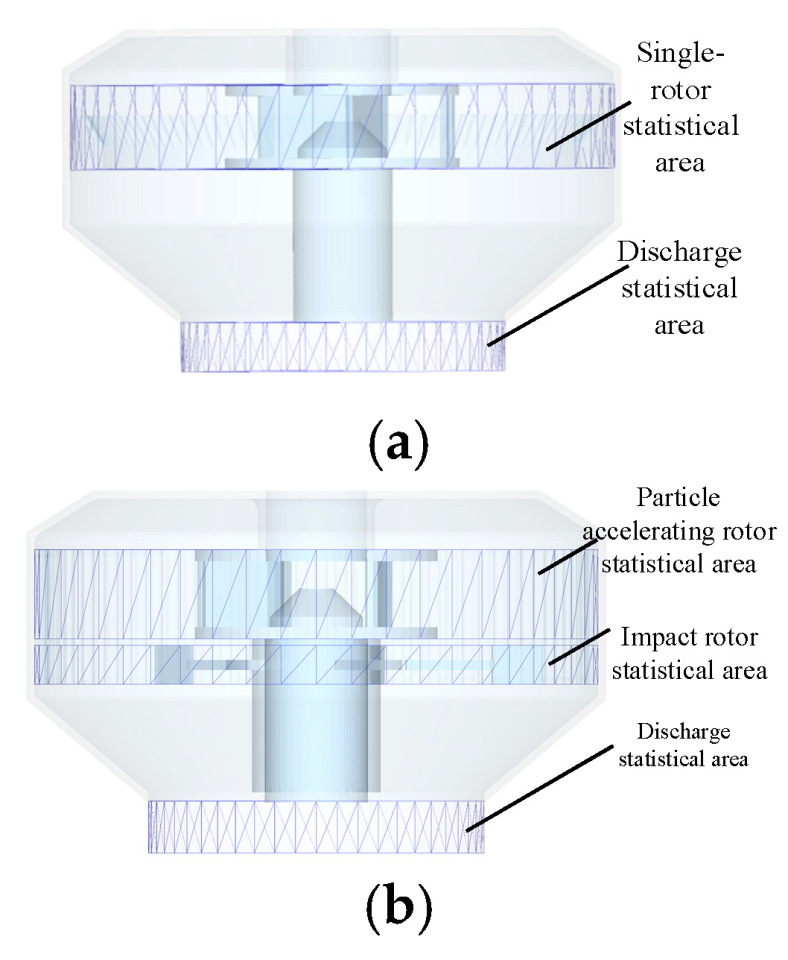
| Level Factor | G/(pcs) | α/(°) | β/(°) | T/(pcs) |
|---|---|---|---|---|
| 1 | 3 | 0 | 0 | 70 |
| 2 | 4 | 15 | 3 | 80 |
| 3 | 5 | 30 | 6 | 90 |
| 4 | 6 | 45 | 10 | 100 |
| Scheme | G/(pes) | α/(°) | β/(°) | C/(mm) | Blank Column | Sand Production Rate (%) |
|---|---|---|---|---|---|---|
| 1 | 3 | 0 | 0 | 70 | 1 | 78.88 |
| 2 | 3 | 15 | 3 | 80 | 2 | 78.43 |
| 3 | 3 | 30 | 6 | 90 | 3 | 76.06 |
| 4 | 3 | 45 | 10 | 100 | 4 | 75.85 |
| 5 | 4 | 0 | 3 | 90 | 4 | 79.86 |
| 6 | 4 | 15 | 0 | 100 | 3 | 79.06 |
| 7 | 4 | 30 | 10 | 70 | 2 | 75.84 |
| 8 | 4 | 45 | 6 | 80 | 1 | 76.11 |
| 9 | 5 | 0 | 6 | 100 | 2 | 79.72 |
| 10 | 5 | 15 | 10 | 90 | 1 | 79.72 |
| 11 | 5 | 30 | 0 | 80 | 4 | 77.96 |
| 12 | 5 | 45 | 3 | 70 | 3 | 77.06 |
| 13 | 6 | 0 | 10 | 80 | 3 | 80.03 |
| 14 | 6 | 15 | 6 | 70 | 4 | 78.20 |
| 15 | 6 | 30 | 3 | 100 | 1 | 77.98 |
| 16 | 6 | 45 | 0 | 90 | 2 | 77.58 |
| I | 77.31 | 79.62 | 78.37 | 77.50 | 78.17 | |
| II | 77.72 | 78.85 | 78.33 | 78.13 | 77.89 | |
| III | 78.62 | 76.96 | 77.52 | 78.31 | 78.05 | |
| IV | 78.45 | 76.65 | 77.86 | 78.15 | 77.97 | |
| Range | 1.31 | 2.20 | 0.85 | 0.81 | 0.28 |
| G/(pcs) | α/(°) | β/(°) | C/(mm) | |
|---|---|---|---|---|
| Scheme 4 Parameters | 3 | 45 | 10 | 100 |
| Scheme 13 Parameters | 6 | 0 | 10 | 80 |
| Optimized Parameters | 6 | 0 | 0 | 89 |
| Test No. | Column No. | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 4 | 7 | 8 |
| 2 | 2 | 4 | 8 | 5 | 7 |
| 3 | 3 | 6 | 3 | 3 | 6 |
| 4 | 4 | 8 | 7 | 1 | 5 |
| 5 | 5 | 1 | 2 | 8 | 4 |
| 6 | 6 | 3 | 6 | 6 | 3 |
| 7 | 7 | 5 | 1 | 4 | 2 |
| 8 | 8 | 7 | 5 | 2 | 1 |
| Number of Factors | Column No. | Deviation | |||
|---|---|---|---|---|---|
| 2 | 1 | 3 | 0.1445 | ||
| 3 | 1 | 3 | 4 | 0.2000 | |
| 4 | 1 | 2 | 3 | 5 | 0.2709 |
| Column No. | Rotational Speed (r/min) | |
|---|---|---|
| Accelerating Rotor | Impact Rotor | |
| 1 | 500 | 800 |
| 2 | 600 | 1200 |
| 3 | 700 | 700 |
| 4 | 800 | 1100 |
| 5 | 900 | 600 |
| 6 | 1000 | 1000 |
| 7 | 1100 | 500 |
| 8 | 1200 | 900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Wu, X.; Song, H.; Tian, Z.; Xie, F.; Chen, Z. Design and Crushing Characteristics of Double-Rotor Vertical-Shaft-Impact Sand-Making Machine. Processes 2025, 13, 2974. https://doi.org/10.3390/pr13092974
Wang Q, Wu X, Song H, Tian Z, Xie F, Chen Z. Design and Crushing Characteristics of Double-Rotor Vertical-Shaft-Impact Sand-Making Machine. Processes. 2025; 13(9):2974. https://doi.org/10.3390/pr13092974
Chicago/Turabian StyleWang, Qian, Xiangfan Wu, Hairong Song, Zuzhi Tian, Fangwei Xie, and Zibo Chen. 2025. "Design and Crushing Characteristics of Double-Rotor Vertical-Shaft-Impact Sand-Making Machine" Processes 13, no. 9: 2974. https://doi.org/10.3390/pr13092974
APA StyleWang, Q., Wu, X., Song, H., Tian, Z., Xie, F., & Chen, Z. (2025). Design and Crushing Characteristics of Double-Rotor Vertical-Shaft-Impact Sand-Making Machine. Processes, 13(9), 2974. https://doi.org/10.3390/pr13092974






