Optimal Placement and Sizing of Reactive Power Compensation Devices in Power Grids with High Penetration of Distributed Generation
Abstract
1. Introduction
2. Short-Circuit Ratio Index
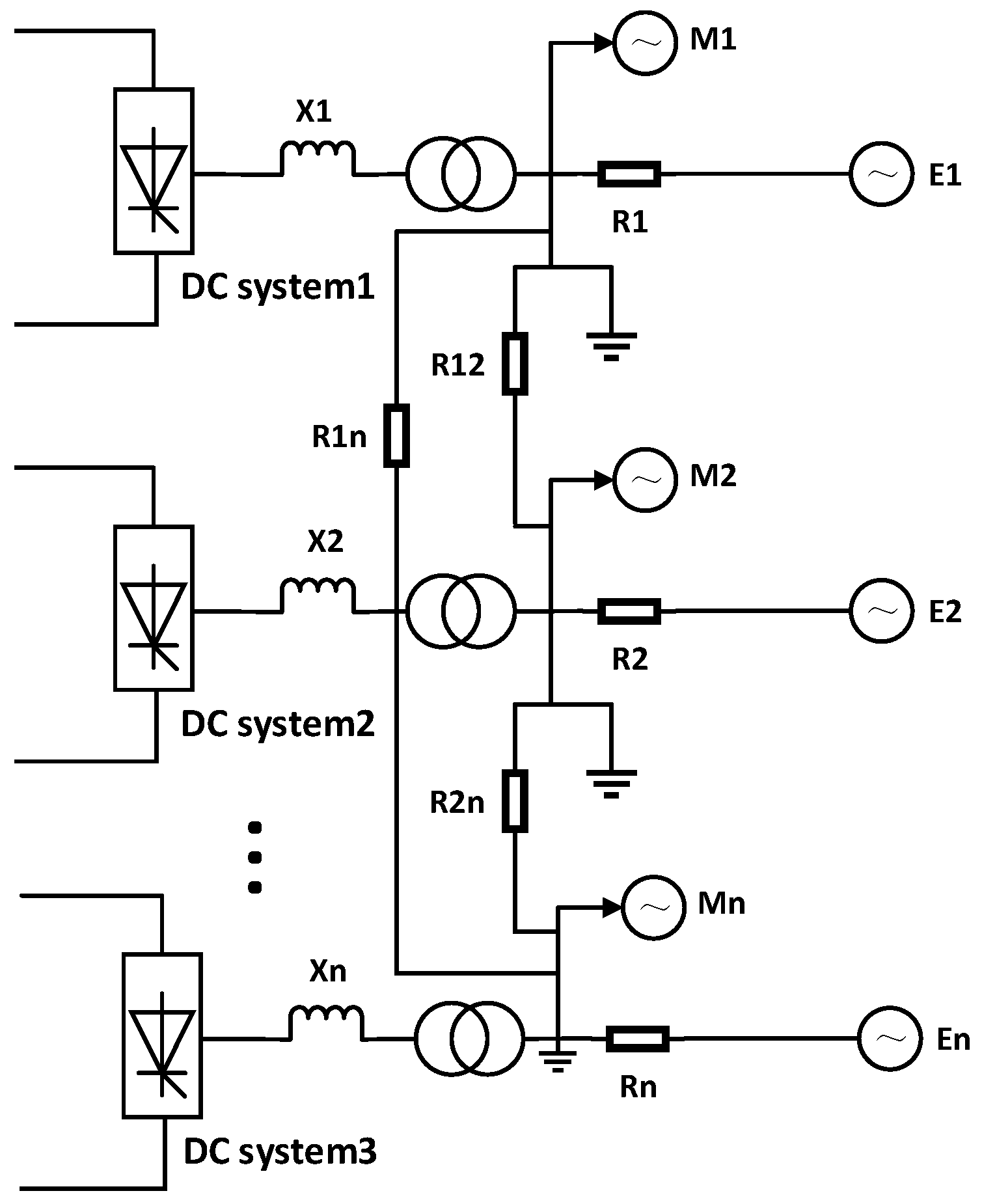
2.1. Multi-Infeed HVDC Systems
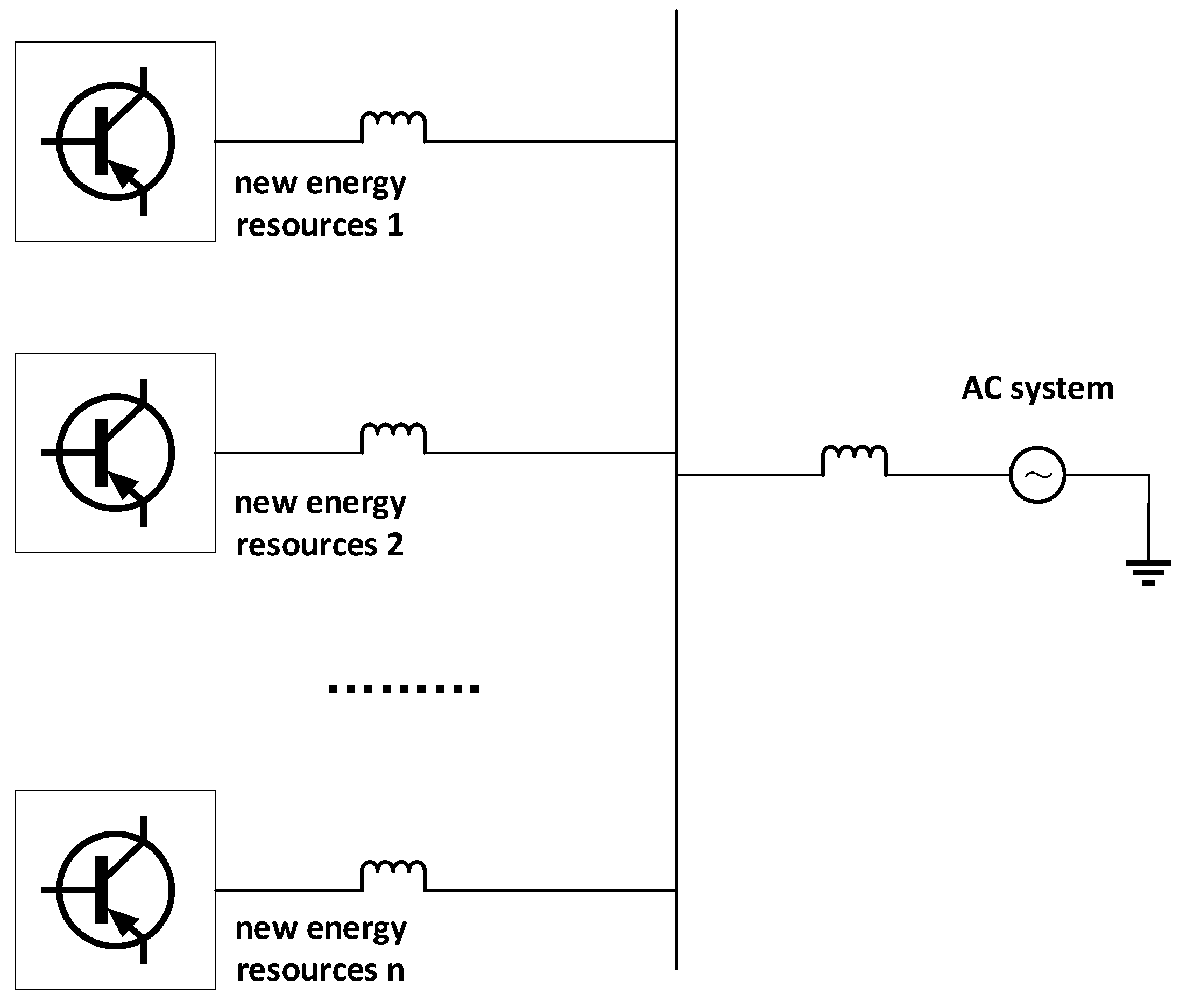
2.2. Multiple Renewable Plants Systems
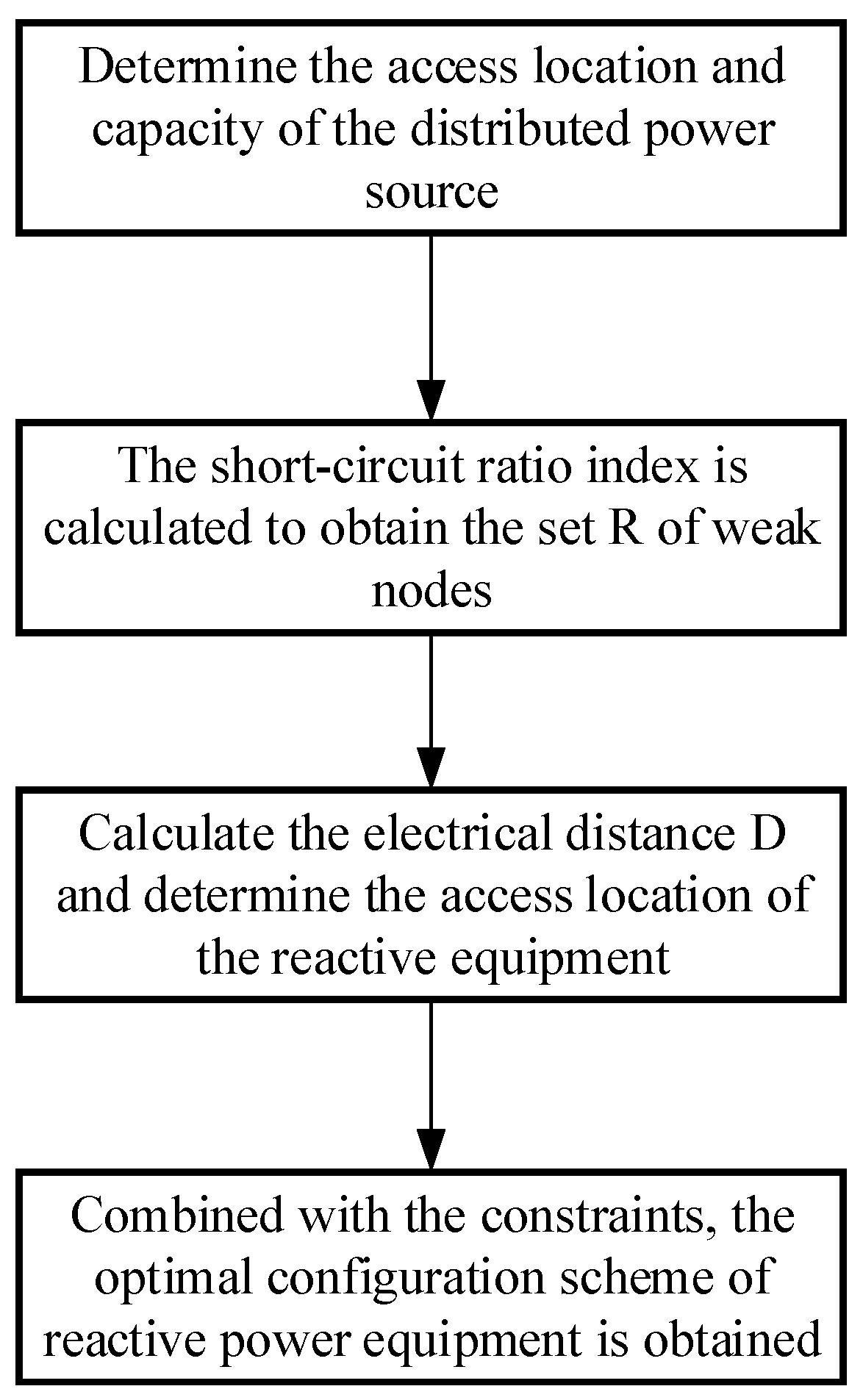
3. Selection of Installation Nodes for Reactive Compensation Devices
4. Optimization Method for Reactive Compensation Device Configuration
4.1. Chance-Constrained Programming
4.2. Constraints
4.3. Reactive Power Allocation Capacity
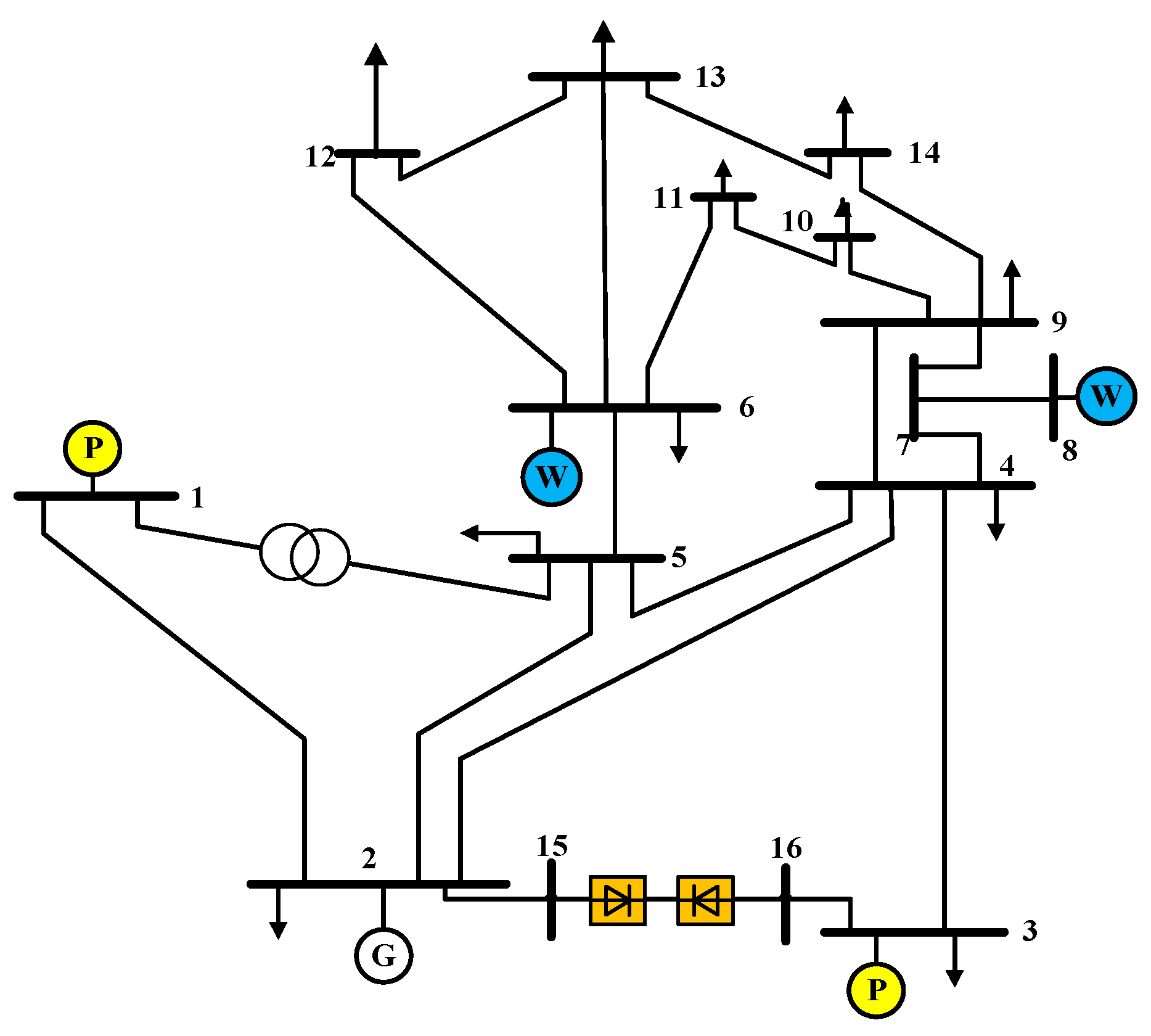
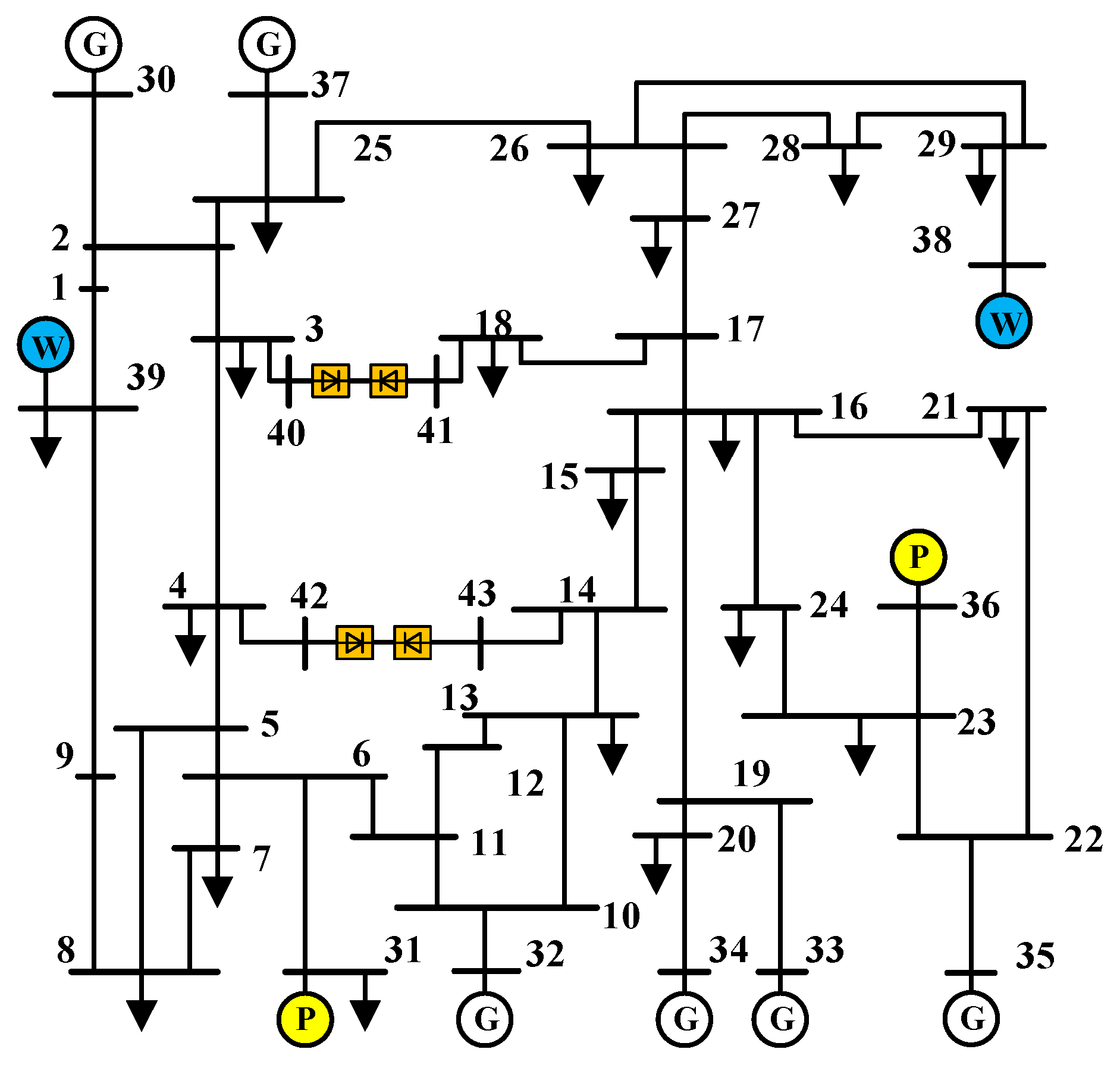
5. Case Study Analysis
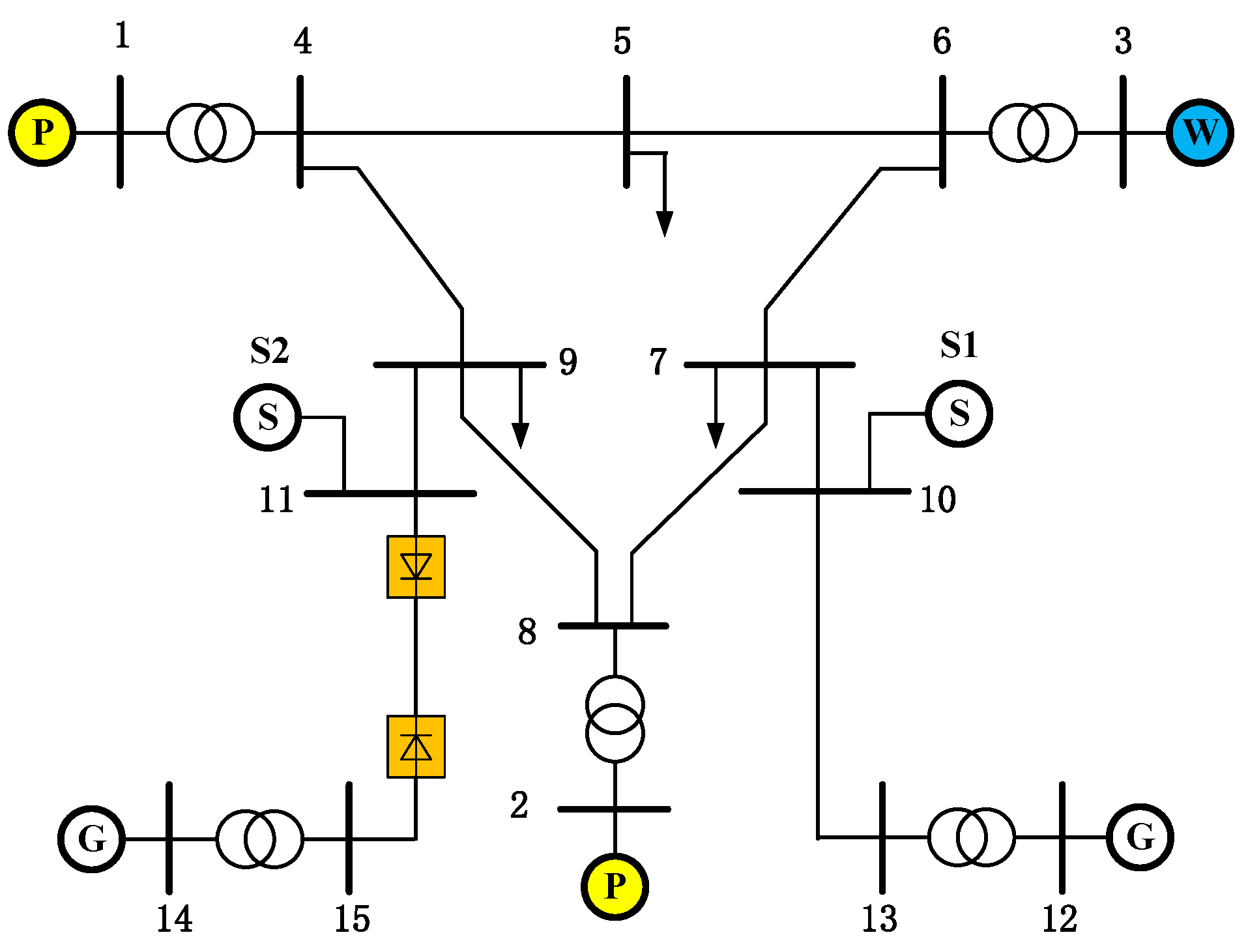
5.1. System Analysis
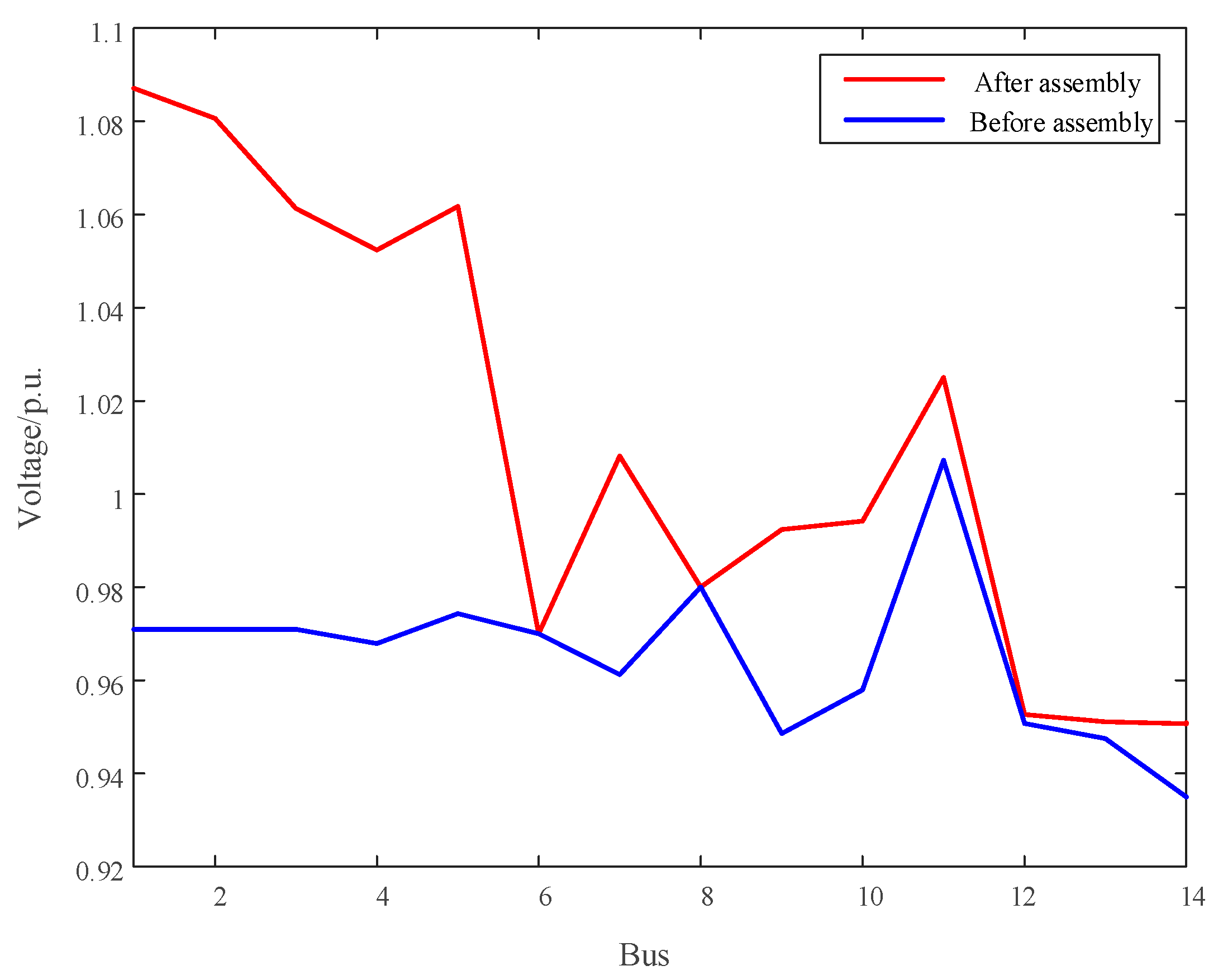
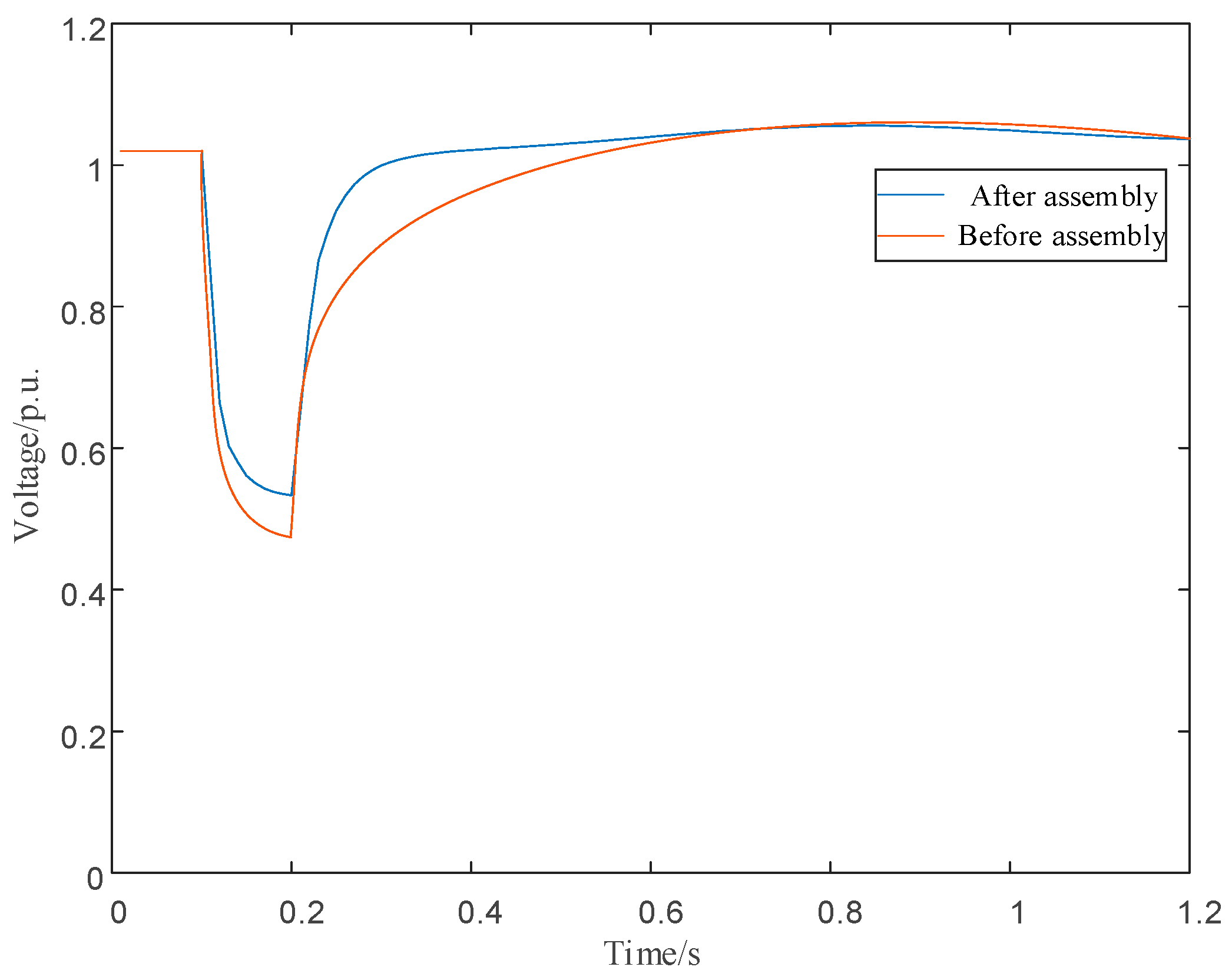
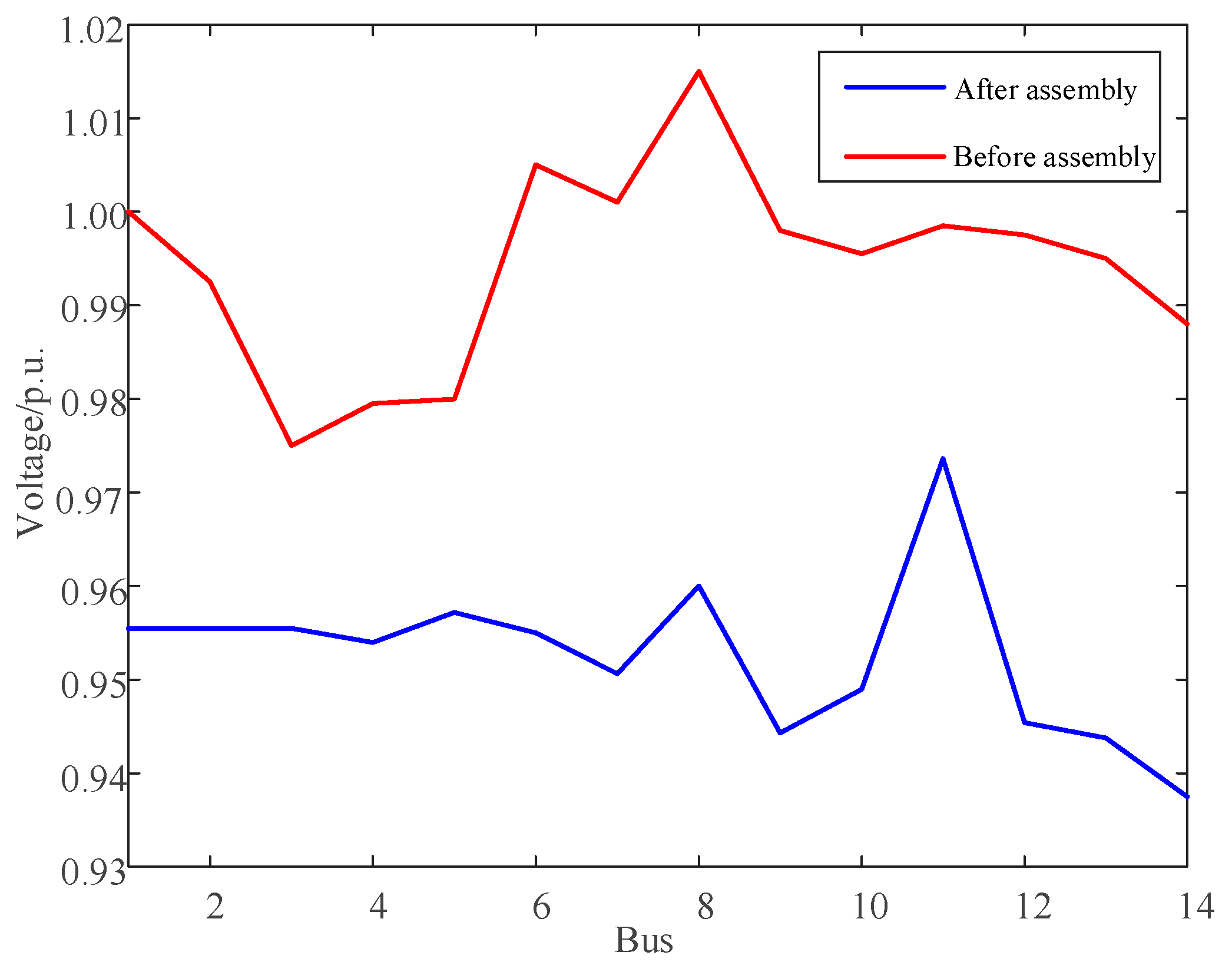
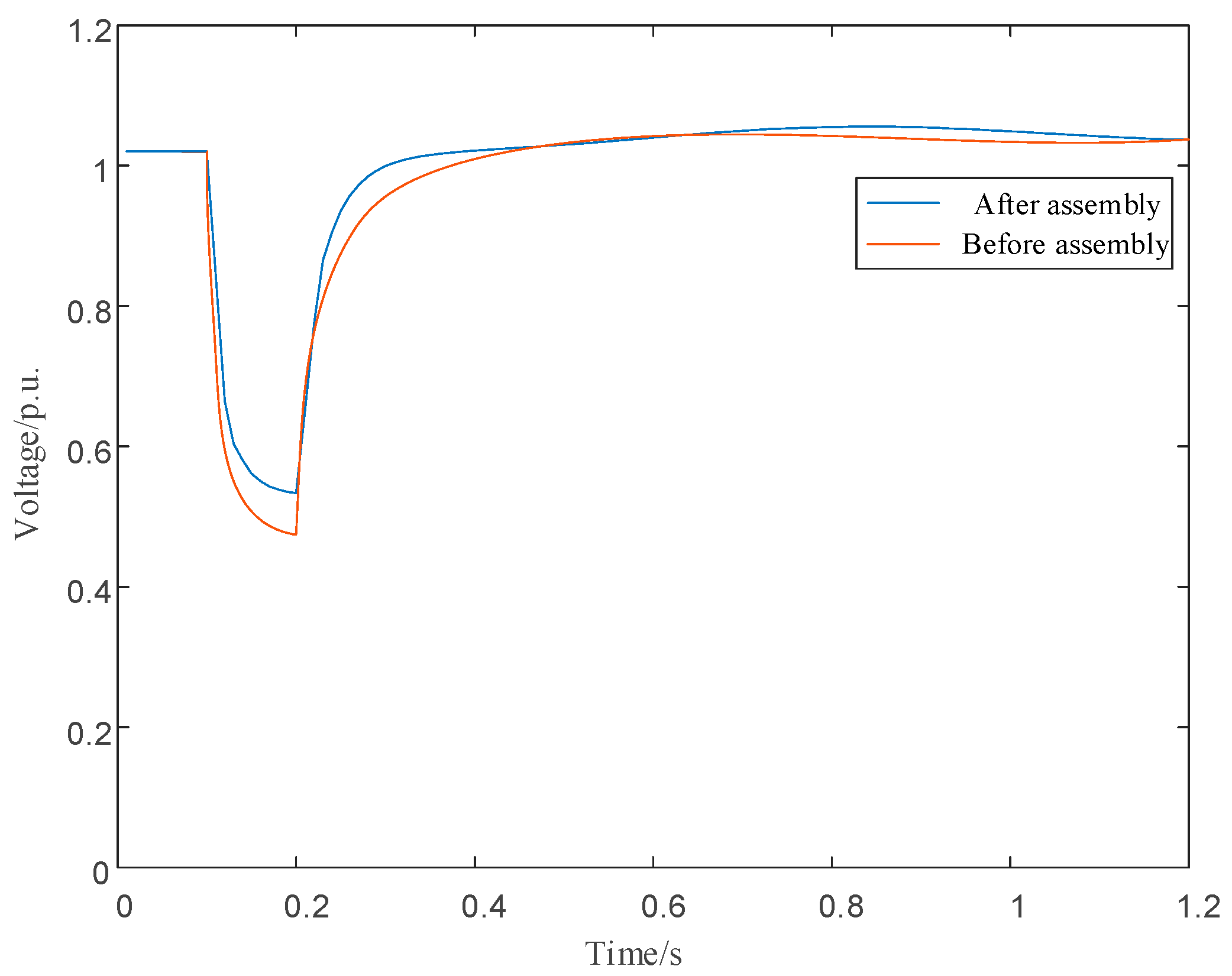
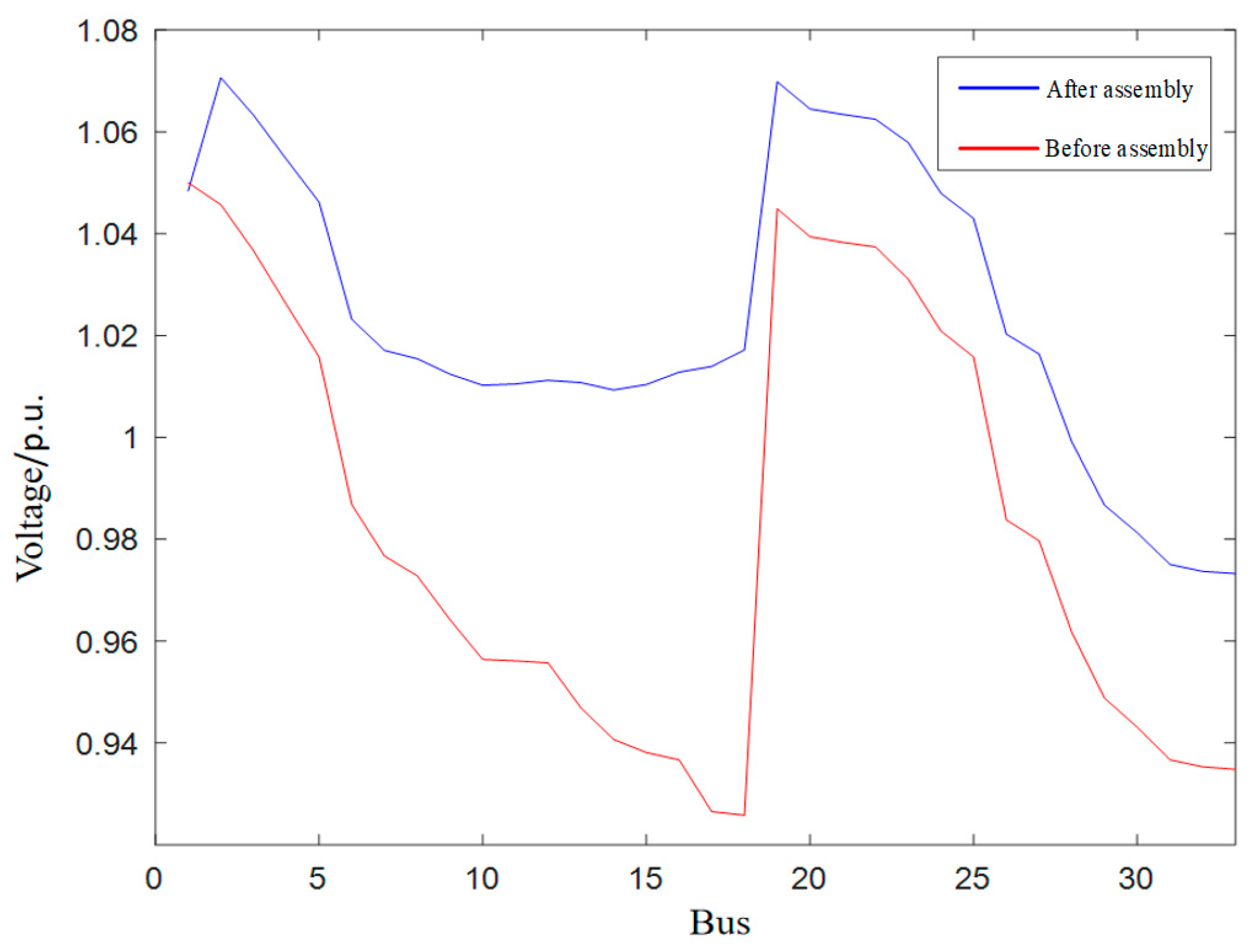
5.2. Validation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shyamal, P.; Krishna, M.; Sukumar, K. Distributed control of distributed energy resources in active power distribution system for local power balance with optimal spectralclustering. IEEE Trans. Power Syst. 2022, 58, 5395–5408. [Google Scholar] [CrossRef]
- Zhang, C.; Dou, X.; Wang, L.; Dong, Y.; Ji, Y. Distributed cooperative voltage control for grid-following and grid-forming DGs in islanded microgrids. IEEE Trans. Power Syst. 2022, 38, 589–602. [Google Scholar] [CrossRef]
- Wang, Y.C.; Zhang, S.; Lin, Z.Z.; Jiang, C.W.; Tang, L.; Wen, F.S. Market mechanisms and implementation methodsfor distributed sources and loads participating in ancillary services. Autom. Electr. Power Syst. 2023, 47, 3–16. [Google Scholar] [CrossRef]
- Hao, W.; Meng, Z.; Zhang, Y.; Xie, B.; Peng, P.; Wei, J. Carrying capacity evaluation of multipledistributed power supply access to the distribution network with the background of a new power system. Power Syst. Prot. Control 2023, 51, 23–33. [Google Scholar] [CrossRef]
- Zhang, S.; Gu, W.; Zhang, X.; Chung, C.Y.; Yu, R.; Lu, S.; Palma-Behnke, R. Analysis for integrated energy system: Benchmarking methods and implementation. Energy Internet 2024, 1, 63–80. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, N.; Zhao, Y.; Ding, X.; Zhang, R.; Zhang, X. Review of methodology and best practice of power system restoration plan. Energy Internet 2024, 1, 123–140. [Google Scholar] [CrossRef]
- Safari, Z.; Javareshk, S.M.A.N.; Pourbagheri, M.; Niaemanesh, M.; Pakseresht, M. Congestion Management in Distribution Network: An Exploration of Distributed Generation and Demand Response Programs by Using the MOPSO Algorithm. In Proceedings of the 2023 27th International Electrical Power Distribution Networks Conference (EPDC), Mashhad, Iran, 12–15 June 2023; pp. 173–177. [Google Scholar] [CrossRef]
- Bayati, N.; Savaghebi, M. A Transient Component-Based Technique for Fault Detection in Distributed Generation Systems. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Yuan, L.; Sun, Y.; Liu, Z.; Shao, C.; Liu, B. Influence and Optimization of Low-voltage Distributed Photovoltaic Reactive Power in Active Distribution Network Based on the Power Flow Reverse Point. Shandong Electr. Power 2023, 50, 11–19+41. [Google Scholar] [CrossRef]
- Li, S.; Qiao, Y.; Xu, M.; Wu, L.; Lu, Z.; Xian, W. Hierarchical multi-objective safety margin optimization of renewable energy island collecting delivery system by VSC-HVDC. Power Syst. Technol. 2020, 44, 4513–4520. [Google Scholar] [CrossRef]
- Xue, L.; Niu, T.; Fang, S.; Chen, J. Master-Slave Cooperative Dynamic Reactive Power Optimization Method Considering Transient Voltage Security of High Proportion of Wind Power. Autom. Electr. Power Syst. 2023, 47, 57–66. [Google Scholar] [CrossRef]
- Hong, L.; Wu, M.; Wang, Y.; Shahidehpour, M.; Chen, Z.; Yan, Z. MADRL-Based DSO-Customer Coordinated Bi-Level Volt/VAR Optimization Method for Power Distribution Networks. IEEE Trans. Sustain. Energy 2024, 15, 1834–1846. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Li, Y.; Hu, J.; Ma, S.; Wang, T. Wang, Study on AC Transient Overvoltage Suppression of LCC-HVDC Sending End System Based on DC Current Control Optimization. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 2419–2424. [Google Scholar] [CrossRef]
- Yin, C.; Li, F. Analytical expression on transient overvoltage peak value of converter buscaused by DC faults. IEEE Trans. Power Syst. 2021, 36, 2741–2744. [Google Scholar] [CrossRef]
- Ibrahim, T.M.S.; De Rubira, T.T.; Del Rosso, A.; Patel, M.; Guggilam, S.; Mohamed, A.A. Alternating Optimization Approach for Voltage-Secure Multi-Period Optimal Reactive Power Dispatch. IEEE Trans. Power Syst. 2022, 37, 3805–3816. [Google Scholar] [CrossRef]
- Zhu, K.; Li, L.; Xu, Y.; Zhang, T.; Zhou, L. Multi-Connection Based Scalable Video Streaming in UDNs: A Multi-Agent Multi-Armed Bandit Approach. IEEE Trans. Wirel. Commun. 2022, 21, 1156–1169. [Google Scholar] [CrossRef]
- Wu, D. Research on New Energy Development Planning Technology. In Proceedings of the 2024 3rd Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 25–27 October 2024; pp. 638–642. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, C.; Li, F.; Han, L.; Liu, J.; Shi, Y. A simultaneous commutation failure assessment method considering reactive powerand voltage characteristics in multi-infeed HVDC systems. Power Syst. Prot. Control 2024, 52, 170–187. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Yu, X.; Zhou, Y.; Zhang, W. Research on optimization method of new energy grid-connected output of the receiving power grid based on short-circuit ratio constraint. Renew. Energy Resour. 2023, 41, 1658–1664. [Google Scholar] [CrossRef]
- Huang, Q.; Cao, S.; Wu, Y.; Lin, X.; Wei, F.; Yang, D.; Cui, T. A New Multi-Infeed Short Circuit Ratio Index Taking into Account the Amplitude and Phase Characteristics of New Energy. Proc. CSEE 2024, 44, 5960–5973. [Google Scholar] [CrossRef]
- Dong, X.; Li, G.; Qiao, R.; Liu, S.; Kan, C. Urban Distribution Network Dynamic Reactive Power Optimization Considering Electrical Vehicle Station. Shandong Electr. Power 2024, 51, 1–9. [Google Scholar] [CrossRef]
- IEEE Std 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018; pp. 1–138. [CrossRef]
- Rayati, M.; Bozorg, M.; Cherkaou, R.; Carpita, M. Distributionally Robust Chance Constrained Optimization for Providing Flexibility in an Active Distribution Network. IEEE Trans. Smart Grid 2022, 13, 2920–2934. [Google Scholar] [CrossRef]

| Bus | SCR | Bus | SCR |
|---|---|---|---|
| Bus 1 | 2.156 | Bus 9 | 1.785 |
| Bus 2 | 2.037 | Bus 10 | 2.012 |
| Bus 3 | 1.456 | Bus 11 | 1.874 |
| Bus 4 | 2.135 | Bus 12 | 1.984 |
| Bus 5 | 2.564 | Bus 13 | 2.121 |
| Bus 6 | 1.795 | Bus 14 | 2.254 |
| Bus 7 | 2.125 | Bus 15 | 2.214 |
| Bus 8 | 1.845 |
| Bus | SCR | Bus | SCR |
|---|---|---|---|
| Bus 1 | 2.178 | Bus 9 | 2.231 |
| Bus 2 | 2.037 | Bus 10 | 2.090 |
| Bus 3 | 2.009 | Bus 11 | 2.186 |
| Bus 4 | 2.184 | Bus 12 | 2.232 |
| Bus 5 | 2.245 | Bus 13 | 2.091 |
| Bus 6 | 1.245 | Bus 14 | 2.270 |
| Bus 7 | 2.066 | Bus 15 | 2.121 |
| Bus 8 | 1.365 | Bus 16 | 2.200 |
| Bus | SCR | Bus | SCR | Bus | SCR |
|---|---|---|---|---|---|
| Bus 1 | 2.178 | Bus 16 | 2.207 | Bus 31 | 2.027 |
| Bus 2 | 2.037 | Bus 17 | 2.195 | Bus 32 | 2.024 |
| Bus 3 | 2.009 | Bus 18 | 2.293 | Bus 33 | 2.193 |
| Bus 4 | 2.184 | Bus 19 | 2.169 | Bus 34 | 2.192 |
| Bus 5 | 2.245 | Bus 20 | 2.189 | Bus 35 | 2.290 |
| Bus 6 | 2.006 | Bus 21 | 2.074 | Bus 36 | 2.140 |
| Bus 7 | 2.066 | Bus 22 | 2.043 | Bus 37 | 2.111 |
| Bus 8 | 2.063 | Bus 23 | 2.231 | Bus 38 | 1.432 |
| Bus 9 | 2.219 | Bus 24 | 2.090 | Bus 39 | 1.356 |
| Bus 10 | 2.056 | Bus 25 | 2.186 | Bus 40 | 2.048 |
| Bus 11 | 2.126 | Bus 26 | 2.232 | Bus 41 | 1.982 |
| Bus 12 | 2.132 | Bus 27 | 2.091 | Bus 42 | 2.079 |
| Bus 13 | 2.298 | Bus 28 | 2.270 | Bus 43 | 2.145 |
| Bus 14 | 2.236 | Bus 29 | 2.121 | ||
| Bus 15 | 2.122 | Bus 30 | 2.200 |
| Bus | Initial Value |
|---|---|
| Bus 1 | 0.1548 |
| Bus 2 | 0.1546 |
| Bus 3 | 0.412 |
| Bus | Initial Value |
|---|---|
| Bus 1 | 0.1542 |
| Bus 2 | 0.1246 |
| Bus 3 | 0.1620 |
| Bus | Initial Value |
|---|---|
| Bus 1 | 0.1330 |
| Bus 2 | 0.1387 |
| Bus 3 | 0.2820 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, N.; Niu, T.; Yan, J.; Zhang, Y.; Feng, Y.; Lei, Y. Optimal Placement and Sizing of Reactive Power Compensation Devices in Power Grids with High Penetration of Distributed Generation. Processes 2025, 13, 2953. https://doi.org/10.3390/pr13092953
Feng N, Niu T, Yan J, Zhang Y, Feng Y, Lei Y. Optimal Placement and Sizing of Reactive Power Compensation Devices in Power Grids with High Penetration of Distributed Generation. Processes. 2025; 13(9):2953. https://doi.org/10.3390/pr13092953
Chicago/Turabian StyleFeng, Nan, Tao Niu, Jun Yan, Yufan Zhang, Yuyao Feng, and Yuli Lei. 2025. "Optimal Placement and Sizing of Reactive Power Compensation Devices in Power Grids with High Penetration of Distributed Generation" Processes 13, no. 9: 2953. https://doi.org/10.3390/pr13092953
APA StyleFeng, N., Niu, T., Yan, J., Zhang, Y., Feng, Y., & Lei, Y. (2025). Optimal Placement and Sizing of Reactive Power Compensation Devices in Power Grids with High Penetration of Distributed Generation. Processes, 13(9), 2953. https://doi.org/10.3390/pr13092953





