Superstructure Optimization Based on Hierarchical Accelerated Branch and Bound Algorithm and Its Application in Feedstock Scheduling
Abstract
1. Introduction
2. Materials and Methods
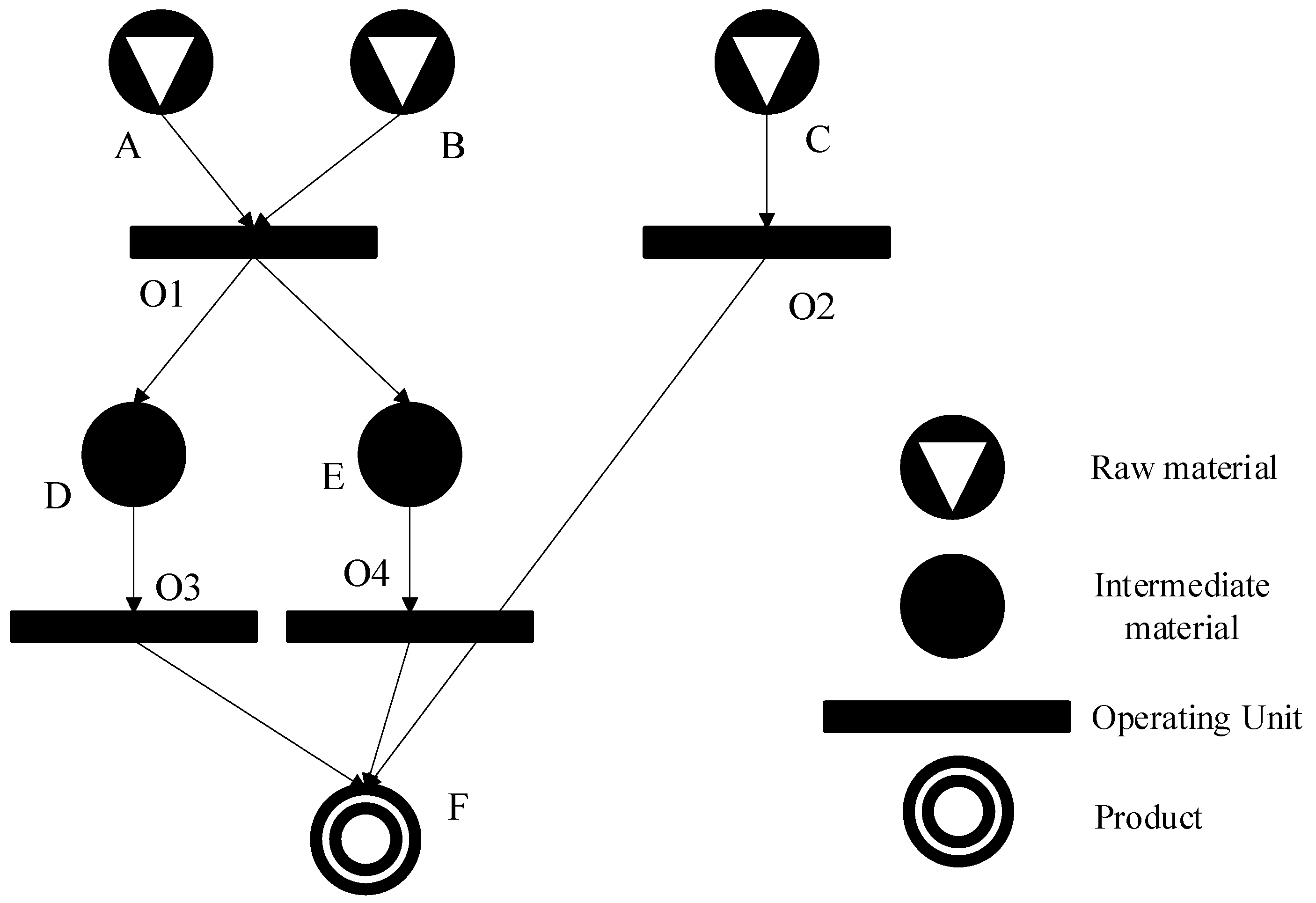
2.1. P-Graph Theory
- (1)
- The topological network of the structure must include every element in the product set P;
- (2)
- If a material is in the output set of the operating unit, then this material cannot be in the raw material set;
- (3)
- All operating units in the topology structure of the process network need to be explained;
- (4)
- Any element in the operating unit and product set must have at least one path connected;
- (5)
- Material must be interconnected with at least one operating unit.
2.2. Accelerated Branch and Bound
- (1)
- Set the root node as the initial structural space and initialize the current optimal solution to infinity.
- (2)
- Calculate the objective function value for each possible structure and determine the objective function value for each structure based on the objective function.
- (3)
- Compare the objective function values of each structure and update the current optimal solution to the structure with the minimum objective function value.
- (4)
- Perform branching operations on the structural space based on the current optimal solution. Calculate the objective function value for the branched structure and define it accordingly.
- (5)
- If the objective function value of a branch has exceeded the current optimal solution, the branch can be pruned. If a better structure is found, update the current optimal solution.
- (6)
- Repeat the steps of (2–5) until the termination condition is reached.
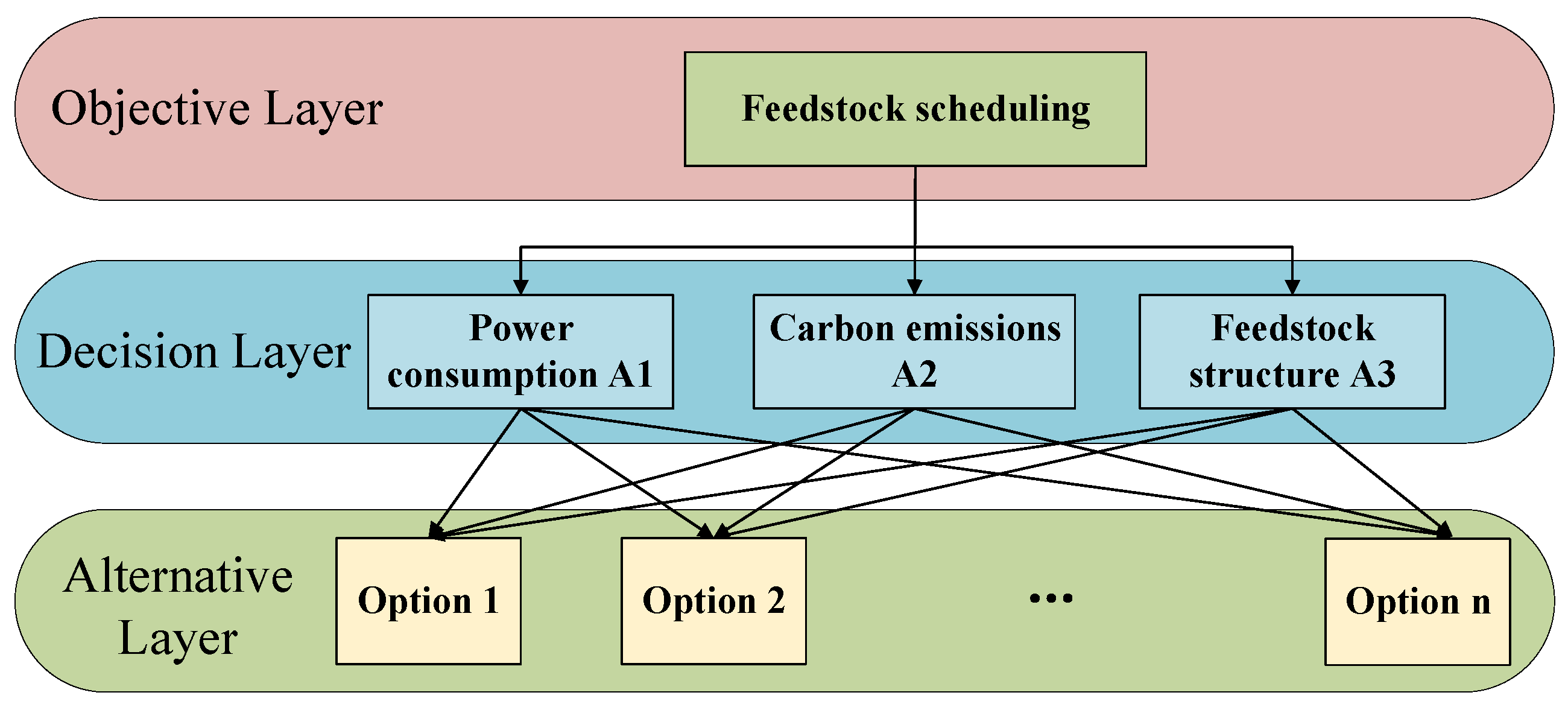
2.3. Analytic Hierarchy Process
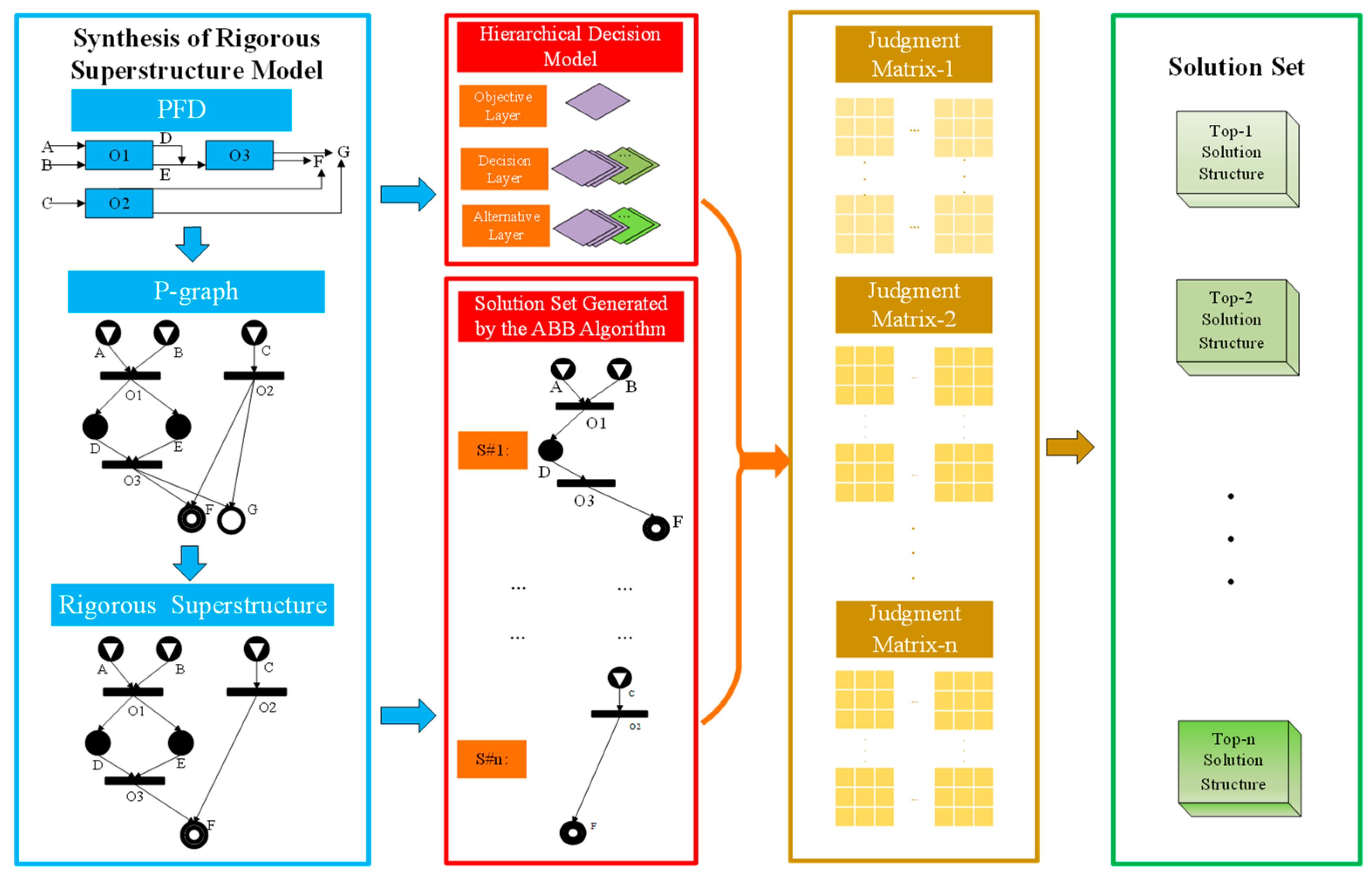
3. Methodology and Case Study
3.1. Methodology
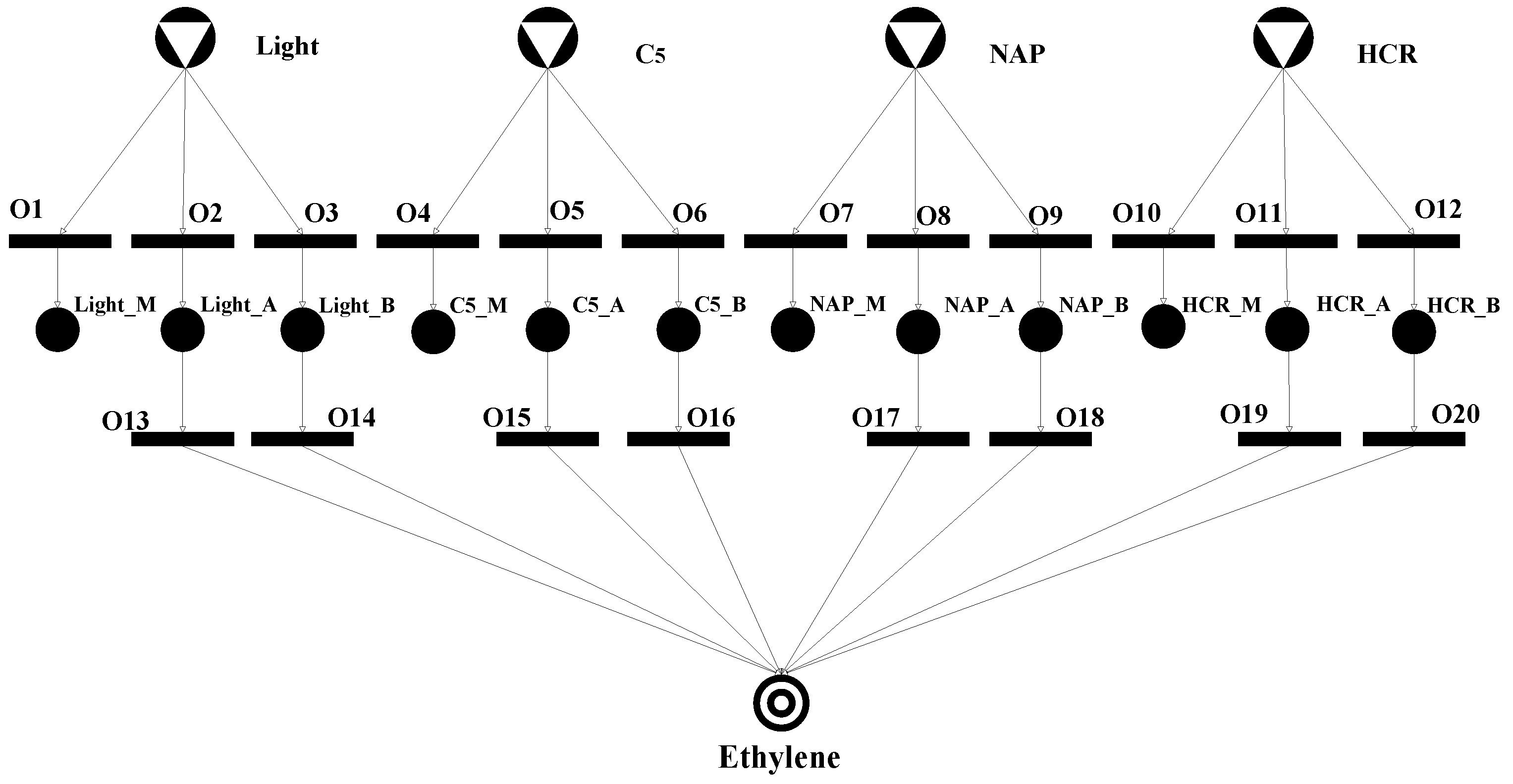
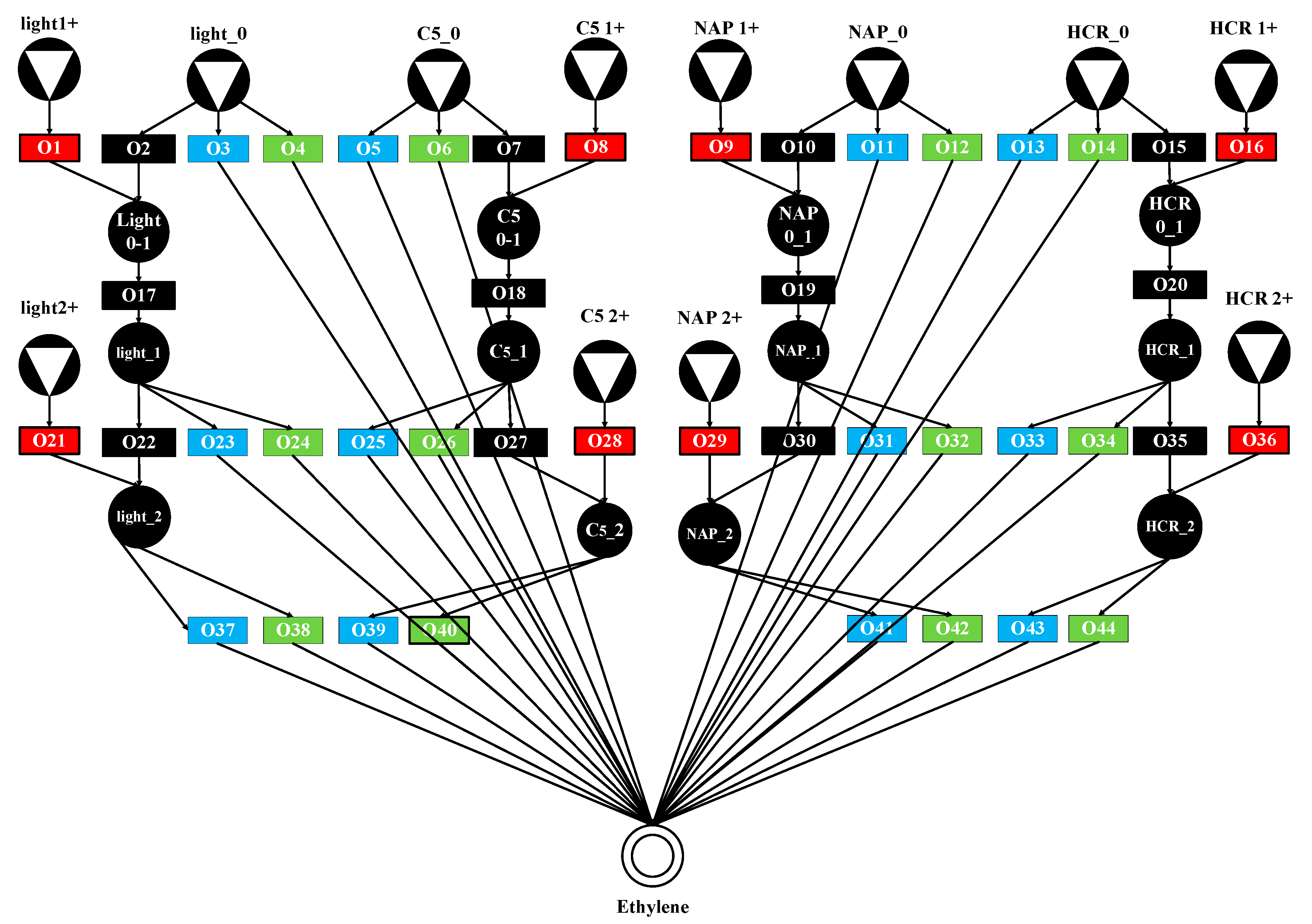
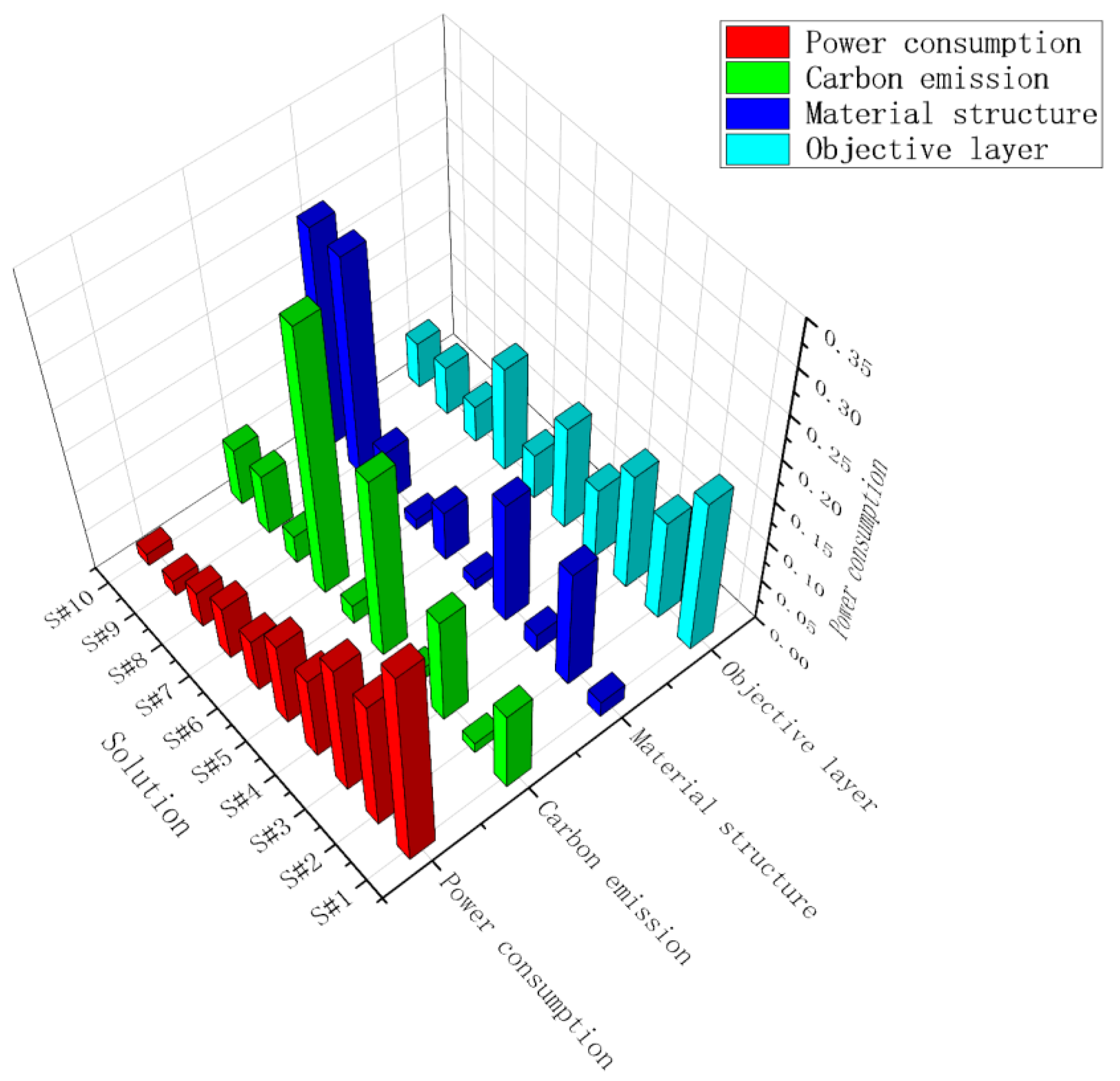
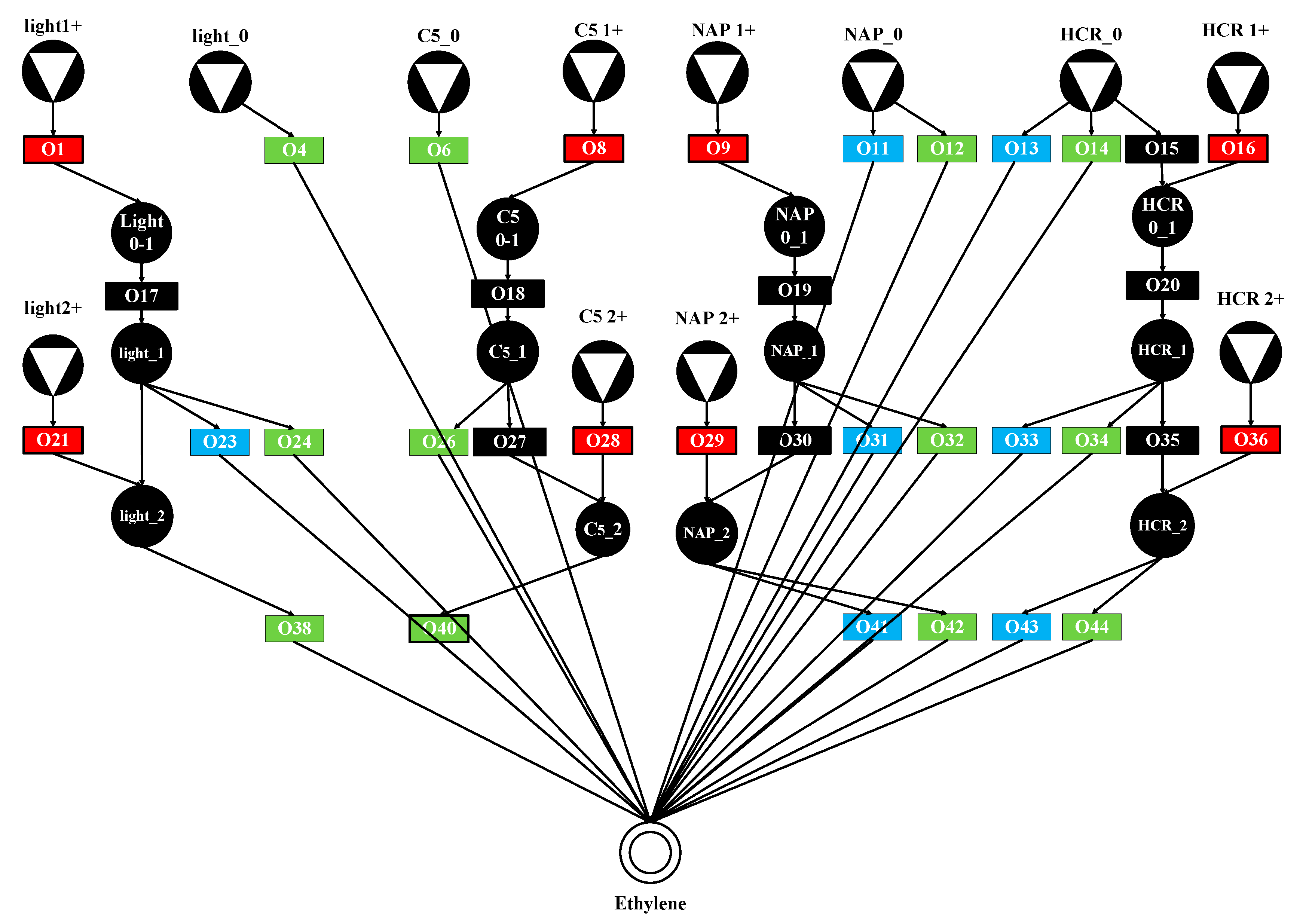
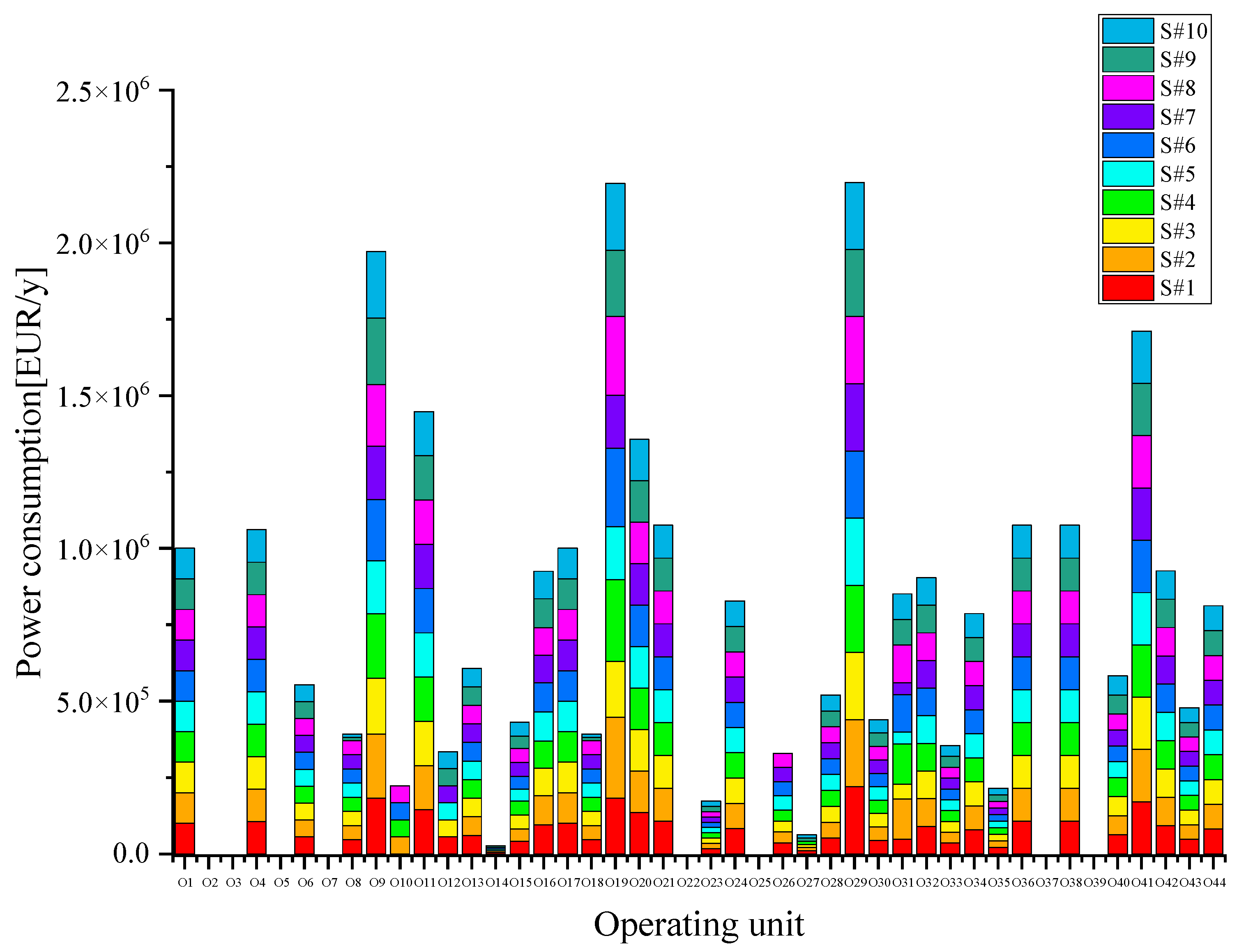
3.2. Case Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PNS | process network synthesis |
| P-graph | Progress graph |
| MINLP | The Mixed Integer Nonlinear Programming |
| ABB | Accelerated Branch and Bound |
| BB | Branch and Bound |
| AHP | The Analytic Hierarchy Process |
| PFD | process flow diagram |
| MSG | Maximum Structure Generation |
| SSG | Solution Structure Generation |
| ETS | Emissions Trading Scheme |
| MEA | monoethanolamine |
| CAP | chilled ammonia process |
| MEM | membrane assisted liquefaction |
| HCR | hydrogenated tail oil |
| light | light diesel oil |
| C5 | C3C4C5 |
| NAP | naphtha |
References
- Mallapragada, D.S.; Dvorkin, Y.; Modestino, M.A.; Biddinger, E.; Esposito, D.V.; Smith, W.A.; Hodge, B.M.; Harold, M.P.; Donnelly, V.M.; Nuz, A.; et al. Decarbonization of the chemical industry through electrification: Barriers and opportunities. Joule 2023, 7, 23–41. [Google Scholar] [CrossRef]
- Prawitasari, D.A. Potensi Limbah Hasil Pertanian Padi menjadi Sumber Bioenergi melalui Konsep Biorefineri dengan Pendekatan P-Graph dan Analisis Ekonomi Teknik di Kabupaten Sleman, Yogyakarta. Asian J. Innov. Entrep. 2025, 9, 16–32. [Google Scholar] [CrossRef]
- Velázquez, J.J.H.; Durán, F.M.Z.; Díaz, L.A.C.; Ruiz, J.C.; Avila, J.R.A. Hybrid two-step optimization of internally heat-integrated distillation columns. J. Taiwan Inst. Chem. Eng. 2022, 130, 103967. [Google Scholar] [CrossRef]
- Xu, Y.; Li, J.; Cui, G.; Zhang, G.; Yang, Q. An improved treble-level assisting optimization strategy to enhance algorithm search ability in heat exchanger network design. J. Taiwan Inst. Chem. Eng. 2021, 129, 162–170. [Google Scholar] [CrossRef]
- Friedler, F.; Fan, L.T.; Imreh, B. Process network synthesis: Problem definition. Networks 1998, 31, 119–124. [Google Scholar] [CrossRef]
- Orosz, Á.; How, B.S.; Friedler, F. Multiple-solution heat exchanger network synthesis using P-HENS solver. J. Taiwan Inst. Chem. Eng. 2022, 130, 103859. [Google Scholar] [CrossRef]
- Ali, R.A.; Nik Ibrahim, N.N.L.; Wan Ab Karim Ghani, W.A.; Lam, H.L.; Sani, N.S. Utilization of process network synthesis and machine learning as decision-making tools for municipal solid waste management. Int. J. Environ. Sci. Technol. 2022, 19, 1985–1996. [Google Scholar] [CrossRef]
- Camisa, A.; Notarnicola, I.; Notarstefano, G. Distributed primal decomposition for large-scale MILPs. IEEE Trans. Autom. Control 2021, 67, 413–420. [Google Scholar] [CrossRef]
- Yuan, T.J.; Mao, Y.L. A review of pinch analysis techniques and extended application in power systems. Renew. Sustain. Energy Rev. 2024, 202, 114684. [Google Scholar] [CrossRef]
- Daoutidis, P.; Lee, J.H.; Rangarajan, S.; Chiang, L.; Gopaluni, B.; Schweidtmann, A.M.; Harjunkoski, I.; Mercangöz, M.; Mesbah, A.; Boukouvala, F.; et al. Machine learning in process systems engineering: Challenges and opportunities. Comput. Chem. Eng. 2024, 181, 108523. [Google Scholar] [CrossRef]
- Friedler, F.; Tarjan, K.; Huang, Y.W. Graph-theoretic approach to process synthesis: Polynomial algorithm for maximal structure generation. Comput. Chem. Eng. 1993, 17, 929–942. [Google Scholar] [CrossRef]
- Tan, R.R.; Aviso, K.B.; Klemes, J.J.; Lam, H.L.; Varbanov, P.S.; Friedler, F. Towards generalized process networks: Prospective new research frontiers for the P-graph framework. Chem. Eng. Trans. 2018, 70, 91–96. [Google Scholar] [CrossRef]
- Tick, A.; Molnár, G. Improving Efficiency: P-Graph Modeling for Business Workflows with Dynamic and Fuzzy Extensions. Acta Polytech. Hung. 2025, 22, 79–100. [Google Scholar] [CrossRef]
- Rohman, F.S.; Alwi, S.R.W.; Er, H.A.; Ahmad Termizi, S.N.A.; Abd Manan, Z.; Lim, J.S.; Muhammad, D. Cogeneration system’s energy performance improvement by using P-graph and advanced process control. Chem. Prod. Process Model. 2025, 20, 1–37. [Google Scholar] [CrossRef]
- Lim, S.Y.; Chemmangattuvalappil, N.G.; Tapia, J.F.D.; Khoiroh, I.; Chai, P.V.; Ng, L.Y. Optimal chemical reaction pathway for palm process residue recovery using Process Graph (P-graph) framework. Comput. Chem. Eng. 2025, 194, 109000. [Google Scholar] [CrossRef]
- Aviso, K.B.; Marfori III, I.A.V.; Tan, R.R.; Ubando, A.T. Optimizing abnormal operations of off-grid community utility systems with fuzzy P-graph. Energy 2020, 202, 117725. [Google Scholar] [CrossRef]
- Pimentel, J.; Rodríguez, G.; Gil, I. Synthesis of Alternative Cost-Effective Process Flowsheets for Lactic Acid Valorization by Means of the P-graph Methodology. Ind. Eng. Chem. Res. 2020, 59, 5921–5930. [Google Scholar] [CrossRef]
- Vance, L.; Cabezas, H.; Heckl, I.; Bertok, B.; Friedler, F. Synthesis of Sustainable Energy Supply Chain by the P-graph Framework. Ind. Eng. Chem. Res. 2013, 52, 266–274. [Google Scholar] [CrossRef]
- Phuang, Z.X.; Sang, K.; Wang, X.C.; You, F.; Woon, K.S. Sustaining regional infrastructure resiliency with externality for plastic waste circularity via geospatially-enhanced P-graph-life cycle optimization framework. J. Clean. Prod. 2025, 486, 144413. [Google Scholar] [CrossRef]
- Bertok, B.; Barany, M.; Friedler, F. Generating and Analyzing Mathematical Programming Models of Conceptual Process Design by P-graph Software. Ind. Eng. Chem. Res. 2013, 52, 166–171. [Google Scholar] [CrossRef]
- Strouvalis, A.M.; Heckl, I.; Friedler, F.; Kokossis, A.C. An accelerated Branch-and-Bound algorithm for assignment problems of utility systems. Comput. Chem. Eng. 2002, 26, 617–630. [Google Scholar] [CrossRef]
- Belkhiri, H.; Chergui, M.E.A.; Ouaïl, F.Z. Optimizing a linear function over an efficient set. Oper. Res. 2022, 22, 3183–3201. [Google Scholar] [CrossRef]
- Bakhtari, A.R.; Waris, M.M.; Sanin, C.; Szczerbicki, E. Evaluating industry 4.0 implementation challenges using interpretive structural modeling and fuzzy analytic hierarchy process. Cybern. Syst. 2021, 52, 350–378. [Google Scholar] [CrossRef]
- Ba, Z.; Wang, Y.; Fu, J.; Liang, J. Corrosion risk assessment model of gas pipeline based on improved AHP and its engineering application. Arabian J. Sci. Eng. 2022, 47, 10961–10979. [Google Scholar] [CrossRef]
- Huang, M.Y.; Huang, L.Y.; Zhong, Y.X.; Yang, H.W.; Chen, X.M.; Huo, W.; Wang, J.Z.; Zhang, F.; Bai, B.; Shi, L. MILP acceleration: A survey from perspectives of simplex Initialization and learning-based branch and bound. J. Oper. Res. Soc. China 2025, 13, 1–55. [Google Scholar] [CrossRef]
- Tavana, M.; Soltanifar, M.; Santos-Arteaga, F.J. Analytical hierarchy process: Revolution and evolution. Ann. Oper. Res. 2023, 326, 879–907. [Google Scholar] [CrossRef]
- Hemmati, S.; Elnegihi, M.M.; Lee, C.H.; Chong, D.Y.L.; Foo, D.C.Y.; How, B.S.; Yoo, C. Synthesis of Large-Scale Bio-Hydrogen Network Using Waste Gas from Landfill and Anaerobic Digestion: A P-Graph Approach. Processes 2020, 8, 505. [Google Scholar] [CrossRef]
- Sitoh, Y.; Tan, V.W.G.; Tapia, J.F.D.; Tan, R.R.; Foo, D.C.Y. Optimal Pathways for Nitric Acid Synthesis Using P-Graph Attainable Region Technique (PART). Processes 2023, 11, 2684. [Google Scholar] [CrossRef]
- Ji, M.; Zhang, W.; Xu, Y.; Liao, Q.; Klemeš, J.J.; Wang, B. Optimisation of multi-period renewable energy systems with hydrogen and battery energy storage: A P-graph approach. Energy Convers. Manag. 2023, 281, 116826. [Google Scholar] [CrossRef]
- Pimentel, J.; Orosz, Á.; Aviso, K.B.; Tan, R.R.; Friedler, F. Conceptual Design of a Negative Emissions Polygeneration Plant for Multiperiod Operations Using P-Graph. Processes 2021, 9, 233. [Google Scholar] [CrossRef]
- Tóth, Á.; Suta, A.; Pimentel, J.; Argoti, A. A comprehensive, semi-automated systematic literature review (SLR) design: Application to P-graph research with a focus on sustainability. J. Clean. Prod. 2023, 415, 137741. [Google Scholar] [CrossRef]
- Friedler, F.; Varga, J.B.; Fan, L.T. Decision-mapping: A tool for consistent and complete decisions in process synthesis. Chem. Eng. Sci. 1995, 50, 1755–1768. [Google Scholar] [CrossRef]
- Ahn, J.; Kim, H.J. A branch and bound algorithm for scheduling of flexible manufacturing systems. IEEE Trans. Autom. Sci. Eng. 2024, 21, 4382–4396. [Google Scholar] [CrossRef]
- Friedler, F.; Varga, J.B.; Feher, E.; Fan, L.T. Combinatorially accelerated branch-and-bound method for solving the MIP model of process network synthesis. In State of the Art in Global Optimization; Springer: Boston, MA, USA, 1996; Volume 7, pp. 609–626. [Google Scholar] [CrossRef]
- Saaty, T.L. Deriving the AHP 1–9 scale from first principles. In Proceedings of the 6th ISAHP, Berna, Switzerland, 2–4 August 2001. [Google Scholar] [CrossRef]
- Roco, J.B.A.; Promentilla, M.A.B. Philippine Energy Network Design via an Integrated P-graph and Analytic Hierarchy Process (AHP) Framework. In Proceedings of the DLSU Research Congress 2022, Manila, Philippines, 6–8 July 2022; Available online: https://www.dlsu.edu.ph/wp-content/uploads/pdf/conferences/research-congress-proceedings/2022/SEE-05.pdf (accessed on 10 September 2025).
- Estrella, E.T.; Belaro, C.M.; Promentilla, M.A.B. Retrofitting of Cement Plant with Carbon Capture Technology and Emissions Trading Scheme (ETS): An Integrated P-Graph and AHP Approach. Chem. Eng. Trans. 2023, 103, 397–402. [Google Scholar] [CrossRef]
- Chen, Y.; Kuo, M.J.; Lobo, R.; Ierapetritou, M. Ethylene production: Process design, techno-economic and life-cycle assessments. Green Chem. 2024, 26, 2903–2911. [Google Scholar] [CrossRef]
- Cao, J.; He, Y.L.; Zhu, Q.X. Feedstock scheduling optimization based on novel extensible P-Graph reasoning in ethylene production. Ind. Eng. Chem. Res. 2020, 59, 18965–18976. [Google Scholar] [CrossRef]
- Eisman, E.M.; Navarro, M.; Castro, J.L. A multi-agent conversational system with heterogeneous data sources access. Expert Syst. Appl. 2016, 53, 172–191. [Google Scholar] [CrossRef]
- Xi, J.; Gong, H.; Zhang, Y.; Dai, X.; Chen, L. The evaluation of GHG emissions from Shanghai municipal wastewater treatment plants based on IPCC and operational data integrated methods (ODIM). Sci. Total Environ. 2021, 797, 148967. [Google Scholar] [CrossRef]
- Yu, X.; Tan, C. China’s process-related greenhouse gas emission dataset 1990–2020. Sci. Data 2023, 10, 55. [Google Scholar] [CrossRef]
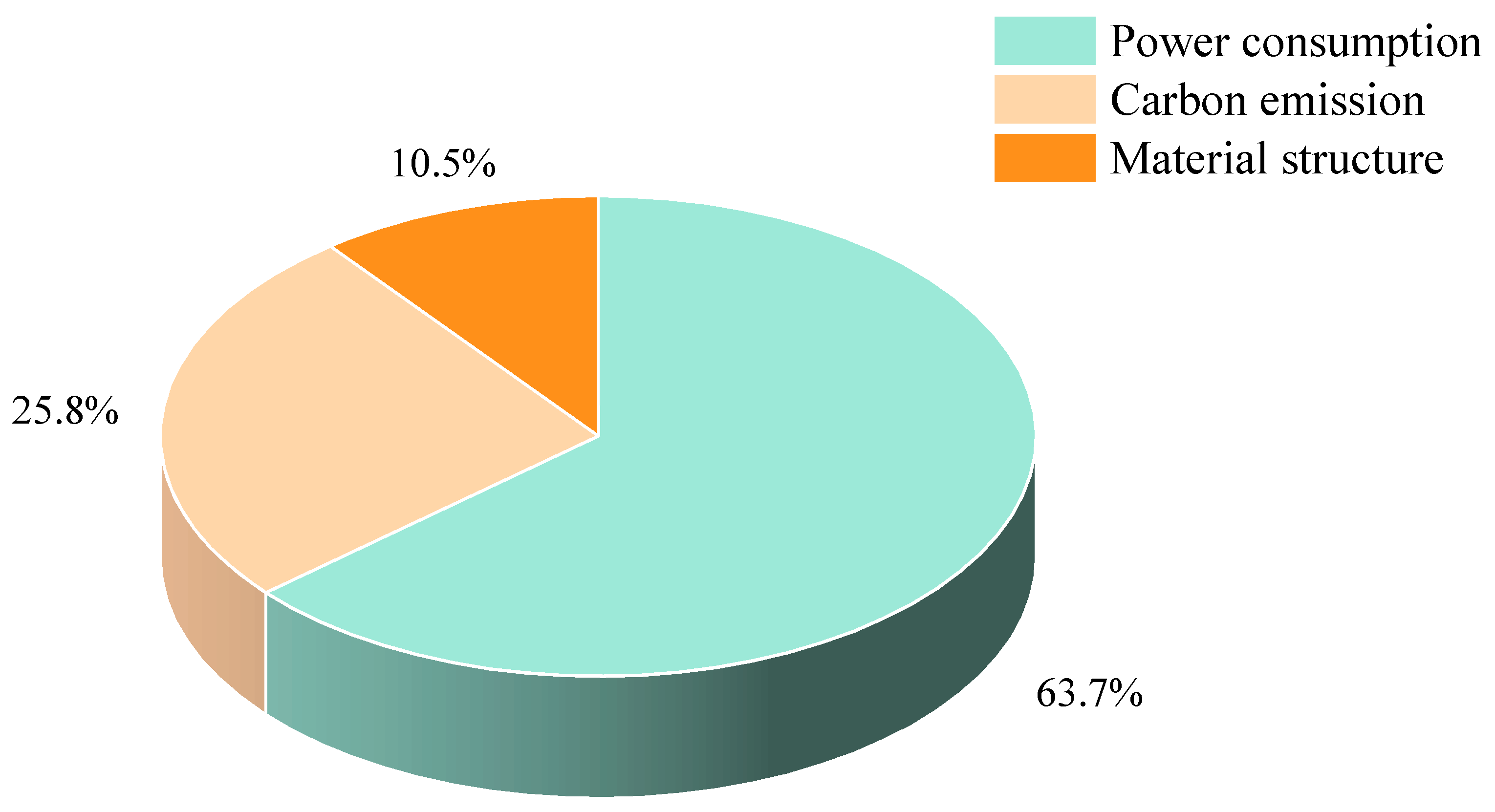
| Numerical Rating | Relative Importance Between Elements i and j |
|---|---|
| 1 | Equal importance |
| 3 | i is slightly more important than j |
| 5 | i is obviously more important than j |
| 7 | i is extremely more important than j |
| 9 | i is absolutely more important than j |
| 2, 4, 6, 8 | The median of the adjacent judgments mentioned above |
| Reciprocal of 1–9 | The importance of comparing the exchange order between i and j |
| Matrix Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| R.I. | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
| Subscript | Content |
|---|---|
| _A | Material for plant A |
| _B | Material for plant B |
| _M | Remaining material after allocating to plant A and B |
| _0 | Raw status |
| _1 | Status after one month |
| _2 | Status after two months |
| 1+ | Raw for second month |
| 2+ | Raw for the third month |
| 0_1 | Status after the first month |
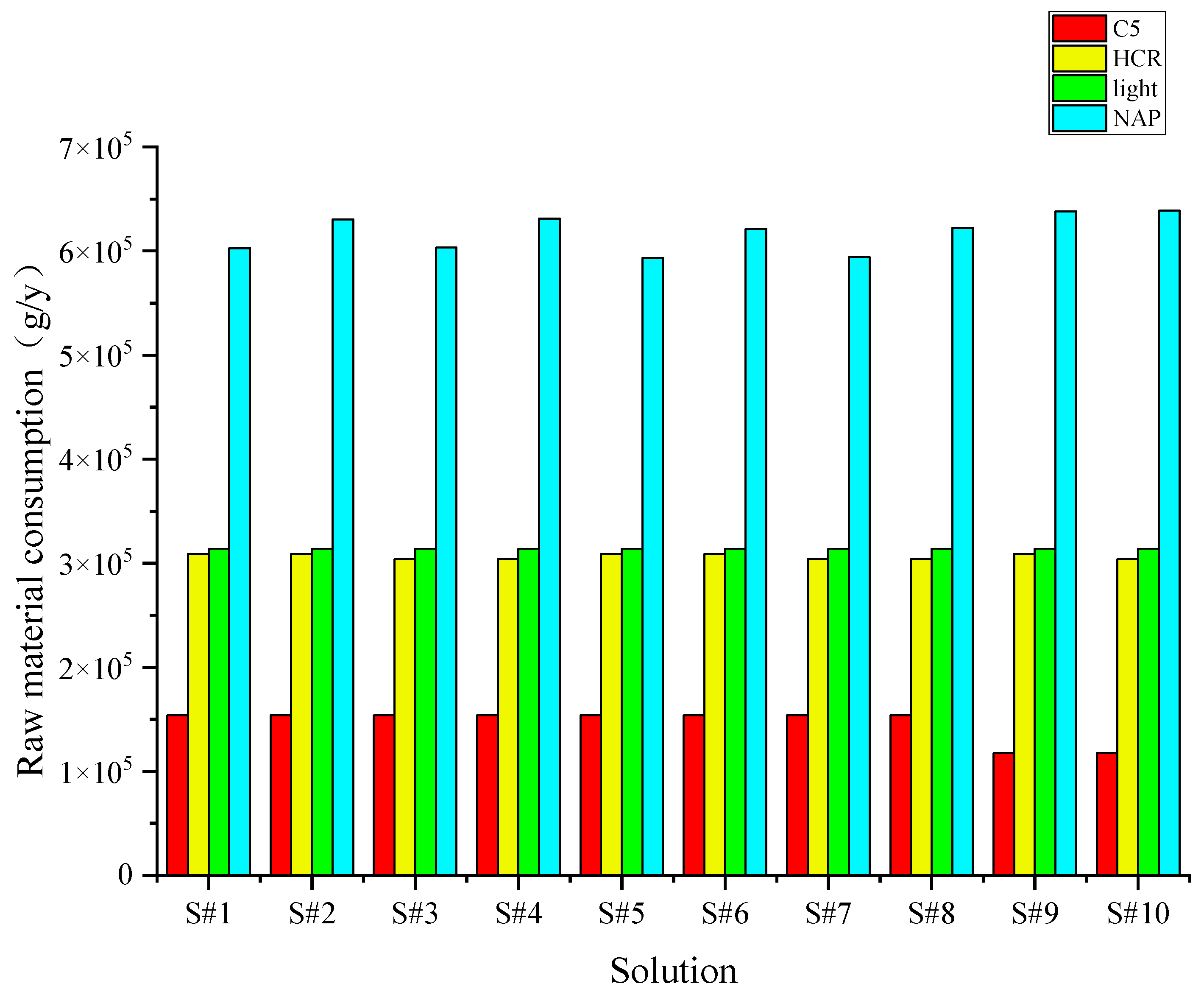
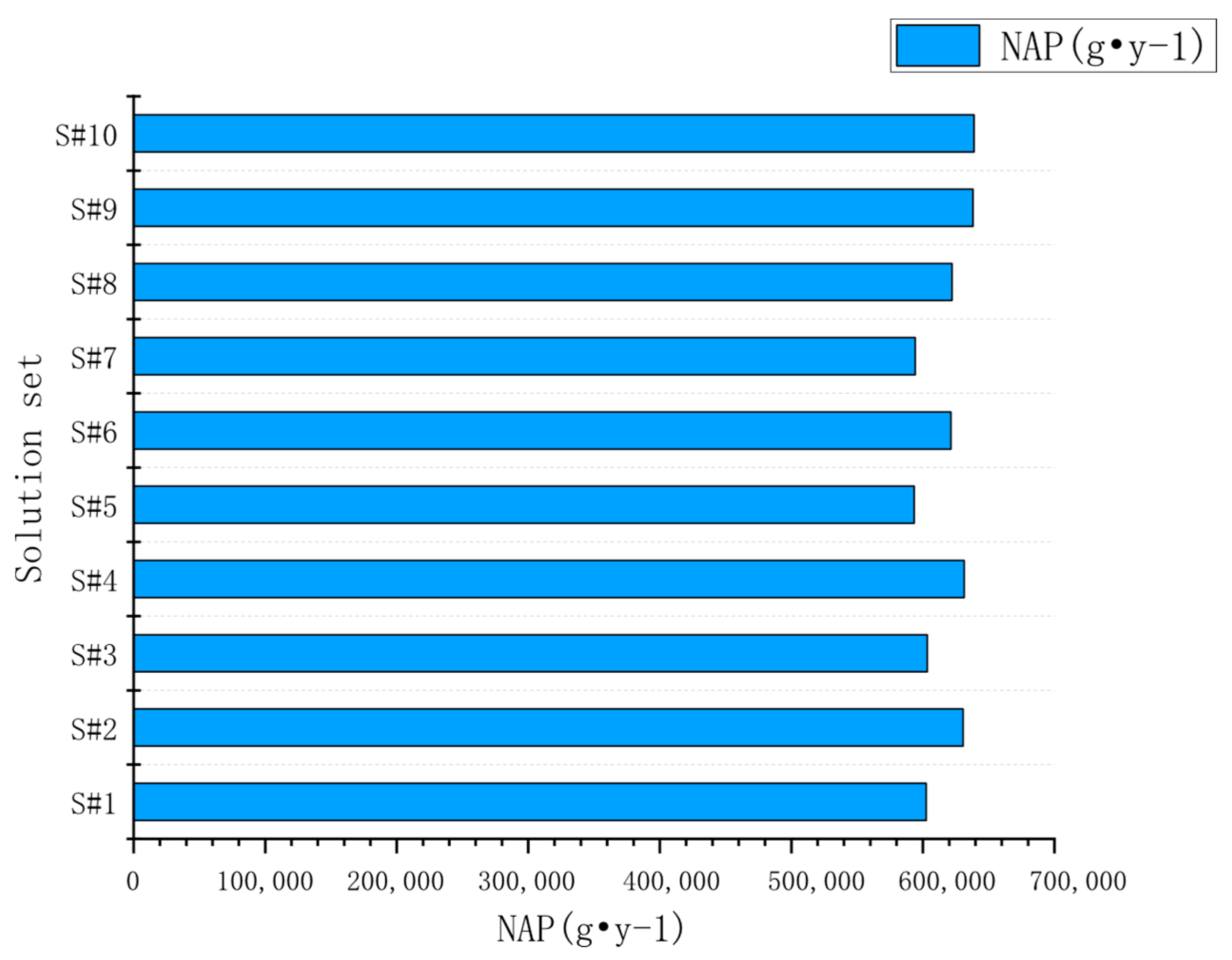
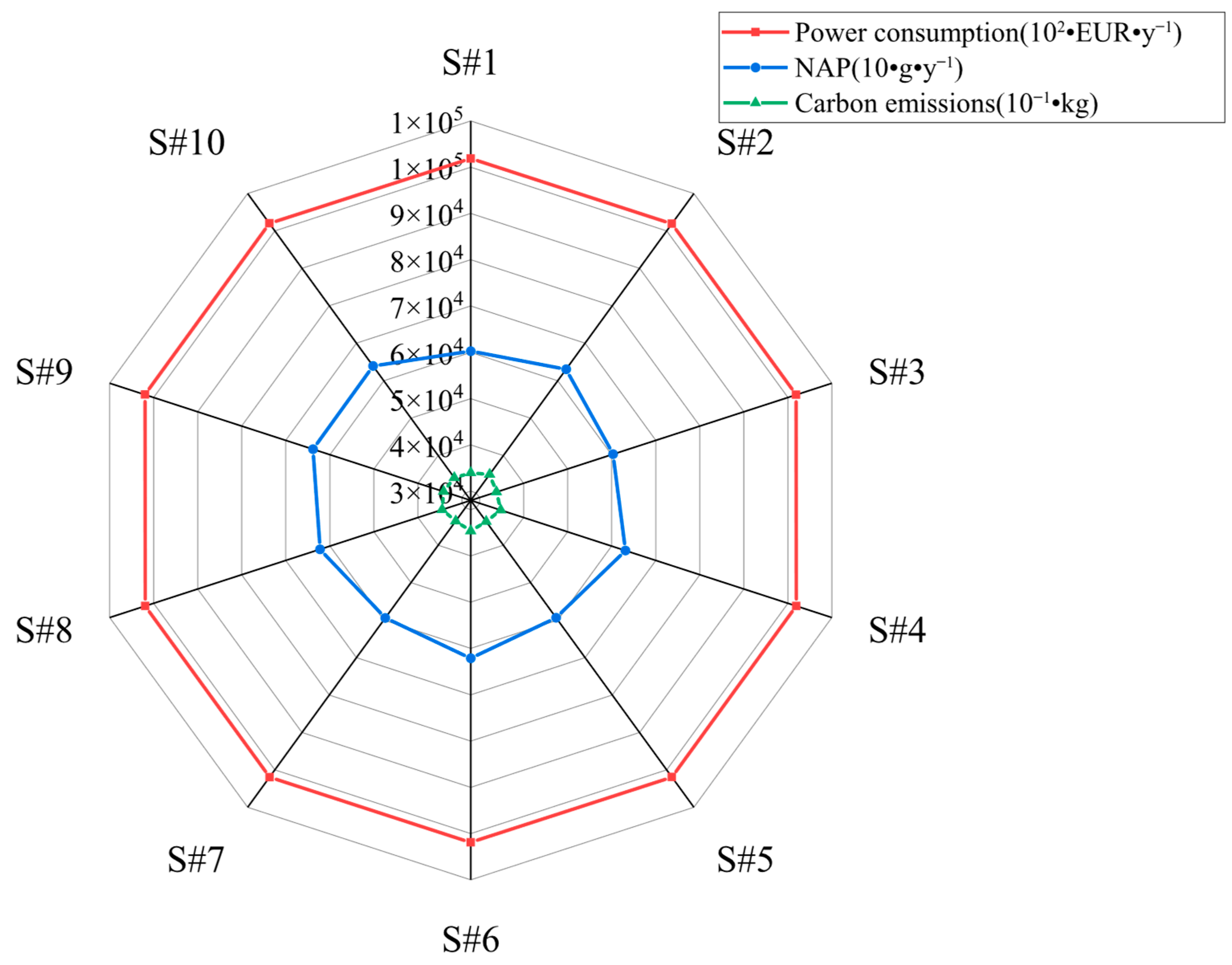
| Solution | Light (g·y−1) | C5 (g·y−1) | NAP (g·y−1) | HCR (g·y−1) | Cost (EUR·y−1) |
|---|---|---|---|---|---|
| S#1 | 313,728.00 | 153,817.00 | 602,552.00 | 309,120.00 | 10,188,700.00 |
| S#2 | 313,728.00 | 153,817.00 | 630,553.00 | 309,120.00 | 10,189,900.00 |
| S#3 | 313,728.00 | 153,817.00 | 603,380.00 | 303,960.00 | 10,190,300.00 |
| S#4 | 313,728.00 | 153,817.00 | 631,381.00 | 303,960.00 | 10,191,400.00 |
| S#5 | 313,728.00 | 153,817.00 | 593,357.00 | 309,120.00 | 10,192,100.00 |
| S#6 | 313,728.00 | 153,817.00 | 621,358.00 | 309,120.00 | 10,193,200.00 |
| S#7 | 313,728.00 | 153,817.00 | 594,186.00 | 303,960.00 | 10,193,700.00 |
| S#8 | 313,728.00 | 153,817.00 | 622,187.00 | 303,960.00 | 10,194,800.00 |
| S#9 | 313,728.00 | 117,836.80 | 638,079.00 | 309,120.00 | 10,197,900.00 |
| S#10 | 313,728.00 | 117,836.80 | 638,907.00 | 303,960.00 | 10,199,500.00 |
| Fuel Type | Carbon Content(kg/GJ) | Carbon Oxidation Factor | Effective CO2 Emission Factor(kg/TJ) | ||
|---|---|---|---|---|---|
| Default Value | 95% Confidence Interval | ||||
| A | B | A·B·44/12 × 1000 | lower | upper | |
| Gas/Diesel Oil | 20.1 | 1 | 74,100 | 72,600 | 74,800 |
| Liquefied Petroleum Gases | 17.2 | 1 | 63,100 | 61,600 | 65,600 |
| Ethane | 16.8 | 1 | 61,600 | 56,500 | 68,600 |
| Naphtha | 20.0 | 1 | 73,300 | 69,300 | 76,300 |
| Refinery Gas | 15.7 | 1 | 57,600 | 48,200 | 69,000 |
| Other Petroleum Products | 20.0 | 1 | 73,300 | 72,200 | 74,400 |
| Refinery Feedstocks | 20.0 | 1 | 73,300 | 69,300 | 76,300 |
| Solution | Carbon Emissions (kg) |
|---|---|
| S#1 | 3395.7 |
| S#2 | 3492.7 |
| S#3 | 3384.0 |
| S#4 | 3481.1 |
| S#5 | 3363.8 |
| S#6 | 3460.9 |
| S#7 | 3352.2 |
| S#8 | 3449.2 |
| S#9 | 3416.2 |
| S#10 | 3404.6 |
| Maximum Eigenvalue | C.R. | Consistency | |
|---|---|---|---|
| Rule 1 | 10.34 | 0.025 | True |
| Rule 2 | 10.86 | 0.064 | True |
| Rule 3 | 11.27 | 0.094 | True |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Yang, H.; Ji, Y. Superstructure Optimization Based on Hierarchical Accelerated Branch and Bound Algorithm and Its Application in Feedstock Scheduling. Processes 2025, 13, 2936. https://doi.org/10.3390/pr13092936
Cao J, Yang H, Ji Y. Superstructure Optimization Based on Hierarchical Accelerated Branch and Bound Algorithm and Its Application in Feedstock Scheduling. Processes. 2025; 13(9):2936. https://doi.org/10.3390/pr13092936
Chicago/Turabian StyleCao, Jian, Haitao Yang, and Yi Ji. 2025. "Superstructure Optimization Based on Hierarchical Accelerated Branch and Bound Algorithm and Its Application in Feedstock Scheduling" Processes 13, no. 9: 2936. https://doi.org/10.3390/pr13092936
APA StyleCao, J., Yang, H., & Ji, Y. (2025). Superstructure Optimization Based on Hierarchical Accelerated Branch and Bound Algorithm and Its Application in Feedstock Scheduling. Processes, 13(9), 2936. https://doi.org/10.3390/pr13092936





