Low-Carbon, High-Efficiency, and High-Quality Equipment Selection for Milling Process Based on New Quality Productivity Orientation
Abstract
1. Introduction
2. Equipment Selection Model Based on NQP
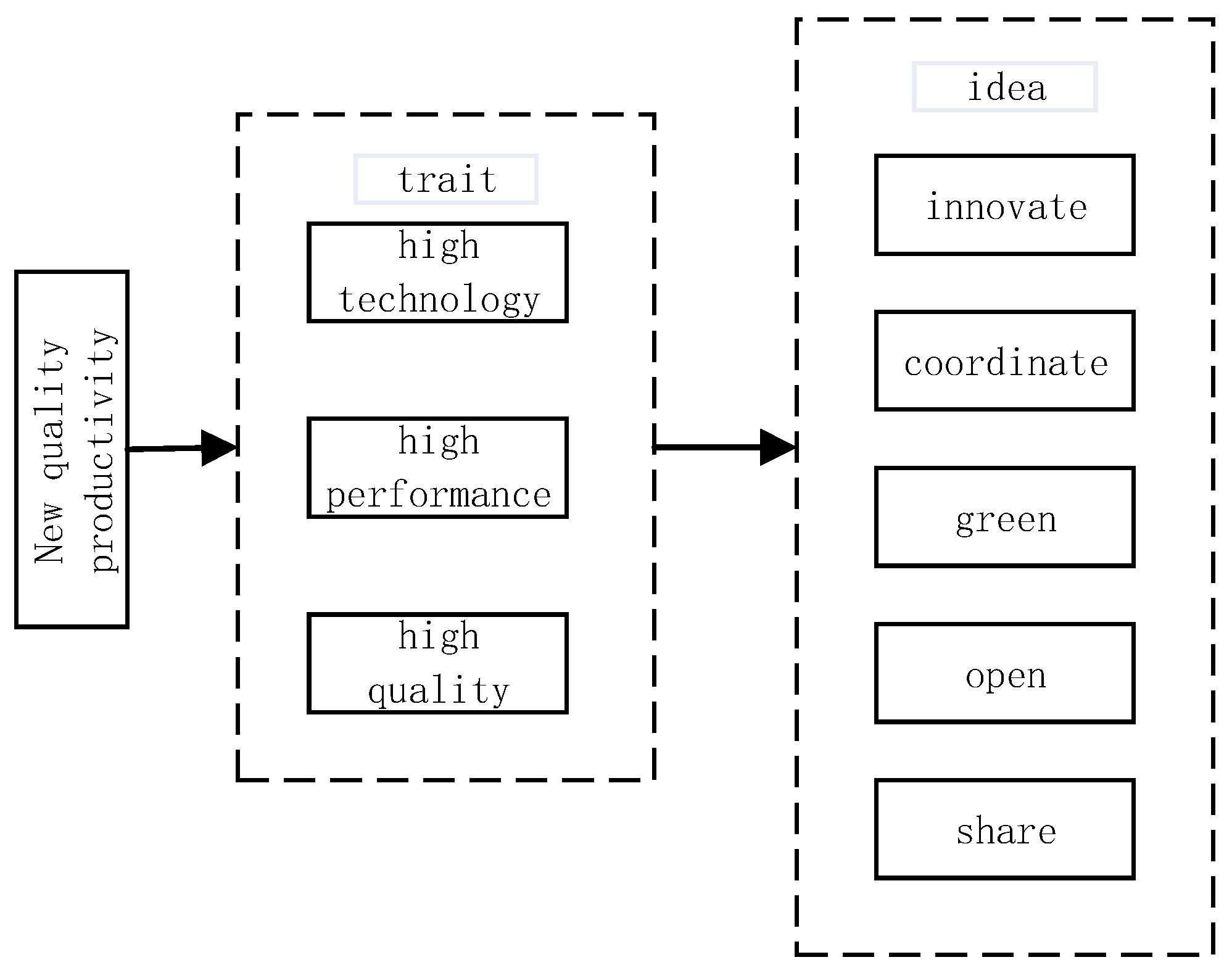
2.1. New Quality Productivity
2.2. Equipment Selection Model Based on NQP Framework
3. Carbon Emissions and Efficient Milling Calculation Model
3.1. Carbon Emissions
3.1.1. Carbon Emissions from Processing Electrical Energy
3.1.2. Other Energy Consumption Carbon Emissions in the Milling Process
3.2. Time Function
3.3. Quality Function
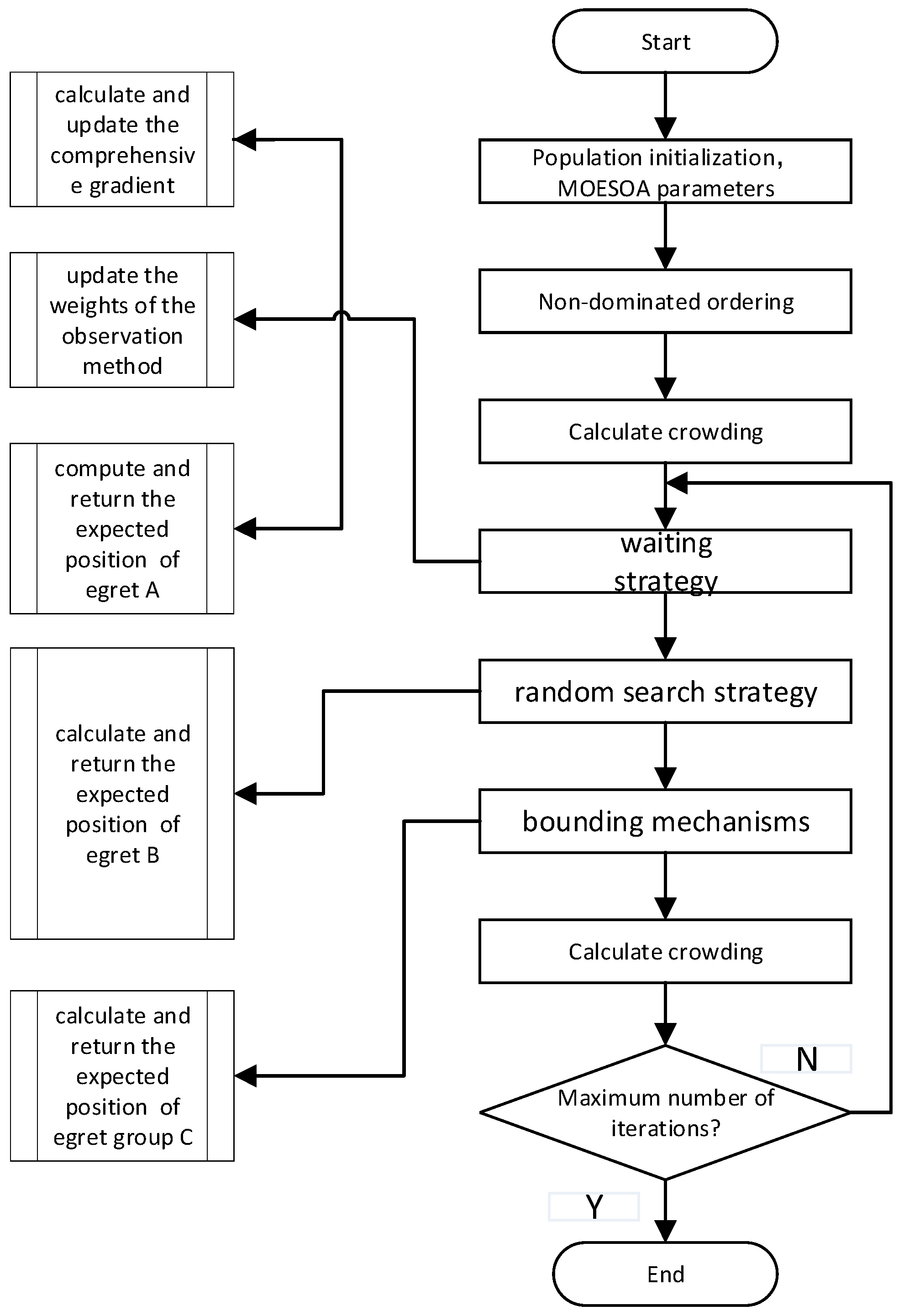
4. Egret Swarm Algorithm
- (1)
- Population initialization: The initial population is randomly generated, where each individual in the population represents an egret squad. The position of the squad represents a combination of cutting parameters, and the fitness of the squad is calculated using the machining result prediction model. The population size is set to N and the maximum iterations to maxGen, where N is in [20, 200] and maxGen is in [100, 5000]. The optimization objectives are set to minimize the energy consumption E, manufacturing cost C, and product quality degradation.
- (2)
- Screening outstanding individuals: According to the fitness values of individuals in the initial population, non-dominated sorting is performed, and a non-dominated solution set with rank 1 is generated. Then, the crowding degree of the sample is calculated using the following formula:where is the crowding degree of the ith egret squad; is the total number of optimization objectives; are the fitness value of egret squads i + 1 and i − 1 for optimization target , respectively; and and are the maximum and minimum fitness values for optimization target , respectively.
- (3)
- Calculate the expected position: Each egret squad consists of three egrets. Egret A adopts the forward guidance strategy, egret B adopts the random walk strategy, and egret C adopts the encircle strategy; in particular, each egret is defined according to the following equations:where , , and are the expected positions of each egret; is the current position of the squad , , and ; is the maximum number of iterations; is the scope of the current search space; is the gradient; is a random number in (−π/2,π/2); is the number of current iterations; and are random numbers in [0,0.5); is the best position of the current egret squad; and is the best position of all egret squads (randomly selected from the non-dominated solution set).
- (4)
- Decision making: Calculate the fitness of each egret in its expected position, select the non-dominated solution according to the fitness values, and the egret team moves to the corresponding position. Then, the non-dominated solution is added to the Pareto solution set and redundant solutions in the Pareto solution set are eliminated according to the crowding ranking result. The best positions are compared before the egret team moves to the current position of the egret team, and the non-dominated solution of the two is set as the best position after the egret team moves.
- (5)
- Iteration: Iterate the above process repeatedly until the maximum number of iterations is reached.
5. Case Study
5.1. Problem Background
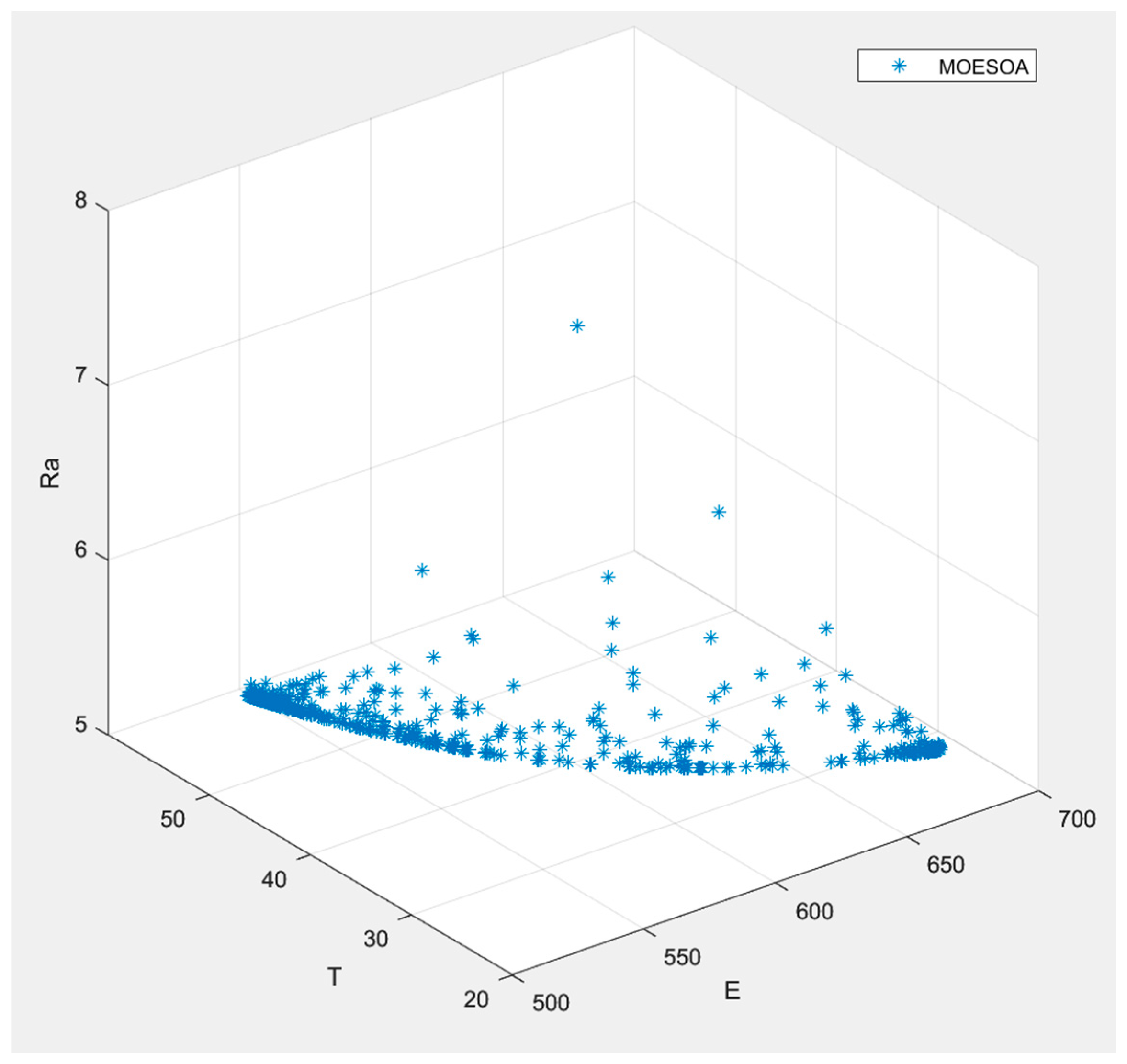
5.2. Optimization Results
5.3. Practical Implications
6. Conclusions
- Based on the NQP concept, a model for enterprise milling equipment selection was created, and the realization path of enterprise management was analyzed through the integration of enterprise management and equipment selection.
- A calculation model for the carbon emissions and processing time for the same product produced with different milling equipment was established and verified through an example involving the machining of a fixture cavity.
- The ESA was used to optimize the energy consumption and processing time of a multi-equipment process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPQ | New Quality Productivity |
| ESA | Egret Swarm Algorithm |
| GA | Genetic Algorithm |
| SAA | Simulated Annealing Algorithm |
| DSA | Distributed Search Algorithm |
| CNC | Computer Numerical Control |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| MEOA | Multi-objective Optimization Algorithms |
| PSO | Particle Swarm Optimization |
| MEC | Minimum Energy Consumption |
| maxGen | Max Generation |
References
- Luo, W.; Zuo, S.; Tang, S.; Li, C. The Formation of New Quality Productivity of Agriculture Under the Perspectives of Digitalization and Innovation: A Dynamic Qualitative Comparative Analysis Based on the “Technology-Organization-Environment” Framework. Sustainability 2025, 17, 597. [Google Scholar] [CrossRef]
- Chen, F. Can New Quality Productivity Promote the Carbon Emission Performance—Empirical Evidence from China. Sustainability 2025, 17, 567. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, Y.; Fu, G.; Li, J.; Luo, F. New quality productivity in the new era enabling scientific instruments “domestic substitution”. Exp. Technol. Manag. 2024, 41, 1–6. [Google Scholar] [CrossRef]
- Yao, H.; Wu, J. An Analysis of Innovative Contributions to the Important Discourse on the Development of New Quality Productivity. J. Contemp. Educ. Res. 2024, 8, 135–141. [Google Scholar] [CrossRef]
- Liu, Z. Sustainable Evolution of China’s Provincial New Quality Productivity Based on Three Dimensions of Multi-Period Development and Combination Weights. Sustainability 2024, 16, 11259. [Google Scholar] [CrossRef]
- Niroomand, S. Hybrid artificial electric field algorithm for assembly line balancing problem with equipment model selection possibility. Knowl. Based Syst. 2021, 219, 106905. [Google Scholar] [CrossRef]
- Sahin, Y.; Aydemir, E. A Comprehensive Solution Approach for CNC Machine Tool Selection Problem. Informatica 2021, 33, 81–108. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, Y.; Luo, S.; Zou, W.; Liu, J.; Ran, Z.; Liu, W. A Data-Driven Strategy Assisted by Effective Parameter Optimization for Cable Fault Diagnosis in the Secondary Circuit of a Substation. Processes 2025, 13, 2407. [Google Scholar] [CrossRef]
- Zheng, Y.-H.; Hu, F.-H.; Wang, M.-H.; Wang, X.-Y. Research on the machine tool selection optimization method based on fuzzy analytic hierarchy process and fuzzy comprehensive assessment. Chin. J. Eng. Des. 2015, 22, 405–411. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.-C.; Niu, Y.; Zhao, J.-P. Optimization Selection of CNC Machine Tool Equipment Based on FAHP. Modul. Mach. Tool Autom. Manuf. Tech. 2014, 334, 133–136. [Google Scholar] [CrossRef]
- Zheng, Y.; Han, F.; Ma, Y. The Application of improved Gray Associated Models in Equipment Selection. Mach. Tool Hydraul. 2009, 37, 41–43. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, H.; Zhang, R.; Liu, H.; Zhang, G. Research on Optimization Evaluation of Machine Tool Equipment for Intelligent Manufacturing. Comb. Mach. Tool Autom. Process. Technol. 2020, 144–148. [Google Scholar] [CrossRef]
- Önüt, S.; Soner Kara, S.; Efendigil, T. A hybrid fuzzy MCDM approach to machine tool selection. J. Intell. Manuf. 2008, 19, 443–453. [Google Scholar] [CrossRef]
- Zhao, X.; Shen, M.; Wang, J. Machining process evaluation model based on low carbon manufacturing and application. J. Mech. Des. Manuf. 2013, 81–83. [Google Scholar] [CrossRef]
- Klink, A.; Arntz, K.; Johannsen, L.; Holsten, M.; Chrubasik, L.; Winands, K.; Wollbrink, M.; Bletek, T.; Gerretz, V.; Bergs, T. Technology-based assessment of subtractive machining processes for mold manufacture. Procedia CIRP 2018, 71, 401–406. [Google Scholar] [CrossRef]
- Vafadar, A.; Hayward, K.; Tolouei-Rad, M. Drilling reconfigurable machine tool selection and process parameters optimization as a function of product demand. J. Manuf. Syst. 2017, 45, 58–69. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Fan, L.; Li, Q.; Chen, X. A novel hybrid MCDM model for machine tool selection using fuzzy DEMATEL, entropy weighting and later defuzzification VIKOR. Appl. Soft Comput. 2020, 91, 106207. [Google Scholar] [CrossRef]
- Zanuto, R.D.S.; Hassui, A.; Lima, F.; Dornfeld, D.A. Environmental impacts-based milling process planning using a life cycle assessment tool. J. Clean. Prod. 2019, 206, 349–355. [Google Scholar] [CrossRef]
- Zhang, B.-P.; Guan, S.-X.; Zhang, B.; Wang, B.; Tian, T. Machine tool selection based on fuzzy evaluation and optimization of cutting parameters. J. Meas. Sci. Instrum. 2015, 6, 384. [Google Scholar]
- Wang, L.P.; Kong, X.Y.; Yu, G. Motor servo control parameter tuning for parallel and hybrid machine tools based on a genetic algorithm. J. Tsinghua Univ. Sci. Technol. 2021, 61, 1106–1114. [Google Scholar]
- Sel, A.; Gurkan, M.E.; Hamzaday, A. Energy-aware production lot-sizing and parallel machine scheduling with the product-specific machining tools and power requirements. Comput. Ind. Eng. 2024, 196, 110503. [Google Scholar] [CrossRef]
- Chen, M.C. Optimization machining economics models of turning operations using the scatter search approach. Int. J. Prod. Res. 2004, 42, 2611–2625. [Google Scholar] [CrossRef]
- Gontarz, S.; Patyk, R.; Bohdal, L.; Jackiewicz, D. Multiparameter optimization of mechanical cutting process of grain-oriented silicon steel. Acta Phys. Pol. A 2020, 137, 930–932. [Google Scholar] [CrossRef]
- Wang, X.; Gu, X.; Liu, Z.; Wang, Q.; Xu, X.; Zheng, M. Production Process Optimization of Metal Mines Considering Economic Benefit and Resource Efficiency Using an NSGA-II Model. Processes 2018, 6, 228. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, L. Research on the impact of digital innovation and entrepreneurship on the development of new quality productivity. Econ. Issues Explor. 2025, 46, 37–49. Available online: http://www.jjwtts.com/CN/Y2025/V46/I1/37 (accessed on 1 January 2025).
- Wang, J.; Qiao, L.; Zhu, G.; Di, K.; Zhang, X. Research on the driving factors and impact mechanisms of green new quality productive forces in high-tech retail enterprises under China’s Dual Carbon Goals. J. Retail. Consum. Serv. 2025, 82, 104092. [Google Scholar] [CrossRef]
- Wu, F.-P.; Song, Y.; Huang, R. Construction of new quality productivity evaluation index system under new development concept. Water Resour. Prot. 2019, 41, 85–91. [Google Scholar]
- Sun, Y.B.; Ye, J.N.; Hu, J. Optimization of Mechanical processing Technology and Application of digital Twin technology. Chin. Mach. 2023, 27, 36–39. [Google Scholar]
- Liu, J.F.; Zhao, P.; Zhou, H.G.; Liu, X.-J.; Feng, F. The evaluation method of mechanical processing technology driven by digital twins. Comput. Integr. Manuf. Syst. 2019, 25, 1600–1610. [Google Scholar] [CrossRef]
- Song, Z.; Liu, D.; Sha, H.; Jiang, X.; Tian, Z.; Yang, G. Carbon emission warning method for machine tool manufacturing process based on dynamic adaptive EWMA control chart. Environ. Sci. Pollut. Res. 2024, 31, 53156–53176. [Google Scholar] [CrossRef]
- Hu, S.H.; Liu, F.; He, Y. Study on the characteristics of no-load energy parameters of variable frequency main drive system of CNC ma-chine tools. Comput. Integr. Manuf. Syst. 2012, 18, 326–331. [Google Scholar]
- Ai, X.; Xiao, S.G. Handbook of Cutting Usage Concise; Mechanical Industry Press: Beijing, China, 1994; p. 110. [Google Scholar]
- Huang, Z.T. Research on Modeling and Cutting Parameters Optimization of CNC Milling Process for Low Carbon Manufacturing. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2016. [Google Scholar] [CrossRef]
- Ansho, P.M.; Nisha, M.G. Egret Swarm Optimized Distributed Power Flow Controller for Power Quality Enhancement in Grid Connected Hybrid System. J. Electr. Eng. Technol. 2024, 19, 2047–2057. [Google Scholar]
- Chen, Z.; Francis, A.; Li, S.; Liao, B.; Xiao, D.; Ha, T.T.; Li, J.; Ding, L.; Cao, X. Egret Swarm Optimization Algorithm: An Evolutionary Computation Approach for Model Free Optimization. Biomimetics 2022, 7, 144. [Google Scholar] [CrossRef] [PubMed]
- Alajlan, A.M.; Razaque, A. ESOA-HGRU: Egret swarm optimization algorithm-based hybrid gated recurrent unit for classification of diabetic retinopathy. Artif. Intell. Rev. 2023, 56, 1617. [Google Scholar] [CrossRef]
- Manivannan, K.; Sathiamoorthy, S. Automated Tuberculosis classification using Egret Swarm Optimization with deep learning based fusion model on chest X-ray images. J. Intell. Fuzzy Syst. Appl. Eng. Technol. 2023, 45, 10335–10347. [Google Scholar] [CrossRef]
- Xiao, Y.M.; Chen, G.H.; Zhang, H.; Zhu, X.Y. Optimization of Low-Carbon and Highly Efficient Turning Production Equipment Selection Based on Beetle Antennae Search Algorithm (BAS). Processes 2023, 11, 911. [Google Scholar] [CrossRef]
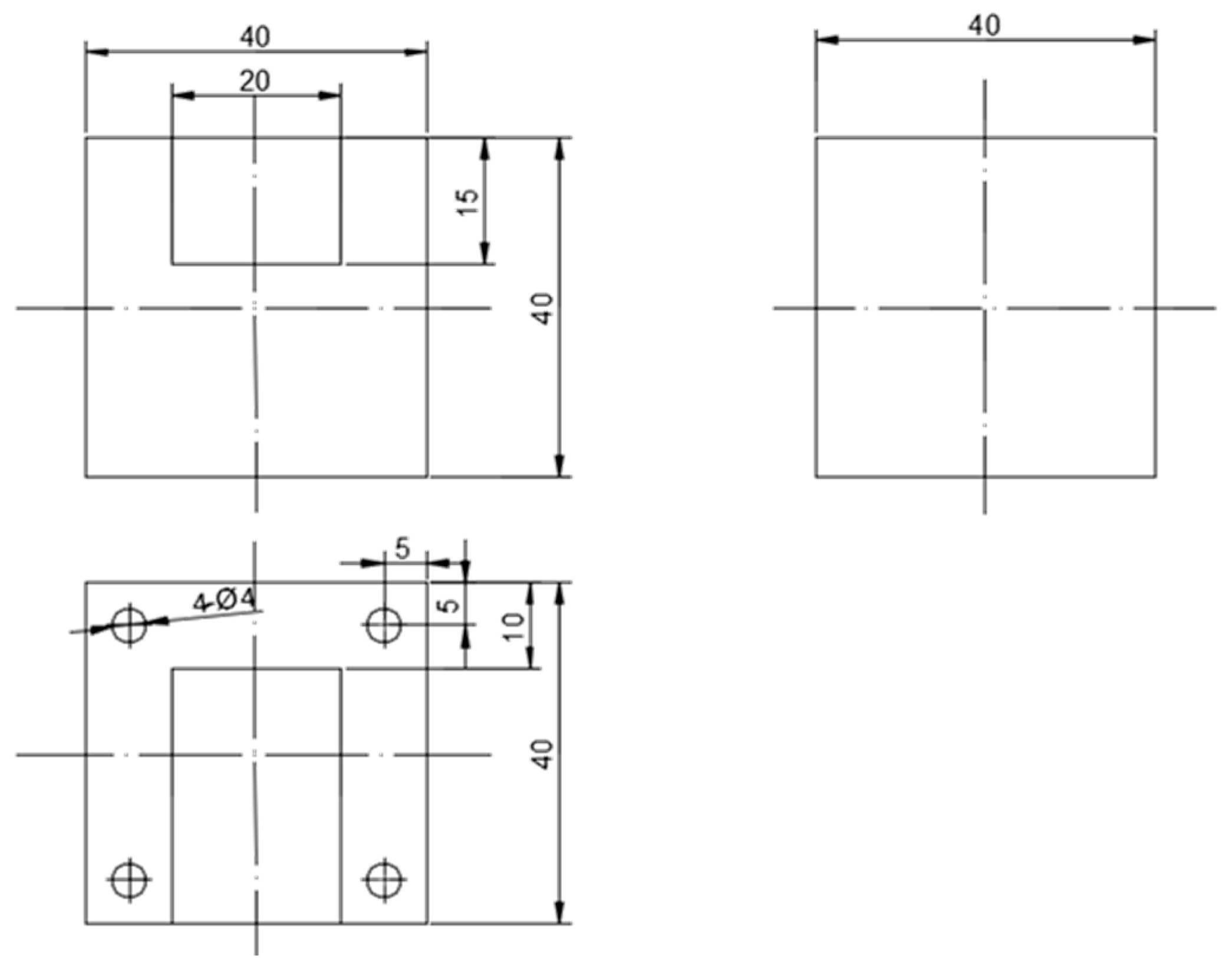
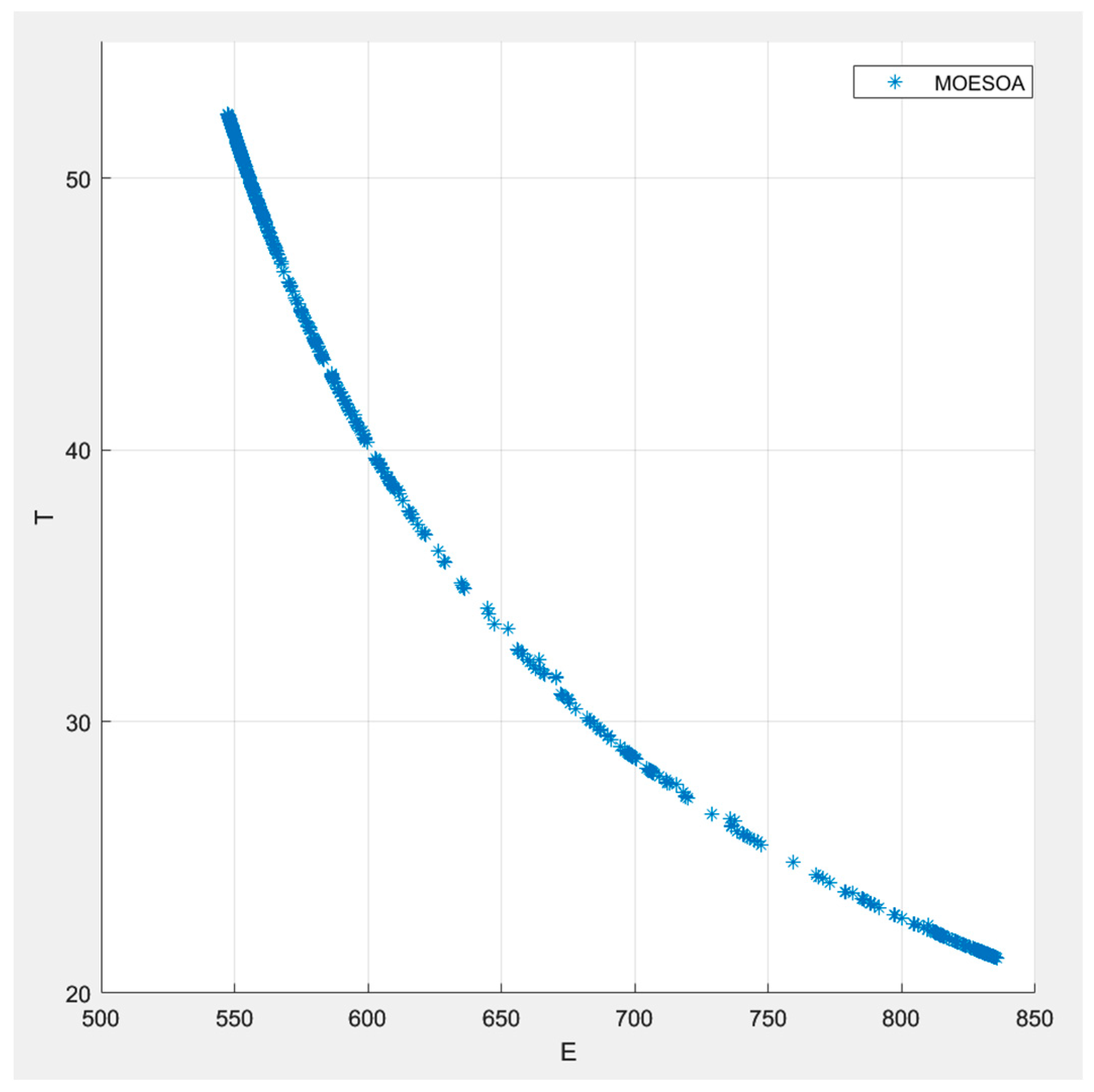
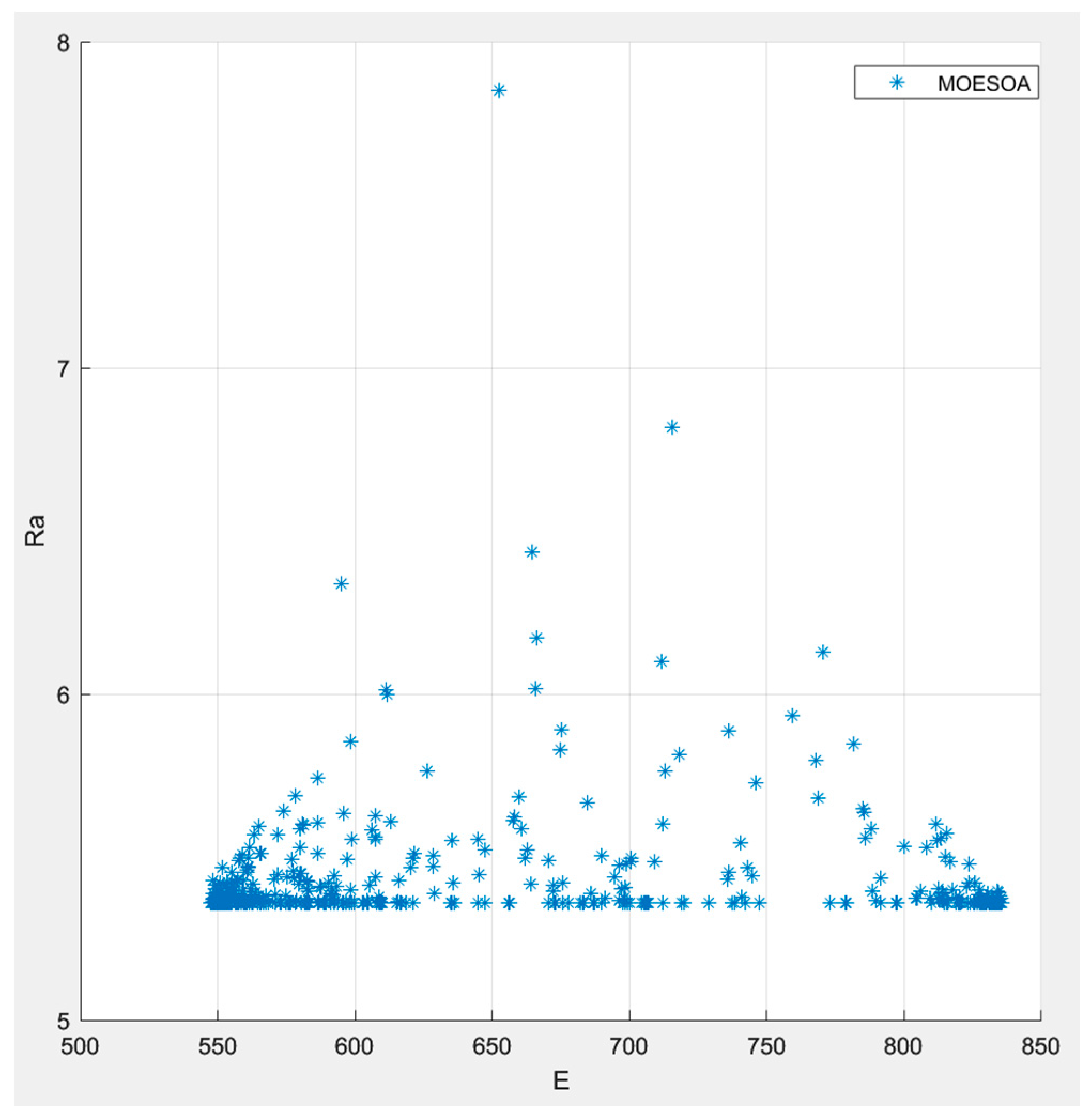
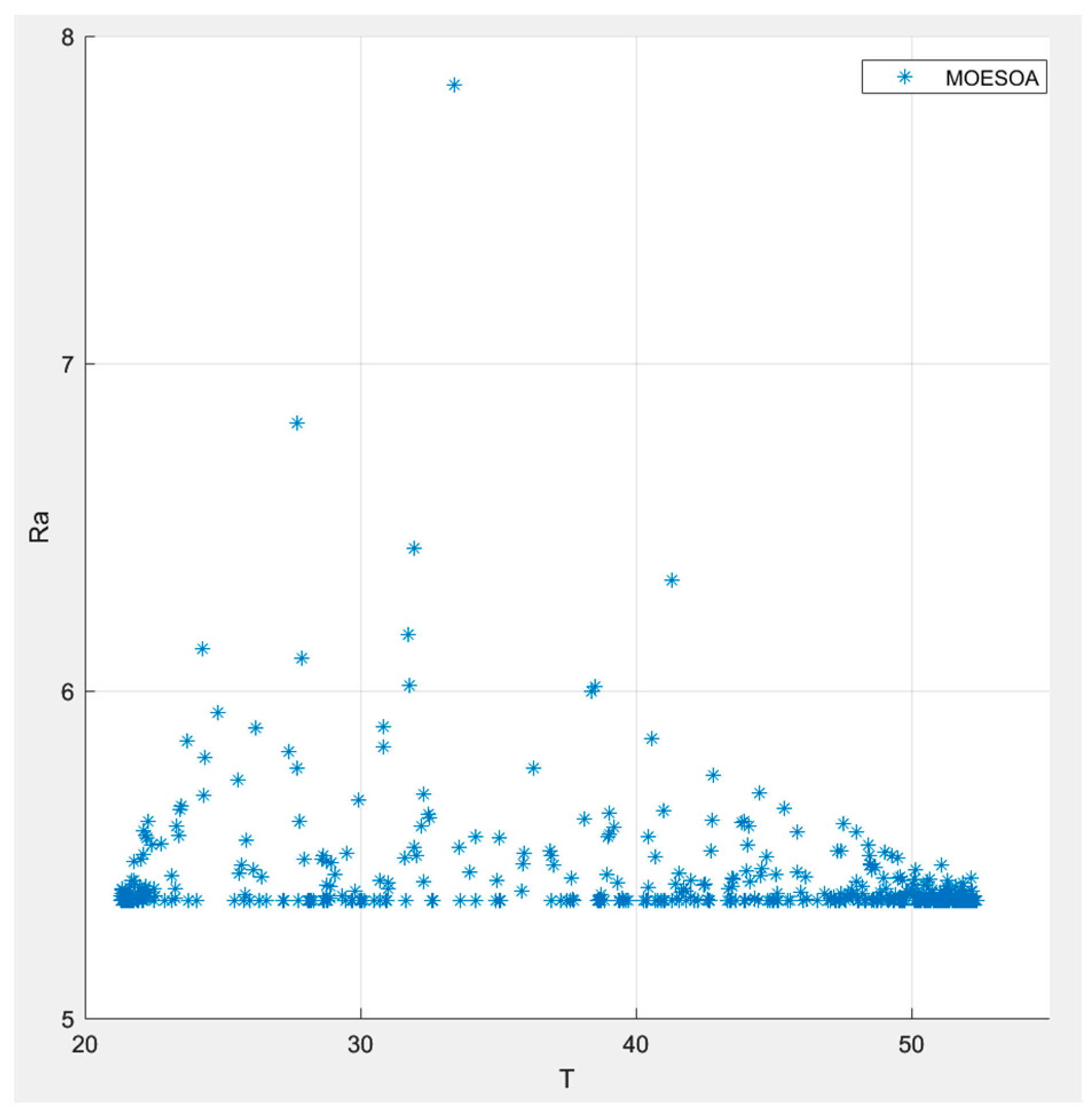
| 50–3500 | 2 | 0.02–5 | 0.8 | 0.2 | 20 |
| 100–6000 | 5.5 | 0.02–5 | 0.8 | 0.2 | 28.5 |
| Tool Type | Tool Diameter (mm) | Tool Teeth | Tip Radius rε (/mm) |
|---|---|---|---|
| YT15 carbide | 125 | 4 | 3 |
| Term | n (r/min) | ap (mm) | (s) | (gco2e) | ||
|---|---|---|---|---|---|---|
| M1 | 400 | 0.40 | 2 | 25.1 | 6.2 | 832.9 |
| M2 (ESA) | 424 | 0.40 | 2 | 23.7 | 5.4 | 723.38 |
| M1 (BSA) | 417 | 0.41 | 2 | 24.6 | 5.4 | 813.25 |
| M2 (BSA) | 419 | 0.41 | 2 | 24.3 | 5.4 | 739.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, W.; Ni, Z. Low-Carbon, High-Efficiency, and High-Quality Equipment Selection for Milling Process Based on New Quality Productivity Orientation. Processes 2025, 13, 2935. https://doi.org/10.3390/pr13092935
Qu W, Ni Z. Low-Carbon, High-Efficiency, and High-Quality Equipment Selection for Milling Process Based on New Quality Productivity Orientation. Processes. 2025; 13(9):2935. https://doi.org/10.3390/pr13092935
Chicago/Turabian StyleQu, Wenyue, and Zhongjin Ni. 2025. "Low-Carbon, High-Efficiency, and High-Quality Equipment Selection for Milling Process Based on New Quality Productivity Orientation" Processes 13, no. 9: 2935. https://doi.org/10.3390/pr13092935
APA StyleQu, W., & Ni, Z. (2025). Low-Carbon, High-Efficiency, and High-Quality Equipment Selection for Milling Process Based on New Quality Productivity Orientation. Processes, 13(9), 2935. https://doi.org/10.3390/pr13092935







